Quantum Support Vector Regression for Disability Insurance

Abstract

We propose a hybrid classical-quantum approach for modeling transition probabilities in health and disability insurance. The modeling of logistic disability inception probabilities is formulated as a support vector regression problem. Using a quantum feature map, the data are mapped to quantum states belonging to a quantum feature space, where the associated kernel is determined by the inner product between the quantum states. This quantum kernel can be efficiently estimated on a quantum computer. We conduct experiments on the IBM Yorktown quantum computer, fitting the model to disability inception data from a Swedish insurance company.

1. Introduction

Support vector machines (SVM) were first introduced as part of Vapnik’s Statistical Learning Framework (Vapnik 2013). Support vector classification aims to classify data, e.g., to determine if a picture contains a cat or a dog, whereas support vector regression (SVR) is used to model real-valued quantities, such as mortality rates or financial asset returns. All SVMs exploit the so-called kernel trick, where an optimization problem with data that have been mapped into a high- or even infinite-dimensional feature space may be efficiently solved by considering its Wolfe-dual (Schölkopf et al. 2000), for which the necessary input is reduced to a so-called kernel matrix consisting of inner products in the feature space between all data pairs. For cases where the kernel matrix can be readily determined, the corresponding optimization problem can be efficiently solved.

Rebentrost et al. (2014) showed that an SVM can be implemented on a quantum computer. This work was recently expanded on by Schuld and Killoran (2019) and Havlíček et al. (2019). In essence, two related methods have been proposed. The first method consists of encoding data in a high-dimensional quantum feature space, calculating a quantum kernel, and subsequently using a variational quantum circuit to find a separating hyperplane. A second approach proposes to use a quantum computer to estimate the kernel, and to implement the resulting SVM optimization on a classical computer, a so-called hybrid classical-quantum implementation. Quantum kernel methods can be efficiently used to solve some optimization problems where the kernel cannot efficiently be determined on a classical computer. This was recently demonstrated by Liu et al. (2021).

In the insurance literature, SVMs have been used as a mortality graduation technique (Kostaki et al. 2011). They could equally well be used to model other transition probabilities, such as disability inception or termination rates. These quantities are often estimated using classical techniques such as maximum likelihood or splines, see e.g., Aro et al. (2015); Djehiche and Löfdahl (2018); Christiansen et al. (2012); Renshaw and Haberman (1995, 2000). In this paper, we propose a hybrid classical-quantum SVR model for logistic disability inception probabilities, using a quantum kernel that can be estimated on a quantum computer. We conduct experiments on the IBM Yorktown quantum computer using disability inception data from a Swedish insurance company. The kernel that we use in this paper is simple enough that it can also be evaluated using classical methods. This allows us to readily compare the analytically derived kernel to the one estimated on a quantum computer. However, the proposed approach is general and is in theory capable of estimating complex kernels based on high-dimensional data, where classical methods are intractable.

This paper is organised as follows. In Section 2 and Section 3, we review kernel theory, support vector regression, and quantum kernel estimation. In Section 4, we propose a support vector regression model with a quantum kernel for disability inception rates. In Section 5, we estimate the kernel matrix associated with disability inception data from a Swedish insurance company on a quantum computer. This kernel is then used in a support vector regression to estimate disability inception rates. The results are compared to those from classical support vector regression.

2. Kernels and Support Vector Regression

In this section, we review kernel theory and support vector regression. Closely following Schuld and Killoran (2019), we let $x_i\in {\mathbb{R}}^d,i=1,\dots ,n,$ denote observations in a data set and let the mapping $\Phi :{\mathbb{R}}^d\mapsto \mathcal{F}$ be a feature map that maps a sample data point x to a feature vector $\Phi (x)$ in a (usually higher-dimensional) feature space $\mathcal{F}$, usually taken as a Hilbert space. The mapping $\Phi$ naturally gives rise to a so-called kernel through the relation

$$K(x,z)=⟨\Phi (x),\Phi (z)⟩,$$

(1)

where $⟨·,·⟩$ denotes the inner product on $\mathcal{F}$. Note that, since $K(x,z)$ is determined by the inner product of $\Phi (x)$ and $\Phi (z)$, it can be seen as a similarity measure between x and z in the feature space. The reproducing kernel Hilbert space (RKHS) associated with $\Phi$ is defined by

$$\mathcal{R}=\{f:{\mathbb{R}}^d\mapsto \mathbb{C};f(x)=⟨w,\Phi (x)⟩\forall x\in {\mathbb{R}}^d,w\in \mathcal{F}\}.$$

(2)

Note that the functions $⟨w,\Phi (x)⟩$ can be interpreted as linear models in the feature space $\mathcal{F}$. Now, assume that we are given a cost function $\mathcal{C}$ that measures the goodness of fit of a model by comparing predicted values ${\{f(x_i)\}}_i$ with observed values ${\{y_i\}}_i$ and that has a regularization term $g(\Vert f\Vert )$, where g is a strictly increasing function. Then, any function $f\in \mathcal{R}$ that minimizes the cost function $\mathcal{C}$ can be written as

$$f(x)=\sum _{i=1}^n{\alpha }_{i}K(x,x_i),$$

(3)

for some parameters ${\alpha }_i\in \mathbb{R},i=1,\dots ,n.$

Perhaps the most famous application of the kernel approach is support vector regression (Vapnik 2013). SVR can be formulated as a convex optimization problem of the form

$$\begin{array}{ccc}\hfill \mathrm{P}:\underset{w,b,\xi ,{\xi }^{\prime }}{min}& \frac{1}{2}\Vert w^2\Vert +C\sum _{i=1}^n({\xi }_i+{\xi }_i^{\prime })\hfill & \\ \hfill \mathrm{s}.\mathrm{t}.& (w^T\Phi (x_i)+b)-y_i\le \epsilon -{\xi }_i,\hfill & \hfill i=1,\dots ,n,\\ \hfill & y_i-(w^T\Phi (x_i)+b)\le \epsilon -{\xi }_i^{\prime },\hfill & \hfill i=1,\dots ,n,\\ \hfill & {\xi }_i,{\xi }_i^{\prime }\ge 0,\hfill & \hfill i=1,\dots ,n,\end{array}$$

where $\epsilon$ determines the error tolerance of the solution, C is a regularization parameter, and ${\xi }_i\in \mathbb{R}$ and ${\xi }_i^{\prime }\in \mathbb{R},i=1,\dots ,n$, are slack variables. It can be shown (Schölkopf et al. 2000) that the dual formulation of P is given by

$$\begin{array}{ccc}\hfill \mathrm{D}:\underset{\lambda ,{\lambda }^{\prime }}{max}& -\frac{1}{2}\sum _{i,j=1}^n({\lambda }_i-{\lambda }_i^{\prime })({\lambda }_j-{\lambda }_j^{\prime })K(x_i,x_j)-\epsilon \sum _{i=1}^n({\lambda }_i-{\lambda }_i^{\prime })+\sum _{i=1}^n{y}_i({\lambda }_i-{\lambda }_i^{\prime })\hfill & \\ \hfill \mathrm{s}.\mathrm{t}.& \sum _{i=1}^n({\lambda }_i-{\lambda }_i^{\prime })=0,\hfill & \\ \hfill & 0\le {\lambda }_i\le C,i=1,\dots ,n,\hfill \\ \hfill & 0\le {\lambda }_i^{\prime }\le C,i=1,\dots ,n,\hfill \end{array}$$

and that the solutions of P and D coincide and are given by

$$f(x)=\sum _{i=1}^n{\alpha }_{i}K(x,x_i)+\beta ,$$

(4)

where ${\alpha }_i={\lambda }_i-{\lambda }_i^{\prime }$. In order to fit the model (4) to data, we must first determine the kernel matrix $K=\{K_{ij}\},i,j=1,\dots ,n,$ where $K_{ij}=K(x_i,x_j)$. In the classical paradigm, we would choose a tractable kernel such as the kernel corresponding to radial basis functions (the so-called Gaussian kernel), evaluate the kernel matrix, and finally, fit the model to data by solving the optimization problem D. An alternative to classical kernels is provided by the so-called quantum kernels, which we will briefly review in the following section.

3. Quantum Kernel Estimation

In quantum kernel estimation, the kernel is determined by a quantum feature map. Following Rebentrost et al. (2014); Schuld and Killoran (2019) and Havlíček et al. (2019), we let $\Phi :x\mapsto \Phi (x)$ (or $|\Phi (x)$ using Dirac’s notation) denote a quantum feature map that maps a data point to a quantum state which is an element $\Phi (x)$ of a Hilbert space $\mathcal{H}$. Any quantum state $\psi \in \mathcal{H}$ naturally satisfies the famous Schrödinger equation

$$i\hslash \frac{\partial }{\partial t}\psi (t,x)=H\psi (t,x),\psi (0,·)\in \mathcal{H}\mathrm{is}\mathrm{given},$$

(5)

where H is the Hamiltonian operator associated with the quantum system. If H is time-independent, the solution to (5) is given by

$$\psi (t,x)=U(t)\psi (0,x),$$

(6)

where the operator U defined by

$$U(t)=e^{-iHt/\hslash },$$

(7)

which is the unitary time evolution operator associated with H. Thus, in analogy with (6), using the characterization of reproducing kernel Hilbert spaces (RKHS), it can be shown (see Schölkopf et al. (2001); Schuld and Killoran (2019), and the references therein) that, for every pair $(\Phi ,x)$, there is an operator $U_{\Phi }(x)$, known in the field of quantum computing as a feature embedding circuit, that is implicitly determined by the relation

$$\Phi (x)=U_{\Phi }(x){\Omega }_0,$$

(8)

where ${\Omega }_0$ (also denoted $|0\dots 0⟩$ using Dirac’s notation) denotes the ground state, i.e., the quantum state with the lowest energy level (associated with the smallest eigenvalue of the generator of the operator $U_{\Phi }(x)$). Further, let the kernel K corresponding to $\Phi$ be given by

$$K(x,z)={|⟨\Phi (x),\Phi (z)⟩|}^2.$$

(9)

As mentioned above, $K(x,z)$ it is essentially a similarity measure between x and z in the quantum feature space $\mathcal{H}$. It should be noted that the definition of the kernel (9) deviates from the form (1) that is common in the classical literature, in that it involves taking the absolute value squared of the inner product. This is due to the following: Using (8), the kernel can be written as

$$K(x,z)={|⟨\Phi (x),\Phi (z)⟩|}^2={|{\Omega }_0^{†}{U}_{\Phi }^{†}(z)U_{\Phi }(x){\Omega }_0|}^2,$$

(10)

that is, $K(x,z)$ is given by the probability of obtaining the measurement outcome ${\Omega }_0$ when measuring the quantum state $\Psi (x,z)$ defined by

$$\Psi (x,z)=U_{\Phi }^{†}(z)U_{\Phi }(x){\Omega }_0,$$

(11)

where $U^{†}$ denotes the adjoint operator of U. The probability (10) can be estimated on a quantum computer by loading the state $\Psi (x,z)$ into a quantum circuit. This circuit is then run multiple times, and (10) is estimated by the frequency of ${\Omega }_0$-measurements. We note that the form of the kernel (9) is what allows us to readily estimate it using a quantum computer.

Naturally, the procedure outlined above introduces a sampling error. Assuming that the measurements are independent, we have that ${\widehat{p}}_n$, the frequency of ${\Omega }_0$-measurements after n trials (or shots), has standard error $\sqrt{\frac{{\widehat{p}}_n(1-{\widehat{p}}_n)}{n}}$. Today’s noisy and rather primitive quantum computers are unfortunately quite error prone, which means that, in addition to the sampling error, there is a large and often systematic error arising from imperfect hardware. Given a large enough number of trials, these hardware errors tend to dominate the sampling error. The hardware-related errors can be partially mitigated using error correction techniques (see, e.g., Temme et al. (2017)).

4. Model Description

We consider a population of insured individuals, divided into subgroups based on some common characteristics. Let $E_i$ be the number of healthy individuals from the population subgroup $i,i=1,\dots ,n,$ in a given disability insurance scheme. We denote by $D_i$ the number of individuals falling ill amongst the $E_i$ insured healthy individuals. For each population subgroup i, there is some associated data $x_i\in {\mathbb{R}}^d$, which may, e.g., contain information about age, gender, and other characteristics of the population subgroup at hand. We assume that the conditional distribution of $D_i$ given $E_i$ is binomial:

$$D_i\sim \mathrm{Bin}(E_i,p(x_i)),$$

(12)

where $p(x_i)$ is the probability that an individual randomly selected from $E_i$ falls ill. We propose to model the logistic disability inception probabilities using support vector regression:

$$\mathrm{logit}p(x)=log\frac{p(x)}{1-p(x)}=\sum _{i=1}^n{\alpha }_{i}K(x,x_i)+\beta ,$$

(13)

where $K\in {\mathbb{R}}^{n\times n}$ is a kernel matrix associated with the data ${\{x_i\}}_i,$, and $\beta \in \mathbb{R}$ and ${\alpha }_i\in \mathbb{R},i=1,\dots ,n,$ are parameters to be estimated from historical data. We propose to fit the model using a weighted support vector regression, with the weight for each sample proportional to the population subgroup size $E_i$, placing higher importance on large subgroups where the sampling errors of the observed inception probabilities are lower. The logistic transform guarantees that the probabilities estimated from the model lie in their natural interval $(0,1)$.

In the classical paradigm we would choose a tractable kernel such as the kernel corresponding to radial basis functions or the linear kernel. We propose instead that this kernel be calculated using a quantum feature map, to be evaluated on a quantum computer. In order to fit the model (13) on a quantum computer, we must first choose a specific quantum feature map. This, in turn, determines the layout of our quantum circuit through (8). There are many ways to choose a suitable feature map (see, e.g., Schuld and Killoran (2019)). We suggest to choose $\Phi$, such that it captures the richness of the data x while still being simple enough to be run on today’s limited and noisy quantum computers. For simplicity, we will now assume that our data are two-dimensional, i.e., $x_i\in {\mathbb{R}}^2$. Then, it is enough to use a two-qubit unitary operator to obtain estimates of K. To this end, we choose the unitary operator given by

$$U_{\Phi }(x_i)=\left(I\otimes {\mathrm{R}}_{\mathrm{Y}}(\pi x_{i,2})\right)C_{{\mathrm{R}}_{\mathrm{Z}}}(\pi x_{i,2})\left({\mathrm{R}}_{\mathrm{Y}}(\pi x_{i,2})\otimes {\mathrm{R}}_{\mathrm{Y}}(\pi x_{i,1})\right),$$

(14)

where ${\mathrm{R}}_{\mathrm{Y}}$ and ${\mathrm{R}}_{\mathrm{Z}}$ denote rotations around the $\mathrm{Y}$ and $\mathrm{Z}$ axes of the Bloch sphere (a.k.a. the Riemann sphere), respectively, and $C_{{\mathrm{R}}_{\mathrm{Z}}}$ denotes a controlled ${\mathrm{R}}_{\mathrm{Z}}$ operation on the second qubit, using the first qubit as a control. A graphical representation of the quantum circuit that implements this unitary is presented as follows:

To facilitate interpretation, we let $x_{i,1}$ be a dummy variable taking the value 1 if the population subgroup is male, and 0 otherwise, and $x_{i,2}$ be the associated age of the population subgroup, measured in centuries. First, we apply a ${\mathrm{R}}_{\mathrm{Y}}(\pi x_{i,1})$-gate to $q_0$. This flips $q_0$ from |0⟩ to |1⟩ for male subgroups. Then, we perform a ${\mathrm{R}}_{\mathrm{Y}}(\pi x_{i,2})$ rotation on $q_1$. This operation rotates the state of $q_1$ from |0⟩ towards |1⟩, with the angle of rotation increasing as the age of the subgroup increases. The $C_{{\mathrm{R}}_{\mathrm{Z}}}(\pi x_{i,2})$ performs an additional rotation around the $\mathrm{Z}$-axis of the Bloch sphere, with the angle of rotation increasing as the age of the subgroup increases. Note that this rotation is only performed if $q_0$ is in the state |1⟩, i.e., if the subgroup is male. Finally, we perform a ${\mathrm{R}}_{\mathrm{Y}}(\pi x_{i,2})$ rotation on $q_0$.

For each data pair $(x_i,x_j)$, we run this quantum circuit inserting the values of $x_i$ and then run the adjoint circuit inserting the values of $x_j$. Finally, we perform a measurement on the two qubits. This circuit is run multiple times, and $K(x_i,x_j)$ is estimated by the frequency of obtaining the measurement ${\Omega }_0:=|00⟩$. The resulting quantum circuit can be graphically represented as

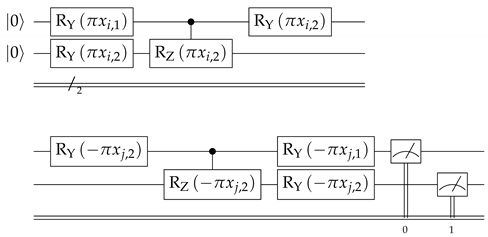
This circuit is designed to clearly separate male and female subgroups and to gradually increase the dissimilarity between different age groups as the difference in ages increases. Note that, for $i=j$, all rotations cancel out, and the circuit will measure the state |00⟩ with probability 1, i.e., $K(x_i,x_i)=1$ as expected.

5. Numerical Results

In this section, we estimate the kernel matrix associated with disability inception data from a Swedish insurance company. This kernel is then used in a support vector regression to estimate the logistic disability inception rates. The data consist of inception counts for 81 groups of individuals as well as the associated age and gender for each group.

5.1. Estimating the Kernel Matrix

We estimate the kernel matrix using the circuit from the previous section with two different techniques. Using (10) and (14), we classically compute $K(x_i,x_j)$ for each pair $(x_i,x_j)$ by matrix multiplication. Here, classically computing the kernel is possible due to the simple structure and low dimension of the unitary operator (14). This procedure is hereafter referred to as a state vector simulation. Figure 1 displays the estimated kernel matrix. This matrix has an interesting structure: it is block-diagonal. This is due to the fact that the second quadrant of the matrix correspond to the inner products of the female population groups. These share the common characteristic ’female’, and each row is similar to its neighbours due to the encoding: similar ages are also similar in the quantum feature space. Analogously, the fourth quadrant of the matrix contains the male population groups. The first and third quadrants contain the inner products between male and female population groups and so are dissimilar in the quantum feature space.

Figure 1. Kernel matrix determined by state vector simulation.

Next, we run multiple experiments on the IBM Yorktown five-qubit quantum computer (of which we use two qubits) to obtain an estimate of (10). For each data pair $(x_i,x_j)$, we run the circuit 8192 times, measure the outcomes, and estimate $K(x_i,x_j)$ with the observed frequency of the ground state. Note, especially, that, for an ideal quantum computer without hardware related errors, this frequency converges to the probability of measuring the ground state when the number of shots goes to infinity. This means that any difference between the kernel from the state vector simulation and the kernel estimated on the quantum computer is related to sampling error and hardware-related errors. Indeed, for an ideal quantum computer using an infinite number of shots, the estimated kernels would be identical.

Figure 2 displays the estimated kernel matrix. We note that, as expected, this matrix deviates somewhat from the kernel matrix obtained by state vector simulation, but it has the same characteristics of the block-diagonal structure and an increasing dissimilarity with increasing age difference. We also note that, using 8192 shots, the maximum standard error under the assumption of ideal hardware (obtained at $\widehat{p}=0.5$) is given by $\sqrt{\frac{0.5(1-0.5)}{8192}}\approx 0.0055$. Noting that this error is small compared to the errors resulting from imperfect hardware, we will focus on the systematic error from now on.

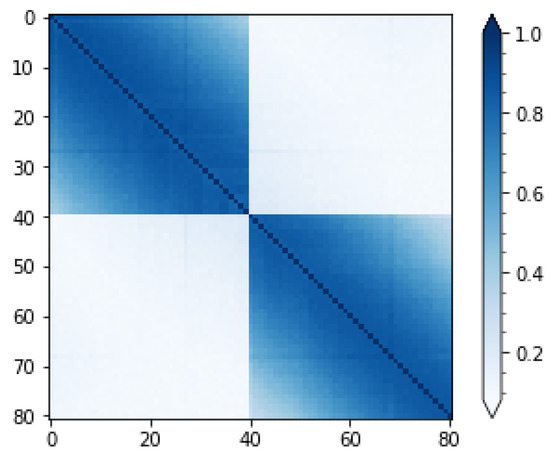
Figure 2. Kernel matrix estimated on the IBM Yorktown quantum computer.

On a five-qubit quantum computer, the natural ground state is the |00000⟩ state. When running a circuit that only performs operations on, say, the first two qubits, we would expect that qubits three through five are always measured to be in their respective |0⟩ state. However, due to measurement error, this is not the case. Hence, we propose to mitigate this problem through the following simple approach: Instead of measuring the frequency of the natural ground state, we measure the sum of the frequencies of all $|00m_1{m}_2{m}_3⟩$ states for $m_k\in \{0,1\},k=1,2,3$.

Figure 3 displays the first row of the kernel matrix, estimated from state vector simulation and from the Yorktown quantum computer, as well as the corresponding error-mitigated kernel. The error mitigation procedure vastly improves the kernel estimate for the first half of the columns and only slightly worsens it for the second half of the columns. The estimation error, measured as the distance from the state vector simulation kernel in the Frobenius norm, is reduced from 15.18 to 8.07, indicating that the approach is functioning as intended.

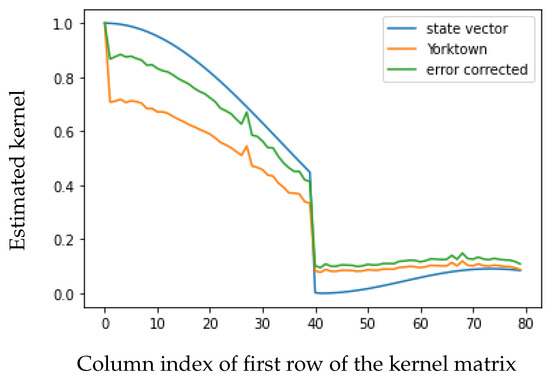
Figure 3. First row of the kernel matrix, estimated from state vector simulation and from the Yorktown quantum computer, as well as the corresponding error-mitigated kernel.

5.2. Fitting Swedish Disability Inception Rates

We now fit the disability inception model (13) to data with support vector regression, using four classical kernel methods, i.e., the linear kernel, a polynomial kernel of rank 3, the radial basis functions kernel, and a sigmoid kernel. In addition, we fit the model to data using the quantum kernels based on a state vector simulation as well as from the IBM Yorktown 5-qubit quantum computer. The models are fit using leave-one-out cross-validation, so that, for each train–test split, a single out-of-sample logistic disability inception rate is estimated. After applying the inverse logistic function to obtain a disability inception rate, we then calculate the weighted R² statistic for the out-of-sample rates, again using the population counts as weights. The results are presented in Table 1. The state vector quantum kernel performs better than three out of the four classical kernels, the exception being the polynomial kernel. The Yorktown quantum kernel is only slightly worse compared to the state vector simulation.

Table 1. Weighted out-of-sample R² for the classical and quantum kernels.

Kernel	R2
linear	0.426
polynomial	0.550
radial basis functions	0.529
sigmoid	0.494
state vector quantum kernel	0.541
Yorktown quantum kernel	0.518

The out-of-sample estimates are displayed in Figure 4. Note that, due to confidentiality, the actual values of the estimates are not reported. The support vector regression approach manages to capture the difference between the genders, as well as finding a pattern in the age dimension. The middle-aged population groups are larger than the others, meaning that the highest weights will be placed on these ages for the purposes of calibrating the model. The observations with very high or very low ages are considered as outliers by the model and so are virtually ignored.

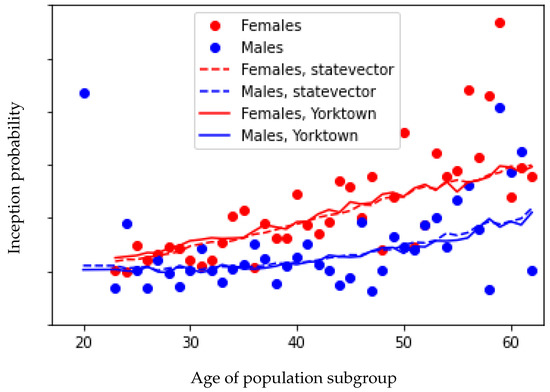
Figure 4. Out-of-sample disability inception rates estimated by state vector simulation and from the IBM Yorktown quantum computer.

We note, especially, that the estimated inception rates from the Yorktown quantum kernel are comparable to the ones obtained from the state vector simulation, even though the estimated quantum kernels were themselves quite different. We believe that this is due to the fact that the characteristics of the kernel, namely the block-diagonal structure and the increasing dissimilarity with increasing age difference, were preserved, even though the actual kernel estimates differed significantly from each other. This fact proposes some degree of robustness to the model: even though the quantum kernel is estimated with significant error, the resulting disability inception estimates are only marginally impacted.

6. Conclusions

We have proposed a hybrid classical-quantum approach for modeling transition probabilities in health and disability insurance. We formulated the modeling of logistic disability inception probabilities as a support vector regression problem. The associated kernel is determined by the inner product between the quantum states from a quantum feature space. This procedure is made possible due to the ability to construct a ‘quantum’ feature map between the data points and the quantum states.

The kernel used in this paper is simple enough that it can also be evaluated using classical methods. This is what allows us to compare the analytically derived kernel to the one estimated on a quantum computer. However, the proposed approach is general and is, in theory, capable of estimating complex kernels based on high-dimensional data, where classical methods are intractable.

Since our proposed model fits the data well and produces errors that are comparable to today’s classical methods, we conclude that estimating disability inception rates with quantum support vector regression is a viable statistical method, even on today’s noisy quantum computers. This bodes well for the future where complex and high-dimensional data might well be modeled and fitted accurately to data in a timely fashion using quantum computers.