Abstract
The paper features an examination of the link between the behaviour of the FTSE 100 and S&P500 Indexes in both an autoregressive distributed lag ARDL, plus a nonlinear autoregressive distributed lag NARDL framework. The attraction of NARDL is that it represents the simplest method available of modelling combined short- and long-run asymmetries. The bounds testing framework adopted means that it can be applied to stationary and non-stationary time series vectors, or combinations of both. The data comprise a daily FTSE adjusted price series, commencing in April 2009 and terminating in March 2021, and a corresponding daily S&P500 Index adjusted-price series obtained from Yahoo Finance. The data period includes all the gyrations caused by the Brexit vote in the UK, beginning with the vote to leave in 2016 and culminating in the actual agreement to withdraw in January 2020. It was then followed by the impact of the global spread of COVID-19 from the beginning of 2020. The results of the analysis suggest that movements in the contemporaneous levels of daily S&P500 Index levels have very significant effects on the behaviour of the levels of the daily FTSE 100 Index. They also suggest that negative movements have larger impacts than do positive movements in S&P500 levels, and that long-term multiplier impacts take about 10 days to take effect. These effects are supported by the results of quantile regression analysis. A key result is that weak form market efficiency does not apply in the second period.
JEL Classification:
C22; G12
1. Introduction
The paper explores the link between the S&P500 and FTSE 100 Indexes in a nonlinear autoregressive distributed lag (NARDL) framework. () suggested a method for modelling asymmetric cointegration and dynamic multipliers in a NARDL framework. The approach introduces short- and long-run nonlinearities via positive and negative partial sum decompositions of the explanatory variables. () demonstrate that their model is estimable by OLS, and that reliable long-run inference can be achieved by bounds-testing, regardless of the integration orders of the variables.
() begin by drawing attention to the vast literature that has developed around the analysis of non-stationary variables, which commenced with the work of (; ; ; ), (), which represent major theoretical landmarks.
Since the mid-1990s, a substantial body of work has considered the joint issues of nonstationarity and nonlinearity. Three regime-switching models have had a dominant influence: the threshold ECM associated with (), the Markov-switching ECM of (), and the smooth transition regression ECM developed by ().
The approach reflects a general concern that simple linear adjustment processes may be excessively restrictive in a wide range of economically interesting situations. () note that there is not a great deal of work on nonlinear cointegration. One exception is provided by (, ), who proposed a bivariate asymmetric cointegrating regression of unemployment on output, in which output is decomposed into partial sum processes of positive and negative changes.
() suggested that the cointegrating relationship may be defined between the positive and negative components of the underlying variables, an effect that they termed ‘hidden cointegration’. They note that variables are cointegrated because they respond to shocks together displaying common stochastic trends. (, p. 5) query what would be the implications if they respond differently to positive and negative shocks. They suggest that there may be cointegration between the nonstationary components of a data series, which they refer to as being ’hidden cointegration’, and suggest that standard cointegration is a special case of hidden cointegration, which is a simple example of nonlinear cointegration.
() extend the work in this area and develop a simple and flexible nonlinear dynamic framework that is capable of simultaneously and coherently modelling asymmetries both in the underlying long-run relationship and in the patterns of dynamic adjustment. They derive the dynamic error correction representation associated with the asymmetric long-run cointegrating regression, resulting in the nonlinear autoregressive distributed lag (NARDL) model.
They follow () and use a bounds testing approach to test for the existence of a stable long-run relationship, which is valid irrespective of whether the underlying regressors are I(0), I(1), or mutually cointegrated. The two sets of critical values, as suggested by (), provide a band covering all these three possible classifications. They also derive asymmetric cumulative dynamic multipliers that permit the display of the asymmetric adjustment patterns following positive and negative shocks to the explanatory variables.
Prior to the development of this flexible approach suggested by (), there had been a few other studies that employed a NARDL framework. () used a NARDL model to analyse asymmetric wealth effects on US consumption. (, ) used a NARDL technique in their analysis of long-run asymmetries in the pass-through from exchange rates to consumer prices in developed economies. () applied NARDL models to high frequency exchange rate data, to explore patterns of asymmetry in the pricing impacts of the order flow.
() in a parallel study apply a NARDL analysis of cointegration between the inflation-adjusted levels of the DOWJONES Index and the WEST TEXAS INTERMEDIATE Crude oil price series. In this paper, we examine the link between the S&P500 and FTSE Indexes in a nonlinear autoregressive distributed lag (NARDL) framework.
The sample time frame is of interest because it covers the impact of Brexit in the UK, and then the massive dislocation in the two markets caused by the global spread of COVID-19 commencing in January 2020. For this reason, we decided to split the sample, which commenced in April 2009 into two segments, pre-Brexit which runs up to 2016, and then post-Brexit and COVID-19, which runs from 2016 to date.
2. Previous Work and Econometric Models
2.1. The Transmission of Shocks across Markets and Economies
The United States and the United Kingdom are the world’s first and fifth largest economies who trade over $260 billion worth of goods and services each year, according to the US Department of State (https://www.state.gov/u-s-relations-with-united-kingdom/, accessed 3 April 2021). The United States is the UK’s largest trading partner, and accounted for over 14 percent of its total trade in 2020. It is therefore not surprising that economic and financial shocks are likely to be transmitted between these two economies.
The manner in which these shocks are assessed depends on the economic or financial time series used. Many recent studies have adopted a cointegration framework since () developed the concept, and helped promote awareness of the dangers of combining stationary and non-stationary series. () used cointegration to show links between markets in the USA, Germany, the Netherlands and Japan, over the period October 1979–June 1986. Another early study, by (), used dividend series to provide evidence of a common stochastic trend driving the equity markets of the USA, Japan, England, Germany and Canada. () used fractional cointegration and reported linkages between India and the USA, the UK and Japan. () examined the long-memory properties of US and European stock indices, as well as their linkages, using fractional integration and fractional cointegration techniques, and reported that the relationships changed over time. They suggested that this might be caused by various factors, such as diverging growth and monetary policy.
() uses an estimated dynamic stochastic general equilibrium model, to show that shocks to a common international stochastic trend explain on average about 10% of the variability of output in several small developed economies but suggests that country-specific disturbances account for the bulk of the volatility in the data. Their research motivation is partly drawn from a desire to explore whether there is a common component to international business cycles that affects most economies to a degree.
It may be the case that information about exchange rate movements, commodity price changes, stock market cycles, or various political and economic global events, all contribute to change expectations about individual company prospects. These changes in expected risks or projected cash flows will have impacts on company share prices. Stock market indices are mere weighted aggregations of the price behaviour of the company share prices that make up their constituents. Thus, factors that affect company share prices will also potentially impact stock market indices.
() use pairwise Engle–Granger cointegration tests to examine Granger causality between each pair of US, UK and Eurozone stock markets from 1980 to 2015 using a rolling-window technique. They conclude that the potential for diversifying risk by investing in the US, UK and Eurozone stock markets is limited during the periods of economic, financial and political shocks because they exhibit high degrees of correlation during periods of shocks.
This study will also adopt a cointegration and autoregressive distributed lag approach to examine the recent relationship between the US and UK financial markets, and explore the extent to which it has varied across the two distinct time periods: pre-Brexit which runs from April 2009 up to December 2015, and then post-Brexit and the COVID-19 pandemic, which runs from January 2016 to 11 March 2021.
2.2. Stock Price Changes and Volatility Changes
One of the frequently occurring empirical regularities in equity markets is the inverse relationship between stock prices and volatility, first documented by (), who suggested it reflected the effects of financial leverage. If a company has any debt in its capital structure, when a company’s stock price declines, it becomes more highly leveraged given a fixed level of debt, and this increase in leverage produces higher equity-return volatility.
() proposes two possible explanations for this relationship. In an argument he refers to as ’direct causation’, he suggests there is a causal relation from stock returns to volatility changes. If the firm’s equity value drops, the change in value of the firm’s equity will cause a negative return on its stock and will increase the leverage of the stock. In effect, its debt/equity ratio will rise. The increase in the debt/equity ratio will lead to a rise in the volatility of the stock.
() provides a second explanation he calls the “reverse causation” effect. In this case, the causality runs from volatility changes to stock returns. Black suggests that changes in tastes and technology may lead to an increase in the uncertainty about the expected payoffs from investments. If there is an increase in future volatility, it will cause stock prices to fall. It follows that the expected return from the stock must rise to induce investors to continue to hold it.
Many other authors have reported on this effect, and early studies include (; ; ; ), to mention a few.
Other studies have questioned whether it is a genuine ’leverage’ effect. For example, () examine whether the effects apply to the individual stocks in the S&P100 (OEX) index, and to the index itself. They report a strong “leverage effect” associated with falling stock prices, but also numerous anomalies that they suggest call into question leverage changes as the explanation. They cite the fact that, in their study, the effect is much weaker or nonexistent when positive stock returns reduce leverage; it is too small with measured leverage for individual firms, but much too large for OEX implied volatilities. They report that the volatility change associated with a given change in leverage seems to die out over a few months; moreover, there is no apparent effect on volatility when leverage changes because of a change in outstanding debt or shares, and it is only apparent when stock prices change. Thus, () conclude that the “leverage effect” is really a “down market effect” that may have little direct connection to firm leverage.
A similar conclusion is made by (), who investigate a sample of all-equity-financed companies from January 1972 to December 2008, and report that the leverage effect is just as strong if not stronger, implying that the inverse relationship between price and volatility is not driven by financial leverage.
The current study examines the relationship between the movements of two major national stock market indices using the recently developed NARDL framework. The advantage of using the NARDL approach, as opposed to that of using a standard VAR approach using differenced series, which in this case would be returns on the two indices, is that it loses any information that may be captured in relationships between the levels of the series, as revealed by cointegration. One of the attractions of the NARDL approach is that it reveals differences in the responses to positive and negative changes, and also how these change in the short and long term.
The adoption of the bounds test also means that it can capture relationships between both stationary and non-stationary variables, as explained in the next sub-section. However, we will also use quantile regression to explore whether the ’leverage’ effect is apparent across the extreme quantiles. This means we can explore, at the index level, whether responses to stock index level movements are symmetric. If they are not, this will provide further evidence that the effect is a ’down-market’ effect as opposed to a leverage one, as discussed above.
In the next two sections, we will discuss the bounds testing approach to the testing of levels relationships, as first suggested by (), and then the NARL approach.
2.3. Bounds Tests
() developed a novel approach to the problem of testing the existence of a level relationship between a dependent variable and a set of regressors, when it is not known with certainty whether regressors are trend- or first-difference stationary. Two sets of asymptotic critical values are provided for the two polar cases which assume the regressors are, on the one hand, purely I(1) and, on the other, purely I(0). Since the two sets of critical values provide bounds for all classifications of the regressors in I(1), purely I(0) or mutually cointegrated, we propose a bounds testing procedure. If the Wald or F-statistic falls outside the critical value bounds, a conclusive inference can be drawn without needing to know the integration/cointegration status of the underlying regressors.
In the empirical analysis that follows, we apply the bounds testing procedure using am R library package Dynamac developed by (). They stress that autoregressive distributed lag (ARDL) models are a useful tool for estimating scientific processes over time. However, as the models become more complex by adding richness in dynamic specifications (through multiple lags of variables, either in levels or differences, or lags of the dependent variable), it becomes more difficult to draw meaningful inferences from coefficients alone. The Dynamac program uses the estimated model coefficients to simulate the impact of a shock to one of the variables in the regression. This “shock” means that, at a time specified, the value of an x variable will move to some level. If the variable is in levels or lagged levels, this means that its new value becomes the pre-shock average plus whatever the shock value is. If the variable is in differences or lagged differences, the shock lasts for one period (as a permanent change in a differenced variable would imply that it is changing every period!).
We fit an ARDL model to the two market index series, and simulate the impact of shocks to the US market and the resultant impacts on the UK market in the two time periods.
2.4. NARDL Approach
() commence by considering an asymmetric long-run regression:
where and are scalar I(1) variables, and is decomposed as where and are partial sum processes of positive and negative changes in
The above provides a simple approach for modelling asymmetric cointegration based on partial sum decompositions. () generalizes this concept and defines the following stationary linear combination of the partial sum components:
If is stationary, then and are said to be ‘asymmetrically cointegrated’. It follows that standard linear (symmetric) cointegration is a special case of (4), obtained only if and . () consider the case where the following restriction holds: In expression (4), this implies that and .
() use this foundation to propose the following nonlinear ARDL (p,q) model:
where is a vector of multiple regressors, defined such that , is the autoregressive parameter, and are the asymmetric distributed lag parameters, and is an process with zero mean and constant variance, . () focus on the case in which is decomposed into and around a threshold of zero, thereby distinguishing between positive and negative changes in the rate of growth of .
They follow (), and write (5) in the error correction form as:
where for for for and is the nonlinear error correction term, where and are the associated asymmetric long-run parameters.
In order to deal with the possibility of non-zero contemporaneous correlation between the regressors and the residuals in (6), () propose the following reduced form data generation process for :
where with being a positive definite covariance matrix. In terms of their focus on conditional modelling, they express in terms of as:
where is uncorrelated with , by construction. If we substitute (8) into (6) and rearrange, we obtain a nonlinear conditional ECM:
where and for
It is clear that (9) corrects for the weak endogeneity of any nonstationary explanatory variables, and that the choice of an appropriate lag structure will free the model from any residual correlation. The model is capable of explaining both long-run and short-run asymmetries and, as it is linear in all the parameters, can be estimated by OLS.
2.5. Quantile Regression
(, p. 145) note that quantiles seem inseparably linked to the operations of ordering and sorting the sample observations that are usually used to define them: ‘The symmetry of the piecewise linear absolute value function implies that the minimization of the sum of absolute residuals must equate the number of positive and negative residuals, thus assuring that there are the same number of observations above and below the median’.
They then ask about the other quantiles? Since the symmetry of the absolute value yields the median, it follows that minimizing the sum of asymmetrically weighted absolute residual by simply giving differing weights to positive and negative residuals provides the other quantiles. The solution to:
where the function is the titled absolute value function, shown in Figure 1, gives the sample quantile function as its solution.
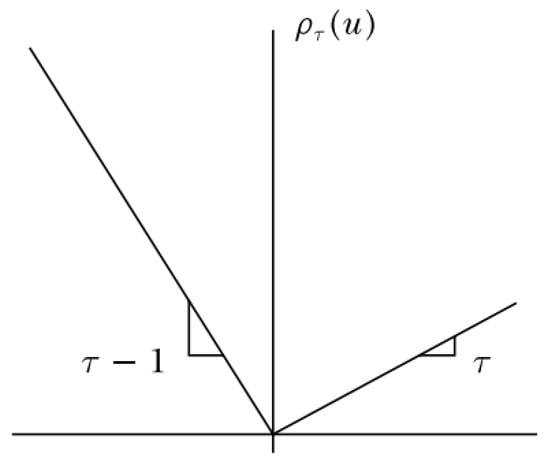
Figure 1.
Quantile Regression function.
An estimate of the conditional median function can be obtained by replacing the scalar in Equation (10) by the parametric function , and setting to Estimates of the other conditional quantile functions can be obtained by replacing the absolute values by , and solving expression (11) by linear programming:
We apply quantile regression to investigate the relationship between the logarithmic differences, or continuously compounded returns, on the FTSE and S&P500 Indexes.
3. Results of the Analysis
3.1. Preliminary Analysis
The sample data set consists of approximately thirteen years of daily data for the S&P500 and the FTSE 100 Indexes from 24 April 2009 through to 11 March 2021, sourced from Yahoo Finance via the R quantmod library. This was divided into two components, a pre-Brexit and COVID-19 period, the former running from 24 April 2009 until 31 December 2015, a total of 1659 observations. The second component of the sample ran from 4 January 2016 until 11 March 2021 and comprises 1290 observations, while the total sample comprises 2949 observations. The Brexit vote took place on 23 June 2016 and, on the following day, the British Prime Minister David Cameron announced his resignation. This immediately led to greater uncertainty in the UK financial market.
The plots of the two series in Figure 2 show that they initially appear to trend together. At the end of 2015, around observation 1660, the UK stock market starts to reflect the uncertainties associated with the Brexit vote. Both appear to be suitable for NARDL analysis in that they do not embody uniformly positive or negative changes. However, a strong upward trend in both markets is evident after their recovery from the Global Financial Crisis of 2007–2008. Things changed in 2016 in the UK following the Brexit vote, the start of the Global Pandemic of COVID-19 at the beginning of 2020, and the onset of massive shocks to the two economies in the form of lockdowns that led to slumps in stock market prices.
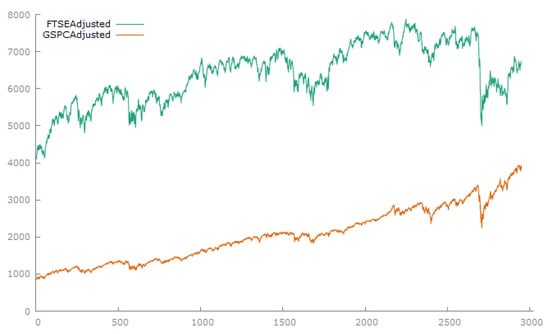
Figure 2.
Plots of daily values of the S&P500 and FTSE Indexes.
Traditionally, cointegration analysis is undertaken with levels of series that are I(1). However, if we are going to make suggestions about the relative volatility of our two base series, in different periods of time, it makes no sense to use the levels of the series which may display infinite variances. We therefore analyse the relative variances of the continuously compounded returns of the two series. These are obtained by calculating their respective logarithmic differences.
Summary statistics for the continuously compounded on the two series, for various sub-samples, are presented in Table 1. In the first sub-period, from 24 April 2009 until 31 December 2015, the mean value of the daily continuously compounded return on the S&P500 index series is 0.00050218, and the corresponding mean value of the daily level of the FTSE 100 index, in period 1, is 0.00021978. The standard deviation of the continuously compounded return on the S&P500 in the first period, is 0.010271, while the standard deviation of the FTSE 100 index, in the first period is 0.010517. In the second period, the mean value of the S&P500 return is 0.00053136, while the corresponding mean value of the return on the FTSE is The standard deviations of the two return series in the second period are 0.012454, for the S&P500, and 0.010834 for the FTSE, respectively. It is noteworthy that both the standard deviations of the S&P500 and of the FTSE returns increase in the second period, but the S&P500 return variance shows a relatively greater increase. This was contrary to our expectations. Our prior was that the prospect of Brexit would have been accompanied by increased uncertainty which would have resulted in relatively increased volatility. The results of ANOVA tests of the equality of variances for the two series across the two periods, reported at the bottom of Table 1, show that the differences in their respective variances across the two periods, are significant at the one percent level, in two-tailed tests for the S&P500 return, but are not significantly different for the FTSE return variance.

Table 1.
Descriptive Statistics for the continuously compounded returns on the S&P500 and FTSE100 indices and analysis of variance tests.
We estimated these tests using a pre-COVID-19 sample period up to the end of 2019, and post COVID from January 2020 on, and found that the variances of both return series were significantly different in the pre-and post COVID periods, but this would have left only 386 daily observations for the post-COVID sample period. (Results available from the authors on request). We decided to stick with the pre and post-Brexit periods which afforded a relatively larger sample in the second period.
The Augmented Dickey–Fuller (ADF) test results shown in Table 2, for the two sub-periods, which are undertaken with both a constant, and a constant and a trend, uniformly fail to reject the null hypothesis of a unit root, in both periods in the case of the S&P500, and in the second period for the FTSE 100 Index, as indicated by the asymptotic probability values in parentheses. However, if both a constant, and a constant and trend, are included, the null hypothesis of a unit root is rejected in the first period for the FTSE 100 Index. Thus, the adoption of a bounds testing procedure appears to be justified on the basis of the differences in the results of the unit root tests on the levels of the two series in the two sub-periods.

Table 2.
Augmented Dickey–Fuller (ADF) Tests.
Table 3 presents the results of simple Engle–Granger tests of cointegration between the two series, using models with a constant, and with a constant and trend. The results in Table 3 appear promising, in that most of the coefficients estimated in the Engle–Granger two-step cointegration test procedure appear to be highly significant, whether the equation includes a constant, or a constant and a time trend, apart from period 2, in which the test with a constant rejects the existence of cointegration, and does not reject the null of a unit root in the residuals. Otherwise, the other three unit root tests on the residuals from the two sets of regressions all reject the null hypothesis of a unit root, which suggests that the two series are cointegrated.

Table 3.
Engle–Granger Tests of Cointegration.
However, () note that they develop a simple and flexible nonlinear dynamic framework capable of simultaneously and coherently modelling asymmetries, both in the underlying long-run relationship and in the patterns of dynamic adjustment. They claim that the approach makes four contributions: the first is the derivation of a dynamic error correction representation associated with the asymmetric long-run cointegrating regression, resulting in the nonlinear autoregressive distributed lag (NARDL) model.
The second is that, in the process, they employ a pragmatic bounds-testing procedure for the existence of a stable long-run relationship, which is valid irrespective of whether the underlying regressors are I(0), I(1), or are mutually cointegrated.
Their third contribution is that they derive asymmetric cumulative dynamic multipliers that permit the tracing out of the asymmetric adjustment patterns following positive and negative shocks to the explanatory variables. Their approach is sufficiently flexible to accommodate the four general combinations of long- and short-run asymmetry.
Finally, by means of Monte Carlo experiments, they validate their estimation and inferential framework, and reveal little bias in estimation and considerable power in the key test statistics. They also compute empirical p-values for the cointegration tests and confidence intervals for the dynamic multipliers by means of a non-parametric bootstrap. Thus, their approach is sufficiently general to permit its application to our two series and will be valid whether or not the two series are cointegrated.
3.2. ARDL Analysis
We commence the analysis using autoregressive distributed lag models (ARDL). For the initial analysis, we use a R package by () called Dynamac. They suggest that, in a typical ARDL model, the number of lags of the dependent variable in levels is given by p, the number of lags of the dependent variable in differences is given by m, the number of lags of the independent variables in levels is given by l, and the number of lags of the independent variables in differences is given by If we restricted all but the contemporaneous and first lag of each series to be zero, a simple ARDL model could be written as:
where is a constant and is a trend term. The usual convention is to add sufficient lags to the system to whiten the residuals.
There are a number of R library packages which undertake cointegration analysis using the bounds testing approach, including () ARDL, ECM and Bounds-Test for Cointegration (ARDL) package, plus Sun’s asymmetric price transmission R package (), which facilitates the assessment of asymmetric price transmissions between two time series, and includes several functions for linear and nonlinear threshold cointegration analysis.
The R package dynamac provides a means to use the coefficients from an estimated model to simulate meaningful responses in the dependent variable to counterfactual changes in an independent variable, x, allowing the change, to filter through the various forms of the x variable in the model, as well as different forms of the y variable (like differences and lagged levels) that might be included. We fit an ARDL model in ECM form using the bounds approach, and then simulate the impact of one standard deviation shocks to the variable in question.
The results of the analysis using dynamac are shown in Table 4 and suggests that the models for both period 1, 2009–2015, and period 2, 2016 to 2021 are significant and successfully capture the relationship between the two indices. In the first period, a constant, plus lagged values of the FTSE in levels, the S&P500 in differences and trend variable, are highly significant. The adjusted R-squared is 0.017, which is low, but is consistent with () concept of market efficiency. If the market is weak-form efficient, it should not be possible to predict price movements in London by changes in prices in New York.

Table 4.
Dynamic analysis using Dynamac.
The results for period 2 in Table 4 suggest that the intercept, the lagged FTSE in levels and two lags of the S&P500 in differences are significant. In this model, the estimate of the trend variable is not significant. The Breusch–Godfrey LM Test test suggests that autocorrelation is not a problem in the model estimates in either period, although the Shapiro–Wilk test results suggest that the residuals do not conform to a Gaussian distribution in either period.
A startling result for the second period is the very high value of the adjusted R-squared of 19.59 per cent, which is not consistent with the () concept of weak form market efficiency. It should not be possible to explain 20 percent of the variation in the value of one market index by movements in the other. This suggests that the relationship between FTSE and S&P500 changed dramatically in the period marked by Brexit and the COVID-19 pandemic.
The plots in Figure 3 present the results of a one standard deviation shock to the level of the S$P500. The graph at the top left-hand-side of the figure displays the level of the FTSE, and the middle plot in the figure shows changes from the mean value of the dependent variable, in this case the level of FTSE. The final plot on the top line of Figure 3 shows changes in the level of FTSE. The lower set of plots in the figure show on the L.H.S the size of the shock, the cumulative change in FTSE, and finally the cumulative absolute change in FTSE. The window has been set to represent the changes through the following 30 days.
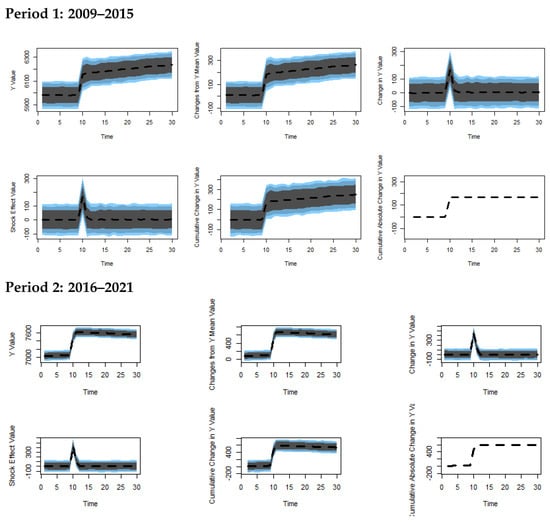
Figure 3.
Dynamac simulations.
The plots suggest that it takes about ten days for a shock to work through the system. The impact of a shock seems to be greater in the second period. One thousand simulations are used to produce the plots, and 95 percent confidence intervals are included in the graphs.
The most notable feature of the two sets of simulations is the increase in the size of the response in the second period, and the fact that explanatory power of the model, as measured by the adjusted R-squared values, is greatly increased.
As a further check, we ran a regression of the continuously compounded returns on FTSE on those of S&P500 in this period. The results are shown in Table 5. The results in the first period are consistent with weak form efficiency in that the adjusted R-squared coefficient is 0.026, indicating that changes in S&P500 returns explain only 2.6% of FTSE returns. The picture changes dramatically in the second period, which captures the uncertainties associated with the BREXIT process and the COVID-19 pandemic. In this period, the adjusted R-squared of the regression jumps to over which is not at all consistent with weak form market efficiency.

Table 5.
Tests of weak-form efficiency.
3.3. NARDL Analysis
We applied the R package ’nardl’ by () to implement the estimation procedures for the nonlinear relationship between the daily levels of S&P500 and FTSE over the two periods. The results of estimation are shown in Table 6.

Table 6.
NARDL Analysis.
The results in Table 6 suggest that the NARDL model successfully captures asymmetries in the response of the level of the FTSE index to changes in the levels of the S&P500 index. In period 1, the response to lagged negative changes is not significant, whereas the responses to lagged positive changes are. This is apparent in the values of the long-run coefficients presented in the RHS of Table 4, in which the coefficient of the lagged positive change in S&P500 (GSPC.Adjusted_p_1) is 52.54374, the coefficient of the second lag is negative, but smaller with a value of −45.84362, while the coefficient of the lagged negative change in S&P500 (GSPC.Adjusted_n_1) is approximately −0.68924, which is much smaller and insignificant. The long term trend coefficient is positive and significant. The Wald test of asymmetry suggests that there is a signifcant difference between the responses to positive and negative movements. The upper bound terminates at an F value of 6.36, whereas the F value of 6.85 shows that there is significant evidence of cointegration.
We tried a number of alternative specifications for the model, but including a constant and trend seemed to be optimal. The adjusted R-squared for the fitted model for the first period is 0.024, and the F statistic for the model is highly significant. The Jarque–Bera (JB) test rejects the hypothesis that the residuals conform to a Gaussian distribution, the Lagrange Multiplier (LM) test finds no evidence of serial correlation, while the ARCH test shows the presence of autoregressive conditional heteroscedasticity.
It has to be borne in mind that we are regressing the levels of a major market index, FTSE, on those of another one, S&P500. The regression is significant, but the Adjusted R-square is small. This is not surprising, and is also consistent with empirical work on market efficiency, for example (). If we could predict the level of FTSE efficiently, we would have a money-making machine, which would not be consistent with the concept of market efficiency. It also has to be borne in mind that () demonstrated that traditional tests of market efficiency typically have low power. He was referring to tests based on returns, not level regressions. The use of cointegration and the error correction mechanism does have the power of super-consistency, but, even so, his cautions have to be borne in mind.
The estimates for period 2 are more puzzling. The coefficients on positive lags of levels of the S&P500 net out to zero, as do the coefficients on negative lags of the levels. All the coefficients in the short run are highly significant, but not in the long run. The trend coefficient is significant in the short run but not in the long run. The adjusted R-squared is very high with a value of 0.22, which, as noted in the previous analysis reported in the paper, is not consistent with the existence of market efficiency. Once again, the Jarque–Bera (JB) test rejects the hypothesis that the residuals conform to a Gaussian distribution, but the Lagrange Multiplier (LM) test finds no evidence of serial correlation, while the ARCH test shows the presence of autoregressive conditional heteroscedasticity. The Wald test suggests the presence of long-run asymmetry, while the F statistic with a value of 34.42 is well outside the bound of 6.36, suggesting the existence of cointegation.
Figure 4 plots the CUSUM test of the residuals, which reveals that, as the model progresses through the observations of the total sample of daily values in the two periods, the residuals remain well within the red borderline boundary at the 5% level, which suggests they are stationary. The simple Engle–Granger tests of cointegration, whether with a constant, or with a constant and trend, did not reject the null of cointegration between the two series.
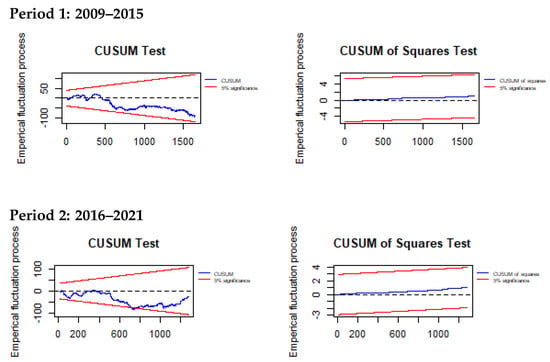
Figure 4.
CUSUM and CUSUM of squares tests.
Similarly, the CUSUM Sum of Squares test, as shown in Figure 4, also suggests that the residuals from the model are stationary. The conclusion drawn from these tests is that something strange was happening to the relationship between FTSE and S&P500 in the BREXIT and COVID-19 periods, which was inconsistent with market efficiency and suggests that movements in FTSE could be predicted in this period.
() note the well-established power dominance of the ECM-based tests, which arises from their inclusion of potentially valuable information relating to the correlation between the regressors and the underlying disturbances, as opposed to the simple Engle–Granger test. In support, they cite the work of (; ; ; ). Thus, the NARDL specification, as used in this paper, can even detect evidence in support of cointegration in circumstances in which the simple Engle–Granger approach might fail to do so, but this is not the case with this data set, as the Engle–Granger tests confirmed the existence of cointegration between the two series.
One of the advantages of the NARDL framework, as used in this paper, is that it has the merit of including both the levels and differences of the relevant series, and that the bounds testing framework means that it can accommodate I(0) and I(1) sequences of variables, or combinations of both. It is consistent but is more powerful than efficient market tests that only use differences or returns series.
However, the results of the NARDL analysis could be consistent with both leverage effects, and the previously mentioned ’downmarket’ effects, mentioned by (). To further explore this issue, we undertake some quantile regression analysis on the differences of the series, which are reported in the next subsection.
3.4. Quantile Regression Results
The results of quantile regressions, of the continuously compounded return on FTSE on the continuously compounded return on S&P500, for both periods, are reported in Table 7. In both periods, the slope coefficients on S&P500 are the highest in the 95% quantile, with values of 0.361510 and 0.479784, respectively, and are both significant at the 1 percent level. The coefficients fall continuously as we move across the quantiles, but remain highly significant, apart from period 1 in the 95th quantile. In this case, in the 95 percent quantile, which represents the highest returns, the slope coefficient is only 0.0154164 and is not significant. This is consistent with the ’down market’ hypothesis, since the leverage effect would imply a significant effect right across the quantiles.

Table 7.
Quantile regression results of regression of FTSE on S&P500.
Figure 5 shows the behaviour of the coefficients of S&P500 as we move across the quantiles. These quantile regression results suggest that there is a larger response to negative returns than to positive ones, and both are consistent with () and the ‘down-market’ hypothesis.
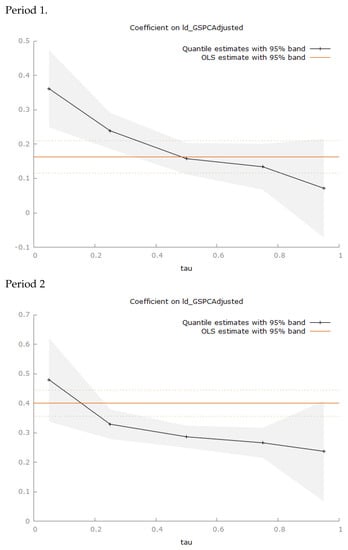
Figure 5.
Tau Sequence—Quantile Regression.
4. Conclusions
The paper featured an examination of the link between the behaviour of the S&P500 and FTSE Indexes in both a linear ARDL and a nonlinear autoregressive distributed lag NARDL framework, as suggested by (). The attraction of NARDL is that it represents the simplest method available of modelling combined short- and long-run asymmetries. As mentioned previously, the bounds testing framework means that it can be applied to stationary and non-stationary time series vectors, or combinations of both. The results reported in the paper suggest that movements in the levels of daily S&P500 index levels have very significant effects on the behaviour of the FTSE Index. They also suggest that long-term multiplier impacts take about 10 days to take effect.
The results of the quantile regressions also support these findings and further suggest that downward movements in S&P500 have a larger impact on FTSE than upward movements do. The results appear to support () and the concept of ’down-market’ effects, as opposed to leverage effects.
The most striking result of the analysis, whether they be undertaken in a cointegration framework using levels of indices, or in a simple linear regression format using continuously compounded returns, is that the hypothesis of simple weak form market efficiency appears to be rejected in the second sample period, namely 2016 to 2021. The observance of increased correlation between markets in times of crisis is consistent with the findings of ().
Author Contributions
Conceptualization, D.E.A. and M.M.; methodology, D.E.A. and M.M.; software, D.E.A.; validation, D.E.A.; formal analysis, D.E.A.; investigation, D.E.A. and M.M.; resources, M.M.; data curation, D.E.A.; writing—original draft preparation, D.E.A.; writing—review and editing, M.M.; visualization, D.E.A.; supervision, D.E.A.; project administration, M.M.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data is publically available on Yahoo Finance.
Acknowledgments
The authors are grateful to three reviewers for helpful comments and suggestions. Vale: Michael McAleer passed away on 8 July 2021, aged 68, after a decade plus struggle against cancer. He was a remarkable scholar with interests in econometrics, economics, financial econometrics, finance, tourism economics, energy economics, the economics of patents, bibliometrics, and more recently statistical applications in COVID-19 research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, David E., and Michael McAleer. 2020. A Nonlinear Autoregressive Distributive Lag Analysis (NARDL) of West Texas Intermediate Oil Prices and the Dow Jones Index. Energies 13: 4011. [Google Scholar] [CrossRef]
- Balke, Nathan S., and Thomas B. Fomby. 1997. Threshold cointegration. International Economic Review 38: 627–45. [Google Scholar] [CrossRef]
- Banerjee, Anindya, Juan Dolado, and Ricardo Mestre. 1998. Error-correction mechanism tests for cointegration in a single-equation framework. Journal of Time Series Analysis 19: 267–83. [Google Scholar] [CrossRef]
- Black, Fischer. 1976. Studies of Stock Price Volatility Changes. In Proceedings of the Business and Economics Section. Washington, DC: American Statistical Association, pp. 177–81. [Google Scholar]
- Braun, Phillip A., Daniel B. Nelson, and Alain M. Sunier. 1995. Good news, bad news, volatility and betas. Journal of Finance 50: 1575–603. [Google Scholar] [CrossRef]
- Chen, Yanhua, Rosario N. Mantegna, Athanasios A. Pantelous, and Konstantin M. Zuev. 2018. A dynamic analysis of S&P 500, FTSE 100 and EURO STOXX 50 indices under different exchange rates. PLoS ONE 13: e0194067. [Google Scholar] [CrossRef] [PubMed]
- Caporale, Guglielmo Maria, Luis A. Gil-Alana, and James C. Orlando. 2016. Linkages between the US and European stock markets: A fractional cointegration approach. International Journal of Finance and Economics 21: 143–53. [Google Scholar] [CrossRef]
- Christie, Andrew A. 1982. The stochastic behavior of common stock variances: Value, leverage and interest rate effects. Journal of Financial Economics 3: 407–32. [Google Scholar] [CrossRef]
- Delatte, Anne-Laure, and Antonia López-Villavicencio. 2010. Asymmetric Responses of Prices to Exchange Rate Variations: Evidence from the G7 Countries. Mimeo: Rouen University Business School. [Google Scholar]
- Delatte, Anne-Laure, and Antonia López-Villavicencio. 2011. Asymmetric Exchange Rate Pass-Through: Evidence from Major Economies. Mont-Saint-Aignan: Rouen University Business School. [Google Scholar]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Engle, Robert F., and Clive W. J. Granger. 1987. Co-integration and error correction: Representation, estimation and testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1965. The behaviour of stock market prices. Journal of Business 38: 34–105. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Figlewski, Steven, and Xiaozu Wang. 2000. Is the “Leverage Effect” a Leverage Effect? Unpublished Working Paper. New York: University and Fudan University. [Google Scholar]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1992. On the relation between the expected value and the volatility of the nominal excess return on stocks. Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Gawon Yoon. 2002. Hidden Cointegration. San Diego: University of California San Diego. [Google Scholar]
- Guerron-Quintana, Pablo A. 2013. Common and idiosyncratic disturbances in developed small open economies. Journal of International Economics 90: 33–49. [Google Scholar] [CrossRef][Green Version]
- Hansen, Bruce E. 1995. Rethinking the univariate approach to unit root tests: How to use covariates to increase power. Econometric Theory 11: 1148–71. [Google Scholar] [CrossRef]
- Hasanhodzic, Jasmina, and Andrew W. Lo. 2011. Black’s Leverage Effect Is Not Due to Leverage. Available online: https://ssrn.com/abstract=1762363 (accessed on 14 April 2021).
- Johansen, Søren. 1988. Statistical analysis of cointegration vectors. Journal of Economic Dynamics and Control 12: 231–54. [Google Scholar] [CrossRef]
- Jordan, Soren, and Andrew Q. Philips. 2020. Dynamac: Dynamic Simulation and Testing for Single-Equation ARDL Models. R Package Version 0.1.11. Available online: https://CRAN.R-project.org/package=dynamac (accessed on 14 April 2021).
- Kapetanios, George, Yongcheol Shin, and Andy Snell. 2006. Testing for cointegration in nonlinear smooth transition error correction models. Econometric Theory 22: 279–303. [Google Scholar] [CrossRef]
- Kasa, Kenneth. 1992. Common stochastic trends in international stock markets. Journal of Monetary Economics 29: 95–124. [Google Scholar] [CrossRef]
- Konker, Roger, and Kevin F. Hallock. 2001. Quantile Regression. Journal of Economic Perspectives 15: 143–56. [Google Scholar] [CrossRef]
- Kremers, Jeroen J. M., Neil R. Ericsson, and Juan J. Dolado. 1992. The power of cointegration tests. Oxford Bulletin of Economics and Statistics 54: 325–48. [Google Scholar] [CrossRef]
- Kwiatkowski, Denis, Peter C. B. Phillips, Peter Schmidt, and Yongcheol Shin. 1992. Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Natsiopoulos, Kleanthis, and Nickolaos Tzeremes. 2021. ARDL: ARDL, ECM and Bounds-Test for Cointegration. R Package Version 0.1.1. Available online: https://CRAN.R-project.org/package=ARDL (accessed on 14 April 2021).
- Nguyen, Viet Hoang, and Yongcheol Shin. 2010. Asymmetric Price Impacts of Order Flow on Exchange Rate Dynamics. Mimeo. Leeds: Leeds University Business School. [Google Scholar]
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Psaradakis, Zacharias, Martin Sola, and Fabio Spagnolo. 2004. On Markov error-correction models with an application to stock prices and dividends. Journal of Applied Econometrics 19: 69–88. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., and Bruce E. Hansen. 1990. Statistical inference in instrumental variables regression with I(1) processes. Review of Economic Studies 57: 99–125. [Google Scholar] [CrossRef]
- Schorderet, Yann. 2001. Revisiting Okun’s Law: An Hysteretic Perspective. San Diego: University of California San Diego. [Google Scholar]
- Schorderet, Yann. 2003. Asymmetric Cointegration. Geneva: University of Geneva. [Google Scholar]
- Schwert, G. William. 1989. Why Does Stock Market Volatility Change over Time? Journal of Finance 44: 1115–53. [Google Scholar] [CrossRef]
- Shin, Yongcheol, Byungchul Yu, and Matthew Greenwood-Nimmo. 2014. Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework. In The Festschrift in Honor of Peter Schmidt.: Econometric Methods and Applications. Edited by Robin C. Sickles and William C. Horrace. New York: Springer, pp. 281–314. [Google Scholar]
- Summers, Lawrence H. 1986. Does the stock market rationally reflect fundamental values. Journal of Finance 41: 591–601. [Google Scholar] [CrossRef]
- Sun, Changyou. 2020. apt: Asymmetric Price Transmission. R Package Version 3.0. Available online: https://CRAN.R-project.org/package=apt (accessed on 14 April 2021).
- Taylor, Mark P., and Ian Tonks. 1989. The internationalisation of stock markets and the abolition of U.K. exchange control. The Review of Economics and Statistics 71: 332–36. [Google Scholar] [CrossRef]
- Van Treeck, Till. 2008. Asymmetric Income and Wealth Effects in a Non-Linear Error Correction Model of US Consumer Spending. Working Paper no. 6/2008. Dusseldorf: Macroeconomic Policy Institute in the Hans-Bockler Foundation. [Google Scholar]
- Wong, Wing-Keung, Aman Agarwal, and Jun Du. 2005. Financial Integration for INDIA Stock Market, a Fractional Cointegration Approach. Paper 0501. Singapore: National University of Singapore Working, pp. 1–29. [Google Scholar]
- Zaghdoudi, Taha. 2021. nardl: Nonlinear Cointegrating Autoregressive Distributed Lag Model. R Package Version 0.1.6. Available online: https://CRAN.R-project.org/package=nardl (accessed on 10 January 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).