3.1. Frequency Models
The general definition of the concordance probability will in this section be modified to a concordance probability that can be used for frequency models. The basic definition (
1) requires the definition of two groups, based on the number of events that occurred during the duration of the policy. However, non-life insurance contracts typically have an exposure of maximum one year. Hence, it is unlikely that more than two events will take place during this (short) period. Therefore, three groups will be defined: policies that experienced zero events, one event, and two events or more, respectively represented by the 0-, 1- and 2-group. These groups result in the following three definitions of the concordance probability for frequency models:
where
refers to the predicted frequency of the frequency model and
to the observed claim number. The set of definitions (
3) has several interesting interpretations. First of all,
(
) evaluates the ability of the model to discriminate policies that did not encounter accidents from policies that encountered at least one (two) accident(s). Furthermore,
quantifies the ability of the model to discriminate policies that encountered one accident from policies that encountered multiple accidents. In other words,
quantifies the ability of the model to discriminate clients that could just have been unfortunate versus clients that are (probably) accident-prone.
However, these concordance probabilities do not take the concept of exposure into account. This is the duration of a policy or insurance contract, and plays a pivotal role in frequency models. In order to make sure that the pair is comparable, the definition of the concordance probability needs to be extended to deal with the concept of exposure as well. As such, two main possibilities can be imagined which ensures comparability of the given pair. For the first possibility, the member of the pair that experienced the most accidents needs to have an exposure that is equal to or lower than the exposure of the other member of the pair. These pairs are sort of comparable since the member of the pair that experienced the most accidents did not have a longer policy duration than the member of the pair that experienced the fewest accidents. The set of definitions (
3) can then be altered as:
where
corresponds to the exposure of observation
i. However, the above set of definitions (
4) runs into trouble for pairs where there is a considerable difference in exposure. In order to understand why this is the case, we need to have a look at the structure of the predictions of a Poisson regression model, which corresponds for observation
i to
. This reveals that the prediction is mainly determined by the exposure
and the linear predictor
. Therefore, when the predictions of a Poisson regression model of a pair of observations are compared, two possibilities can occur when the pair is comparable according to the above set of definitions (
4). One member of the pair can have a higher prediction than the other member due to a difference in risk, as expressed by the linear predictor and as is desirable, or due to a mere difference in exposure, which would obscure the analysis. A possible solution would be to set the exposure values of all observations equal to 1 when making predictions, such that one only focuses on the difference in risk between the different observations. However, this is undesirable as we would like to evaluate the predictions of the Poisson model that are used to compute the expected cost of the insurance policy, and for this the exposure is a key ingredient. In other words, the set of definitions (
4) are of little practical use within the domain of insurance and will no longer be considered.
For the second possibility, the exposure
of both members of the pair need to be more or less the same, in order to ensure their comparability. Incorporated in the set of definitions (
3), we get:
Here, is a tuning parameter representing the maximal difference in exposure between both members of a pair that is considered to be negligible.
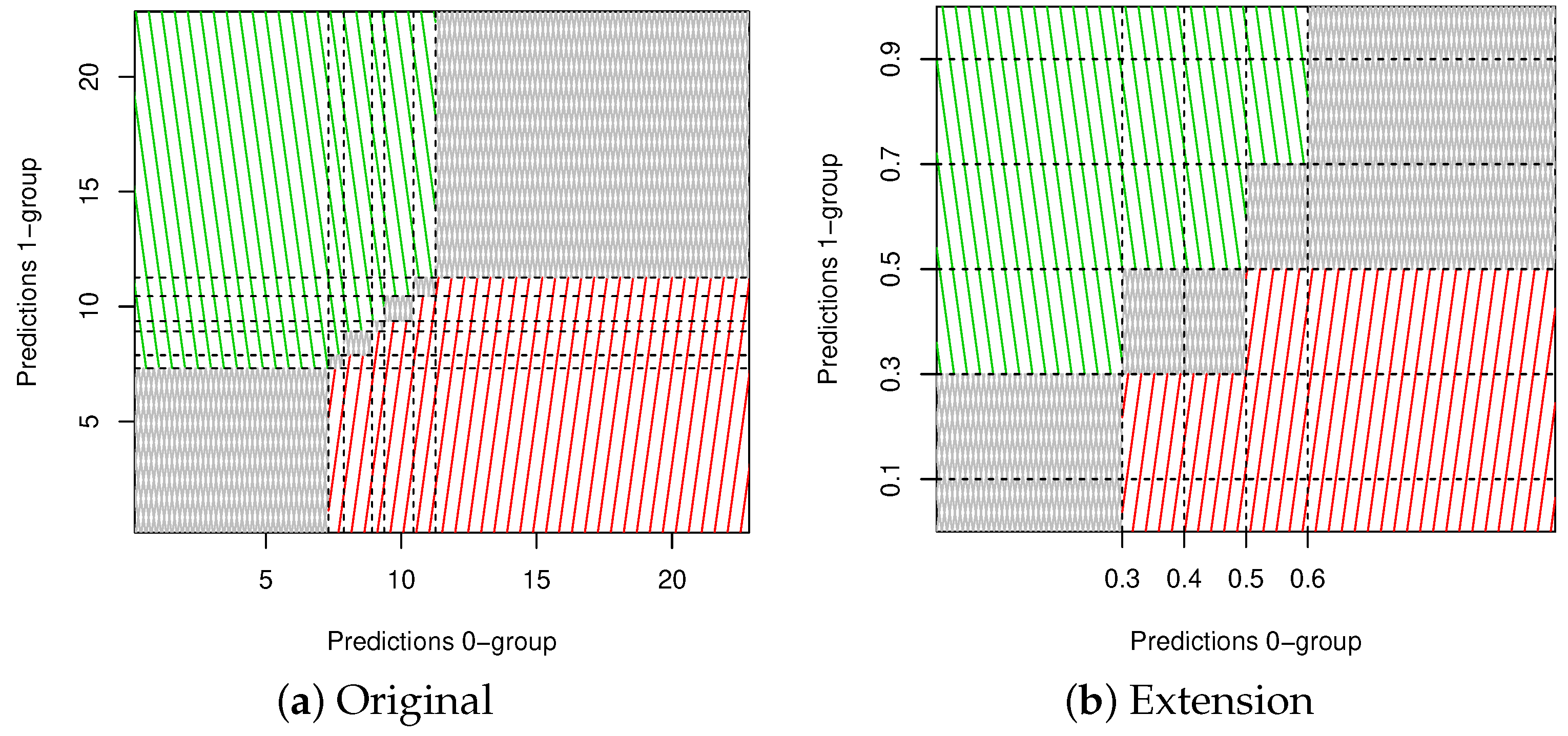
All former definitions are global measures, meaning that the concordance probability is computed over all observations of the dataset, where comparability is considered as the sole exclusion criterion for a given pair. The following definitions show a local concordance probability, by taking a subset of the complete dataset based on the exposure:
In the above set of definitions, is the parameter corresponding to the exposure value for which the local concordance probability needs to be computed. In practice, because the main mass of the data is located at a full exposure. The appealing aspect of this set of definitions is that it allows the construction of a (, ) table, i.e., an evolution of the local concordance probabilities in function of the exposure. However, the disadvantage of this plot is that one has to choose the values of and . Assume one takes equal to 0.05 and . In this case, observations with for example exposure 0.49 and 0.51 will not be comparable, although their exposures are very close to each other. To eliminate this issue, we first define two groups:
-group: group with the largest number of elements, hence the group with the smallest number of events,
-group: group with the smallest number of elements, hence the group containing the largest number of events.
When we consider for example , the -group consists of the elements with and the -group of the elements with . Next, we apply following steps to construct a better (, ) plot:
Determine the pairs of observations and predictions belonging to the -group and the ones to the -group.
Define the number of unique exposures within and apply a for-loop on them:
Select the elements in with exposure .
Select the elements in with exposure in .
Determine , the concordance probability on these two subsets.
Define , the number of comparable pairs used to calculate .
The global concordance probability
can be rewritten as:
where
n equals the number of observations,
(
) the number of observations in
(
),
the number of unique exposures in
and
.
Construct the plot of in function of .
Since the loop iterates over all unique exposures in the
-group, which is the smallest one, the
x-axis can have a rather rough grid. Therefore, one can also easily adapt the previous steps by looping over the unique exposures in the
-group, resulting in a plot with an
x-axis that has possibly a finer grid. In
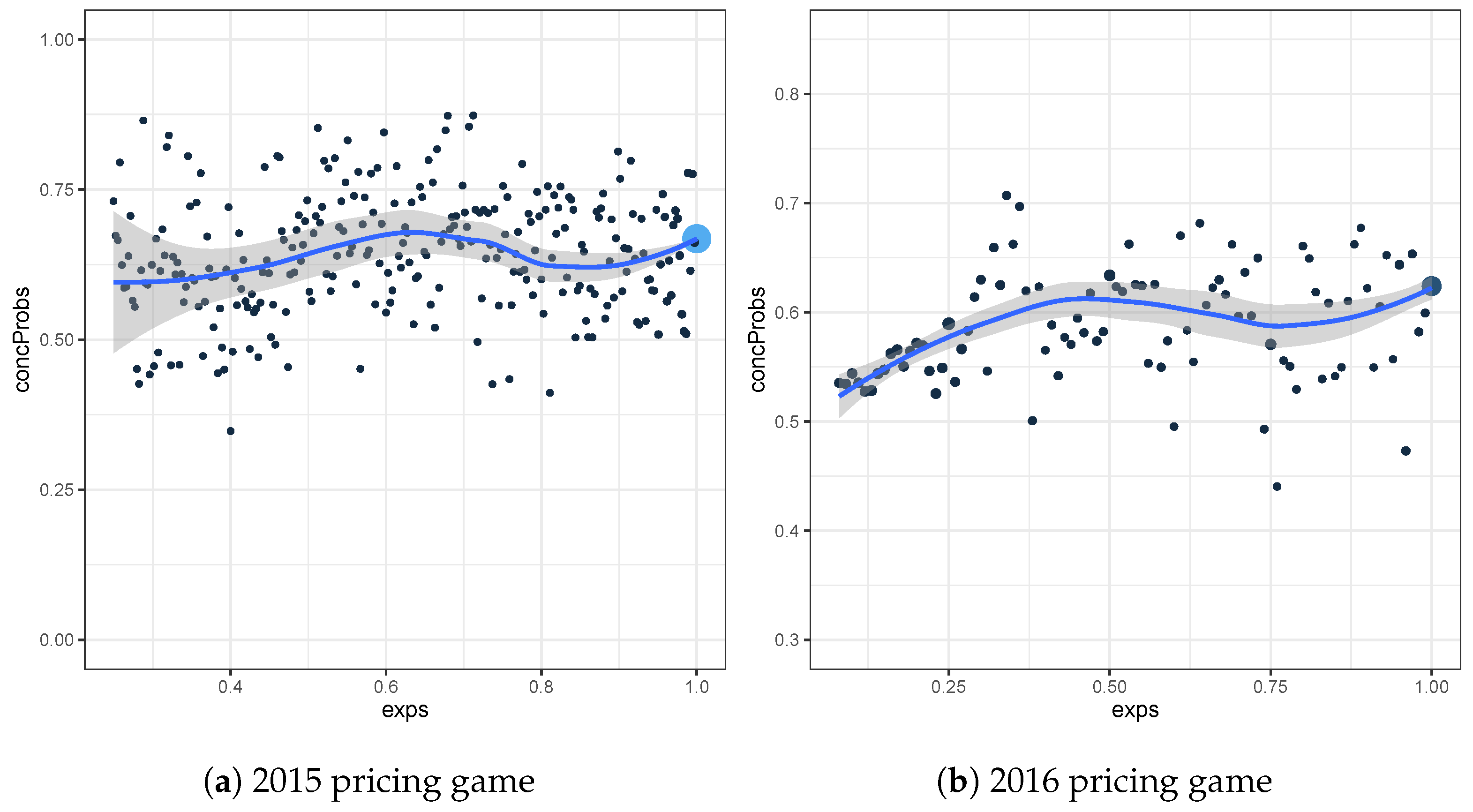
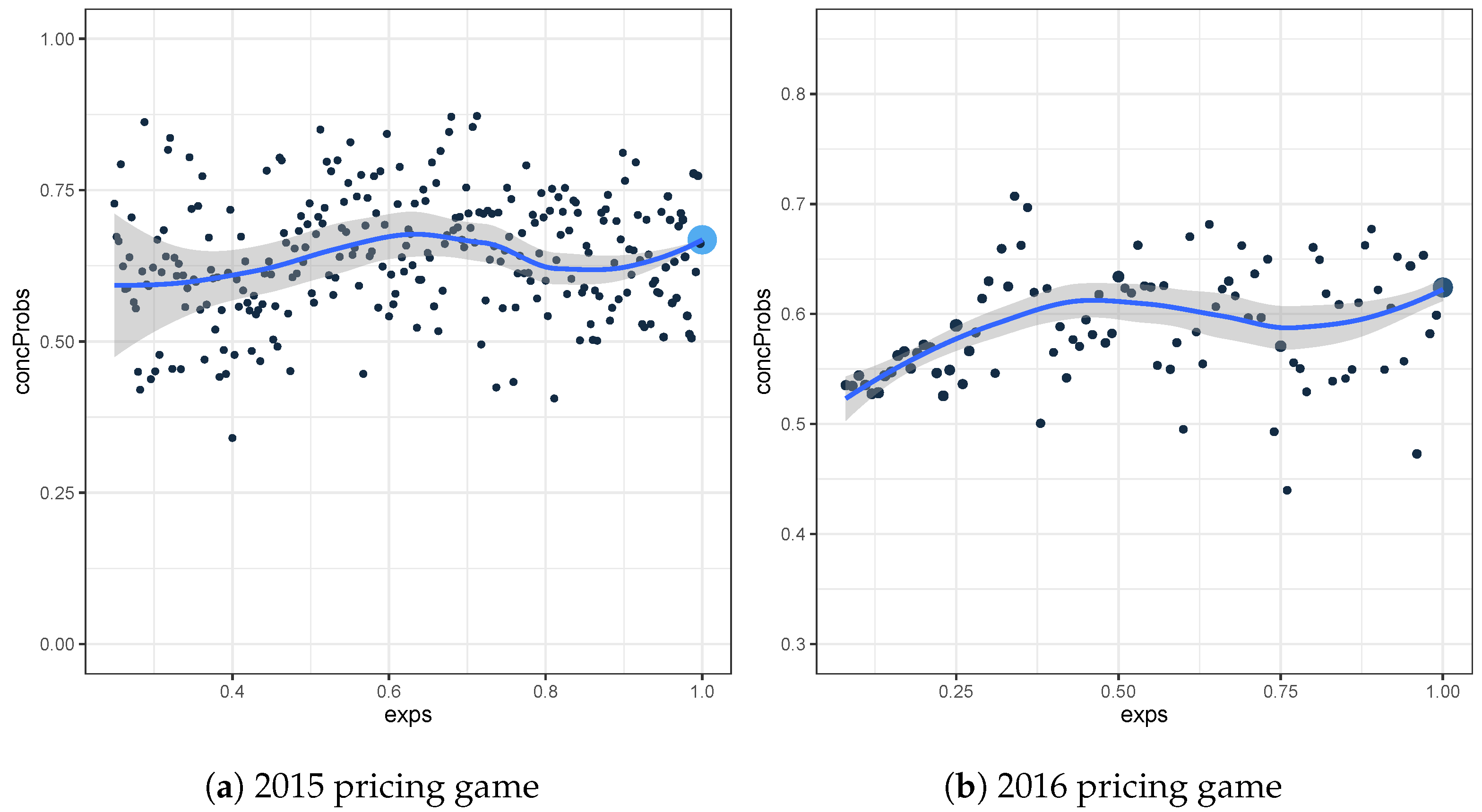
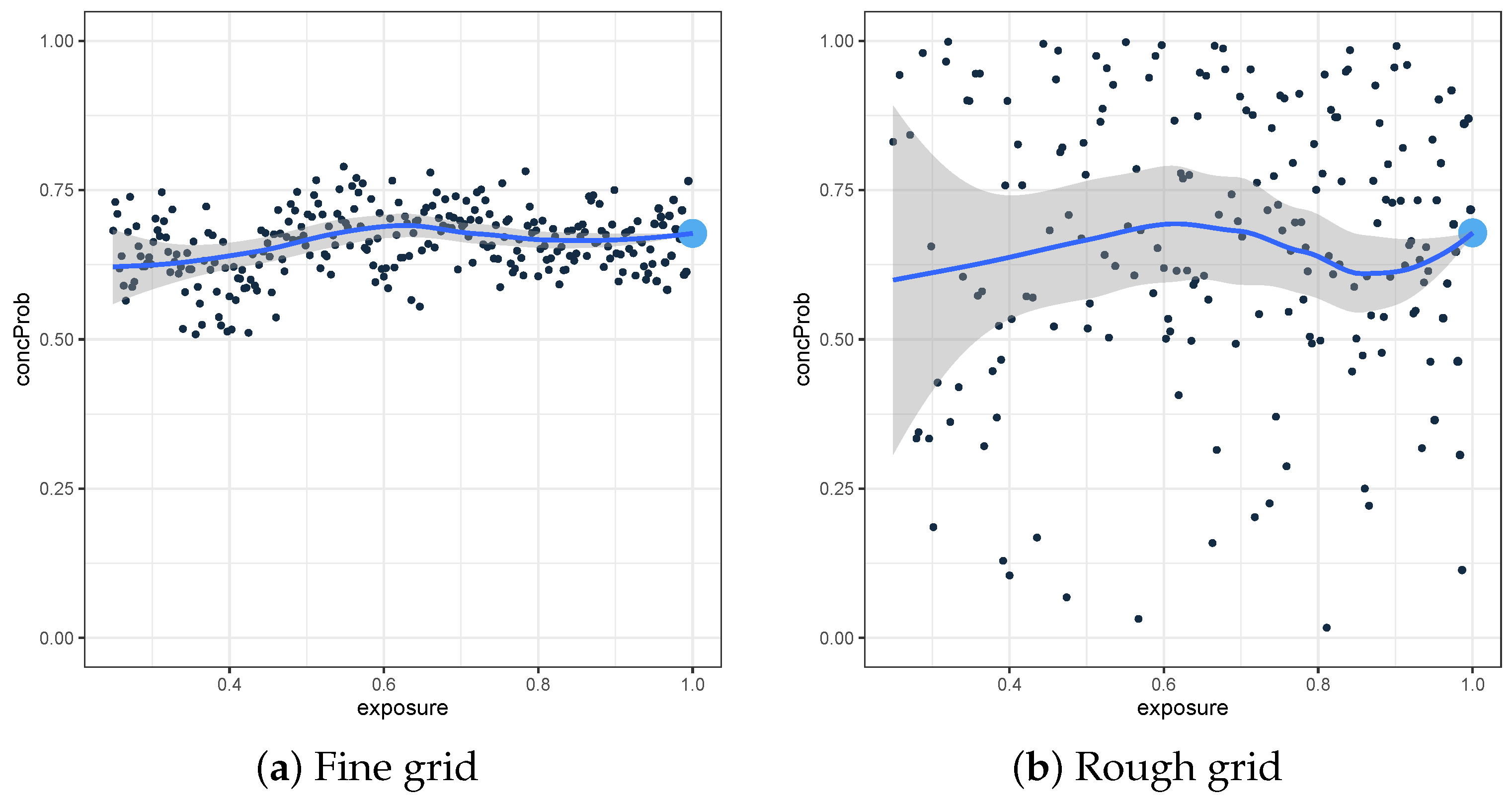
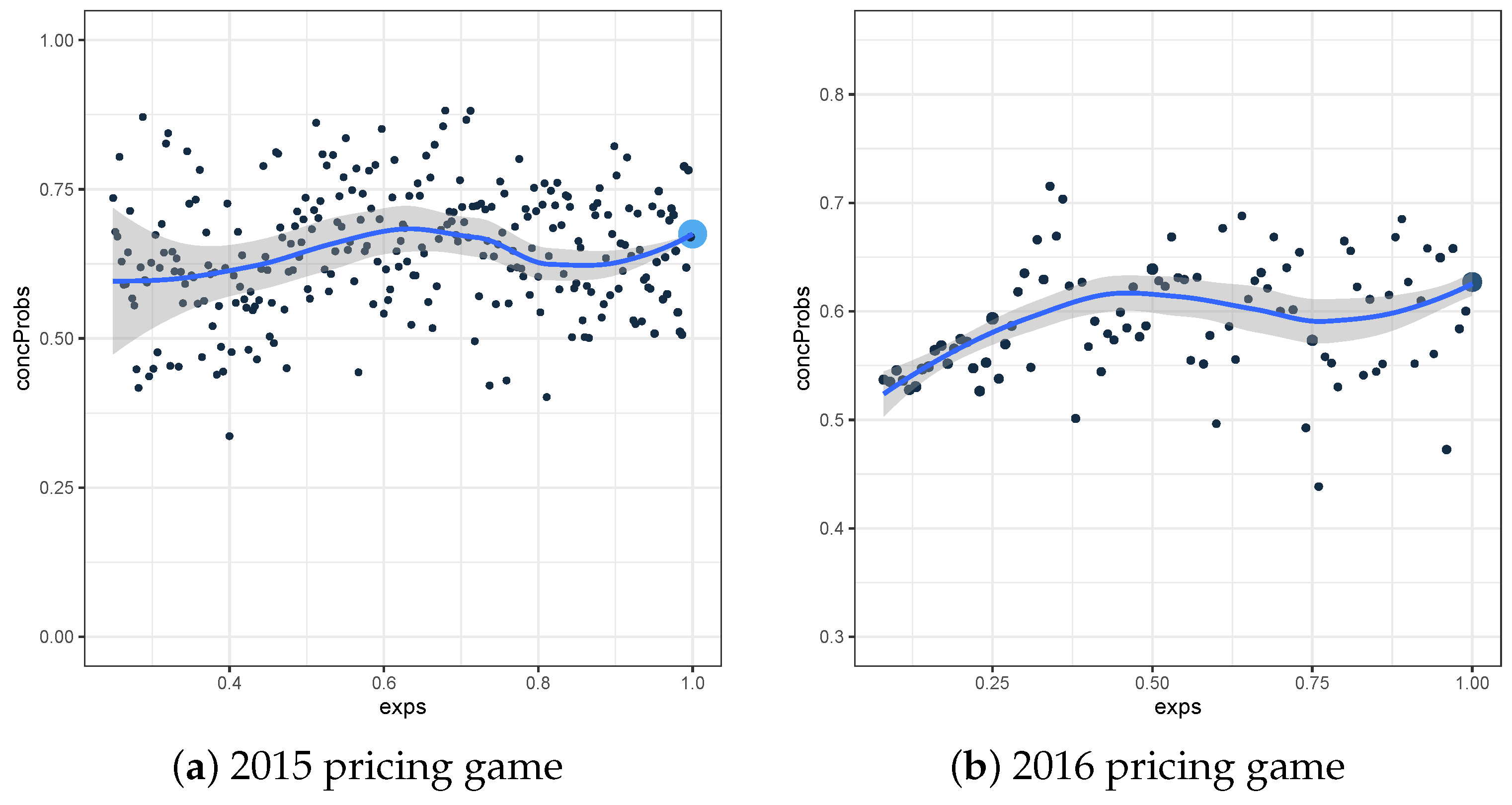
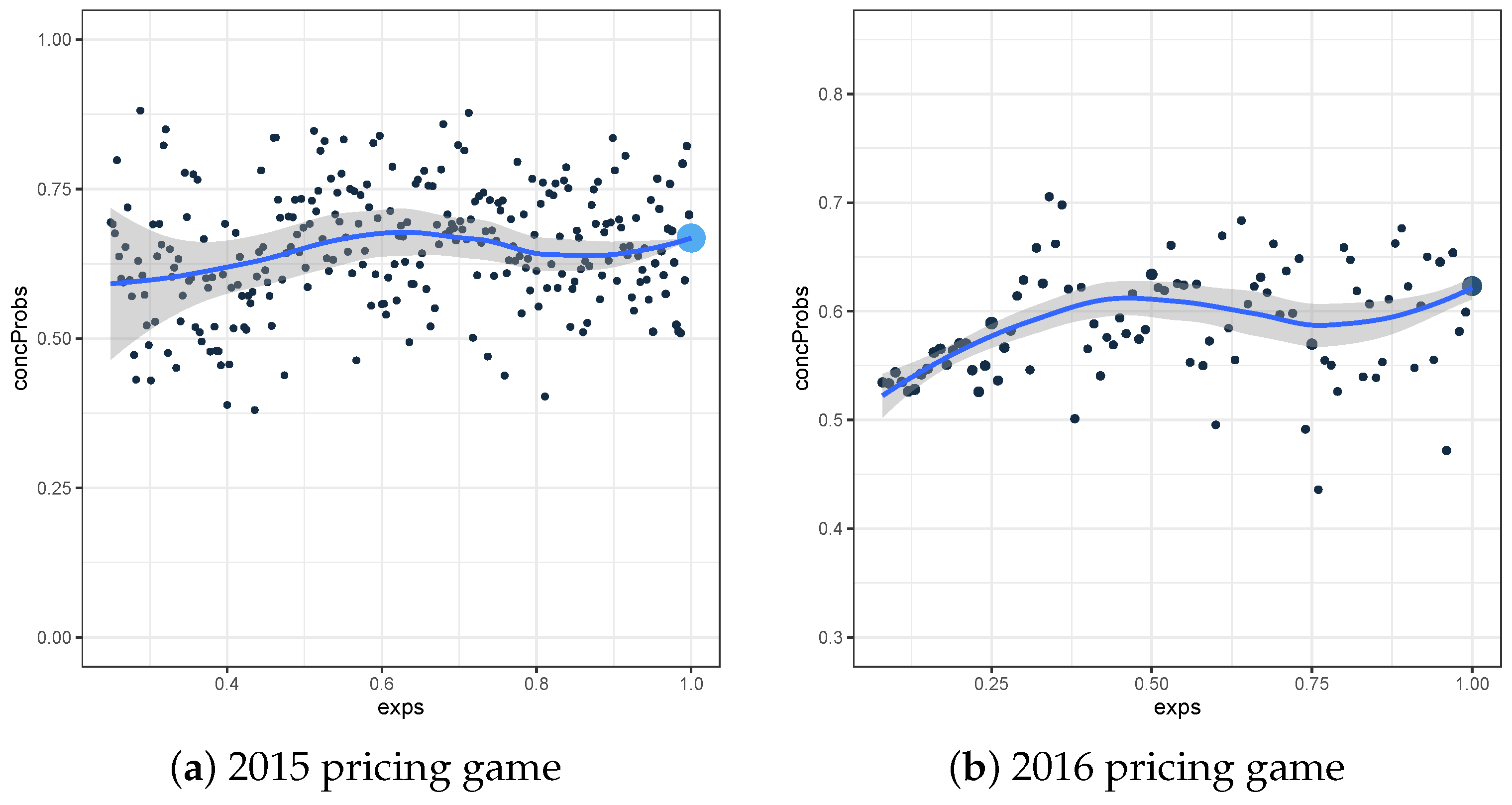
Figure 1 and
Figure 2, both the rough and the fine version of the (
,
) plot are constructed for the test sets of the 2015 and 2016 pricing game respectively. We choose
to be 0.05, which is approximately equal to the length of one month. For the test set of the 2015 (2016) pricing game, the maximal weight
is 0.96 (0.32) for the observations with exposure 1.
However, the plots are hard to interpret, since there are large differences depending on which group is iterated. Especially in
Figure 2, we see that for example
is much larger when iterating over the
-group (fine grid), than when iterating over the
-group (rough grid). For the fine grid version, we use the elements of the
-group with exposure equal to 0.08, together with the elements of the
-group with an exposure between 0.08 and 0.13. This subset leads to a high value for
, meaning that the selected elements of the
-group have in general a higher prediction than the ones of the
-group. However, for the rough grid version, we use the elements of the
-group with an exposure between 0.08 and 0.13, together with the elements of the
-group with an exposure equal to 0.08. This is yet another subset, and this time we often see higher predictions for the elements in the
-group, leading to a small value for
. Considering different subgroups, leads to a difficult interpretation of these plots. However, it is important to know that both versions of this local plot lead to the same global concordance probability, based on equality (
7).
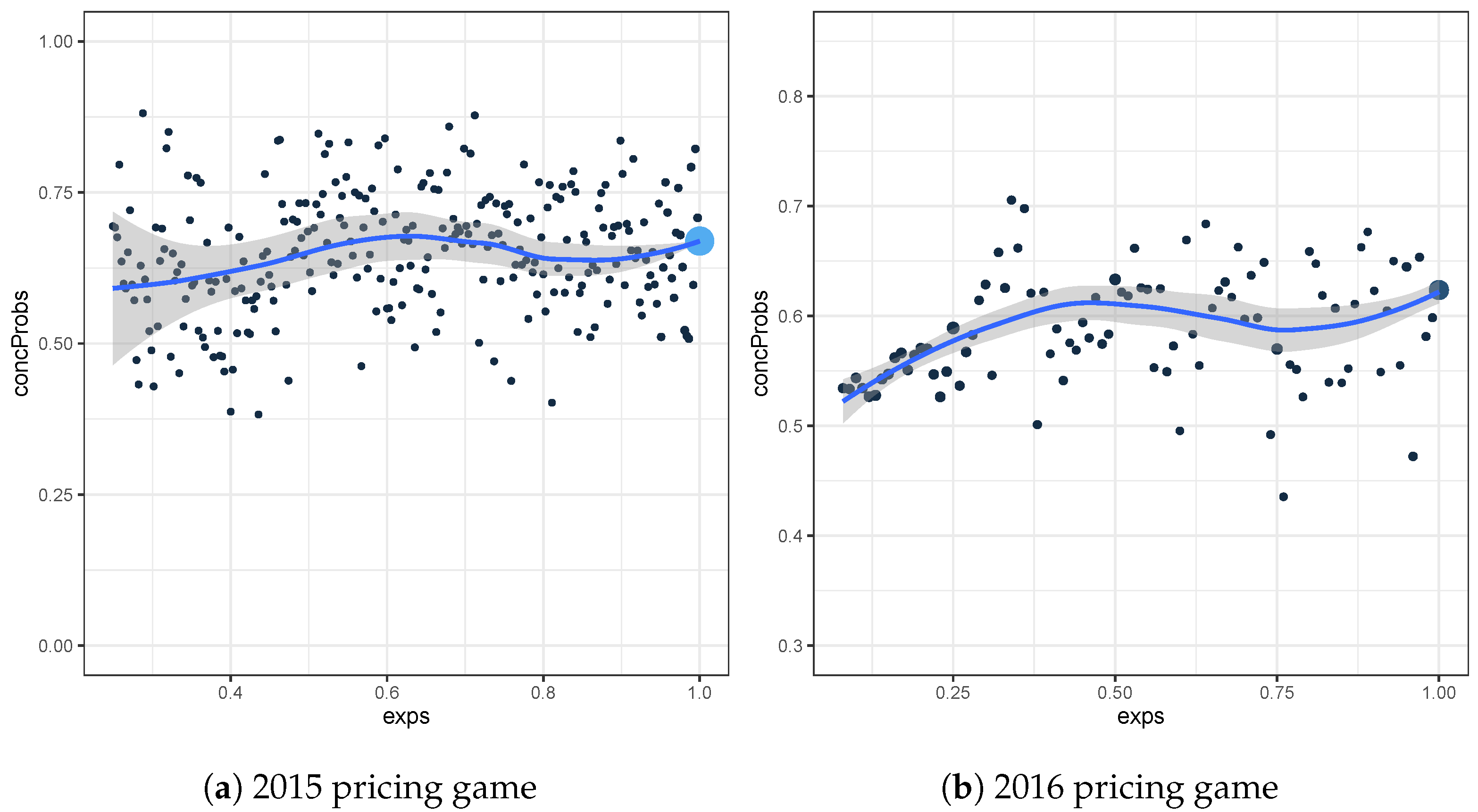
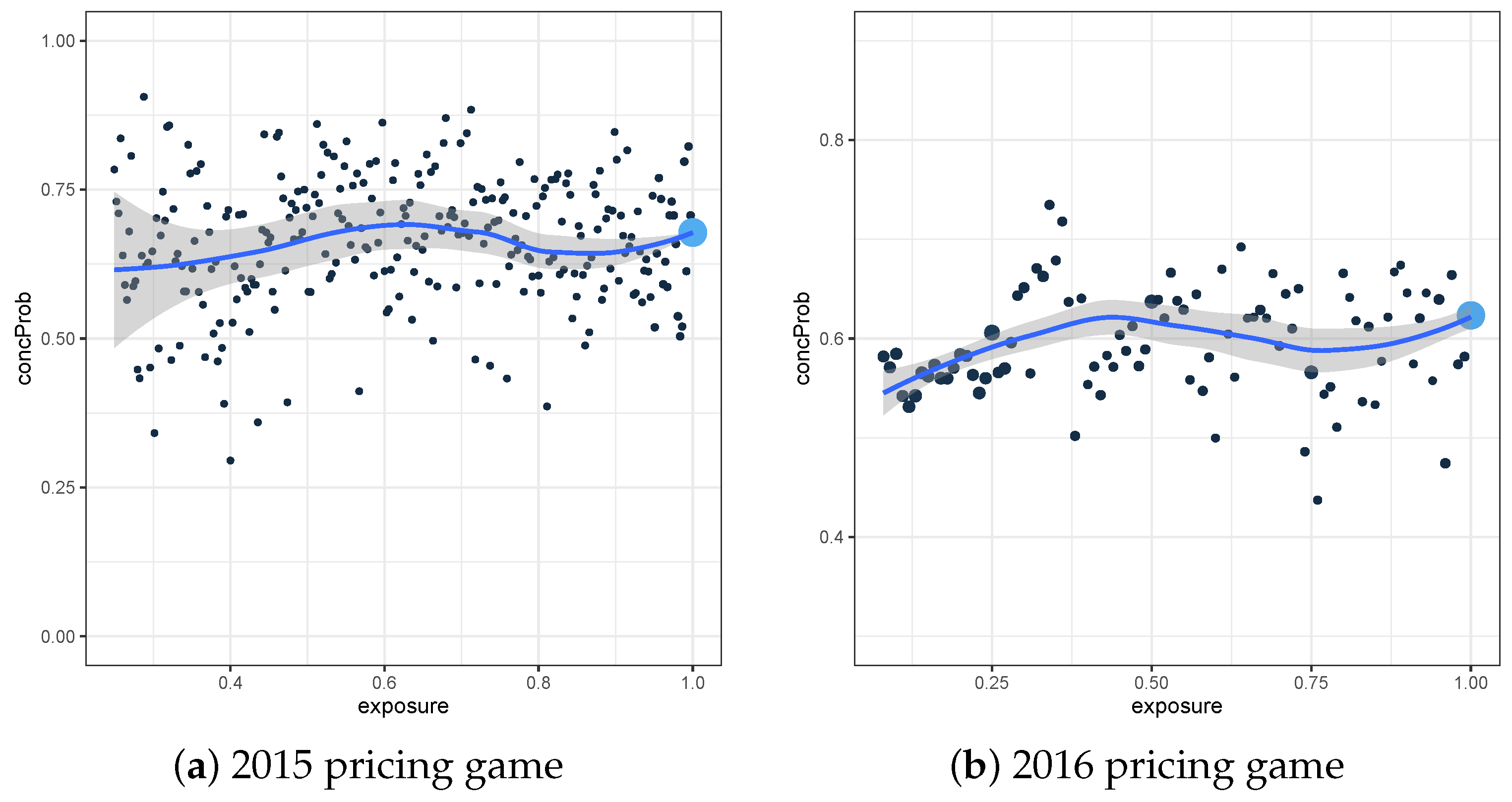
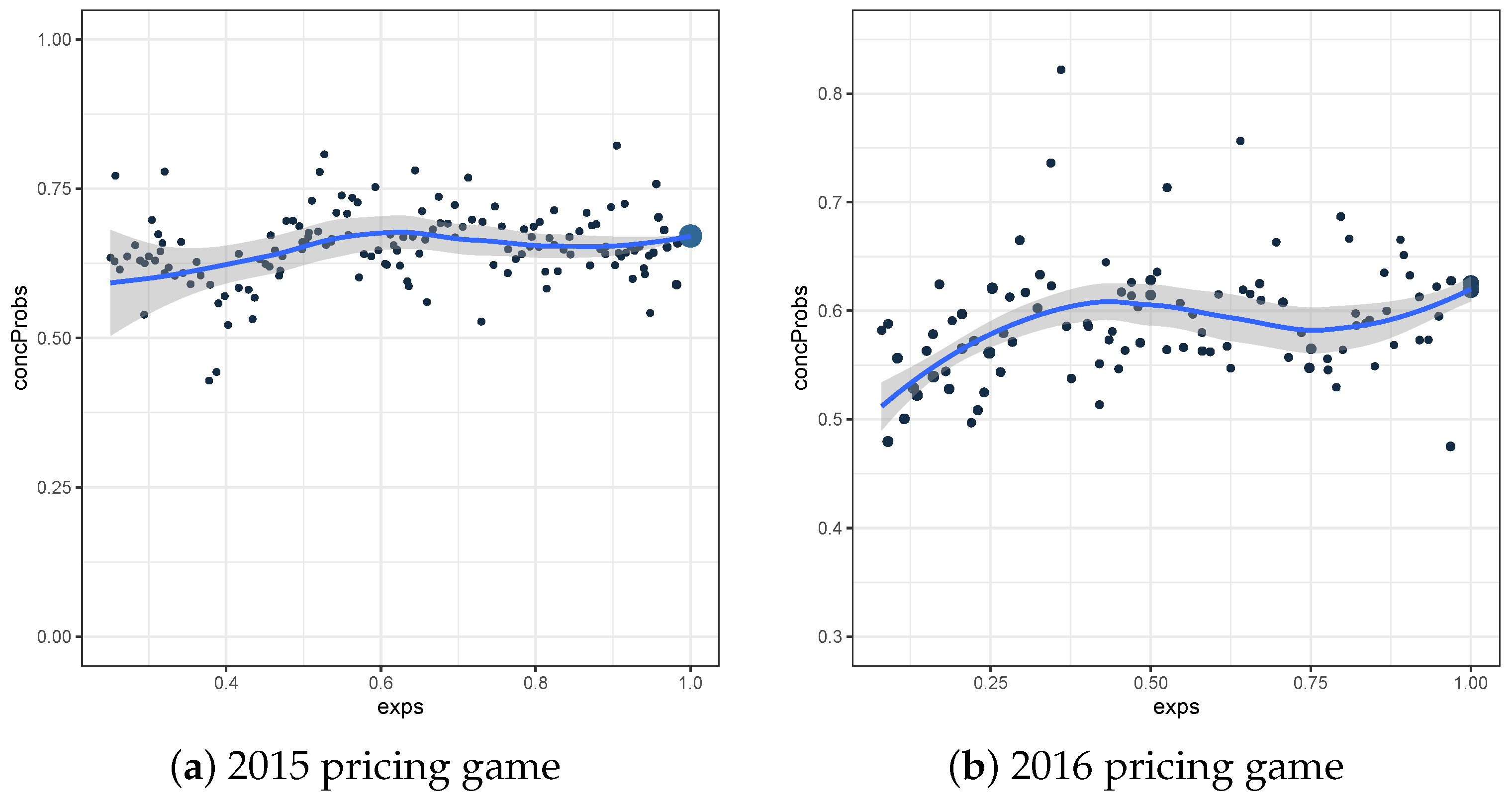
A solution to the lack of interpretability of both local plots (fine and rough grid), is to consider a weighted mean of them, with the weights based on the number of comparable pairs. This weighted-mean-plot is constructed for both datasets and can be seen in
Figure 3. For the interpretability, it is important to see that the weighted-mean-plot is equivalent with applying the following two steps:
For every observation i, construct , with the exposure of the considered element.
For every considered exposure , determine the weighted mean of , where the weights are based on the total number of comparable pairs.
From
Figure 3b, we see that the basic Poisson model for the frequency model based on the dataset of the 2016 pricing game results in small concordance probabilities when considering observations with an exposure around 0.25 or 0.75. Hence, near these exposure values, the model has a hard time distinguishing the two considered groups.
3.2. Severity Models
The general definition (
2) of the concordance probability will in this section be modified to a concordance probability that can be used for severity models. Since it might be of little practical importance to distinguish claims from one another that only slightly differ in claim cost, the basic definition can be extended to a version introduced by
Van Oirbeek et al. (
2021):
where
. Furthermore,
refers to the predicted claim size of the severity model and
to the observed claim size. In other words, the claims that are to be considered are those of which the claim size has a difference of at least a value
. Hereby, pairs of claims that makes more sense from a business point of view are selected. Also, a (
,
) plot can be constructed where different values for the threshold
are chosen, as to investigate the influence of
on (
8). Interestingly,
corresponds to a global version of the concordance probability (as expressed by definition (
2)), while any value of
results in a more local version of the concordance probability.
Focusing on the datasets introduced in
Section 2, we determine the value of
such that
x% of the pairwise absolute differences of the observed values is smaller than
, with
. Note that
equal to zero is not a popular choice in business, since they are not interested in comparing claims that are nearly identical. The size of the considered test sets still allow to consider all possible pairs between the observations in order to determine the absolute differences between observations belonging to the same pair. However, this is no longer the case for the bootstrapped versions, since this would result in 499,999,500,000 pairs and corresponding differences. Since the observations are all sampled from the original test sets, we know that the number of unique values is much lower than 1,000,000. Hence, we can use the technique discussed in
Van Oirbeek et al. (
2021), resulting in a fast calculation of the values of
represented in
Table 1. As can be seen, the difference between the values for
determined on the original test set or on the bootstrapped dataset is very small. Therefore, we will from here on only focus on the bootstrapped versions of the test sets.