Discrete-Time Risk Models with Claim Correlated Premiums in a Markovian Environment

Abstract

In this paper we consider a discrete-time risk model, which allows the premium to be adjusted according to claims experience. This model is inspired by the well-known bonus-malus system in the non-life insurance industry. Two strategies of adjusting periodic premiums are considered: aggregate claims or claim frequency. Recursive formulae are derived to compute the finite-time ruin probabilities, and Lundberg-type upper bounds are also derived to evaluate the ultimate-time ruin probabilities. In addition, we extend the risk model by considering an external Markovian environment in which the claims distributions are governed by an external Markov process so that the periodic premium adjustments vary when the external environment state changes. We then study the joint distribution of premium level and environment state at ruin given ruin occurs. Two numerical examples are provided at the end of this paper to illustrate the impact of the initial external environment state, the initial premium level and the initial surplus on the ruin probability.

1. Introduction

The commonly adopted bonus-malus system in the general insurance industry is based on a principal that insurance premiums can be adjusted based on the historical claims record of individual policyholders. To be specific, the policyholders, who make no claim or small claims in the latest policy year, will be offered a premium discount (also called ‘bonus’) on renewal. On the other hand, policyholders who make more claims than the given thresholds in the current policy year may need to pay higher premiums (also called ‘malus’) if they decide to renew their policies. The bonus-malus system plays an important role in the insurance industry, in particular in motor vehicle insurance sector, because this system defines risk specific premium levels that help to sustain the total premium pool in covering all motor insurance claims of the given insurance portfolio. The discount in premium acts as an incentive to retain low-risk policyholders and to attract new customers; on the other hand, the malus component prevents high-risk policyholders from taking advantage of the low-risk policyholders by receiving disproportionate insurance benefits. The purpose of the bonus-malus system is to create heterogeneity by low-risk policyholders and high-risk policyholders. In other words, it acts as a posteriori classifier that differentiates the policyholders according to their driving behaviours besides the a priori variables. In addition, in terms of commercial purpose, the bonus-malus system is widely adopted in pricing by motor vehicle insurance companies to enhance their competitiveness in the insurance market.

The bonus-malus system related problems have remained a popular research field for decades. De Pril (1979) proposed a continuous-time model for the bonus-malus system, which considers the phenomenon called ‘bonus-hunger’. Lemaire and Zi (1994) conducted a comparative analysis of 30 bonus-malus systems of 22 countries, and Lemaire (1995) provided insurance companies models to design their own bonus-malus systems that meet their objectives. Pinquet et al. (2001) considered the age of claims in their proposed model for the bonus-malus system. Baione et al. (2002) proposed the optimal bonus-malus system, which maximised the ‘transparency’ between policyholders and insurers and ‘financial balance conditions’. Pitrebois et al. (2006) designed a bonus-malus system with different types of claims. Dionne and Ghali (2005) conducted an empirical evaluation of the 1992 bonus-malus system in Tunisia. More recently, Denuit et al. (2019) considered multivariate credibility modelling for usage-based motor insurance pricing with behavioural data, Vilar-Zanon et al. (2020) discussed an average model approach to experience based premium rates discounts using the Spanish agricultural insurance data, and Ágoston and Gyetvai (2020) studied a joint optimisation problem of transition rules and the premium scale in a bonus-malus system. A lot more research work can be found in the references therein.

The bonus-malus system has also been studied by many researchers in the context of risk models with claim-dependent premiums. As for the continuous-time setting, Afonso et al. (2009) studied the finite-time ruin probabilities in a continuous- time risk model that allows the premiums to be adjusted according to historical surplus levels. Li et al. (2015) studied the ruin probabilities under a continuous-time risk model with premium rate adjusted to the historical number of claims. Specifically, they applied the Bayesian credibility theory to find the posteriori expected number of claims and then adjusted the premium rate according to the posteriori estimator of claim numbers. They studied the impact of the two risks classified by ‘defectiveness’, i.e., the ‘historical’ stream and the ‘unforeseeable’ stream, on ruin probabilities. Constantinescu et al. (2016) studied the ruin probability in a regenerative risk process. They assume that the inter-arrival times of the process depend on the inter-arrival time between the current and previous claim. In other words, the distribution of the next claim waiting time depends on the waiting time between the current claim and the previous one. This assumption allows the premium rate to be adjusted according to the change of the inter-arrival time distribution. However, only two levels of premium rates are evaluated in their model: the bonus (discount) state and the base state. Moreover, Kučerovský and Najafabadi (2017) studied the continuous-time risk model for a long term bonus-malus system in a steady state. They obtained the ruin probability in terms of closed-form solutions of an integral equation by the method of complex analysis. In addition, Afonso et al. (2017) analysed the impact of the different well-known bonus-malus scales and transition rules on the finite-time ruin probability in a continuous-time risk model. The posteriori premiums in their model are modified according to the historical claim record of each individual policyholder. In the most recent literature, Afonso et al. (2020) studied ruin probabilities and capital requirement for open automobile portfolios with a bonus-malus system based on claim counts.

Under the discrete-time setting, Dufresne (1988) proposed the recursive algorithm to compute the ruin probabilities by using the stationary distributions of the bonus-malus system. Wagner (2002) considered a two-state Markov chain risk model and derived recursive formulae for ruin probabilities. Trufin and Loisel (2013) studied the ruin probabilities with premiums adjusted to the claims by Bühlmann credibility theory. They derived the asymptotic formulae for the ultimate ruin probabilities and the Lundberg coefficients for the light-tailed claims. In addition, they also derived the asymptotic formulae for the ultimate ruin probabilities for heavy-tailed claims. Further, Wu et al. (2015) derived recursive formulae and explicit formulae for the ultimate ruin probabilities in the case that premiums are correlated to claim amounts by using the two-state Markov Chain model.

First of all, this paper is an extension of the models of Wu et al. (2015). As for the models of Wu et al. (2015), there are some strong assumptions regarding claim amounts and premiums. For example, the claims were assumed to take only three integer values and the differences between claims amount and premiums must be multiples of the lowest premium level. In addition, there are only three premium levels in their models. Taking into account these limitations, this paper aims to relax the strict assumptions such that the individual claims can take any non-negative integer values and the premiums vary according to claims record in a broader bonus-malus context. Recursive equations are derived to calculate the finite-time ruin probabilities in the discrete-time setting. A similar approach was adopted in (Cai and Dickson (2004), sct. 2). In addition to considering premium adjustments according to aggregate claim amounts, this paper also considers the option of adjusting premiums based on recorded claim numbers, whereas Wu et al. (2015) only focused on the former case.

Secondly, this paper combines inhomogeneity in claims experience with the bonus-malus system by introducing an external Markovian environment, which could see more applications in the real world. This is inspired by the fact that the external environment can affect the implementation of the bonus-malus system and should be taken into account by the insurers. As being said in Niemiec (2017), the external environment can affect the claim frequency and the bonus-malus system should be evaluated according to this factor. The term ‘external environment’ in this context means the factor that the insurers are not able to control but have an impact on the performance of the bonus-malus system. It can include economic conditions, weather conditions, regulations, competitiveness of competitors and so on. The topics about a bonus-malus system within an external environment have been studied by various researchers in the literature. For example, Viswanathan and Lemaire (2005) used a diffusion theory to study the evolution of market shares and claim frequencies of a two-company market when one insurance company applies the aggressive bonus-malus system. Park et al. (2010) used principal components analysis and regression models to evaluate the toughness of the bonus-malus system in Asia and its correlation with economic and cultural variables. Lee and Kim (2016) studied the impact of the change in a regulation of the bonus-malus system in Korea on moral hazard in motor vehicle insurance. Vilar-Zanon et al. (2020) introduced the new experience rating system, which is more suitable to the agricultural insurance in Spain and some other EU countries when high losses occur due to extreme weather. As for the studies of the risk of ruin within a Markovian environment, the most recent literature of Markov-modulated risk models includes Nie et al. (2020) and Li and Li (2020). In the former paper, the authors studied a discrete Markov-modulated risk model with delayed claims, random premium income, and a constant dividend barrier; whilst in the latter one, the authors studied some state-specific one-sided exit probabilities as well as the corresponding two-sided first exit probabilities in a Markov-modulated risk process.

In this paper, we only focus on external environments that affect the implementation of the bonus-malus system in terms of varying the aggregate claims distribution such as economic environment and weather conditions. Regarding our proposed premium adjustment rules, we assume that the external environment is governed by an external Markov process. When the policies are renewed, the insurers will apply certain premium correction rules that correspond to the current external environment condition to determine the renewal premiums. As for a real-world application, it is not an issue in practice due to the short-term nature of most non-life insurance contracts. It means that the insurers are able to frequently modify the premium adjustment rules when the external environment changes. By applying this principle, it helps the insurers to better address the systematic risk when implementing the bonus-malus system in pricing. However, it can be tricky when insurers explain the environment-dependent premium changing rules to their policyholders since the rules are likely to change over time.

The main goal of this paper is to numerically evaluate the impact of bonus-malus system on the ruin probabilities of the proposed risk models within an external Markovian environment. We aim to explore the following questions that may arise when implementing the bonus-malus system in practice through some numerical studies based on hypothetical assumptions:

-

What should the initial premium level be for new policyholders?

-

Which premium adjustment criterion is better in the proposed risk models: premiums adjusted by aggregate claims amount or premiums adjusted by claim frequency only?

-

What is the likely impact of the initial external environment condition on the risk of ruin when the proposed premium adjustment rules are implemented?

The main findings of our numerical studies are:

-

The choice of initial premium level for new policyholders is not an easy task. A low initial premium level tends to be very risky when the company’s initial capital amount is small. However, when the initial capital amount is sufficiently large, the insurer has more flexibility to lower the initial premium level that can attract more new policyholders and help with boosting the insurance business without significantly increasing the risk of insolvency.

-

The initial external environment condition does have a significant impact on the risk of ruin under the proposed premium adjustment rules, but the impact could be different from our first guess.

-

Adjusting premiums according to claim frequency can be riskier than the case of adjusting premiums by aggregate claims.

This paper is organised as follows. Section 2 presents the models and assumptions of our study. Section 3 presents the finite-time ruin probabilities in a Markovian environment. Section 4 presents Lundberg inequalities for ruin probabilities. Section 5 presents the joint distribution of time of ruin, deficit, premium level and environment state at ruin. Section 6 provides some numerical studies with detailed comments. Concluding remarks and future research are given in Section 7.

2. Models and Assumptions

Let c denote a premium level set where $\mathbf{c}={\left\{c_i\right\}}_{i\in \mathcal{𝓛}}$, $\mathcal{𝓛}=\{1,2,\dots ,l\}$, $l\in {\mathbb{N}}^{+}$, $c_i\in {\mathbb{R}}^{+}$. Here $c_i$, $i=1,\dots ,l$, are premium levels per unit volume of risk. Let the external economic environmental status in time period $[t-1,t)$, $t\in {\mathbb{N}}^{+}$ be represented by a homogeneous and irreducible discrete-time Markov chain ${\left\{J_t\right\}}_{t\in \mathbb{N}}$ with a finite state space $\mathbf{R}=\{1,2,\dots ,r\}$ and a transition probability matrix $P_J={\left[p_J(g,h)\right]}_{g,h\in \mathbf{R}}$, where $p_J(g,h)=\mathbb{P}(J_t=h|J_{t-1}=g)$. The stationary probability distribution of the Markov process is denoted by $\mathit{\lambda }=[{\lambda }_1,\dots ,{\lambda }_r]$ where $0\le {\lambda }_i\le 1,i=1,2,\dots ,r$, and ${\sum }_{i=1}^r{\lambda }_i=1$. Let ${\left\{L_t\right\}}_{t\in {\mathbb{N}}^{+}}$ be a stochastic process monitoring the premium levels that the insurance company charges over time. Here $L_t\in \mathbf{c}$ for any $t\in {\mathbb{N}}^{+}$ and this premium level applies in the time period $[t-1,t)$.

Consider a general insurance surplus process of which the level of surplus at time k, $k=0,1,\dots ,$ is defined by

$$\begin{array}{c}\hfill U_k=U_0+\sum _{t=1}^k(C_t-S_t),\mathrm{for}k\in {\mathbb{N}}^{+},\end{array}$$

(1)

where $S_t$ is the aggregate claims amount for time period $[t-1,t)$ payable at time t, $t\in {\mathbb{N}}^{+}$; $U_0=u\ge 0$, $u\in \mathbb{N}$ is the initial surplus level; $C_t$ is the total premium for time period $[t-1,t)$ received at time $t-1$ and $C_t=L_{t}E\left[S_t\right]$, $t\in {\mathbb{N}}^{+}$. Further, $S_t$ has probability mass function (P.M.F.) ${\mathbb{P}}_{S,J_t}\left(s\right)$ and mean ${\mu }_{S,J_t}$, for $J_t\in \mathbf{R}$ and $s\in \mathbb{N}$.

The timing of all cash flows involved in the above insurance surplus process is illustrated through the following timeline given in Figure 1 where year t denotes the period of $[t-1,t)$, $t\in {\mathbb{N}}^{+}$.

Given $L_1=c_i$ and $J_1=g$, $i\in \mathcal{𝓛}$, $g\in \mathbf{R}$, the first premium amount $C_1$ can be determined as follows

$$C_1=c_{i}E\left[S_1\right]=c_i{\mu }_{S,g}:={\alpha }_{i,g}.$$

(2)

According to (2), theoretically ${\alpha }_{i,g}$ can be a non-integer value. However, an integer-valued ${\alpha }_{i,g}$ is required for the computation of numerical results. There are two feasible ways to convert non-integer ${\alpha }_{i,g}$ to an integer. Firstly, certain scaling-up can be applied to make sure that ${\alpha }_{i,g}$ for all $i\in \mathcal{𝓛}$ and $g\in \mathbf{R}$ are integer-valued. However, this method may heavily increase the required computational time if the multiplier is a large number. Another way is to round each of ${\alpha }_{i,g}$ to its nearest integer, but this method potentially reduces the level of accuracy in the computations. This negative impact might be minimal when considering large insurance portfolios. We remark that in this paper, we always assume that the parameters are integer-valued when necessary. In addition, all variables in our models are assumed to be integers to suit the derivations of the main recursive formulae in this paper. Non-integer valued parameters are not feasible in the recursive computational framework.

The n-period finite-time ruin probability with initial surplus u, initial environment state g and initial premium level $c_i$ is defined by, $n\in {\mathbb{N}}^{+}$,

$$\begin{array}{c}\hfill {\psi }_{i,g}(u,n)={\mathbb{P}}_u\left\{\bigcup _{k=1}^n(U_k<0)|L_1=c_i,J_1=g\right\},\end{array}$$

(3)

where $U_k$ is defined by (1) and the subscript u represents the condition $U_0=u$. By convention, for any $i\in \mathcal{𝓛}$ and $g\in \mathbf{R}$,

$${\psi }_{i,g}(u,n)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}u\ge 0,n\le 0,\hfill \\ 1\hfill & \mathrm{if}u<0,n\ge 0.\hfill \end{array}\right.$$

Further, we assume that the aggregate claim amounts $S_t$, $t\in {\mathbb{N}}^{+}$, are non-negative integer-valued random variables that follow a collective risk model structure:

$$\begin{array}{c}\hfill S_t=\sum _{i=1}^{M_t}{W}_{it},\end{array}$$

(4)

where $M_t$ is the total number of claims recorded in time period $[t-1,t)$, $t\in {\mathbb{N}}^{+}$, with P.M.F. ${\mathbb{P}}_{M,J_t}\left(m\right)$ for $J_t\in \mathbf{R}$ and $m\in \mathbb{N}$; ${\left\{W_{it}\right\}}_{i\in {\mathbb{N}}^{+}}$, are individual claim sizes settled in time period $[t-1,t)$. For the purpose of simplification, conditional on $J_t$, we assume that ${\left\{W_{it}\right\}}_{i\in {\mathbb{N}}^{+}}$ are independent and identically distributed (i.i.d.) with common P.M.F. ${\mathbb{P}}_{W,J_t}\left(w\right)$, $w\in {\mathbb{N}}^{+}$ and $J_t\in \mathbf{R}$. The claims number $\left\{M_t\right\}$ and individual claim sizes $\left\{W_{it}\right\}$ are assumed to be independent of each other given $J_t$.

For simplicity, we will use the symbol $f_{g,m}$ to denote ${\mathbb{P}}_{M,g}\left(m\right)$ within the rest of this paper. One can show that, for $s\in \mathbb{N}$,

$${\displaystyle {\mathbb{P}}_{S,g}\left(s\right)=\sum _{m=0}^s{f}_{g,m}{\mathbb{P}}_{W,g}^{*m}\left(s\right)}$$

with ${\mathbb{P}}_{W,g}^{*m}\left(s\right)$ being the m-fold convolution of ${\mathbb{P}}_{W,g}\left(w\right)$ and ${\mathbb{P}}_{W,g}^{*0}\left(0\right)=1$.

2.1. Premiums Adjusted by Aggregate Claims

As introduced previously, this paper aims to consider a general bonus-malus premium system in a discrete-time setting. Let ${\left\{t_{ij}(s,g)\right\}}_{i,j\in \mathcal{𝓛};s\in \mathbb{N};g\in \mathbf{R}}$ denote a general set of time-homogeneous rules for premium variations, where $t_{ij}(s,g)=1$ if the aggregate claim $S_t=s$ and environment state $L_t=g$ lead to the transition from the premium level $L_t=i$ to $L_{t+1}=j$ and $t_{ij}(s,g)=0$ otherwise. According to the definition, we have ${\sum }_{j=1}^l{t}_{ij}(s,g)=1$ for any $i\in \mathcal{𝓛},g\in \mathbf{R},s\in \mathbb{N}$. Let $p_{C,g,h}(i,j)$ denote the probability that the premium level moves from level i in initial environment state g to level j in environment state h, which can be expressed as, for any $t\in {\mathbb{N}}^{+}$,

$$\begin{array}{ccc}\hfill p_{C,g,h}(i,j)& =& \mathbb{P}\{L_{t+1}=j,J_{t+1}=h|L_t=i,J_t=g\}\hfill \\ & =& p_J(g,h)\sum _{s=0}^{\infty }{t}_{ij}(s,g){\mathbb{P}}_{S,g}\left(s\right),\mathrm{for}i,j\in \mathcal{𝓛},g,h\in \mathbf{R},\hfill \end{array}$$

(5)

where ${\mathbb{P}}_{S,g}\left(s\right)$, $s\in \mathbb{N}$, is the P.M.F. of aggregate claims in the environment state h with mean ${\mu }_{S,h}$. The function $t_{ij}(s,g)$ is determined according to the given transition rule. From the definition of $p_{C,g,h}(i,j)$, considering a state space of ${\left\{(i,g)\right\}}_{i\in \mathcal{𝓛},g\in \mathbf{R}}$, its one-step transition probability matrix has the form

$$\begin{array}{ccc}\hfill P_C& =& \left[p_{C,g,h}(i,j)\right]{}_{(l\times r)\times (l\times r)}\hfill \\ & =& \left[\begin{array}{ccccccc}{p}_{C,1,1}(1,1)& \cdots & p_{C,1,1}(1,l)& \cdots & p_{C,1,r}(1,1)& \cdots & p_{C,1,r}(1,l)\\ ⋮& \ddots & ⋮& & ⋮& \ddots & ⋮\\ p_{C,1,1}(l,1)& \cdots & p_{C,1,1}(l,l)& \cdots & p_{C,1,r}(l,1)& \cdots & p_{C,1,r}(l,l)\\ ⋮& & ⋮& & ⋮& & ⋮\\ p_{C,r,1}(1,1)& \cdots & p_{C,r,1}(1,l)& \cdots & p_{C,r,r}(1,1)& \cdots & p_{C,r,r}(1,l)\\ ⋮& \ddots & ⋮& & ⋮& \ddots & ⋮\\ p_{C,r,1}(l,1)& \cdots & p_{C,r,1}(l,l)& \cdots & p_{C,r,r}(l,1)& \cdots & p_{C,r,r}(l,l)\end{array}\right].\hfill \end{array}$$

(6)

Note that the above matrix is constructed based on the combined statuses of pairs of premium level and environment state, which is a generalised version of the usual transition matrix for individual premium levels or transition matrix for individual environment states. The associated stationary probability distribution of $P_{C,g,h}$ is denoted by $\mathbf{\pi }={\left[{\pi }_{ig}\right]}_{l\times r}$, for $i\in \mathcal{𝓛}$ and $g\in \mathbf{R}$. From (5) we have, for $j\in \mathcal{𝓛},h\in \mathbf{R}$,

$$\begin{array}{ccc}\hfill {\pi }_{jh}& =& \sum _{i=1}^l\sum _{g=1}^r{\pi }_{ig}{p}_{C,g,h}(i,j)\hfill \\ & =& \sum _{i=1}^l\sum _{g=1}^r{\pi }_{ig}{p}_J(g,h)\sum _{s=0}^{\infty }{t}_{ij}(s,g){\mathbb{P}}_{s,g}\left(s\right).\hfill \end{array}$$

Following a common practice, we would also assume that the surplus process (1) satisfies the positive safety loading conditions, for any $i\in \mathcal{𝓛},g\in \mathbf{R}$,

$${\alpha }_{ig}>{\mu }_{S,g}.$$

Remark 1.

The above positive safety loading condition assumption is more conservative than it usually appears in the Markov modulated risk model literature, because it needs to be in such form to enable the generalised Lundberg inequalities discussed in Section 4.

2.2. Premiums Adjusted by Claim Frequency

When periodic premiums adjust according to the claim frequency experience rather than the aggregate claim amounts, the transition probability $p_{C,g,h(i,j)}$ in (5) needs to be modified as

$$\begin{array}{c}\hfill p_{C,g,h}(i,j)=p_J(g,h)\sum _{m=0}^{\infty }{t}_{ij}(m,g)f_{g,m},\mathrm{for}i,j\in \mathcal{𝓛}\mathrm{and}g,h\in \mathbf{R},\end{array}$$

(7)

where $f_{g,m}$, for $m\in \mathbb{N}$, is the P.M.F. of the claims number in the environment state g.

3. Finite-Time Ruin Probabilities

In this section, we shall derive recursive formulae to compute the finite-time ruin probabilities that are defined by (3). We consider the two options of varying premiums separately.

3.1. Premiums Adjusted by Aggregate Claims

According to the assumptions in Section 2.1, the n-period finite-time ruin probability ${\psi }_{i,g}(u,n)$, satisfies the following recursive formula.

Theorem 1.

For $u\ge 0$, $n\in {\mathbb{N}}^{+}$, $i\in \mathcal{𝓛}$ and $g\in \mathbf{R}$,

$$\begin{array}{ccc}\hfill {\psi }_{i,g}(u,n+1)& =& \sum _{h=1}^r{p}_J(g,h)\sum _{j=1}^l\sum _{s=0}^{u+{\alpha }_{i,g}}{t}_{ij}(s,g){\psi }_{j,h}(u+{\alpha }_{i,g}-s,n){\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & & +\sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)\hfill \end{array}$$

(8)

with ${\psi }_{i,g}(u,1)={\sum }_{s=u+{\alpha }_{i,g}+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right).$

Proof of Theorem 1.

From (3), we have

$$\begin{array}{ccc}& & {\psi }_{i,g}(u,n+1)={\mathbb{P}}_u\left\{\bigcup _{k=1}^{n+1}(U_k<0)|L_1=c_i,J_1=g\right\}\hfill \\ & =& \sum _{s=0}^{u+{\alpha }_{i,g}}{\mathbb{P}}_u\left\{\bigcup _{k=1}^{n+1}(U_k<0)|L_1=c_i,J_1=g,S_1=s\right\}{\mathbb{P}}_{S,g}\left(s\right)+\sum _{s=u+c_i{\mu }_{S,h}+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & =& \sum _{j=1}^l\sum _{s=0}^{u+{\alpha }_{i,g}}{t}_{ij}(s,g){\mathbb{P}}_{u+{\alpha }_{i,g}-s}\left\{\bigcup _{k=2}^{n+1}(U_k<0)|L_2=c_j,J_1=g\right\}{\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & & +\sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & =& \sum _{h=1}^r{p}_J(g,h)\sum _{j=1}^l\sum _{s=0}^{u+{\alpha }_{i,g}}{t}_{ij}(s,g){\mathbb{P}}_{u+{\alpha }_{i,g}-s}\left\{\bigcup _{k=2}^{n+1}(U_k<0)|L_2=c_j,J_2=h\right\}{\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & & +\sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & =& \sum _{h=1}^r{p}_J(g,h)\sum _{j=1}^l\sum _{s=0}^{u+{\alpha }_{i,g}}{t}_{ij}(s,g){\psi }_{j,h}(u+{\alpha }_{i,g}-s,n){\mathbb{P}}_{S,g}\left(s\right)+\sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right).\hfill \end{array}$$

Since ${\psi }_{i,g}(u,1)$ only measures the probability of ruin of the business within one time period, the verification of the given boundary condition is trivial. □

3.2. Premiums Adjusted by Claim Frequency

For this section, we change the transition rule for premium adjustment from considering the aggregate claims to number of claims. According to the assumptions in Section 2.2, the n-period-finite-time ruin probability with premiums adjusted according to claims numbers, initial premium level i and initial environment state g satisfies the following the recursive formulae.

Theorem 2.

For $u\ge 0$, $n\in {\mathbb{N}}^{+}$, $i\in \mathcal{𝓛}$ and $g\in \mathbf{R}$,

$$\begin{array}{ccc}\hfill {\psi }_{i,g}(u,n+1)& =& \sum _{h=1}^r{p}_J(g,h)\sum _{j=1}^l\sum _{m=0}^{u+{\alpha }_{i,g}}{f}_{g,m}{t}_{ij}(m,g)\sum _{s=m}^{u+{\alpha }_{i,g}}{\mathbb{P}}_{W,g}^{*m}\left(s\right){\psi }_{j,h}(u+{\alpha }_{i,g}-s,n)\hfill \\ & & +\sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)\hfill \end{array}$$

(9)

with ${\displaystyle {\psi }_{i,g}(u,1)=\sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)}$.

Proof of Theorem 2.

Since the proof of Theorem 2 is largely similar to the proof of Theorem 1, we omit the details here. Its full proof can be found in Appendix A. □

4. Lundberg Inequalities for Ruin Probabilities

In previous sections, we studied the finite-time ruin probabilities, which reflect the risk of ruin for insurers within finite terms. However, in practice, insurers and insurance regulators also concern about the risk of ruin in the long term, where ultimate ruin probabilities are the appropriate measurement instead of the finite-time ones. The ultimate ruin probabilities can be defined by letting $n=\infty$ in (3), which is denoted by ${\psi }_{i,g}\left(u\right)$, $i\in \mathcal{𝓛}$ and $g\in \mathbf{R}$. Due to the general settings of premium changing rules and aggregate claim distributions, neither explicit results nor recursive formulae for the ultimate ruin probabilities can be obtained easily. How to extend our finite-time ruin probability recursive formulae to the infinite-time context remains an open problem for the future.

Instead of calculating the ultimate ruin probabilities directly, we would derive some upper bounds for them in this section. It is inspired by the Lundberg inequality result in the classical risk model. Some Lundberg-type upper bounds, named as generalised Lundberg inequalities, are obtained with the induction method in both cases of premium variations. A similar approach was used in Cai and Dickson (2004). To calculate the generalised Lundberg inequalities, the stationary distribution $\mathbf{\pi }$ defined in Section 2.1 is needed, which represents the long-term probabilities of premium levels and environment states.

We consider the case of premiums adjusted by aggregate claims first. Following the classical risk model Lundberg inequality approach, to derive an upper bound for the ultimate-time ruin probabilities, we need to find the corresponding adjustment coefficient for our generalised risk model first. Let ${\gamma }_{i,g}>0$, $i\in \mathcal{𝓛},g\in \mathbf{R}$, be constants satisfying the following equation,

$$e^{-{\gamma }_{i,g}{\alpha }_{i,g}}\mathbb{E}\left[e^{{\gamma }_{i,g}{S}_1}|J_1=g\right]=1.$$

(10)

Then $\gamma =\underset{i\in \mathcal{𝓛};g\in \mathbf{R}}{inf}\left\{{\gamma }_{i,g}\right\}$ is a generalised adjustment coefficient. It can be shown that, by the log-convexity property of the moment generating functions, for any $i\in \mathcal{𝓛},g\in \mathbf{R}$,

$$e^{-\gamma {\alpha }_{i,g}}\mathbb{E}\left[e^{\gamma S_1}|J_1=g\right]\le 1.$$

(11)

We can obtain the following main result:

Theorem 3.

Let $\gamma >0$ be the generalised adjustment coefficient defined above, then for any $i\in \mathcal{𝓛},g\in \mathbf{R}$,

$$\begin{array}{c}\hfill {\psi }_{i,g}\left(u\right)\le \beta e^{-\gamma u},\end{array}$$

(12)

where ${\displaystyle \beta =\underset{t\ge 0;g\in \mathbf{R}}{sup}\frac{e^{\gamma t}{\sum }_{s=t+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)}{{\sum }_{s=t+1}^{\infty }{e}^{\gamma s}{\mathbb{P}}_{S,g}\left(s\right)}}$.

Proof of Theorem 3.

Firstly, we need to prove by induction that for any $n>0$, ${\psi }_{i,g}(u,n)\le \beta e^{-\gamma u}.$

When $n=1$, we have, for $i\in \mathcal{𝓛},g\in \mathbf{R}$,

$$\begin{array}{ccc}\hfill & & {\psi }_{i,g}(u,1)=\sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & =& e^{-\gamma (u+{\alpha }_{i,g})}\sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{e}^{\gamma s}{\mathbb{P}}_{S,g}\left(s\right)\left[\frac{e^{\gamma (u+{\alpha }_{i,g})}{\sum }_{t=u+{\alpha }_{i,g}+1}^{\infty }{\mathbb{P}}_{S,g}\left(t\right)}{{\sum }_{t=u+{\alpha }_{i,g}+1}^{\infty }{e}^{\gamma t}{\mathbb{P}}_{S,g}\left(t\right)}\right]\hfill \\ & \le & \beta e^{-\gamma (u+{\alpha }_{i,g})}\sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{e}^{\gamma s}{\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & \le & \beta e^{-\gamma u}{e}^{-\gamma {\alpha }_{i,g}}\mathbb{E}\left[e^{\gamma S_1}|J_1=g\right]\hfill \\ & \le & \beta e^{-\gamma u}.\hfill \end{array}$$

(13)

Assume the result holds true for the case of $n\ge 1$, i.e.,

$$\begin{array}{c}\hfill {\psi }_{i,g}(u,n)\le \beta e^{-\gamma u},i\in \mathcal{𝓛},g\in \mathbf{R}.\end{array}$$

We only need to show that it also holds for the case of $n+1$. From (8) and (13), we have

$$\begin{array}{ccc}\hfill {\psi }_{i,g}(u,n+1)& =& \sum _{h=1}^r{p}_J(g,h)\sum _{j=1}^l\sum _{s=0}^{u+{\alpha }_{i,g}}{t}_{ij}(s,g){\psi }_{j,h}(u+{\alpha }_{i,g}-s,n){\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & & +\sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & \le & \beta \sum _{s=0}^{u+{\alpha }_{i,g}}{e}^{-\gamma (u+{\alpha }_{i,g}-s)}\sum _{h=1}^r{p}_J(g,h)\sum _{j=1}^l{t}_{ij}(s,g){\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & & +\beta \sum _{s=u+{\alpha }_{i,g}+1}^{\infty }{e}^{-\gamma (u+{\alpha }_{i,g}-s)}{\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & =& \beta \sum _{s=0}^{\infty }{e}^{-\gamma (u+{\alpha }_{i,g}-s)}{\mathbb{P}}_{S,g}\left(s\right)\hfill \\ & =& \beta e^{-\gamma u}{e}^{-\gamma {\alpha }_{i,g}}\mathbb{E}\left[e^{\gamma S_1}|J_1=g\right]\hfill \\ & \le & \beta e^{-\gamma u}.\hfill \end{array}$$

By induction, we conclude that for any $n>0$,

$${\psi }_{i,g}(u,n)\le \beta e^{-\gamma u}.$$

Since ${\psi }_{i,g}\left(u\right)=\underset{n\to \infty }{lim}{\psi }_{i,g}(u,n)$, this upper bound also holds for ${\psi }_{i,g}\left(u\right)$. □

Remark 2.

From the similarity between the recursive formulae given in Theorems 1 and 2, one can see that the Lundberg inequality (12) also applies to the ultimate ruin probabilities in the case of premiums adjusted by claims frequency.

5. The Joint Distribution of Premium Level and Environment State at Ruin

In this section, given that ruin occurs, the joint distribution of the premium level and environment state at ruin is studied.

5.1. Premiums Adjusted by Aggregate Claims

Let $T_u=min\left\{k:U_k<0|U_0=u\right\}$ be the time of ruin with initial surplus u. Define

$${\chi }_{i,g}(u,n,j,h)={\mathbb{P}}_u\left\{T_u\le n,L_{T_u}=c_j,J_{T_u}=h|L_1=c_i,J_1=g\right\}$$

to be the probability that ruin occurs within the first n time periods with the premium level $c_j$ and the environment state h at ruin given the initial surplus u, initial premium level i and initial environment state g, where $u\ge 0$, $n\in {\mathbb{N}}^{+}$, $i,j\in \mathcal{𝓛}$ and $g,h\in \mathbf{R}$. Then, the joint probability of premium level $c_j$ and environment state h at ruin given that ruin occurs within the next n periods with initial surplus u, initial premium level $c_i$ and initial environment state g, denoted by ${\chi }_{i,g}^{\prime }(u,n,j,h)$, takes the form

$${\chi }_{i,g}^{\prime }(u,n,j,h)=\frac{{\chi }_{i,g}(u,n,j,h)}{{\psi }_{i,g}(u,n)},$$

where ${\psi }_{i,g}(u,n)$ can be computed using (8).

A trivial relationship between ${\chi }_{i,g}(u,n,j,h)$ and ${\psi }_{i,g}(u,n)$ is that, for $u\ge 0$, $n\in {\mathbb{N}}^{+}$, $i,j\in \mathcal{𝓛}$ and $g,h\in \mathbf{R}$,

$$\sum _{j=1}^l\sum _{h=1}^r{\chi }_{i,g}(u,n,j,h)={\psi }_{i,g}(u,n).$$

Parallel to Theorem 1, we can show that ${\chi }_{i,g}(u,n,j,h)$ satisfies the following recursive formula.

Theorem 4.

For $u\ge 0$, $n\in {\mathbb{N}}^{+}$, $i,j\in \mathcal{𝓛}$ and $g,h\in \mathbf{R}$,

$$\begin{array}{ccc}\hfill {\chi }_{i,g}(u,n+1,j,h)& =& \sum _{h^{\prime }=1}^r{p}_J(g,h^{\prime })\sum _{s=0}^{u+c_i}{\mathbb{P}}_{S,g}\left(s\right)\sum _{j^{\prime }=1}^l{t}_{i{j}^{\prime }}(s,g){\chi }_{j^{\prime },h^{\prime }}(u+c_i-s,n,j,h)\hfill \\ & & +{\mathbb{𝟙}}_{\{i=j\}}{\mathbb{𝟙}}_{\{g=h\}}\sum _{s=u+c_i+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right),\hfill \end{array}$$

(14)

where ${\chi }_{i,g}(u,1,j,h)={\mathbb{𝟙}}_{\{i=j\}}{\mathbb{𝟙}}_{\{g=h\}}{\sum }_{s=u+c_i+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)$.

Proof of Theorem 4.

Following the definition of ${\chi }_{i,g}(u,n,j,h)$, we have, for $u\ge 0$, $n\in {\mathbb{N}}^{+}$, $i,j\in \mathcal{𝓛}$ and $g,h\in \mathbf{R}$,

$$\begin{array}{ccc}& & {\chi }_{i,g}(u,n+1,j,h)\hfill \\ & =& {\mathbb{P}}_u\left\{T_u\le n+1,L_{T_u}=c_j,J_{T_u}=h|L_1=c_i,J_1=g\right\}\hfill \\ & =& \sum _{h^{\prime }=1}^r{p}_J(g,h^{\prime })\left[\sum _{s=0}^{u+c_i}{\mathbb{P}}_{S,g}\left(s\right)+\sum _{s=u+c_i+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)\right]\hfill \\ & & \times {\mathbb{P}}_u\left\{T_u\le n+1,L_{T_u}=c_j,J_{T_u}=h|L_1=c_i,J_2=h^{\prime },S_1=s\right\}\hfill \\ & =& {\mathbb{𝟙}}_{\{i=j\}}{\mathbb{𝟙}}_{\{g=h\}}\sum _{s=u+c_i+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)+\sum _{h^{\prime }=1}^r{p}_J(g,h^{\prime })\sum _{s=0}^{u+c_i}{\mathbb{P}}_{S,g}\left(s\right)\sum _{j^{\prime }=1}^l{t}_{i{j}^{\prime }}(s,g)\hfill \\ & & \times {\mathbb{P}}_u\left\{T_u\le n+1,L_{T_u}=c_j,J_{T_u}=h|L_2=c_{j^{\prime }},J_2=h^{\prime },S_1=s\right\}\hfill \\ & =& {\mathbb{𝟙}}_{\{i=j\}}{\mathbb{𝟙}}_{\{g=h\}}\sum _{s=u+c_i+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)+\sum _{h^{\prime }=1}^r{p}_J(g,h^{\prime })\sum _{s=0}^{u+c_i}{\mathbb{P}}_{S,g}\left(s\right)\sum _{j^{\prime }=1}^l{t}_{i{j}^{\prime }}(s,g)\hfill \\ & & \times {\mathbb{P}}_{u+c_i-s}\left\{T_{u+c_i-s}\le n,L_{T_{u+c_i-s}}=c_j,J_{T_{u+c_i-s}}=h|L_2=c_{j^{\prime }},J_2=h^{\prime }\right\}\hfill \\ & =& \sum _{h^{\prime }=1}^r{p}_J(g,h^{\prime })\sum _{s=0}^{u+c_i}{\mathbb{P}}_{S,g}\left(s\right)\sum _{j^{\prime }=1}^l{t}_{i{j}^{\prime }}(s,g){\chi }_{j^{\prime },h^{\prime }}(u+c_i-s,n,j,h)\hfill \\ & & +{\mathbb{𝟙}}_{\{i=j\}}{\mathbb{𝟙}}_{\{g=h\}}\sum _{s=u+c_i+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right).\hfill \end{array}$$

The verification of the boundary condition is trivial. □

5.2. Premiums Adjusted by Claim Frequency

The notations and definitions are same as the case of premiums adjusted according to aggregate claims. The corresponding ${\chi }_{i,g}^{\prime }(u,n,j,h)$ is also computed by $\frac{{\chi }_{i,g}(u,n,j,h)}{{\psi }_{i,g}(u,n)}$, where ${\psi }_{i,g}(u,n)$ is calculated by (9) and ${\chi }_{i,g}(u,n,j,h)$ satisfied the following recursive formulae.

Theorem 5.

For $u\ge 0$, $n\in {\mathbb{N}}^{+}$, $i,j\in \mathcal{𝓛}$ and $g,h\in \mathbf{R}$,

$$\begin{array}{ccc}\hfill {\chi }_{i,g}(u,n+1,j,h)& =& {\mathbb{𝟙}}_{\{i=j\}}{\mathbb{𝟙}}_{\{g=h\}}\sum _{s=u+c_i+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)+\sum _{h^{\prime }=1}^r{p}_J(g,h^{\prime })\sum _{m=0}^{u+c_i}{f}_{g,m}\sum _{s=m}^{u+c_i}{\mathbb{P}}_{W,g}^{*m}\left(s\right)\hfill \\ & & \times \sum _{j^{\prime }=1}^l{t}_{i{j}^{\prime }}(m,g){\chi }_{j^{\prime },h^{\prime }}(u+c_i-s,n,j,h),\hfill \end{array}$$

(15)

where ${\chi }_{i,g}(u,1,j,h)={\mathbb{𝟙}}_{\{i=j\}}{\mathbb{𝟙}}_{\{g=h\}}{\sum }_{s=u+c_i+1}^{\infty }{\mathbb{P}}_{S,g}\left(s\right)$.

Proof of Theorem 5.

Since the proof of Theorem 5 is largely similar to the proof of Theorem 4, we omit the details here. Its full proof can be found in Appendix B. □

6. Some Numerical Results

In this section we shall provide two numerical examples that represent the two varying premium cases discussed previously in this paper and the numerical results regarding the ruin probabilities are given with some concluding remarks.

6.1. An Example for Premiums Adjusted by Aggregate Claims

This example is designed for the case that premiums are adjusted according to aggregate claims. We assume that the economic state is fixed over a year from the beginning, and the economic state affects the aggregate claims distribution in the year. It implies that the yearly aggregate claims distribution changes whenever the economic state changes. The aggregate claims are assumed to be negative binomial distributed as follows:

• Economic state 1 (normal): mean $=10$, variance $=101.743$;
• Economic state 2 (deflation): mean $=5$, variance $=54.664$;
• Economic state 3 (inflation): mean $=15$, variance $=268.187$.

The one-step transition probability matrix of the economic state is

$$\begin{array}{ccc}\hfill P_J& =& {\left[p_J(g,h)\right]}_{g,h=1,2,3}=\left[\begin{array}{ccc}0.8& 0.1& 0.1\\ 0.3& 0.65& 0.05\\ 0.3& 0.05& 0.65\end{array}\right],\hfill \end{array}$$

with stationary distribution $\mathbf{\lambda }=[{\lambda }_1=0.6,{\lambda }_2=0.2,{\lambda }_3=0.2]$. The expected long-term aggregate claim amount is: $(0.6\times 10)+(0.2\times 5)+(0.2\times 15)=10$.

Suppose the set of premium loading is $\mathbf{c}=\{120\%,140\%,160\%,180\%,200\%\}$. The rules for adjusting the premiums are given as follows.

• If the recorded aggregate claims in the current period is no more than the 30th percentile of the aggregate claim distribution, then the premium level for the next period will move to the lower premium level or stay in the lowest one;
• If the recorded aggregate claims in the current period is more than the 30th percentile but no more than the 70th percentile of the aggregate claim distribution, then the premium level for the next period will remain in the current premium level;
• If the recorded aggregate claims in the current period is more than the 70th percentile of the aggregate claim distribution, then the premium level for the next period will move to the higher premium level or stay in the highest one.

Remark 3.

• The transition matrix of economic state given above is a hypothetical one. Different matrices will generate different sequences of premiums in the future. How to obtain a reliable estimate of such a transition matrix in real-life is beyond the scope of this study. Econometric studies could possibly provide answers to this question.
• The above set of premium rules is again a hypothetical one and is a much simplified version of the real-life bonus-malus rules. This helps to simplify the computational process and can sufficiently showcase our key results obtained in the main text before.
• The premium loadings given in c do not indicate the bonus or malus cases directly. Only when the initial premium level (or base level) is chosen, then we can tell whether a given premium level is a bonus (lower than base level) or a malus case (higher than base level).

According to the above transition rule, we can calculate the transition matrix among premium levels, i.e., $P_C=\left[p_{C,g,h}(i,j)\right]{}_{(l\times r)\times (l\times r)}$, defined in (6) in Appendix C. Using $P_C$, we can find the long-term stationary joint distribution of the premium levels and economics conditions:

$$\begin{array}{c}\hfill \mathbf{\pi }={\left[{\pi }_{ig}\right]}_{i\in \mathcal{𝓛},g\in \mathbf{R}}=\left[\begin{array}{ccccc}0.1270,& 0.1234,& 0.1199,& 0.1165,& 0.1132\\ 0.0421,& 0.0411,& 0.0400,& 0.0389,& 0.0379\\ 0.0424,& 0.0411,& 0.0400,& 0.0388,& 0.0377\end{array}\right].\end{array}$$

The expected long-term premium income calculated from $\mathbf{\pi }$ is 15.89 per time unit, which is roughly 60% greater than the expected long-term aggregate claim amount per time unit. Assuming the initial economic state is 1 (normal condition), using (8) we calculate the finite-time ruin probabilities ${\psi }_{i1}(u,40)$, $i=1,\dots ,5$, and the associated Lundberg upper bounds for the ultimate ruin probabilities ${\psi }_{ig}\left(u\right)$ can be found using (12). These results are summarised in

Table 1. ${\psi }_{i,1}(u,40)$ values with upper bounds (UB).

u	${\mathit{\psi }}_{1,1}(\mathit{u},40)$	${\mathit{\psi }}_{2,1}(\mathit{u},40)$	${\mathit{\psi }}_{3,1}(\mathit{u},40)$	${\mathit{\psi }}_{4,1}(\mathit{u},40)$	${\mathit{\psi }}_{5,1}(\mathit{u},40)$	UB
0	0.581516	0.485600	0.370290	0.278787	0.220787	0.982500
10	0.346148	0.268051	0.189482	0.135426	0.106381	0.823486
20	0.202262	0.147489	0.097952	0.067067	0.052281	0.690207
30	0.117224	0.081516	0.051458	0.034011	0.026317	0.578500
40	0.067836	0.045466	0.027558	0.017698	0.013597	0.484872
50	0.039369	0.025658	0.015062	0.009450	0.007212	0.406397
70	0.013508	0.008491	0.004769	0.002893	0.002181	0.285494
90	0.004775	0.002943	0.001609	0.000954	0.000713	0.200560
120	0.001052	0.000638	0.000340	0.000197	0.000146	0.118091
150	0.000240	0.000144	0.000075	0.000043	0.000031	0.069532
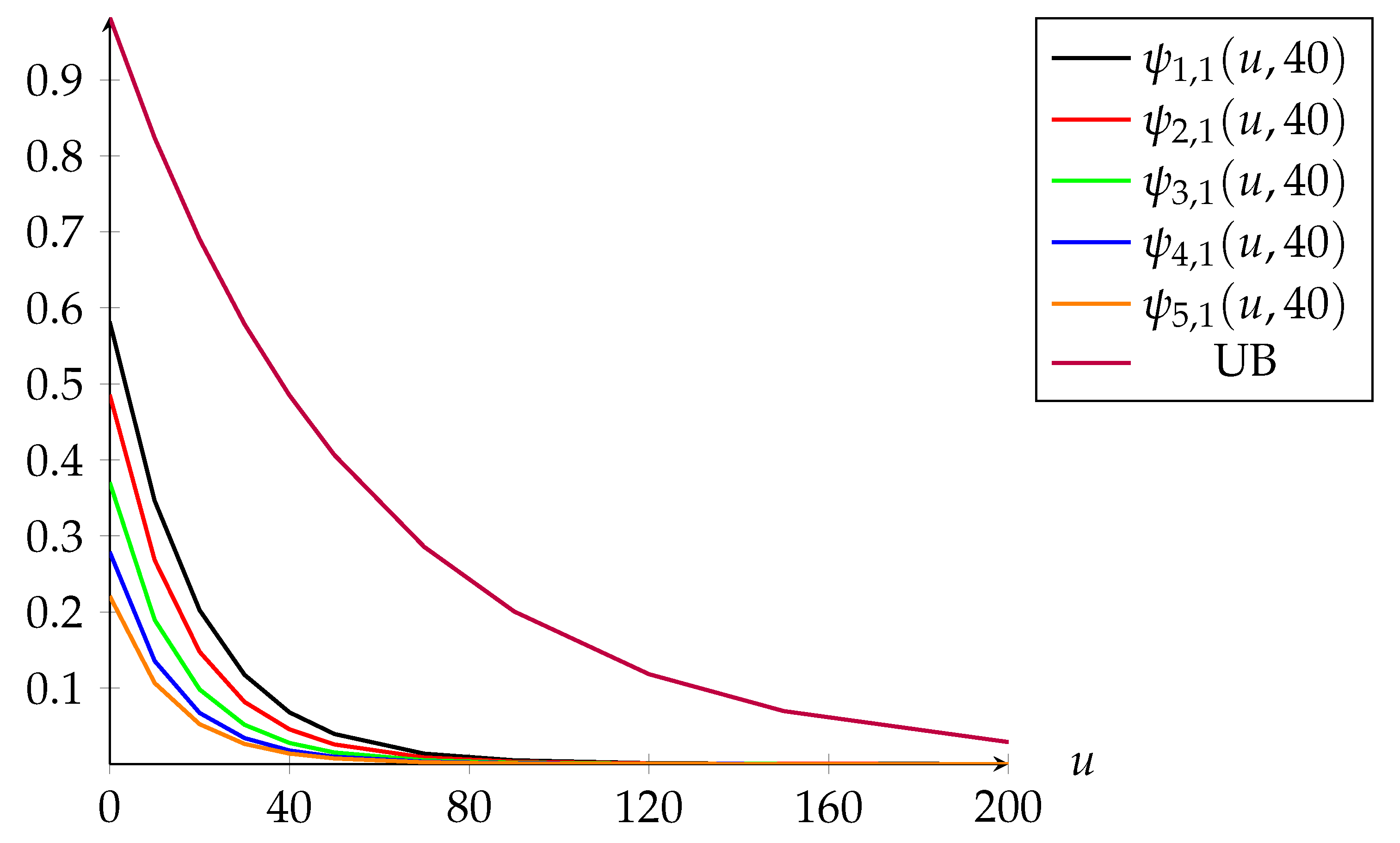
200	0.000021	0.000012	0.000006	0.000004	0.000003	0.028761

and Figure 2 below.

As shown in Table 1 and Figure 2, one can see that ${\psi }_{i1}(u,40)$, $i=1,\dots ,5$ are ordered by their initial premium levels, the lower the initial premium level is, the higher the finite-time ruin probabilities. Secondly, the initial surplus level u has a significant impact on differentiating the five finite-time ruin probabilities: these probabilities differ more from each other when u is small, but this impact tends to wear off when u becomes larger. For example, for $u=0$, ${\psi }_{1,1}(0,40)=0.581516$, whereas ${\psi }_{5,1}(0,40)=0.220787$ (around 0.36 in difference). On the other hand, for $u=50$, ${\psi }_{1,1}(50,40)=0.039369$ and ${\psi }_{5,1}(50,40)=0.007212$ (only 0.03 in difference). Its implications coincide with the practical concerns when choosing the initial premium level with different u levels: a low initial premium level tends to be very risky when u is small. However, when the initial surplus u is sufficiently large, the insurer has more flexibility to lower the initial premium level that can attract more new policyholders and help with boosting the insurance business without significantly increasing the risk of insolvency.

One obvious observation in Figure 2 regarding the upper bound is that it is very loose for all five versions of finite-time ruin probabilities. An argument for this is that the generalised adjustment coefficient $\gamma$ adopted in (12) is quite conservative, since it is determined by the scenario that has the highest ruin probabilities by its definition. Also, the upper bound given in (12) is for the ultimate time ruin probabilities, so tend to be fairly loose for finite-time ruin probabilities with $n=40$. In practice, the insurer can use these upper bounds to evaluate the worst-scenario risk of ruin in the long run.

First of all, given each initial economic state, we make similar observations in the trending in finite-time ruin probabilities when u and i change. Following that, comparing the three cases with different initial economic states, we have some interesting findings. Firstly, when $u=0$ and three i cases of $u=10$, the deflation economic state (state 2) leads to the highest finite-time ruin probabilities whilst the inflation economic state (state 3) has the lowest finite-time ruin probabilities. Secondly, when the initial premium level is at the lowest one ($i=1$) and $u\ge 10$, the inflation economic state leads to the highest ruin probabilities whilst the deflation state has the lowest ones. For remaining cases, the inflation state usually ranks the highest in finite-time ruin probabilities and the normal economic state ranks the lowest. We struggle to find intuitive reasons behind these observations. One contributing factor is the initial premium amount. The ranking of ruin probabilities when $u=0$ coincides with the ranking of the initial premium amounts correspond to the three initial economic states, which again confirms the significant role of the early premium income in keeping solvency when there is no capital buffer in the first place. Based on these observations, it is fair to say that both initial economic state and initial premium level play important roles in determining the finite-time ruin probabilities of the insurance business. Therefore, the insurers must keep a close eye on this matter when optimising their premium-changing strategies. Next, we shall dig further into the relationship between u, the premium level and economic state at ruin given ruin occurs. As an example, we calculate the joint distribution of the premium level and economic state at ruin given the ruin occurs within 10 periods, i.e., ${\chi }_{i,g}^{{}^{\prime }}(0,10,j,h)$, making use of the result (14).

For the initial economics state 2 (deflation condition) and state 3 (inflation condition), the finite-time ruin probability results are given in

Table 2. ${\psi }_{i,2}(u,40)$ values with upper bounds (UB).

u	${\mathit{\psi }}_{1,2}(\mathit{u},40)$	${\mathit{\psi }}_{2,2}(\mathit{u},40)$	${\mathit{\psi }}_{3,2}(\mathit{u},40)$	${\mathit{\psi }}_{4,2}(\mathit{u},40)$	${\mathit{\psi }}_{5,2}(\mathit{u},40)$	UB
0	0.602651	0.530232	0.432010	0.346695	0.290467	0.982500
10	0.340618	0.280003	0.210953	0.159843	0.132489	0.823486
20	0.194130	0.151662	0.107550	0.077895	0.063776	0.690207
30	0.110690	0.083187	0.056257	0.039292	0.031786	0.578500
40	0.063296	0.046186	0.030090	0.020401	0.016316	0.484872
50	0.036402	0.025979	0.016437	0.010875	0.008605	0.406397
70	0.012333	0.008554	0.005196	0.003313	0.002573	0.285494
90	0.004325	0.002954	0.001750	0.001087	0.000832	0.200560
120	0.000946	0.000638	0.000369	0.000223	0.000168	0.118091
150	0.000215	0.000143	0.000082	0.000049	0.000036	0.069532
200	0.000019	0.000012	0.000007	0.000004	0.000003	0.028761

and

Table 3. ${\psi }_{i,3}(u,40)$ values with upper bounds (UB).

u	${\mathit{\psi }}_{1,3}(\mathit{u},40)$	${\mathit{\psi }}_{2,3}(\mathit{u},40)$	${\mathit{\psi }}_{3,3}(\mathit{u},40)$	${\mathit{\psi }}_{4,3}(\mathit{u},40)$	${\mathit{\psi }}_{5,3}(\mathit{u},40)$	UB
0	0.536216	0.441881	0.338071	0.259681	0.209647	0.982500
10	0.362565	0.284586	0.209476	0.157582	0.127362	0.823486
20	0.240562	0.181306	0.129259	0.095593	0.077312	0.690207
30	0.157427	0.114621	0.079529	0.057972	0.046900	0.578500
40	0.101979	0.072065	0.048833	0.035150	0.028439	0.484872
50	0.065557	0.045126	0.029942	0.021312	0.017240	0.406397
70	0.026650	0.017546	0.011225	0.007835	0.006334	0.285494
90	0.010669	0.006769	0.004198	0.002881	0.002327	0.200560
120	0.002651	0.001606	0.000957	0.000643	0.000519	0.118091
150	0.000647	0.000377	0.000217	0.000144	0.000116	0.069532
200	0.000060	0.000033	0.000018	0.000012	0.000009	0.028761

, respectively.

In

Table 4. Results for ${\chi }_{1,1}^{{}^{\prime }}(0,10,j,h)$.

	$\mathit{j}=1$	2	3	4	5
$h=1$	0.758260	0.066721	0.017378	0.004019	0.000892
$h=2$	0.031033	0.015421	0.005128	0.001372	0.000344
$h=3$	0.062983	0.026394	0.007770	0.001865	0.000421

, ${\chi }_{1,1}^{{}^{\prime }}(0,10,1,1)$ is the highest one among all 15 cases, much larger than all the other cases. It means that, given that $u=0$ and ruin occurs by time 10, the most likely premium level and economic state combination at ruin is the same as the initial combination $(i=1,g=1)$. The second and third most likely cases are $(j=2,h=1)$ and $(j=1,h=3)$ that are adjacent combinations of $(i=1,g=1)$. This implies that without any capital buffer at the beginning and charging the lowest level of premium, if ruin occurs early, then it will occur within the first few time units before making many transitions in either premium levels or economic states. Of course, the initial premium level and initial economic state as well as u all play an important roles in this. We shall continue this investigation in our next scenario.

Scenario 1.

Let $u=0$, $i=1$ and $g=1$. Values of ${\chi }_{1,1}^{{}^{\prime }}(0,10,j,h)$ are summarised in Table 4.

Scenario 2.

Keep u and g unchanged, but let $i=5$, the highest level of premium. The corresponding results are given in

Table 5. Results for ${\chi }_{5,1}^{{}^{\prime }}(0,10,j,h)$.

	$\mathit{j}=1$	2	3	4	5
$h=1$	0.000113	0.000726	0.004665	0.047550	0.800367
$h=2$	0.000037	0.000231	0.001394	0.008976	0.038254
$h=3$	0.000408	0.001594	0.005976	0.024634	0.065076

.

In Table 5, ${\chi }_{5,1}^{{}^{\prime }}(0,10,5,1)$ is the highest one among all 15 cases, much larger than all the others. Again, given that $u=0$ and ruin occurs by time 10, the most likely premium level and economic state combination at ruin is the same as the initial combination. The second and third most likely cases are $(j=5,h=3)$ and $(j=4,h=1)$, the adjacent combinations of $(i=5,g=1)$. It looks like when $u=0$, even charging the given highest level of premium, if we know ruin occurs early, then it will still occur within the first few time units. This is a similar observation to Scenario 1. This implies that, under our model assumptions, the initial surplus plays a more important role in the insolvency risk than the initial premium level. For the purpose of comparison, we shall consider one more scenario of $u=100$ to see any different observations from the $u=0$ scenarios.

Scenario 3.

Let $u=100$, $i=1$ and $g=1$. The corresponding results are given in

Table 6. Results for ${\chi }_{1,1}^{{}^{\prime }}(100,10,j,h)$.

	$\mathit{j}=1$	2	3	4	5
$h=1$	0.016169	0.053910	0.071874	0.054714	0.043763
$h=2$	0.002011	0.008437	0.013755	0.012849	0.012611
$h=3$	0.098078	0.218514	0.204083	0.118145	0.071086

.

In contrast to the previous two scenarios, in Table 6, the top four most likely combinations of premium level and economic state at ruin are $(j=2,h=3)$, $(j=3,h=3)$, $(j=4,h=3)$, and $(j=1,h=3)$. It implies that when the initial surplus is large, given ruin occurs, then ruin would most likely occur under the worst economic state, i.e., $h=3$, which by assumption has the highest expected aggregate claim amount per time unit. Again, the premium level at ruin seems relatively less influential than the economic state regarding insolvency. Moreover, the values of ${\chi }_{1,1}^{{}^{\prime }}(100,10,j,h)$ in Table 6 are more evenly spread out than the results in Table 4 and Table 5. This is because with $u=100$, there are more chances that the insurance business could stay solvent in the first few periods and ruin would occur later. The longer the surplus process runs, then the less predictable it is, thus the premium level and economic state combination at ruin.

6.2. An Example for Premiums Adjusted by Claim Frequency

In this example, we shall consider automobile insurance business and we replace the external economic environment by weather conditions. We assume that the premium levels are adjusted according to the claim frequency and the weather condition has a significant impact on the claim frequency of automobile insurance policyholders.

• The claim frequency is modelled by Poisson distribution with mean 1.57, 0.785 and 2.355 for weather state 1 (normal condition), 2 (less severe condition) and 3 (severe weather condition) respectively.
• The one-step transition probability matrix of weather states (environment state) with the corresponding stationary probability distribution are the same as the ones for the external economic states in the previous example. Similar to the previous example, the weather state is assumed to be fixed over a year from the beginning and the premiums depend on the current weather state.
• The individual claim size distribution under each weather state is assumed to be geometric with P.M.F. ${\mathbb{P}}_W\left(w\right)=\left(\frac{1.57}{10}\right){(1-\frac{1.57}{10})}^{(w-1)}$ for $w\ge 1$ and mean $\frac{10}{1.57}$. Then the expected aggregate claim amount under weather state 1, 2, and 3 is 10, 5 and 15, respectively. The expected long-term aggregate claim amount is 10, which is the same as the one in the previous example as well.

We continue to use the same set of premium loading as the one in the previous example, i.e., $\mathbf{c}=\{120\%,140\%,160\%,180\%,200\%\}$. The rules for adjusting premiums are given as follows:

• If the number of claims in the current period is 0, then the premium level for the next period will move to the lower premium level or stay in the lowest one;
• If the number of claims in the current period is greater than 0 but no more than 2, then the premium level for the next period will remain in the current premium level;
• If the number of claims in the current period is more 2, then the premium level for the next period will move to the higher premium level or stay in the highest one.

According to the above transition rules for premium adjustments, we can also find its associated transition matrix among the premium levels in the Appendix D, and the following long-term stationary joint distribution of the premium levels and weather states:

$$\begin{array}{c}\hfill \mathbf{\pi }={\left[{\pi }_{ig}\right]}_{i\in \mathcal{𝓛},g\in \mathbf{R}}=\left[\begin{array}{ccccc}0.1429,& 0.1214,& 0.1119,& 0.1089,& 0.1150\\ 0.0702,& 0.0394,& 0.0350,& 0.0314,& 0.0241\\ 0.0328,& 0.0374,& 0.0373,& 0.0380,& 0.0545\end{array}\right].\end{array}$$

Using $\mathbf{\pi }$, one can see that the expected long-term premium is around 15.9 per time unit, which is about 60% greater than the expected long-term aggregate claims per time unit. Remarkably, the expected long-term premium loading in this example is comparable to the one in the previous example. We make the expected long-term premium income and expected long-term aggregate claims of these two examples comparable on purpose such that a comparison is feasible between the two different types of premium transition rules regarding their impact on the ruin probabilities. Similarly, in the following we use the result (9) to calculate ${\psi }_{i,1}(u,40)$ and use (12) to calculate the upper bounds for the ultimate time ruin probabilities ${\psi }_{i,1}\left(u\right)$. The results are summarised in

Table 7. ${\psi }_{i,1}(u,40)$ values with upper bounds (UB).

u	${\mathit{\psi }}_{1,1}(\mathit{u},40)$	${\mathit{\psi }}_{2,1}(\mathit{u},40)$	${\mathit{\psi }}_{3,1}(\mathit{u},40)$	${\mathit{\psi }}_{4,1}(\mathit{u},40)$	${\mathit{\psi }}_{5,1}(\mathit{u},40)$	UB
0	0.605971	0.509785	0.394719	0.299570	0.235311	0.971992
10	0.388786	0.299805	0.209603	0.146053	0.110407	0.731630
20	0.236054	0.167432	0.106238	0.068367	0.050195	0.550706
30	0.137875	0.090424	0.052377	0.031307	0.022445	0.414523
40	0.078166	0.047692	0.025389	0.014180	0.009959	0.312016
50	0.043249	0.024708	0.012176	0.006393	0.004407	0.234858
70	0.012487	0.006372	0.002750	0.001299	0.000865	0.133065
90	0.003391	0.001581	0.000614	0.000266	0.000172	0.075391
120	0.000441	0.000186	0.000064	0.000025	0.000015	0.032152
150	0.000053	0.000021	0.000007	0.000002	0.000001	0.013712
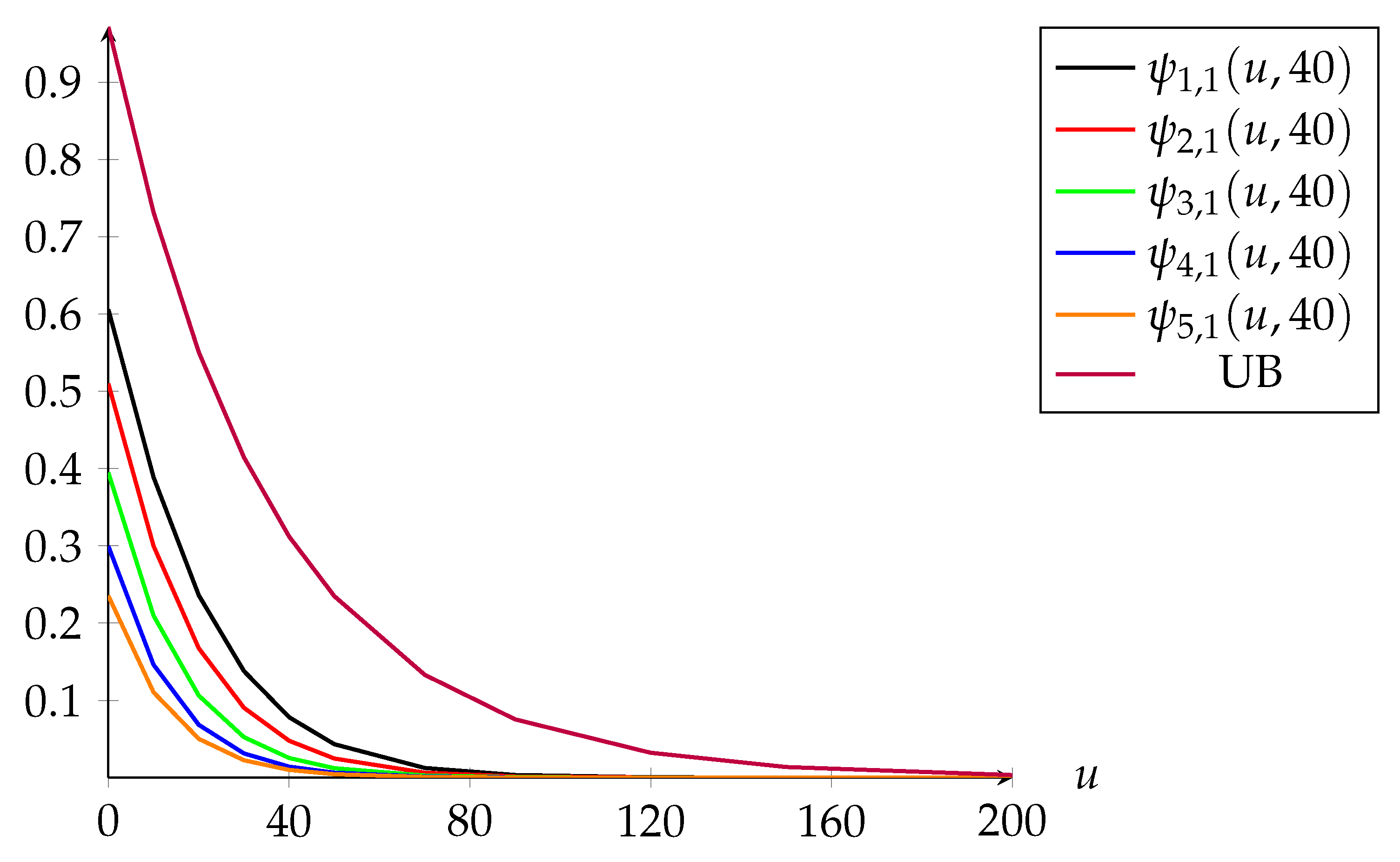
200	0.000001	0.000001	0.000000	0.000000	0.000000	0.003313

and Figure 3 below.

Firstly, our main findings in Table 7 and Figure 3 are consistent with those in Table 1 and Figure 2 in terms of the impact of the initial premium level and initial surplus level on ruin probabilities. Secondly, given the same initial external environment state, when u is small the premium adjustment rules based on claim frequency have a negative impact on the finite-time ruin probabilities comparing with the rules by aggregate claim amounts. Also, this effect becomes more significant when the initial premium level is lower. For instance when $i=1$ this effect applies to $u\le 50$ but it only takes effect for $u\le 20$ when $i=5$. This is reasonable since the transition rules that adjust the premiums according to the claim frequency can not fully reflect the historical claims experience, which causes higher risk of ruin when u is small. On the contrary, when u is large enough, the premium rules by claim frequency seems to lower the insolvency risk of the insurer comparing with the other type of rules. This implies that, in practice, the insurers should carefully design their bonus-malus rules by taking into account factors like the capital adequacy level since the proposed rules could have significant impact on insolvency risk. Next, we shall investigate the finite-time ruin probabilities with initial weather state 2 and 3, which are shown in

Table 8. ${\psi }_{i,2}(u,40)$ values with upper bounds (UB).

u	${\mathit{\psi }}_{1,2}(\mathit{u},40)$	${\mathit{\psi }}_{2,2}(\mathit{u},40)$	${\mathit{\psi }}_{3,2}(\mathit{u},40)$	${\mathit{\psi }}_{4,2}(\mathit{u},40)$	${\mathit{\psi }}_{5,2}(\mathit{u},40)$	UB
0	0.647608	0.600217	0.511647	0.414121	0.332302	0.971992
10	0.410970	0.362287	0.281517	0.204813	0.150624	0.731630
20	0.251122	0.211238	0.150889	0.099501	0.067739	0.550706
30	0.148774	0.119900	0.079446	0.047947	0.030482	0.414523
40	0.085828	0.066553	0.041270	0.023024	0.013769	0.312016
50	0.048375	0.036238	0.021204	0.011040	0.006249	0.234858
70	0.014483	0.010237	0.005448	0.002533	0.001305	0.133065
90	0.004064	0.002744	0.001359	0.000580	0.000276	0.075391
120	0.000550	0.000353	0.000162	0.000063	0.000027	0.032152
150	0.000069	0.000042	0.000018	0.000007	0.000003	0.013712
200	0.000002	0.000001	0.000000	0.000000	0.000000	0.003313

and

Table 9. ${\psi }_{i,3}(u,40)$ values with upper bounds (UB).

u	${\mathit{\psi }}_{1,3}(\mathit{u},40)$	${\mathit{\psi }}_{2,3}(\mathit{u},40)$	${\mathit{\psi }}_{3,3}(\mathit{u},40)$	${\mathit{\psi }}_{4,3}(\mathit{u},40)$	${\mathit{\psi }}_{5,3}(\mathit{u},40)$	UB
0	0.555437	0.430304	0.315517	0.231635	0.179284	0.971992
10	0.354335	0.249205	0.167191	0.115193	0.087273	0.731630
20	0.212928	0.136511	0.084156	0.054739	0.040872	0.550706
30	0.122699	0.072029	0.040953	0.025268	0.018672	0.414523
40	0.068509	0.037011	0.019486	0.011455	0.008399	0.312016
50	0.037306	0.018650	0.009134	0.005138	0.003744	0.234858
70	0.010434	0.004543	0.001955	0.001019	0.000736	0.133065
90	0.002749	0.001066	0.000411	0.000202	0.000144	0.075391
120	0.000343	0.000116	0.000039	0.000018	0.000013	0.032152
150	0.000040	0.000012	0.000004	0.000002	0.000001	0.013712
200	0.000001	0.000000	0.000000	0.000000	0.000000	0.003313

.

According to the results in Table 8 and Table 9, the trending of finite-time ruin probabilities when u and i change is still consistent with Table 7. In contrast to the previous premium-changing category (by aggregate claims), when the premiums change according to claim frequency experience, there is an overall consistent ranking in the finite-time ruin probabilities among the three initial weather conditions, i.e., less severe initial weather condition (state 2) leads to the highest ruin probabilities whilst the severe initial weather condition (state 3) has the lowest ruin probabilities. This ranking can be explained by the level of right-skewness of the Compound Poisson distributions corresponding to the aggregate claims under each weather condition. Apparently, state 2 has the highest right-skewness whilst state 3 has the lowest, which relates to the risk of insolvency.

At last, we shall use the (15) to compute the joint distribution of the premium level and weather condition at ruin given ruin occurs within 10 time periods. The results are given in

Table 10. Results for ${\chi }_{1,1}^{{}^{\prime }}(0,10,j,h)$.

	$\mathit{j}=1$	2	3	4	5
$h=1$	0.788065	0.069503	0.012257	0.002256	0.000437
$h=2$	0.041473	0.010975	0.002007	0.000384	0.000077
$h=3$	0.045738	0.020304	0.005216	0.001088	0.000220

,

Table 11. Results for ${\chi }_{5,1}^{{}^{\prime }}(0,10,j,h)$.

	$\mathit{j}=1$	2	3	4	5
$h=1$	0.000410	0.001394	0.005025	0.039455	0.863448
$h=2$	0.000204	0.000681	0.002484	0.010320	0.034591
$h=3$	0.000116	0.000389	0.001216	0.006851	0.033414

and

Table 12. Results for ${\chi }_{1,1}^{{}^{\prime }}(100,10,j,h)$.

	$\mathit{j}=1$	2	3	4	5
$h=1$	0.066714	0.193377	0.205458	0.115465	0.057055
$h=2$	0.017125	0.033472	0.034556	0.020260	0.010142
$h=3$	0.020572	0.071252	0.082757	0.047871	0.023924

, where the scenarios considered are the same as Scenario 1–3 in the previous example.

From Table 10 and Table 11, one can see that under Scenario 1 and Scenario 2 (both with $u=0$) we get similar main findings to those in the previous example. It is worth noting that in Scenario 3 where $u=100$, we get opposite findings comparing with our previous example. The top four most likely combinations of premium level and weather conditions at ruin are $(j=3,h=1)$, $(j=2,h=1)$, $(j=4,h=1)$ and $(j=3,h=3)$, mostly associated with the normal weather conditions under which the claim experience should be the middle one. This is totally different from the previous example where in Scenario 3 the most likely combinations come from the worst economic state under which the claim experience is the worst. The most likely explanation lies in the way premiums are being adjusted as well as the claim experience assumptions under different weather conditions. To be more specific, we assume that individual claim amounts are not affected by weather conditions, but claim frequency does. Under the normal weather condition ($i=1$), the current premium level is likely to stay unchanged. However, under severe weather condition ($i=3$), average claim frequency is high, which leads to moving the next premium level up. To a certain extent, the worsened claim experience is off-set by the increased premium amount, which leads to a lower overall insolvency risk than the normal weather condition. We remark that this observation might not hold when the parameter assumptions are changed, which result in a different trade-off between the claim experience and premium adjustment.

Last but not least, we make a further comparison between the above two numerical examples, as the risk models constructed in those two examples are in general comparable, for example, equal average aggregate claim amounts as well as the same premium levels. We can see that the case of adjusting premiums according to claim frequency is riskier than the case of adjusting premiums according to aggregate claims under our assumptions. This finding also has some material implication for the insurance companies on how to choose an appropriate premium adjustment strategy.

7. Conclusions and Discussions

In this paper we considered a discrete-time risk model, which allows the premium to be adjusted according to claims experience. The premium correction was based on the well-known bonus-malus system and the claims experience was assumed to depend on an external Markovian environment (economic and/or natural environment). As a result, the evaluation of this unusual bonus-malus framework, which has non-homogeneous premium transition rules, became the main objective of this paper. To have a better coverage, two types of premium changing criteria were examined throughout the paper: aggregate claims criterion vs. claim frequency criterion. The basis of our evaluation is the risk of ruin for the proposed risk model with the given set of initial parameters, i.e., initial surplus, initial premium level and initial environment state. On the one hand, recursive formulae were obtained to calculate the finite-time ruin probabilities and Lundberg-type upper bounds were derived to evaluate the ultimate ruin probabilities in both cases. On the other hand, the joint distribution of premium level and environment state at ruin was also studied. Through our numerical studies, we find that both the initial premium level and the initial environment state have a significant impact on the insolvency risk. We observed that there is no straightforward ordering on the insolvency risk among cases with different initial environmental state, which can be seen as the consequence of a combined effect of non-homogeneous loss distributions, premium rule assumptions as well as the initial surplus level. This shed a light on the importance of determining the proper base premium level in a given external environment when insurers implement the bonus-malus system in premium corrections.

This paper focused on the ruin probabilities when evaluating the proposed bonus-malus system within a Markovian environment. However, how to implement the premium corrections in real life based on the main findings in this paper remains a very challenging task, as there will be no fixed premium changing rules when the external environment changes. A possible solution is that the insurer designs a special scoring system and uses it to evaluate its policyholders’ claim experience. For instance, at the end of each policy year a policyholder receives a certain score based on the ordering of his/her claim experience in the whole insurance portfolio, and then a bonus or malus can be offered in the renewal premium based on the scores. This type of score-based premium rules can effectively address the impact of external environment on premium corrections. This non-standard premium correction practice needs to be carefully communicated with the policyholders in practice.

There are some limitations in the above study that are worth addressing in the future research. Firstly, the two numerical examples given above were based on a number of assumptions, including aggregate claims distribution, claim frequency distribution, transition rules for premium adjustment, number of premium levels and the specific external environment processes. Whether or not these assumptions hold in real practice need to be verified and more appropriate assumptions may be required to improve the model results. Secondly, in real life the parameters associated with the assumptions need to be estimated using real-life data. For instance, we used hypothetical transition probabilities among different environment states in both our numerical examples, but in real life these probabilities need to be estimated using real-life economic data or meteorological data. Moreover, if the environment-initiated non-homogeneity does exhibit in the claim experiences, then the claim frequency and claim severity modelling would become more complicated and generally long-term data would be needed to obtain reliable parameter estimates.

Another potential future research could be constructing a continuous-time risk model with the same features as the discrete-time model in this paper. Then we could study the impact of the bonus-malus system and the external Markovian environment on the ultimate-time ruin probability.