1. Introduction
There have been various approaches to determine loss reserve for a single line of business with statistical models. According to
Mack (
1993), the chain-ladder method, which has been used as a rule of thumb for the determination of reserve, can be interpreted as a nonparameteric stochastic model. After that, many univariate stochastic reserving models have been developed and used for both determination of point estimates of reserve and risk management. For detailed discussions on univariate stochastic reserving models, see
England and Verrall (
2002).
However, it is also certain that most of the insurance companies do not run only a single line of business so one needs to consider possible dependence among the lines of business in reserve modeling. Consequently, stochastic reserving models need to be extended to multivariate frameworks. In this regard, some actuarial literature focused on the extension of the chain-ladder method to multivariate cases, such as
Braun (
2004),
Schmidt (
2006), and
Merz and Wüthrich (
2008) which are followed by
Shi et al. (
2012), which used a bivariate normal distribution to model multi-line reserves. Besides the dependence among multiple lines of business, there have been some works on the dependence between paid claim triangles and incurred claim triangles such as
Zhang (
2010) and
Merz and Wüthrich (
2010).
Note that the methods mentioned above are less flexible since it is not allowed to disentangle marginal distributions and multivariate association structure. Therefore, use of a copula was introduced to the multivariate reserving problem since this allows us to consider marginal distribution and association structure in a separate way. Based on this idea,
Shi and Frees (
2011) proposed the use of a bivariate Gaussian copula to model dependence among multi-line reserves where the marginal distributions are chosen as Gaussian and gamma, respectively.
Peters et al. (
2014) considered dependence between paid-incurred claim triangles via bivariate copula. Further,
Abdallah et al. (
2015) used the idea of the hierarchical archimedian copula to capture calendar year effect and multi-line dependence simultaneously.
Although there have been some works on the multivariate reserving in actuarial literature, applications of all the aforementioned works are restricted only to possible dependence between two lines of business. Indeed, it is natural that a property and casualty insurance company runs more than two lines of business, so we need to incorporate such a high-dimensional dependence structure in our reserve modeling.
In that regard, we apply the idea of a vine copula in this article, which uses bivariate copulas as its building blocks and connects them with vine structure to describe the high-dimensional association in a flexible way. The vine copula has been widely used in the actuarial and financial literature.
Loaiza Maya et al. (
2015) investigated dependency among the exchange rates of Latin American countries using the vine copula.
Reboredo and Ugolini (
2016),
Arreola Hernandez et al. (
2017), and
Trucíos et al. (
2020) used the vine copula to assess systemic risks due to possible dependence among economic subjects. Surprisingly, usage of the vine copula in property and casualty insurance literature does exist but is scarce. For example,
Shi and Yang (
2018) used a vine copula to capture the serial dependence of claim amounts and derive the experience ratemaking factor.
This paper has been organized as follows. In
Section 2, basic concept of the vine copula is introduced and the model selection procedure to be implemented is specified. In
Section 3, we describe the data used for our empirical analysis. In
Section 4, we go through the model selection procedure to determine marginal distributions and the vine copula structure to be used in our analysis. In
Section 5, we discuss the implications of estimation results from the perspective of enterprise risk management using the predictive distribution of unpaid claims.
Section 6 addresses practical issues for implementing the proposed methodology. Finally, we conclude this article in
Section 7 by providing some future directions of research.
2. Proposed Methodology
Suppose an insurance company owns a portfolio which consists of
N multiple lines of business. By assuming balanced observations in multiple triangles, one can write the multivariate cumulative paid claims as
where
indicates a claim triangle from the
line of business,
means the
accident years, and
denotes
development lag. In general, it is of interest to predict the cumulative paid claim for the next year given information up to the current year, which can be written as
. Therefore, instead of working with
, one can directly model the incremental development of claims, or age-to-age factors as follows:
where
so that
. Since each of
are observed from the same business line, it is natural that we model the marginal distribution of
and the dependence structure among
via copulas to jointly model
.
According to
Sklar (
1959), if all marginal distribution functions are continuous, then there is a unique function
such that
where
denotes marginal distribution function of
and
H denotes joint distribution function of
. Therefore, use of copulas allows us to capture the association among the joint response random variables, which may follow different marginal distributions. In that sense, by letting
, where
is the parameter vector for the marginal distribution of
and
is the copula parameter, the likelihood for joint distribution is given as follows:
Here
h means the joint density of
and we assume that
are independent for fixed
n.
Depending on the sign of dependence, we may use different families of copulas. For example, in order to capture positive dependence, one can suggest the following bivariate copulas:
Although those two copulas can only capture positive dependence, one can easily rotate those in order to capture reversed tail behavior and negative dependence as follows:
Further, the Gaussian copula and Frank copula are also prevalent choices which can capture both positive and negative dependence:
where
stands for the cumulative distribution function of a bivariate, standard, normal, random variable with correlation
and
stands for the cumulative distribution function of a univariate, standard, normal random variable.
Given families of copulas, allow us to consider various facets of possible dependence among the lines of business, including the upper and lower tail dependence properties. For example, the Clayton copula can capture a positive association and has lower tail dependence but no upper tail dependence. The Gumbel copula can capture positive associations and has upper tail dependence but no lower tail dependence. Further, both Frank and Gaussian copulas are symmetric and able to capture positive and negative dependence, but they have no tail dependencies. Note that upper tail dependence of original copulas corresponds to lower tail dependence of survival copulas, and vice versa. Further, if an original copula can capture a positive association, then the corresponding
or
rotated copula can capture a negative association; for example,
rotated Clayton and
rotated Gumbel copulas can be used to capture negative associations. We refer the readers to
Nelsen (
1999),
Embrechts et al. (
2001), and
Hua and Joe (
2011) for a more detailed explanation. The variability of tail behaviors is potentially important considering the data used in our empirical analysis. Here we capture the dependencies among the incremental development factors of different lines of business so that it is natural that the incremental development factors will be quite large in the initial years and become smaller in the mature years. In this regard, upper tail dependence corresponds to the associations among the loss development factors in the initial years, whereas lower tail dependence corresponds to the associations among the loss development factors in the mature years.
If
, then the dependence can be captured by a bivariate copula, which has been explored in previous works such as
Shi and Frees (
2011). However, we may not preclude the possibility that
, and one can suggest the use of vine copula when we have more than two lines of business to capture the multiple dependence. The concept of vine copula was introduced by
Aas et al. (
2009) who extended the research conducted by
Bedford and Cooke (
2001) and
Bedford and Cooke (
2002) to show how multivariate data, which exhibit complex patterns of dependence in the tails, can be modeled using a cascade of pair-copulas, acting on two variables at a time. Later
Czado (
2010) and
Joe and Kurowicka (
2011) developed this idea further and provided us with a definite road map for constructing vine copulas to represent complex multivariate data. The core concept behind construction of vine copulas is that a
d-dimensional density
can be represented as a product of pair copula densities and marginal densities. For example, let us consider
dimension. A possible way to represent the joint density
is as follows:
Additionally, since
where
is the joint copula density of random variables
and
. One can write out the joint density of
as follows:
Note that in general,
is affected by
, not only through
and
, but also directly through
. However, such a general form of conditional coplula density is cumbersome to be used in statistical inference. For this reason, it is tempting to use a simplified form of conditional copula density so that
is affected by
only through
and
.
Haff et al. (
2010) showed that we may write each conditional pair copula density in a simplified form for elliptical distributions with a positive definite scale matrix. Further, it was also shown that use of the simplified form could be a good approximation even in a case wherein such an assumption could not be fully validated. Hence, we will use a simplified form of conditional copula density in this article hereafter.
The sequential dependence structure via pair copulas is described with a regular vine, or R-vine. Let
be a set of trees where each tree
is connected and
. Here
and
mean the nodes and edges of
, respectively. If
for
,
is called a vine. Further, if
then
is called a R-vine. There are two important subclasses of R-vine, C-vine and D-vine. If there is a node
so that the degree of that node is
in an R-vine, it is called a C-vine. D-vine is an R-vine wherein the degree of every node is at most 2.
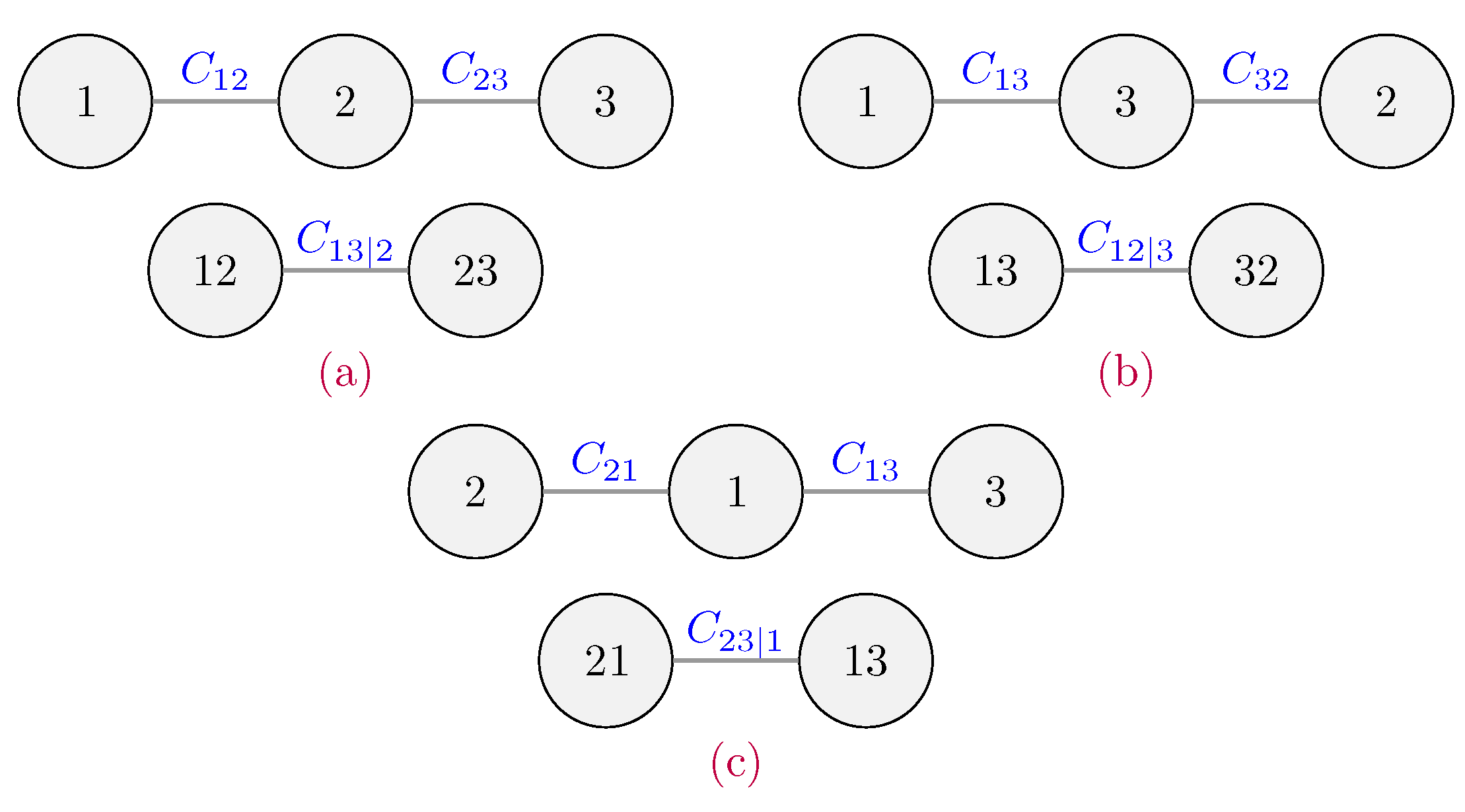
The above decomposition of the joint density in terms of vine structure is not unique. For example, when
, we have the following three available R-vine structures as in
Figure 1. Note that in the case of 3-dimensional R-vine structures, C-vine and D-vine are identical, which is no more true for
.
Note that the number of regular vine structures on
d-dimensional variables grows super-exponentially so that there are
regular vine structures on
d variables, as shown in
Joe and Kurowicka (
2011). Therefore, it is already meaningless to display every possible vine structure if
.
Therefore, for the calibration of vine copula model, we need to carefully determine the following components based on observed data:
Marginal distribution for each of ;
Optimal d-dimensional vine structure;
Copula family for each of pair copula in the selected vine structure.
For statistical inference, one may consider either the frequentist or the Bayesian approach and subsequently choose the optimal structure via a model selection procedure. However, it can be quite computationally demanding to choose an optimal model in both approaches. For example, as mentioned in Table 1 of
Gruber and Czado (
2015), the size of search space of vine copula model for
is already (1.3559 × 10
) when we consider seven families of copula for each of the pair copulas, which is definitely computationally infeasible. In this regard,
Dissmann et al. (
2013) proposed a top-down approach to choose the vine structure from a frequentist view.
Gruber and Czado (
2018) proposed sequential vine copula model selection from a Bayesian perspective.
Schamberger et al. (
2017) also considered a Bayesian approach to model dependence structure with a factor copula in order to handle the dimensionality issue. Recently,
Kreuzer and Czado (
2019) showed that the pair copula family can be chosen together with their parameters using the Hamiltonian MCMC.
The Bayesian approach can be beneficial in reserve modeling since it can incorporate the uncertainty of parameter estimation and reflect it to compute the predictive distribution of future unpaid claims, as proposed in
Shi et al. (
2012). Therefore, we propose the following two-step approach, which can be considered as a compromise of
Dissmann et al. (
2013) and
Gruber and Czado (
2018):
3. Data Description
For the empirical analysis, we used a publicly available dataset from
ACE Limited 2013 Global Loss Triangles, which consists of aggregated claim developments for insurance operations in North America (4 lines of business), insurance operations overseas (3 lines of business), and global reinsurance operations (2 lines of business). A description and the corresponding index for each line of business are given in
Table 1. We incorporate a 9-dimensional vine copula structure to capture possible dependence among all lines of business. Indeed, the current COVID-19 situation could be a clear example of showing the inappropriateness of ignoring potential dependencies among different countries. Note that the dataset and code for data analysis are attached as
Supplementary Materials.
Although we consider all possible lines of business simultaneously here, an actuary who applies vine copulas to model dependence among the lines of business should be careful, since the complexity of the vine copula structure increases super-exponentially as the dimensionality grows. Therefore, it is a role of an actuary to apply his/her industrial experience or knowledge for the dependence modeling. Further, it is also possible to observe more than 10 lines of business according to the classification in Schedule P of the National Association of Insurance Commissioners (NAIC) annual report, including but not limited to:
Therefore, it is also possible to merge some lines of business into one category in order to not only enhance homogeneity and credibility in the analysis but also avoid too much complexity of the vine structure due to the large number of lines of business.
The loss development triangles, which are training sets in terms of predictive analytics, can be expressed as follows:
Our task is to predict the cumulative paid claims for the next years, which are described as follows:
For enterprise risk management (ERM) purposes, insurance companies are usually interested in the distribution of aggregate unpaid claims after one year of loss development, which is determined by incremental paid losses defined as follows:
This formulation validates us to model
rather than
because one can see that
A simple approach for the analysis of
L is the silo approach, which means we just aggregate all lines of business so that the paid losses of the same development lag and accident year are merged and modeled altogether. In this case, one can write
L as follows:
where
and
. However, such an approach ignores the heterogeneity of the lines of business and could be problematic. Suppose there are two lines of business, personal and commercial auto insurances, and reported losses of these lines are given in
Table 2. Note that the incremental development is calculated as
. One can see that due to the difference in volume, the volatility of loss development for the commercial auto line is wiped out if we analyze the aggregated data. Therefore, the vine copula model can be considered as a flexible generalization of two extreme models, silo and independent approaches, so that one can consider possible dependence and heterogeneity among the lines of business simultaneously.
4. Model Selection and Parameter Estimation
For marginal distribution, we apply the idea of the cross-classified model for each line of business as in
Shi and Frees (
2011) and
Taylor and McGuire (
2016), which regresses
to linear predictor
as follows:
where
corresponds to the effect for the
accident year and
corresponds to the cumulative effect up to
development lag, for
line of business, respectively.
Recall that it is in our interests to predict
. Therefore, one can rewrite (
6) in the following way:
where
and
. Therefore,
can be interpreted as the incremental loss development factor from
lag to
lag. In this regard, we utilize two candidate distributions in (
7) and compare the model selection diagnostics to choose a suitable distribution for each of marginal models.
Further, it is natural to expect that for a fixed accident year, paid claim amounts gradually increase until they are fully mature and developed, while the magnitude of development gets smaller as development lag increases, which means the incremental loss development factor is expected to be greater than 1 but monotonically decreasing until it converges to 1. In terms of cross-classified model, such a statement is equivalent to the following mathematical condition:
for a large enough integer
, or there are
for
and
such that
. Therefore, we may suggest the following four models as the candidates for marginal distribution of each line of business:
LNU: The cross-classfied lognormal model in (
7);
LNC: The cross-classfied lognormal model in (
7) with (
8);
GamU: The cross-classfied gamma model in (
7);
GamC: The cross-classfied gamma model in (
7) with (
8).
All of the four models are fitted via
RStan because of its flexibility. For example, one can incorporate the constraint in (
8) by forcing a lower limit of
as 0 in
RStan and using a diffuse uniform prior on a positive real number for
,
, and
. For the unconstrained models, a diffuse uniform prior on the positive real number is directly used for
,
, and
. For each marginal model, four chains with 1000 iterates are used; the first 500 iterates are discarded for burn-in, which usually requires computation time for MCMC sampling of less than a second.
Table 3 provides a summary of the estimates of parameters in all models for the marginal components, which are summarized with posterior mean and upper/lower bounds of
of the Bayesian credible interval for each parameter. One can see that
tends to be greater than or equal to
in the unconstrained models, whereas
for all
in the constrained models, which is a more natural pattern in loss development analysis.
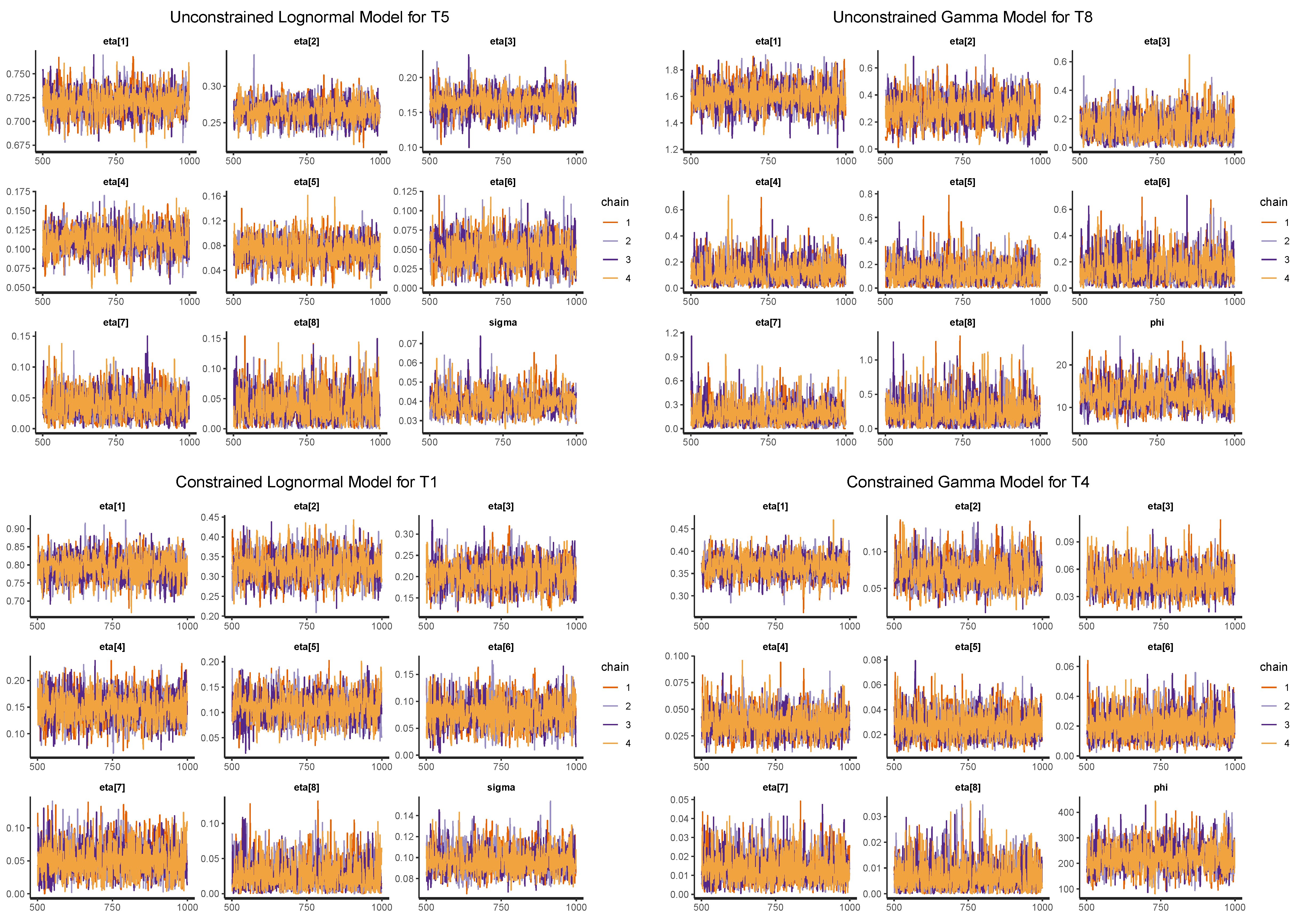
When posterior MCMC samples of parameters are obtained, it is quite important to make sure that these samples converge to (proper) posterior distributions. In this regard, we use
statistics proposed by
Gelman and Rubin (
1992) and traceplots which enable us to judge the convergence of MCMC sampling with the generated samples. Basically,
statistics tell us that the samples from distinct chains are well-mixed so that the chains are considered converged if
.
Table A1 in
Appendix A shows that
for all parameters, which tells us that the chains are well-mixed. One can also see that MCMC chains are well-mixed by looking at selected traceplots of maginal models, as shown in
Figure A1. It indicates different MCMC chains end up with similar empirical distributions, which is a necessary condition of the convergence of the MCMC algorithm to the correct posterior distribution.
After the convergence of Bayesian models is assessed, we compare the goodness-of-fit of Bayesian models using DIC and LPML. Based on the DIC and LPML values for fitted marginal models in
Table 4, it turns out that lognormal distribution is favored compared to gamma distribution. Further, DIC values of constrained lognormal distribution are always less than ones of unconstrained lognormal distribution, while LPML values have no definitive patterns between constrained and unconstrained lognormal distributions. Therefore, we suggest to use constrained lognormal distribution as the marginal distribution of every line of business, based on the model selection diagnostics and interpretability of the regression coefficients while unconstrained lognormal distributions are considered as a benchmark.
Once a marginal distribution for each triangle is specified, the dependence structure can be modeled with a 9-dimensional vine copula. Since marginal distributions are fixed and calibrated, it is possible to optimize (
2). For the optimization routine, we use the algorithm of
Dissmann et al. (
2013) which is readily available in an
R package
VineCopula, as a function
RVineStructureSelect, which explores both the optimal vine structure and the choice of family for each of the pair copulas sequentially. For a detailed explanation of such an implementation, see Chapter 8 of
Czado (
2019).
In our search for the vine structure, we also consider the sparsity of the vine copula. Since we need
pair copulas to construct a
d-dimensional vine structure, the number of required pair copulas quadratically increases as the dimension increases, which adds both complexity and computational burden to the optimization scheme. Therefore, in this article, we also incorporate the idea of a sparse copula so that a pair copula is considered to be an independent copula unless the estimated association Kendall’s Tau is significantly different from 0 for the pair copula. More specifically, we use the following test statistic
T based on the estimated value of Kendall’s Tau,
as proposed in
Genest and Favre (
2007):
where
T asymptotically follows a standard normal distribution if
m is large enough. For more approaches of incorporating sparsity in a high-dimensional vine copula, see
Gruber and Czado (
2018) and
Nagler et al. (
2019).
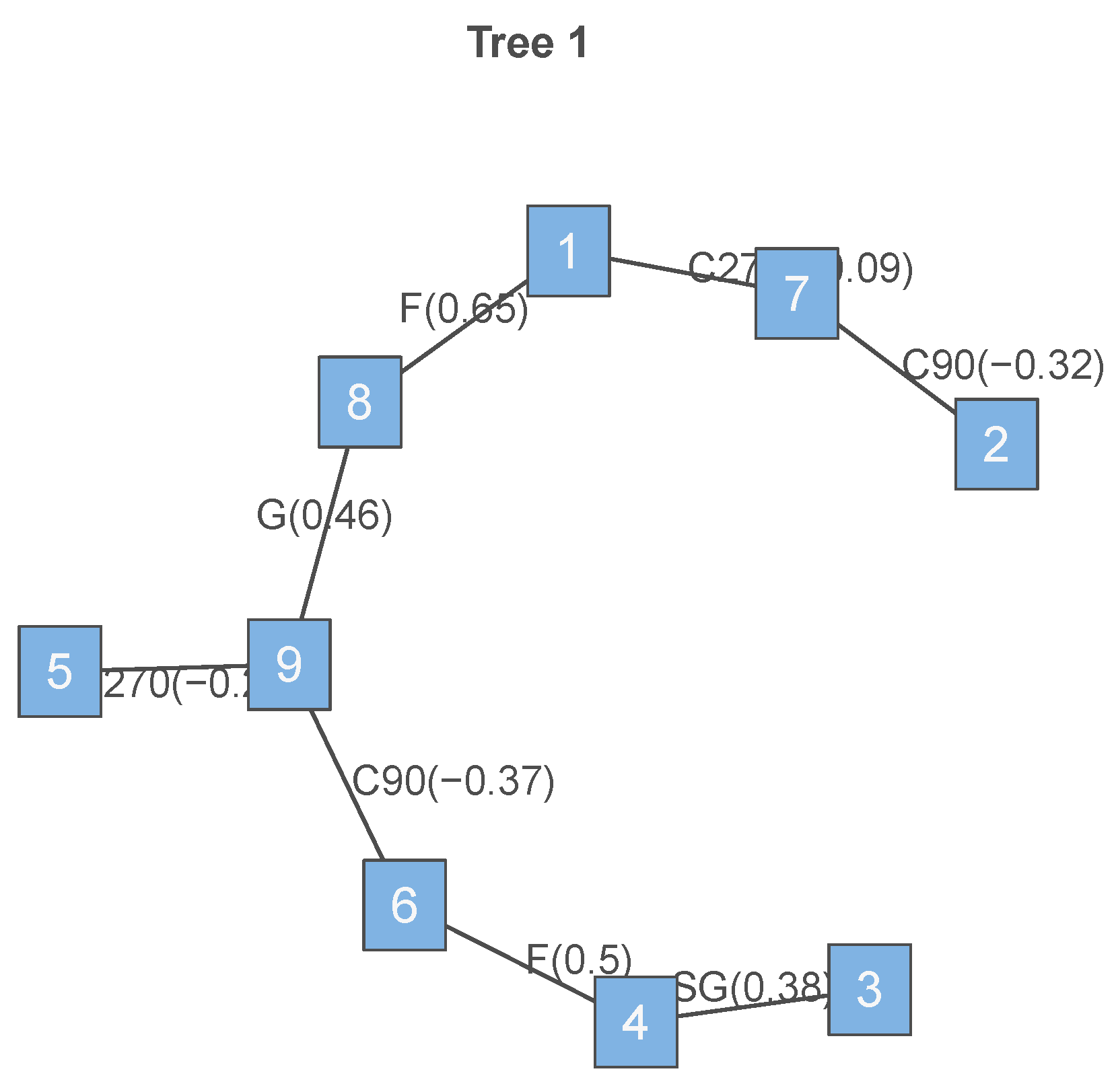
According to the optimization with the data, the optimal vine structure is given
Table 5 which only displays non-independent pair copulas. In the table,
and
mean estimated copula parameter and Kendall’s Tau for each pair copula, respectively. Some empirical relationships are observed by the estimated copula parameters, which seem intuitive considering the nature of the lines of business. For example, it might be quite natural to have strongly positive dependence among the development patterns of line 4 (North American non-casualty) and line 6 (overseas general non-casualty) due to inherent characteristics of the same claim type. Dependence between line 8 (global reinsurance property) and line 9 (global reinsurance non-property) is captured by the Gumbel copula, which indicates there is positive association between claim settlements in the initial years (that corresponds to upper tail part) for a global reinsurance business unit. Such a positive tail dependence might have originated from an internal decision on the claim processing in the same business unit. Note that a company has limited resources to deal with ligitations related to the claim adjustments so that claim adjustments can be delayed in a line by focusing on expediation in claim adjustments in another line, which might explain negative associations between lines 6 and 9, lines 2 and 7, and lines 5 and 9. One can see that the estimated vine structure exhibits enough of a degree of sparsity because only 10 pair copulas are non-independent among
pair copulas in the vine structure so that most of the dependencies arise from tree 1, as shown in
Figure 2. There are nine lines of business that correspond to the nodes of tree 1 so that we have nine nodes and eight edges as an R-vine structure which captures the first layer of dependence among the lines of business. Since the dependence of a pair of copulas is quite weak except for those in tree 1, we only display the R-vine structure for tree 1.
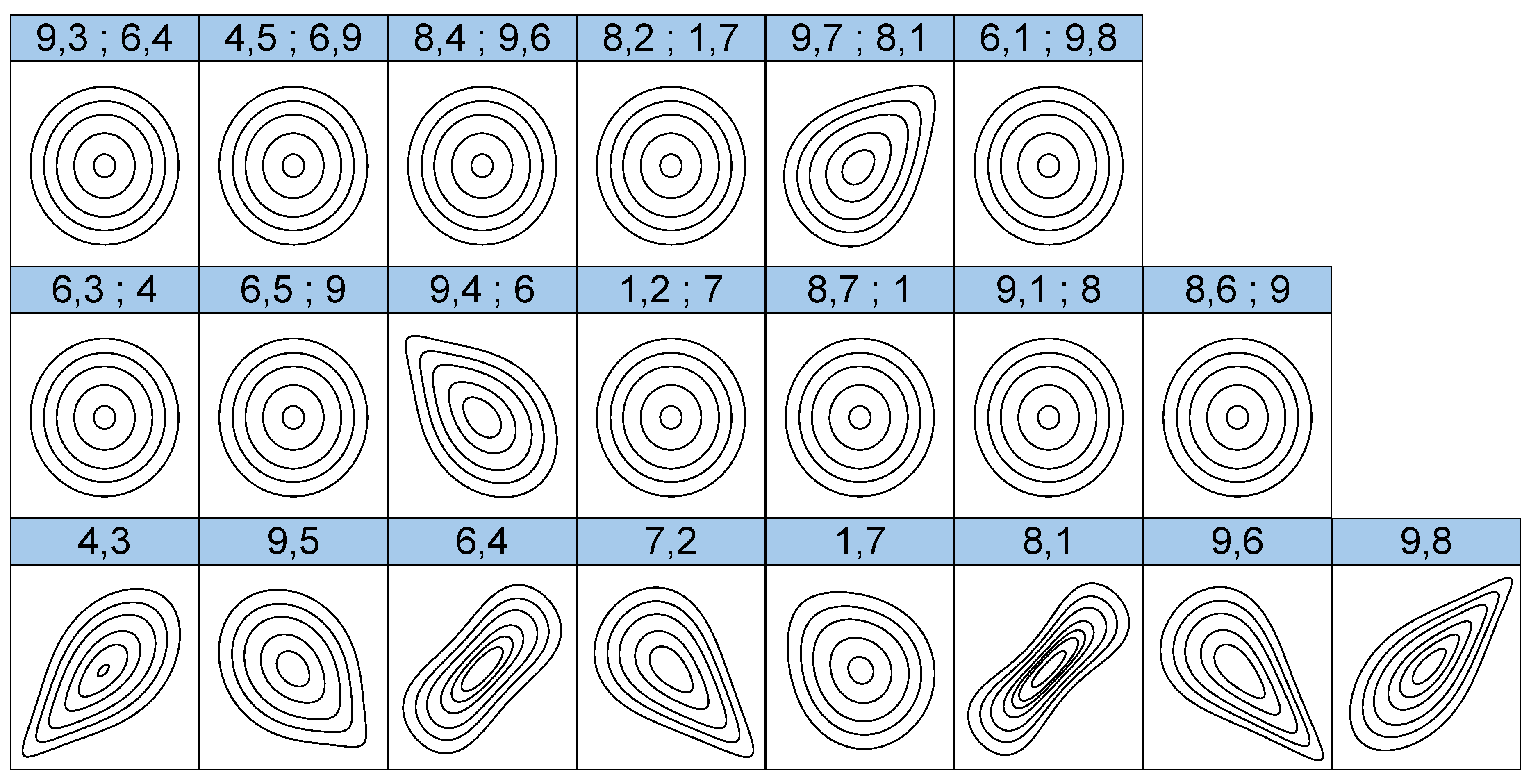
We also visualize the dependence structure via normalized contour plots in
Figure 3, which displays the association between two probabilty integral transforms in a normalized scale. For example, if a pair copula
is given, then the corresponding normalized contour plot gives us a contour plot with the following density
g:
Normalized contour plots for trees 1, 2, and 3 in the chosen vine structure are provided in
Figure 3. One can see that some pair copulas (for example,
and
) demonstrate strong tail dependence or skewed shape of the contours, which cannot be captured with naive use of eillptical copulas such as Gaussians or
copulas. Therefore,
Figure 3 substantiates that the choice of pair copula families are enough to describe the dependence structure observed in the data. In the figure, the first row corresponds to normalized contour plots for tree 3 where one can see concentric circles as contour plots, which indicates independence of corresponding pair copulas. On the other hand, one can see many skewed contour plots for tree 3 from the third row of the figure, which indicates varying dependence of corresponding pair copulas.
5. Validation and Actuarial Implication
Once a predictive model is calibrated based on the upper loss triangles
, which is defined in (
3), it needs to be validated based on available
, which is defined in (
4). For this purpose,
, the latest diagonals are used as a validation set.
Under the proposed lognormal model for marginal components, one can show that
so that a point estimate of
is given as
, where
and
are obtained as posterior means from the MC samples of parameters. Since it is of interest to predict the future unpaid claim
L as defined in (
5), here we apply three models to project the unpaid claims; the independent model which assumes independence among all lines of business, the silo model which assumes a perfect positive association among all lines of business, and the copula model which utilizes the vine copula structure specified and optimized in
Section 4.
Due to linearity of expectation, it is natural to expect that point estimates of reserves under the copula model would be more or less the same as the estimates under independent model. However, insurance companies are often interested in not only the predictive mean, but also the confidence interval of the estimated mean and risk measures for enterprise risk management. In this regard, the proposed vine copula model allows us to consider the impacts of associations among the lines of business that might lead to more accurate estimation of risk measures. For example, if there are positive associations among the lines of business, then the independent model will underestimate Value at Risk (VaR) or Conditional tail expectation (CTE) since a worse scenario can affect all lines of business adversely.
Table 6 summarizes the point estimates of unpaid claims for the subsequent calendar year based on the copula model and the silo model. Note that point estimates of unpaid claims from the independent model should be the same as ones from the copula model, as long as we model each line of business with the same marginal distribution. Further, although we primarily use constrained models for the marginal components, here we also provide the point estimates of unpaid claims from the models where we do not impose any constraints on the parameters.
From the table, it is shown that copula model with constraints turns out to be the best model in terms of prediction of aggregate unpaid claims for the subsequent year. We observe that under unconstrained models, the predicted values of unpaid claims can be severely exaggerated, especially for mature years (in our case, AY = 2005). That is because the value of
can be overestimated in the unconstrained models, as observed in
Table 3. Therefore, it implies that naive implementation of unconstrained model for multi-line reserving problem may end up with poor prediction.
In order to evaluate the prediction performance, here we use validation measures such as root mean squared error (RMSE) and mean absolute error (MAE) defined as follows:
where
is the estimate of
under each method. We prefer the models with smaller values of RMSE and/or MAE. According to
Table 7, the copula model with constraints still turns out to be the best model in terms of RMSE and MAE, which evaluate the performance of predicting the point estimates.
However, it is of less concern to get point estimates of
L, the aggregate unpaid claims. Actuaries (and companies) want to know a range of estimates, or the predictive distribution of the aggregate unpaid claims to assess the quality of decision making on reserve and retain appropriate amounts of risk capital for the whole company. Thus, here we provide a way to simulate predictive samples of
and describe the predictive distribution of
for
and subsequently
with the following steps, which are similar to those of
Gao (
2018):
Generate a 9-dimensional uniform random vector
based on the specified copula structure in a sequential way. For example, one can first generate
from
. After that,
is generated subsequently due to the following identity:
where
. One can continue such implementation to obtain a random sample of
d-dimensional uniform vector, which is readily available with
RVineSim function in
R package
VineCopula. (For details, see Chapter 6 of
Czado (
2019).)
Based on the lognormal assumption of marginal components, are generated as follows; where and are MC samples of and from the marginal model for the line of business, respectively.
Repeat steps 1 to 2 to get
, the MC samples of
for
where
Since , only needs to be simulated to describe the distribution of L. In the simulation scheme, possible uncertainties of estimated parameter values are already considered since the marginal parameters are estimated with the Bayesian approach.
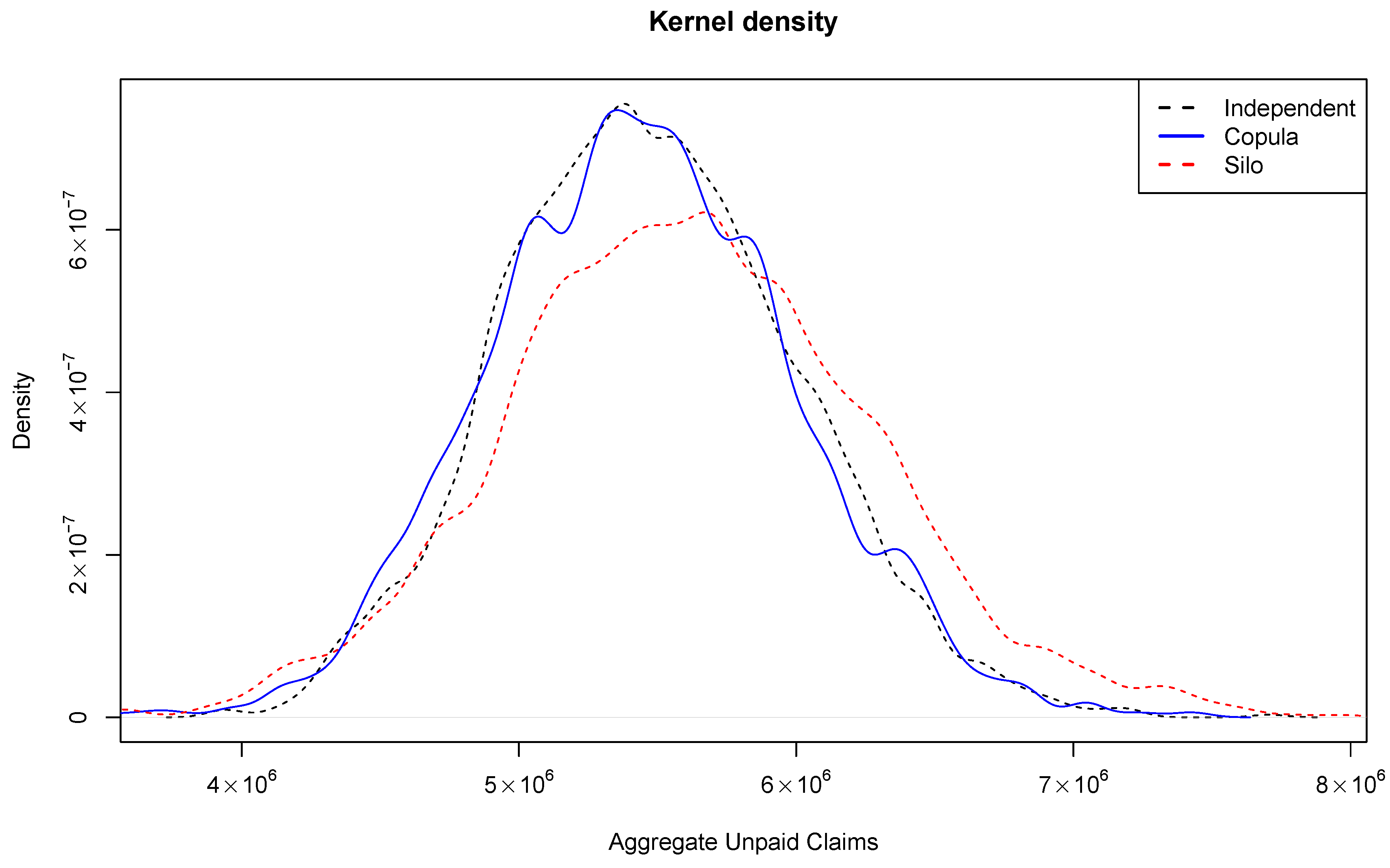
Figure 4 shows the predictive kernel densities of
L based on the Monte Carlo samples generated with the aforementioned approach from the constrained model. In the silo approach, all nine triangles are aggregated into one triangle based on the development lags and accident years, so that loss development patterns of all business lines are implicitly assumed to be identical, which may not be true in some cases. One can see that the predictive distribution of
L under the copula model is more jagged than one under the independent model, but the copula model is still closer to the independent model than the silo model. It agrees with the proposed vine copula structure described in
Figure 2, which shows a sufficient degree of sparsity.
The discrepancy among predictive distributions based on copula, independent, and silo models also can be quantified via Hellinger distance. Hellinger distance, originally proposed by
Hellinger (
1909), is used to quantify the "distance" between two distributions. For example, if there are two functions
f and
g which are probability density functions of two distributions
F and
G, the square of Hellinger distance is calculated as follows:
One can see that
is always satisfied with Hellinger distance so that it is well calibrated and interpreted, where
means
F and
G are identical almost surely and
means
F and
G are totally different. Due to this property, Hellinger distance has been widely used in the statistics literature, such as
Beran (
1977), and estimation of
using generated samples from
F and
G can be easily implemented via
R packages such as
statip. Here,
, the square of the Hellinger distance between the kernel density of
L under copula model with constraints (illustrated with blue solid line in
Figure 4) and the density under the independent model with constraints (illustrated with black dotted line in
Figure 4) is about
while
. Therefore, one can see that the proposed vine copula structure can capture weak dependencies among the lines of business.
Note that Hellinger distance is a special case of the functional Bregman divergence proposed in
Goh and Dey (
2014) and
Jeong (
2020), which is given as follows:
where
is a strictly convex and differentiable function with positive support and
. One can see that
if
, and
is Kullback–Leibler divergence if
.
Based on the predictive distributions of
L and
for
, one can calculate the risk margins for the unpaid claims as in
Table 8. Both VaR and CTE are estimated in an empirical way—in other words, based on the generated samples of the predictive distribution of
L or
. Usually, it is expected that a company can get a benefit from the diversification of risks for multiple lines of business so that the risk capital for aggregate reserve is less than the sum of the risk capitals for the reserve of each line, which is known as subadditivity of risk measure. Although subadditivity is not guaranteed for VaR, it is guaranteed for CTE and we can quantify the diversification effects by taking the differences of risk capitals by subtracting the risk capital for aggregate reserve from the sum of the risk capitals for the reserve of each line.
Table 9 summarizes measured diversification effects for given models. We can observe that the measured diversification effect of the copula model is much greater than that of the silo model because of weak dependence captured in the vine structure, although it is still less than that of the independent model, which assumes perfect independence among the lines of business.
7. Conclusions
In this article, we explored and introduced a novel approach which considered possible dependence among the multiple lines of business via vine copula. Use of a vine copula is very flexible and it allows us to model high-dimensional dependence among the business lines, not only bivariate dependence. In the case of traditional copula models, one needs to calibrate many copula models with different families, and go through model validation procedure to choose the best one among the candidates. On the other hand, our proposed vine copula structure enables us to explore the optimal copula structure for the given data in a unified manner.
For model selection, a stepwise approach can be applied to choose the marginal distributions, copula structure, and family for each pair of copulas subsequently. Our empirical analysis on a synthetic insurance portfolio consisting of nine lines of business showed weak associations among the lines.
Further, it was also shown that the naive implementation of a cross-classified model may result in a counterintuitive pattern of loss development, so one might consider a constrained cross-classified model to mitigate this issue. In our work, constraints on the development lag parameters are naturally incorporated via prior elicitation in a Bayesian framework. We expect that a more thorough discussion of the constrained cross-classified model in terms of variable selection could be one of the future directions of this work.