A Longitudinal Analysis of the Impact of Distance Driven on the Probability of Car Accidents
Abstract
1. Introduction
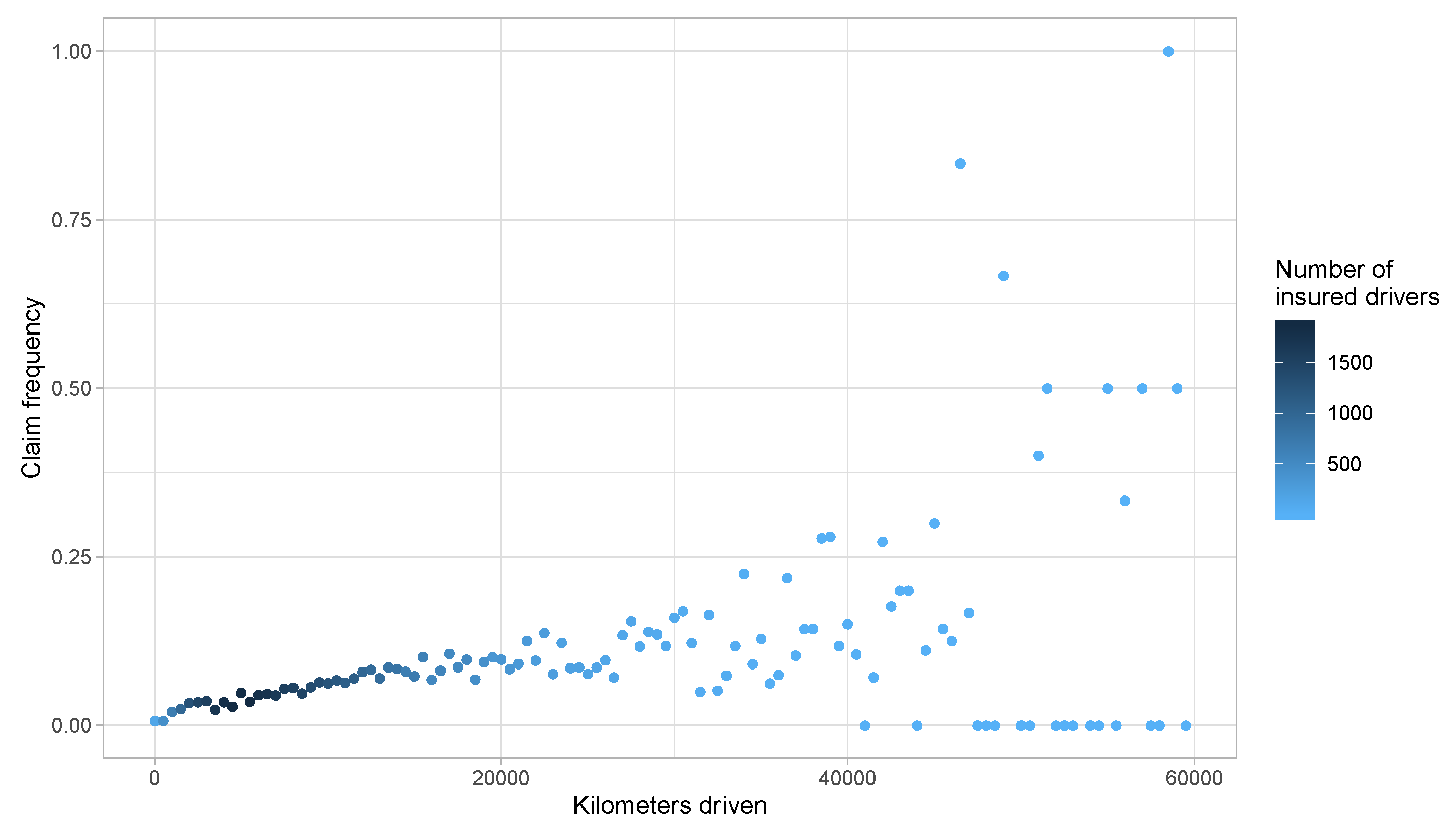
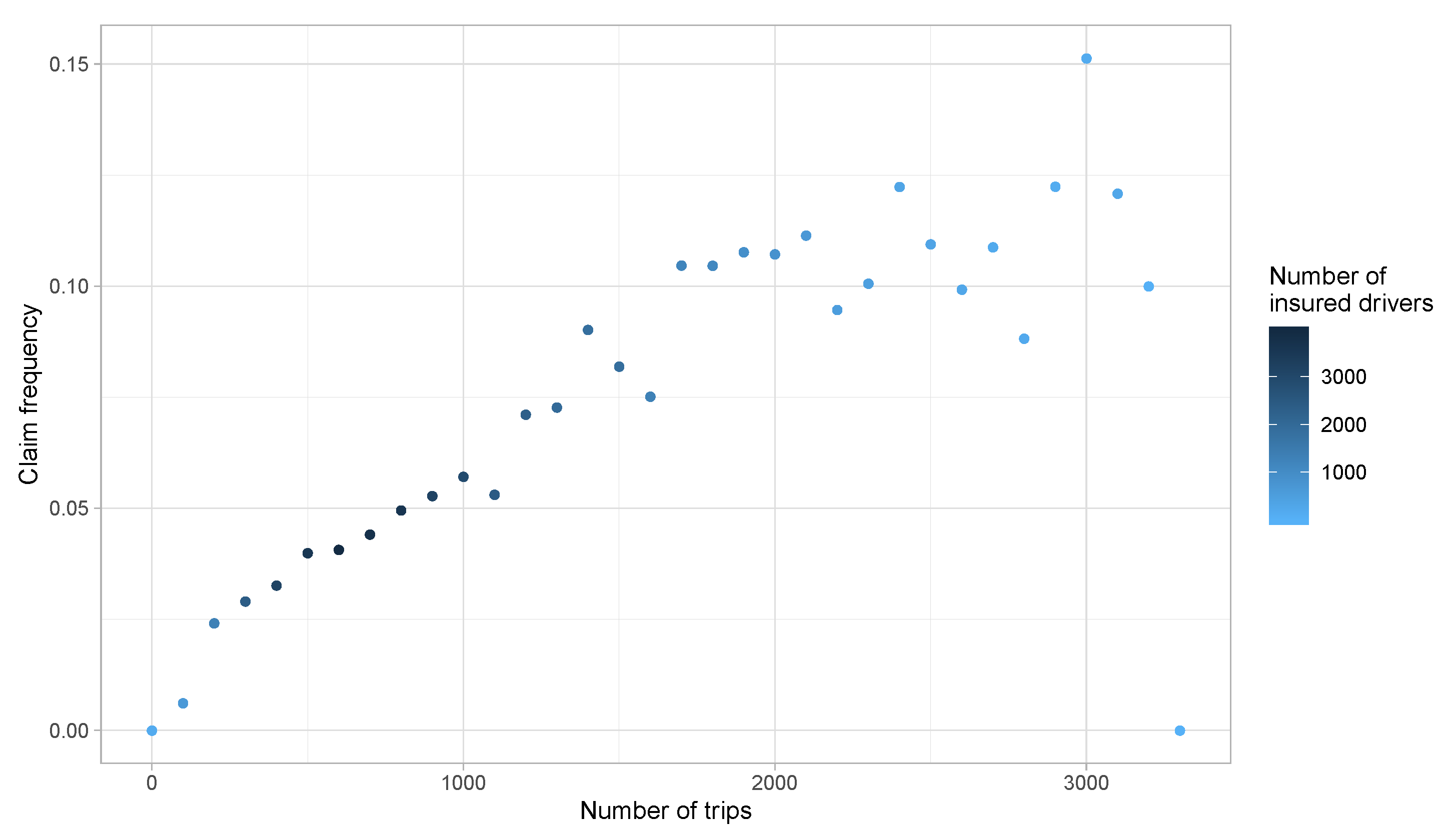
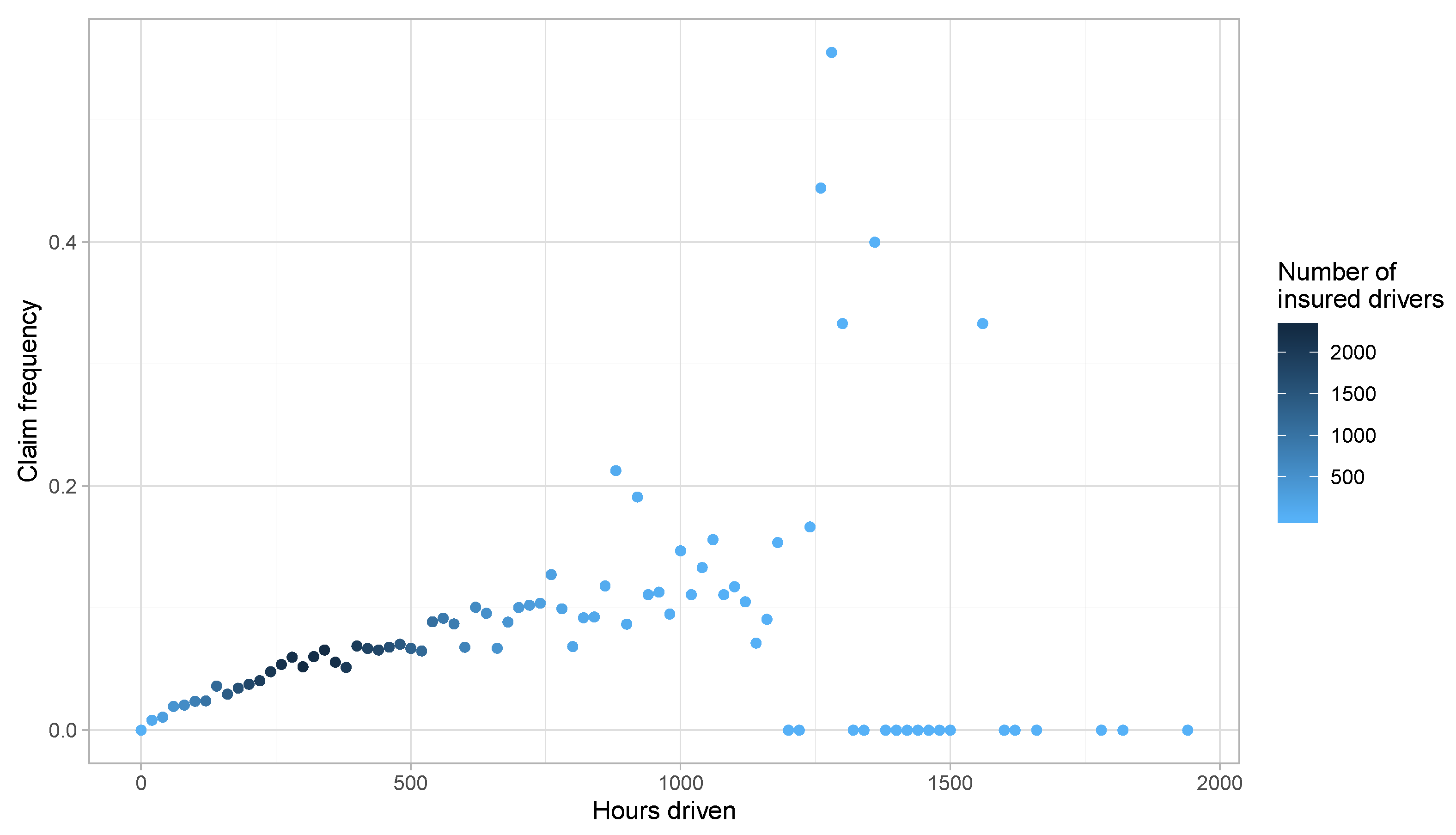
2. Summary of the Database
- Policyholders who are technophiles: they love new telematics technology, and want detailed information about their driving habits. Summary driving data is indeed continuously available to policyholders via a website.
- Young and/or bad drivers. To motive policyholders to buy the telematics option, insurance companies often offer an initial discount, and the renewal discounts range from 0% to 25% depending on driving experience.1 Because auto insurance in Ontario is very expensive and often unaffordable for some drivers, all discounts are welcome for policyholders with high insurance premiums. As a result, an unusually high proportion of risky insureds uses telematics devices or telematics app.
Risk Exposure Measures
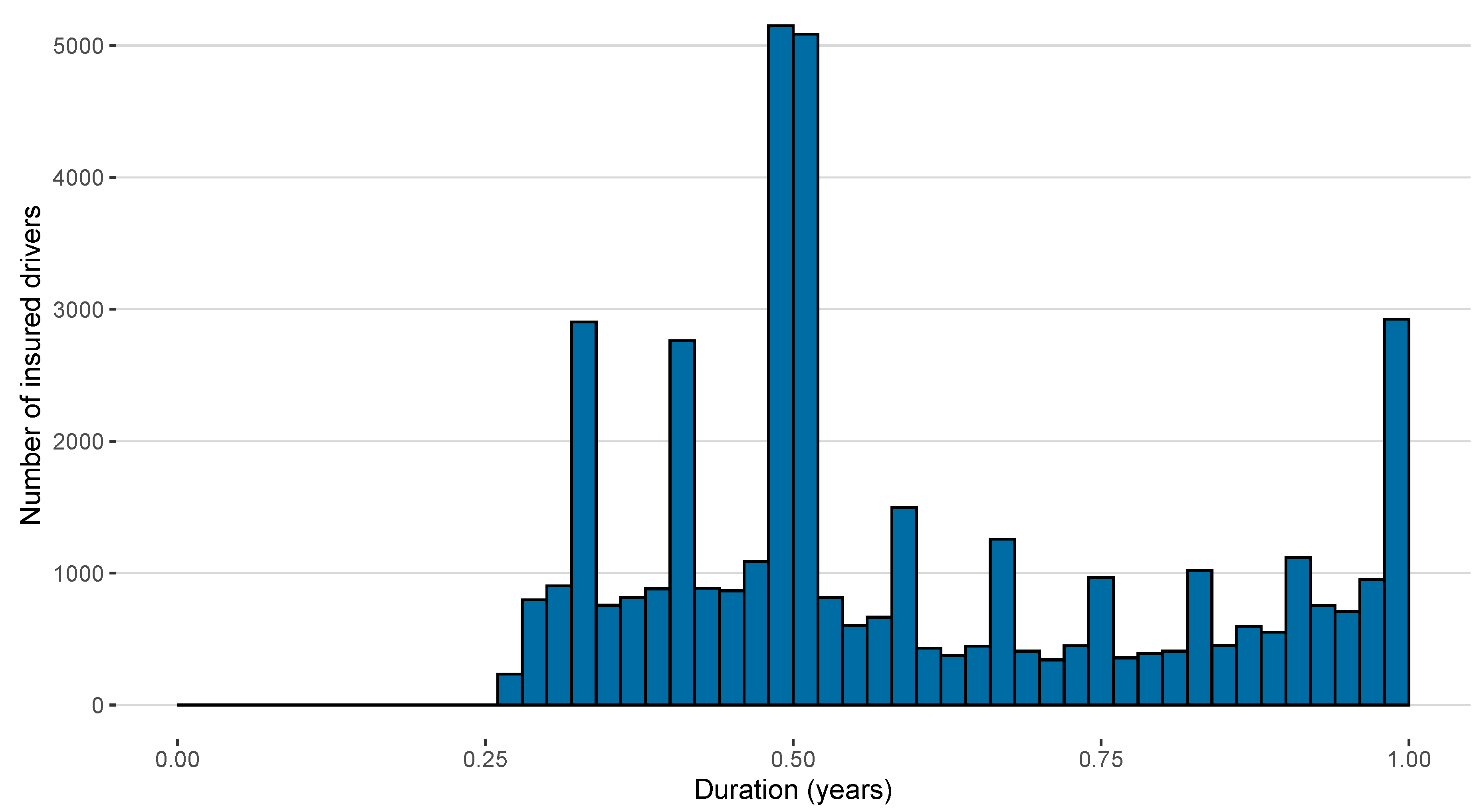
- Exposure time (the time between the start and the end of the insurance contract)
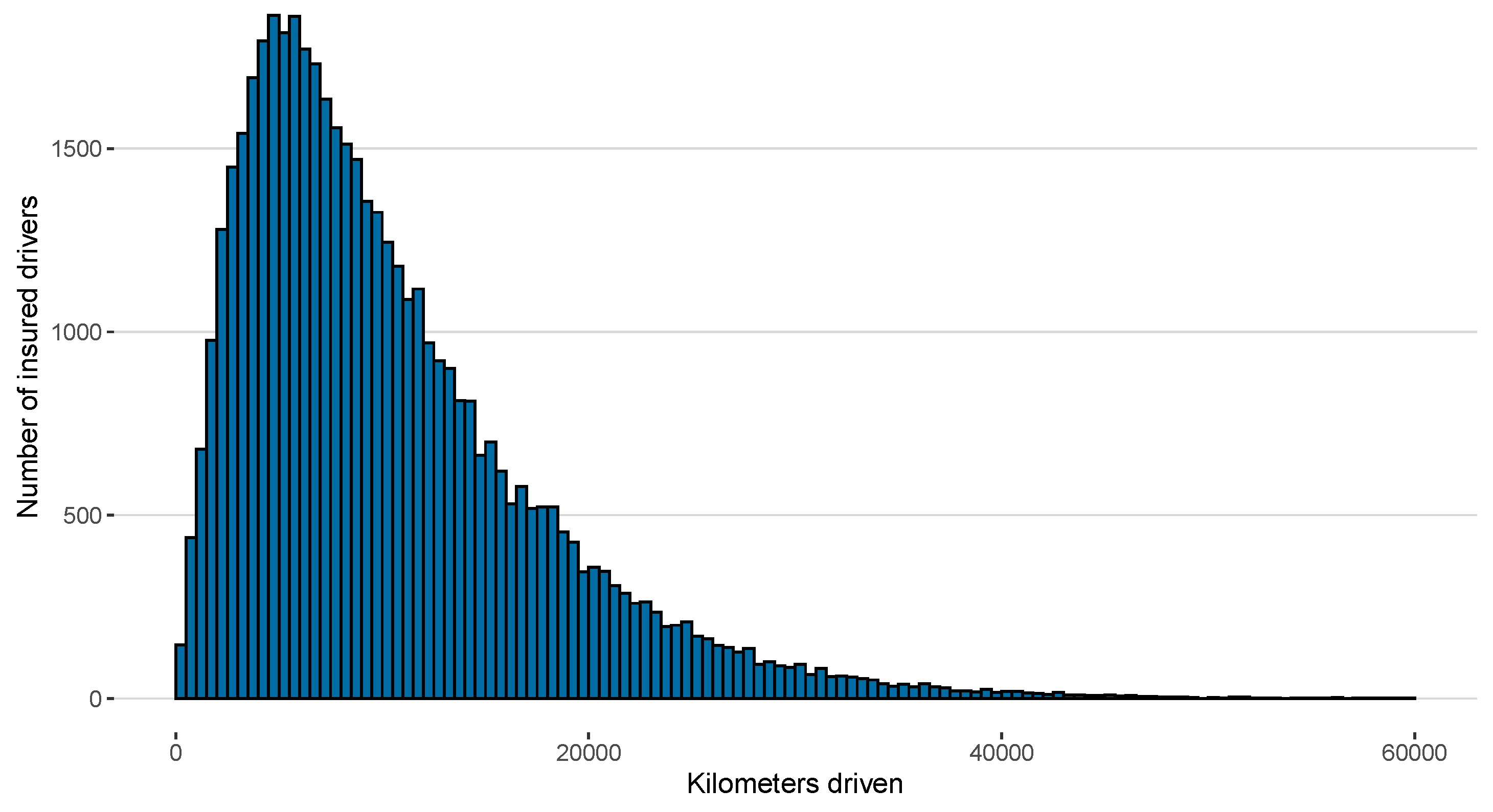
- Distance driven
- Number of trips
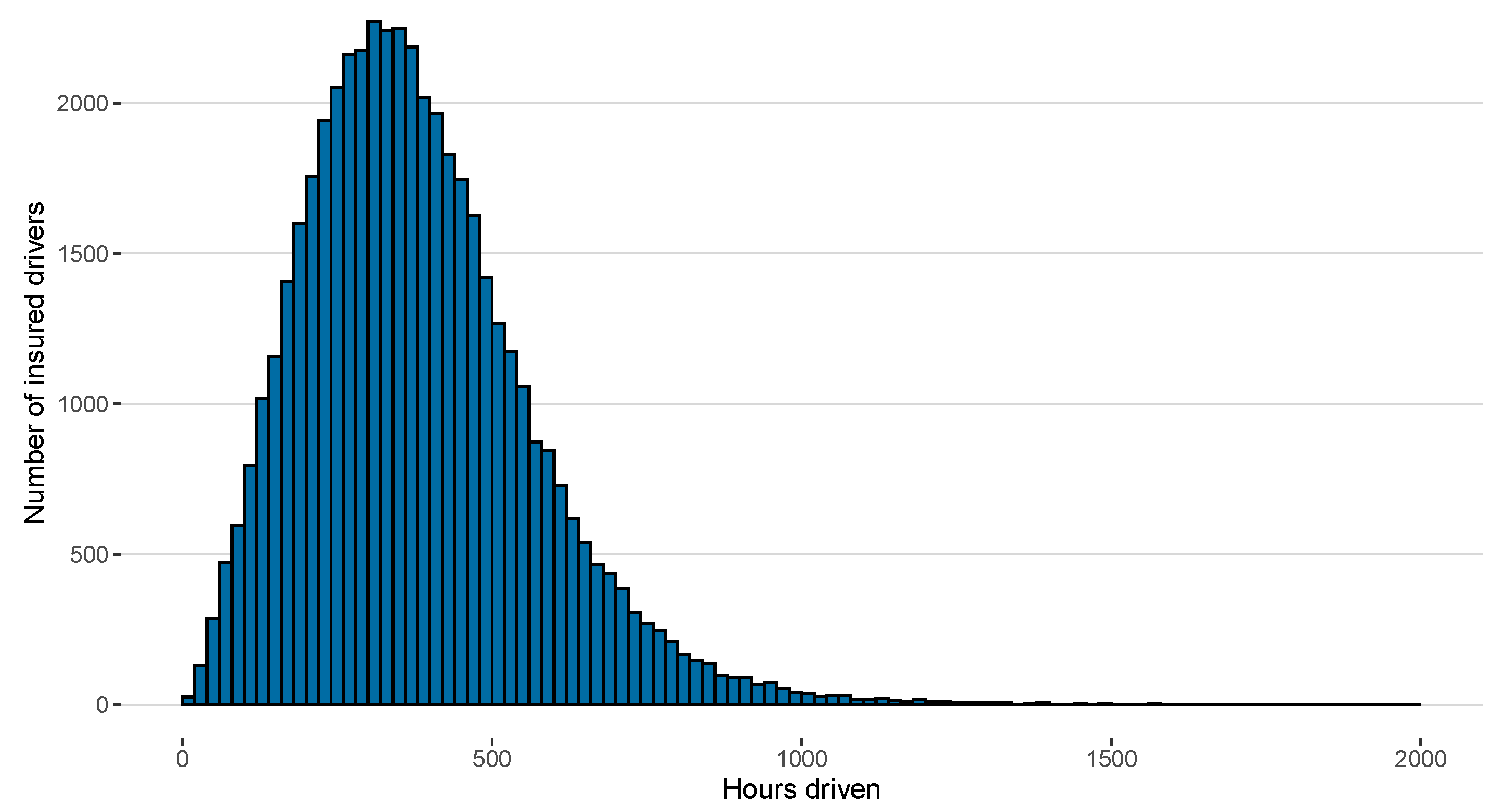
- Hours driven.
- The maximum number of trips observed is 3317 while another one only used his car 15 times for a single insured period.
- A policyholder drove the car for only for one hour for the whole insured period, while another driver used the car for more than 3000 h.
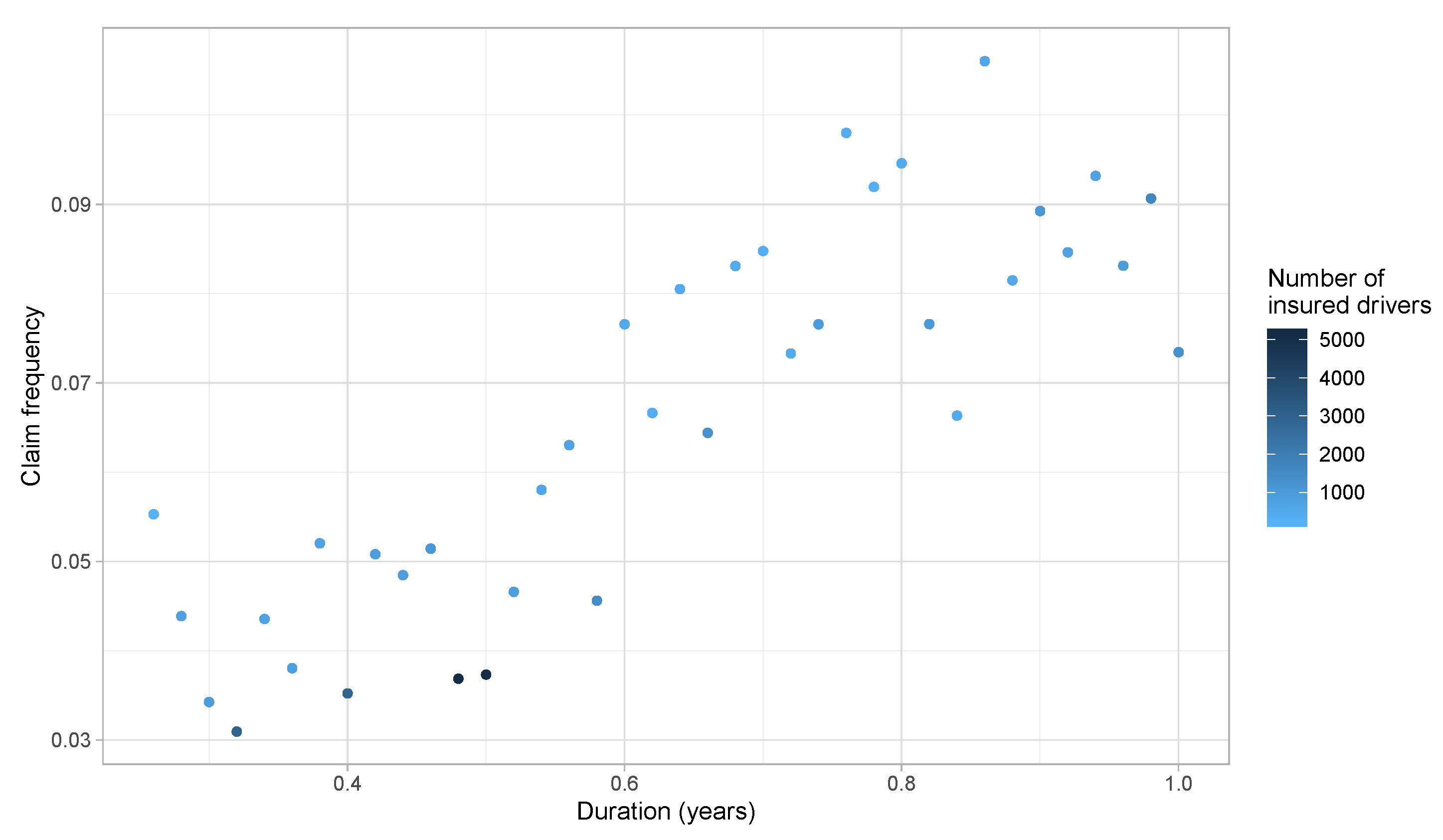
3. Preliminary Risk Exposure Analysis
4. Panel Data Modeling
5. Random Effects
5.1. Model Specification
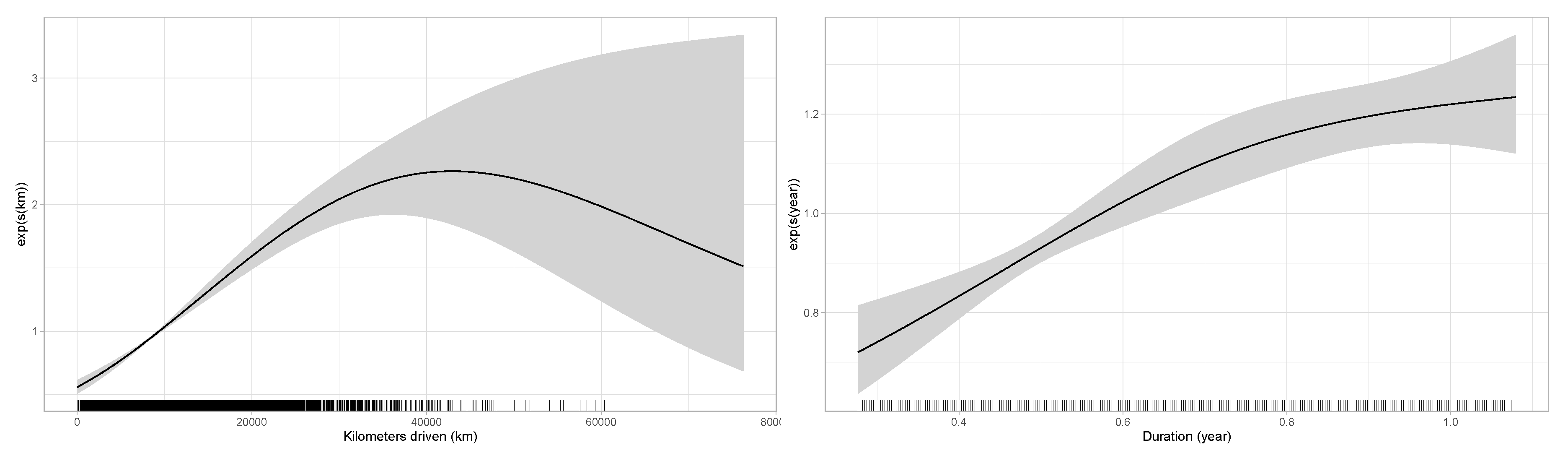
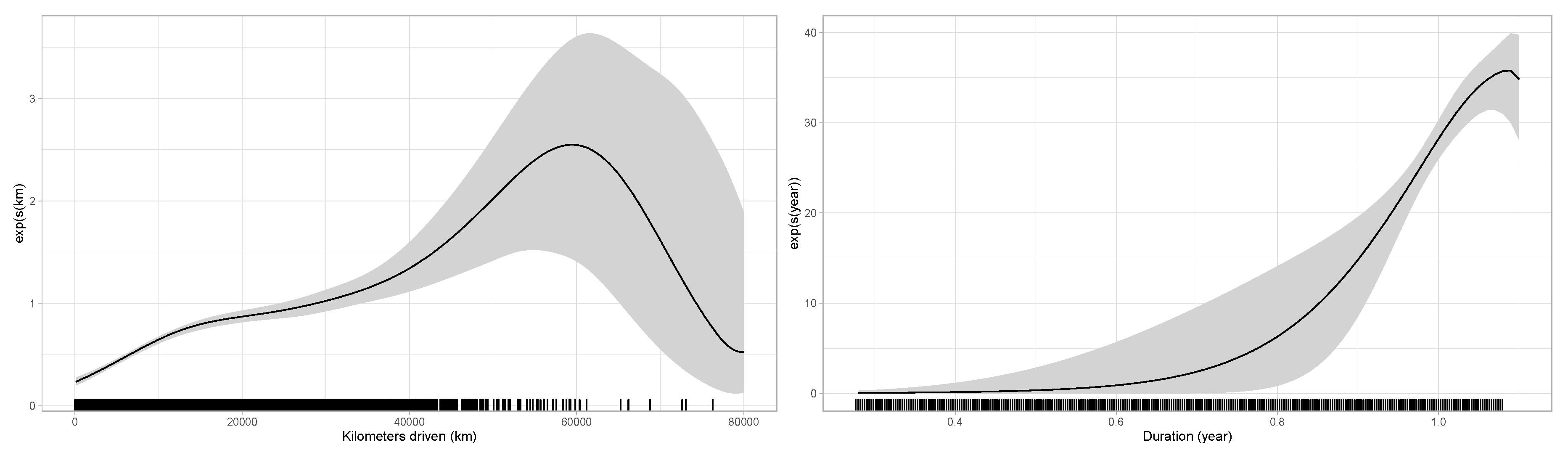
5.2. Numerical Illustration
6. Fixed Effects
6.1. Model Specification
- (1)
- When we compare Equations (4) (first-order condition equation of the random effects model) and (8), we see that when T is large, or when , random and fixed effects models are equivalent. However, in our data, the number of contracts observed for each insured i is small, while is significantly greater than zero. This results in different estimation equations between the two models.
- (2)
- Individuals observed for a single insured period, i.e., with , are not considered in the estimation of the parameters;
- (3)
- Individuals who have not filed claims with the insurer do not contribute to the estimation either. Indeed, for an individual i that does not have a claim, we have which is constant, whatever the value of .
- (4)
- It is necessary to restrict the covariates included in to those that change over time. Consequently, this also rules out the inclusion of an intercept in the model.
- (5)
- If does not change over for an individual i, this policyholder does not contribute to the estimation (even if they claimed). The ratio is the key element in the estimation of , where it is used to find the best “weight” to apply at each to approximate . In other words, to measure the specific effect of a covariate , the driving experience of an insured must be measured with and without the effect of . For the distance driven, this seems to be exactly what we are looking for. Indeed, as mentioned in Section 3, we are looking for the marginal impact of each extra kilometer driven when insureds decide to use their car rather than leaving it at home.
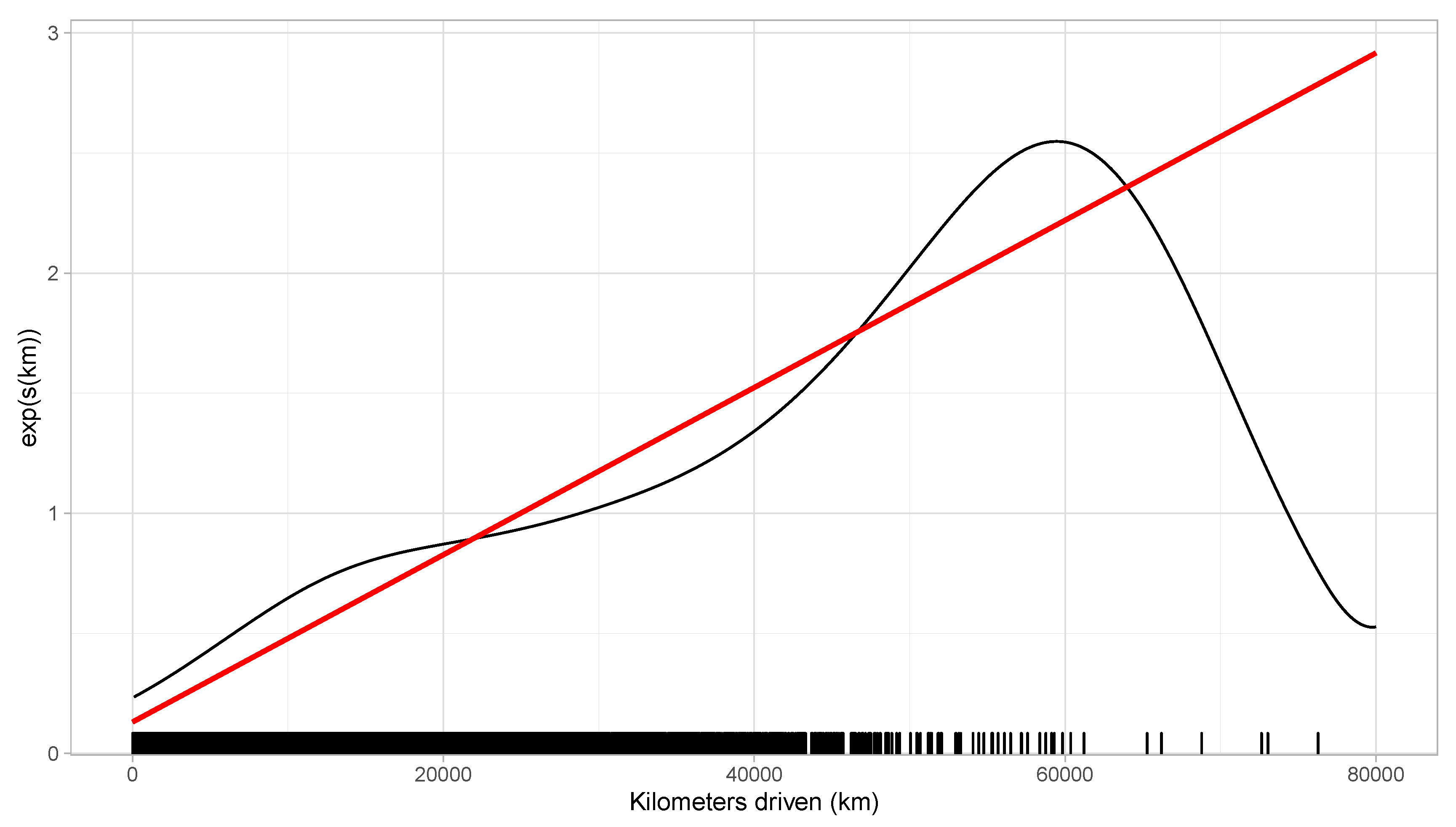
6.2. Poisson Fixed Effects and Smoothing Functions
- removing insureds without claim,
- removing insured observed for only one insured period ,
- adding a factor covariate for insured identification,
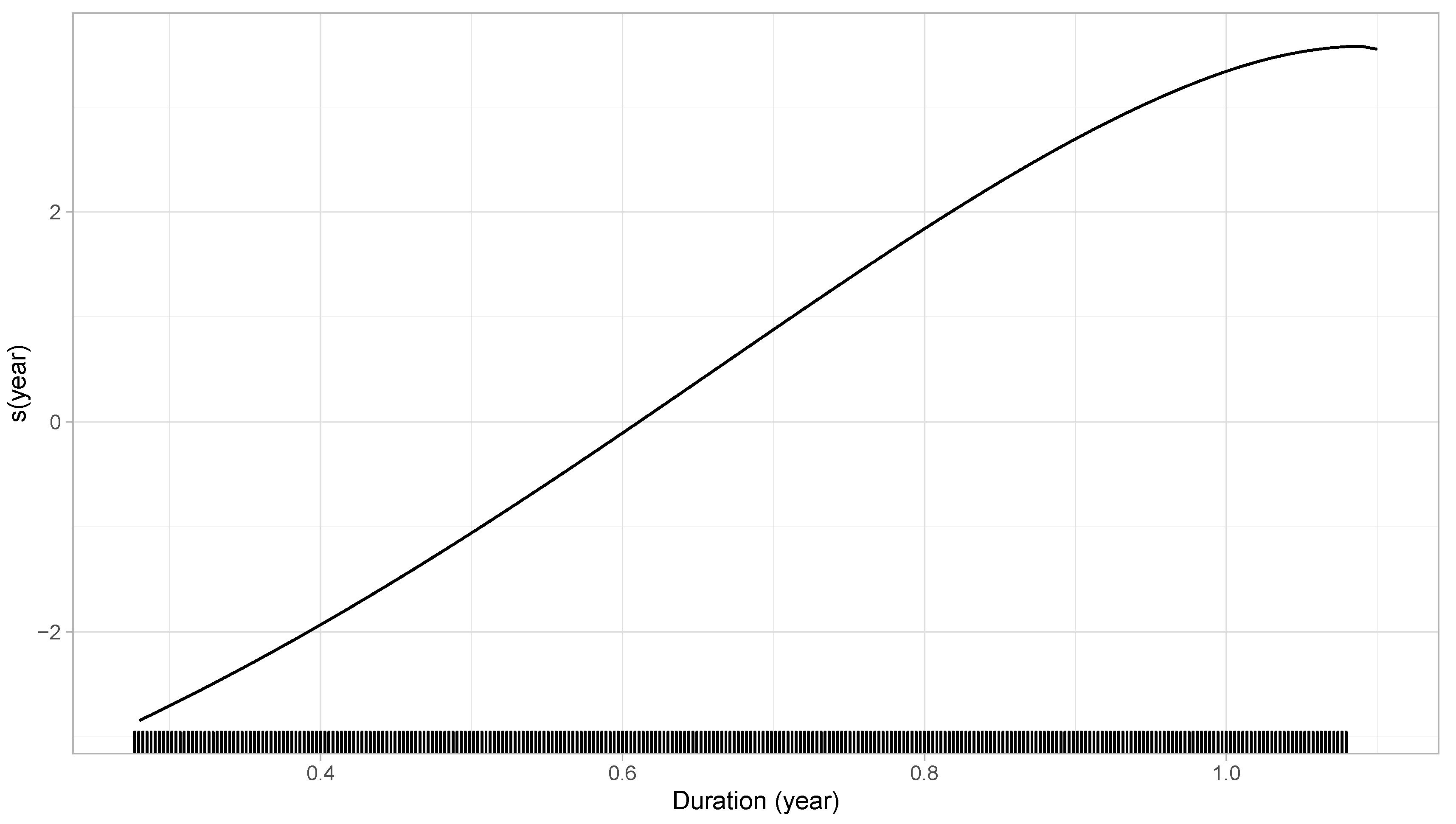
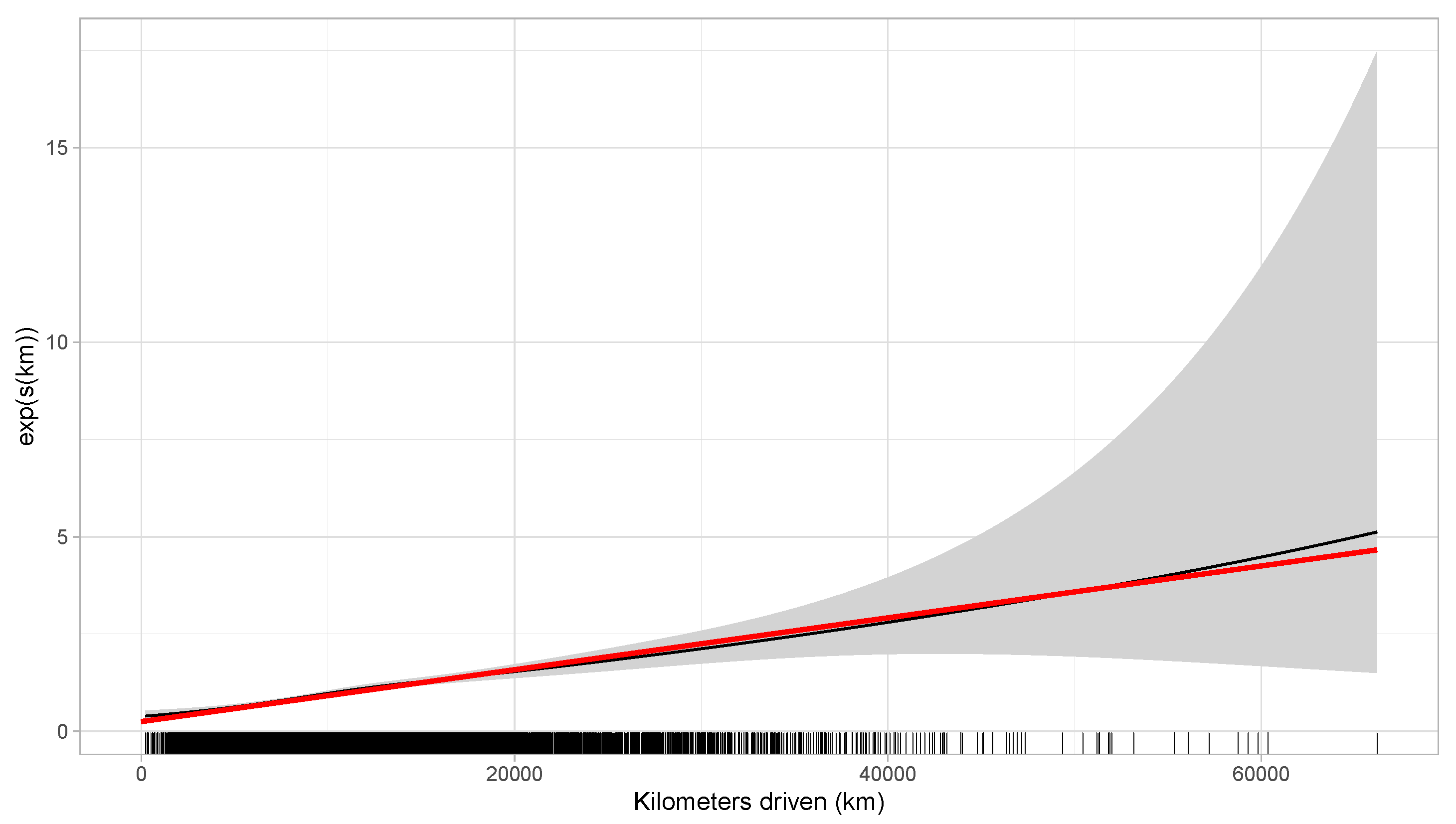
6.3. Numerical Illustration
6.4. Which Effect Should Be Used in Practice?
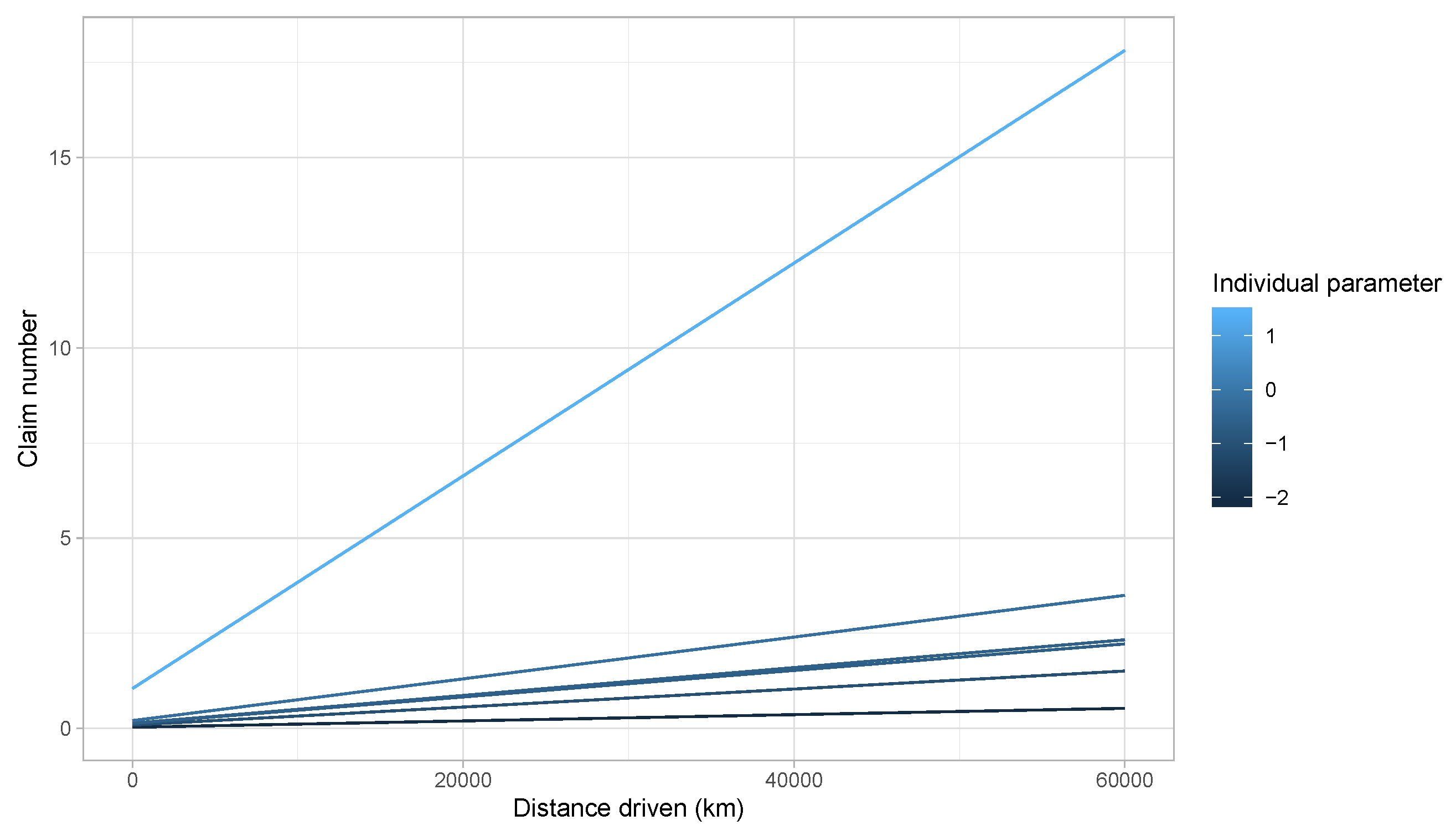
- The model requires evaluating an individual parameter for each insured i in the portfolio. This raises a problem for new policyholders.
- For a small value of , may be incorrectly estimated.
- As the model estimates each individual as , policyholders without claims will have an expected number of claims of 0, meaning that the premium of these insureds should be zero.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ayuso, Mercedes, Montserrat Guillén, and Ana María Pérez-Marín. 2014. Time and distance to first accident and driving patterns of young drivers with pay-as-you-drive insurance. Accident Analysis & Prevention 73: 125–31. [Google Scholar]
- Ayuso, Mercedes, Montserrat Guillen, and Ana María Pérez Marín. 2016a. Using gps data to analyse the distance travelled to the first accident at fault in pay-as-you-drive insurance. Transportation Research Part C: Emerging Technologies 68: 160–67. [Google Scholar] [CrossRef]
- Ayuso, Mercedes, Montserrat Guillen, and Ana María Pérez-Marín. 2016b. Telematics and gender discrimination: Some usage-based evidence on whether men’s risk of accidents differs from women’s. Risks 4: 10. [Google Scholar] [CrossRef]
- Ayuso, Mercedes, Montserrat Guillen, and Jens Perch Nielsen. 2019. Improving automobile insurance ratemaking using telematics: Incorporating mileage and driver behaviour data. Transportation 46: 735–52. [Google Scholar] [CrossRef]
- Bolderdijk, Jan Willem, Jasper Knockaert, E. M. Steg, and Erik T. Verhoef. 2011. Effects of pay-as-you-drive vehicle insurance on young drivers’ speed choice: Results of a dutch field experiment. Accident Analysis & Prevention 43: 1181–86. [Google Scholar]
- Boucher, Jean-Philippe, and Michel Denuit. 2006. Fixed versus random effects in poisson regression models for claim counts: A case study with motor insurance. ASTIN Bulletin: The Journal of the IAA 36: 285–301. [Google Scholar] [CrossRef][Green Version]
- Boucher, Jean-Philippe, Ana Maria Pérez-Marín, and Miguel Santolino. 2013. Pay-as-you-drive insurance: The effect of the kilometers on the risk of accident. In Anales del Instituto de Actuarios Españoles. 19 vols. Madrid: Instituto de Actuarios Españoles, pp. 135–54. [Google Scholar]
- Boucher, Jean-Philippe, Steven Côté, and Montserrat Guillen. 2017. Exposure as duration and distance in telematics motor insurance using generalized additive models. Risks 5: 54. [Google Scholar] [CrossRef]
- Cameron, A. Colin, and Pravin K. Trivedi. 2013. Regression Analysis of Count Data. 53 vols. Cambridge: Cambridge University Press. [Google Scholar]
- Denuit, Michel, Montserrat Guillen, and Julien Trufin. 2019. Multivariate credibility modelling for usage-based motor insurance pricing with behavioural data. Annals of Actuarial Science 13: 378–99. [Google Scholar] [CrossRef]
- Denuit, Michel, Xavier Maréchal, Sandra Pitrebois, and Jean-François Walhin. 2007. Actuarial Modelling of Claim Counts: Risk Classification, Credibility and Bonus-Malus Systems. Hoboken: John Wiley & Sons. [Google Scholar]
- Eilers, Paul H. C., and Brian D. Marx. 1996. Flexible smoothing with b-splines and penalties. Statistical Science 11: 89–102. [Google Scholar] [CrossRef]
- Ferreira, Joseph, and Eric Minikel. 2010. Pay-as-You-Drive Auto Insurance in Massachusetts: A Risk Assessment and Report on Consumer, Industry and Environmental Benefits. Boston: Conservation Law Foundation. [Google Scholar]
- Gao, Guangyuan, and Mario V. Wüthrich. 2018. Feature extraction from telematics car driving heatmaps. European Actuarial Journal 8: 383–406. [Google Scholar] [CrossRef]
- Gao, Guangyuan, Shengwang Meng, and Mario V. Wüthrich. 2019. Claims frequency modeling using telematics car driving data. Scandinavian Actuarial Journal 2019: 143–62. [Google Scholar] [CrossRef]
- Green, Peter J., and Bernard W. Silverman. 1993. Nonparametric Regression and Generalized Linear Models: A Roughness Penalty Approach. Boca Raton: Chapman and Hall/CRC. [Google Scholar]
- Hastie, Trevor, and Robert Tibshirani. 1986. Generalized additive models. Statistical Science 1: 297–310. [Google Scholar] [CrossRef]
- Inouye, David I., Eunho Yang, Genevera I. Allen, and Pradeep Ravikumar. 2017. A review of multivariate distributions for count data derived from the poisson distribution. Wiley Interdisciplinary Reviews: Computational Statistics 9: e1398. [Google Scholar] [CrossRef] [PubMed]
- Lemaire, Jean, Sojung Carol Park, and Kili C. Wang. 2016. The use of annual mileage as a rating variable. ASTIN Bulletin 46: 39–69. [Google Scholar] [CrossRef]
- Ma, Yu-Luen, Xiaoyu Zhu, Xianbiao Hu, and Yi-Chang Chiu. 2018. The use of context-sensitive insurance telematics data in auto insurance rate making. Transportation Research Part A: Policy and Practice 113: 243–58. [Google Scholar] [CrossRef]
- Molenberghs, Geert, and Geert Verbeke. 2006. Models for Discrete Longitudinal Data. Berlin: Springer Science & Business Media. [Google Scholar]
- Rigby, Robert A., and D. Mikis Stasinopoulos. 2005. Generalized additive models for location, scale and shape. Journal of the Royal Statistical Society: Series C (Applied Statistics) 54: 507–54. [Google Scholar] [CrossRef]
- Tselentis, Dimitrios I., George Yannis, and Eleni I. Vlahogianni. 2016. Innovative insurance schemes: Pay as/how you drive. Transportation Research Procedia 14: 362–71. [Google Scholar] [CrossRef]
- Verbelen, Roel, Katrien Antonio, and Gerda Claeskens. 2018. Unravelling the predictive power of telematics data in car insurance pricing. Journal of the Royal Statistical Society: Series C (Applied Statistics) 67: 1275–304. [Google Scholar] [CrossRef]
- Weidner, Wiltrud, Fabian W. G. Transchel, and Robert Weidner. 2016. Classification of scale-sensitive telematic observables for riskindividual pricing. European Actuarial Journal 6: 3–24. [Google Scholar] [CrossRef]
- Wood, Simon N. 2017. Generalized Additive Models: An Introduction with R. Boca Raton: Chapman and Hall/CRC. [Google Scholar]
- Wüthrich, Mario V. 2017. Covariate selection from telematics car driving data. European Actuarial Journal 7: 89–108. [Google Scholar] [CrossRef]
| 1 | Please note that it is not legally possible for an Ontario insurance company to increase the insurance premium based on the telematics information collected. |

| Number of Insurance Periods | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Number of policyholders | 12,562 | 9746 | 3420 | 844 | 415 | 11 |
| Proportion (%) | 46.5 | 36.1 | 12.7 | 3.1 | 1.5 | 0.0 |
| Average | Variance | Min. | Max. | 25th pct | 50th pct | 75th pct | |
|---|---|---|---|---|---|---|---|
| Exp. Time (in years) | 0.645 | 0.060 | 0.277 | 1.079 | 0.463 | 0.540 | 0.912 |
| Dist. Driven (in km) | 10,398 | 55,138,376 | 7.1 | 76,272 | 5026 | 8561 | 13,836 |
| Nb. of Trips | 1083 | 383,165 | 15 | 3317 | 621 | 946 | 1434 |
| Time Driven (in hours) | 380 | 34,740 | 1 | 2159 | 248 | 356 | 483 |
| Nb. of claims | 0.060 | 0.061 | 0.000 | 3 | 0 | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boucher, J.-P.; Turcotte, R. A Longitudinal Analysis of the Impact of Distance Driven on the Probability of Car Accidents. Risks 2020, 8, 91. https://doi.org/10.3390/risks8030091
Boucher J-P, Turcotte R. A Longitudinal Analysis of the Impact of Distance Driven on the Probability of Car Accidents. Risks. 2020; 8(3):91. https://doi.org/10.3390/risks8030091
Chicago/Turabian StyleBoucher, Jean-Philippe, and Roxane Turcotte. 2020. "A Longitudinal Analysis of the Impact of Distance Driven on the Probability of Car Accidents" Risks 8, no. 3: 91. https://doi.org/10.3390/risks8030091
APA StyleBoucher, J.-P., & Turcotte, R. (2020). A Longitudinal Analysis of the Impact of Distance Driven on the Probability of Car Accidents. Risks, 8(3), 91. https://doi.org/10.3390/risks8030091




