Price Discovery and Market Reflexivity in Agricultural Futures Contracts with Different Maturities
Abstract
1. Introduction
2. Methodology
3. Empirical Application
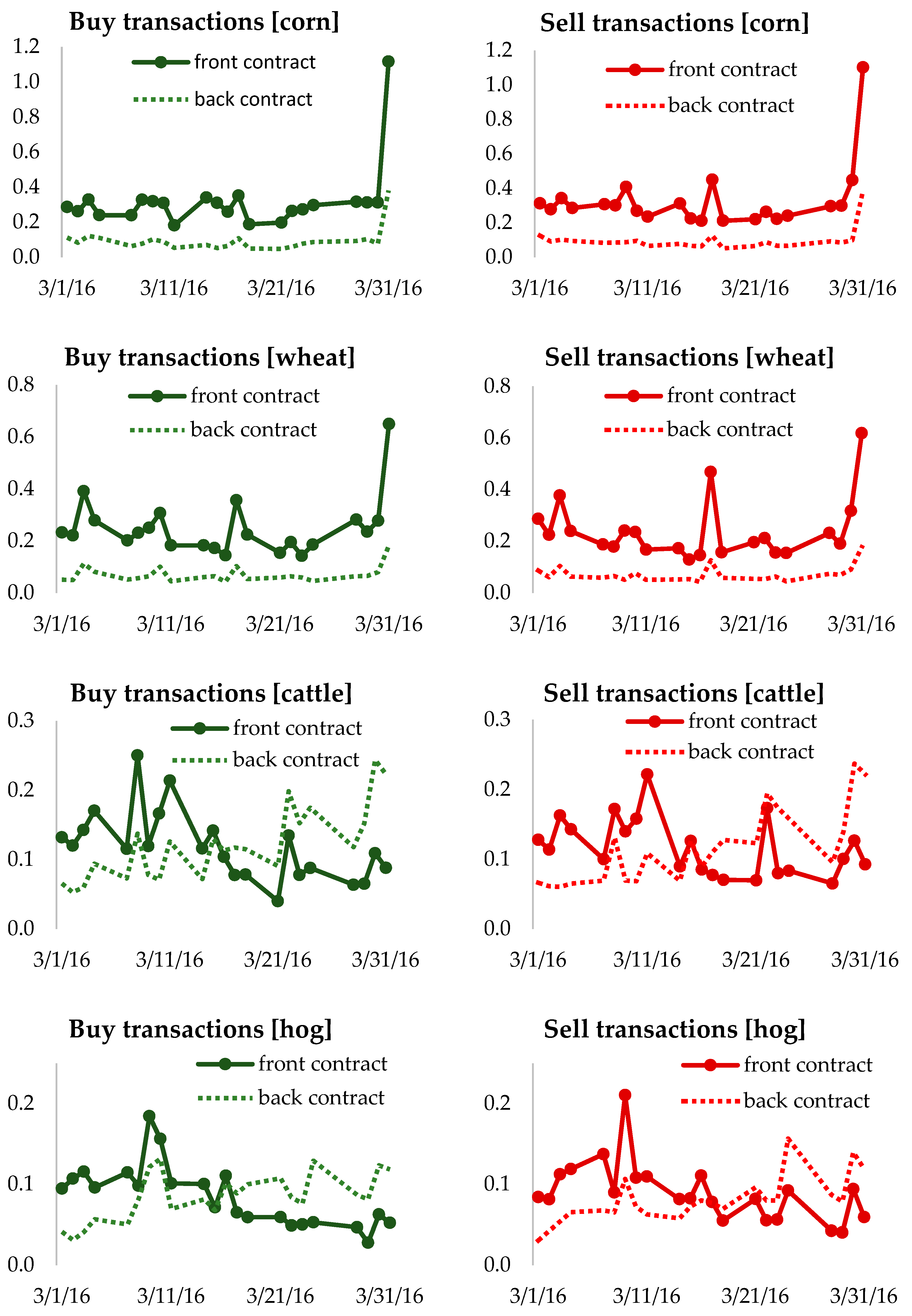
3.1. Data
3.2. Descriptive Statistics
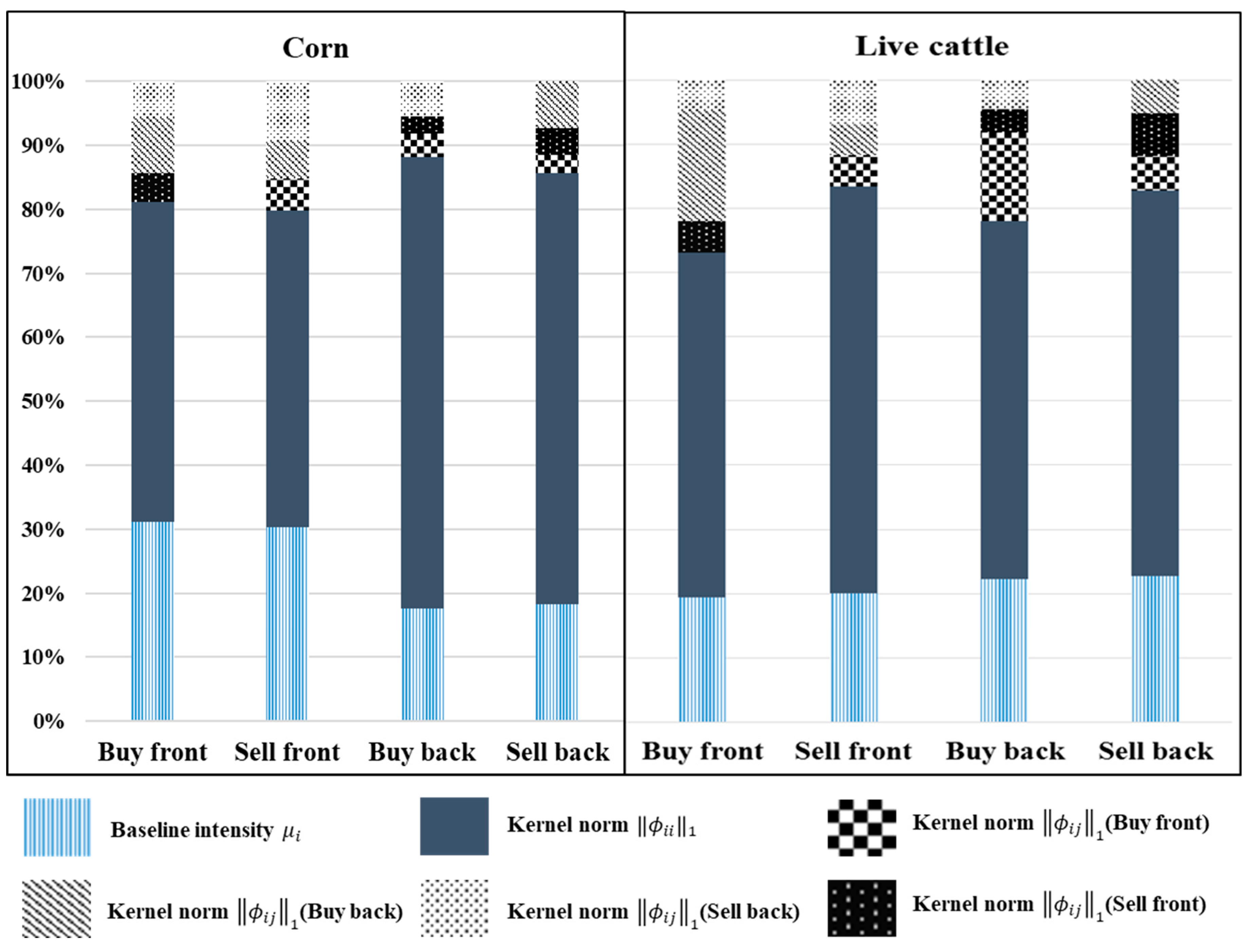
3.3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Contract | Front | Back | Front | Back | ||||
|---|---|---|---|---|---|---|---|---|
| Transaction | Buy | Sell | Buy | Sell | Buy | Sell | Buy | Sell |
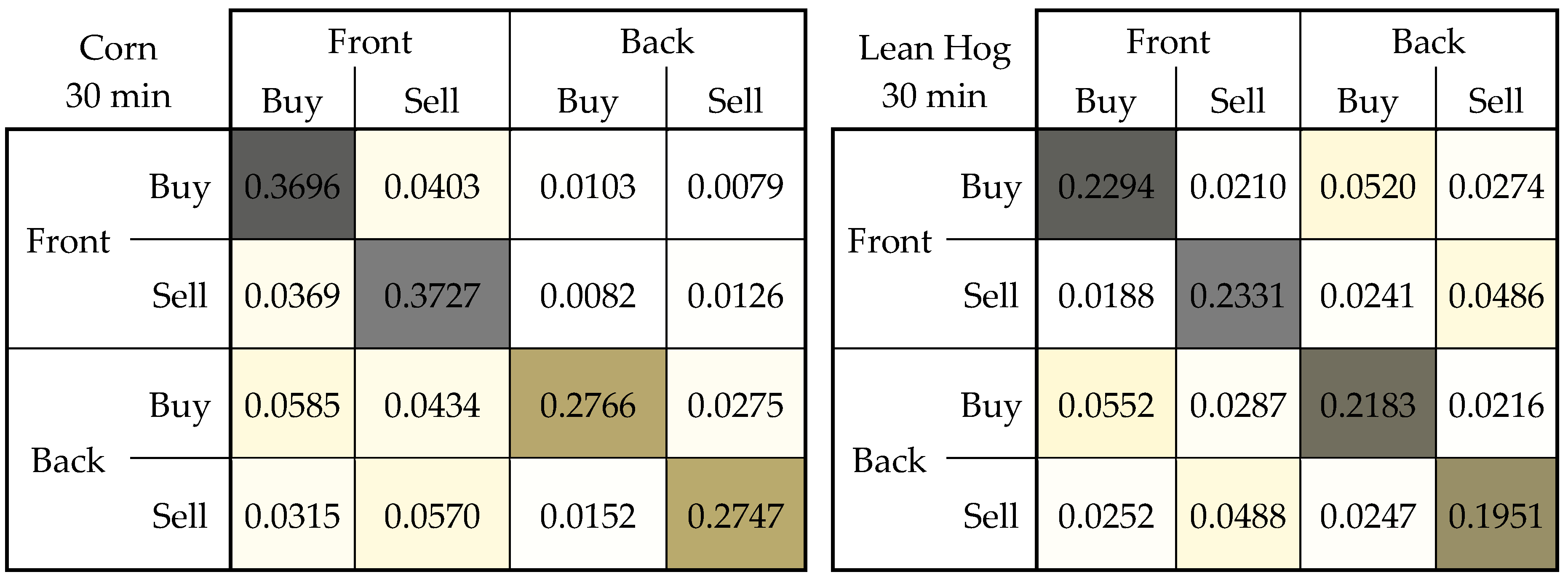
| Commodity | Corn (30-min interval) | Lean Hog (30-min interval) | ||||||
| Baseline intensity | 0.164 | 0.163 | 0.054 | 0.056 | 0.052 | 0.058 | 0.054 | 0.052 |
| Average intensity | 0.303 | 0.312 | 0.089 | 0.093 | 0.087 | 0.091 | 0.087 | 0.082 |
| Exogeneity ratio | 0.567 | 0.565 | 0.643 | 0.638 | 0.669 | 0.681 | 0.683 | 0.697 |
| Contract | Front | Back | Front | Back | ||||
|---|---|---|---|---|---|---|---|---|
| Transaction | Buy | Sell | Buy | Sell | Buy | Sell | Buy | Sell |
| Commodity | Corn (30-min interval) | Lean Hog (30-min interval) | ||||||
| Kolmogorov–Smirnov | 0.460 | 0.465 | 0.758 | 0.757 | 0.830 | 0.800 | 0.794 | 0.790 |
| Ljung–Box | 0.373 | 0.374 | 0.791 | 0.770 | 0.807 | 0.785 | 0.829 | 0.860 |
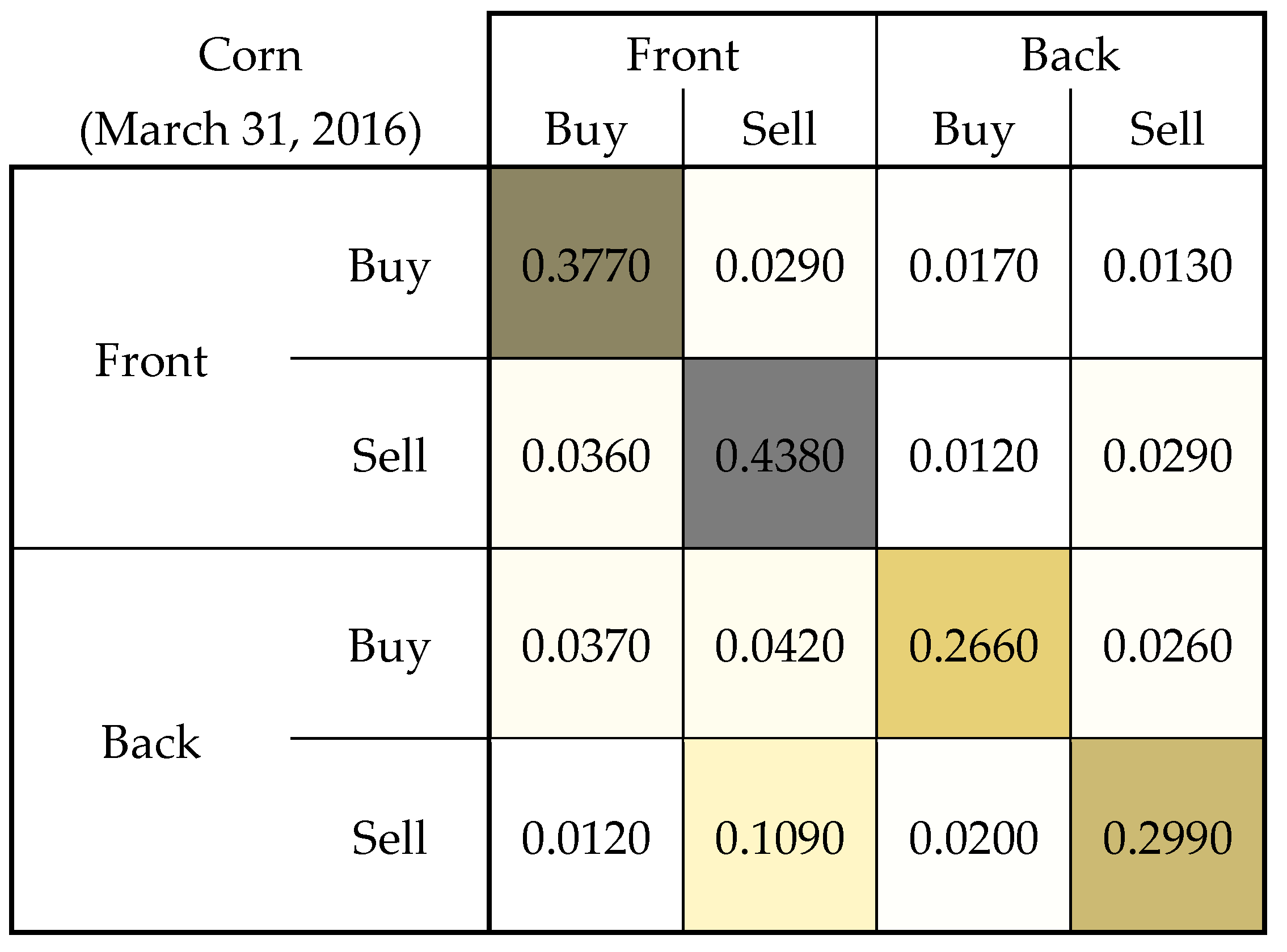
| 1 | An inclusion of further contracts with longer maturities would be desirable to obtain a clearer picture of price discovery along the entire term structure curve. However, this comes at the cost of increasing the dimension of the Hawkes model. Moreover, the number of transactions becomes rather small for futures contracts with longer maturity, which renders the estimation unreliable. |
References
- Bacry, Emmanuel, Martin Bompaire, Stéphane Gaıffas, and Soren Poulsen. 2017. Tick: A Python library for statistical learning, with a particular emphasis on time-dependent modeling. arXiv arXiv:1707.03003. [Google Scholar]
- Bacry, Emmanuel, Thibault Jaisson, and Jean–François Muzy. 2016. Estimation of slowly decreasing Hawkes kernels: Aplication to high-frequency order book dynamics. Quantitative Finance 16: 1179–201. [Google Scholar] [CrossRef]
- Bauwens, Luc, and Nikolaus Hautsch. 2007. Modelling Financial High Frequency Data Using Point Processes. SFB 649 Discussion Paper 2007-066. Available online: http://sfb649.wiwi.hu-berlin.de/papers/pdf/SFB649DP2007-066.pdf (accessed on 29 October 2018).
- Bicchetti, David, and Nicolas Maystre. 2013. The synchronized and long-lasting structural change on commodity markets: Evidence from high frequency data. Algorithmic Finance 2: 233–39. [Google Scholar] [CrossRef]
- Bowsher, Clive G. 2007. Modelling Security Markets in Continuous Time: Intensity-based, Multivariate Point Process Models. Journal of Econometrics 141: 876–912. [Google Scholar] [CrossRef]
- Couleau, Anabelle, Teresa Serra, and Philip Garcia. 2019. Microstructure noise and realized variance in the live cattle futures market. American Journal of Agricultural Economics 101: 563–78. [Google Scholar] [CrossRef]
- Brennan, M. J. 1958. The supply of storage. American Economic Review 48: 50–72. [Google Scholar]
- Diebold, Francis X., and Canlin Li. 2006. Forecasting the term structure of government bond yields. Journal of Econometrics 130: 337–64. [Google Scholar] [CrossRef]
- Easley, David, and Maureen O’Hara. 1992. Time and the process of security price adjustment. Journal of Finance 47: 577–604. [Google Scholar] [CrossRef]
- Engle, Robert F., and Jeffrey R. Russell. 1998. Autoregressive conditional duration: A new model for irregularly spaced transaction data. Econometrica 66: 1127–62. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1987. Commodity Futures Prices: Some Evidence on Forecast Power, Premiums, and the Theory of Storage. The Journal of Business 60: 55–73. [Google Scholar] [CrossRef]
- Filimonov, Vladimir, and Didier Sornette. 2012. Quantifying reflexivity in financial markets: Toward a prediction of flash crashes. Physical Review E 85: 056108. [Google Scholar] [CrossRef]
- Filimonov, Vladimir, David Bicchetti, Nicolas Maystre, and Didier Sornette. 2014. Quantification of the high level of endogeneity and of structural regime shifts in commodity markets. Journal of International Money and Finance 42: 174–92. [Google Scholar] [CrossRef]
- Geman, Helyette, and Vu-Nhat Nguyen. 2005. Soybean Inventory and Forward Curve Dynamics. Management Science 51: 1076–91. [Google Scholar] [CrossRef]
- Gibson, Rajna, and Eduardo S. Schwartz. 1990. Stochastic Convenience Yield and the Pricing of Oil Contingent Claims. Journal of Finance 45: 959–76. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., and Paul R. Milgrom. 1985. Bid, Ask, and Transaction Prices in a Specialist Market with Heterogeneously Informed Agents. Journal of Financial Economics 14: 71–100. [Google Scholar] [CrossRef]
- Gray, Roger W., and David J. S. Rutledge. 1971. The economics of commodity futures markets: A survey. Review of Marketing and Agricultural Economics 39: 57–108. [Google Scholar]
- Gurgul, Henryk, and Robert Syrek. 2017. Trading volume and volatility patterns across selected Central European stock markets from microstructural perspective. Managerial Economics 18: 87. [Google Scholar] [CrossRef][Green Version]
- Hardiman, Stephen J., Nicolas Bercot, and Jean-Philippe Bouchard. 2013. Critical reflexivity in financial markets: A Hawkes process analysis. The European Physical Journal B 86: 442. [Google Scholar] [CrossRef]
- Harris, Frederick H. deB., Thomas H. McInish, and Robert A. Wood. 2002. Security price adjustment across exchanges: An investigation of common factor components for Dow stocks. Journal of Financial Markets 5: 277–308. [Google Scholar] [CrossRef]
- Hasbrouck, Joel. 1995. One Security, Many Markets: Determining the Contributions to Price Discovery. The Journal of Finance 50: 1175–95. [Google Scholar] [CrossRef]
- Hautsch, Nikolaus. 2004. Modelling Irregularly Spaced Financial Data. Berlin: Springer. [Google Scholar]
- Hawkes, Alan G. 1971. Point spectra of some mutually-exciting point processes. Journal of the Royal Statistical Society 33: 438–43. [Google Scholar] [CrossRef]
- Hawkes, Alan G., and David Oakes. 1974. A cluster process representation of a self-exciting process. Journal of Applied Probability 11: 493–503. [Google Scholar] [CrossRef]
- Haynes, Richard, and John S. Roberts. 2015. Automated Trading in Futures Markets. CFTC White Paper. Available online: https://www.cftc.gov/sites/default/files/idc/groups/public/@economicanalysis/documents/file/oce_automatedtrading.pdf (accessed on 25 October 2019).
- Hu, Zhepeng, Mindy Mallory, Teresa Serra, and Philip Garcia. 2017. Measuring Price Discovery between Nearby and Deferred Contracts in Storable and Non-Storable Commodity Futures Markets. arXiv arXiv:1711.03506. [Google Scholar]
- Karstanje, Dennis, Michel van der Wel, and Dick J. C. van Dijk. 2017. Common Factors in Commodity Futures Curves. SSRN Working Paper. [Google Scholar] [CrossRef][Green Version]
- Kendall, David Laurence. 1982. Intertemporal Price Relationships in Noninventory Futures Markets. Ph.D. thesis, North Carolina State University, Raleigh, NC, USA. [Google Scholar]
- Kyle, Albert S., and Anna Obizhaev. 2019. Large Bets and Stock Market Crashes. Working Paper. Available online: https://ssrn.com/abstract=2023776 (accessed on 25 October 2019).
- Large, Jeremy. 2007. Measuring the Resiliency of an Electronic Limit Order Book. Journal of Financial Markets 10: 1–25. [Google Scholar] [CrossRef]
- Lee, Charles M. C., and Mark J. Ready. 1991. Inferring trade direction from intraday data. The Journal of Finance 46: 733–46. [Google Scholar] [CrossRef]
- Mallory, Mindy, Philip Garcia, and Teresa Serra. 2015. Nearby and Deferred Quotes: What They Tell Us about Linkages and Adjustments to Information. Proceedings of the NCCC-134 Conference on Applied Commodity Price Analysis, Forecasting, and Market Risk Management. Available online: http://www.farmdoc.illinois.edu/nccc134/conf_2015/pdf/Mallory_Garcia_Serra_NCCC_134_2015.pdf (accessed on 25 October 2019).
- Meyer, Paul-André. 1971. Démonstration simplifiée d’un théorème Knight. Lecture Notes in Mathematics 191: 191–95. [Google Scholar]
- Nelson, Charles R., and Andrew F. Siegel. 1987. Parsimonious modeling of yield curve. Journal of Business 60: 473–89. [Google Scholar] [CrossRef]
- Ogata, Yosihiko. 1989. Statistical Models for Earthquake Occurrences and Residual Analysis for Point Processes. Journal of the American Statistical Association 83: 9–27. [Google Scholar] [CrossRef]
- Ogata, Yosihiko. 1998. Space-time point-process models for earthquake occurrences. Annals of the Institute of Statistical Mathematics 50: 379–402. [Google Scholar] [CrossRef]
- Russell, Jeffrey R. 1999. Econometric Modeling of Multivariate Irregularly-Spaced High-Frequency Data. Working Paper, University of Chicago. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.202.486&rep=rep1&type=pdf (accessed on 5 November 2018).
- Schwartz, Eduardo S. 1997. The Stochastic Behavior of Commodity Prices: Implications for Valuation and Hedging. The Journal of Finance 52: 923–73. [Google Scholar] [CrossRef]
- Sorensen, Carsten. 2002. Modeling seasonality in agricultural commodity futures. The Journal of Futures Markets 22: 393–426. [Google Scholar] [CrossRef]
- Soros, George. 1987. The Alchemy of Finance: Reading the Mind of the Market. New York: John Wiley & Sons. [Google Scholar]
- Tang, Ke, and Wei Xiong. 2012. Index investment and the financialization of commodities. Financial Analysts Journal 68: 54–74. [Google Scholar] [CrossRef]
- USDA. 2016a. Prospective Plantings (March 2016). United States Department of Agriculture, National Agricultural Statistics Service. Available online: https://downloads.usda.library.cornell.edu/usda-esmis/files/x633f100h/9c67wq58w/rx913s37m/ProsPlan-03-31-2016.pdf (accessed on 25 October 2019).
- USDA. 2016b. United States Department of Agriculture, National Agricultural Statistics Service. Available online: https://downloads.usda.library.cornell.edu/usda-esmis/files/3t945q76s/zs25x8827/d504rk71k/wasde-03-09-2016.pdf (accessed on 25 October 2019).
- USDA. 2016c. United States Department of Agriculture, National Agricultural Statistics Service. Available online: https://downloads.usda.library.cornell.edu/usda-esmis/files/m326m174z/8623j006q/q524jq148/CattOnFe-03-18-2016.pdf (accessed on 25 October 2019).
- USDA. 2016d. United States Department of Agriculture, National Agricultural Statistics Service. Available online: https://downloads.usda.library.cornell.edu/usda-esmis/files/xg94hp534/08612q46m/fj236409h/GraiStoc-03-31-2016.pdf (accessed on 25 October 2019).
- Volkenand, Steffen, Günther Filler, Marlene Kionka, and Martin Odening. 2019. Duration dependence among agricultural futures with different maturities. Applied Economics Letters. [Google Scholar] [CrossRef]
- Wang, Xiaoyang, Philip Garcia, and Scott H. Irwin. 2016. Are agricultural futures getting noisier? The impact of high frequency quoting in the corn market. Working paper, University of Illinois, Urbana-Champaign. Available online: https://legacy.farmdoc.illinois.edu/irwin/research/Wang_Garcia_Irwin_Oct%202016.pdf (accessed on 25 October 2019).
- Working, Hoolbrock. 1949. The theory of price of storage. The American Economic Review 39: 1254–62. [Google Scholar]


| Variable | Commodity | Corn | Wheat | ||||||
| Contract | Front | Back | Front | Back | |||||
| Type | Buy | Sell | Buy | Sell | Buy | Sell | Buy | Sell | |
| Number of Transactions | Total | 102,778 | 105,822 | 30,607 | 31,762 | 80,038 | 77,586 | 22,873 | 23,273 |
| Min. | 14 | 34 | 1 | 4 | 12 | 11 | 1 | 1 | |
| Mean | 194.655 | 200.420 | 58.078 | 60.155 | 145.524 | 141.065 | 41.815 | 42.469 | |
| Max. | 2127 | 2519 | 946 | 889 | 1237 | 1392 | 349 | 277 | |
| Std Dev | 177.603 | 191.665 | 67.799 | 66.629 | 129.876 | 127.539 | 37.675 | 36.888 | |
| CV | 1.096 | 1.046 | 0.857 | 0.903 | 1.120 | 1.106 | 1.110 | 1.151 | |
| Volume (number of contracts) | Min. | 149 | 110 | 4 | 12 | 50 | 84 | 8 | 4 |
| Mean | 1991 | 2083 | 402 | 434 | 781 | 763 | 180 | 175 | |
| Max. | 22,131 | 29,561 | 5926 | 7546 | 6771 | 6,206 | 2127 | 1468 | |
| Std Dev | 2009 | 2467 | 516 | 596 | 775 | 714 | 197 | 174 | |
| CV | 1.009 | 1.185 | 1.284 | 1.372 | 0.993 | 0.937 | 1.099 | 0.995 | |
| Mid-quotes (cents per bushel) | Min. | 348 | 352 | 446 | 453 | ||||
| Mean | 364 | 369 | 466 | 472 | |||||
| Max. | 373 | 377 | 479 | 486 | |||||
| Std Dev | 5.683 | 5.594 | 8.199 | 8.341 | |||||
| CV | 0.016 | 0.015 | 0.018 | 0.018 | |||||
| Variable | Commodity | Live Cattle | Lean Hog | ||||||
| Contract | Front | Back | Front | Back | |||||
| Type | Buy | Sell | Buy | Sell | Buy | Sell | Buy | Sell | |
| Number of Transactions | Total | 35,801 | 35,474 | 36,426 | 35,025 | 25,077 | 26,892 | 25,160 | 23,845 |
| Min. | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Mean | 70.061 | 69.285 | 71.424 | 68.811 | 49.364 | 52.833 | 49.237 | 46.755 | |
| Max. | 426 | 373 | 532 | 584 | 371 | 371 | 261 | 328 | |
| Std Dev | 52.744 | 50.727 | 52.819 | 54.116 | 44.705 | 43.991 | 36.408 | 34.376 | |
| CV | 1.328 | 1.366 | 1.352 | 1.272 | 1.104 | 1.201 | 1.352 | 1.360 | |
| Volume (number of contracts) | Min. | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 |
| Mean | 248 | 249 | 237 | 232 | 171 | 179 | 152 | 142 | |
| Max. | 2532 | 1512 | 1962 | 2416 | 1586 | 1661 | 106 | 1343 | |
| Std Dev | 225 | 210 | 209 | 214 | 181 | 179 | 135 | 128 | |
| CV | 0.905 | 0.842 | 0.882 | 0.922 | 1.058 | 1.003 | 0.883 | 0.898 | |
| Mid-quotes (cents per pound) | Min. | 131 | 123 | 68 | 80 | ||||
| Mean | 137 | 127 | 70 | 82 | |||||
| Max. | 142 | 131 | 73 | 84 | |||||
| Std Dev | 2.553 | 2.131 | 0.937 | 1.040 | |||||
| CV | 0.019 | 0.017 | 0.013 | 0.013 | |||||
| Contract | Front | Back | Front | Back | ||||
|---|---|---|---|---|---|---|---|---|
| Transaction | Buy | Sell | Buy | Sell | Buy | Sell | Buy | Sell |
| Commodity | Corn | Wheat | ||||||
| Baseline intensity | 0.194 | 0.193 | 0.061 | 0.062 | 0.15 | 0.149 | 0.046 | 0.048 |
| Average intensity | 0.327 | 0.337 | 0.097 | 0.101 | 0.25 | 0.241 | 0.071 | 0.072 |
| Exogeneity ratio | 0.636 | 0.629 | 0.663 | 0.67 | 0.654 | 0.657 | 0.704 | 0.726 |
| Commodity | Live cattle | Lean Hog | ||||||
| Baseline intensity | 0.077 | 0.078 | 0.083 | 0.081 | 0.058 | 0.063 | 0.061 | 0.059 |
| Average intensity | 0.119 | 0.117 | 0.121 | 0.117 | 0.085 | 0.09 | 0.085 | 0.08 |
| Exogeneity ratio | 0.701 | 0.699 | 0.714 | 0.733 | 0.743 | 0.741 | 0.76 | 0.772 |
| Commodity | Corn | Wheat | ||||||
| Baseline intensity | 0.194 | 0.193 | 0.061 | 0.062 | 0.150 | 0.149 | 0.046 | 0.048 |
| Average intensity | 0.327 | 0.337 | 0.097 | 0.101 | 0.250 | 0.241 | 0.071 | 0.072 |
| Exogeneity ratio | 0.636 | 0.629 | 0.663 | 0.670 | 0.654 | 0.657 | 0.704 | 0.726 |
| Commodity | Live cattle | Lean Hog | ||||||
| Baseline intensity | 0.077 | 0.078 | 0.083 | 0.081 | 0.058 | 0.063 | 0.061 | 0.059 |
| Average intensity | 0.119 | 0.117 | 0.121 | 0.117 | 0.085 | 0.090 | 0.085 | 0.080 |
| Exogeneity ratio | 0.701 | 0.699 | 0.714 | 0.733 | 0.743 | 0.741 | 0.760 | 0.772 |
| Contract | Front | Back | Front | Back | ||||
|---|---|---|---|---|---|---|---|---|
| Transaction | Buy | Sell | Buy | Sell | Buy | Sell | Buy | Sell |
| Commodity | Corn | Wheat | ||||||
| Kolmogorov–Smirnov | 0.84 | 0.84 | 0.88 | 0.89 | 0.87 | 0.83 | 0.89 | 0.89 |
| Ljung–Box | 0.64 | 0.67 | 0.94 | 0.92 | 0.78 | 0.80 | 0.94 | 0.94 |
| Commodity | Live cattle | Lean Hog | ||||||
| Kolmogorov–Smirnov | 0.91 | 0.87 | 0.91 | 0.88 | 0.93 | 0.93 | 0.91 | 0.90 |
| Ljung–Box | 0.92 | 0.91 | 0.91 | 0.91 | 0.94 | 0.93 | 0.93 | 0.93 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volkenand, S.; Filler, G.; Odening, M. Price Discovery and Market Reflexivity in Agricultural Futures Contracts with Different Maturities. Risks 2020, 8, 75. https://doi.org/10.3390/risks8030075
Volkenand S, Filler G, Odening M. Price Discovery and Market Reflexivity in Agricultural Futures Contracts with Different Maturities. Risks. 2020; 8(3):75. https://doi.org/10.3390/risks8030075
Chicago/Turabian StyleVolkenand, Steffen, Günther Filler, and Martin Odening. 2020. "Price Discovery and Market Reflexivity in Agricultural Futures Contracts with Different Maturities" Risks 8, no. 3: 75. https://doi.org/10.3390/risks8030075
APA StyleVolkenand, S., Filler, G., & Odening, M. (2020). Price Discovery and Market Reflexivity in Agricultural Futures Contracts with Different Maturities. Risks, 8(3), 75. https://doi.org/10.3390/risks8030075





