Abstract
This paper investigates dynamic correlations of stock–bond returns for different stock indices and bond maturities. Evidence in the US shows that stock–bond relations are time-varying and display a negative trend. The stock–bond correlations are negatively correlated with implied volatilities in stock and bond markets. Tests show that stock–bond relations are positively correlated with economic policy uncertainty, however, are negatively correlated with the monetary policy and fiscal policy uncertainties. Correlation coefficients between stock and bond returns are positively related to total policy uncertainty for returns of the Dow-Jones Industrial Average (DJIA) and the S&P 500 Value stock index (VALUE), but negatively correlated with returns of S&P500 (Total market), the NASDAQ Composite Index (NASDAQ), and the RUSSELL 2000 (RUSSELL).
Keywords:
stock–bond correlation; VIX; economic policy uncertainty; monetary policy uncertainty; fiscal policy uncertainty JEL Classification:
C12; C13; G10; G11
1. Introduction
The investigation on correlations of stock and bond returns has long been a key concern of portfolio managers and financial market strategists (Connolly et al. 2005; Panchenko and Wu 2009; Baur and Lucey 2009; Li et al. 2019, among others). This is because the derived parametric relations could provide useful guidance in portfolio selection, dynamic asset allocation, and risk management. For most of this time, two questions have dominated the literature. First, are stock returns and bond returns positively or negatively correlated? Second, what are the factors that cause correlations to vary over time? The theoretical claim of the first issue contends that both required rates of return for stock and bond yields are viewed as part of a discount factor to calculate the future cash flows of investments. This argument is based on the valuation model that has been adopted and used in the “Fed model” (Kwan 1996; Yardeni 1997). It is observed that any economic shocks, such as income, inflation rate, policy innovation, or external shock that disturb an existing equilibrium, will cause investors to reallocate their funds between assets with lower returns to ones with higher returns. An efficient arbitrage will eliminate the return differentials and establish return parity conditions after executing full adjustment (Tobin 1969). This view focuses on economic fundamentals analyzed over a long-run perspective.
However, evidence of the decoupling phenomenon observed by Gulko (2002) finds a negative sign for the correlation that obviously occurred in the crisis period; this finding reflects a short run “flight-to-quality” process (Baur and Lucey 2009). To advance the study, Connolly et al. (2005) examine the US market and discover that the implied stock volatility (VIX) spikes during periods of market turmoil leads to decline in stock prices (Whaley 2009). It is argued that the VIX variable has a power in predicting stock returns (Connolly et al. 2005) and find that VIX displays a negative effect on the stock–bond correlation. Further study by Chiang et al. (2015) documents that both implied volatility of stock and conditional volatility of bond returns have significantly negative effects on variations in stock–bond returns.
To distinguish their work from previous models, some researchers identify economic policy uncertainty (EPU) as a key factor that dictates the time-varying correlations between stock and bond returns (Antonakakis et al. 2013; Jones and Olson 2013; Li et al. 2015). Antonakakis et al. (2013) show that the dynamic correlation between EPU and S&P500 returns is consistently negative over time, with exception of a financial crisis period. Li et al. (2015) report that innovations in EPU have a negative and asymmetrical impact on subsequent stock–bond correlations, since a rise in EPU will likely prompt risk averse investors to sell off risky stocks and purchase lower risk bonds, leading to a negative correlation.1
Considering the above evidence of risk/uncertainty on stock returns, this paper attempts to contribute to the study of the effects of policy uncertainty on stock–bond relations. This study differs from existing models in the following ways. First, this study focus on broad information in developing measures of financial risks such as VIX, Merrill Lynch Option Volatility Estimate (MOVE) and uncertainty (EMU) to explain the time-varying correlations between stock and bond returns. Second, in addition to EPU, this study investigates the impact of categorical policy uncertainties, including both fiscal policy uncertainty (FPU) and monetary policy uncertainty (MPU). The testing result suggests that the FPU and MPU give rise to different effects vis-à-vis that of EPU. Third, instead of testing a correlation coefficient derived from a single measure of aggregate stock returns that covaries with a specific bond yield, this study conducts tests on the return correlations involving different measures of aggregate stock returns and a spectrum of bond yields for different maturities. Thus, the estimated results will provide broad coverage of dynamic correlation behavior. Fourth, the net effect of various policy uncertainty is summarized in total policy uncertainty (TPU). Evidence demonstrates that the results are mixed due to the different impact, which the income and substitution effects have on stock–bond return correlations.
The remainder of the paper is structured as follows. Section 2 describes a dynamic correlation model and derives the time-varying correlations. Section 3 provides rationales for using risk and uncertainty variables to explain the time-varying behavior of stock–bond return correlation. Section 4 describes the sample data. Section 5 reports the estimates developed from the use of policy uncertainty to explain the dynamic stock–bond correlations. Section 6 provides robustness tests. Section 7 concludes the paper.
2. The Relationship between Stock Returns and Bond Returns
As mentioned earlier, stock and bond returns are positively correlated since both stock and bond markets commonly react to economic news, such as changes in inflation rate, economic growth, the real interest rate, and business cycle, in similar ways. When investors perceive that economic prospects are good, demand for bonds increase, as does demand for stocks, leading to a positive correlation. Experience from the late 1990s suggests that an upward shift in the wealth effect encourages investors to hold both types of assets simultaneously. Campbell and Ammer (1993), Kwan (1996), and d’Addona and Kind (2006) document this phenomenon.
Historical experience also reveals a negative correlation between stock–bond returns, which is especially noticeably in the stock market during a downturn period or a financial crisis. When the stock market plummets, risk averse investors may move funds from the stock market to safer assets and increase the demand for bond market, forming a “flight-to-quality” phenomenon (Baur and Lucey 2009; Hakkio and Keeton 2009). On the contrary, when the economy recovers and stock prices start to rally, investors become less risk averse and opt to switch back to stock market, leading to a “flight-from-quality” phenomenon. Thus, the correlation between stock and bond returns displays a negative relation. Evidence by Gulko (2002), Connolly et al. (2005), Baur and Lucey (2009), and Chiang et al. (2015) support this hypothesis.
Despite their contributions, which use VIX as a measure to explain the time-varying correlation of stock–bond returns, their work appears to inadequately capture all the necessary information associated with uncertainty. For instance, President Trump revealed in the first week of October that high-level trade negotiations between the US and China had concluded in a “very substantial phase one deal” and that phase two would start almost immediately after phase one was signed. This statement, a sure sign of reduced uncertainty, would be expected to improve investors’ sentiment, and indeed, Wall Street stocks closed higher on 11 October 2019 as the S&P 500 gained 32.14 points (or 1.09%), DJIA moved ahead 319.92 points (or 1.21%) and Nasdaq 106.26 advanced points (1.34%). This episode motivates this study to investigate the role of economic policy uncertainty on asset prices. In addition, the impacts of monetary policy uncertainty (MPU) and fiscal policy uncertainty (FPU) are also included to the test equation as a way of differentiating the impact of dynamic correlation behavior of stock–bond returns.
It is generally recognized that a sudden rise in EPU is likely to impede the smoothness of operations in economic activities and hence cause income uncertainty, which tamps down liquidity (Brunnermeier and Pedersen 2009) and leads to a decline in demand for assets (Bloom 2009, 2014; Chiang 2019). This phenomenon may be called the income uncertainty effect. Conversely, as EPU lessens, investors feel less uncertain about the future and more encouraged to increase their demand for assets, driving a positive correlation between stock and bond returns (Hong et al. 2014).
On the other hand, the substitution effect describes a phenomenon in which stock and bond returns move in opposite directions as uncertainty about economic activity changes in the market. This occurs as uncertainty heightens; investors then sell off their riskier assets (stock) and move their funds into safer assets (bond). This shift results in a negative relation between stock and bond returns. Further, as uncertainty declines, investors then switch from lower return assets (bond) to higher return assets (stocks), causing a negative relation between stock and bond returns (Li et al. 2015). Thus, the substitution effect tends to produce a negative relation between stock and bond returns. In fact, the concept of income effect is essentially derived from Tobin (1969) and then applied by Barsky (1989), Hong et al. (2014), and Li et al. (2015) to analyze the impact of economic uncertainty, triggered by economic policy uncertainty, on asset returns. The analysis can be extended to examine the impacts of monetary policy uncertainty (MPU) and fiscal policy uncertainty (FPU). As stated above, the impacts of MPU and FPU on stock return and bond return could also be attributed to the income effect and substitution effect; the ultimate impact on the returns of these two asset classes depends on the relative influence of these two forces.
3. A Dynamic Conditional Correlation Model
To derive the dynamic correlation series, the literature follows a seminal study by Engle (2002) who proposes a dynamic conditional correlation model, which is designed to estimate asset market returns (de Goeij and Marquering 2004; Chiang et al. 2007; Yu et al. 2010; Antonakakis et al. 2013; Jones and Olson 2013; Li et al. 2015; Ehtesham and Siddiqui 2019; Allard et al. 2019). This model is frequently used because of its ability to capture a vector of return correlations and describe the volatility clustering phenomenon. Moreover, it could alleviate the heteroscedasticity problem (Forbes and Rigobon 2002). In this study, {Rt} represents a bivariate return series, expressed as
where Rt = [ is a 2 × 1 vector for stock market returns, is the mean value of asset 1 or 2, which has the conditional expectation of multivariate time series properties2, ut is the information set up for (and including) time t − 1. In the context of this study, it is convenient to treat as the return on stocks and as the bond return for one of the bond instruments. In the multivariate DCC-GARCH structure, the conditional variance-covariance matrix Ht is assumed to be
where = diag{ is the 2 × 2 diagonal matrix of time-varying standard deviations from univariate models, and Pt is the time-varying conditional correlation matrix, which satisfies the following conditions:
Now in Equation (3) is a correlation matrix with ones on the diagonal and off-diagonal elements that have an absolute value less than one. Use of an asymmetric DCC model recognizes a shock dynamic adjustment of correlation for negative shock may be different than it is for a positive outcome (Cappiello et al. 2006; Engle 2009).3 In this expression, it can be written as:
where the is positive definite and .
The product of will be nonzero; only these two variables are negative. Thus, a positive value of indicates that correlations increase more in response to market falls than they do to market rises. The equation is written as
where = is the 2 × 2 time-varying covariance matrix of , = E[ is the 2 × 2 unconditional variance matrix of (where , i = 1 and 2), is the 2 × 2 unconditional variance matrix of ; , are non-negative scalar parameters satisfying The substitution of Equation (5) for four yields
which can be used to calculate the correlations for the two assets. As proposed by Engle (2002, 2009) and Cappiello et al. (2006), the asymmetric dynamic correlation (ADCC) model can be estimated by using a two-stage approach to maximize the log-likelihood function.
4. Data
The data in this study cover the US aggregate stock market index (TTMK-US$RI) for the monthly observations spanning from January 1990 through June 2019. To measure the risks in the stock and bond markets, I use the implied stock market volatility (VIXt) obtained from the S&P 500 index options and MOVEt, the one-month Merrill Lynch Option Volatility Estimate of bond volatility. To conduct robustness tests, the US aggregate stock market indices also include the Dow-Jones Industrial Average (DJIA), the NASDAQ Composite Index (NASDAQ), the RUSSELL 2000 (RUSSELL), and the S&P 500 Value stock index (VALUE). For bond markets, the data cover the bond price indices of maturities for 30 years, 10 years, seven years, five years, and two years. The data for the total stock market, VIX, MOVE, and bond markets indices are obtained from Thomson Reuters’ Datastream. Returns are constructed by taking the log-difference of the price indices times 100.
The data for the categorical uncertainty indices are equivalent to the economic policy uncertainty (EPU) data used by Baker et al. (2016). The construction of the EPU index is based on the following components: newspaper coverage of policy-related economic uncertainty, which is based on 10 large newspapers; the number of federal tax code provisions set to expire in future years; and disagreements among economic forecasters, which are used as a proxy for uncertainty. Based on a similar procedure, Baker, Bloom, and Davis (BBD) construct categorical indices, including the MPU and FPU indices. Of these indices, the MPU and FPU are based on several dimensions of information: (i) the Access World News database of over 2000 newspapers; (ii) a balanced panel of 10 major national and regional US papers, including a broader set of terms designed to capture domestic and foreign sources of monetary policy and fiscal policy uncertainties; and (iii) data scaled by the total number of articles. The term sets for economic policy, monetary policy, and fiscal policy uncertainty indices are given in the Appendix A. These data can be downloaded from the link given below: http://www.policyuncertainty.com/categorical_terms.html.
Note that the choice of the US data is based on the rationale that these data can be used to construct a dynamic correlation between stocks and bonds with combinations of different stock indices and maturities of bonds. More importantly, our goal is to use policy uncertainty, including economic policy uncertainty, fiscal policy uncertainty and monetary policy uncertainty to explain the dynamic correlations. These data are more consistently available in the US market and not as accessible in other markets. The data constraint limits our research scope.
5. Empirical Estimations
5.1. Estimated Stock–Bond Dynamic Correlations
Table 1 provides different correlation matrices of stock returns, bond returns, risk and uncertainty. Panel A. reports the correlations of total stock market (TTMK) return and bond returns with different maturities. The statistics show negative correlation coefficients ranging from −0.12 to −0.15. The corresponding t-ratios are statistically significant, the only exception is the coefficient of a two-year bond. The other elements in this table are the correlations of bond returns, which range between 0.59 and 0.98. Panel B presents the correlations among different measures of stock returns and range from 0.74 to 0.95 (VALUE and DJIA). Due to the high correlation in both types of assets, most researchers tend to use only one type of stock measure, i.e., total market return, and one type of bond return, i.e., 10-year bond, to engage empirical analysis. Panel C provides a correlation matrix that illustrates the correlation of VIX and different categorical policy uncertainties. It shows that FPU and MPU are highly correlated with EPU, and VIX has the highest correlation with MOVE. To visually demonstrate, Figure 1 presents time varying correlations for VIX, MOVE, EPU, FPU, and MPU in the US market. Panel D reports the summary of statistics for VIX and uncertainty variables. Among them, the FPU surprisingly has the highest standard deviation, while the VIX has the lowest. The information is not usually observable by the public.
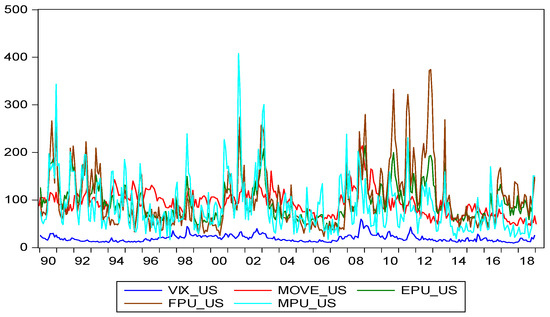
Figure 1.
Time-varying VIX, MOVE, EPU, FPU, and MPU in the US market.
5.2. Estimated Stock–Bond Correlation Coefficients
Table 2 contains parametric estimates of the covariance between stock and various bond returns using the ADCC-GARCH model as represented by the system of Equations (1)–(5). Estimates in Table 2 are pairwise covariances between TTMK stock returns and one of the bond returns from 30 year to two year bonds, , , , , and The reported statistics for conditional variances indicate that the lagged conditional variance, , and the lagged shock squared, , are largely statistically significant except for . This result indicates that the GARCH-type model is relevant. Turning to the asymmetric impact of shocks on conditional variance, we find that most of the estimated coefficients in the stock and bond markets are highly significant. The exception is which is not consistent with the expected sign. Judging from the estimated coefficient and the associated t-statistics, the variance equation is apparently dominated by the predictive power from the lagged variance term.4 Having estimated , it can derive: .

Table 2.
Estimates of the asymmetric dynamic correlation (ADCC) models parameters for stock–bond return correlations.
The estimated result for model is given by:
The parameter is the variance and covariance of asset i and j in the estimated equation (subscripts i = ) and j = , which stand for stock and bond returns, respectively); , and are the parameters for the conditional variance equation; and is an asymmetric parameter. The first column is the estimated parameters and the second column is the t-statistics. The critical values at the 1%, 5%, and 10% are 2.60, 1.97, and 1.65, respectively. LLF denotes the log-likelihood function.
Figure 2 shows time series plots of dynamic conditional correlations for the monthly data between TTMK return and bond returns with different maturities based on Equation (6). Correlations between the returns of the two assets display noticeable variations throughout the sample period. In general, the plots clearly show a downward slope up to the time of 2004. During the beginning of the 2000s when the US market suffered from the dotcom collapse, the stock market dropped dramatically, and there was less of a decline in bond returns, causing the correlation to move downward as shown in the Figure 2 in this period. These results are consistent with the findings of Connolly et al. (2005), Chiang et al. (2015), and Li et al. (2015). However, during the global financial crisis period in 2008–2010, the stock market plummeted again, and the correlation coefficient also deepened in this period. After this crisis time the relationships become stationary and fluctuate around a very mild negative regime. A special feature derived from this study is that despite of their common movement around turning points, the dynamic paths show that the stock–bond return correlations vary with different bond maturities, which reflect different market conditions and preferences for bond maturities with different bondholders. These results suggest that the path of is based on only one stock return and one bond return, as is the case in conventional studies, which could produce a misleading and biased estimator.
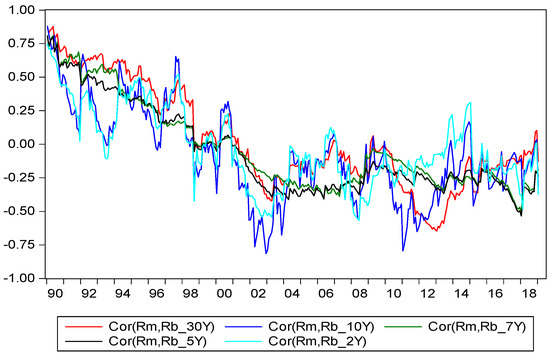
Figure 2.
Dynamic correlations between stock (TTMK) and various bond returns in the US.
5.3. The Role of Uncertainty
Early studies by Connolly et al. (2005), Andersson et al. (2008), and Chiang et al. (2015) stress the notion of using volatility measure as a proxy for uncertainty. Connolly et al. (2005) find that the correlation between stock and bond returns declines during periods with substantial increases in VIX. Andersson et al. (2008), Chiang et al. (2015), and Dimic et al. (2016) report that periods of elevated stock market uncertainty cause a decoupling between the relation of stock and bond returns, which is consistent with the “flight-to-quality” phenomenon. Antonakakis et al. (2013) and Li et al. (2015) employ the economic policy uncertainty in modeling the dynamic correlations. The current study extends this approach by adding monetary policy uncertainty and fiscal policy uncertainty in the test equation to explain the dynamic correlations between stock and bond returns. This notion is summarized in the regression model as follows:
where is a Fisher transformation of stock–bond correlation coefficient, that is, = ln[ and is bound to interval [−1,+1]. and are the 1-month implied volatility in stock and bond markets, respectively. The is the economic policy uncertainty at time t − 1, while and are the monetary policy and fiscal policy uncertainties at time t − 1. Two special features are included in Equation (7). First, the financial risk and uncertainty are treated as independent factors to explain the stock–bond return correlations; second, in addition to the , the categorical policy impacts, such as the and , are included to highlight their distinctive effects. In the last term, the trend factor is added to capture of the presence of non-stationarity.
Table 3 presents consistent estimates (Newey and West 1987) of Equation (7) without including and , while Table 4 shows results for this equation where the restriction of has been relaxed. Both models perform very well, the adjusted R-squares for the unrestricted model, which range from 0.48 to 0.81, are notably higher than those of the restricted model, indicating that the inclusion of the uncertainty variables helps to increase their explanatory power. Since the results in Table 3 are nested in Table 4, our interpretations focus on Table 4. Several points are noteworthy.

Table 3.
Estimates of aggregate and categorical EPU, FPU, and MPU and on stock (TTMK)–bond return correlations.

Table 4.
Estimates of aggregate and categorical EPU, FPU, and MPU, and on stock (TTMK)–bond return correlations.
First, the coefficients of the trend factor are negative, indicating that in general the correlations between stock and bond returns slope downward, although feathering in the stochastic process is present. This result is consistent with the findings reported by Connolly et al. (2005) and Chiang et al. (2015).
Second, the risk variables of and are negative, revealing that investors are actively switching between stock and bond depending on the level of risk in the market. This movement resembles a flight-to-quality as risk increases and flight-from-quality as risk declines. This finding is consistent with the results in the literature (Gulko 2002; Connolly et al. 2005; Andersson et al. 2008; Chiang et al. 2015).
Third, the estimated coefficients of are positive and highly significant. This conforms with a market phenomenon in which a sudden rise in uncertainty impedes prospects for economic activities, thereby dampening output production and future cash flows. Facing weakening liquidity, investors tend to sell off stocks and bonds. The dominance of this income effect will lead to a positive movement between stock and bond prices, a reaction that is consistent with a study by Hong et al. (2014), which emphasizes the response to market volatile.
Fourth, the estimated coefficients for and are negative and significant at the one percent level. This should not be surprising, since a rise in MPU tends to increase uncertainty in interest rate, which is more likely to create a strong substitution effect that causes a shift from high uncertainty asset-stocks to relatively low uncertainty asset-bonds and leads to a decoupling of stock and bond returns. A similar shift also holds true for an upward shift in FPU, especially in the case of bond financing of government deficits. It is recognized that an increase in and could create an income effect; however, the negative coefficients imply that the substitution effect dominates the income effect.
Fifth, the estimated results favor the inclusion of uncertainty variables as incremental variables. This can be seen in the reported statitic, which tests the joint significance of the coefficients with 0. The p-values of the Chi-squared test, which are in brackets, indicate the rejection of the null, suggesting that the inclusion of the uncertainty variables helps to improve the explanation of the dynamic correlations between stock and bond returns. Evidence thus indicates that the exclusion of uncertainty variables in the literature (Connolly et al. 2005; Andersson et al. 2008; Chiang et al. 2015) is subject to an omitted variable problem. In addition, the statistic for testing equality of coefficients for 0 against alternatives is also significant in all of cases, this test indicates the exclusion of categorical uncertainty even in the case of (Antonakakis et al. 2013; Li et al. 2015) suffers from a missing variable problem.
In summary, this study contributes to the literature in two ways. First, the effect of risk is separated from the uncertainty effect, showing both types of variables contribute to the variations of stock–bond correlations. Second, unlike the EPU, evidence shows the coefficients of FPU and MPT are negative, which provides an incremental contribution in the ability to predict time-varying correlations of stock and bond returns, These categorical uncertainty variables have not been explored in the literature.
6. Robustness Tests
6.1. Difference of Stock Indices
Despite of successful outcomes of the time-varying behavior of in relation to the risk/uncertainty, it is important to examine the robustness of the parametric relations, which can be done by using alternative measures of stock indices. In this section, the test equations apply to stock indices including the DJIA, NASDAQ, RUSSELL, and VALUE. Pairings of stock returns with bond returns of maturities of 30 years, 10 years, seven years, five years, and two years are used to derive . The estimated equations are reported in Table 5, Table 6, Table 7 and Table 8, and the test results are summarized as follows.

Table 5.
Estimates of aggregate and categorical EPU, FPU, and MPU and on stock (DJIA)–bond return correlations.

Table 6.
Estimates of aggregate and categorical EPU, FPU and MPU and on stock (NASDAQ)–bond return correlations.

Table 7.
Estimates of aggregate and categorical EPU, FPU, and MPU and on stock (RUSSELL)–bond return correlations.

Table 8.
Estimates of aggregate and categorical EPU, FPU, and MPU and on stock (VALUE)–bond return correlations.
First, the evidence clearly indicates that the coefficients of stock–bond return correlations slope downward as indicated by the negative sign and are statistically significant. However, the coefficients of have mixed signs. Although most of them are negative, yet, the coefficients of in the NASDAQ and RUSSELL stock returns are positive, reflecting the possibility that investors with different stocks holding have different degrees of sensitivity to financial shock and react differently. From an econometric point of view, this may also result from a spurious correlation. Another financial risk variable, , however, presents consistent results. Except (in Table 7 and Table 8), the coefficients show negative signs and are statistically significant.
Turning to the performance of the coefficients of EPUt−1, FPUt−1, and MPUt−1, the signs are consistent with the results in Table 4. That is, the coefficients of EPUt−1 continue to present positive signs, showing the impact of a positive income effect on the stock–bond return correlation, while the coefficients of FPUt−1 and MPUt−1 display negative signs, revealing that stock and bond returns are dominated by a substitution effect and move in diverse directions. The testing results suggest that a portfolio combination of stocks and bonds are a better hedge against uncertainty if it originates from monetary policy or fiscal policy uncertainty. However, the benefits of stock and bond diversification are less apparent if the uncertainty is the result of a general economic policy uncertainty, since its impact on economic activity is pervasive.5
6.2. Total Policy Uncertainty
The above tests suggest that the EPUt−1 has a positive effect, while FPUt−1 and MPUt−1have a negative effect on the . It is natural to pool all the uncertainty information together regardless of the sources of uncertainty. To this end, I define TPUt = EPUt + FPUt + MPUt as total policy uncertainty (TPUt). Table 9 reports the estimates of the test equation, which uses TPUt as a measure of uncertainty. Consistent with previous findings, the coefficients of have mixed signs. However, the signs for consistently present negative signs and most of them are statistically significant.

Table 9.
Estimates of correlations of total stock market returns and 10-year bond returns in response to financial risk and total policy uncertainty.
With respect to the sign of , evidence shows that the coefficients on TTMK, NASDAQ, and RUSSELL exhibit negative signs and are statistically significant. This result is consistent with market behavior of investors who during a rise in tend to sell off more uncertain stock and move their funds to bonds, effectively exhibiting the substitution effect. However, the coefficients of for the DJIA and VALUE stocks are positive and statistically significant, indicating a dominance of the income effect. A review of the S&P 500 Value index, which has a style-concentrated index designed to track the performance of stocks that exhibit the strongest value, shows that the value of these stocks is very much in line with that of the DJIA. In sum, estimates of correlations between total stock market returns and 10-year bond returns show different signs in response to total policy uncertainty is essentially executed under different degrees of force from income effect and substitution effect.
7. Conclusions
This paper examines the impact of financial market risk and policy uncertainties on the correlation between stock and bond returns. Analyzing the financial data of US markets for the period January 1990–June 2019, I derive several important empirical conclusions. First, empirical estimations based on the asymmetric dynamic correlation model (ADCC) suggest that stock–bond correlations are time-varying and display a negative relation overtime, especially for the period before 2002.
Second, evidence confirms that the stock–bond relationship is negatively correlated with the implied volatility in stock market (VIX), suggesting a higher market risk would cause a “flight-to-safety.” This phenomenon appears in stock markets of TTMK and VALUE. However, for indices such as the DJIA (with two-year and five-year bonds), the NASDAQ and RUSSELL, the sign turns out to be positive. The mixed results reflect differing attitudes toward risks of investors who hold different stock portfolios. This finding suggests that the use of a single stock index to measure stock returns and one specific form of bond maturity (10-year bond) as was done in the previous research (Connolly et al. 2005) could produce a biased estimator and hence a misleading statistical inference.
Third, with respect to the performance of implied bond volatility (MOVEt−1), this study arrives at more consistent results. In this case, the coefficients tend to have negative signs with a couple of exceptions. For this reason, we can reach a more concrete conclusion that a rise in MOVEt−1 leads to a decoupling of stock and bond returns. Thus, MOVEt−1 to some extent reflects different market information and complementarily contributes to explaining movements in stock and bond return correlations.
Fourth, this study find evidence that estimated coefficient of the EPUt−1 has a positive and significant effect on the stock–bond return correlation. This result is consistent with a dominant income effect resulting from a rise in economic policy uncertainty that impedes economic activities and leads to a decline in income. This decline brings about a decrease in liquidity and in turn weakens demand for both stocks and bonds. Therefore, both stock and bond prices move in the same direction.
Fifth, testing results conclude that the estimated coefficients for both FPUt−1 and MPUt−1 are negative and highly significant. The negative sign of this policy uncertainty is mainly due to the dominance of the substitution effect, which prompts investors to replace higher uncertainty assets with lower uncertainty assets due to an upward shift in policy uncertainty. This occurs because of a policy stance that causes a sudden rise in MPUt−1 (or FPUt−1 in bond financing) and increases uncertainty in interest rates, prompting a selloff in stocks and a flight-to-quality phenomenon. Note that this market action essentially stems from a heightened fear from policy uncertainty rather than something of inherent in the asset’s return. It is possible that a rise in MPUt−1 (or FPUt−1) could threaten the future cash flow and reduce the demand for both stocks and bonds. However, the evidence of a negative coefficient indicates the dominant force of the substitution effect. An implication of a negative coefficient suggests that a portfolio can benefit from a combination of stocks and bonds as a way of diversification and hedging against monetary policy or fiscal policy uncertainty.
Sixth, by testing the total policy uncertainty on the dynamic correlations between stock–bond returns, the evidence turns out to display mixed signs. For DJIA and VALUE stocks, the correlation coefficients present positive signs, indicating the dominance of an income effect attributable to general economic policy uncertainty; however, correlations of the TTMK, NASDAQ, and RUSSELL stocks with bond returns display negative signs, suggesting the dominance of a substitution effect, resulting from the reallocation of assets from ones with higher uncertainty to those with lower uncertainty in response to a rise in total policy uncertainty.
In sum, this paper provides significant empirical evidence to support the impact of MPUt−1 and FPUt−1 on stock–bond correlations. In addition to the VIXt−1, MOVEt−1 and EPUt−1, our Chi-squared statistics consistently suggest the rejection of the null, MPUt−1 = FPUt−1 = 0, and support the incremental significance of MPUt−1 and FPUt−1 in the test equation. This evidence has not previously been shown in the literature to explain the stock–bond return correlation.
Further, this study has practical implications for investment firms by tracing the time-varying correlations and is distinct from more commonly taken approaches by calculating the individual, constant correlations (Forbes and Rigobon 2002) within a given period of time. This study identifies categorical policy uncertainties as factors to explain the change in stock–bond correlations over time. Given the model parameters, firms can access information via newspapers to make projections related to stock–bond dynamics.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A

Table A1.
Some major term sets for policy category uncertainty indices.
Table A1.
Some major term sets for policy category uncertainty indices.
| Variable | Description | Source |
|---|---|---|
| EPUt | Economic policy uncertainty index involves: ‘‘economic’’ or ‘‘economy’’; ‘‘uncertain’’ or ‘‘uncertainty’’; and one or more of ‘‘Congress,’’ ‘‘deficit,’’ ‘‘Federal Reserve,’’ ‘‘legislation,’’ ‘‘regulation,’’ or ‘‘White House’’ in 10 major newspapers. | Baker et al. (2016) * |
| Fiscal policy uncertainty index involves terms of “government budget” or discretionary fiscal policy”, “government revenue”, “tax” or “Taxation”, “government deficit”, “government spending” or “government expenditure”, “social security expenditures”, “defense spending”, “Legislation”, “public debt” or “government debt”, “National bonds”, among others. | Davis (2016) ** | |
| Monetary policy uncertainty index involves terms of “monetary policy”, monetary easing”, quantitative easing”, “negative interest rate”, “official discount rate”, “monetary operation(s)”, “inflation target”, among others. | Davis (2016) ** |
* Baker et al. (2016). http://www.policyuncertainty.com. ** Source: ‘Measuring Economic Policy Uncertainty’ by Scott Baker, Nicholas Bloom and Davis, S.J. at www.PolicyUncertainty.com.
References
- Allard, Anne-Florence, Leonardo Iania, and Kristien Smedts. 2019. Stock–Bond Return Correlations: Moving away from ‘One-Frequency-Fits-All’ by Extending the DCC-MIDAS Approach. Available online: https://ssrn.com/abstract=3190071 (accessed on 29 May 2020).
- Andersson, Magnus, Elizaveta Krylova, and Sami Vähämaa. 2008. Why does the correlation between stock and bond returns vary over time? Applied Financial Economics 18: 139–51. [Google Scholar] [CrossRef]
- Antonakakis, Nikolaos, Ioannis Chatziantoniou, and George Filis. 2013. Dynamic co-movements of stock market returns, implied volatility and policy uncertainty. Economics Letters 120: 87–92. [Google Scholar] [CrossRef]
- Baele, Lieven, Geert Bekaert, and Inghelbrecht Koen. 2010. The determinants of stock and bond return comovements. Review of Financial Studies 23: 2374–428. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, and Steven J. Davis. 2016. Measuring economic policy uncertainty. Quarterly Journal of Economics 131: 1593–636. [Google Scholar] [CrossRef]
- Barsky, R. 1989. Why don’t the prices of stocks and bonds movetogether? American Economic Review 79: 1132–45. [Google Scholar]
- Baur, Dirk, and Brian Lucey. 2009. Flight and contagion—An empirical analysis of stock–bond correlations. Journal of Financial Stability 5: 339–52. [Google Scholar] [CrossRef]
- Bloom, Nicholas. 2009. The impact of uncertainty shocks. Econometrica 77: 623–85. [Google Scholar]
- Bloom, Nicholas. 2014. Fluctuations in Uncertainty. Journal of Economic Perspectives 28: 153–76. [Google Scholar] [CrossRef]
- Brunnermeier, Markus, and Lasse H. Pedersen. 2009. Market liquidity and funding liquidity. Review of Financial Studies 22: 2201–38. [Google Scholar] [CrossRef]
- Campbell, John Y., and John Ammer. 1993. What moves the stock and bond markets? A variance decomposition for long-term asset returns. Journal of Finance 48: 3–37. [Google Scholar] [CrossRef]
- Cappiello, Lorenzo, Robert F. Engle, and Kevin Sheppard. 2006. Asymmetric dynamics in the correlations of global equity and bond returns. Journal of Financial Econometrics 4: 537–72. [Google Scholar] [CrossRef]
- Chiang, Thomas Chinan. 2019. Economic policy uncertainty, risk and stock returns: Evidence from G7 stock markets. Finance Research Letters 29: 41–49. [Google Scholar] [CrossRef]
- Chiang, Thomas Chinan, Bang Nam Jeon, and Huimin Li. 2007. Dynamic correlation analysis of financial contagion: Evidence from Asian markets. Journal of International Money and Finance 26: 1206–28. [Google Scholar] [CrossRef]
- Chiang, Thomas Chinan, Jiandong Li, and Sheng-Yung Yang. 2015. Dynamic stock–bond return correlations and financial market uncertainty. Review of Quantitative Finance and Accounting 45: 59–88. [Google Scholar] [CrossRef]
- Connolly, Robert A., Chris T. Stivers, and Licheng Sun. 2005. Stock market uncertainty and the stock–bond return relation. Journal of Financial and Quantitative Analysis 40: 161–94. [Google Scholar] [CrossRef]
- d’Addona, Stefano, and Axel H. Kind. 2006. International stock–bond correlations in a simple affine asset pricing model. Journal of Banking and Finance 30: 2747–65. [Google Scholar] [CrossRef]
- de Goeij, Peter, and Wessel Marquering. 2004. Modeling the conditional covariance between stock and bond returns: A multivariate GARCH approach. Journal of Financial Econometrics 2: 531–64. [Google Scholar] [CrossRef]
- Dimic, Nabojsa, Jarmo Kivisha, Vanja Piljak, and Janne Äijö. 2016. Impact of financial market uncertainty and macroeconomic factors on stock–bond correlation in emerging markets. Research in International Business and Finance 36: 41–51. [Google Scholar] [CrossRef]
- Ehtesham, Qurat, and Danish Siddiqui. 2019. Analyzing Stock–bond Correlation in Emerging Markets. Research in Applied Economics. Available online: https://www.researchgate.net/publication/336283757_Analyzing_Stock–bond_Correlation_in_Emerging_Markets (accessed on 29 May 2020).
- Engle, Robert F. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business and Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Engle, Robert F. 2009. Anticipating Correlations: A New Paradigm for Risk Management. Princeton: Princeton University Press. [Google Scholar]
- Forbes, Kristin, and Roberto Rigobon. 2002. No contagion, only interdependence: measuring stock market comovements. Journal of Finance 57: 2223–61. [Google Scholar] [CrossRef]
- Glassman, Barry. 2018. The Most Confused Identity in Your Portfolio: High Yield Bonds. Available online: https://www.forbes.com/sites/advisor/2018/03/13/the-most-confused-identity-in-your-portfolio-high-yield-bonds/#cccd5ea2b8b6 (accessed on 30 May 2020).
- Gulko, Les. 2002. Decoupling. Journal of Portfolio Management 28: 59–66. [Google Scholar] [CrossRef]
- Hakkio, Craig S., and William R. Keeton. 2009. Financial stress: What is it, how can it be measured, and why does it matter? Federal Reserve Bank of Kansas City Economic Review 2: 5–50. [Google Scholar]
- Hong, GWangheou, Youngsoo Kim, and Bong-Soo Lee. 2014. Correlations between stock returns and bond returns: income and substitution effects. Quantitative Finance 14: 1999–2018. [Google Scholar] [CrossRef]
- Ilmanen, Antti. 2003. Stock–bond correlations. Journal of Fixed Income 13: 55–66. [Google Scholar] [CrossRef]
- Jones, Paul M., and Eric Olson. 2013. The time-varying correlation between uncertainty, output, and inflation: Evidence from a DCC-GARCH model. Economic Letters 118: 33–37. [Google Scholar] [CrossRef]
- Kwan, Simon H. 1996. Firm-specific information and the correlation between individual stocks and bonds. Journal of Financial Economics 40: 63–80. [Google Scholar] [CrossRef]
- Li, Xiao-Ming, Bing Zhang, and Ruzhao Gao. 2015. Economic policy uncertainty shocks and stock–bond correlations: Evidence from the US market. Economics Letters 132: 191–96. [Google Scholar] [CrossRef]
- Li, Erica X.N., Tao Zha, Ji Zhang, and Hao Zhou. 2019. Active Monetary or Fiscal Policy and Stock–bond Correlation. Available online: http://abfer.org/media/abfer-events-2019/annualconference/cebra/AC19P1019_Active_Monetary_or_Fiscal_Policy_and_Stock–bond_Correlation.pdf (accessed on 29 May 2020).
- Newey, Whitney K., and Kenneth D. West. 1987. A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 55: 703–8. [Google Scholar] [CrossRef]
- Panchenko, Valentyn, and Eliza Wu. 2009. Time-varying market integration and stock and bond return concordance in emerging markets. Journal of Banking and Finance 33: 1014–21. [Google Scholar] [CrossRef]
- Pericoli, Marcello. 2018. Macroeconomics Determinants of the Correlation between Stocks and Bonds. Bank of Italy Working Paper No. 1198. Available online: https://ssrn.com/abstract=3429148 (accessed on 31 May 2020).
- Tobin, James. 1969. A general equilibrium approach to monetary theory. Journal of Money Credit and Banking 1: 15–29. [Google Scholar] [CrossRef]
- Whaley, Robert E. 2009. Understanding the VIX. Journal of Portfolio Management 35: 98–105. [Google Scholar] [CrossRef]
- Yang, Jian, Yinggang Zhou, and Zijun Wang. 2009. The stock–bond correlation and macroeconomic conditions: One and a half centuries of evidence. Journal of Banking and Finance 33: 670–80. [Google Scholar] [CrossRef]
- Yardeni, Edward. 1997. Fed’s Stock Market Model Finds Overvaluation. US Equity Research, Deutsche Morgan Grenfell. Available online: http://www.yardeni.com/premiumdata/t_970825.pdf (accessed on 29 May 2020).
- Yu, IP-Win, Kang-Por Fung, and Chi-Sang Tam. 2010. Assessing financial market integration in Asia—Equity markets. Journal of Banking and Finance 34: 2874–85. [Google Scholar] [CrossRef]
| 1 | Li et al. (2015) argue that when EPU declines, a flight from quality could also occur, resulting in a reduction in the correlations. However, the reduction in EPU can signify an improvement in the market environment, which would raise investors’ demand for both stocks and bonds, thereby pushing up their correlations. This could produce an asymmetric effect. |
| 2 | Some researchers use domestic macroeconomic factors, such as inflation rate, business cycle patterns, and policy stance, on the stock–bond correlation (Ilmanen 2003; Yang et al. 2009; Dimic et al. 2016; Pericoli 2018). |
| 3 | This section follows closely to Engle (2009, pp. 45–49). |
| 4 | To illustrate the model, in the footnote of Table 2, one can plug the estimated parameters into the model using . |
| 5 | Instead of stressing the sources of policy uncertainty, Baele et al. (2010) analyze monetary policy impact on the direction of equity-bond correlation by focusing on the effects of inflation. In periods with a contractionary monetary policy, which is usually associated with low inflation rate, the correlation displays a positive relation; nonetheless, during periods of high inflation, the stock–bond correlation presents a negative relation. Thus, it is hard to justify whether inflation plays a role in uncertainty or a real income effect. However, Pericoli (2018) shows that inflation rate is a significant factor. Further, instead of using government bonds, one might use junk bonds to trace the dynamic correlations (Glassman 2018), which will be the subject of future research. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).