A Two-Population Extension of the Exponential Smoothing State Space Model with a Smoothing Penalisation Scheme
Abstract
1. Introduction
2. Model Description
2.1. The Lee-Carter Model
2.2. Exponential Smoothing State Space (ETS) Model
2.3. The Augmented Common Factor, or Lee-Li (LL) Model
2.4. The Coherent Functional Data Model (CFDM)
3. The Two-Population ETS Model
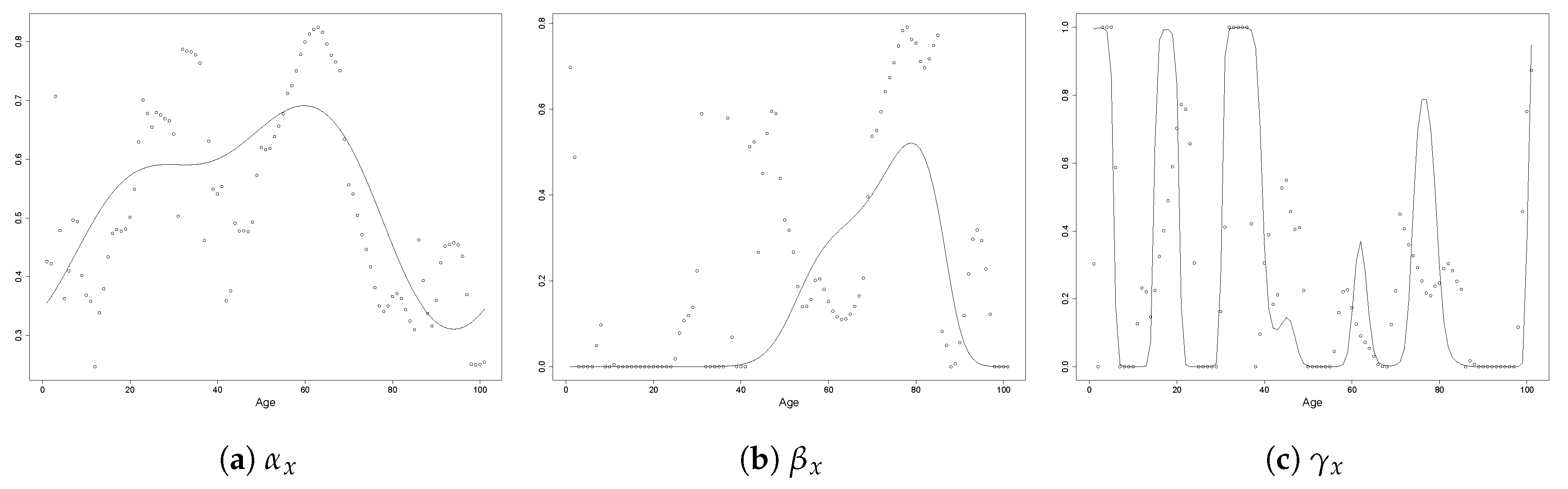
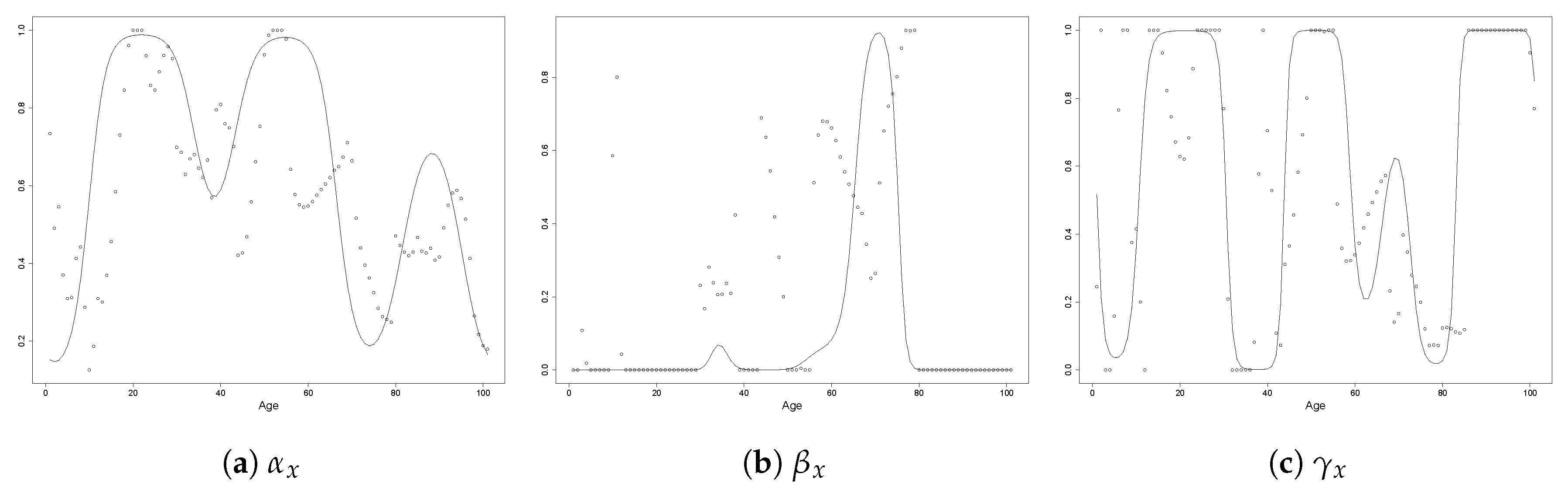
3.1. Model Specification
3.2. Reduction of Dimensionality
3.3. Selection of the Tuning Parameter
- Identify the first training set (e.g., ,,…,) out of the the entire sample;
- Given and , use the training set to fit the 2-ETS model and obtain the 1-step-ahead forecast ;
- Extend the training set to include and refit the 2-ETS model to obtain the 1-step-ahead forecast ;
- Repeat steps 2–3 until is generated; and
- Calculate the root of mean squared error (RMSE) asand are then chosen as those resulting in the smallest RMSE.
3.4. Overall Fitting Procedure
- (1)
- Fit an unpenalised 2-ETS model to obtain , and ;
- (2)
- Select , and as described in Section 3.2;
- (3)
- Given the chosen , and , select the tuning parameters and as described in Section 3.3; and
- (4)
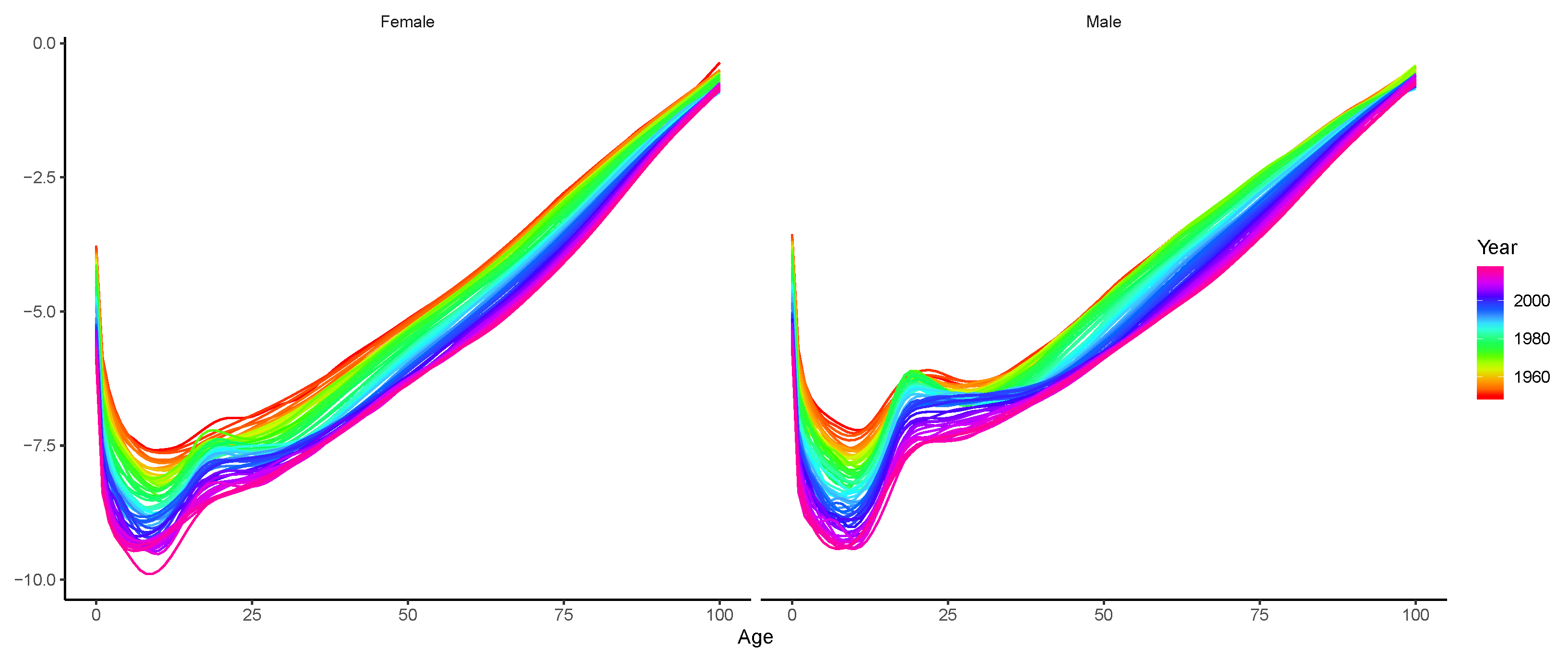
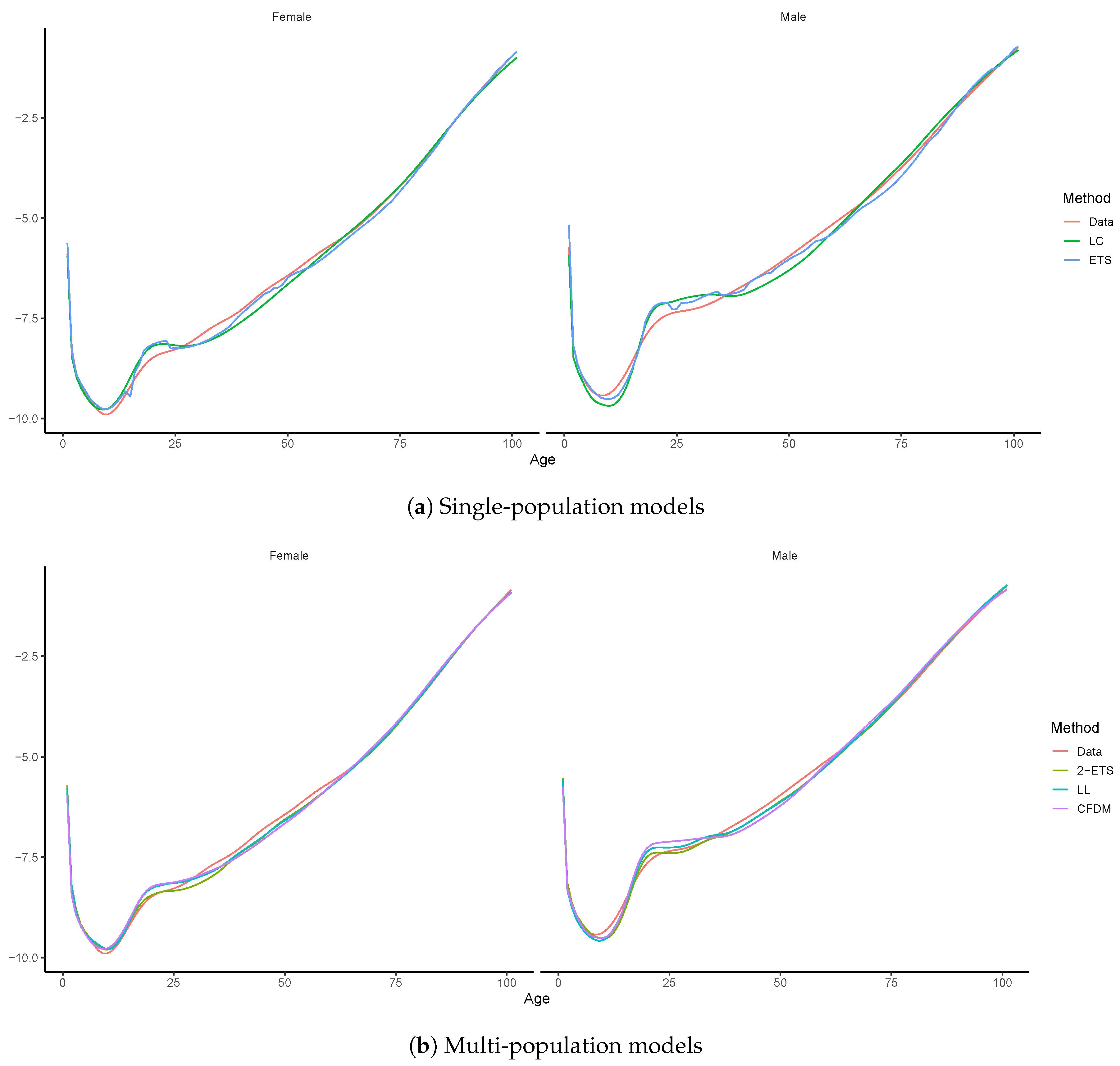
4. Empirical Analysis
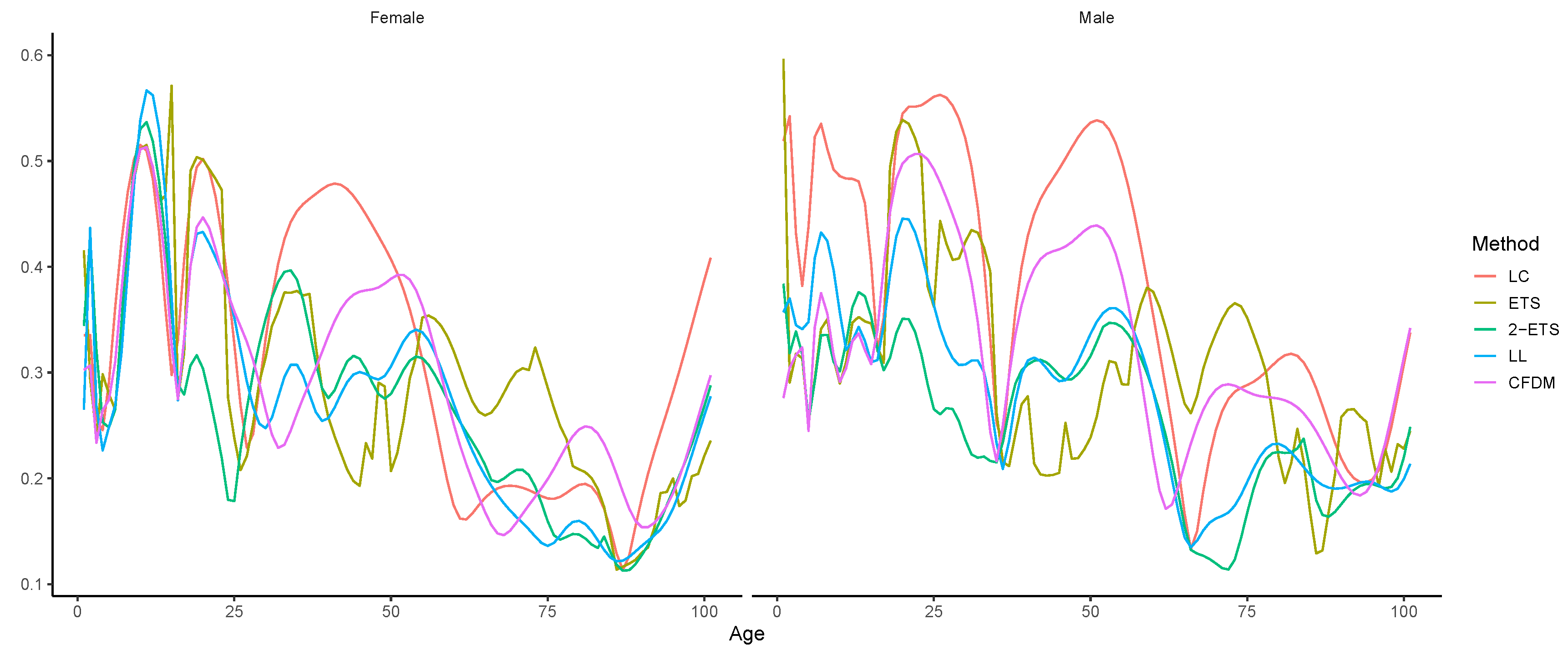
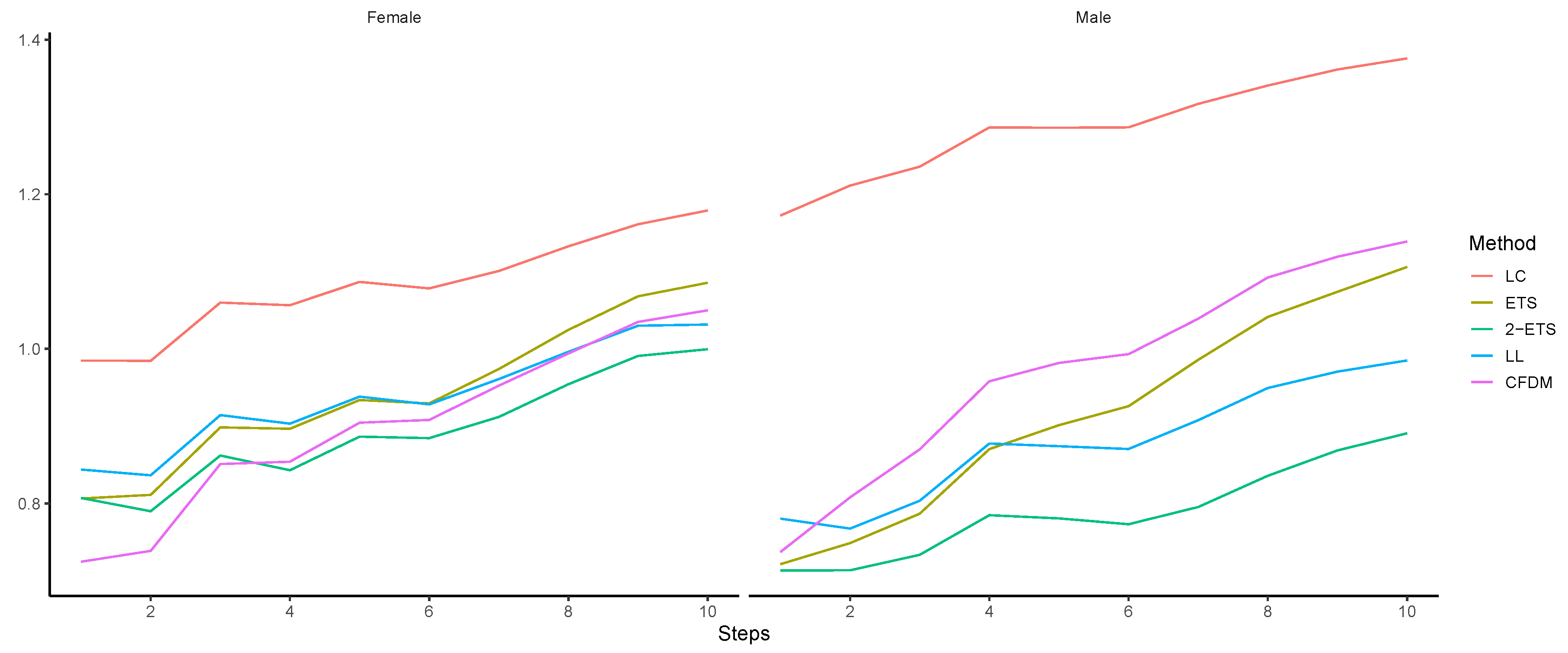
4.1. Forecast Accuracy Comparison
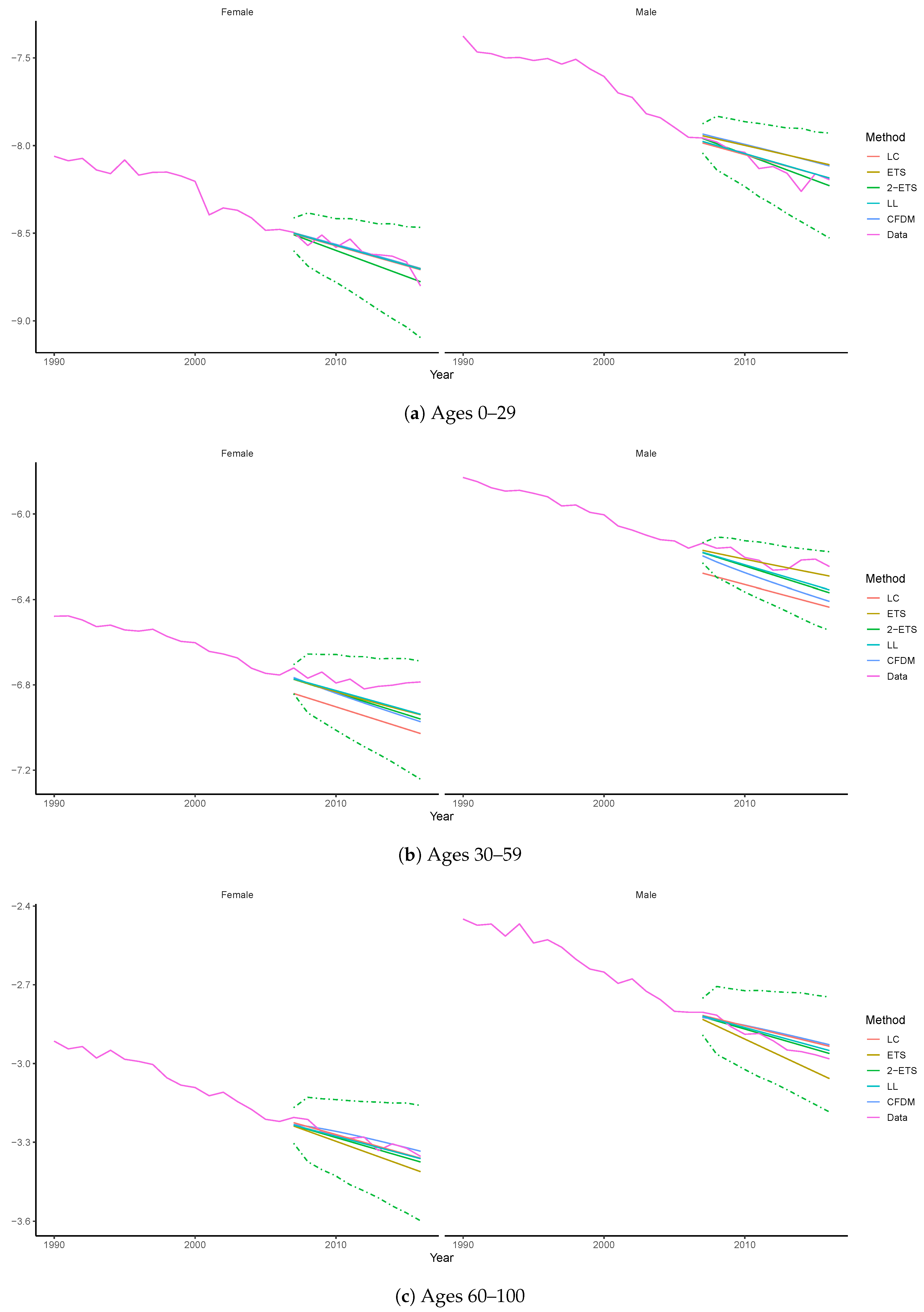
4.2. Prediction Intervals via Simulation
- Given the in-sample period 1950–2006, we estimate the model parameters and calculate the fitted (log) central death rates ;
- The residuals are then collected as , which are assumed to follow a multi-Gaussian distribution with means 0 and covariance computed as sample values from using ;
- Given the assumed distribution, simulate a matrix of error terms, which is applied to the 2-ETS projections from 2007 to 2016, according to (12); and
- The process is repeated until 5000 replicates are produced.
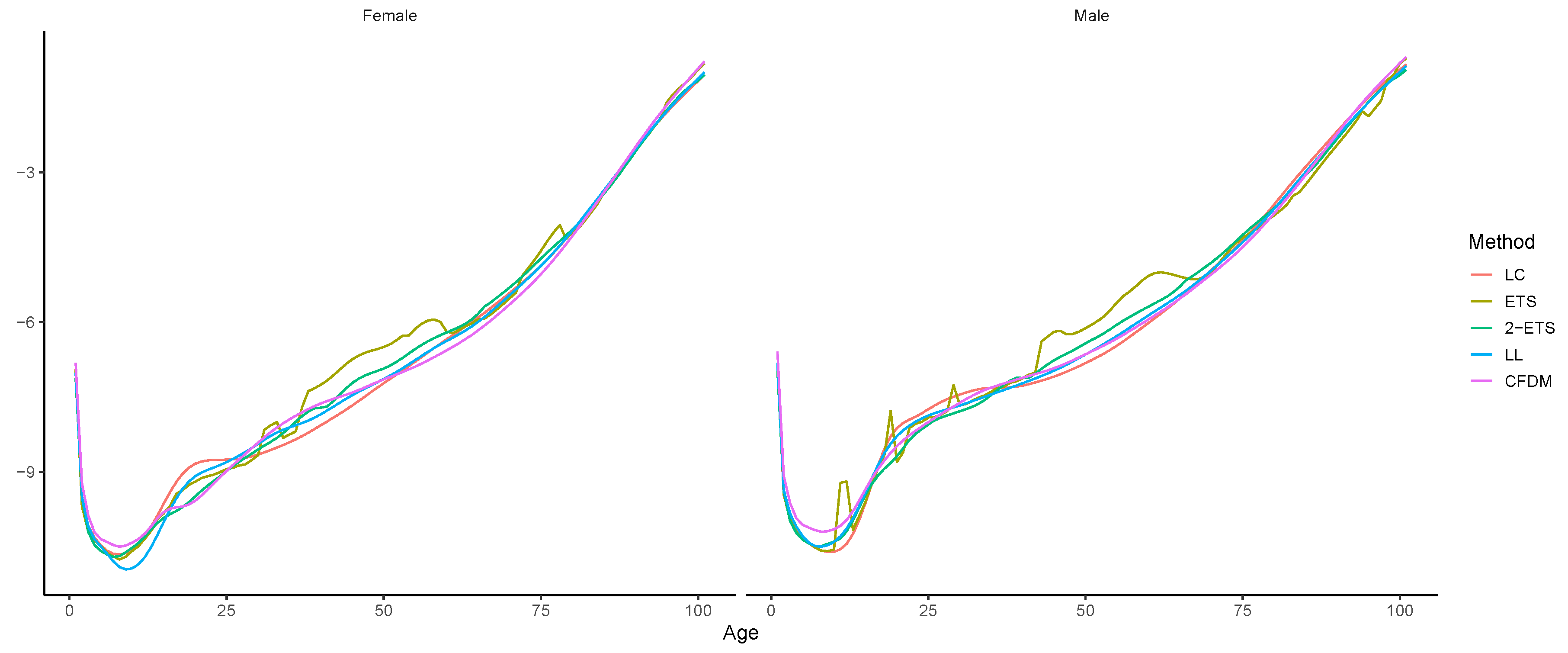
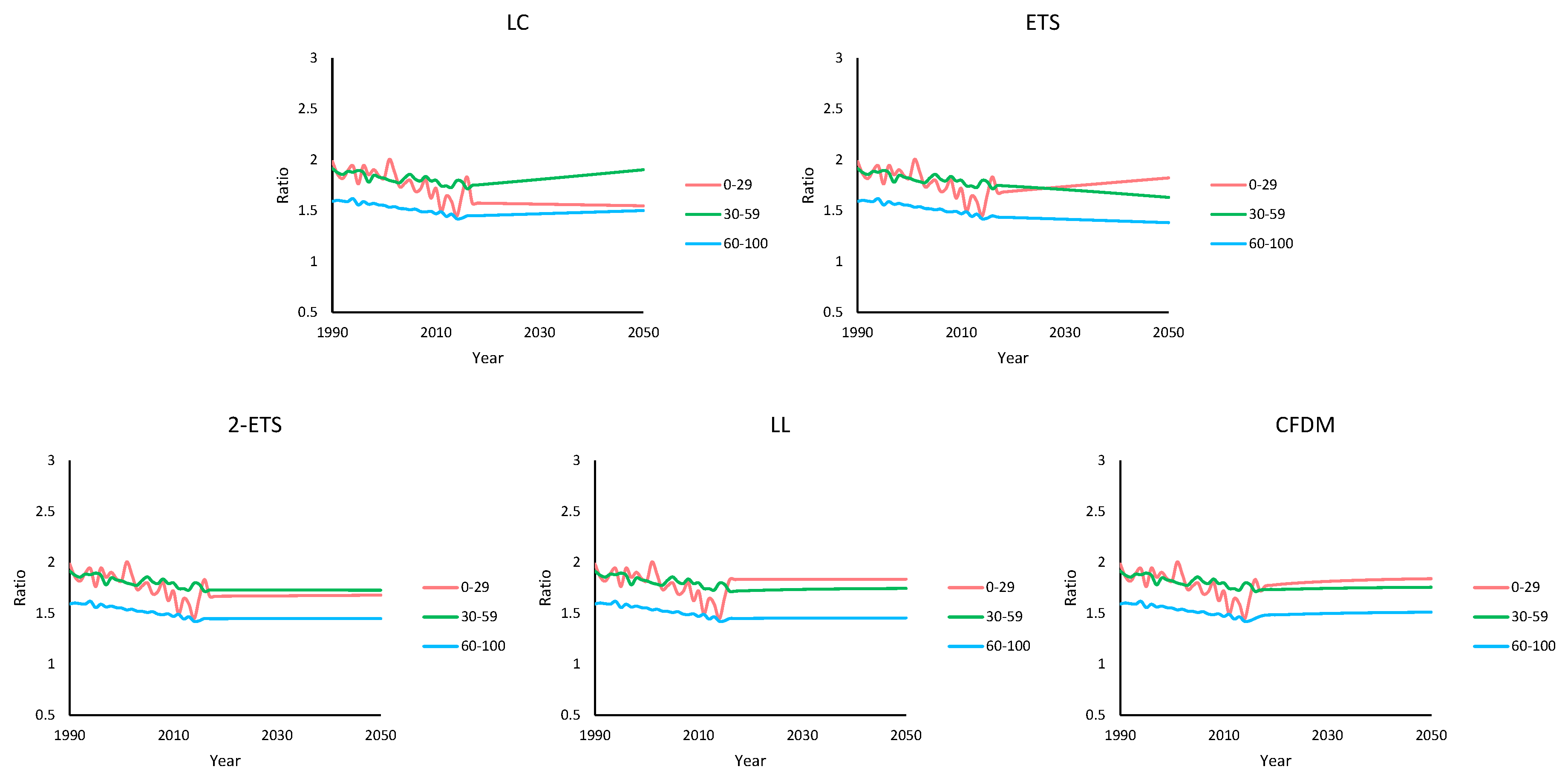
4.3. Long-Term Forecasting Performance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Booth, Heather, Rob Hyndman, Leonie Tickle, and Piet De Jong. 2006. Lee-Carter mortality forecasting: A multi-country comparison of variants and extensions. Demographic Research 15: 289–310. [Google Scholar] [CrossRef]
- Feng, Lingbing, and Yanlin Shi. 2018. Forecasting mortality rates: Multivariate or univariate models? Journal of Population Research 35: 289–318. [Google Scholar] [CrossRef]
- Gardner, Everette S., Jr. 1985. Exponential smoothing: The state of the art. Journal of Forecasting 4: 1–28. [Google Scholar] [CrossRef]
- Gardner, Everette S., Jr., and Ed. McKenzie. 1985. Forecasting trends in time series. Management Science 31: 1237–46. [Google Scholar] [CrossRef]
- Giacometti, Rosella, Marida Bertocchi, Svetlozar Rachev, and Frank Fabozzi. 2012. A comparison of the Lee–Carter model and AR–ARCH model for forecasting mortality rates. Insurance: Mathematics and Economics 50: 85–93. [Google Scholar] [CrossRef]
- Human Mortality Database. 2020. University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). Available online: www.mortality.org (accessed on 23 March 2020).
- Hyndman, Rob, Heather Booth, and Farah Yasmeen. 2012. Coherent mortality forecasting: The product-ratio method with functional time series models. Demography 50: 261–83. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, Rob, and Yeasmin Khandakar. 2008. Automatic time series forecasting: The forecast package for r. Journal of Statistical Software 26. [Google Scholar] [CrossRef]
- Hyndman, Rob, Anne B. Koehler, J. Keith Ord, and Ralph D. Snyder. 2008. Forecasting with Exponential Smoothing: The State Space Approach. Springer Series in Statistics; Berlin and Heidelberg: Springer. [Google Scholar]
- Hyndman, Rob, Anne Koehler, Ralph Snyder, and Simone Grose. 2002. A state space framework for automatic forecasting using exponential smoothing methods. International Journal of Forecasting 18: 439–54. [Google Scholar] [CrossRef]
- Hyndman, Rob, and Md. Shahid Ullah. 2007. Robust forecasting of mortality and fertility rates: A functional data approach. Computational Statistics and Data Analysis 51: 4942–56. [Google Scholar] [CrossRef]
- Hyndman, Rob J., and George Athanasopoulos. 2018. Forecasting: Principles and Practice. Melbourne: OTexts. [Google Scholar]
- Hyndman, Rob J., Anne B. Koehler, J. Keith Ord, and Ralph D. Snyder. 2005. Prediction intervals for exponential smoothing using two new classes of state space models. Journal of Forecasting 24: 17–37. [Google Scholar] [CrossRef]
- Hyndman, Rob J., and Han Lin Shang. 2009. Forecasting functional time series. Journal of the Korean Statistical Society 38: 199–211. [Google Scholar] [CrossRef]
- Lee, Ronald, and Timothy Miller. 2001. Evaluating the performance of the lee-carter method for forecasting mortality. Demography 38: 537–49. [Google Scholar] [CrossRef]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting U.S. mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar] [CrossRef]
- Li, Hong, and Yang Lu. 2017. Coherent forecasting of mortality rates: A sparse vector-autoregression approach. ASTIN Bulletin: The Journal of the IAA 47: 563–600. [Google Scholar] [CrossRef]
- Li, Jackie. 2013. A poisson common factor model for projecting mortality and life expectancy jointly for females and males. Population Studies 67: 111–26. [Google Scholar] [CrossRef]
- Li, Nan, and Ronald Lee. 2005. Coherent mortality forecasts for a group of populations: An extension of the lee-carter method. Demography 42: 575–94. [Google Scholar] [CrossRef]
- Makridakis, Spyros, and Michele Hibon. 2000. The m3-competition: Results, conclusions and implications. International Journal of Forecasting 16: 451–76. [Google Scholar] [CrossRef]
- Pegels, C. Carl. 1969. Exponential forecasting: Some new variations. Management Science 15: 311–15. [Google Scholar]
- Renshaw, Arthur E., and Steven Haberman. 2003. Lee–carter mortality forecasting with age-specific enhancement. Insurance: Mathematics and Economics 33: 255–72. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Steven Haberman. 2006. A cohort-based extension to the Lee-Carter model for mortality reduction factors. Insurance: Mathematics and Economics 38: 556–70. [Google Scholar] [CrossRef]
- Taylor, James W. 2003. Exponential smoothing with a damped multiplicative trend. International Journal of Forecasting 19: 715–725. [Google Scholar] [CrossRef]
- Wong, Kenneth, Jackie Li, and Sixian Tang. 2020. A modified common factor model for modelling mortality jointly for both sexes. Journal of Population Research 37: 1–32. [Google Scholar] [CrossRef]
| 1 | See Hyndman et al. (2002) for a thorough review of exponential smoothing methods. |
| 2 | A maximum likelihood method may also be employed to calibrate the parameters (Renshaw and Haberman 2003). |
| 3 | In our preliminary analysis, all damped parameters essentially approach 1 after a penalised structure is considered as in (14). |
| 4 | In contrast to Li and Lu (2017), we do not penalise , and . One reason is that those parameters will be smoothed after applying the procedure described in Section 3.2. The other reason is that out-of-sample forecasts of do not directly depend on them. In other words, smoothed parameters will not necessarily enforce the smoothness of across x. |
| Model | Mean | Std. Dev. | |||
|---|---|---|---|---|---|
| Panel A: Female | |||||
| LC | 0.1383 | 0.1144 | 0.0781 | 0.0369 | 0.1846 |
| ETS | 0.1173 | 0.0952 | 0.0688 | 0.0448 | 0.1183 |
| 2-ETS | 0.0994 | 0.0802 | 0.0590 | 0.0386 | 0.0980 |
| LL | 0.1059 | 0.0828 | 0.0663 | 0.0288 | 0.1015 |
| CFDM | 0.1097 | 0.0925 | 0.0592 | 0.0456 | 0.1395 |
| Panel B: Male | |||||
| LC | 0.1884 | 0.1625 | 0.0957 | 0.0794 | 0.2524 |
| ETS | 0.1217 | 0.1031 | 0.0649 | 0.0569 | 0.1243 |
| 2-ETS | 0.0789 | 0.0705 | 0.0356 | 0.0379 | 0.0987 |
| LL | 0.0965 | 0.0844 | 0.0472 | 0.0392 | 0.1168 |
| CFDM | 0.1291 | 0.1129 | 0.0628 | 0.0669 | 0.1658 |
| Steps | Female | Male | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LC | ETS | 2-ETS | LL | CFDM | LC | ETS | 2-ETS | LL | CFDM | |
| 1 | 0.0965 | 0.0647 | 0.0648 | 0.0708 | 0.0522 | 0.1368 | 0.0518 | 0.0506 | 0.0606 | 0.0622 |
| 2 | 0.0964 | 0.0662 | 0.0592 | 0.0683 | 0.0562 | 0.1546 | 0.0595 | 0.0507 | 0.0565 | 0.0588 |
| 3 | 0.1374 | 0.1038 | 0.0932 | 0.1052 | 0.0984 | 0.1632 | 0.0718 | 0.0589 | 0.0742 | 0.0774 |
| 4 | 0.1089 | 0.0790 | 0.0600 | 0.0748 | 0.0741 | 0.1981 | 0.1065 | 0.0801 | 0.1054 | 0.1026 |
| 5 | 0.1403 | 0.1097 | 0.1028 | 0.1095 | 0.1098 | 0.1642 | 0.0998 | 0.0580 | 0.0735 | 0.0743 |
| 6 | 0.1061 | 0.0817 | 0.0761 | 0.0757 | 0.0852 | 0.1653 | 0.1048 | 0.0532 | 0.0722 | 0.0681 |
| 7 | 0.1465 | 0.1343 | 0.1076 | 0.1225 | 0.1290 | 0.2139 | 0.1477 | 0.0807 | 0.1137 | 0.1047 |
| 8 | 0.1692 | 0.1580 | 0.1332 | 0.1375 | 0.1425 | 0.2178 | 0.1664 | 0.1045 | 0.1315 | 0.1321 |
| 9 | 0.1780 | 0.1693 | 0.1422 | 0.1493 | 0.1577 | 0.2241 | 0.1592 | 0.1099 | 0.1213 | 0.1189 |
| 10 | 0.1713 | 0.1468 | 0.1137 | 0.1086 | 0.1345 | 0.2205 | 0.1722 | 0.1077 | 0.1189 | 0.1170 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Tang, S.; Li, J. A Two-Population Extension of the Exponential Smoothing State Space Model with a Smoothing Penalisation Scheme. Risks 2020, 8, 67. https://doi.org/10.3390/risks8030067
Shi Y, Tang S, Li J. A Two-Population Extension of the Exponential Smoothing State Space Model with a Smoothing Penalisation Scheme. Risks. 2020; 8(3):67. https://doi.org/10.3390/risks8030067
Chicago/Turabian StyleShi, Yanlin, Sixian Tang, and Jackie Li. 2020. "A Two-Population Extension of the Exponential Smoothing State Space Model with a Smoothing Penalisation Scheme" Risks 8, no. 3: 67. https://doi.org/10.3390/risks8030067
APA StyleShi, Y., Tang, S., & Li, J. (2020). A Two-Population Extension of the Exponential Smoothing State Space Model with a Smoothing Penalisation Scheme. Risks, 8(3), 67. https://doi.org/10.3390/risks8030067






