A New Approach to Risk Attribution and Its Application in Credit Risk Analysis

Abstract

How can risk of a company be allocated to its divisions and attributed to risk factors? The Euler principle allows for an economically justified allocation of risk to different divisions. We introduce a method that generalizes the Euler principle to attribute risk to its driving factors when these factors affect losses in a nonlinear way. The method splits loss contributions over time and is straightforward to implement. We show in an example how this risk decomposition can be applied in the context of credit risk.

1. Introduction

For any company, the decomposition of risk matters. Risk is decomposed to address questions such as: how much do a company’s divisions contribute to the total risk? Or, what portion of the total risk can be attributed to a specific type of risk, such as interest rate risk? Accordingly, we distinguish two dimensions of how risk is decomposed. Risk allocation deals with how risk from some entity is allocated to different sub-entities or divisions. Risk attribution is about identifying and quantifying risk drivers, types of risk, or risk management features.

Table 1. Decomposition of risk along two dimensions: risk allocation and attribution.

illustrates the decomposition of risk along these two dimensions.

Before giving more details on the distinction between risk allocation and risk attribution, let us recall that risk is typically modelled by a risk measure applied to the company’s potential losses. Examples of such risk measures include value-at-risk and expected shortfall. There are important conceptual differences between risk allocation and risk attribution:

• For risk allocation, we note that the company’s profit/loss is the sum of the profits/losses of its divisions so that there is linearity in the underlying loss variable. Risk allocation is about achieving a similar relationship for risk, namely, risk allocated to the divisions sums up to the total risk. The goal is to find a fair split of the diversification benefits along with the specific risk of each division.
• For risk attribution, risk drivers may contribute to a company’s profit/loss in a nonlinear way. Not all diversification effects can or may need to be attributed to the risk drivers. The goal is to identify risk drivers and attribute risk to them while cross effects between risk drivers may remain.

Risk allocation has been well studied in the literature. An often used approach is to allocate to each division its marginal contribution to the total risk, in other words, the risk allocated to a division equals the rate at which the company’s risk is changed when the division’s losses increase. This approach is called Euler risk allocation or Euler principle because Euler’s theorem on homogeneous functions assures that the risks allocated to the divisions under this approach sum up to the total risk if the risk measure is homogenous, which is satisfied for value-at-risk and expected shortfall. Moreover, the Euler risk allocation is well justified economically in that it is compatible with return on risk adjusted capital (Tasche 2008). In fact, it is essentially the only such risk allocation. Additionally, the Euler risk allocation satisfies a desired diversification property in that it does not allocate more risk to any division than the risk that the division would have stand-alone (Denault 2001; Kalkbrener 2005). Zhang and Rachev (2006) give an overview of how different risk measures and distributions affect the risk allocation while Bauer and Zanjani (2016) study the reverse problem of identifying risk measures that yield a risk allocation. A complementary and—in some sense—converse question to risk allocation is risk aggregation, which is also well studied and deals with how to deduce a total risk from individual risk components. Risk aggregation is particularly relevant in the context of systemic and vector-valued risk measures (Cousin and Di Bernardino 2013; Feinstein et al. 2017; Jouini et al. 2004; Landsman et al. 2016), where individual parts and their dependence structure are modelled.

By contrast, there is only scarce literature on risk attribution when risk drivers contribute to the losses in a nonlinear way. When the Euler principle is applied directly, its desirable properties mentioned above are lost when loss contributions are no more additive. A possibility for risk attribution is to use the Shapley value, which is based on a game-theoretic approach to solve the conflict on how to share the diversification effects (Denault 2001; Powers 2007). However, it becomes computationally very demanding when there is a large number of risk drivers. Moreover, in the special case of a linear loss structure, it does not reconcile with the Euler risk allocation.

In this paper, we propose a new method for risk attribution. We employ that risk drivers are typically given as a time series. At each time step, we analyze how much a change in one particular risk driver contributes to the total risk at that time. We aggregate these changes over time to obtain the contribution of each risk driver. This procedure results in a linear approximation of the loss variable in terms of the contributions of the different risk drivers. Because we have a linear approximation of the loss variable, we can apply the Euler principle to this approximation, which in turn gives us the contributions for the risk attribution.

This method has the property that in the special case of a linear loss structure, it gives the same result as the Euler risk allocation. For a general loss structure, the approximation becomes better the larger the number of time steps is in the time series used for the risk drivers. We prove that, under suitable assumptions, the approximation converges to the precise value as the number of time steps goes to infinity. Moreover, the method is easy to apply, as we show in an example in the context of credit risk. The example considers a structural credit risk model, where the obligors’ defaults are driven by idiosyncratic risk and two common risk factors. The computation of the risk attribution for these factors gives meaningful results.

The remainder of this paper is organized as follows. In Section 2, we recall the Euler risk allocation and its economic justification. We also mention several alternative methods for risk allocation. For risk attribution, we introduce in Section 3 a linear approximation of the loss variable, which then allows us to apply the Euler risk allocation to the approximation. Additionally, Section 3 contains the above-mentioned convergence result. Section 4 presents the application of risk attribution in the context of credit risk. Section 5 concludes.

2. Risk Allocation in Divisions

In this section, we recall the Euler principle for risk allocation, which is a well-known approach in the literature; see for example Section 8.5 in McNeil et al. (2015) or Tasche (2008). It is also being used in the context of the Fundamental Review of Trading Book (Li and Xing 2019).

We consider K divisions with loss variables $L^1,\cdots ,L^K$. As is customary, losses are denoted with positive signs so that $L^k>0$ means a loss in the amount of $L^k$ in the kth division. We denote the total loss variable by $L={\sum }_{k=1}^K{L}^k$. For a given risk measure $\rho$, the overall required capital is $\rho (-L)$. We are seeking allocations $x^k$ to the kth division, corresponding to the portion of the total risk that is allocated to the kth division. Mathematically, $x^k$ is the result of a mapping from the loss variables $L^1,\cdots ,L^K$ and the risk measure $\rho$ to the real numbers. The goal of risk allocation is to determine such a suitable mapping. Note that $x^k$ may depend on all loss variables $L^1,\cdots ,L^K$ and not just $L^k$ because the dependence structure between $L^k$ and the other loss variables affects the value of $x^k$. The following two properties are crucial for risk allocation:

• The first property is the full allocation property $\rho (-L)={\sum }_{k=1}^K{x}^k$, which means that exactly the total risk is allocated to the divisions.
• The second property is related to the return on the risk adjusted capital (RORAC) given by

  $${\mathrm{RORAC}}_k=\frac{-E\left[L^k\right]}{x^k}\mathrm{and}\mathrm{RORAC}(-L)=\frac{-E\left[L\right]}{\rho (-L)},$$

  which correspond to the expected returns adjusted for risk of the kth division and of the total company, respectively, as explained in Tasche (2008). Risk allocations $x^1,\cdots ,x^K$ are said to be RORAC compatible if there exists $ϵ>0$ such that

  $${\mathrm{RORAC}}_k>\mathrm{RORAC}(-L)⟹\mathrm{RORAC}(-L-h{L}^k)>\mathrm{RORAC}(-L)$$

  for all $0<h<ϵ$. In words, an allocation is RORAC compatible if increasing the weight of a division that has superior risk-adjusted return will improve the total risk-adjusted return.

Definition 1.

The Euler risk allocation (also called Euler principle ) is defined as

$$x_{\mathrm{Euler}}^k=\frac{\mathrm{d}}{\mathrm{d}\lambda }\rho (-L-\lambda L^k){|}_{\lambda =0}.$$

The Euler principle has a sound economic justification. By Euler’s theorem on homogeneous functions, it satisfies the full allocation property if $\rho$ is homogeneous. For example, value-at-risk (${\mathrm{VaR}}_{\alpha }$) and expected shortfall (${\mathrm{ES}}_{\alpha }$) are homogeneous. It can be checked that the Euler principle is also RORAC compatible. Even more, under suitable technical conditions, the Euler principle is the only allocation which is RORAC compatible; see Proposition 2.1 of Tasche (2008). Note that for this result, the risk measure does not need to be sub-additive.1

If the risk measure is sub-additive and some technical conditions hold, the Euler principle is the only risk allocation that satisfies a strengthened version of the diversification benefit inequality $x^k\le \rho (-L^k)$ for all k (Denault 2001; Kalkbrener 2005).

A potential drawback is that $x_{\mathrm{Euler}}^k$ can be negative when there is negative correlation between $L^k$ and L. From a business perspective, however, it may be reasonable to allocate a negative risk value to a division that reduces the overall risk.

If ${\mathrm{VaR}}_{\alpha }$ is used as the risk measure, then

$$x_{\mathrm{Euler}}^k=E\left[L^k\right|L={\mathrm{VaR}}_{\alpha }\left(L\right)];$$

(1)

see Section 3.2 of Tasche (2008). This means to compute the average of $L^k$ over the scenarios where L realizes ${\mathrm{VaR}}_{\alpha }\left(L\right)$. In this case, issues are that the computation leads to instability and that the conditional expectation may not even be directly computed, as there may not be any scenario or very few scenarios where L takes the value ${\mathrm{VaR}}_{\alpha }\left(L\right)$. In practice, one uses a kernel estimation approach for (1) as explained in Tasche (2008) or replaces (1) by the expected range loss approximation

$$x_{\mathrm{Euler}}^k\approx E\left[L^k|L\in [{\mathrm{VaR}}_{\alpha }\left(L\right)-x/2,{\mathrm{VaR}}_{\alpha }\left(L\right)+x/2]\right]$$

for some range $x>0$. The question then becomes how big the range x should be. A bigger range gives a more stable, but less accurate allocation. If ${\mathrm{ES}}_{\alpha }$ is used as the risk measure, then

$$x_{\mathrm{Euler}}^k=E\left[L^k\right|L\ge {\mathrm{VaR}}_{\alpha }\left(L\right)].$$

For completeness, we mention several alternative approaches, along with their major drawbacks.

• Pro-rata contribution. The simplest allocation approach is the pro-rate contribution

  $$x_{\mathrm{pr}}^k=\frac{\rho (-L^k)}{{\sum }_{\ell =1}^K\rho (-L^{\ell })}\rho (-L).$$
  Because the diversification effects are allocated proportionally to each division’s contribution, this approach does not penalize divisions that are highly correlated and does not reward divisions that increase the diversification. This is a major drawback of this approach.
• Marginal risk contribution. The marginal risk contribution (or with-without principle) is given by

  $$x_{\mathrm{mr}}^k=\rho (-L)-\rho (-(L-L^k)).$$
  It does not satisfy the full allocation property because one can show that ${\sum }_{k=1}^K{x}_{\mathrm{mr}}^k<\rho (-L)$ in general.
• Shapley value. This is a game-theoretic approach to solve the conflict on how to share the diversification effects. It also works in nonlinear structures and will be discussed at the end of the next section. A drawback of this approach is that it becomes computationally very demanding when there is a large number of divisions.

3. Risk Attribution in Risk Drivers

We now consider d random variables $R^1,\cdots ,R^d$, interpreted as risk factors, and assume that the total loss variable $L=f(R^1,\cdots ,R^d)$ is some function of these risk factors. There is again a given risk measure $\rho$ so that the overall required capital is $\rho (-f(R^1,\cdots ,R^d))$. We are seeking attributions $y^j$ to the jth risk factor. The problem from Section 2 corresponds to the special case of linear losses $f(R^1,\cdots ,R^d)={\sum }_{j=1}^d{R}^j$.

The main idea is to approximate $f(R^1,\cdots ,R^d)$ by a sum ${\sum }_{j=1}^d{A}^j$, where $A^j$ isolates the contribution of the jth risk factor, and then apply the Euler principle to this sum. In other words, the goal is to find isolated contributions to the company’s potential losses.

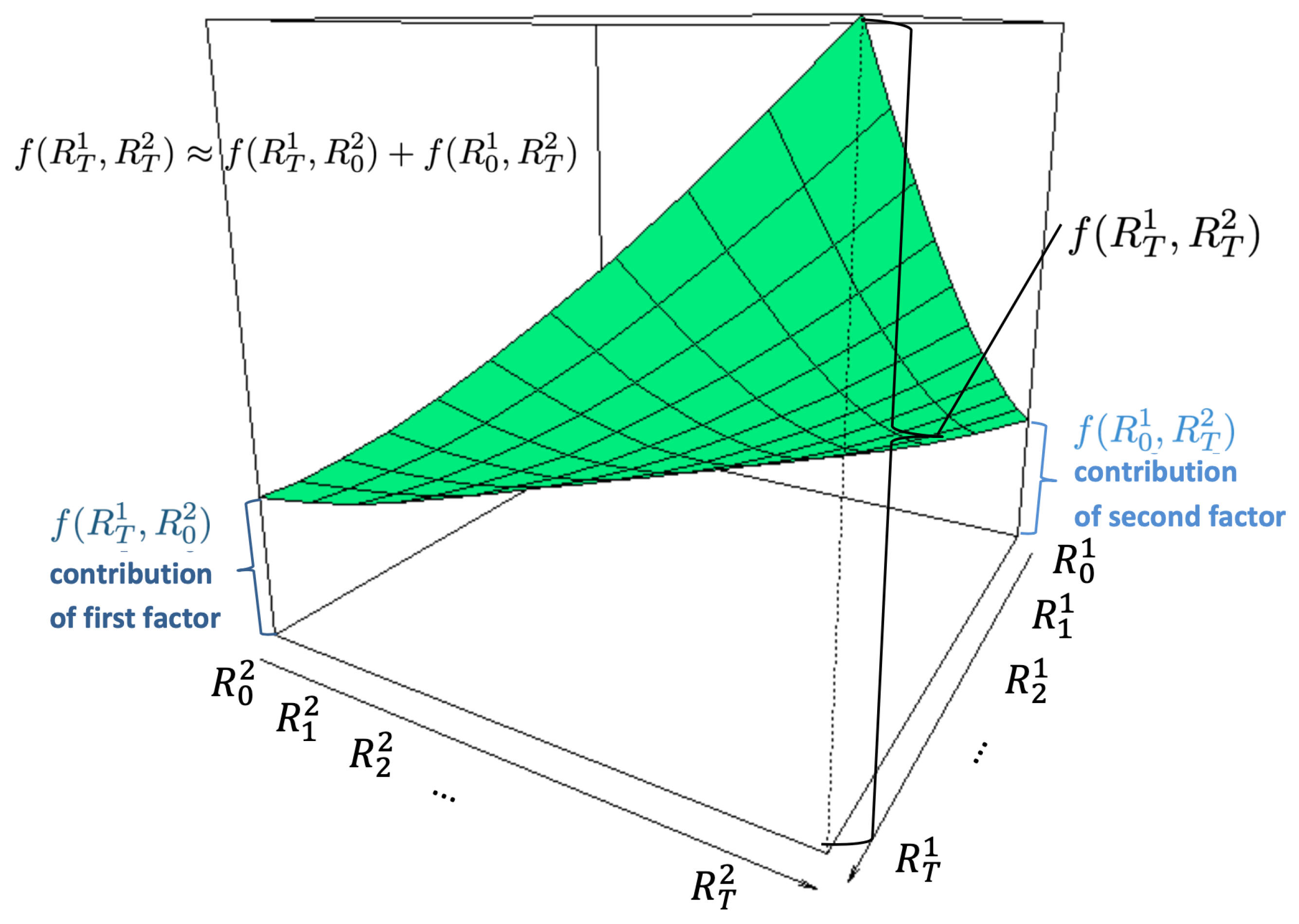
In reality, the risk factors evolve over time. To illustrate, we start by considering two risk factors taking values $R_0^1,R_1^1,\cdots ,R_T^1$ and $R_0^2,R_1^2,\cdots ,R_T^2$ over time. The losses depend on the terminal values of the risk factors: $L=f(R_T^1,R_T^2)$. We aim to linearize the losses $f(R_T^1,R_T^2)\approx A^1+A^2$, where $A^1$ and $A^2$ are the loss contributions of the first and second risk factors, respectively. Once we have such a linearization, we can apply risk allocation as in the previous section to $A^1+A^2$, which results in attributions $y^1$ and $y^2$ to the two risk factors. We now discuss how we can determine $A^1$ and $A^2$.

A possibility would be to define $A^1$ as the losses resulting from changes in $R^1$ while $R^2$ is fixed. Assuming $f(R_0^1,R_0^2)=0$ for simplicity and applying the same idea to define $A^2$, this will lead to an approximation

$$f(R_T^1,R_T^2)\approx \underset{A^1}{\underbrace{f(R_T^1,R_0^2)}}+\underset{A^2}{\underbrace{f(R_0^1,R_T^2)}}.$$

The approximation is exact if the risk factors decouple in an additive way. However, as Figure 1 illustrates, the resulting approximation error can be large when f depends on $R_T^1$ and $R_T^2$ in a nonlinear way. This is relevant in practice, as factors often affect risk in a nonlinear way.

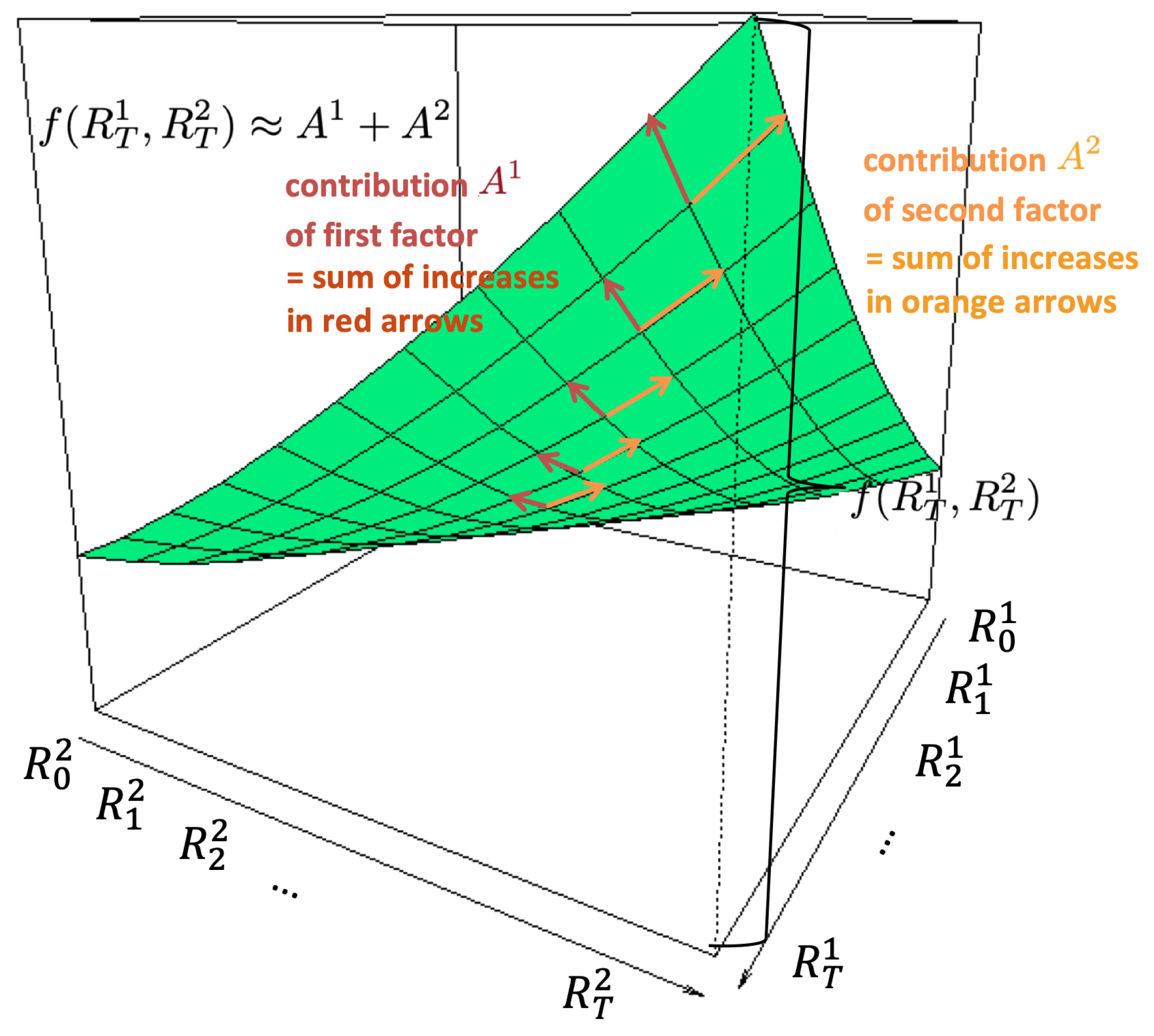
Rather than computing just one step, we define

$$A^1=\sum _{t=0}^{T-1}\underset{\mathrm{change}\mathrm{in}\mathrm{losses}\mathrm{due}\mathrm{to}{R}^1\mathrm{at}\mathrm{time}t}{\underbrace{\left(f(R_{t+1}^1,R_t^2)-f(R_t^1,R_t^2)\right)}}\mathrm{and}{A}^2=\sum _{t=0}^{T-1}\underset{\mathrm{change}\mathrm{in}\mathrm{losses}\mathrm{due}\mathrm{to}{R}^2\mathrm{at}\mathrm{time}t}{\underbrace{\left(f(R_t^1,R_{t+1}^2)-f(R_t^1,R_t^2)\right)}}$$

(2)

which means to consider the marginal changes at the different time steps and sum them up. As Figure 2 on the next page shows, the resulting approximation error will typically be much smaller because we approximate locally the function change at each time step. This approximation is exact when there is a stepwise linear dependence structure. The larger the curvature of f is, the bigger the approximation error will be. However, by making the size of the time steps smaller, the approximation error can be reduced.

We now discuss the general case with d risk factors. Each risk factor corresponds to a time series $R_0^j,R_1^j,\cdots ,R_T^j$. We denote by $R_t^j$ the $j^{\mathrm{th}}$ risk factor at time t, which is a random variable observable at time t. We define $A^j$ by

$$A^j=\sum _{t=0}^{T-1}\left(f(R_{t+1}^j,{\left(R_t^i\right)}_{i\ne j})-f\left({\left(R_t^i\right)}_i\right)\right),$$

(3)

This means that, for each period, we consider the one-dimensional slides

$$f(R_{t+1}^j,{\left(R_t^i\right)}_{i\ne j})-f\left({\left(R_t^i\right)}_i\right)=\mathrm{change}\mathrm{in}\mathrm{losses}\mathrm{due}\mathrm{to}{R}^j\mathrm{at}\mathrm{time}t\mathrm{while}{R}^i\mathrm{for}i\ne j\mathrm{remains}\mathrm{constant}$$

and then sum up over time $t=0,1,\cdots ,T-1$ to obtain $A^j$.

This method has the following properties:

• In the linear case $f\left({\left(R_t^i\right)}_i\right)={\sum }_{j=1}^d{R}_t^j$, we have $A^j=R_T^j-R_0^j$ so that ${\sum }_{j=1}^d{A}^j=f\left({\left(R_T^i\right)}_i\right)-{\sum }_{j=1}^d{R}_0^j$. One could adjust the procedure to achieve ${\sum }_{j=1}^d{A}^j=f\left({\left(R_T^i\right)}_i\right)$ in this linear case, but ${\sum }_{j=1}^d{R}_0^j$ is a constant at time 0, hence affects little the tails of the losses and the risk measure.
• For each period, $A^j$ captures the risk that comes from the $j^{\mathrm{th}}$ risk driver while considering the current values of the other risk factors. Therefore, the overall residual consists of the diversification benefit in each period, summed up over the periods:

  $$f\left({\left(R_T^i\right)}_i\right)-f\left({\left(R_0^i\right)}_i\right)-\sum _{j=1}^d{A}^j=\sum _{t=0}^{T-1}\underset{\mathrm{change}\mathrm{in}\mathrm{loss}\mathrm{from}\mathrm{joint}\mathrm{movement}\mathrm{of}\mathrm{several}\mathrm{risk}\mathrm{drivers}\mathrm{in}\mathrm{period}t}{\underbrace{\left(f\left({\left(R_{t+1}^i\right)}_i\right)-f\left({\left(R_t^i\right)}_i\right)-{\sum }_{j=1}^d\left(f(R_{t+1}^j,{\left(R_t^i\right)}_{i\ne j})-f\left({\left(R_t^i\right)}_i\right)\right)\right)}}$$
• An alternative specification for $A_j$ would be to use an approximation with partial derivatives of the form

  $$\sum _{t=0}^{T-1}\frac{\partial f}{\partial x^j}\left({\left(R_t^i\right)}_i\right)(R_{t+1}^j-R_t^j).$$
  This corresponds to first-order sensitivities while (3) is based on one-dimensional slides.

When we fix the time horizon and make the time grid more and more granular, the approximation ${\sum }_{j=1}^d{A}_j$ converges to the total losses L under suitable conditions. This result is formalized as follows.

Proposition 1.

Let $L=f(R_T^1,\cdots ,R_T^d)$ for a twice continuously differentiable f and let ${(R_t^1,\cdots ,R_t^d)}_{t\in [0,T]}$ be a continuous semimartingale on $[0,T]$ with zero quadratic covariation ${\langle R^i,R^j\rangle }_t=0$ for all $t\in [0,T]$ and $i\ne j$. We set

$$A_N^j=\sum _{n=0}^{N-1}\left(f(R_{t_{n+1}}^j,{\left(R_{t_n}^i\right)}_{i\ne j})-f\left({\left(R_{t_n}^i\right)}_i\right)\right)$$

for $0=t_0\le t_1\le \cdots \le t_N=T$. Then ${\sum }_{j=1}^d{A}_N^j+f(R_0^1,\cdots ,R_0^d)$ converges to L almost surely as $N\to \infty$.

Proof. 

By Itô’s formula, we can write

$$\begin{array}{cc}\hfill f(R_T^1,\cdots ,R_T^d)-f(R_0^1,\cdots ,R_0^d)& =\sum _{j=1}^d{\int }_0^T{f}_{x^j}(R_t^1,\cdots ,R_t^d)\mathrm{d}{R}_t^j+\frac{1}{2}\sum _{i,j=1}^d{\int }_0^T{f}_{x^i{x}^j}(R_t^1,\cdots ,R_t^d)\mathrm{d}{\langle R^i,R^j\rangle }_t\hfill \\ \hfill & =\sum _{j=1}^d{\int }_0^T{f}_{x^j}(R_t^1,\cdots ,R_t^d)\mathrm{d}{R}_t^j+\frac{1}{2}\sum _{j=1}^d{\int }_0^T{f}_{x^j{x}^j}(R_t^1,\cdots ,R_t^d)\mathrm{d}{\langle R^j,R^j\rangle }_t,\hfill \end{array}$$

(4)

using that ${\langle R^i,R^j\rangle }_t=0$ for all $i\ne j$ by assumption. As in the proof of Theorem 3.3 in Karatzas and Shreve (1998), we also have that $A_N^j$ converges almost surely to

$${\int }_0^T{f}_{x^j}(R_t^1,\cdots ,R_t^d)\mathrm{d}{R}_t^j+\frac{1}{2}{\int }_0^T{f}_{x^j{x}^j}(R_t^1,\cdots ,R_t^d)\mathrm{d}{\langle R^j,R^j\rangle }_t$$

so that

$$\begin{array}{cc}\hfill \underset{N\to \infty }{lim}\sum _{j=1}^d{A}_N^j+f(R_0^1,\cdots ,R_0^d)& =\sum _{j=1}^d{\int }_0^T{f}_{x^j}(R_t^1,\cdots ,R_t^d)\mathrm{d}{R}_t^j+\frac{1}{2}\sum _{j=1}^d{\int }_0^T{f}_{x^j{x}^j}(R_t^1,\cdots ,R_t^d)\mathrm{d}{\langle R^j,R^j\rangle }_t\hfill \\ \hfill & +f(R_0^1,\cdots ,R_0^d)\hfill \\ \hfill & =f(R_T^1,\cdots ,R_T^d)\hfill \\ \hfill & =L\hfill \end{array}$$

almost surely, where we used (4) for the penultimate equality. □

We next discuss how risk attribution can be applied within a company’s divisions. Because the total loss variable $L={\sum }_{k=1}^K{L}^k$ is linear in the loss variables $L^k=f^k\left({\left(R_T^i\right)}_i\right)$ of the divisions, we can define an approximation of $L^k$ by ${\sum }_{j=1}^d{A}^{jk}$ with

$$A^{jk}=\sum _{t=0}^{T-1}\left(f^k(R_{t+1}^j,{\left(R_t^i\right)}_{i\ne j})-f^k\left({\left(R_t^i\right)}_i\right)\right),$$

(5)

analogously to (3). Since we have linear approximations ${\sum }_{j=1}^d{A}^j$ and ${\sum }_{j=1}^d{A}^{jk}$ for L and $L^k$, respectively, we can apply the Euler principle to these sums to determine an attribution for the different risk drivers.

For $\rho ={\mathrm{VaR}}_{\alpha }$ (value-at-risk as risk measure), an overview of the formulas for this method of the risk allocation and attribution is given in

Table 2. Risk decomposition along two dimensions: risk allocation and risk attribution. In the table, we used the notations $A^j$ from (3), $A^{jk}$ from (5), $L^k=f^k\left({\left(R_T^i\right)}_i\right)$, and $B=\{f\left({\left(R_T^i\right)}_i\right)\ge {\mathrm{VaR}}_{\alpha }\left(f\left({\left(R_T^i\right)}_i\right)\right)\}$.

. Note that the procedure in Table 2 is commutative in the sense that the order of risk allocation and risk attribution can be interchanged: if risk is allocated first to the different divisions and then attributed to the sources of risk, it leads to the same values as when attribution is done before allocation.

We mention next several other approaches:

• Shapley value. The Shapley value for a risk factor is computed as the average of the contribution of this risk factor when it enters at different stages (Denault 2001; Powers 2007). In the first round, the impact of only a single risk factor is considered. In the second round, the impact is computed that a risk factor has when there are two factors present. Then the stand-alone contribution of the other factor is subtracted from the result. In the third round, the impact of the risk factor is computed when there are three factors present. Then the joint contribution of the other two factors is subtracted. The procedure continues until all factors are considered.
  For linear loss structures, the Shapley value distributes the diversification benefits in a fair way. Moreover, it can be defined axiomatically (Denault 2001).
  A drawback of this method is that it is computationally intense for large d ($d\ge 7$). A possibility is to group the $R^1,\cdots ,R^d$, compute the allocation first for each group and then allocate it within each group. However, this may not lead to the same outcome as when the allocation is done directly for each $R^j$.
• Hájek projection. Assume that $R^1,\cdots ,R^d$ are independent. The Hájek projection is the projection of the total loss variable L onto the set of sums ${\sum }_{j=1}^d{g}^j\left(R^j\right)$ of measurable functions $g^j$(Rosen and Saunders 2010). The Hájek projection is given by $g^j\left(R^j\right)=E\left[L\right|R^j]-\frac{d-1}{d}E\left[L\right]$. One could then apply to ${\sum }_{j=1}^d{g}^j\left(R^j\right)$ the Euler principle using the ideas of Section 2. However, to make use of this approach, one would need to compute $E\left[L\right|R^j]$, which requires knowing the dependence structure between the total losses and the risk factor $R^j$.
• Sensitivity-based approach. As in the Euler risk allocation, we could compute

  $$A_{\mathrm{Euler}}^j=\frac{\mathrm{d}}{\mathrm{d}\lambda }\rho \left(-L(R^1,\cdots ,(1+\lambda )R^j,\cdots ,R^d)\right){|}_{\lambda =0},$$

  but they will not sum up and would need to be scaled. Moreover, the economic justification given in Section 2 is lost for nonlinear L.
• Taylor expansion. For a fixed expansion point $(z^1,\cdots ,z^d)$, the first-order Taylor expansion

  $$L(R^1,\cdots ,R^d)\approx L(z^1,\cdots ,z^d)+\sum _{j=1}^d\frac{\partial L}{\partial z^j}(z^1,\cdots ,z^d)(R^j-z^j)$$

  can be used to interpret $\frac{\partial L}{\partial z^j}(z^1,\cdots ,z^d)(R^j-z^j)$ as approximate risk factors, which can be used similarly to the Hájek projection. There is again an approximation error so that a scaling is needed. Moreover, the approximation will strongly depend on the choice of the expansion point.
• Freezing the margins. The idea of this approach is to “switch off” the randomness of all but one of the sources of risk. The approximate risk factors are of the form $L(z^1,\cdots ,z^{j-1},R^j,z^{j+1},\cdots ,z^d)$ for a fixed point $(z^1,\cdots ,z^d)$. Again, there is an approximation error, the business meaning of the terms is unclear, and the approximation will strongly depend on the choice of $(z^1,\cdots ,z^d)$.

4. Application to Credit Risk

We start by briefly recalling the classical structural approach to credit risk generalizing Merton (1974) to multiple firms, which is widely used in academia and practice, see for example Berg (2010); Frei and Wunsch (2018); Hull et al. (2005), and Vasicek (2002). We consider one rating bucket consisting of homogeneous obligors. We group obligors in the portfolio into homogeneous buckets. We assume that the number of obligors is big enough so that the idiosyncratic risk of obligors is negligible at the bucket level. The normalized asset return of an obligor is given by

$$A=\sqrt{\varrho }R+\sqrt{1-\varrho }ϵ,$$

where $\varrho \in [0,1)$ is the correlation coefficient, R is a standard normally distributed random variable (the systematic factor of the bucket) common to all obligors in the bucket and $ϵ$ is a standard normally distributed random variable (the obligor’s idiosyncratic component) specific to each obligor and independent of R and of the $ϵ$ of other obligors. The systematic factor R captures macroeconomic developments that affect all obligors. An obligor defaults if their return is below a threshold b, which is the same for all obligors in the bucket. Hence, the unconditional default probability of obligors in the bucket is given by

$$p=P[A\le b]=\Phi \left(b\right),$$

where $\Phi$ denotes the standard normal cumulative distribution function, using that A is standard normally distributed. This implies $c={\Phi }^{-1}\left(p\right)$. The loss rate in the bucket conditional on the systematic factor R is given by

$$L=P[A\le b|R]=P\left[ϵ\le \frac{{\Phi }^{-1}\left(p\right)-\sqrt{\varrho }R}{\sqrt{1-\varrho }}|R\right]=\Phi \left(\frac{{\Phi }^{-1}\left(p\right)-\sqrt{\varrho }R}{\sqrt{1-\varrho }}\right),$$

using the independence of $ϵ$ from R. We assume that the systematic return component R is driven by two factors, namely,

$$R=\sqrt{w}{R}^1+\sqrt{1-w}{R}^2,$$

where $R^1$ and $R^2$ are independent and standard normally distributed. We can think of $R^1$ and $R^2$ as the drivers behind two different macroeconomic components. In practice, they can be obtained from a principal component analysis of data used to model asset returns (such as macroeconomic data or data from stock price returns). It follows that

$$L=\Phi \left(\frac{{\Phi }^{-1}\left(p\right)-\sqrt{\varrho }(\sqrt{w}{R}^1+\sqrt{1-w}{R}^2)}{\sqrt{1-\varrho }}\right),$$

where L depends in a nonlinear way on $R^1$ and $R^2$. We are interested in the following questions: What is the risk attributed to the first factor $R^1$? What is the difference between the total risk and the sum of the risk attributions to the two factors $R^1$ and $R^2$? It is natural to expect that the risk attributed to $R^1$ should be close to w, and the sum of the risk attributions to $R^1$ and $R^2$ should be close to the total risk, but it will not be equal because of the nonlinear dependence of L on $R^1$ and $R^2$.

To compute a risk attribution of the first factor, we apply the procedure presented in Section 3. We assume that there are 26 time steps, corresponding to biweekly observations over one year. For the approximate contribution of the first factor to L, we apply (2) by considering what happens to L when $R^1$ changes from time t to $t+1$ while $R^2$ remains at the value of time t, namely

$$A^1=\sum _{t=0}^{25}\left(\Phi \left(\frac{{\Phi }^{-1}\left(p\right)-\sqrt{\varrho }(\sqrt{w}{R}_{t+1}^1+\sqrt{1-w}{R}_t^2)}{\sqrt{1-\varrho }}\right)-\Phi \left(\frac{{\Phi }^{-1}\left(p\right)-\sqrt{\varrho }(\sqrt{w}{R}_t^1+\sqrt{1-w}{R}_t^2)}{\sqrt{1-\varrho }}\right)\right).$$

We do the same procedure for the second factor so that

$$A^2=\sum _{t=0}^{25}\left(\Phi \left(\frac{{\Phi }^{-1}\left(p\right)-\sqrt{\varrho }(\sqrt{w}{R}_t^1+\sqrt{1-w}{R}_{t+1}^2)}{\sqrt{1-\varrho }}\right)-\Phi \left(\frac{{\Phi }^{-1}\left(p\right)-\sqrt{\varrho }(\sqrt{w}{R}_t^1+\sqrt{1-w}{R}_t^2)}{\sqrt{1-\varrho }}\right)\right),$$

and apply the Euler principle to compute the contribution of each factor. For this example, we assume that all obligors in the bucket have the same exposure at default, where the total exposure is normalized to 1. The probability of default is set to $p=$ 1% per year, $\varrho =0.2$ for this example, and the loss given default is set to 100%. Of course, these are simplifications because our focus is on analyzing the contributions of the risk drivers in a simple example. There is an extensive literature on the modelling of the probability of default, the loss given default, and their dependence structure (Cheng and Cirillo 2019; Frye and Jacobs 2012; Metzler and Scott 2020; Miu and Ozdemir 2006; Pykhtin 2003). We use expected shortfall at the 99.5% level as the risk measure.

The results presented in the upper panel of Figure 3 show a good fit of both the risk attribution of the first factor compared to its weight w and the sum of the risk attributions of the two factors compared to the total risk. By contrast, if only one step instead of 26 steps is performed, the lower panel of Figure 3 shows big deviations between the sum of the risk attributions and the total risk. We also observe in

Table 3. Risk attribution to two risk factors. The approximation error is averaged over the weight of the first factor, and expected shortfall at 99.5% level is used as the risk measure.

	1 Step	4 Steps	12 Steps	26 Steps	52 Steps	253 Steps
	Annual	Quarterly	Monthly	Biweekly	Weekly	Daily *
factor 1	0.047	0.052	0.058	0.060	0.061	0.061
factor 2	0.047	0.052	0.058	0.060	0.061	0.061
approximation	0.094	0.104	0.116	0.120	0.121	0.122
total	0.127
absolute error	0.033	0.023	0.011	0.007	0.006	0.005
percentage error	25.6%	17.6%	7.9%	5.5%	4.6%	3.9%

* 253 = approximate number of trading days per year.

that the approximation becomes more precise when the number of steps is increased. This improvement is consistent with Proposition 1, which gives a convergence result when the number of steps goes to infinity. The conditions of Proposition 1 are met in this application because $\Phi$ is infinitely differentiable, and $R^1$ and $R^2$ can be modelled in continuous time as two independent Brownian motions, thus as a continuous semimartingale with zero quadratic covariation, as required by Proposition 1.

Finally, we extend the example by including idiosyncratic risk. So far, we have assumed that all idiosyncratic risk is diversified away. If there is a smaller number of obligors, their idiosyncratic risk will also be present at bucket level. Idiosyncratic risk then constitutes a third risk component, in addition to the risk originating from the two factors. We now apply the Euler principle to all three risk components, resulting in Figure 4 for an example with 20 obligors. We still see a fairly good correspondence of the sum of the risk attributions to the total risk, where we again chose 26 time steps in the procedure.

5. Conclusions

Extending the Euler principle to nonlinear loss dependence structures, we introduced a method for risk attribution, which assigns risk contributions to underlying drivers. To allow for nonlinear loss dependence structure, we use a linearization based on one-dimensional slides, before applying the Euler principle to this linearization. We showed that under suitable conditions the linearization becomes exact for an infinitely granular time grid. The method is straightforward to implement and yields the desired risk split, as we exemplified in the context of credit risk. Compared to other approaches, this method has the following main advantages:

• in practice, it is easy to compute, even for a high number of risk factors, unlike the Hájek projection or the method of the Shapley value;
• being based on the Euler principle, it has a solid economic justification, unlike the approach to freeze the margins.

Interesting questions for future work include the application of this method to different risk types, and the comparison of its results with those of other methods, such as the Shapley value. Another possible future research direction is the analysis of dynamic (over time) properties of the risk attribution.