Bankruptcy Prediction and Stress Quantification Using Support Vector Machine: Evidence from Indian Banks
Abstract
1. Introduction
2. Literature Review
3. Data Descriptions and Methodology
3.1. Two-Step Feature Selection


3.2. Support Vector Machine
3.2.1. Why Support Vector Machine?
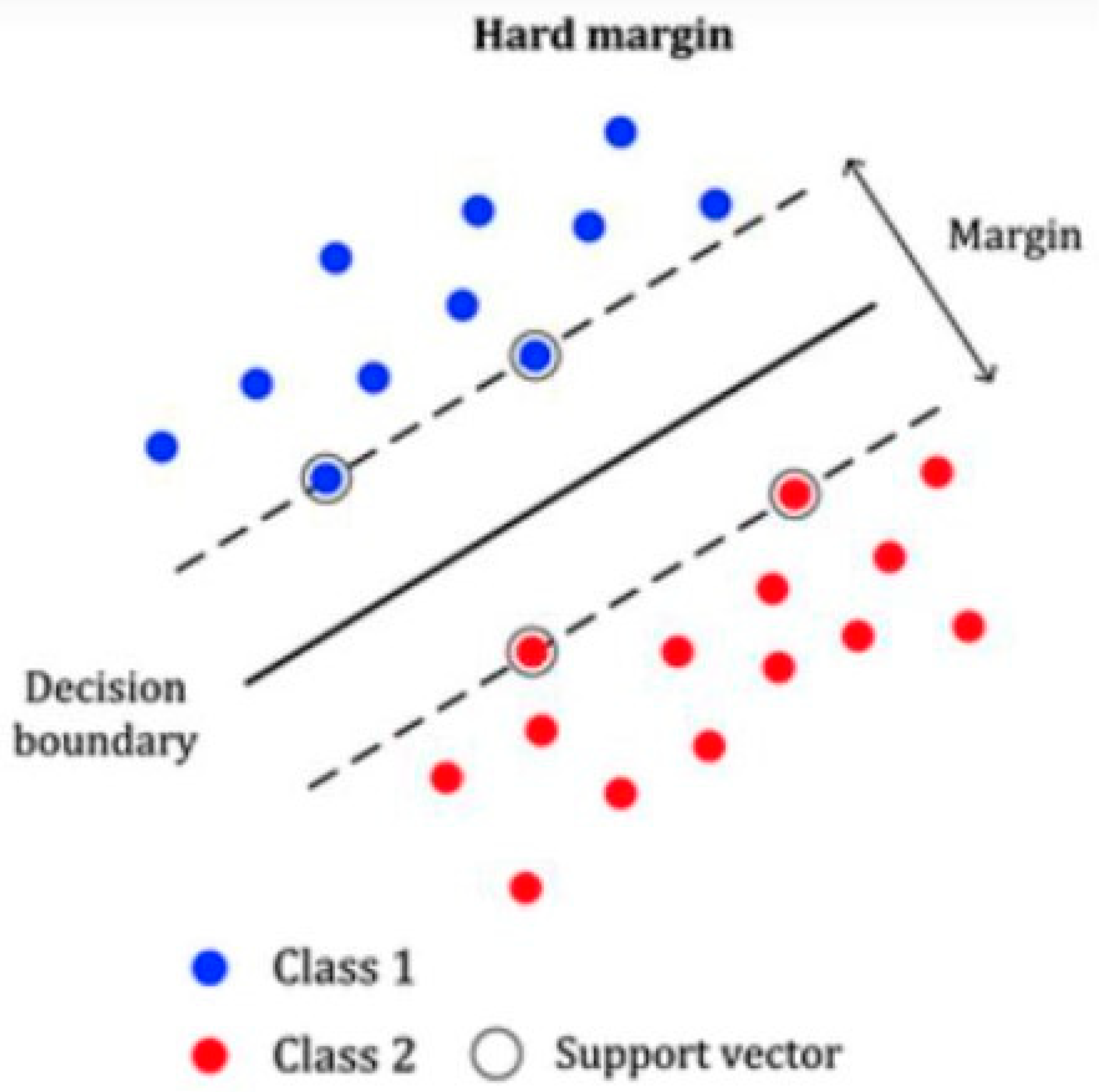
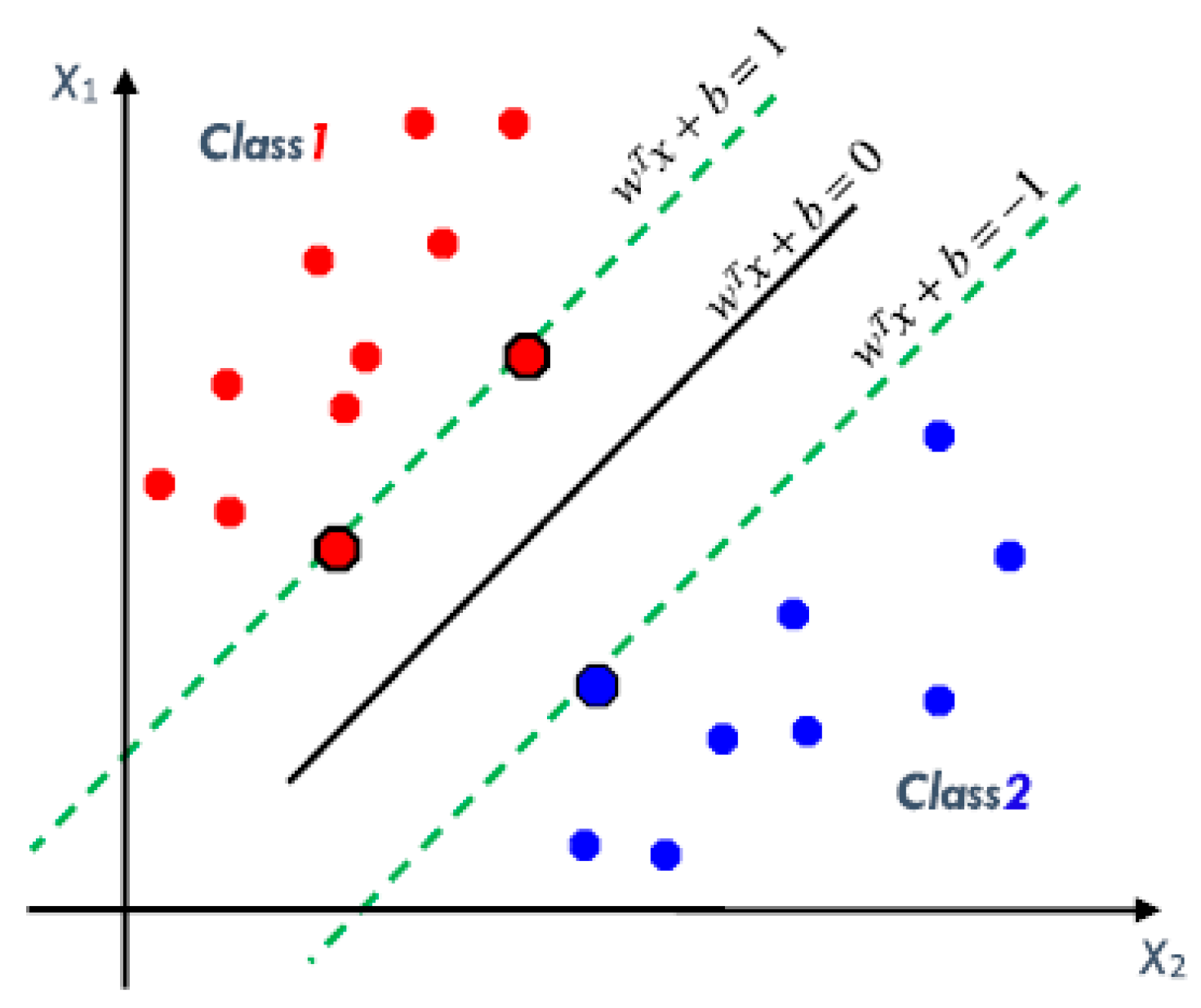
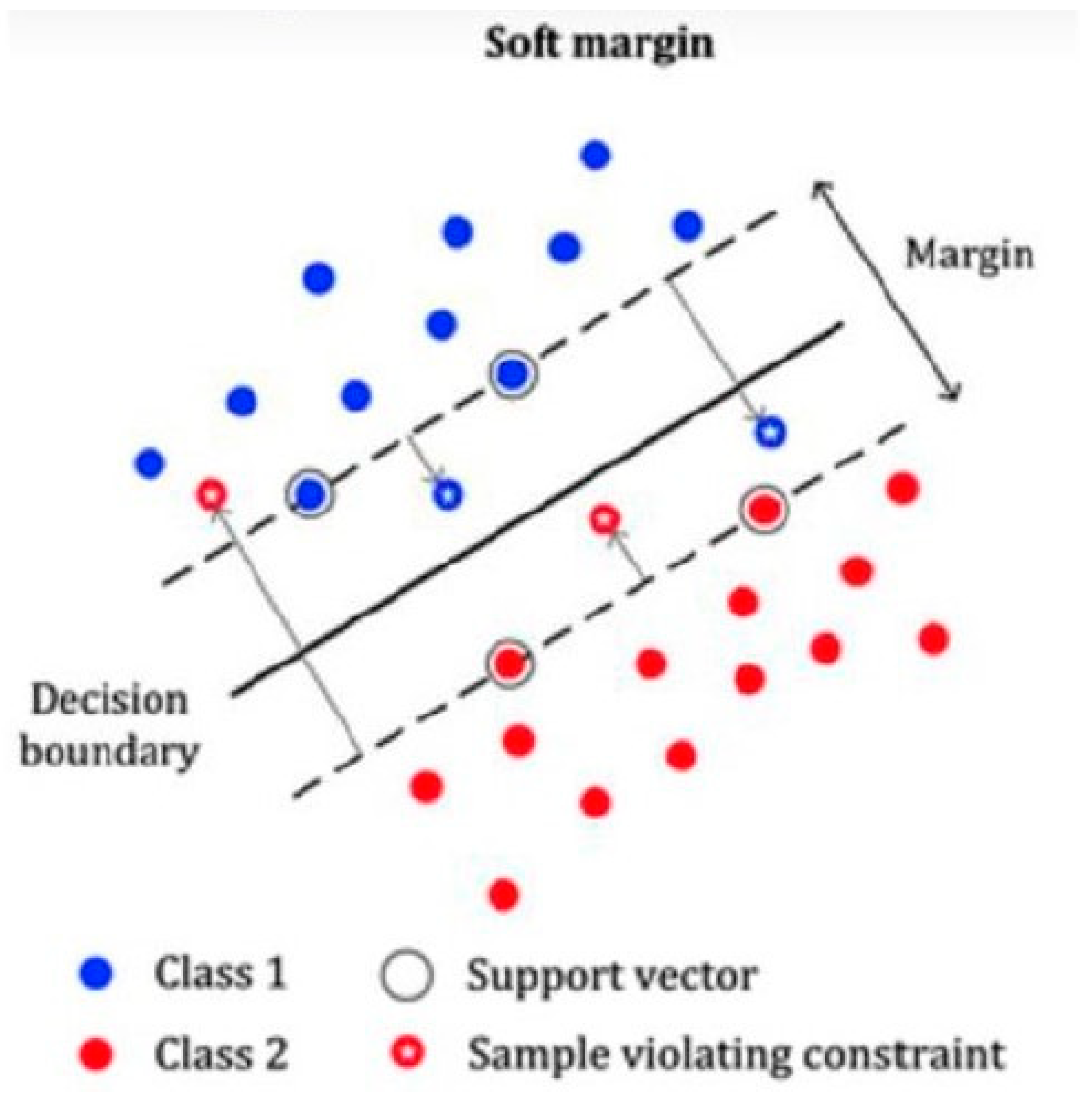
3.2.2. Support Vector Machine for Linearly Separable Data
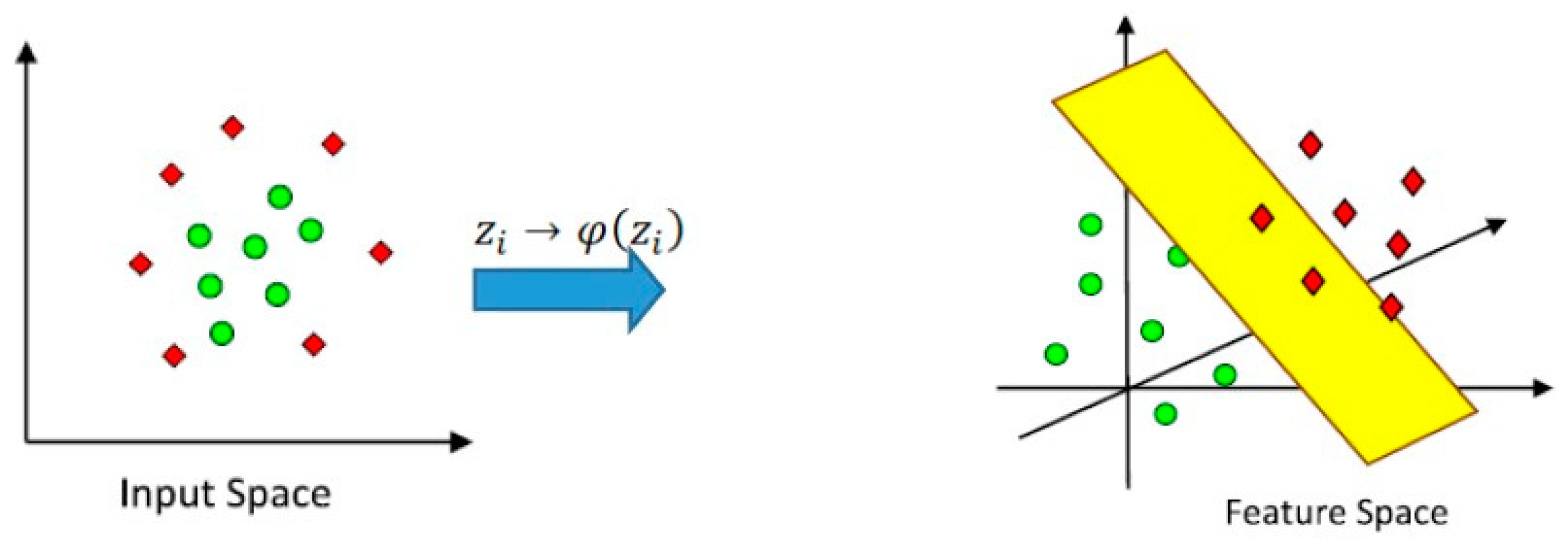
3.3. Support Vector Machine for the Non-Linear Case (Kernel Machine)
Kernel Trick
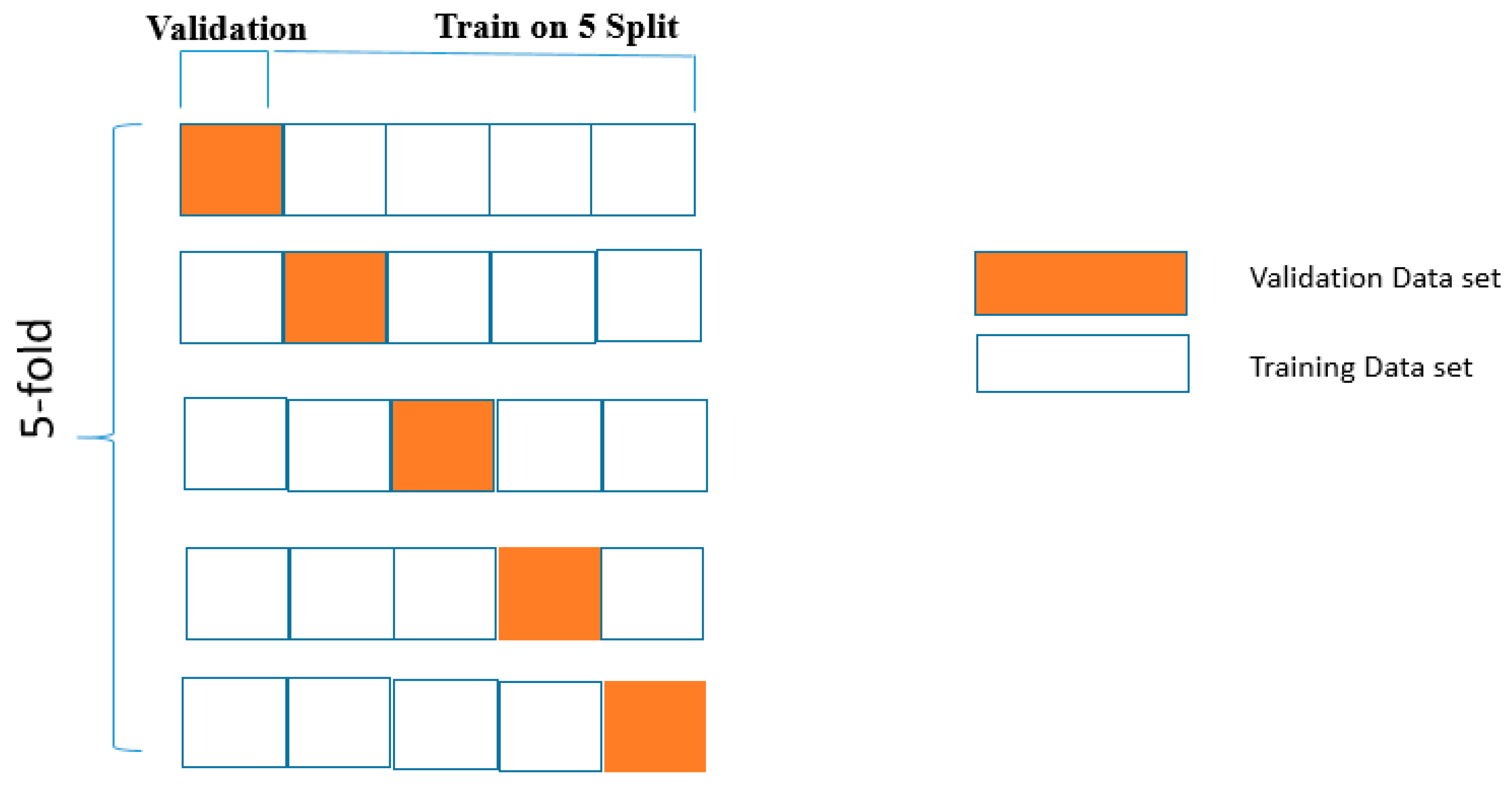
3.4. Overfitting and Cross-Validation
4. Empirical Results and Discussion
4.1. Empirical Results
| Input Features | Coefficient |
| provision_for_loan_Interest_income(t−1) | 6.056 |
| Tier1CAR(t−1) | 4.37 |
| Bias Term | 3.96 |
| Cut-off value | 6.97 |
4.2. Stress Quantification of Banks
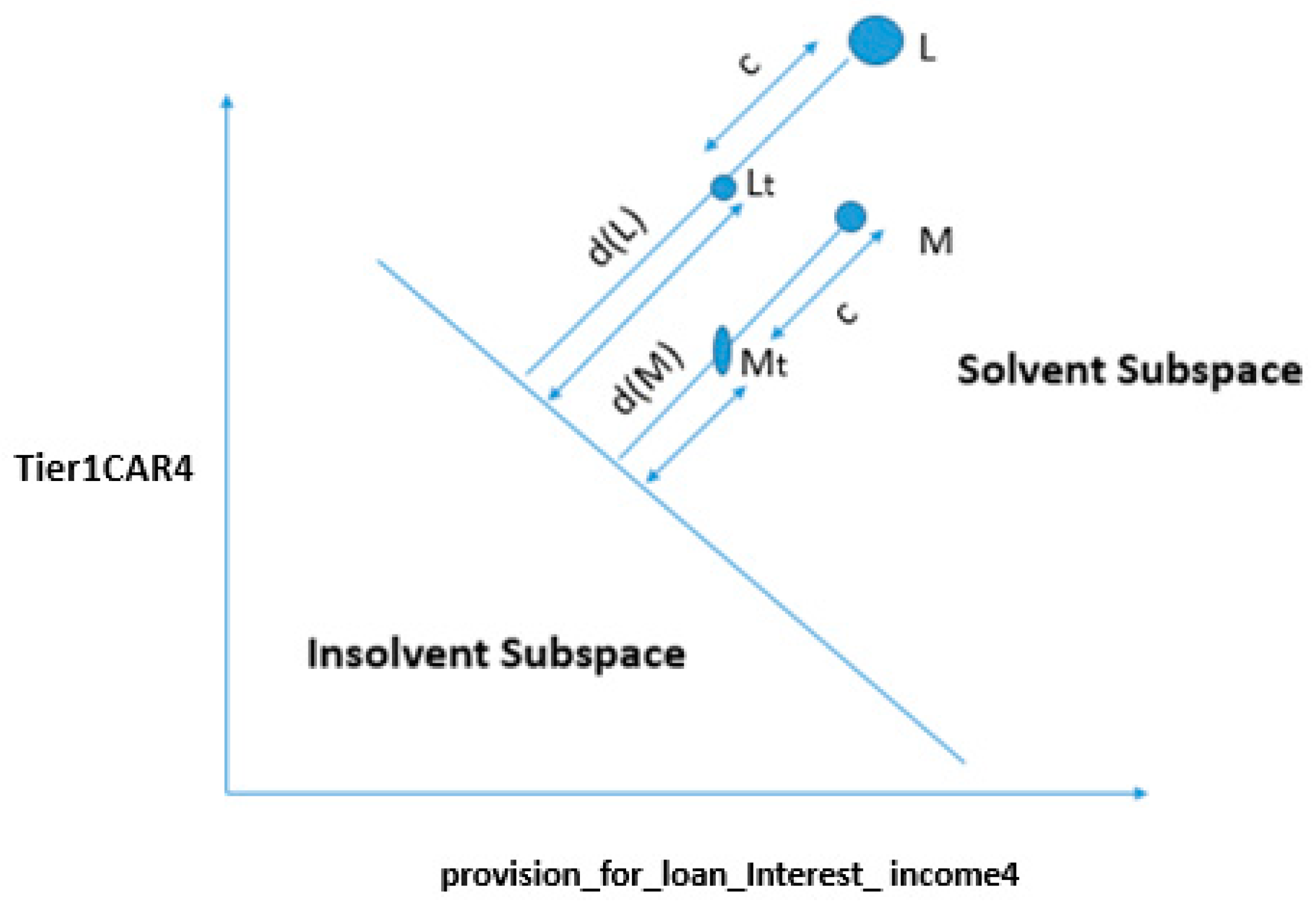
Decision Linear Boundary
- (a)
- By using the SVMLK predictive model, is it possible to find quantitative information about bank features to avoid a predicted bank failure?
- (b)
- How financially strong are the banks that are predicted as survival banks by using SVMLK predictive model?
4.3. Mathematical Approach for Stress Quantification Using SVMLK
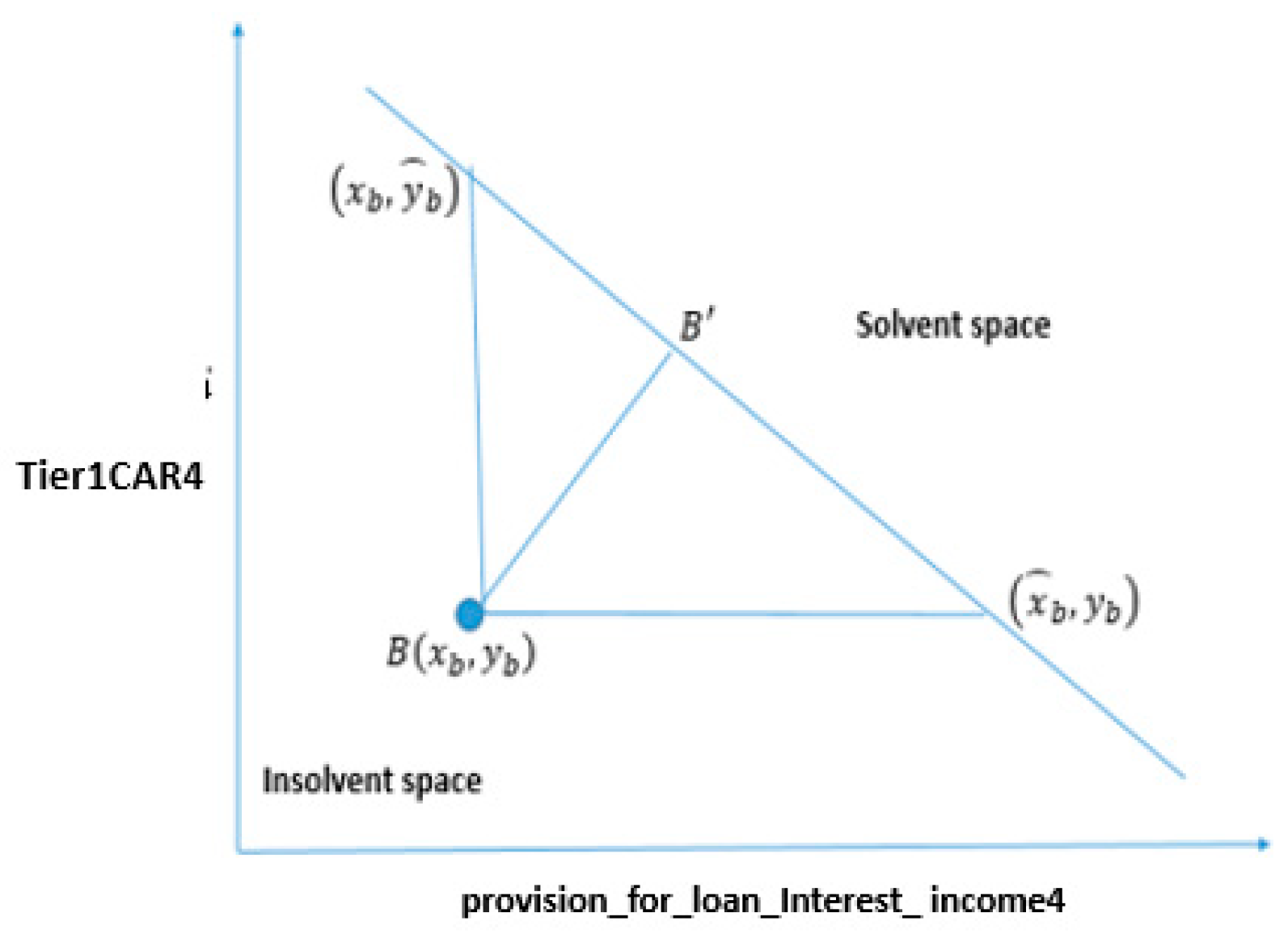
4.3.1. Change in Both Features
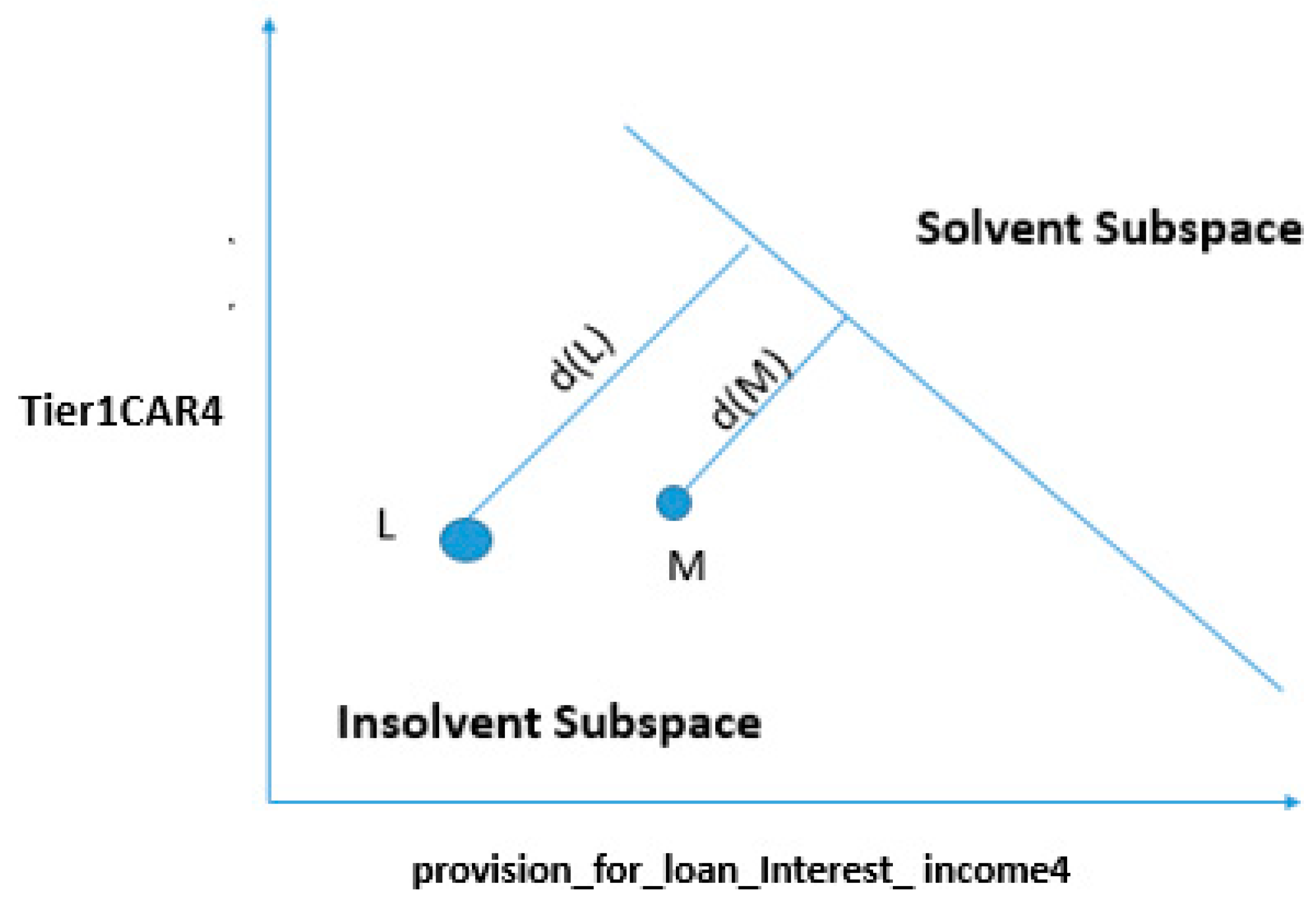
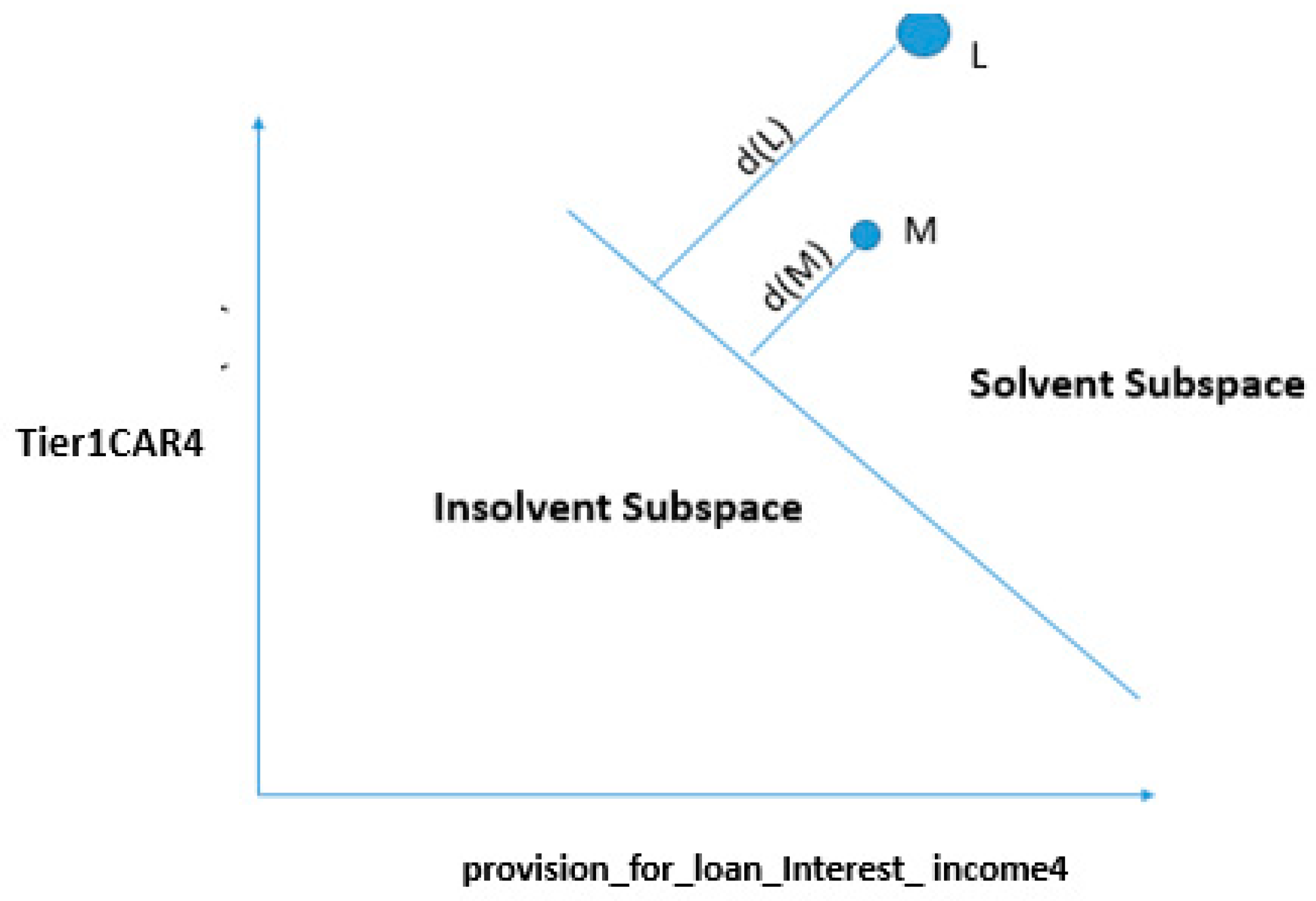
4.3.2. Change in One Feature
4.4. Comparison of Bank Financial Health
4.4.1. Changing the Status of Bank “A” from Insolvent to Solvent by Changing Both Variables
4.4.2. Marginal Cases: Changing the Status of Bank “A” from Insolvent to Solvent by Changing a Single Variable
| Features | Original Values | Critical Values |
| provision_for_loan_Interest_income(t−1) | 0.00123 | 0.49 |
| Tier1CAR(t−1) | 0.1123 | 0.1123 |
| Features | Original Values | Critical Values |
| provision_for_loan_Interest_income(t−1) | 0.00123 | 0.00123 |
| Tier1CAR(t−1) | 0.1123 | 0.54 |
5. Conclusions
6. Limitations of the Study
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Name | Type | Definition |
|---|---|---|
| Financial Status (Failed or Survival) | Categorical | Binary indicator equal to 1 for failed banks and 0 for surviving banks |
| Total_Assets (TA) | Quantitative | Total earning assets |
| Cash_Balance_TA | Quantitative | Cash and due from depository institutions/TA |
| Net_Loan_TA | Quantitative | Net loans /TA |
| Deposit_TA | Quantitative | Total Deposits/TA |
| Subordinated_debt_TA | Quantitative | Subordinated Debt/TA |
| Average_Assets_TA | Quantitative | Average Assets till 2017/Total Assets |
| Tier1CAR | Quantitative | Tier1 risk-based capital/Total Assets |
| Tier2CAR | Quantitative | Tier 2 risk-based capital/Total Assets |
| IntincExp_Income | Quantitative | Total interest expense/total interest income |
| Provision_for_loan_Interest_income | Quantitative | Provision for loan and lease losses/total interest income |
| Nonintinc_intIncome | Quantitative | Total noninterest income/total interest income |
| Return_on_capital_employed | Quantitative | Salaries and employee benefits/total interest income |
| Operating_income_T_Interest_income | Quantitative | net operating income/total interest income |
| Cash_dividend_T_Interest_Income | Quantitative | Cash dividends/total interest income |
| Operating_income_T_Interest_income | Quantitative | Net operating income/total interest income |
| Net_Interest_margin | Quantitative | Net interest margin earned by bank |
| Return_on_assets | Quantitative | Return on total assets of firm |
| Equity_cap_TA | Quantitative | Equity capital to assets |
| Return_on_Assets | Quantitative | Return on total assets of banks |
| Noninteerst_Income | Quantitative | Noninterest Income earned by banks |
| Treasury_income_T_Interest_income | Quantitative | Net income attributable to bank/total interest income |
| Net_loans_Deposits | Quantitative | Net loans and leases to deposits |
| Net_Interest_margin | Quantitative | Net interest income expressed as a percentage of earning assets. |
| Salaries_employees_benefits_Int_income | Quantitative | Salaries and employee benefits/total interest income |
| TA_employee | Quantitative | Total assets per employee of bank |
Appendix B
| Variables Name | Relief Score |
|---|---|
| Tier1CAR(t−1) | 0.18 |
| Subordebt_TA(t−1) | 0.12 |
| Tier2CAR(t−2) | 0.1 |
| Provision_for_loan_Interest_income(t−4) | 0.1 |
| Subordebt_TA(t−3) | 0.09 |
| Provision_for_loan_Interest_income(t−1) | 0.08 |
| Provision_for_loan_Interest_income(t−2) | 0.08 |
| Provision_for_loan_Interest_income(t−3) | 0.07 |
| TA_emplyee(t−3) | 0.07 |
| TA_emplyee(t−2) | 0.06 |
| Tier2CAR(t−1) | 0.06 |
| TA_emplyee(t−4) | 0.05 |
| TA_emplyee(t−1) | 0.05 |
| Noninterest_expences_Int_income(t−3) | 0.04 |
| Subordebt_TA(t−4) | 0.02 |
| Salaries_and_employees_benefits_Int_income(t−3) | 0.01 |
| Tier2CAR(t−3) | 0.00 |
| Return_on_capital_employed_(t−2) | 0.00 |
| Operating_income_T_Interest_income(t−4) | 0.00 |
| Cash_TA(t−3) | 0.00 |
| Noninterest_expences_Int_income(t−4) | 0.00 |
| Deposits_TA(t−2) | 0.00 |
| Return_on_advances_adjusted_to_cost_of_funds(t−1) | 0.00 |
| Operating_income_T_Interest_income(t−3) | 0.00 |
| Return_on_capital_employed(t−3) | 0.00 |
| Salaries_and_employees_benefits_Int_income(t−4) | 0.00 |
| Net_loans_TA(t−3) | 0.00 |
| Deposits_TA(t−1) | 0.00 |
| Treasury_income_T_Interest_income(t−4) | 0.00 |
| Return_on_assets(t−3) | 0.00 |
| Net_loans_TA(t−2) | 0.00 |
| Net_loans_TA(t−1) | 0.00 |
| Return_on_assets(t−1) | 0.00 |
| Return_on_capital_employed(t−4) | 0.00 |
| IntincExp_Income(t−2) | 0.00 |
| Cash_TA(t−2) | 0.00 |
| IntincExp_Income(t−4) | 0.00 |
| Noninterest_expences_Int_income(t−1) | 0.00 |
| Return_on_advances_adjusted_to_cost_of_funds(t−2) | 0.00 |
| Nonintinc_intIncome(t−4) | 0.00 |
| Nonintinc_intIncome(t−1) | 0.00 |
| Deposits_TA(t−3) | 0.00 |
| Equity_cap_TA(t−1) | 0.00 |
| IntincExp_Income(t−3) | 0.00 |
| Operating_income_T_Interest_income(t−1) | 0.00 |
| Avg_Asset_TA(t−2) | 0.00 |
| Total_Assets(t−3) | 0.00 |
| Noninteerst_Income(t−3) | 0.00 |
| Provision_for_loan(t−2) | 0.00 |
| Total_Assets(t−4) | 0.00 |
| Salaries_and_employees_benefits_Int_income(t−1) | 0.00 |
| Noninteerst_Income(t−2) | 0.00 |
| Total_Assets(t−1) | 0.00 |
| Return_on_capital_employed(t−1) | 0.00 |
| Noninteerst_Income(t−4) | 0.00 |
| Subordebt_TA(t−2) | 0.00 |
| Total_Assets(t−2) | 0.00 |
| Noninterest_expences_Int_income(t−2) | 0.00 |
| Equity_cap_TA(t−2) | 0.00 |
| Noninteerst_Income(t−1) | 0.00 |
| Salaries_and_employees_benefits_Int_income(t−2) | 0.00 |
| Nonintinc_intIncome(t−3) | 0.00 |
| Treasury_income_T_Interest_income(t−3) | 0.00 |
| Return_on_assets(t−4) | 0.00 |
| Treasury_income_T_Interest_income(t−1) | 0.00 |
| Tier1CAR(t−3) | 0.00 |
| Avg_Asset_TA(t−3) | 0.00 |
| Tier1CAR(t−4) | 0.00 |
| Equity_cap_TA(t−3) | 0.00 |
| IntincExp_Income(t−1) | 0.00 |
| Return_on_assets(t−2) | 0.00 |
| Treasury_income_T_Interest_income(t−2) | 0.00 |
| Net_Interest_margin(t−4) | 0.00 |
| Tier1CAR(t−2) | 0.00 |
| Cash_TA(t−1) | 0.00 |
| Provision_for_loan(t−4) | 0.00 |
| Net_Interest_margin(t−2) | 0.00 |
| Net_Interest_margin(t−1) | 0.00 |
| Cash_TA(t−4) | 0.00 |
| Deposits_TA(t−4) | 0.00 |
| Equity_cap_TA(t−4) | 0.00 |
| Net_loans_TA(t−4) | 0.00 |
| Return_on_advances_adjusted_to_cost_of_funds(t−4) | 0.00 |
| Return_on_advances_adjusted_to_cost_of_funds(t−3) | 0.00 |
| Provision_for_loan(t−3) | 0.00 |
| Avg_Asset_TA(t−4) | 0.00 |
| Operating_income_T_Interest_income(t−2) | 0.00 |
| Net_loans_Deposits(t−3) | 0.00 |
| Nonintinc_intIncome(t−2) | 0.00 |
| Net_Interest_margin(t−4) | 0.00 |
| Net_loans_Deposits(t−4) | 0.00 |
| Avg_Asset_TA(t−1) | 0.00 |
| Tier2CAR(t−4) | −0.01 |
| Net_loans_Deposits(t−2) | −0.01 |
| Cash_dividend_T_Interest_Income(t−2) | −0.01 |
| Cash_dividend_T_Interest_Income(t−1) | −0.01 |
| Cash_dividend_T_Interest_Income(t−4) | −0.01 |
| Net_loans_Deposits(t−1) | −0.01 |
| Cash_dividend_T_Interest_Income(t−3) | −0.02 |
References
- Aha, David W., Dennis Kibler, and Marc K. Albert. 1991. Instance-based learning algorithms. Machine Learning 6: 37–66. [Google Scholar] [CrossRef]
- Altman, Edward I. 1968. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. The Journal of Finance 23: 589–609. [Google Scholar] [CrossRef]
- Altman, Edward I., Robert G. Haldeman, and Paul Narayanan. 1977. ZETATM analysis A new model to identify bankruptcy risk of corporations. Journal of Banking & Finance 1: 29–54. [Google Scholar]
- Altman, Edward I., Marco Giancarlo, and Giancarlo Varetto. 1994. Corporate distress diagnosis: Comparisons using linear discriminant analysis and neural networks (the Italian experience). Journal of Banking & Finance 18: 505–29. [Google Scholar]
- Antunes, Francisco, Bernardete Ribeiro, and Bernardete Pereira. 2017. Probabilistic modeling and visualization for bankruptcy prediction. Applied Soft Computing 60: 831–43. [Google Scholar] [CrossRef]
- Chaudhuri, Arindam, and Kajal De. 2011. Fuzzy support vector machine for bankruptcy prediction. Applied Soft Computing 11: 2472–86. [Google Scholar] [CrossRef]
- Chen, Ning, Bernardete Ribeiro, Armando Vieira, and An Chen. 2013. Clustering and visualization of bankruptcy trajectory using self-organizing map. Expert Systems with Applications 40: 385–93. [Google Scholar] [CrossRef]
- Cleary, Sean, and Greg Hebb. 2016. An efficient and functional model for predicting bank distress: In and out of sample evidence. Journal of Banking & Finance 64: 101–11. [Google Scholar]
- Cole, Rebel A., and Jeffery Gunther. 1995. A CAMEL Rating’s Shelf Life. Available at SSRN 1293504. Amsterdam: Elsevier. [Google Scholar]
- Cole, Rebel A., and Jeffery W. Gunther. 1998. Predicting bank failures: A comparison of on-and off-site monitoring systems. Journal of Financial Services Research 13: 103–17. [Google Scholar] [CrossRef]
- Cortes, Corinna, and Vladimir Vapnik. 1995. Support-vector networks. Machine Learning 20: 273–97. [Google Scholar] [CrossRef]
- Cristianini, Nello, and John Shawe-Taylor. 2000. An Introduction to Support Vector Machines (and Other Kernel-Based Learning Methods). Cambridge: Cambridge University Press. 190p. [Google Scholar]
- Dash, Mihir, and Annyesha Das. 2009. A CAMELS Analysis of the Indian Banking Industry. Available at SSRN 1666900. Amsterdam: Elsevier. [Google Scholar]
- Du Jardin, Philippe. 2012. Predicting bankruptcy using neural networks and other classification methods: The influence of variable selection techniques on model accuracy. Neurocomputing 73: 2047–60. [Google Scholar] [CrossRef]
- Fletcher, Desmond, and Ernie Goss. 1993. Forecasting with neural networks: an application using bankruptcy data. Information & Management 24: 159–67. [Google Scholar]
- Kim, Myoung-Jong, Dae-Ki Kang, and Hong Bae Kim. 2015. Geometric mean based boosting algorithm with over-sampling to resolve data imbalance problem for bankruptcy prediction. Expert Systems with Applications 42: 1074–82. [Google Scholar] [CrossRef]
- Kira, Kenji, and Larry A. Rendell. 1992. A practical approach to feature selection. In Machine Learning Proceedings 1992. Amsterdam: Elsevier, pp. 249–56. [Google Scholar]
- Kirkos, Efstathios. 2015. Assessing methodologies for intelligent bankruptcy prediction. Artificial Intelligence Review 43: 83–123. [Google Scholar] [CrossRef]
- Korol, Tomasz. 2013. Early warning models against bankruptcy risk for Central European and Latin American enterprises. Economic Modelling 31: 22–30. [Google Scholar] [CrossRef]
- Leshno, Moshe, and Yishay Spector. 1996. Neural network prediction analysis: The bankruptcy case. Neurocomputing 10: 125–47. [Google Scholar] [CrossRef]
- Lin, Wei-Yang, Ya-Han Hu, and Chih-Fong Tsai. 2011. Machine learning in financial crisis prediction: a survey. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews) 42: 421–36. [Google Scholar]
- Mangasarian, Olvi. L. 1969. Nonlinear Programming. New York: McGraw-Hill Book Co. [Google Scholar]
- Martin, Daniel. 1977. Early warning of bank failure: A logit regression approach. Journal of Banking & Finance 1: 249–76. [Google Scholar]
- Meyer, Paul A., and Howard W. Pifer. 1970. Prediction of bank failures. The Journal of Finance 25: 853–68. [Google Scholar] [CrossRef]
- Mercer, James. 1909. Functions of positive and negative type and their connection with the theory of integral equations. Philosophical Transactions of the Royal Society A 209: 415–46. [Google Scholar]
- Moore, Andrew W. 2001. Cross-Validation for Detecting and Preventing Overfitting. Pittsburgh: School of Computer Science Carneigie Mellon University. [Google Scholar]
- Murphy, Kevin P. 2012. Machine Learning: A Probabilistic Perspective. Cambridge: MIT Press. [Google Scholar]
- Nanni, Loris, and Alessandra Lumini. 2009. An experimental comparison of ensemble of classifiers for bankruptcy prediction and credit scoring. Expert Systems with Applications 36: 3028–33. [Google Scholar] [CrossRef]
- Ohlson, James A. 1980. Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research 18: 109–31. [Google Scholar] [CrossRef]
- Papadimitriou, Theophilos, Periklis Gogas, Vasilios Plakandaras, and John C. Mourmouris. 2013. Forecasting the insolvency of US banks using support vector machines (SVM) based on local learning feature selection. International Journal of Computational Economics and Econometrics 3: 1. [Google Scholar] [CrossRef]
- Pappas, Vasileios, Steven Ongena, Marwan Izzeldin, and Ana-Maria Fuertes. 2017. A survival analysis of Islamic and conventional banks. Journal of Financial Services Research 51: 221–56. [Google Scholar] [CrossRef]
- Piramuthu, Selwyn, Harish Ragavan, and Michael J. Shaw. 1998. Using feature construction to improve the performance of neural networks. Management Science 44: 416–30. [Google Scholar] [CrossRef]
- Pradhan, Roli. 2014. Z score estimation for Indian banking sector. International Journal of Trade, Economics, and Finance 5: 516. [Google Scholar] [CrossRef]
- Chelimala, Pramodh, and Vadlamani Ravi. 2007. Modified great deluge algorithm based auto-associative neural network for bankruptcy prediction in banks. International Journal of Computational Intelligence Research 3: 363–71. [Google Scholar]
- Sharda, Ramesh, and Rick L. Wilson. 1993. Performance comparison issues in neural network experiments for classification problems. In [1993] Proceedings of the Twenty-Sixth Hawaii International Conference on System Sciences. Piscataway: IEEE, vol. 4, pp. 649–57. [Google Scholar]
- Shrivastav, Santosh Kumar. 2019. Measuring the Determinants for the Survival of Indian Banks Using Machine Learning Approach. FIIB Business Review 8: 32–38. [Google Scholar] [CrossRef]
- Shrivastava, Santosh, P. Mary Jeyanthi, and Sarabjit Singh. 2020. Failure prediction of Indian Banks using SMOTE, Lasso regression, bagging and boosting. Cogent Economics & Finance 8: 1729569. [Google Scholar]
- Shumway, Tyler. 2001. Forecasting bankruptcy more accurately: A simple hazard model. The Journal of Business 74: 101–24. [Google Scholar] [CrossRef]
- Sun, Yijun, Sinisa Todorovic, and Steve Goodison. 2009. Local-learning-based feature selection for high-dimensional data analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence 32: 1610–26. [Google Scholar]
- Swicegood, Philip, and Jeffrey A. Clark. 2001. Off-site monitoring systems for predicting bank underperformance: a comparison of neural networks, discriminant analysis, and professional human judgment. Intelligent Systems in Accounting, Finance & Management 10: 169–86. [Google Scholar]
- Tam, Kar Yan. 1991. Neural network models and the prediction of bank bankruptcy. Omega 19: 429–45. [Google Scholar] [CrossRef]
- Tian, Yingjie, Yong Shi, and Xiaohui Liu. 2012. Recent advances on support vector machines re-search. Technological and Economic Development of Economy 18: 5–33. [Google Scholar] [CrossRef]
- Tsukuda, Junsei, and Shin-ichi Baba. 1994. Predicting Japanese corporate bankruptcy in terms of financial data using neural network. Computers & Industrial Engineering 27: 445–48. [Google Scholar]
- Vapnik, Vladimir. 1998. The support vector method of function estimation. In Nonlinear Modeling. Boston: Springer, pp. 55–85. [Google Scholar]
- Wang, Gang, Jinxing Hao, Jian Ma, and Hongbing Jiang. 2011. A comparative assessment of ensemble learning for credit scoring. Expert Systems with Applications 38: 223–30. [Google Scholar] [CrossRef]
- Wang, Gang, Jian Ma, and Shanlin Yang. 2014. An improved boosting based on feature selection for corporate bankruptcy prediction. Expert Systems with Applications 41: 2353–61. [Google Scholar] [CrossRef]
- Whalen, Gary. 1991. A proportional hazards model of bank failure: an examination of its usefulness as an early warning tool. Economic Review 27: 21–31. [Google Scholar]
- Yeh, Quey-Jen. 1996. The application of data envelopment analysis in conjunction with financial ratios for bank performance evaluation. Journal of the Operational Research Society 47: 980–88. [Google Scholar] [CrossRef]
- Zmijewski, Mark E. 1984. Methodological issues related to the estimation of financial distress prediction models. Journal of Accounting Research 22: 59–82. [Google Scholar] [CrossRef]
| Mathematical Kernel Equation | Name of Kernel |
|---|---|
| Linear | |
| RBF (Radial Basis Function) |
| Subordebt_TA (t−2) | 0.18 |
| Subordebt_TA (t−1) | 0.12 |
| Tier1CAR(t−2) | 0.1 |
| Provision_for_loan_Interest_income (t−4) | 0.1 |
| Subordebt_TA(t−3) | 0.09 |
| Provision_for_loan_Interest_income(t−1) | 0.08 |
| Provision_for_loan_Interest_income(t−2) | 0.08 |
| Provision_for_loan_Interest_income(t−3) | 0.07 |
| TA_employee(t−3) | 0.07 |
| TA_employee(t−2) | 0.06 |
| Tier1CAR(t−1) | 0.06 |
| TA_employee(t−4) | 0.05 |
| TA_employee(t−1) | 0.05 |
| Noninterest_expences_Int_income(t−3) | 0.04 |
| Subordebt_TA(t−4) | 0.02 |
| Salaries_and_employees_benefits_Int_income(t−3) | 0.01 |
| Total Accuracy | Solvent Predictive Accuracy | Insolvent Predictive Accuracy |
|---|---|---|
| 92.86% | 100% | 75% |
| Total Accuracy | Solvent Predictive Accuracy | Insolvent Predictive Accuracy |
|---|---|---|
| 71.43% | 100% | 0% |
| Features | Original Values | Critical Values |
|---|---|---|
| provision_for_loan_Interest_income(t−1) | 0.00123 | 2.0 |
| Tier1CAR(t−1) | 0.1123 | 1.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrivastav, S.K.; Ramudu, P.J. Bankruptcy Prediction and Stress Quantification Using Support Vector Machine: Evidence from Indian Banks. Risks 2020, 8, 52. https://doi.org/10.3390/risks8020052
Shrivastav SK, Ramudu PJ. Bankruptcy Prediction and Stress Quantification Using Support Vector Machine: Evidence from Indian Banks. Risks. 2020; 8(2):52. https://doi.org/10.3390/risks8020052
Chicago/Turabian StyleShrivastav, Santosh Kumar, and P. Janaki Ramudu. 2020. "Bankruptcy Prediction and Stress Quantification Using Support Vector Machine: Evidence from Indian Banks" Risks 8, no. 2: 52. https://doi.org/10.3390/risks8020052
APA StyleShrivastav, S. K., & Ramudu, P. J. (2020). Bankruptcy Prediction and Stress Quantification Using Support Vector Machine: Evidence from Indian Banks. Risks, 8(2), 52. https://doi.org/10.3390/risks8020052





