Delta Boosting Implementation of Negative Binomial Regression in Actuarial Pricing
Abstract
1. Introduction
2. Literature Review
3. Delta Boosting Implementation of Negative Binomial Regression
3.1. Notation
3.2. Generic Delta Boosting Algorithms
| Algorithm 1 Delta boosting for a single parameter estimation. |
|
3.3. Asymptotic DBM
3.4. Negative Binomial Regression
4. Delta Boosting Implementation of One-Parameter Negative Binomial Regression
4.1. Adaptation to Partial Exposure
4.2. Derivation of the Algorithm
| Algorithm 2 Delta boosting for one-parameter negative binomial regression. |
|
5. Delta Boosting Implementation of Two-Parameter Negative Binomial Regression
5.1. Adaptation to Incomplete Exposure
5.2. Derivation of the Algorithm
5.3. Negative Binomial Does Not Belong to the Two-Parameter Exponential Family
5.4. No Local Minima
5.4.1. Negative Convexity
5.4.2. Co-Linearity
5.4.3. Our Proposal to Saddle Points
5.4.4. The Modified Deltas
5.4.5. Partition Selection
5.5. The Selected Algorithm
| Algorithm 3 Delta boosting for two-parameter negative binomial regression. |
|
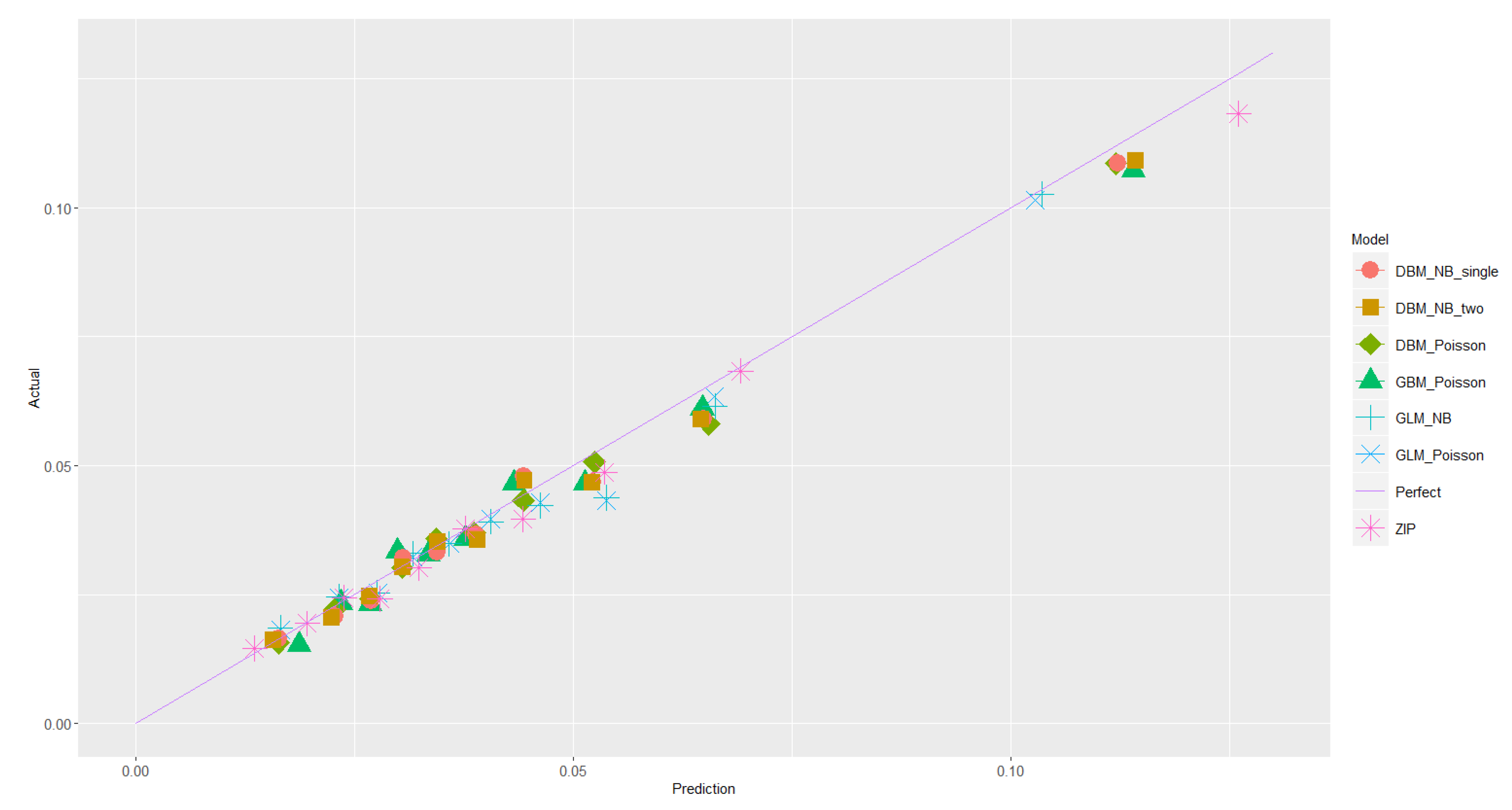
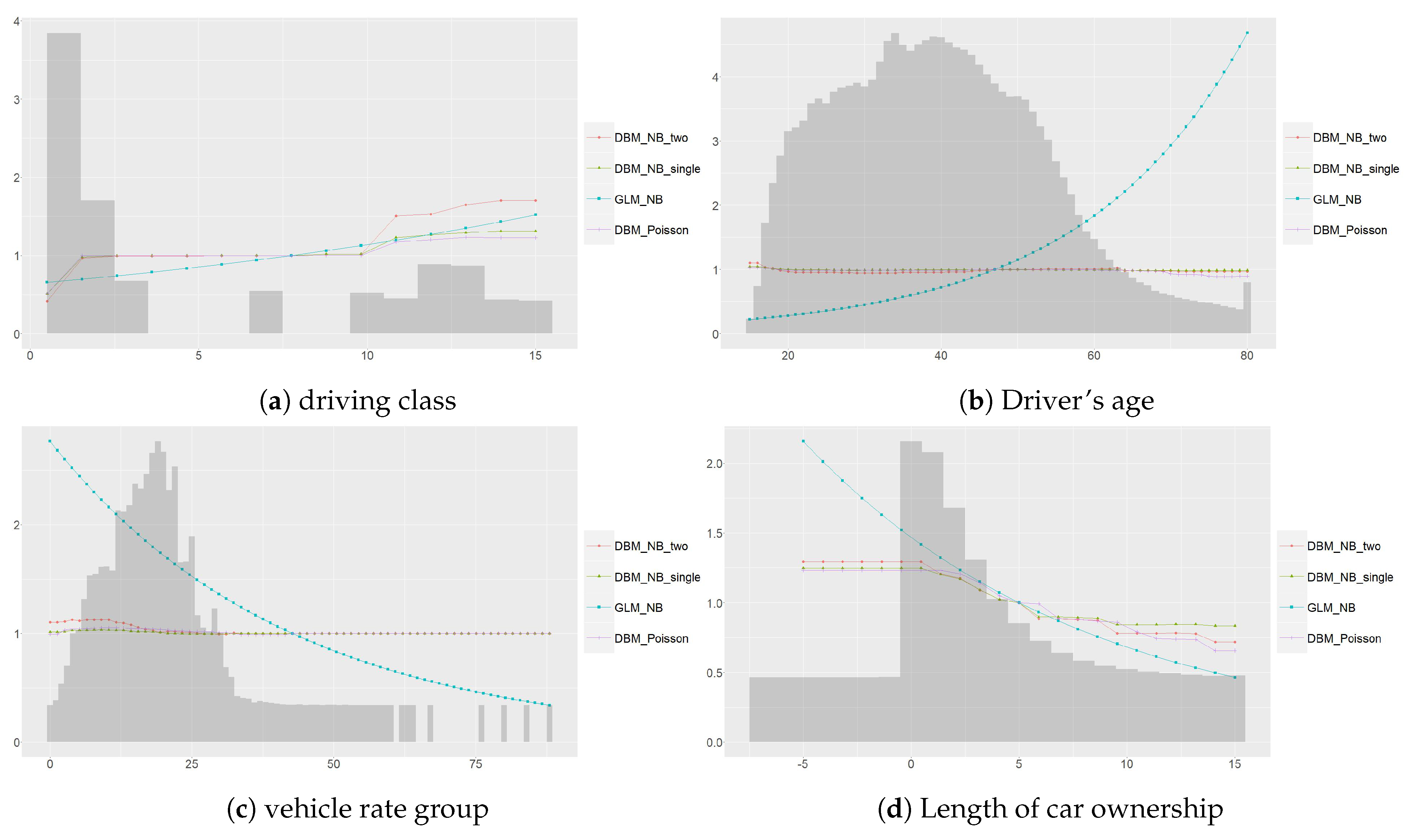
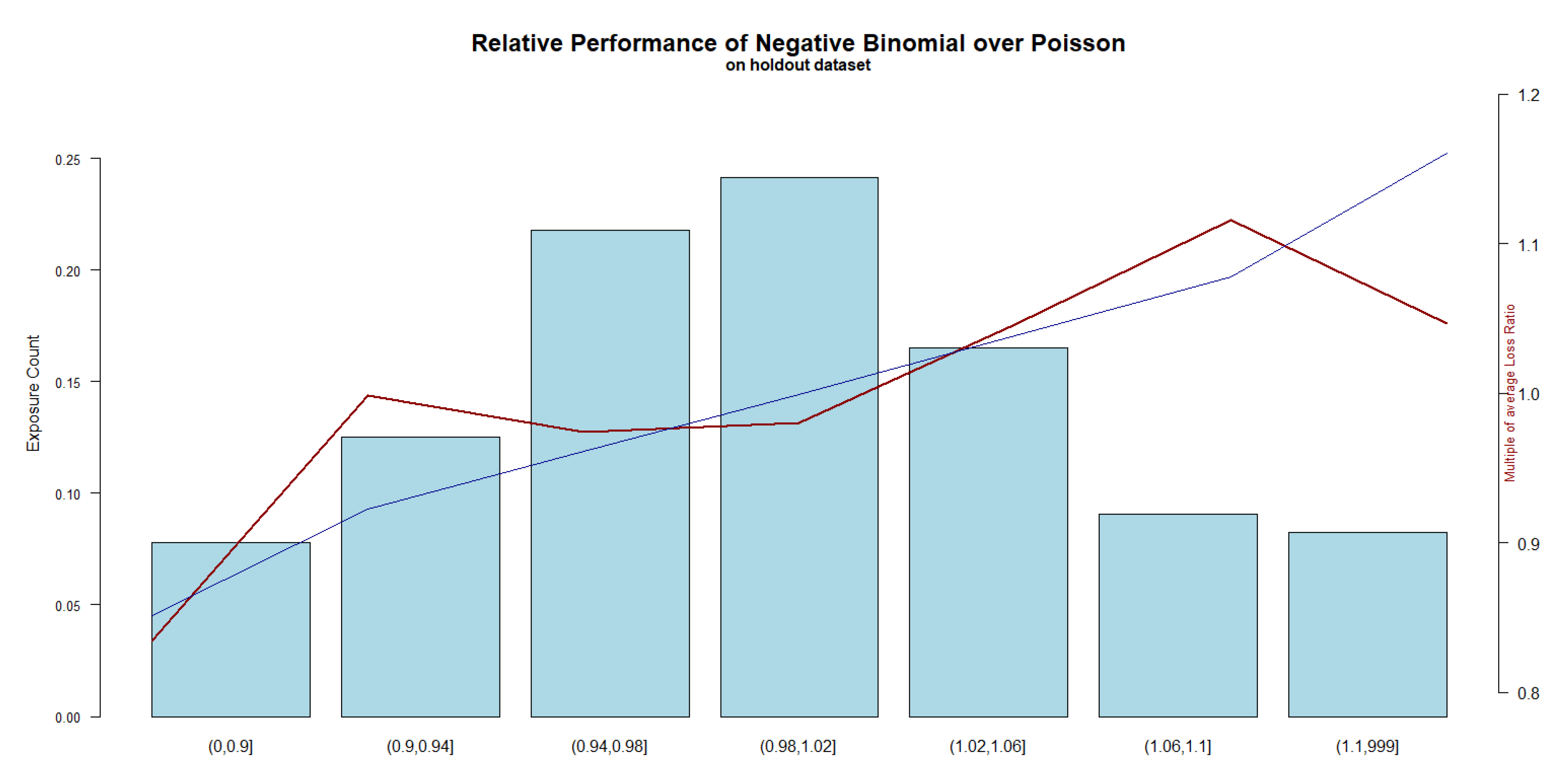
6. Empirical Studies
6.1. Data
6.2. Candidate Algorithms for Benchmarking Studies
7. Concluding Remarks and Directions of Future Research
- Negative binomial regression performs better than the Poisson counterparts A meaningful improvement of metrics is observed with GLM, GAM, and DB, implementation of negative binomial as compared to the GLM, GAM and DB implementation of Poisson which clearly indicates that the negative binomial based models show a better fit for the insurance data, potentially due to the excessive zeros phenomenon described Section 1.
- Existence of non-linearity and interaction In either Poisson or negative binomial based models, GAM outperforms GLM and DB outperforms GAM. The former suggests non-linearity between explanatory variables and the response where the later suggests that the existence of interaction within the data.
- Two-parameter regression offers an additional boost of performance In this paper, we introduce a novel two-parameter regression approach through a simultaneous regression of both and . From the empirical study, assuming a fixed shape parameter may restrict the ability for a machine learning model to search for the best parameter set.
Funding
Conflicts of Interest
References
- Anderson, Duncan, Sholom Feldblum, Claudine Modlin, Doris Schirmacher, Ernesto Schirmacher, and Neeza Thandi. 2007. A Practitioner’s Guide to Generalized Linear Models—A Foundation for Theory, Interpretation and Application. CAS Discussion Paper Program. Arlington: Casualty Actuarial Society. [Google Scholar]
- Baudry, Maximilien, and Christian Y. Robert. 2019. A machine learning approach for individual claims reserving in insurance. Applied Stochastic Models in Business and Industry 35: 1127–55. [Google Scholar] [CrossRef]
- Boucher, Jean-Philippe, Michel Denuit, and Montserrat Guillen. 2009. Number of accidents or number of claims? an approach with zero-inflated poisson models for panel data. Journal of Risk and Insurance 76: 821–46. [Google Scholar] [CrossRef]
- Breslow, Norman. 1990. Tests of hypotheses in overdispersed poisson regression and other quasi-likelihood models. Journal of the American Statistical Association 85: 565–71. [Google Scholar] [CrossRef]
- Casualty Actuarial and Statistical Task Force. 2019. Regulatory Review of Predictive Models White Paper. Technical Report. Kansas City: National Association of Insurance Commissioners. [Google Scholar]
- Darroch, John N., and Douglas Ratcliff. 1972. Generalized iterative scaling for log-linear models. The Annals of Mathematical Statistics 43: 1470–80. [Google Scholar] [CrossRef]
- Dauphin, Yann N., Razvan Pascanu, Caglar Gulcehre, Kyunghyun Cho, Surya Ganguli, and Yoshua Bengio. 2014. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. In Advances in Neural Information Processing Systems. Montreal: Neural Information Processing Systems Conference, pp. 2933–41. [Google Scholar]
- David, Mihaela, and Dănuţ-Vasile Jemna. 2015. Modeling the frequency of auto insurance claims by means of poisson and negative binomial models. Annals of the Alexandru Ioan Cuza University-Economics 62: 151–68. [Google Scholar] [CrossRef]
- De Jong, Piet, and Gillian Z. Heller. 2008. Generalized Linear Models for Insurance Data. Cambridge: Cambridge University Press. [Google Scholar]
- Friedland, Jacqueline. 2010. Estimating Unpaid Claims Using Basic Techniques. Arlington: Casualty Actuarial Society, vol. 201. [Google Scholar]
- Friedman, Jerome H. 2001. Greedy function approximation: A gradient boosting machine. Annals of Statistics 29: 1189–232. [Google Scholar] [CrossRef]
- Gagnon, David R., Susan Doron-Lamarca, Margret Bell, Timothy J. O’ Farrell, and Casey T. Taft. 2008. Poisson regression for modeling count and frequency outcomes in trauma research. Journal of Traumatic Stress 21: 448–54. [Google Scholar] [CrossRef]
- Gini, Corrado. 1936. On the measure of concentration with special reference to income and statistics. Colorado College Publication, General Series 208: 73–79. [Google Scholar]
- Girosi, Federico, Michael Jones, and Tomaso Poggio. 1995. Regularization theory and neural networks architectures. Neural Computation 7: 219–69. [Google Scholar]
- Gourieroux, Christian, Alain Monfort, and Alain Trognon. 1984a. Pseudo maximum likelihood methods: Applications to poisson models. Econometrica: Journal of the Econometric Society 52: 701–20. [Google Scholar] [CrossRef]
- Gourieroux, Christian, Alain Monfort, and Alain Trognon. 1984b. Pseudo maximum likelihood methods: Theory. Econometrica: Journal of the Econometric Society 52: 681–700. [Google Scholar] [CrossRef]
- Haberman, Steven, and Arthur E. Renshaw. 1996. Generalized linear models and actuarial science. Journal of the Royal Statistical Society. Series D (The Statistician) 45: 407–36. [Google Scholar] [CrossRef]
- Hashem, Sherif. 1996. Effects of collinearity on combining neural networks. Connection Science 8: 315–36. [Google Scholar] [CrossRef]
- Henckaerts, Roel, Marie-Pier Côté, Katrien Antonio, and Roel Verbelen. 2019. Boosting insights in insurance tariff plans with tree-based machine learning. arXiv arXiv:1904.10890. [Google Scholar]
- Ismail, Noriszura, and Abdul Aziz Jemain. 2007. Handling overdispersion with negative binomial and generalized poisson regression models. Casualty Actuarial Society Forum 2007: 103–58. [Google Scholar]
- JO, Loyd-Smith. 2007. Maximum likelihood estimation of the negative binomial dispersion parameter for highly overdispersed data, with applications to infectious diseases. PLoS ONE 2: e180. [Google Scholar]
- Kingma, Diederik P., and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv arXiv:1412.6980. [Google Scholar]
- Kuo, Kevin. 2019. Deeptriangle: A deep learning approach to loss reserving. Risks 7: 97. [Google Scholar] [CrossRef]
- Lee, Simon, and Katrien Antonio. 2015. Why high dimensional modeling in actuarial science? Paper presented at the ASTIN, AFIR/ERM and IACA Colloquia, Sydney, Australia, August 23–27. [Google Scholar]
- Lee, Simon C. K., and Sheldon Lin. 2015. Delta boosting machine with application to general insurance. Paper presented at the ASTIN, AFIR/ERM and IACA Colloquia, Sydney, Australia, August 23–27. [Google Scholar]
- Lee, Simon CK, and Sheldon Lin. 2018. Delta boosting machine with application to general insurance. North American Actuarial Journal 22: 405–25. [Google Scholar] [CrossRef]
- Lim, Hwa Kyung, Wai Keung Li, and Philip L. H. Yu. 2014. Zero-inflated poisson regression mixture mode l. Computational Statistics and Data Analysis 71: 151–58. [Google Scholar] [CrossRef]
- Majumdar, Abhijit, Sayantan Chatterjee, Roshan Gupta, and Chandra Shekhar Rawat. 2019. Competing in a New Age of Insurance: How india Is Adopting Emerging Technologies. Technical Report. Chandigarh: PwC and Confederation of Indian Industry Northern Region. [Google Scholar]
- Naya, Hugo, Jorge I. Urioste, Yu-Mei Chang, Mariana Rodrigues-Motta, Roberto Kremer, and Daniel Gianola. 2008. A comparison between poisson and zero-inflated poisson regression models with an application to number of black spots in corriedale sheep. Genetics, Selection, Evolution: GSE 40: 379–94. [Google Scholar]
- Nelder, John Ashworth, and Robert W. M. Wedderburn. 1972. Generalized linear models. Journal of the Royal Statistical Society: Series A (General) 135: 370–84. [Google Scholar] [CrossRef]
- Ridout, Martin, Clarice G. B. Demetrio, Clarice, and John Hindle. 1998. Models for count data with many zeros. Paper presented at the International Biometric Conference, Cape Town, South Africa, December 14–18. [Google Scholar]
- Scollnik, David P. M. 2001. Actuarial modeling with mcmc and bugs. North American Actuarial Journal 5: 96–124. [Google Scholar] [CrossRef]
- Sun, Yanmin, Mohamed S. Kamel, Andrew K. C. Wong, and Yang Wang. 2007. Cost-sensitive boosting for classification of imbalanced data. Pattern Recognition 40: 3358–78. [Google Scholar] [CrossRef]
- Taylor, Greg. 2019. Loss reserving models: Granular and machine learning forms. Risks 7: 82. [Google Scholar] [CrossRef]
- Teugels, Jozef L., and Petra Vynckie. 1996. The structure distribution in a mixed poisson process. International Journal of Stochastic Analysis 9: 489–96. [Google Scholar] [CrossRef]
- Thomas, Janek, Andreas Mayr, Bernd Bischl, Matthias Schmid, Adam Smith, and Benjamin Hofner. 2018. Gradient boosting for distributional regression: Faster tuning and improved variable selection via noncyclical updates. Statistics and Computing 28: 673–87. [Google Scholar] [CrossRef]
- Tihonov, Andrei Nikolajevits. 1963. Solution of incorrectly formulated problems and the regularization method. Soviet Math. 4: 1035–38. [Google Scholar]
- Ver Hoef, Jay M., and Peter Boveng. 2007. Quasi-poisson vs. negative binomial regression: How should we model overdispersed count data? Ecology 88: 2766–72. [Google Scholar] [CrossRef] [PubMed]
- Werner, Geoff, and Claudine Modlin. 2010. Basic ratemaking. Casualty Actuarial Society 4: 1–320. [Google Scholar]
- Wüthrich, Mario V. 2018. Machine learning in individual claims reserving. Scandinavian Actuarial Journal 2018: 465–80. [Google Scholar] [CrossRef]
- Wuthrich, Mario V., and Christoph Buser. 2019. Data Analytics for Non-Life Insurance Pricing. Swiss Finance Institute Research Paper. Rochester: SSRN, pp. 16–68. [Google Scholar]
- Yang, Yi, Wei Qian, and Hui Zou. 2018. Insurance premium prediction via gradient tree-boosted tweedie compound poisson models. Journal of Business & Economic Statistics 36: 456–70. [Google Scholar]
- Yip, Karen CH, and Kelvin KW Yau. 2005. On modeling claim frequency data in general insurance with extra zeros. Insurance: Mathematics and Economics 36: 153–63. [Google Scholar] [CrossRef]

| Notation | Description |
|---|---|
| M | Total number of observations for training |
| In decision tree, is a step function with as the split point. | |
| Index set of observation in Partition (can also be called Node or Leaf) j induced by | |
| as the shape parameter in the case of negative binomial regression. | |
| as the scale parameter in the case of negative binomial regression. | |
| The Loss function of observation i for DB regression. can be a vector of parameters. In negative binomial regression, the loss function is presented as | |
| Aggregate loss function for one parameter regression, equivalent to | |
| and | as an abbreviation of . Similar for |
| , , | as an abbreviation of . Similar for and |
| The exposure length of observation i | |
| The abbreviation of , analogy for other first and second derivatives. | |
| Loss minimizer(delta) for observation i in the case of a single parameter estimation: | |
| Loss minimizer for observations in Node j: | |
| Partition that has a smaller in the case of a 2-node partition (Stunt) | |
| Partition that has a larger in the case of a 2-node partition (Stunt) | |
| for observations in | |
| for observations in |
| Record | yyyymm | Exposure | Policy ID | Age | Conviction | Vehicle Code | Claim | Claim $ |
|---|---|---|---|---|---|---|---|---|
| 1 | 201501 | 0.0849 | 123456 | 35 | 1 | CamrySE2013 | 0 | - |
| 2 | 201502 | 0.0767 | 123456 | 35 | 1 | CamrySE2013 | 0 | - |
| 3 | 201503 | 0.0849 | 123456 | 35 | 1 | CamrySE2013 | 0 | - |
| 4 | 201504 | 0.0274 | 123456 | 35 | 1 | CamrySE2013 | 0 | - |
| 5 | 201504 | 0.0548 | 123456 | 35 | 1 | LexusRX2015 | 0 | - |
| 6 | 201505 | 0.0411 | 123456 | 35 | 1 | LexusRX2015 | 0 | - |
| 7 | 201506 | 0.0438 | 123456 | 35 | 2 | LexusRX2015 | 1 | 50,000.0 |
| 8 | 201507 | 0.0849 | 123456 | 35 | 2 | LexusRX2015 | 0 | - |
| 9 | 201508 | 0.0082 | 123456 | 35 | 2 | LexusRX2015 | 0 | - |
| 10 | 201508 | 0.0767 | 123456 | 36 | 2 | LexusRX2015 | 0 | - |
| Model | Metrics on Train Dataset | Metrics on Test Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| Loss(P) | Loss(NB) | Lift | Gini | Loss(P) | Loss(NB) | Lift | Gini | |
| GLM | 0.00 | - | 5.807 | 0.269 | 0.00 | - | 5.575 | 0.245 |
| GAM | −277.36 | - | 6.739 | 0.286 | −39.79 | - | 6.009 | 0.312 |
| GBM | −764.80 | - | 8.987 | 0.314 | −56.45 | - | 7.022 | 0.292 |
| Poissondbm | −790.97 | 10.520 | 0.317 | −63.88 | 6.945 | 0.329 | ||
| NBGLM | −5.72 | −33.96 | 5.826 | 0.267 | 6.16 | −9.26 | 5.527 | 0.256 |
| NBGAM | −264.75 | −288.39 | 6.780 | 0.295 | −39.12 | −53.25 | 6.087 | 0.259 |
| NBdelta_single | −782.02 | −528.80 | 10.285 | 0.322 | −61.45 | −68.60 | 6.582 | 0.306 |
| NBdelta_double | −901.22 | −599.81 | 10.311 | 0.327 | −62.77 | −75.55 | 6.694 | 0.332 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.C. Delta Boosting Implementation of Negative Binomial Regression in Actuarial Pricing. Risks 2020, 8, 19. https://doi.org/10.3390/risks8010019
Lee SC. Delta Boosting Implementation of Negative Binomial Regression in Actuarial Pricing. Risks. 2020; 8(1):19. https://doi.org/10.3390/risks8010019
Chicago/Turabian StyleLee, Simon CK. 2020. "Delta Boosting Implementation of Negative Binomial Regression in Actuarial Pricing" Risks 8, no. 1: 19. https://doi.org/10.3390/risks8010019
APA StyleLee, S. C. (2020). Delta Boosting Implementation of Negative Binomial Regression in Actuarial Pricing. Risks, 8(1), 19. https://doi.org/10.3390/risks8010019




