1. Introduction
Big data has now become a driver of model building and analysis in a number of areas, including finance. More than half of the markets in today’s highly competitive and relentlessly fast-paced financial world now use a limit order book (LOB) mechanism to facilitate trade. The main problem here is how to deal with big data arising in electronic markets for algorithmic and high-frequency (milliseconds) trading (HFT).
The present paper introduces new different types of general compound Hawkes processes (GCHP)—namely GCHPDO (two fixed ticks,
dependent orders), GCHP2SDO (two non-fixed ticks,
dependent orders) and GCHPnSDO (
n non-fixed ticks,
dependent order)—to model the mid prices
dynamics of the assets in HFT, namely, EBAY, FB, MU, PCAR, SMH, CSCO, (provided by Reference
Cartea et al. (
2015)).
As we mentioned, high-frequency trading happens in milliseconds, as order arrivals and cancellations are very frequent. How we can study and model the dynamics of the mid-prices? One of the ways is to look over a larger time scale, for example, 5, 10 or 20 min, that is, consider time scale
instead of
then
n could be
etc. It means that we consider the dynamics of order flow over large time scales. Thousands of order book events may occur over such large time scales (e.g., for CISCO data on one day in 2014 it is around 500,000, see Reference
Cartea et al. (
2015)). Thus, we can use asymptotic methods to study the link between order flow and price volatility by considering the diffusive limit of the mid-price processes. More precisely, we use the functional central limit theorems for above-mentioned GCHP and present the volatility of price changes in terms of the parameters of initial models.
To estimate the models fitting accuracy we define an error rate for each model and set the threshold value as The model with error rate less than the threshold is considered as well fitted. Thus, we define which of our models is the best fit for our real data.
We also use Maximum Likelihood Estimation (MLE) and Particle Swarm Optimization (PSO) for Hawkes processes and our parameters’ calibration.
There are many papers devoted to the modelling of HFT and applications of Hawkes processes in finance. See Reference
Bacry et al. (
2015) for more details. Below we give an overview of the most relevant literature.
Reference
Cont and De Larrard (
2013) proposed a simple Markovian stochastic model for the dynamics of a limit order book, in which arrivals of market orders, limit orders and order cancellations are independent and inter-arrival times have exponential distribution. They also studied the diffusion limit of the price process and expressed the volatility of price changes in terms of parameters describing the arrival rates of buy and sell orders and cancellations.
As suggested by empirical observations, Reference
Swishchuk and Vadori (
2017) extended their framework to (1) arbitrary distributions for book events inter-arrival times (possibly non-exponential) and (2) both the nature of a new book event and its corresponding inter-arrival time depend on the nature of the previous book event. They did so by resorting to Markov renewal processes to model the dynamics of the bid and ask queues. They kept analytical tractability via explicit expressions for the Laplace transforms of various quantities of interest. They also justified and illustrated their approach by calibrating their model to the five stocks Amazon, Apple, Google, Intel, Microsoft on 21 June 2012, to the 15 stocks from Deutsche Boerse Group (23 September 2013) and to CISCO asset (3 November 2014). As in Reference
Cont and De Larrard (
2013), the bid-ask spread remains constant equal to one tick, only the bid and ask queues are modelled (they are independent from each other and get reinitialized after a price change) and all orders have the same size. We discussed possible extensions of our model for the case when the spread is not fixed, including the diffusion limit of the price dynamics in this case and we also discussed stochastic optimal control and market making problems.
The paper by Swishchuk and Hofmeister
Swishchuk et al. (
2017) considered a general semi-Markov model for limit order books with two states that incorporate price changes that are not fixed to one tick. Furthermore, even more general cases of the semi-Markov model for limit order books was introduced that incorporates an arbitrary number of states for the price changes. For both cases the justifications, diffusion limits, implementations and numerical results were presented for different limit order book data—Apple, Amazon, Google, Microsoft, Intel on 21 June 2012 and Cisco, Facebook, Intel, Liberty Global, Liberty Interactive, Microsoft, Vodafone from 3 November 2014 to 7 November 2014. Reference
Chavez-Casillas et al. (
2019) proposed a simple stochastic model for the dynamics of a limit order book, extending the recent work of
Cont and De Larrard (
2013), where the price dynamics are endogenous, resulting from market transactions. They also showed that the conditional diffusion limit of the price process is the so-called Brownian meander.
Trading activity is not a completely random and memoryless process. That is why the Poisson process is not suitable for modelling trade arrival times. Trading activity also shows clustering behaviour. These properties suggest the use of the Hawkes process, a point process mathematically defined by Reference
Hawkes (
1971), which is an extension of the classical Poisson process that possesses this clustering property. It explains the large number of works on trading activity and more generally high-frequency econometrics based on this process as a modelling framework. (See Reference (
Bacry et al. 2015) for applications of Hawkes processes in finance).
Reference
Da Fonseca and Zaatour (
2013) provided explicit formulas for the moments and the autocorrelation function of the number of jumps over a given interval for a self-excited Hawkes process. The estimation strategy was applied to trade arrival times for major stocks that show a clustering behaviour, a feature the Hawkes process can effectively handle. As the calibration is fast, the estimation was rolled to determine the stability of the estimated parameters. Also, the analytical results enable the computation of the diffusive limit in a simple model for the price evolution based on the Hawkes process. It determines the connection between the parameters driving the high-frequency activity to the daily volatility.
Reference
Swishchuk et al. (
2019) introduced two new Hawkes processes, namely, compound and regime-switching compound Hawkes processes, to model the price processes in limit order books. They proved Law of Large Numbers and Functional Central Limit Theorems (FCLT) for both processes. The two FCLTs were applied to limit order books, where they used these asymptotic methods to study the link between price volatility and order flow in these two models by using the diffusion limits of these price processes. The volatilities of price changes were expressed in terms of parameters describing the arrival rates and price changes. They also presented some numerical examples based on CISCO data (3–7 November 2014).
Reference
Swishchuk and Huffman (
2018) studied various new Hawkes processes. Specifically, they constructed general compound Hawkes processes and investigate their properties in limit order books. With regards to these general compound Hawkes processes, they proved a Law of Large Numbers (LLN) and a Functional Central Limit Theorems (FCLT) for several specific variations. Then they applied several of these FCLTs to limit order books in Lobster data (21 June 2012) to study the link between price volatility and order flow, where the volatility in mid-price changes is expressed in terms of parameters describing the arrival rates and mid-price process. Quantitative and comparative analyses were performed for different models.
When it comes to multivariate cases of Hawkes Processes, Reference
Bacry et al. (
2013) proved a law of large numbers, a functional central limit theorem, and the asymptotic behaviour. Reference
Embrechts et al. (
2011) derived the maximum likelihood estimation and goodness-of-fit. As an Application, they analyzed the data sets from finance and fit the multivariate Hawkes process to daily closing values from the Dow Jones Industrial Average from 1 January 1994 to 31 December 2010. Reference
Zhou et al. (
2013) applied multivariate Hawkes processes to social network analysis and showed that the proposed method performed significantly better on both synthetic and real world datasets.
The rest of the paper is organized as follows. Different type of Hawkes processes and diffusive limits for them are introduced in
Section 2. Applications to limit order books are considered in
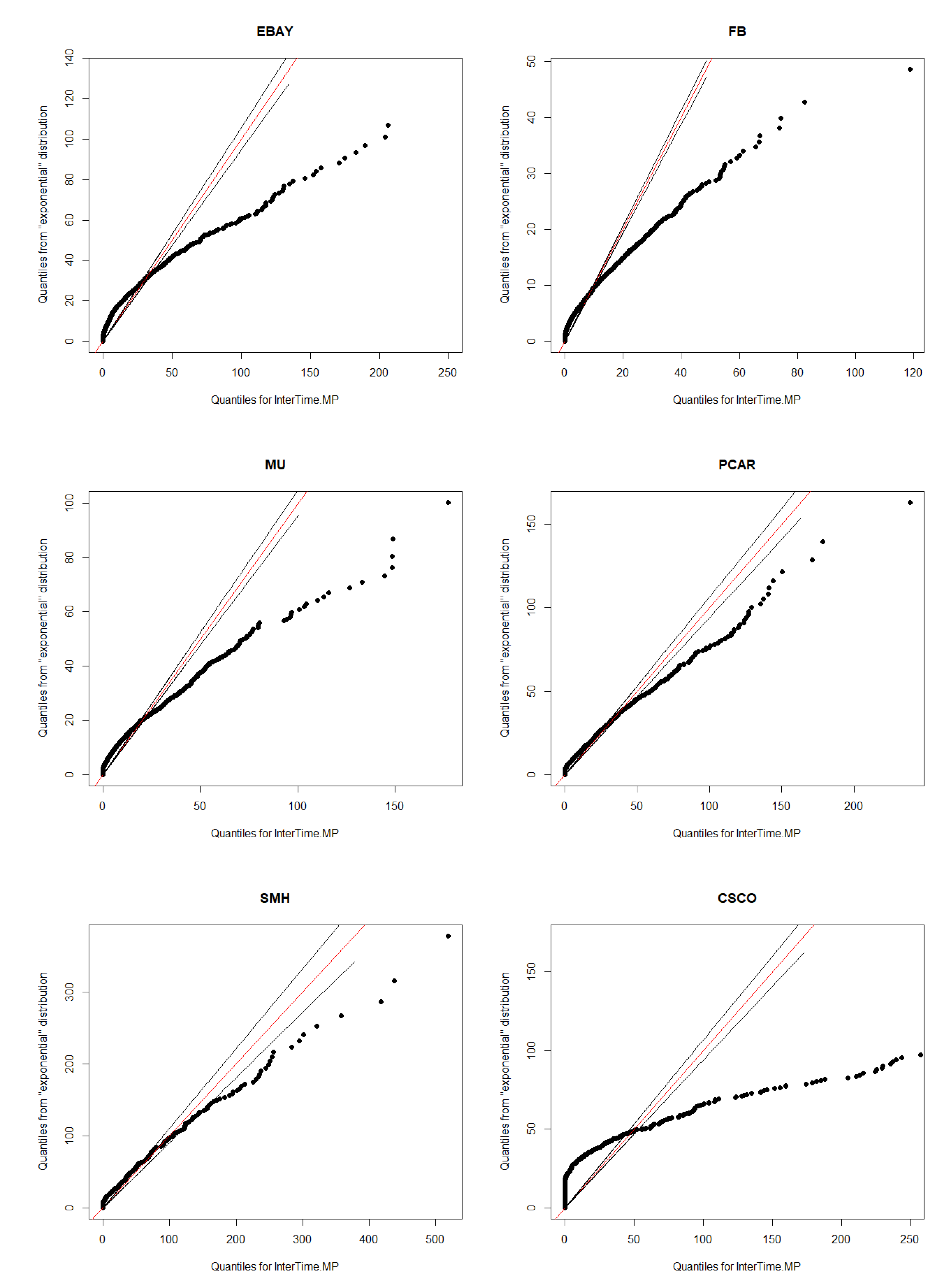
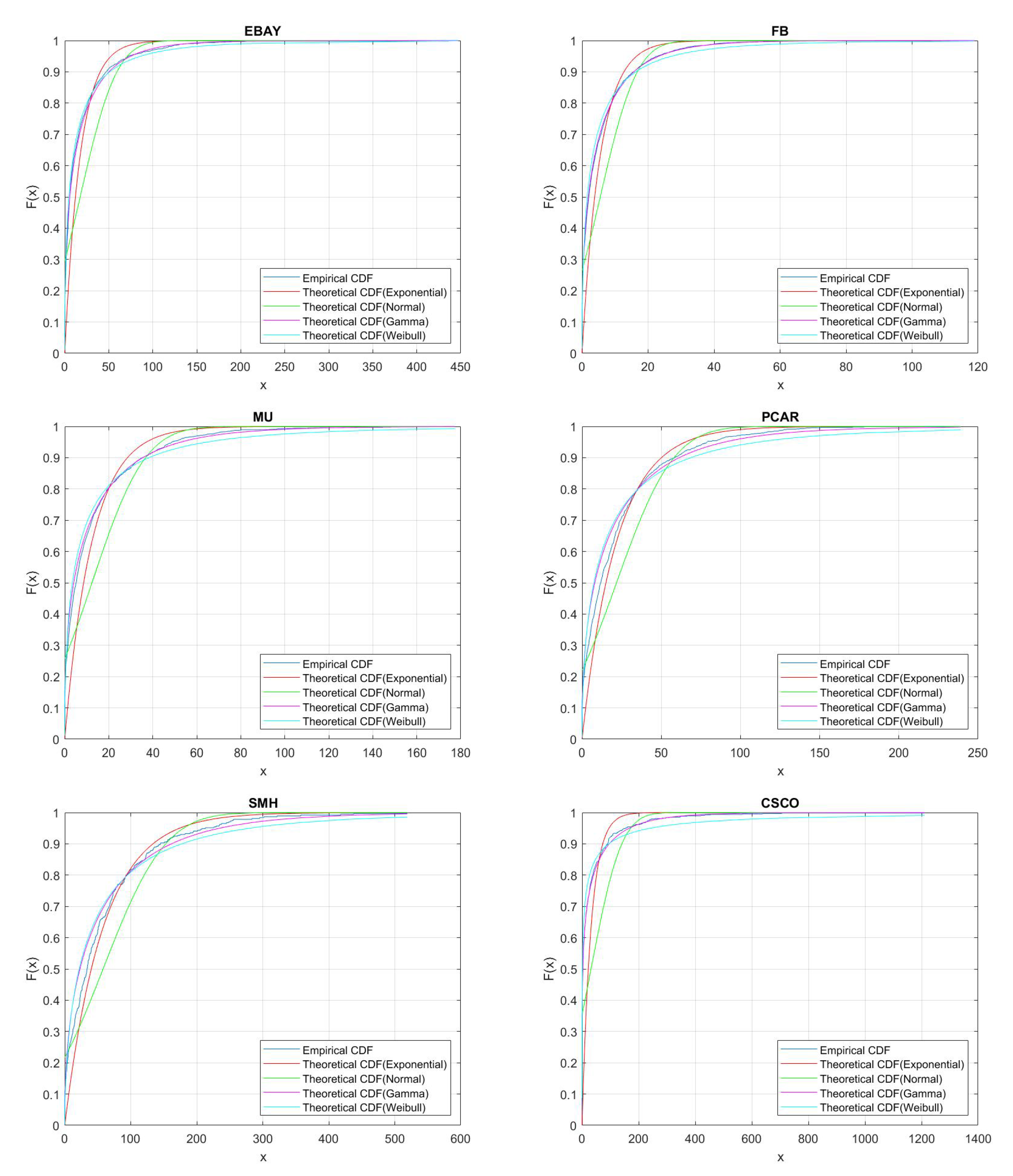
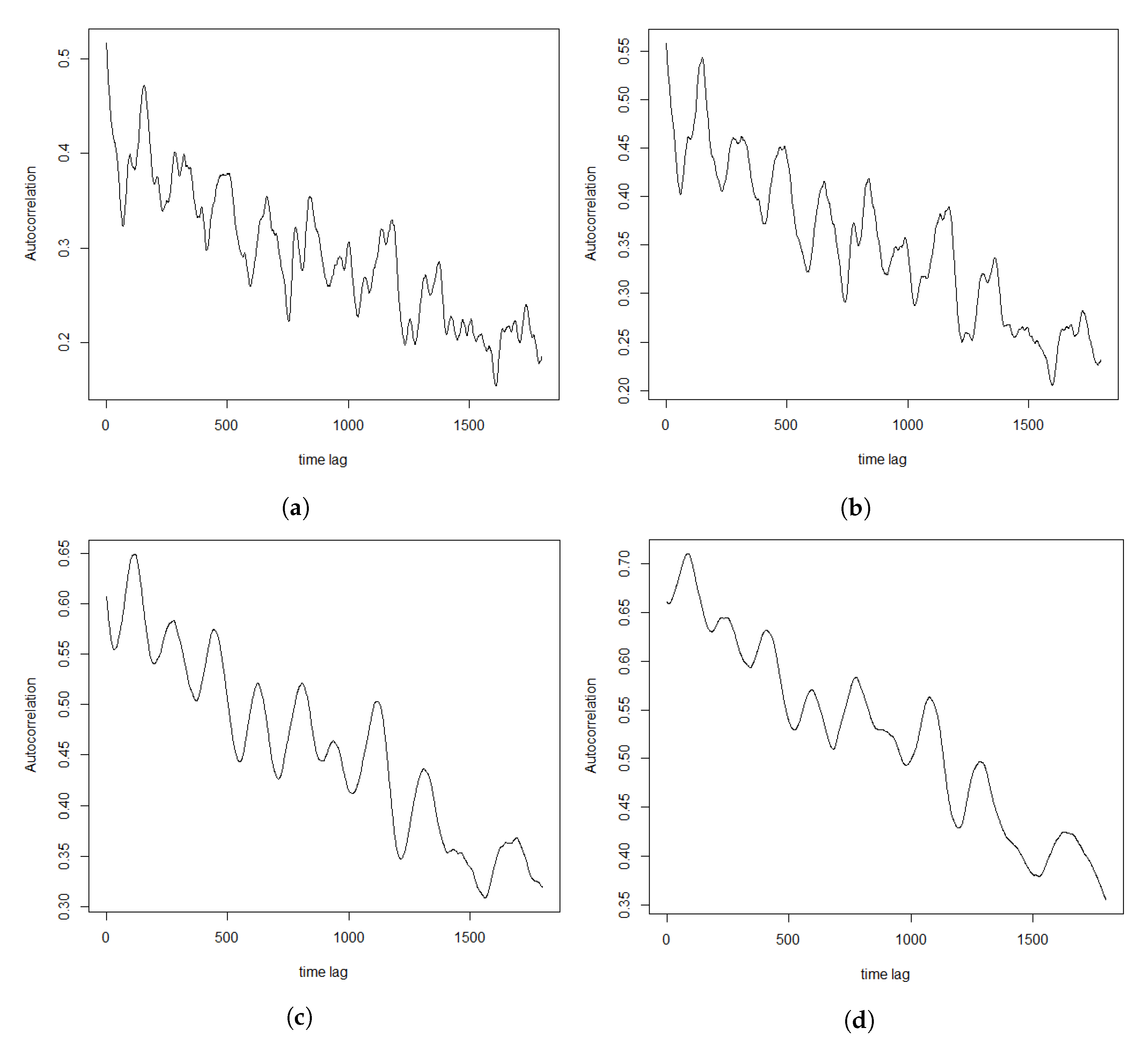
Section 3, including data and their clustering features descriptions, QQ-plots and autocorrelations.
Section 4 presents Hawkes process and different models’ parameters calibration’s results. Error measurements and comparative analysis are considered in
Section 5.
Section 6 concludes the paper.
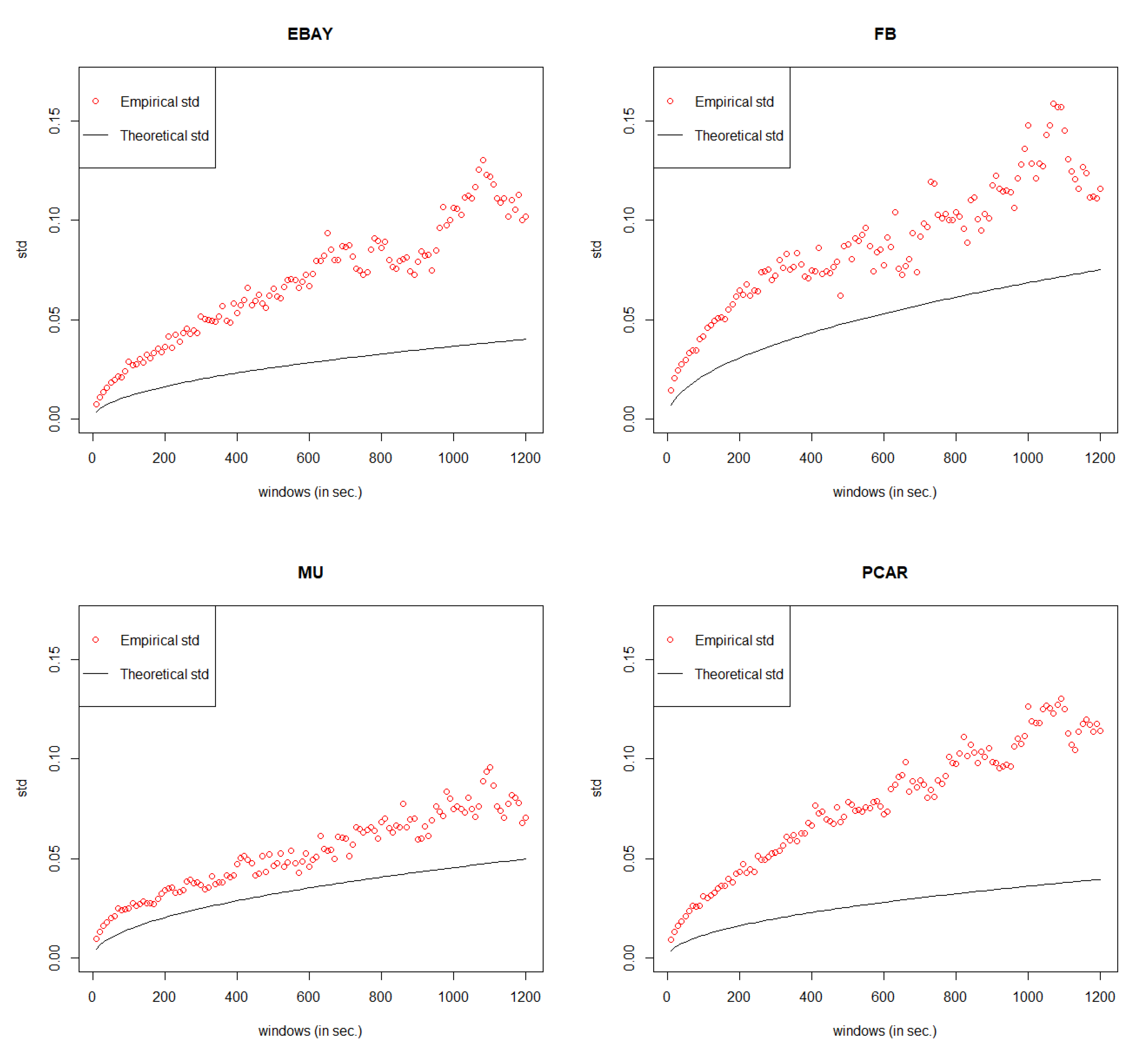
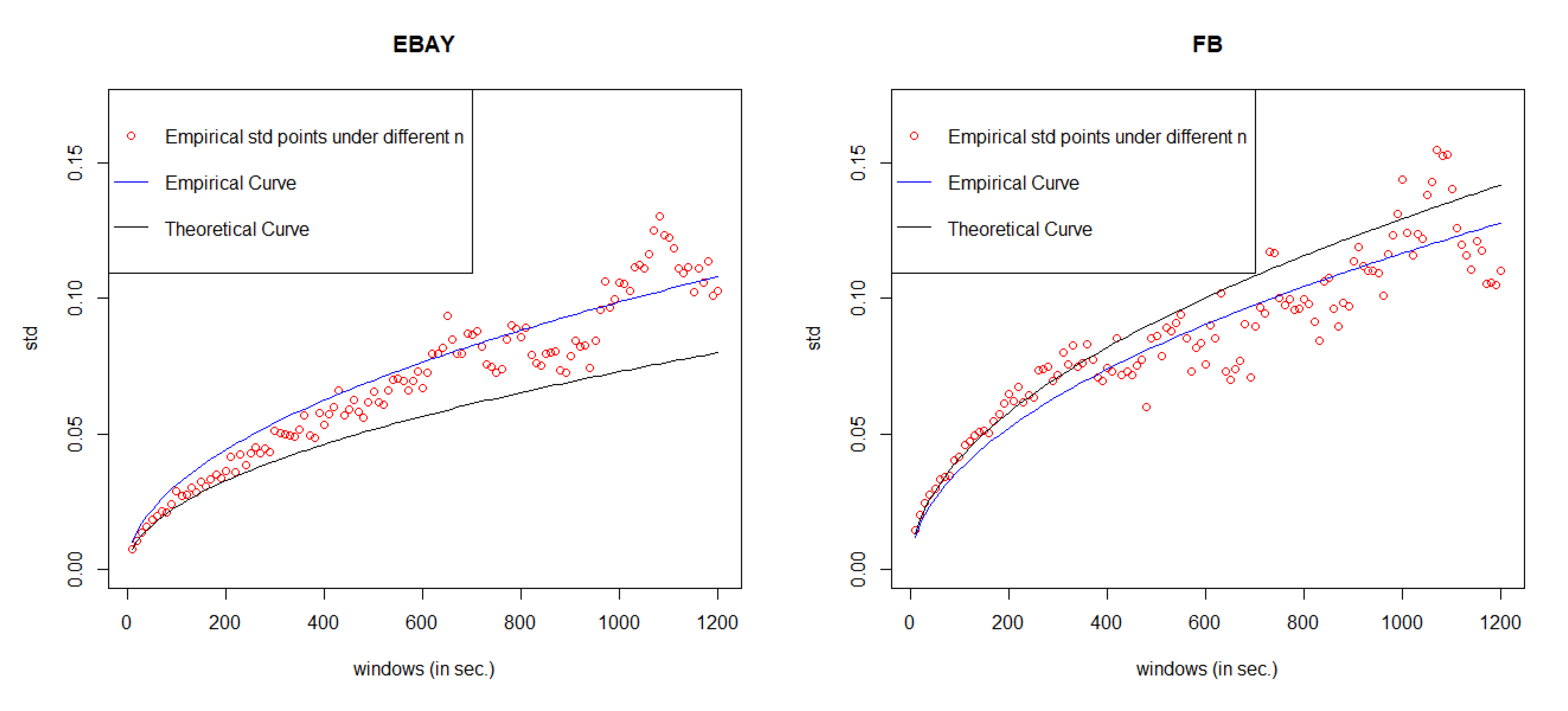
5. Error Measurement
Since the value of MSE is always very small under GCHPDO, GCHP2SDO, and GCHPnSDO models, it makes no sense to measure the correctness of model fitting under the best model only by MSE. Therefore, in this paper, we proposed a new way to measure the correctness. If we take the square of both sides in Equation (
16), we can get
Equation (
18) means that when
n goes to infinity, the square of
converges to a linear regression function
with respective to
n. Therefore, based on the real points
under different
n, we can estimate the linear regression function
by least square method, where
c is the estimated slope. Then, we take the square root of estimated function
, we can get our estimated curve of
. The comparison between the empirical curve and the theoretical curve is shown in
Figure 8.
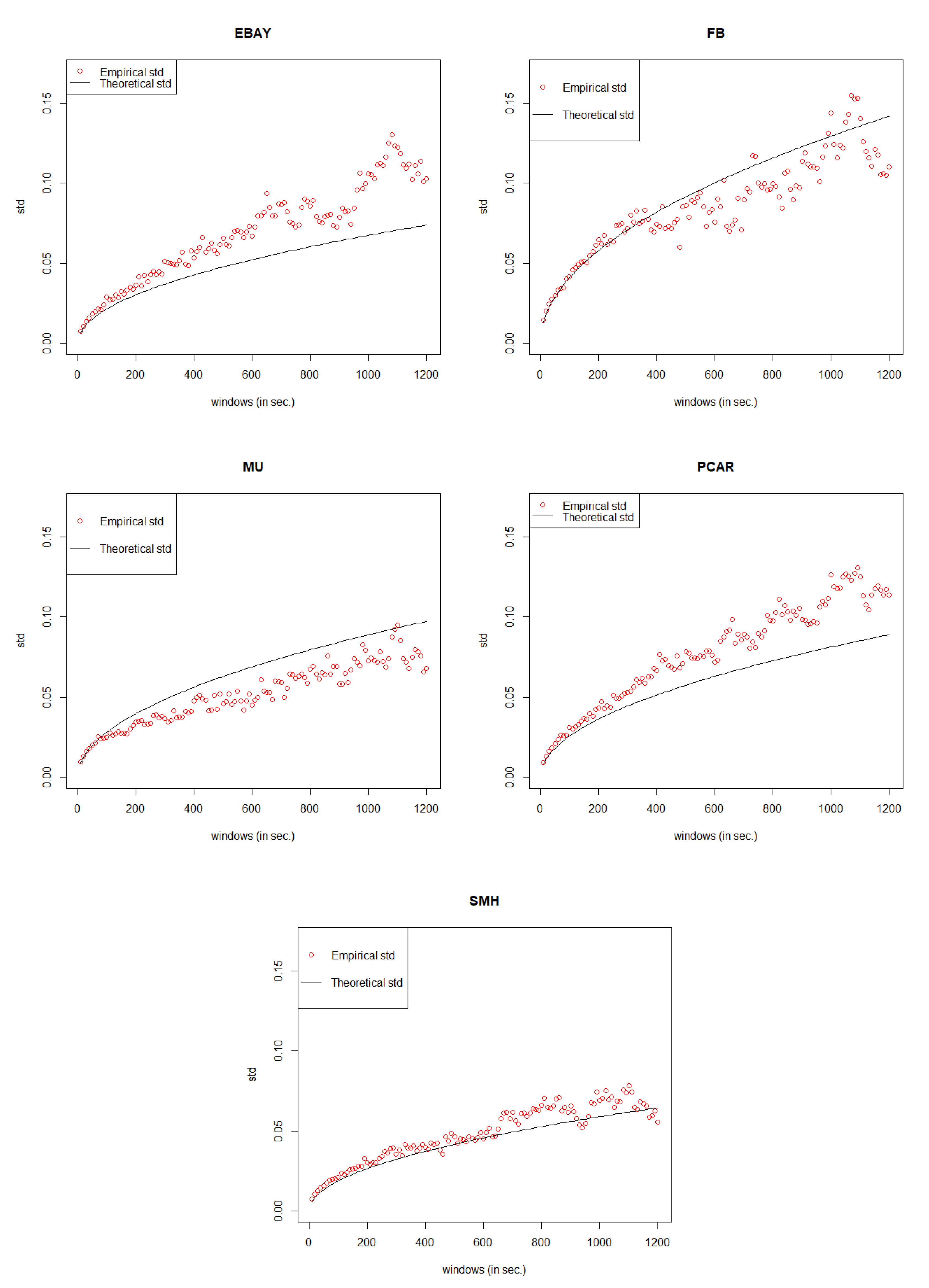
Under the best model, the error rate of each stock is listed in
Table 10. If we set the threshold value as 15%, the model with error rate less than threshold can be considered as well fitted.
Table 10 shows that our General Compound Hawkes Process correctly models the mid price movements of 4 stocks among 6.
We define the error rate as
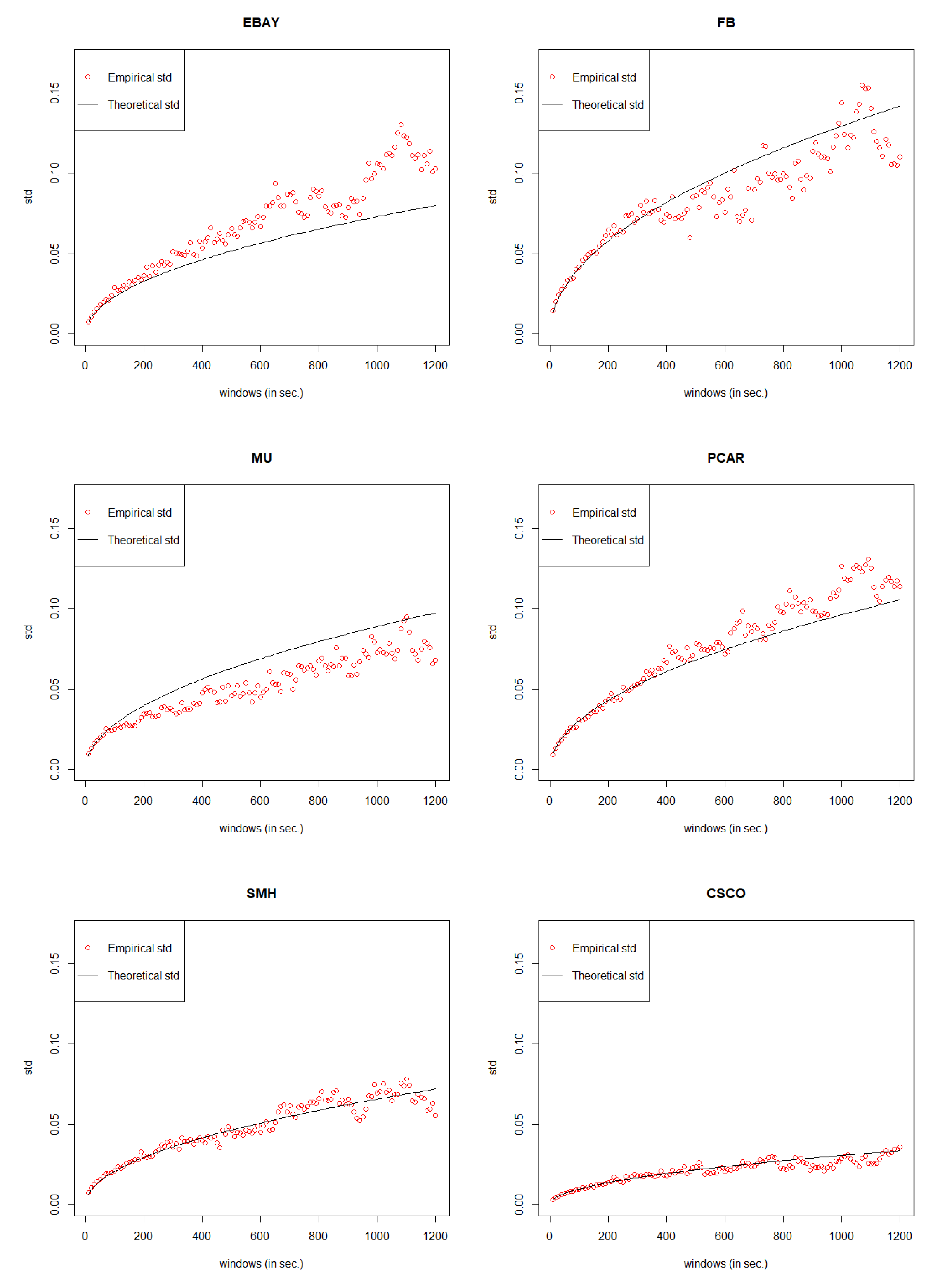
In order to avoid any bias of data selection, we do the simulation again by following the same process mentioned in
Section 3 to
Section 5 to justify our General Compound Hawkes Processes work well not just for one day but also for other days. In the data set of EBAY, FB, MU, PCAR, SMH, we randomly choose the date 18 November 2014; for the data set of CSCO, we randomly choose the date 6 November 2014.
Similarly, for CSCO data, since the intervals of price movements are always
$0.5, the GCHPDO model should be the best fit. To find the best n of the GCHPnSDO model for EBAY, FB, MU, PCAR, SMH, we have tried limited n and then picked up the best n under the smallest MSE. From
Table 12,
Table 13,
Table 14,
Table 15 and
Table 16, we can see that for EBAY, the best GCHPnSDO model is GCHP5SDO; for FB, the best GCHPnSDO model is GCHP4SDO; for MU, the best GCHPnSDO model is GCHP4SDO; for PCAR, the best GCHPnSDO model is GCHP4SDO; for SMH, the best GCHPnSDO model is GCHP6SDO.
Compare the MSE of the best GCHPnSDO models with that of GCHPDO and GCHP2SDO models. Again, pick up the best model for mid price movements under the smallest MSE and then calculate the error rate following the same method derived in Equation (
19). Within the error rate threshold of 15%, in
Table 17, we could see that our General Compound Hawkes Processes successfully track the mid price movements of FB, MU, PCAR, SMH, and CSCO.
6. Conclusions and Future Work
The main contribution and novelty of the paper consists in introducing different new types of General Compound Hawkes Processes (GCHPDO, GCHP2SDO, GCHPnSDO) and their diffusive limits to model the mid price movements. Based on our previous research, we further expand our data sets to justify whether our models still work well on the stocks of EBAY, FB, MU, PCAR, SMH, CSCO (provided by Reference
Cartea et al. (
2015) book). We define the error rates to estimate the models fitting accuracy and set the threshold to 15%. Based on the data sets named EBAY_20141110, FB_20141110, MU_20141110, PCAR_20141110, SMH_20141110, CSCO_20141107, the best model for EBAY is GCHP8SDO; for FB, the best model is GCHP2SDO; for MU, the best model is GCHP2SDO; for PCAR, the best model is GCHP15SDO; for SMH, the best model is GCHP9SDO; for CSCO, the best model is GCHPDO. Under the best model, our General Hawkes Processes successfully track the mid price movements of 4 stocks out of 6. To further avoid any bias of data selection process, again, we randomly choose the data from another date in our data sets, and gain the quite similar results. Those results justify that our General Compound Hawkes Processes could be right and could be applied for the data not just from a specific day but also from other days.
The future work will be devoted to the prediction analysis with different models introduced in this paper, and justifications of those model using real data.