Credit Risk Migration and Economic Cycles
Abstract
1. Introduction
2. Markov Chains and the Movers Stayers Model
- and ;
- ;
- M(t) = exp(tQ) for all t > 0, where exp(.) stands for the exponential matrix function (Golub and Van Loan 1996).
- Embeddability: there is no solution which also satisfies the aforementioned properties of a generating matrix. This drawback arises because not every discrete time Markov chain can be realized as a discretized continuous-time chain (Israel et al. 2001). Hence, it may be impossible from a one-year transition matrix (for example, if it contains zeros in some of the non-default rows) to structure a continuous-time chain which has the one-year transition matrix as its “marginal”.
- Aliasing: more than one continuous time chain exists, from which the discrete process arises. This drawback is caused by the fact that the equation M = exp(Q) may have different solutions.
- it randomly draws from a binomial distribution depending on ;
- it updates to randomly drawing from a probability density function which is a sort of multivariate Dirichlet distribution, with parameters depending on and on the observed starting distribution and the total observed number of transition from i to j, for every couple i and j.
3. Data Description
4. Results
4.1. Estimated Parameters
4.2. The Estimated Annual Transition Matrix
4.3. Comparison between the Markov Chain and Movers Stayers Models
4.4. The Equilibrium Distribution
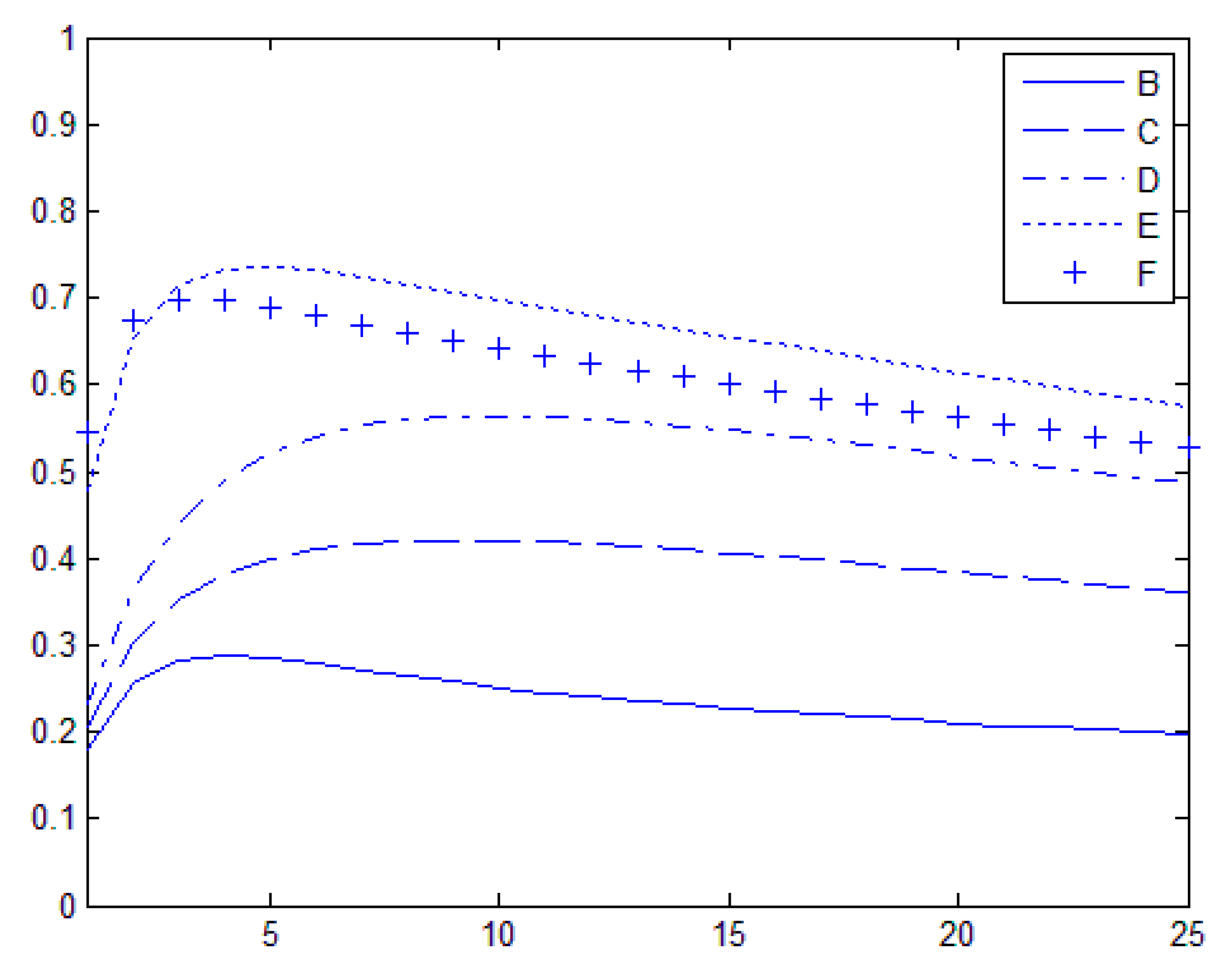
4.5. Time Persistence
4.6. Mobility Measurements
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Altman, Edward I. 1998. The importance and subtlety of credit rating migration. Journal of Banking and Finance 22: 1231–47. [Google Scholar] [CrossRef]
- Altman, Edward, and Duen Li Kao. 1992a. Rating Drift of High Yield Bonds. Journal of Fixed Income 14: 15–20. [Google Scholar] [CrossRef]
- Altman, Edward, and Duen Li Kao. 1992b. The Implications of Corporate Bond Ratings Drift. Financial Analysts Journal 48: 64–75. [Google Scholar] [CrossRef]
- Altman, Edward I., Robert G. Haldeman, and Paul Narayanan. 1977. Zeta-analysis. A new model to identify bankruptcy risk of corporations. Journal of Banking and Finance 1: 29–54. [Google Scholar] [CrossRef]
- Angilella, Silvia, and Sebastiano Mazzù. 2019. A credit risk model with an automatic override for innovative small and medium-sized enterprises. Journal of the Operational Research Society 70: 1784–800. [Google Scholar] [CrossRef]
- Baas, Timo, and Mechthild Schrooten. 2006. Relationship banking and SMEs: A theoretical analysis. Small Business Economics 27: 127–37. [Google Scholar] [CrossRef]
- Bandyopadhyay, Arindam, Tasneem Chherawala, and Asish Saha. 2007. Calibrating asset correlation for Indian corporate exposures. Implications for regulatory capital. The Journal of Risk Finance 8: 330–48. [Google Scholar] [CrossRef]
- Bangia, Anil, Francis X. Diebold, and Til Schuermann. 2002. Ratings migration and the business cycle, with application to credit portfolio stress testing. Journal of Banking and Finance 26: 445–74. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. 2009. Guidelines for Computing Capital for Incremental Risk in the Trading Book. Basel: Bank of International Settlements. [Google Scholar]
- Basel Committee on Banking Supervision. 2011. Basel III: A Global Regulatory Framework for More Resilient Banks and Banking Systems—Revised Version. Basel: Bank of International Settlements. [Google Scholar]
- Berger, Allen N., and Gregory F. Udell. 1995. Relationship lending and lines of credit in small firm finance. Journal of Business 1995: 351–81. [Google Scholar] [CrossRef]
- Berger, Allen N., and Gregory F. Udell. 2002. Small Business Credit Availability and Relationship Lending: The Importance of Bank Organizational Structure. The Economic Journal 112: 32–53. [Google Scholar] [CrossRef]
- Blume, Marshall E., Felix Lim, and A. Craig Mackinlay. 1998. The declining credit quality of U.S. corporate debt: Myth or reality. Journal of Finance 53: 1389–1413. [Google Scholar] [CrossRef]
- Blumen, Isadore, Marvin Kogan, and Philip McCarthy J. 1955. The Industrial Mobility of Labor as a Probability Process. Ithaca: Cornell University Press. [Google Scholar]
- Boot, Arnoud. 2000. Relationship lending: What do we know? Journal of Financial Intermediation 9: 7–25. [Google Scholar] [CrossRef]
- Boreiko, Dmitri, Serguei Kaniovski, Yuri Kaniovski, and Georg C. Pflug. 2018. Business Cycles and Conditional Credit-Rating Migration Matrices. Quarterly Journal of Finance 8: 1–19. [Google Scholar] [CrossRef]
- Carty, Lea V. 1997. Moody’s Rating Migration and Credit Quality Correlation, 1920–1996. New York: Moody’s Investor Service. [Google Scholar]
- Carty, Lea V., and Jerome S. Fons. 1993. Measuring Changes in Corporate Credit Quality. New York: Moody’s Investor Service. [Google Scholar]
- Cipollini, Fabrizio, Camilla Ferretti, Piero Ganugi, and Mario Mezzanzanica. 2013. A Continuous Time Mover Stayer Model for Labor Market in a Northern Italian Area, Classification and Data Mining. Edited by Giusti Antonio, Ritter Gunter and Vichi Maurizio. Berlin and Heidelberg: Springer, pp. 181–88. [Google Scholar]
- Cole, Rebel A., Lawrence G. Goldberg, and Lawrence J. White. 2004. Cookie cutter vs. character: The micro-structure of small business lending by large and small banks. Journal of Financial and Quantitative Analysis 39: 227–51. [Google Scholar] [CrossRef]
- D’Amico, Guglielmo, Jacques Janssen, and Raimondo Manca. 2016. Downward migration credit risk problem: A non-homogeneous backward semi-Markov reliability approach. Journal of the Operational Research Society 67: 393–401. [Google Scholar] [CrossRef]
- Das, Sanjiv, and Peter Tufano. 1996. Pricing credit sensitive debt when interest rates, credit ratings and credit spreads are stochastic. The Journal of Financial Engineering 5: 161–98. [Google Scholar]
- Degryse, Hans, and Patrick Van Cayseele. 2000. Relationship lending within a bank-based system: Evidence from European small business data. Journal of Financial Intermediation 9: 90–109. [Google Scholar] [CrossRef]
- Dietsch, Michel, and Jöel Petey. 2004. Should SME exposures be treated as retail or corporate exposures? A comparative analysis of default probabilities and asset correlations in French and German SMEs. Journal of Banking & Finance 28: 773–88. [Google Scholar]
- Elsas, Ralf, and Jan Pieter Krahnen. 1998. Is relationship lending special? Evidence from credit-file data in Germany. Journal of Banking & Finance 22: 1283–316. [Google Scholar]
- Fei, Fei, Ana-Maria Fuertes, and Elena Kalotychou. 2012. Credit Rating Migration Risk and Business Cycles. Journal of Business Finance and Accounting 39: 229–63. [Google Scholar] [CrossRef]
- Ferretti, Camilla, and Piero Ganugi. 2013. A new mobility index for transition matrices. Statistical Methods and Applications 2: 403–25. [Google Scholar] [CrossRef]
- Figlewski, Stephen, Halina Frydman, and Weijian Liang. 2006. Modeling the Effect of Macroeconomic Factors on Corporate Default and Credit Rating Transitions. Available online: http://dx.doi.org/10.2139/ssrn.934438 (accessed on 29 October 2018).
- Fougère, Denis, and Thierry Kamionka. 2003. Bayesian inference for the Mover-Stayer model of continuous time. Journal of Applied Economics 18: 697–723. [Google Scholar] [CrossRef]
- Frydman, Halina, and Ashay Kadam. 2002. Estimation in the continuous time Mover Stayer model with an application to bond rating migration. Applied Stochastic Models in Business and Industry 20: 155–70. [Google Scholar] [CrossRef]
- Frydman, Halina, and Anna Matuszyk. 2018. Estimation and status prediction in a discrete Mover-Stayer model with covariate effects on stayers probability. Applied Stochastic Models in Business and Industry 34: 196–205. [Google Scholar] [CrossRef]
- Frydman, Halina, Jarl G. Kallberg, and Duen-Li Kao. 1985. Testing the adequacy of Markov Chain and Mover-Stayer models as representation of credit behavior. Operations Research 33: 1203–14. [Google Scholar] [CrossRef]
- Frydman, Halina, Anna Matuszyk, Chang Li, and Weicheng Zhu. 2019. Mover Stayer model with covariate effects on stayer’s probability and mover’s transitions. Applied Stochastic Models in Business and Industry 35: 1171–84. [Google Scholar] [CrossRef]
- Fuertes, Ana-Maria, and Elena Kalotychou. 2007. On sovereign credit migration: A study of alternative estimators and rating dynamics. Computational Statistics & Data Analysis 51: 3448–69. [Google Scholar]
- Gabbi, Giampaolo, and Richard Levich. 2019. Controlling risks to ensure financial stability and reducing volatility. Journal of International Financial Management and Accounting 30: 183–87. [Google Scholar] [CrossRef]
- Gabbi, Giampaolo, and Andrea Sironi. 2005. Which factors affect corporate bonds pricing? Empirical evidence from eurobonds primary market spreads. The European Journal of Finance 11: 59–74. [Google Scholar] [CrossRef]
- Gabbi, Giampaolo, and Pietro Vozzella. 2013. Asset Correlation and Bank Capital Adequacy. European Journal of Finance 19: 55–74. [Google Scholar] [CrossRef]
- Gabbi, Giampaolo, Matthias Massimo, and Giammarino Michele. 2019. Modeling Hard and Soft Facts for SMEs. Some International Evidence. Journal of International Financial Management and Accounting 30: 203–22. [Google Scholar]
- Golub, Gene, and Charles F. Van Loan. 1996. Matrix Computation, 3rd ed. Baltimore: Johns Hopkins University Press. [Google Scholar]
- Gómez-González, José E., and Nicholas M. Kiefer. 2009. Evidence of non-Markovian behavior in the process of bank rating migrations. Cuadernos de Economia Latin American Journal of Economics 46: 33–50. [Google Scholar] [CrossRef]
- Grimmett, Geoffrey, Geoffrey R. Grimmett, and David Stirzaker. 1992. Probability and random Processes. Oxford: Clarendon Press. [Google Scholar]
- Harhoff, Dietmar, and Timm Körting. 1998. Lending relationships in Germany–Empirical evidence from survey data. Journal of Banking & Finance 22: 1317–53. [Google Scholar]
- Israel, Robert, Jeffrey S. Rosenthal, and Jason Z. Wei. 2001. Finding generators for Markov Chains via empirical transition matrices, with application to credit ratings. Mathematical Finance 11: 245–65. [Google Scholar] [CrossRef]
- Ivashina, Victoria. 2009. Asymmetric information effects on loan spreads. Journal of Financial Economics 92: 300–19. [Google Scholar] [CrossRef]
- Jarrow, Robert A., David Lando, and Stuart M. Turnbull. 1997. A Markov model for the term structure of credit risk spreads. Review of Financial Studies 10: 481–523. [Google Scholar] [CrossRef]
- Kremer, Alexander, and Rafael Weißbach. 2013. Consistent estimation for discretely observed Markov jump processes with an absorbing state. Statistical Papers 54: 993–1007. [Google Scholar] [CrossRef]
- Lando, David. 1998. On Cox processes and credit risky securities. Review of Derivatives Research 2: 99–120. [Google Scholar] [CrossRef]
- Lando, David, and Torben M. Skødeberg. 2002. Analyzing rating transitions and rating drift with continuous observations. Journal of Banking and Finance 26: 423–44. [Google Scholar] [CrossRef]
- Lin, Chen, Yue Ma, Paul Malatesta, and Yuhai Xuan. 2011. Ownership structure and the cost of corporate borrowing. Journal of Financial Economics 100: 1–23. [Google Scholar] [CrossRef]
- Lucas, Douglas J., and John G. Lonski. 1992. Changes in corporate credit quality 1970–1990. The Journal of Fixed Income 1: 7–14. [Google Scholar] [CrossRef]
- Nickell, Pamela, William Perraudin, and Simone Varotto. 2000. Stability of ratings transitions. Journal of Banking and Finance 24: 203–27. [Google Scholar] [CrossRef]
- Petersen, Mitchell A., and Raghuram G. Rajan. 1994. The benefits of lending relationships: Evidence from small business data. The Journal of Finance 49: 3–37. [Google Scholar] [CrossRef]
- Petersen, Mitchell A., and Raghuram G. Rajan. 1995. The effect of credit market competition on lending relationships. The Quarterly Journal of Economics 110: 407–43. [Google Scholar] [CrossRef]
- Shorrocks, Anthony F. 1978. The measurement of Mobility. Econometrica 46: 1013–24. [Google Scholar] [CrossRef]
| 1 | In Fei et al. (2012) data are derived from the S&P CreditPro 7.7 database. In Dietsch and Petey (2004), relating to the empirical studies on asset correlation, data were collected from the internal rating system of Coface for France and Creditform for Germany. Similarly, in Bandyopadhyay et al. (2007), results were based on CRISIL’s (a lending credit rating agency in India) annual ratings of long-term bonds. For more details on the process we applied to compute PD, see (Gabbi and Vozzella 2013). |
| 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | absolute | 19,265 | 17,950 | 12,433 | 13,136 | 13,194 | 13,298 | 13,367 | 13,136 | 13,565 | 16,860 | 17,297 | 16,892 |
| relative | 43.6% | 40.6% | 28.1% | 29.7% | 29.9% | 30.1% | 30.2% | 29.7% | 30.7% | 38.2% | 39.1% | 38.2% | |
| B | absolute | 7804 | 7906 | 9457 | 9346 | 9275 | 9208 | 9152 | 8940 | 8709 | 8581 | 7954 | 8044 |
| relative | 17.7% | 17.9% | 21.4% | 21.1% | 21.0% | 20.8% | 20.7% | 20.2% | 19.7% | 19.4% | 18.0% | 18.2% | |
| C | absolute | 8313 | 8715 | 10679 | 9930 | 9571 | 9508 | 9490 | 9500 | 9212 | 7431 | 6896 | 6984 |
| relative | 18.8% | 19.7% | 24.2% | 22.5% | 21.7% | 21.5% | 21.5% | 21.5% | 20.8% | 16.8% | 15.6% | 15.8% | |
| D | absolute | 7268 | 7551 | 9188 | 8579 | 8471 | 8129 | 7764 | 7804 | 7373 | 5482 | 5506 | 5601 |
| relative | 16.4% | 17.1% | 20.8% | 19.4% | 19.2% | 18.4% | 17.6% | 17.7% | 16.7% | 12.4% | 12.5% | 12.7% | |
| E | absolute | 975 | 966 | 1062 | 1168 | 1135 | 973 | 950 | 956 | 1012 | 965 | 1220 | 1186 |
| relative | 2.2% | 2.2% | 2.4% | 2.6% | 2.6% | 2.2% | 2.1% | 2.2% | 2.3% | 2.2% | 2.8% | 2.7% | |
| F | absolute | 567 | 468 | 147 | 270 | 290 | 250 | 263 | 281 | 201 | 317 | 303 | 414 |
| relative | 1.3% | 1.1% | 0.3% | 0.6% | 0.7% | 0.6% | 0.6% | 0.6% | 0.5% | 0.7% | 0.7% | 0.9% | |
| Default | absolute | 0 | 636 | 1226 | 1763 | 2256 | 2826 | 3206 | 3575 | 4120 | 4556 | 5016 | 5071 |
| relative | 0.0% | 1.4% | 2.8% | 4.0% | 5.1% | 6.4% | 7.3% | 8.1% | 9.3% | 10.3% | 11.4% | 11.5% | |
| TOT | 44,192 | 44,192 | 44,192 | 44,192 | 44,192 | 44,192 | 44,192 | 44,192 | 44,192 | 44,192 | 44,192 | 44,192 |
| Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | Year 6 | Year 7 | Year 8 | Year 9 | Year 10 | Year 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel 1: Failed firms over time by rating class | |||||||||||
| A | 0.0055 | 0.0045 | 0.0020 | 0.0013 | 0.0015 | 0.0011 | 0.0004 | 0.0014 | 0.0010 | 0.0008 | 0.0002 |
| B | 0.0083 | 0.0072 | 0.0027 | 0.0031 | 0.0049 | 0.0025 | 0.0027 | 0.0044 | 0.0032 | 0.0044 | 0.0005 |
| C | 0.0123 | 0.0114 | 0.0124 | 0.0088 | 0.0101 | 0.0074 | 0.0060 | 0.0107 | 0.0100 | 0.0100 | 0.0013 |
| D | 0.0359 | 0.0335 | 0.0290 | 0.0277 | 0.0290 | 0.0201 | 0.0222 | 0.0237 | 0.0308 | 0.0275 | 0.0047 |
| E | 0.0615 | 0.0621 | 0.0593 | 0.0634 | 0.0793 | 0.0586 | 0.0674 | 0.0868 | 0.0445 | 0.0736 | 0.0082 |
| F | 0.0741 | 0.0855 | 0.1701 | 0.1778 | 0.2483 | 0.2120 | 0.1711 | 0.4199 | 0.1493 | 0.3565 | 0.0099 |
| Panel 2: Firms leaving their states (up and downgrading) | |||||||||||
| A | 0.2309 | 0.5871 | 0.1226 | 0.1411 | 0.1217 | 0.1186 | 0.1282 | 0.0986 | 0.0616 | 0.0861 | 0.1024 |
| B | 0.4231 | 0.3368 | 0.3956 | 0.3808 | 0.3556 | 0.3502 | 0.3596 | 0.3656 | 0.4881 | 0.4192 | 0.3306 |
| C | 0.3920 | 0.2997 | 0.4360 | 0.4037 | 0.3644 | 0.3552 | 0.3399 | 0.3669 | 0.6303 | 0.4427 | 0.3475 |
| D | 0.3361 | 0.2512 | 0.3537 | 0.3146 | 0.3147 | 0.3105 | 0.2727 | 0.3134 | 0.6240 | 0.3320 | 0.2933 |
| E | 0.6190 | 0.5169 | 0.5394 | 0.6352 | 0.7657 | 0.6137 | 0.5554 | 0.5247 | 0.6363 | 0.4369 | 0.5919 |
| F | 0.9573 | 2.8299 | 0.3667 | 0.6724 | 0.8200 | 0.5817 | 0.5409 | 1.1045 | 0.3785 | 0.7690 | 0.4251 |
| Panel 3: Firms never moving from their starting state (“potential stayers”) | |||||||||||
| A | B | C | D | E | F | ||||||
| 0.3009 | 0.0160 | 0.0206 | 0.0527 | 0.0308 | 0.0000 | ||||||
| Panel 1: Estimated generating matrix for the MC model | |||||||
| A | B | C | D | E | F | Default | |
| A | −0.1853 | 0.1376 | 0.0195 | 0.0213 | 0.0022 | 0.0037 | 0.0010 |
| Se | 0.0012 | 0.0012 | 0.0007 | 0.0005 | 0.0002 | 0.0002 | 0.0001 |
| B | 0.2532 | −0.5433 | 0.2776 | 0.0000 | 0.0063 | 0.0031 | 0.0030 |
| Se | 0.0020 | 0.0031 | 0.0024 | 0.0000 | 0.0005 | 0.0004 | 0.0003 |
| C | 0.0081 | 0.2934 | −0.5676 | 0.2461 | 0.0080 | 0.0048 | 0.0072 |
| Se | 0.0009 | 0.0025 | 0.0032 | 0.0022 | 0.0008 | 0.0005 | 0.0004 |
| D | 0.0182 | 0.0066 | 0.2893 | −0.4541 | 0.1010 | 0.0124 | 0.0267 |
| Se | 0.0007 | 0.0012 | 0.0026 | 0.0030 | 0.0018 | 0.0009 | 0.0007 |
| E | 0.0276 | 0.0360 | 0.0272 | 0.6555 | −0.9634 | 0.1525 | 0.0646 |
| Se | 0.0030 | 0.0038 | 0.0061 | 0.0117 | 0.0129 | 0.0072 | 0.0037 |
| F | 0.1762 | 0.0955 | 0.1402 | 0.2190 | 0.3870 | −1.3138 | 0.2959 |
| Se | 0.0113 | 0.0111 | 0.0135 | 0.0179 | 0.0211 | 0.0301 | 0.0131 |
| Default | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | −0.0002 |
| Se | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| probability of embeddability = 1 | |||||||
| number of possible models (aliasing) = 1 | |||||||
| Panel 2: Estimated generating matrix and probability to be a Stayers for the MS model | |||||||
| A | B | C | D | E | F | Default | |
| A | −0.2978 | 0.2223 | 0.0300 | 0.0346 | 0.0034 | 0.0060 | 0.0016 |
| Se | 0.0023 | 0.0021 | 0.0011 | 0.0008 | 0.0004 | 0.0004 | 0.0002 |
| B | 0.2721 | −0.5661 | 0.2818 | 0.0000 | 0.0065 | 0.0027 | 0.0030 |
| Se | 0.0022 | 0.0033 | 0.0024 | 0.0000 | 0.0005 | 0.0004 | 0.0003 |
| C | 0.0071 | 0.3015 | −0.5828 | 0.2550 | 0.0072 | 0.0048 | 0.0072 |
| Se | 0.0010 | 0.0026 | 0.0033 | 0.0023 | 0.0009 | 0.0005 | 0.0004 |
| D | 0.0203 | 0.0047 | 0.3075 | −0.4824 | 0.1093 | 0.0125 | 0.0280 |
| Se | 0.0008 | 0.0013 | 0.0029 | 0.0034 | 0.0020 | 0.0009 | 0.0008 |
| E | 0.0297 | 0.0372 | 0.0209 | 0.7006 | −1.0165 | 0.1611 | 0.0670 |
| Se | 0.0034 | 0.0041 | 0.0063 | 0.0131 | 0.0141 | 0.0075 | 0.0039 |
| F | 0.1876 | 0.0855 | 0.1392 | 0.2122 | 0.3971 | −1.3175 | 0.2959 |
| Se | 0.0122 | 0.0110 | 0.0138 | 0.0190 | 0.0221 | 0.0305 | 0.0135 |
| Default | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | −0.0002 |
| Se | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Stayers | 0.2625 | 0.0115 | 0.0167 | 0.0424 | 0.0318 | 0.0018 | 0.5015 |
| Se | 0.0036 | 0.0014 | 0.0016 | 0.0027 | 0.0056 | 0.0019 | 0.2884 |
| probability of embeddability = 1 | |||||||
| number of possible models (aliasing) = 1 | |||||||
| Panel 1: Estimated annual transition matrixfor the MC | |||||||
| A | B | C | D | E | F | Default | |
| A | 84.46% | 10.02% | 2.89% | 1.94% | 0.27% | 0.22% | 0.19% |
| B | 18.13% | 61.68% | 16.67% | 2.43% | 0.49% | 0.22% | 0.40% |
| C | 3.24% | 17.52% | 61.28% | 15.53% | 1.15% | 0.35% | 0.93% |
| D | 1.92% | 3.24% | 18.23% | 67.70% | 5.36% | 0.91% | 2.64% |
| E | 3.02% | 3.12% | 7.22% | 34.67% | 40.79% | 5.22% | 5.96% |
| F | 10.14% | 6.17% | 8.93% | 15.97% | 13.32% | 27.92% | 17.54% |
| Default | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 100.00% |
| Panel 2: Estimated annual transition matrixfor the MS | |||||||
| A | B | C | D | E | F | Default | |
| A | 82.62% | 11.19% | 3.22% | 2.19% | 0.30% | 0.25% | 0.22% |
| B | 18.04% | 61.63% | 16.62% | 2.61% | 0.49% | 0.22% | 0.40% |
| C | 3.23% | 17.48% | 61.33% | 15.54% | 1.15% | 0.35% | 0.93% |
| D | 1.92% | 3.24% | 18.19% | 67.76% | 5.36% | 0.91% | 2.63% |
| E | 3.01% | 3.11% | 7.21% | 34.56% | 40.98% | 5.20% | 5.93% |
| F | 10.11% | 6.16% | 8.92% | 15.95% | 13.29% | 28.06% | 17.51% |
| Default | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 100.00% |
| Panel 1: Estimated distribution for the MC model | |||||||||||
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | |
| A | 41.14% | 39.32% | 37.91% | 36.77% | 35.82% | 35.01% | 34.31% | 33.68% | 33.11% | 32.58% | 32.10% |
| B | 19.24% | 19.97% | 20.27% | 20.35% | 20.30% | 20.18% | 20.02% | 19.83% | 19.64% | 19.43% | 19.23% |
| C | 19.00% | 19.26% | 19.45% | 19.57% | 19.61% | 19.59% | 19.53% | 19.43% | 19.30% | 19.16% | 19.01% |
| D | 16.30% | 16.21% | 16.15% | 16.11% | 16.07% | 16.03% | 15.97% | 15.90% | 15.82% | 15.72% | 15.61% |
| E | 2.37% | 2.38% | 2.36% | 2.34% | 2.33% | 2.32% | 2.31% | 2.30% | 2.29% | 2.27% | 2.26% |
| F | 0.82% | 0.70% | 0.67% | 0.65% | 0.65% | 0.64% | 0.64% | 0.63% | 0.63% | 0.62% | 0.62% |
| Default | 1.12% | 2.17% | 3.19% | 4.21% | 5.22% | 6.23% | 7.23% | 8.23% | 9.22% | 10.21% | 11.18% |
| Panel 2: Estimated distribution for the MS model | |||||||||||
| A | 40.32% | 38.17% | 36.68% | 35.58% | 34.74% | 34.06% | 33.50% | 33.01% | 32.59% | 32.21% | 31.85% |
| B | 19.73% | 20.54% | 20.77% | 20.72% | 20.55% | 20.32% | 20.07% | 19.80% | 19.54% | 19.27% | 19.01% |
| C | 19.14% | 19.52% | 19.79% | 19.92% | 19.94% | 19.88% | 19.77% | 19.62% | 19.44% | 19.25% | 19.04% |
| D | 16.45% | 16.46% | 16.46% | 16.46% | 16.44% | 16.40% | 16.33% | 16.24% | 16.12% | 16.00% | 15.85% |
| E | 2.39% | 2.40% | 2.39% | 2.38% | 2.37% | 2.36% | 2.35% | 2.34% | 2.32% | 2.30% | 2.28% |
| F | 0.84% | 0.72% | 0.68% | 0.67% | 0.66% | 0.65% | 0.65% | 0.64% | 0.63% | 0.63% | 0.62% |
| Default | 1.13% | 2.19% | 3.23% | 4.27% | 5.30% | 6.32% | 7.34% | 8.35% | 9.35% | 10.35% | 11.33% |
| Transition Matrix Estimation Model | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MC | 3.58 | 25.49 | 18.21 | 15.36 | 12.80 | 10.62 | 10.36 | 6.93 | 12.94 | 16.22 | 14.75 |
| MS | 4.07 | 23.14 | 15.64 | 12.85 | 10.48 | 8.57 | 8.59 | 5.51 | 14.07 | 16.99 | 15.29 |
| Error gap | −0.49 | 2.35 | 2.57 | 2.51 | 2.32 | 2.05 | 1.77 | 1.42 | −1.13 | −0.77 | −0.54 |
| A | B | C | D | E | F | Default | |
|---|---|---|---|---|---|---|---|
| MC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 100.00 |
| MS | 11.78 | 0.52 | 0.64 | 0.97 | 0.11 | 0.02 | 85.96 |
| Time | 1 | 2 | 3 | 4 | 5 | 10 | 20 | 50 | 100 | 500 | 1000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | MC | 0.19 | 0.53 | 0.98 | 1.53 | 2.15 | 6.1 | 15.33 | 39.28 | 65.18 | 99.59 | 100 |
| MS | 0.22 | 0.58 | 1.05 | 1.6 | 2.23 | 5.94 | 13.94 | 33.24 | 52.61 | 73.64 | 73.75 | |
| B | MC | 0.4 | 0.96 | 1.66 | 2.47 | 3.34 | 8.15 | 17.69 | 41.03 | 66.19 | 99.6 | 100 |
| MS | 0.4 | 0.99 | 1.75 | 2.63 | 3.6 | 9.01 | 19.8 | 45.33 | 70.92 | 98.7 | 98.85 | |
| C | MC | 0.93 | 2.11 | 3.4 | 4.71 | 6.01 | 11.91 | 21.62 | 43.91 | 67.84 | 99.62 | 100 |
| MS | 0.93 | 2.13 | 3.44 | 4.79 | 6.13 | 12.35 | 23.01 | 47.36 | 71.73 | 98.19 | 98.33 | |
| D | MC | 2.63 | 5.08 | 7.27 | 9.2 | 10.93 | 17.6 | 27.07 | 47.86 | 70.1 | 99.65 | 100 |
| MS | 2.63 | 5.05 | 7.2 | 9.1 | 10.79 | 17.44 | 27.39 | 49.51 | 71.63 | 95.63 | 95.77 | |
| E | MC | 5.96 | 10.3 | 13.36 | 15.64 | 17.47 | 23.88 | 32.65 | 51.85 | 72.39 | 99.68 | 100 |
| MS | 5.93 | 10.2 | 13.19 | 15.42 | 17.23 | 23.67 | 32.99 | 53.63 | 74.28 | 96.68 | 96.81 | |
| F | MC | 17.53 | 23.77 | 26.65 | 28.42 | 29.75 | 34.54 | 41.8 | 58.36 | 76.12 | 99.72 | 100 |
| MS | 17.51 | 23.79 | 26.73 | 28.55 | 29.94 | 35.07 | 43.15 | 61.47 | 79.81 | 99.71 | 99.82 |
| Panel 1: Mobility indices by starting rating (and global), for the annual estimated transition matrices(percentages) | |||||||
| Rating | A | B | C | D | E | F | Default |
| −6.32 | −1.65 | 0.68 | 5.35 | 13.76 | 25.98 | 0 | |
| 23.56 | 38.82 | 39.33 | 33.66 | 60.96 | 72.07 | 0 | |
| −4.66 | −1.63 | 0.67 | 5.12 | 13.32 | 25.93 | 0 | |
| 17.38 | 38.37 | 38.68 | 32.24 | 59.03 | 71.94 | 0 | |
| Global Mobility Indices | −2.54 | 38.34 | −1.67 | 36.8 | |||
| Panel 2: Mobility indices by starting rating (and global), for the 10-years estimated transition matrices(percentages) | |||||||
| Rating | A | B | C | D | E | F | Default |
| −29.36 | −17.42 | −3.11 | 18.43 | 31.89 | 37.23 | 0 | |
| 72.20 | 77.06 | 77.56 | 80.74 | 97.32 | 99.42 | 0 | |
| −21.65 | −17.21 | −3.06 | 17.65 | 30.88 | 37.17 | 0 | |
| 53.25 | 76.17 | 76.28 | 77.32 | 94.24 | 99.25 | 0 | |
| Global Mobility Indices | −16.71 | 72.04 | −12.56 | 68.07 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferretti, C.; Gabbi, G.; Ganugi, P.; Sist, F.; Vozzella, P. Credit Risk Migration and Economic Cycles. Risks 2019, 7, 109. https://doi.org/10.3390/risks7040109
Ferretti C, Gabbi G, Ganugi P, Sist F, Vozzella P. Credit Risk Migration and Economic Cycles. Risks. 2019; 7(4):109. https://doi.org/10.3390/risks7040109
Chicago/Turabian StyleFerretti, Camilla, Giampaolo Gabbi, Piero Ganugi, Federica Sist, and Pietro Vozzella. 2019. "Credit Risk Migration and Economic Cycles" Risks 7, no. 4: 109. https://doi.org/10.3390/risks7040109
APA StyleFerretti, C., Gabbi, G., Ganugi, P., Sist, F., & Vozzella, P. (2019). Credit Risk Migration and Economic Cycles. Risks, 7(4), 109. https://doi.org/10.3390/risks7040109





