Option Implied Stock Buy-Side and Sell-Side Market Depths
Abstract
1. Introduction
2. Model
2.1. The Economic Foundations
2.2. Parsimonious Stochastic Volatility-Liquidity Models
2.2.1. A stochastic Liquidity Model (SL)
2.2.2. A Stochastic Volatility-Liquidity Model (SVL)
2.2.3. A Stochastic Volatility-Liquidity Model with the Leverage Effect (SVLL)
2.3. Short Summary
2.4. Extension
2.5. Generalization
2.6. Valuation
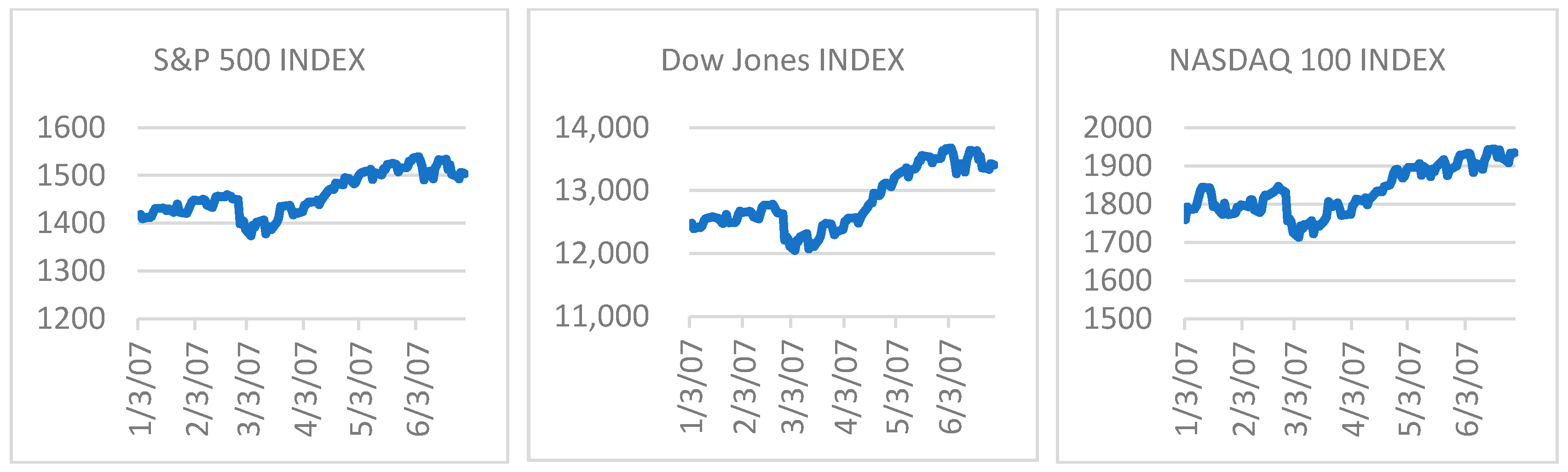
3. Data and Methodology
3.1. Data Description
3.2. Methodology
3.2.1. Estimation for Illiquidity in Intraday Markets
3.2.2. Estimation for the Behavior of Statistical Price Process
3.2.3. Calibration of Option Models
4. Results
4.1. Estimates in Intraday Markets
4.2. Estimates in Daily Markets
4.3. Calibration in Index Option Markets
4.4. Event Days
4.5. Market-to-Model
4.6. Comparison between Two Events
4.7. Short Summary
4.8. Implication for Asymmetric Liquidity
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Abudy, Menachem, and Yehuda Izhakian. 2013. Pricing stock options with stochastic interest rate. International Journal of Portfolio Analysis and Management 1: 250–77. [Google Scholar] [CrossRef]
- Acharya, Viral, and Lasse Heje Pedersen. 2005. Asset pricing with liquidity risk. Journal of Financial Economics 77: 375–410. [Google Scholar] [CrossRef]
- Amihud, Yakov, Haim Mendelson, and Lasse Heje Pedersen. 2013. Market Liquidity: Asset Pricing, Risk, and Crises. Cambridge: Cambridge University Press. [Google Scholar]
- Ane, Thierry, and Hélyette Geman. 2000. Order flow, transaction clock and normality of asset returns. Journal of Finance 55: 2259–84. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, Charles Cao, and Zhiwu Chen. 1997. Empirical performance of alternative option pricing models. Journal of Finance 52: 2003–49. [Google Scholar] [CrossRef]
- Black, Fischer. 1976. Studies of stock price volatility changes. In Proceedings of the 1976 Meetings of the Business and Economic Statistics Section. Washington: American Statistical Association, pp. 177–81. [Google Scholar]
- Brennan, Michael, and Avanidhar Subrahmanyam. 1996. Market microstructure and asset pricing: on the compensation for illiquidity in stock returns. Journal of Financial Economics 41: 441–64. [Google Scholar] [CrossRef]
- Brennan, Michael, Tarun Chordia, Avanidhar Subrahmanyam, and Qing Dong. 2012. Sell-order Liquidity and the Cross-Section of Expected Stock Returns. Journal of Financial Economics 105: 523–41. [Google Scholar] [CrossRef]
- Carr, Peter, and Dilip B. Madan. 1999. Option valuation using the fast Fourier transform. Journal of Computational Finance 2: 61–73. [Google Scholar] [CrossRef]
- Carr, Peter, Hélyette Geman, Dilip B. Madan, and Marc Yor. 2003. Stochastic volatility for Levy processes. Mathematical Finance 13: 345–82. [Google Scholar] [CrossRef]
- Cetin, Umut, Robert A. Jarrow, and Philip Protter. 2004. Liquidity risk and arbitrage pricing theory. Finance and Stochastics 8: 311–41. [Google Scholar] [CrossRef]
- Cetin, Umut, Robert A. Jarrow, Philip Protter, and M. Warachka. 2006. Pricing options in an extended Black Scholes economy with illiquidity: theory and empirical evidence. The Review of Financial Studies 19: 493–529. [Google Scholar] [CrossRef]
- Chacko, George C., Jakub W. Jurek, and Erik Stafford. 2008. The price of immediacy. The Journal of Finance 63: 1253–90. [Google Scholar] [CrossRef]
- Chang, Carolyn W., Jack S. K. Chang, and Kian Guan Lim. 1998. Information-time option pricing: Theory and empirical evidence. Journal of Financial Economics 48: 211–42. [Google Scholar] [CrossRef]
- Christoffersen, Peter, Ruslan Goyenko, Kris Jacobs, and Mehdi Karoui. 2018. Illiquidity premia in the equity options market. The Review of Financial Studies 31: 811–51. [Google Scholar] [CrossRef]
- Clark, Peter K. 1973. A subordinated stochastic process model with finite variance for speculative prices. Econometrica 41: 135–55. [Google Scholar] [CrossRef]
- Easley, David, Soeren Hvidkjaer, and Maureen O’Hara. 2002. Is information risk a determinant of asset returns? Journal of Finance 57: 2185–221. [Google Scholar] [CrossRef]
- Engle, Robert. 2004. Risk and volatility: Econometric models and financial practice. The American Economic Review 94: 405–20. [Google Scholar] [CrossRef]
- Gradshetyn, Izrail Solomonovich, and Iosif Moiseevich Ryzhik. 1980. Table of Integrals, Series, and Products. New York: Academic Press. [Google Scholar]
- Harris, Larry. 2003. Trading and Exchanges: Market Microstructure for Practitioners. New York: Oxford University Press. [Google Scholar]
- Hasbrouck, Joel. 2007. Empirical Market Microstructure: The Institutions, Economics, and Econometrics of Securities Trading. New York: Oxford University Press. [Google Scholar]
- Jagannathan, Raj. 2008. A class of asset pricing models governed by subordinate processes that signal economic shocks. Journal of Economic Dynamics and Control 32: 3820–46. [Google Scholar] [CrossRef]
- Kyle, Albert S. 1985. Continuous auctions and insider trading. Econometrica 53: 1315–36. [Google Scholar] [CrossRef]
- Lee, Charles M., and Mark J. Ready. 1991. Inferring trade direction from intraday data. Journal of Finance 46: 733–46. [Google Scholar] [CrossRef]
- Luciano, Elisa, and Wim Schoutens. 2006. A multivariate jump-driven financial asset model. Quantitative Finance 6: 385–402. [Google Scholar] [CrossRef]
- Madan, Dilip B., Peter Carr, and Eric C. Chang. 1998. The variance gamma process and option pricing. European Finance Review 2: 79–105. [Google Scholar] [CrossRef]
- Pastor, Ľuboš, and Robert F. Stambaugh. 2003. Liquidity risk and expected stock returns. Journal of Political Economy 111: 642–85. [Google Scholar] [CrossRef]
- Schoutens, Wim. 2003. Levy Processes in Finance: Pricing Financial Derivatives. West Sussex: John Wiley & Sons Ltd. [Google Scholar]
- Watanabe, Masahiro. 2007. A Model of Stochastic Liquidity. Yale ICF Working Paper No. 03-18; EFA 2003 Glasgow Annual Conference Paper. Available online: https://ssrn.com/abstract=413983 (accessed on 26 October 2019).
| 1 | I also run the following regression with fixed cost and the conclusion does not change: |
| 2 | The results are verified using the Nelder-Mead simplex approach as well as the simulated annealing method. |
| Company Name | ||
|---|---|---|
| IBM | 0.0138 (9.45) | 0.1414 (50.61) |
| KO | 0.0320 (13.25) | 0.2064 (20.64) |
| FDX | 0.0433 (11.81) | 0.1859 (17.34) |
| BKS | 0.0994 (15.46) | 0.1814 (11.25) |
| BA | 0.0270 (20.27) | 0.2722 (38.90) |
| DIS | 0.0447 (26.16) | 0.2583 (45.71) |
| Parameter Estimated | IBM | KO |
|---|---|---|
| −0.0670 (0.0003) | −0.0871 (0.0003) | |
| 0.1000 (0.0003) | 0.1086 (0.0003) | |
| 2.6168 (0.0001) | 1.9070 (0.0002) | |
| m | −0.0652 (0.0003) | −0.3190 (0.0003) |
| Implied / | 0.0447/0.1118 | 0.0447/0.1318 |
| Log likelihood value | 103.9537 | 158.2823 |
| Parameter estimated | FDX | BKS |
| −0.2178 (0.0003) | 0.1615 (0.0001) | |
| 0.1615 (0.0003) | 0.1021 (0.0001) | |
| 2.3168 (0.0002) | 3.4623 (0.0000) | |
| m | −0.1850 (0.0003) | 0.2849 (0.0001) |
| Implied / | 0.0489/0.2667 | 0.1891/0.0276 |
| Log likelihood value | 107.1581 | 87.2402 |
| Parameter estimated | BA | DIS |
| −0.0084 (0.0002) | 0.0794 (0.0003) | |
| 0.0512 (0.0001) | 0.2296 (0.0003) | |
| 2.1419 (0.0000) | 1.6606 (0.0001) | |
| m | 0.0252 (0.0002) | 0.1951 (0.0003) |
| Implied / | 0.0322/0.0406 | 0.2068/0.1274 |
| Log likelihood value | 136.8132 | 98.7784 |
| Model | Index | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|---|
| BS | SPX | 0.1287 | 9.8557 | ||||||
| SL | SPX | 0.0920 | 0.0354 | 0.1194 | 9.7068 | ||||
| SVL | SPX | 0.0718 | 2.0205 | 0.0930 | 2.0032 | 0.0283 | 0.0912 | 7.6090 | |
| SVLL | SPX | 0.0131 | 1.6976 | 0.4792 | 0.6444 | −0.20 | 0.0017 | 0.0514 | 6.4715 |
| MSVLL | SPX | 0.0086 | 1.6019 | 0.7849 | 0.9085 | −0.18 | 0.0009 | 0.0430 | 7.7160 |
| DJX | 0.0089 | 2.4375 | 0.4602 | 0.4552 | −0.36 | 0.0006 | 0.0688 | ||
| NDX | 0.0198 | 0.4503 | 0.4895 | 0.4392 | −0.47 | 0.0041 | 0.0474 |
| Date|Index | |||||||
|---|---|---|---|---|---|---|---|
| 2/26 SPX | 3.0661 | 1.1183 | 1.1744 | 1.5414 | 0.8265 | −0.10 | |
| 2/26 DJX | 3.0661 | 0.0915 | 0.1441 | 1.5393 | 0.7729 | −0.13 | |
| 2/26 NDX | 3.0661 | 0.5553 | 0.5836 | 0.7651 | 1.1170 | −0.14 | |
| 2/27 SPX | 4.1101 | 0.0071 | 0.0033 | 0.0124 | 0.5539 | 0.9766 | −0.13 |
| 2/27 DJX | 4.1101 | 0.0525 | 0.0823 | 0.6733 | 0.6754 | −0.19 | |
| 2/27 NDX | 4.1101 | 0.0205 | 0.0230 | 0.0270 | 0.8568 | 0.6662 | −0.25 |
| 2/28 SPX | 2.8288 | 0.8360 | 0.8780 | 1.1523 | 0.0132 | 1.0733 | −0.12 |
| 2/28 DJX | 2.8288 | 0.0886 | 0.1347 | 1.2108 | 0.9183 | −0.14 | |
| 2/28 NDX | 2.8288 | 0.4334 | 0.4543 | 0.5979 | 0.1839 | 1.1247 | −0.16 |
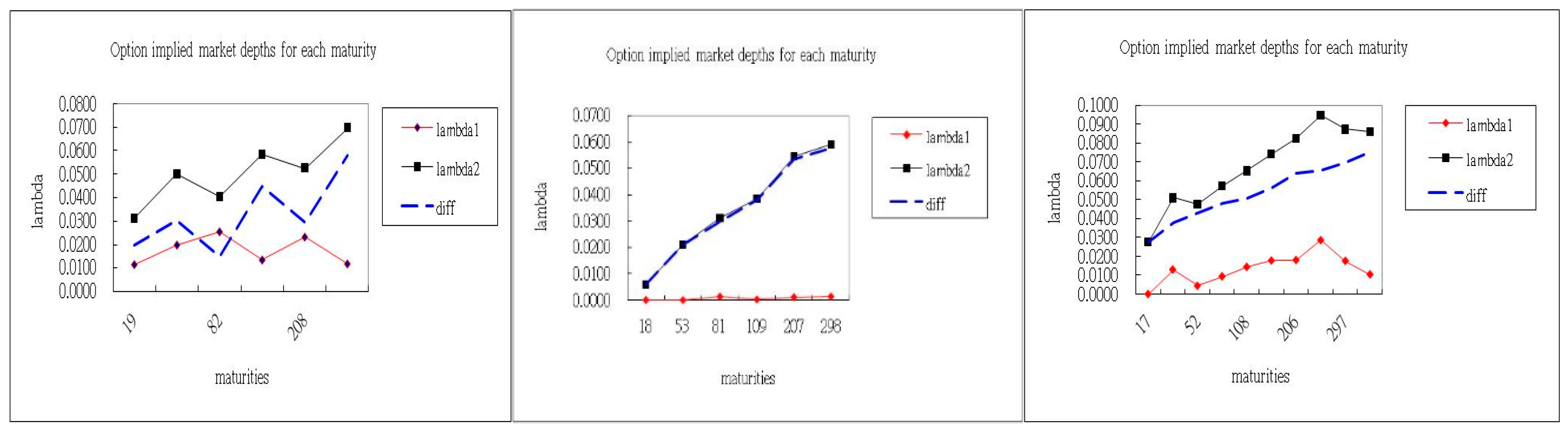
| Date | Maturity | RMSE | ARPE (%) | APE (%) | AAE | |||
|---|---|---|---|---|---|---|---|---|
| 10 September | 40 | 11.00 | 0.0317 | 0.0883 | 0.6963 | 9.05 | 0.99 | 0.5540 |
| 68 | 7.97 | 0.0349 | 0.0982 | 0.3794 | 6.02 | 0.92 | 0.3902 | |
| 103 | 5.50 | 0.0372 | 0.1158 | 0.2767 | 2.48 | 0.46 | 0.2910 | |
| 187 | 3.53 | 0.0457 | 0.1346 | 0.1668 | 0.78 | 0.27 | 0.1623 | |
| 285 | 2.77 | 0.0448 | 0.1476 | 0.2794 | 0.66 | 0.41 | 0.3139 | |
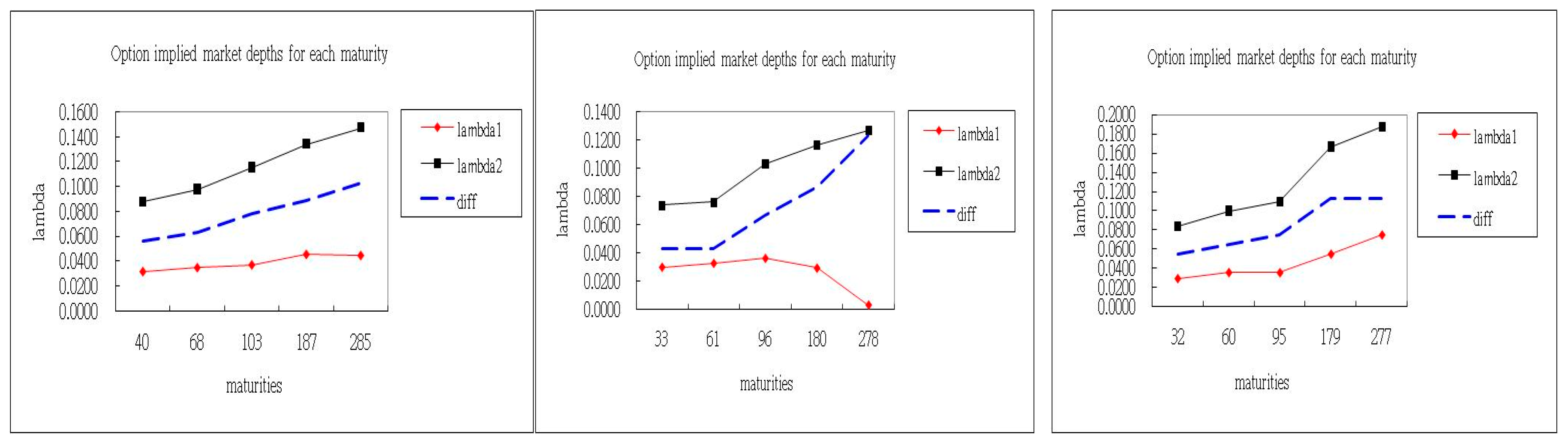
| 17 September | 33 | 22.31 | 0.0300 | 0.0740 | 0.2825 | 3.75 | 1.07 | 0.4280 |
| 61 | 15.98 | 0.0327 | 0.0763 | 0.1537 | 2.12 | 0.40 | 0.1939 | |
| 96 | 8.59 | 0.0362 | 0.1033 | 0.2641 | 1.79 | 0.93 | 0.5449 | |
| 180 | 5.99 | 0.0294 | 0.1167 | 0.2517 | 2.00 | 0.62 | 0.3708 | |
| 278 | 5.04 | 0.0035 | 0.1270 | 0.4307 | 1.59 | 1.13 | 0.9207 | |
| 18 September | 32 | 17.25 | 0.0288 | 0.0841 | 0.2171 | 4.03 | 0.64 | 0.2870 |
| 60 | 10.23 | 0.0352 | 0.1000 | 0.2137 | 3.37 | 0.54 | 0.3021 | |
| 95 | 7.72 | 0.0351 | 0.1096 | 0.3114 | 2.32 | 0.79 | 0.4279 | |
| 179 | 3.10 | 0.0546 | 0.1664 | 0.2564 | 1.76 | 0.71 | 0.3964 | |
| 277 | 2.16 | 0.0747 | 0.1869 | 0.3767 | 1.15 | 0.80 | 0.6142 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, F.-T. Option Implied Stock Buy-Side and Sell-Side Market Depths. Risks 2019, 7, 108. https://doi.org/10.3390/risks7040108
Tsai F-T. Option Implied Stock Buy-Side and Sell-Side Market Depths. Risks. 2019; 7(4):108. https://doi.org/10.3390/risks7040108
Chicago/Turabian StyleTsai, Feng-Tse. 2019. "Option Implied Stock Buy-Side and Sell-Side Market Depths" Risks 7, no. 4: 108. https://doi.org/10.3390/risks7040108
APA StyleTsai, F.-T. (2019). Option Implied Stock Buy-Side and Sell-Side Market Depths. Risks, 7(4), 108. https://doi.org/10.3390/risks7040108




