4.1. Data
We analyzed a North American database consisting of
claims occurred from 1 Januar 2004 to 31 December 2016. We therefore let
, the starting point, be 1 January 2004 meaning that all dates are expressed in number of years from this date. These claims are related to
general liability insurance policies for private individuals. We focus only on the accident benefits coverage that provides compensation if the insured is injured or killed in an auto accident. It also includes coverage for passengers and pedestrians involved in the accident. Claims involve one (
), two (
) or
parties (
) resulting in a total of
files in the database. Consequently, there is a possibility of dependence between some payments in the database. Nevertheless, we assume in this paper that all files are independent claims, and we postpone the analysis of this dependence. Thus, we analyze a portfolio of
independent claims that we denote by
. An example of the structure of the dataset is given in
Table A1 in
Appendix A.
The data are longitudinal, and each row of the database corresponds to a snapshot of a file. For each element in , a snapshot is taken at the end of every quarter, and we have information from the reporting date until 31 December 2016. Therefore, a claim is represented by a maximum of 52 rows. A line is added in the database even if there is no new information, i.e., it could be possible that two consecutive lines provide precisely the same information. During the training of our models, we do not consider these replicate rows because they do not provide any relevant information for the model.
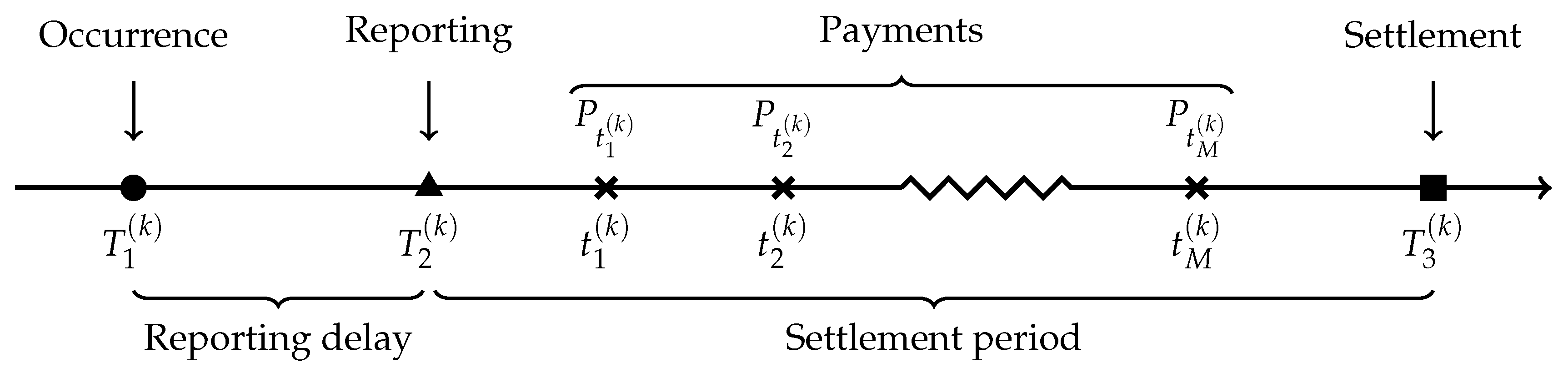
The information vector for claim k, at time t is given by . Therefore, the information matrix about the whole portfolio at time t is given by . Because of the discrete nature of our dataset, it contains information , where t is the number of years since .
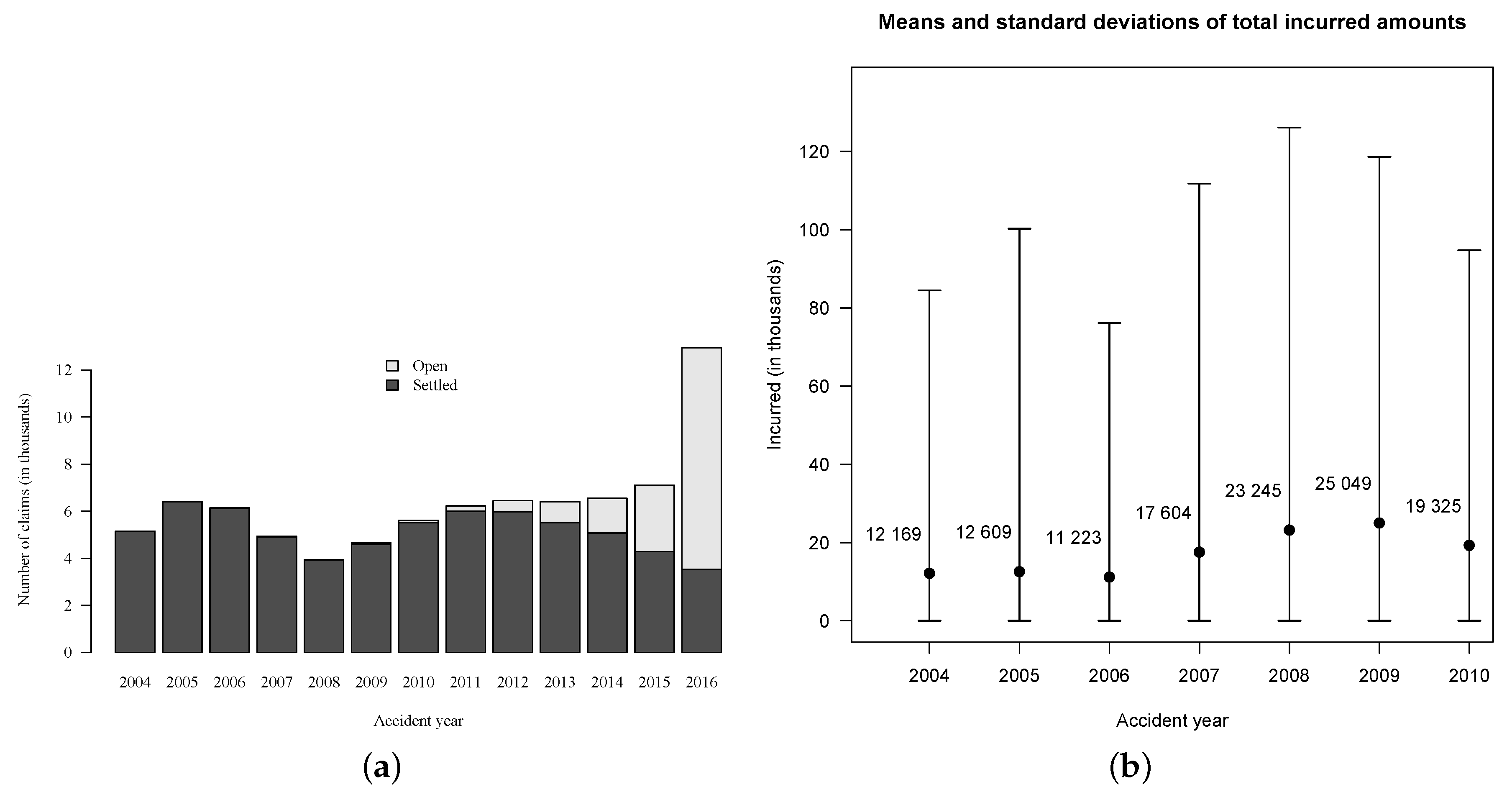
In order to validate models, we need to know how much has actually been paid for each claim. In portfolio
, the total paid amount
is still unknown for
of the cases because they are related to claims that were open on 31 December 2016 (see
Figure 2). To overcome this issue, we use a subset
of
, i.e., we consider only accident years from 2004 to 2010 for both training and validation. This subset contains
files related to
claims of which
are still open on 31 December 2010. Further, only
of the files are associated with claims that are still open as of the end of 2016, so we know the exact total paid amount for
of them, assuming no reopening after 2016. For the small proportion of open claims, we assume that the incurred amount set by experts is the true total paid amount. Hence, the evaluation date is set at 31 December 2010 and
. This is the date at which the reserve must be evaluated for files in
. This implies that the models are not allowed to use information past this date for their training. Information past the evaluation date is used only for validation.
For simplicity and for computational purposes, the quarterly database is summarized to form a yearly database , where . We randomly sampled of the claims to form the training set of indices , and the other forms the validation set of indices , which gives the training and validation datasets and .
In partnership with the insurance company, we selected 20 covariates in order to predict total paid amount for each of the claims. To make all models comparable, we use the same covariates for all claims. Some covariates are characteristics of the insured, such as age and gender, and some pertain to the claim such as the accident year, the development year, and the number of healthcare providers in the file. For privacy reasons, we cannot discuss the selected covariates further in this paper.
4.2. Training of XGBoost Models
In order to train XGBoost models, we analyze the training dataset . Because some covariates are dynamic, the design matrix changes over time, that is to say for . Unless otherwise stated, the models are all trained using , which is the latest information we have about files, assuming information after is unknown.
Although a model using real responses is not usable in practice, it is possible to train it because we set the evaluation date to be in the past. Model A acts as a benchmark model in our case study because it is fit using as training responses and it is best model we can hope for. Therefore, in order to train model A, data is input into the XGBoost algorithm, which learns the prediction function .
Model B, which is biased, is fit using as training responses, but only on the set of claims for which the claim is settled at time . Hence, model B is trained using , where , giving the prediction function . This model allows us to measure the extent of the selection bias.
In the next models, we develop claims that are still open at , i.e., we predict pseudo-responses using training set , and these are subsequently used to fit the model.
In model C, claims are developed using the Mack’s model. We only develop open files at the evaluation date, i.e., we assume no reopening for settled claims. More specifically, information from data
is aggregated by accident year and by development year to form a cumulative run-off triangle. Based on this triangle, we use the bootstrap approach described in
England and Verrall (
2002) and involving Pearson’s residuals to generate
bootstrapped triangles
. On each of those triangles, the Mack’s model is applied to obtain vectors of development factors
,
, with
where
and
are from bootstrapped triangle
. From each vector
, we compute empirical cumulative distribution function
and we set
,
and where
is a hyperparameter estimated using cross-validation. Finally, we calculate pseudo-responses
using
In model D, claims are projected using an individual quasi-Poisson GLM as described in
Section 3.1 and including all 20 covariates. We discretize the amounts by rounding in order to be able to use a counting distribution even if the response variable is theoretically continuous. This approach is common in the literature associated with loss reserving and does not have a significant impact on the final results. Unlike in model C, we also develop settled claims at
. This is because in this model, the status (open or closed) of the file is used, which means the models will be able to make the difference between open and settled claims. More specifically, model D uses an individual quasi-Poisson GLM to estimate the training dependent variable. The GLM is fit on data
, where
,
and
is the yearly aggregate payment at year
t for claim
k. A logarithm link function is used and coefficients are estimated by maximizing the Poisson log-likelihood function. Therefore, the estimation of the expected value for a new observation is given by
and a prediction is made according to
, which is the level
empirical quantile of the distribution of
. This quantile can be obtained using simulation or bootstrap procedure. Finally, for the claim
k, the pseudo-response is
Model E is constructed in the same way as model C but it uses prospective information about the 4 dynamic stochastic covariates available in the dataset. It is analogous to model A in the sense that it is not usable in practice. However, fitting this model indicates whether an additional model that would project censored dynamic covariates would be useful. In
Table 1, we summarize the main specifications of the models.
4.3. Learning of Prediction Function
In
Section 4.2, we showed how to train the XGBoost models having the dataset
. However, no details were given on how we obtain the prediction function for each model. In this section, we dive one abstraction level lower by explaining the general idea behind the algorithm. Our presentation is closely inspired by the TreeBoost algorithm developed by
Friedman (
2001), which is based on the same principles as XGBoost using regression trees as weak learners. The main difference between the two algorithms is the computation time: XGBoost is usually faster to train. In order to get through this, we take model A as an example. The explanation is nevertheless easily transferable to all other models since only the dataset given as input changes.
In the regression framework, a TreeBoost algorithm combines many regression trees together in order to optimize some objective function and thus learn a prediction function. The prediction function for model A takes the form of a weighted sum of regression tress
where
and
are the weights and the vectors of parameters characterizing the regression trees, respectively. The vector of parameters associated with the
tree contains
regions (or leaves)
as well as the corresponding prediction constants
, which means
. Notice that a regression tree can be seen as a weighted sum of indicator functions:
Ref.
Friedman (
2001) proposed to slightly modify Equation (
5) in order to choose a different optimal value
for each of the tree’s regions. Consequently, each weight
can be absorbed into the prediction constant
. Assuming a constant number of regions
J in each tree (which is almost always the case in practice), Equation (
5) becomes
With a loss function
, we need to solve
which is, most of the time, too expensive computationally. The TreeBoost algorithm overcomes this issue by building the prediction function iteratively. In order to avoid overfitting, it also adds a learning rate
,
. The steps needed to obtain the prediction function for model A are detailed in Algorithm 1.
algorithmAlgorithm
| Algorithm 1: Obtaining with least square TreeBoost. |
![Risks 07 00079 i001]() |
4.4. Results
From
, which was the training dataset before the evaluation date, it is possible to obtain a training run-off triangle by aggregating payments by accident and by development year, presented in
Table 2.
We can apply the same principle for validation dataset
, which yields the validation run-off triangle displayed in
Table 3.
Based on the training run-off triangle, it is possible to fit many collective models, see
Wüthrich and Merz (
2008) for an extensive overview. Once fitted, we scored them on the validation triangle. In the validation triangle (
Table 3), data used to score models are displayed in black and aggregated payments observed after the evaluation date are displayed in gray. Payments have been observed for six years after 2010, but this was not long enough for all claims to be settled. In fact, on 31 December 2016,
of files were associated with claims that are still open, mostly from accident years 2009 and 2010. Therefore, amounts in column “
” for accident years 2009 and 2010 in
Table 3 are in fact too low. Based on available information, the observed RBNS amount was
$67,619,905 (summing all gray entries), but we can reasonably think that this amount would be closer to
$70,000,000 if we could observe more years. The observed IBNR amount was
$3,625,983 for a total amount of
$71,245,888.
Results for collective models are presented according to two approaches:
Mack’s model, for which we present results obtained with the bootstrap approach developed by
England and Verrall (
2002), based on both quasi-Poisson and gamma distributions; and
generalized linear models for which we present results obtained using a logarithmic link function and a variance function with (quasi-Poisson), (gamma), and (Tweedie).
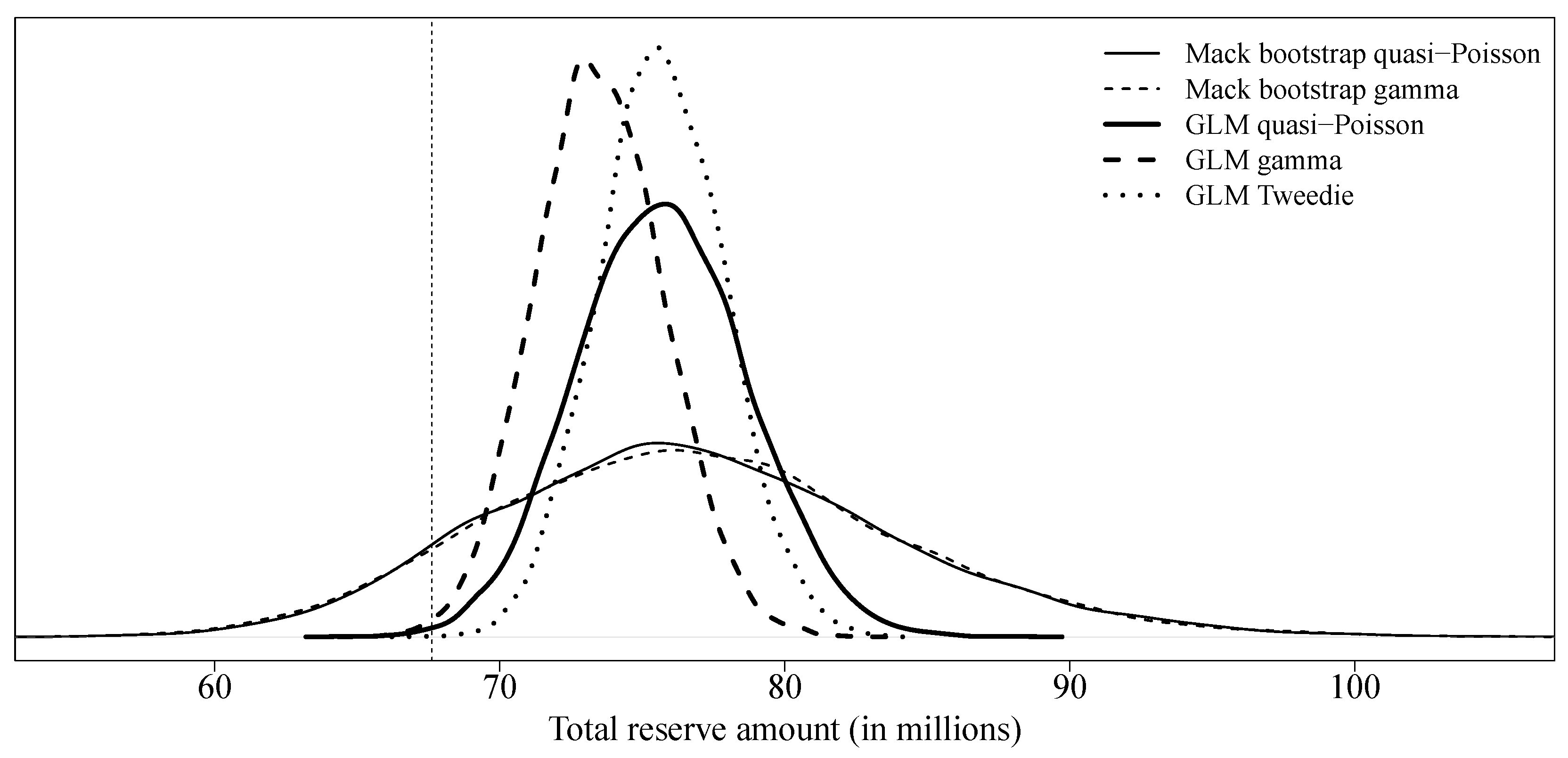
For each model,
Table 4 presents the expected value of the reserve, its standard error, and the
and the
quantiles of the predictive distribution of the total reserve amount. As is generally the case, the choice of the distribution used to simulate the process error in the bootstrap procedure for Mack’s model has no significant impact on the results. Reasonable practices, at least in North America, generally require a reserve amount given by a high quantile (
,
or even
) of the reserve’s predictive distribution. As a result, the reserve amount obtained by bootstrapping Mack’s model is too high (between
$90,000,000 and
$100,000,000) compared to the observed value (approximately
$70,000,000). Reserve amounts obtained with generalized linear models were more reasonable (between
$77,000,000 and
$83,000,000), regardless of the choice of the underlying distribution. The predictive distribution for all collective models is shown in
Figure 3.
In
Table 4, we also present in-sample results, i.e., we used the same dataset to perform both estimation and validation. The results were very similar, which tends to indicate stability of the results obtained using these collective approaches.
Individual models were trained on the training set and scored on the validation set . In contrast to collective approaches, individual methods used micro-covariates and, more specifically, the reporting date. This allows us to distinguish between IBNR claims and RBNS claims and, as previously mentioned, in this project we mainly focus on the modeling of the RBNS reserve. Nevertheless, in our dataset, we observe very few IBNR claims ($3,625,983) and therefore, we can reasonably compare the results obtained using both micro- and macro-level models with the observed amount ($67,619,905).
We considered the following approaches:
individual generalized linear models (see
Section 3.1), for which we present results obtained using a logarithmic link function and three variance functions:
(Poisson) and
with
(quasi-Poisson) and
with
(Tweedie); and
XGBoost models (models A, B, C, D and E) described in
Section 4.2.
Both approaches used the same covariates described in
Section 4.1, which makes them comparable. For many files in both training and validation sets, some covariates are missing. Because generalized linear models cannot handle missing values, median/mode imputation has been performed for both training and validation sets. No imputation has been done for XGBoost models because missing values are processed automatically by the algorithm.
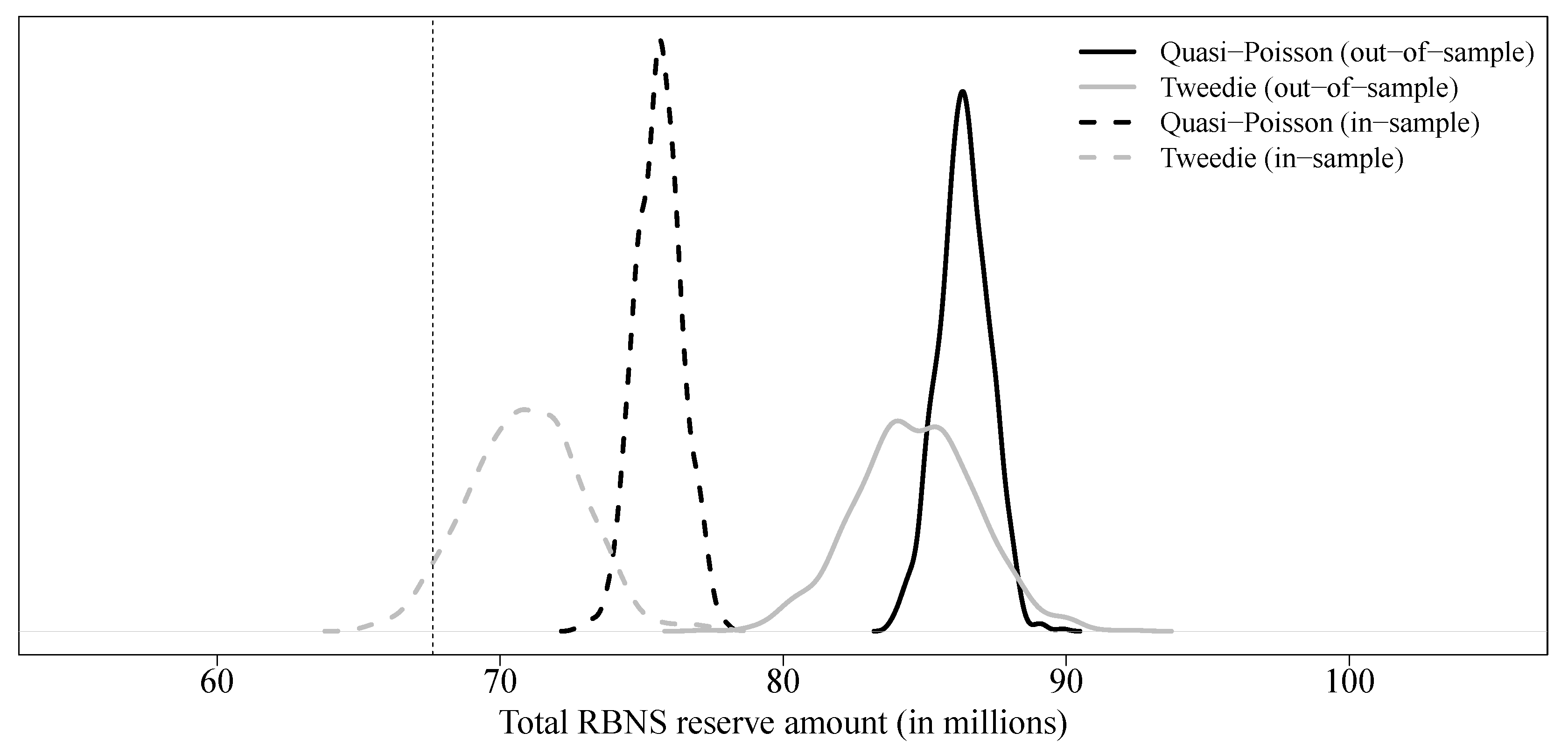
Results for individual GLM are displayed in
Table 5, and predictive distributions for both quasi-Poisson and Tweedie GLM are shown in
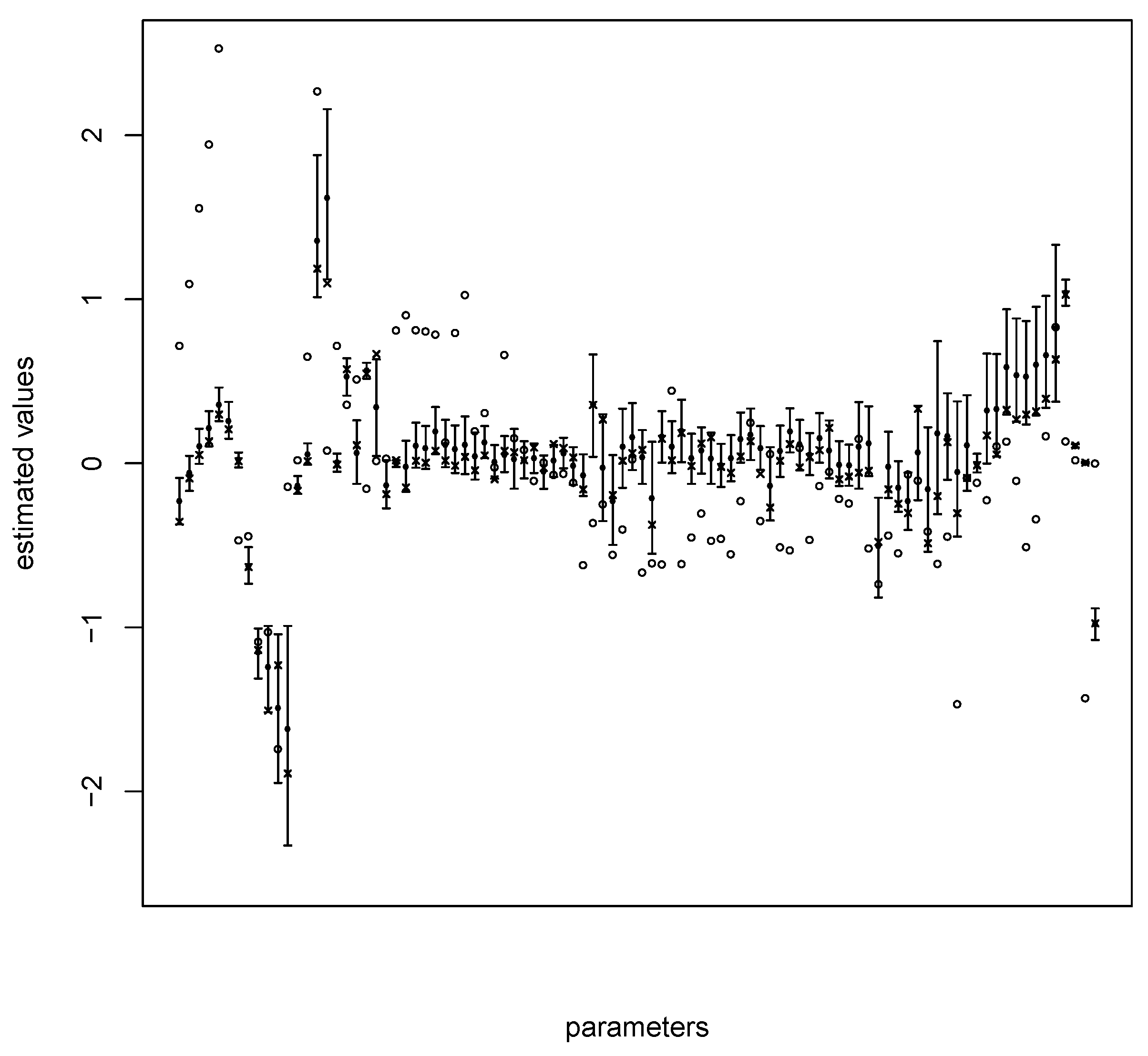
Figure 4. Predictive distribution for the Poisson GLM is omitted because it is the same as the quasi-Poisson model, but with a much smaller variance. Based on our dataset, we observe that the estimated value of the parameter associated to some covariates is particularly dependent on the database used to train the model, e.g., in the worst case, for the quasi-Poisson model, we observe
(
) with the out-of-sample approach and
(
) with the in-sample approach. This can also be observed for many parameters of the model, as shown in
Figure 5 for the quasi-Poisson model. These results were obtained by resampling from the training database and the quasi-Poisson model. Crosses and circles represent the estimated values of the parameters if the original training database is used, and the estimated values of the parameters if the validation database is used, respectively. On this graph, we observe that, for most of the parameters, the values estimated on the validation set are inaccessible when the model is adjusted on the training set. In
Table 5, we display results for both in-sample and out-of-sample approaches. As the results shown in
Figure 4 suggest, there are significant differences between the two approaches. Particularly, the reserves obtained from the out-of-sample approach are too high compared with the observed value. Although it is true that in practice, the training/validation set division is less relevant for an individual generalized linear model because the risk of overfitting is lower, this suggests that some caution is required in a context of loss reserving.
Out-of-sample results for XGBoost models are displayed in
Table 6. For all models, the learning rate is around
, which means our models are quite robust to overfitting. We use a maximum depth of 3 for each tree. A higher value would make our model more complex but also less robust to overfitting. All those hyperparameters are obtained by cross-validation. Parameters
and
are obtained using cross-validation over a grid given by
.
Not surprisingly, we observe that model B is completely off the mark, underestimating the total reserve by a large amount. This confirms that the selection bias, at least in this example, is real and substantial.
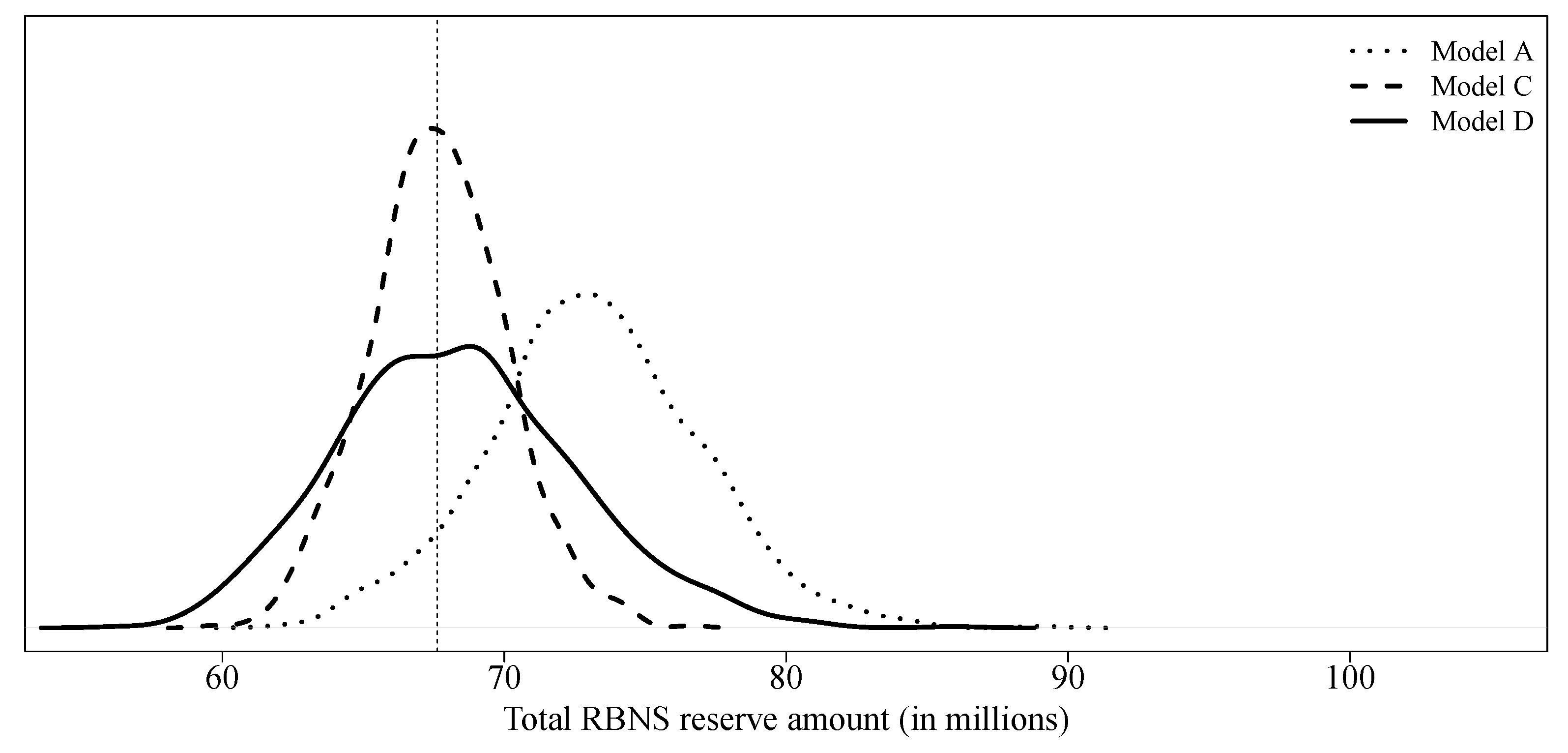
model C considers a collective model, i.e., without micro-covariates, to create pseudo-responses and uses all covariates available in order to predict final paid amounts. With a slightly lower expectation and variance, model C is quite similar to model A. Because the latter model uses real responses for its training, the method used for claim development appears to be reasonable. Model D uses an individual model, a quasi-Poisson GLM, using all covariates available to obtain both, pseudo-responses and final predictions. Again, results are similar to those of model A. In
Figure 6 we compare the predictive distributions of model A, model C and model D.
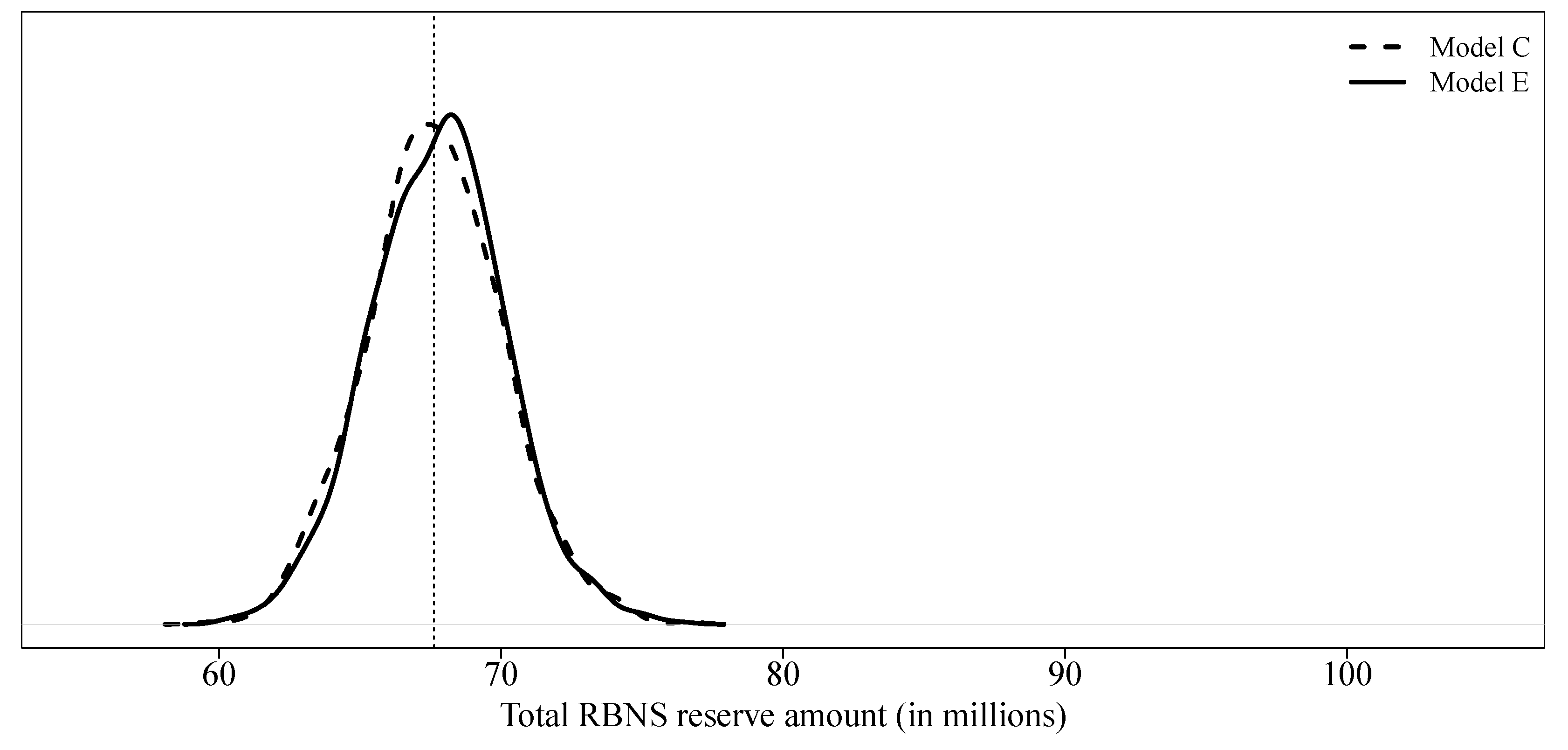
Model E is identical to model C with the exception of dynamic variables whose value at the evaluation date was artificially replaced by the ultimate value. At least in this case study, the impact is negligible (see
Figure 7). There would be no real interest in building a hierarchical model that allows, first, to develop the dynamic variables and, second, to use one XGBoost models to predict final paid amounts.