Market-Risk Optimization among the Developed and Emerging Markets with CVaR Measure and Copula Simulation
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Generalized Pareto Distribution Copula Approach
3.2. Portfolio Optimization
4. Results and Interpretations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Elliptical Copula Parameters
- ■
- The bivariate Gaussian copula (N)—it has no tail dependence, hence = = 0. Therefore, modeling the dependence structure of the series by a Gaussian (normal) copula is consistent with the estimation of this dependence by the linear correlation coefficient such that . The copula density is given by (see e.g., Cherubini et al. (2004))where represents the univariate standard normal distribution function with correlation .
- ■
- The t-copula—it also has a correlation coefficient such that however, it shows some tail dependence. Specifically, it has symmetric tail dependence. It may be expressed as follows (see e.g., Cherubini et al. (2004)):where is a univariate Student-t distribution function with degrees of freedom and . The symmetric tail dependence is . As the t-copula allows for symmetric non-zero dependence in the tails and it represents a generalization of the Gaussian-copula.
| Family | Parameters | |
|---|---|---|
| Upper Tail Dependence | Lower Tail Dependence | |
| Gaussian-copula | = 0 | |
| t-copula | ||
References
- Acharya, Viral V., Lasse H. Pedersen, Thomas Philippon, and Matthew Richardson. 2009. Regulating Systemic Risk, Restoring Financial Stability: How to Repair a Failed System. Hoboken: Wiley, pp. 283–304. [Google Scholar]
- Adrian, Tobias, and Markus K. Brunnermeier. 2016. CoVaR. American Economic Review 106: 1705–41. [Google Scholar] [CrossRef]
- Alexander Siddharth, Coleman Thomas F., and Yuying Li. 2006. Minimizing CVaR and VaR for a Portfolio of Derivatives. Journal of Banking & Finance 30: 583–605. [Google Scholar]
- Aloui, Riadh, Duc Khuong Nguyen, and Mohamed Ben Aïssa. 2011. Global financial crisis, extreme interdependences, and contagion effects: The role of economic structure? Journal of Banking & Finance 35: 130–41. [Google Scholar]
- Bedford, Tim, and Roger M. Cooke. 2002. Vines—A new graphical model for dependent random variables. Annals of Statistics 30: 1031–68. [Google Scholar] [CrossRef]
- Bellini, Fabio, Klar Bernhard, and Müller Alfred. 2017. Expectiles, Omega ratios, and stochastic ordering. In Methodology and Computing in Applied Probability. Berlin: Springer. [Google Scholar]
- Boubaker, Heni, and Nadia Sghaier. 2013. Portfolio Optimization in the Presence of Dependent Financial Returns with Long Memory: A Copula Based Approach. Journal of Banking & Finance 37: 361–77. [Google Scholar]
- Cao, Jinsheng. 2015. Portfolio Optimization Model Based on CVaR Programming and Limits of MAD. Paper presented at the International Conference on Education Technology, Management and Humanities Science (ETMHS), Xi’an, China, 21–22 March. [Google Scholar]
- Chen, James Ming. 2018. On Exactitude in Financial Regulation: Value-at-Risk, Expected Shortfall, and Expectiles. Risks 6: 61. [Google Scholar] [CrossRef]
- Chen, Yi-Hsuan, and Anthony Tu. 2013. Estimating Hedged Portfolio Value-at-Risk Using the Conditional Copula: An Illustration of Model Risk. International Review of Economics & Finance 27: 514–28. [Google Scholar]
- Chen, F., X. Chen, Z. Sun, T. Yu, and M. Zhong. 2013. Systemic risk, financial crisis, and credit risk insurance. Financial Review 48: 417–42. [Google Scholar] [CrossRef]
- Cherubini, Umberto, Elisa Luciano, and Walter Vecchiato. 2004. Copula Methods in Finance. New York: John Wiley & Sons. [Google Scholar]
- Clemente, Annalisa Di, and Claudio Romano. 2004. Measuring and optimizing portfolio credit risk: A copula-based approach. Economic Notes by Banca Monte dei Paschi di Siena SpA 33: 325–57. [Google Scholar] [CrossRef]
- Cox, Samuel H., Yijia Lin, Ruilin Tian, and Luis Zuluaga. 2009. Portfolio Risk Management with CVaR-Like Constraints. North American Actuarial Journal 14: 86–106. [Google Scholar] [CrossRef]
- Demarta, Stefano, and Alexander J. McNeil. 2005. The t-copula and related copulas. International Statistical Review 73: 111–29. [Google Scholar] [CrossRef]
- Embrechts, Paul, Claudia Klüppelberg, and Thomas Mikosch. 1997. Modelling Extremal Events for Insurance and Finance. Berlin: Springer. [Google Scholar]
- Fernando, A. B. Sabino da Silva, Flávio A. Ziegelmann, and Cristina Tessari. 2017. Robust Portfolio Optimization with Multivariate Copulas: A Worst-Case Cvar Approach. Working Paper, unpublished. [Google Scholar] [CrossRef]
- Gandy, Robin. 2005. Portfolio Optimization with Risk Constraints. Ph.D. dissertation, Universität ULM, Denmark. Available online: http://vts.uni-ulm.de/docs/2005/5427/vts5427.pdf (accessed on 13 December 2005).
- Goetzmann, William, Lingfing Li, and K. Geert Rouwenhorst. 2005. Long-term global market correlations. Journal of Business 78: 1–38. [Google Scholar] [CrossRef]
- Hallinan, Kelly. 2011. The Role of Emerging Market in Investment Portfolios. Honours Scholar thesis. Available online: http://digitalcommons.uconn.edu/srhonors_theses/200 (accessed on 5 August 2011).
- He, Xubiao, and Pu Gong. 2009. Measuring the coupled risks: A copula-based CVaR model. Journal of Computational and Applied Mathematics 223: 1066–80. [Google Scholar] [CrossRef]
- Hotta, Luiz Koodi, Edimilson C. Lucas, and Helder P. Palaro. 2008. Estimation of VaR using copula and extreme value theory. Multinational Finance Journal 12: 205–21. [Google Scholar] [CrossRef]
- Huang, Jen Jsung, Jung Kuo, Hueimei Liang, and Wei-Fu Lin. 2009. Estimating Value at Risk of Portfolio by Conditional Copula-GARCH Method. Insurance 45: 315–24. [Google Scholar] [CrossRef]
- Komang, Dharmawan. 2013. Measuring and Optimizing Conditional Value at Risk Using Copula Simulation. Paper presented at South East Asian Conference on Mathematics and Its Application (SEACMA 2013), Surabaya, Indonesia, 11–15 November. [Google Scholar]
- Krokhmal, Pavlo, Jonas Palquist, and Stanislav Uryasev. 2003. Portfolio Optimization with Conditional Value-at-Risk Objective and Constraints. Journal of Risk 4. [Google Scholar] [CrossRef]
- Li, Jing, and Mingxin Xu. 2013. Optimal Dynamic Portfolio with Mean-CVaR Criterion. Risks 1: 119–47. [Google Scholar] [CrossRef]
- Markowitz, H. 1952. Portfolio selection. Journal of Finance 7: 77–91. [Google Scholar]
- McNeil, Alexander J., and Johanna Nešlehová. 2009. Multivariate Archimedean copulas, $d$-monotone functions and $l_1$-norm symmetric distributions. Annals of Statistics 37: 3059–97. [Google Scholar] [CrossRef]
- Najafi, Amir Abbas, and Siamak Mushakhian. 2015. Multi-stage stochastic mean-semivariance-CVaR Optimization under Transaction Costs. Applied Mathematics and Computation 256: 445–58. [Google Scholar] [CrossRef]
- Nikusokhan, Moien. 2018. GJR-Copula-CVaR Model for Portfolio Optimization: Evidence for Emerging Stock Markets. Iranian Economic Review 22: 990–1015. [Google Scholar]
- Natalia, Nolde, and Johanna F. Ziegel. 2017. Elicitability and backtesting: Perspectives for banking regulation. The Annals of Applied Statistics 11: 1833–74. [Google Scholar]
- Rockafellar, R. Tyrrel, and Stanilav Uryasev. 2000. Optimization of conditional value-at-risk. Journal of Risk 2: 21–41. [Google Scholar] [CrossRef]
- Rockafellar, R. Tyrrel, and Stanislav Uryasev. 2002. Conditional value-at-risk for general loss distributions. Journal of Banking and Finance 26: 1443–71. [Google Scholar] [CrossRef]
- Sahamkhadam, Maziar, Andreas Stephan, and Ralf Ostermark. 2018. Portfolio optimization based on GARCH-EVT-Copula forecasting models. International Journal of Forecasting 34: 497–506. [Google Scholar] [CrossRef]
- Scarrott, Carl, and Anna MacDonald. 2012. A review of extreme value threshold estimation and uncertainty quantification. REVSTAT—Statistical Journal 10: 33–59. [Google Scholar]
- Sklar, Abe. 1959. Fonctions de répartition à n dimensions et leurs marges. Publications de l’Institut Statistique de l’Université de Paris 8: 229–31. [Google Scholar]
- Ted, Smith. 2016. Building a Better Emerging Markets Portfolio. Available online: http://www.ashmoregroup.com/ (accessed on 1 November 2016).
- Zhang, Qiqi. 2016. Multi-portfolio Optimization with CVaR Risk Measure. Electronic Theses and Dissertations. p. 5685. Available online: https://scholar.uwindsor.ca/etd/5685 (accessed on 15 April 2016).
- Zheng, Harry. 2009. Efficient frontier of utility and CVaR. Mathematical Methods of Operations Research. 70: 129. [Google Scholar] [CrossRef]
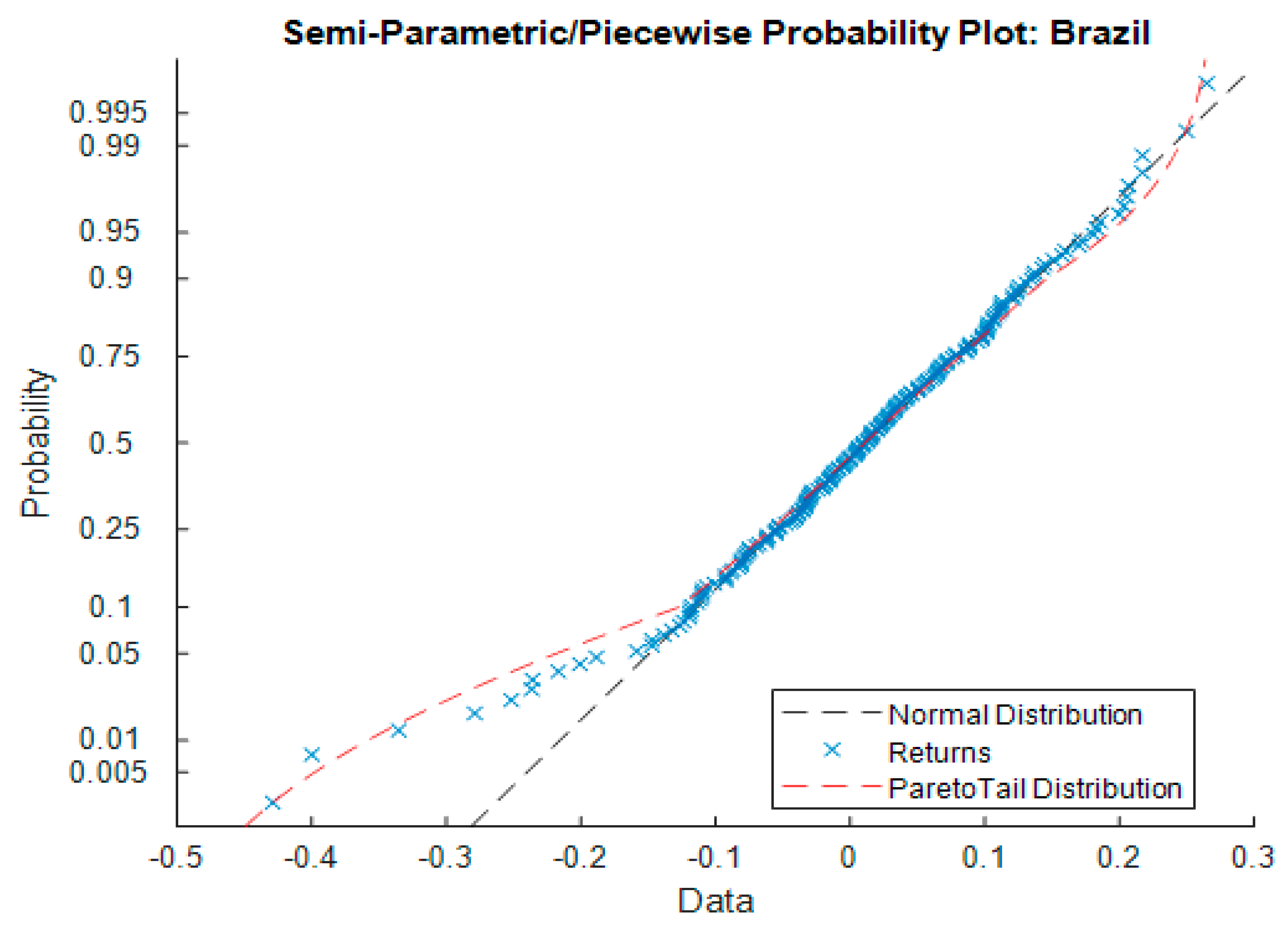
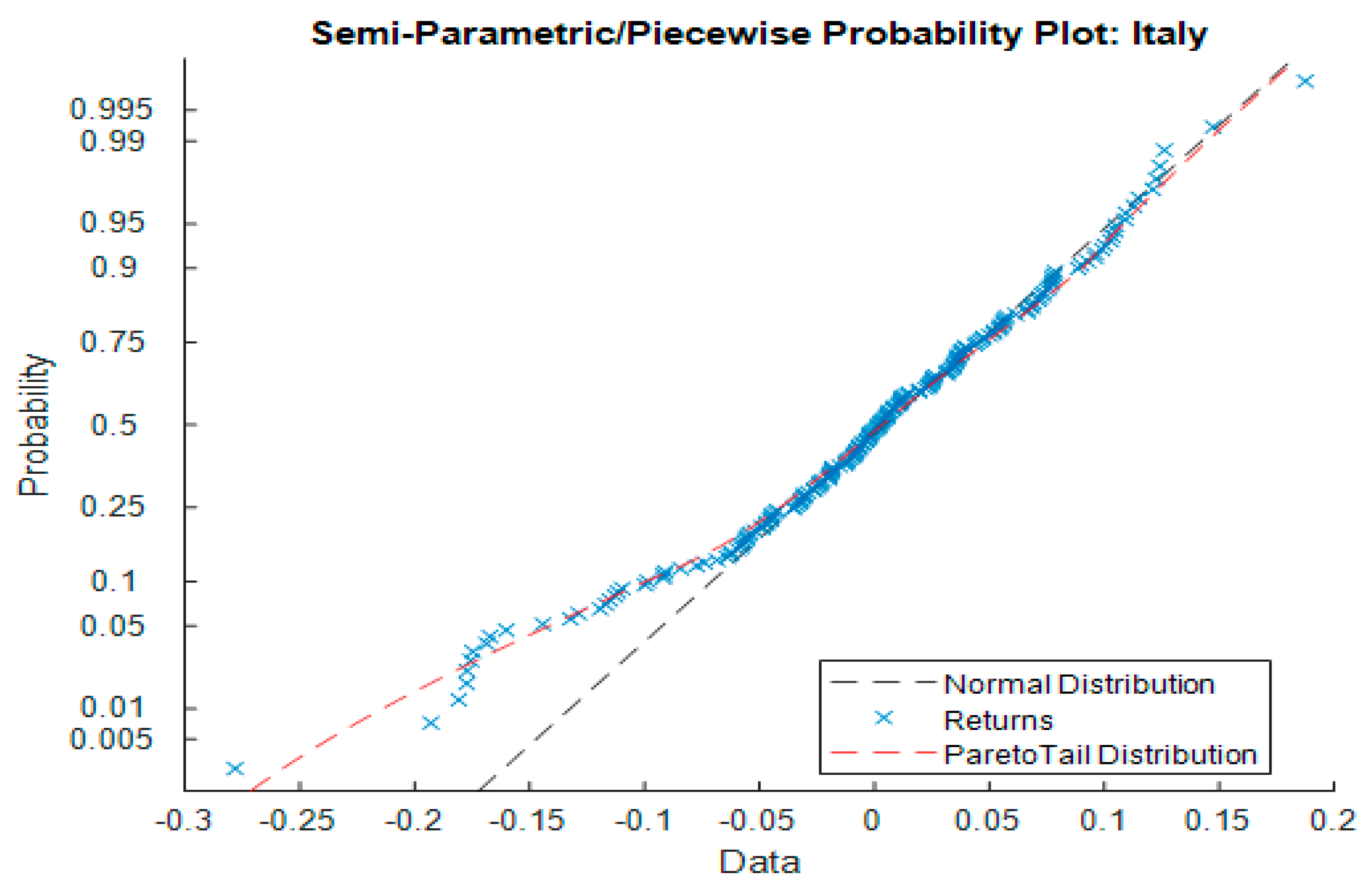

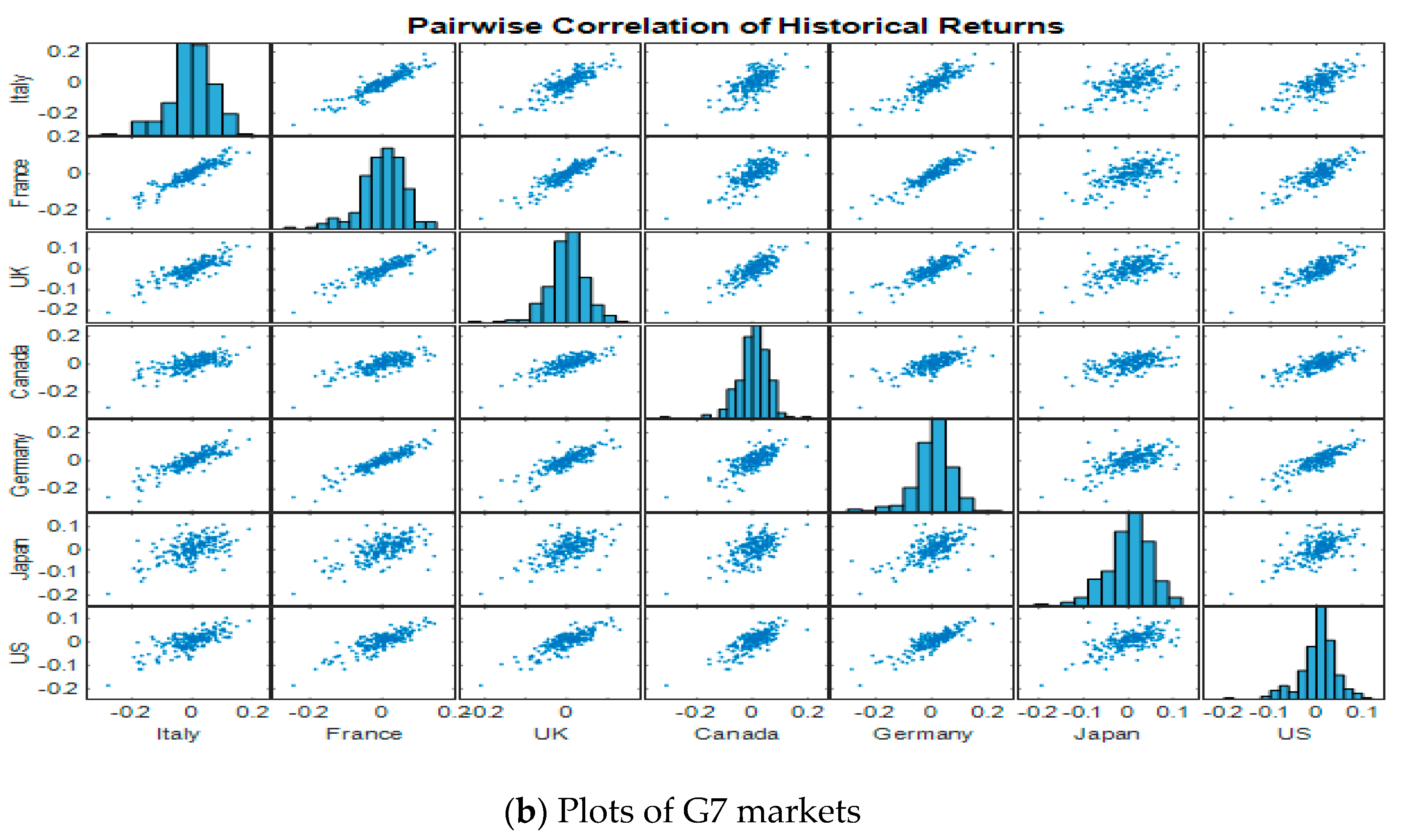
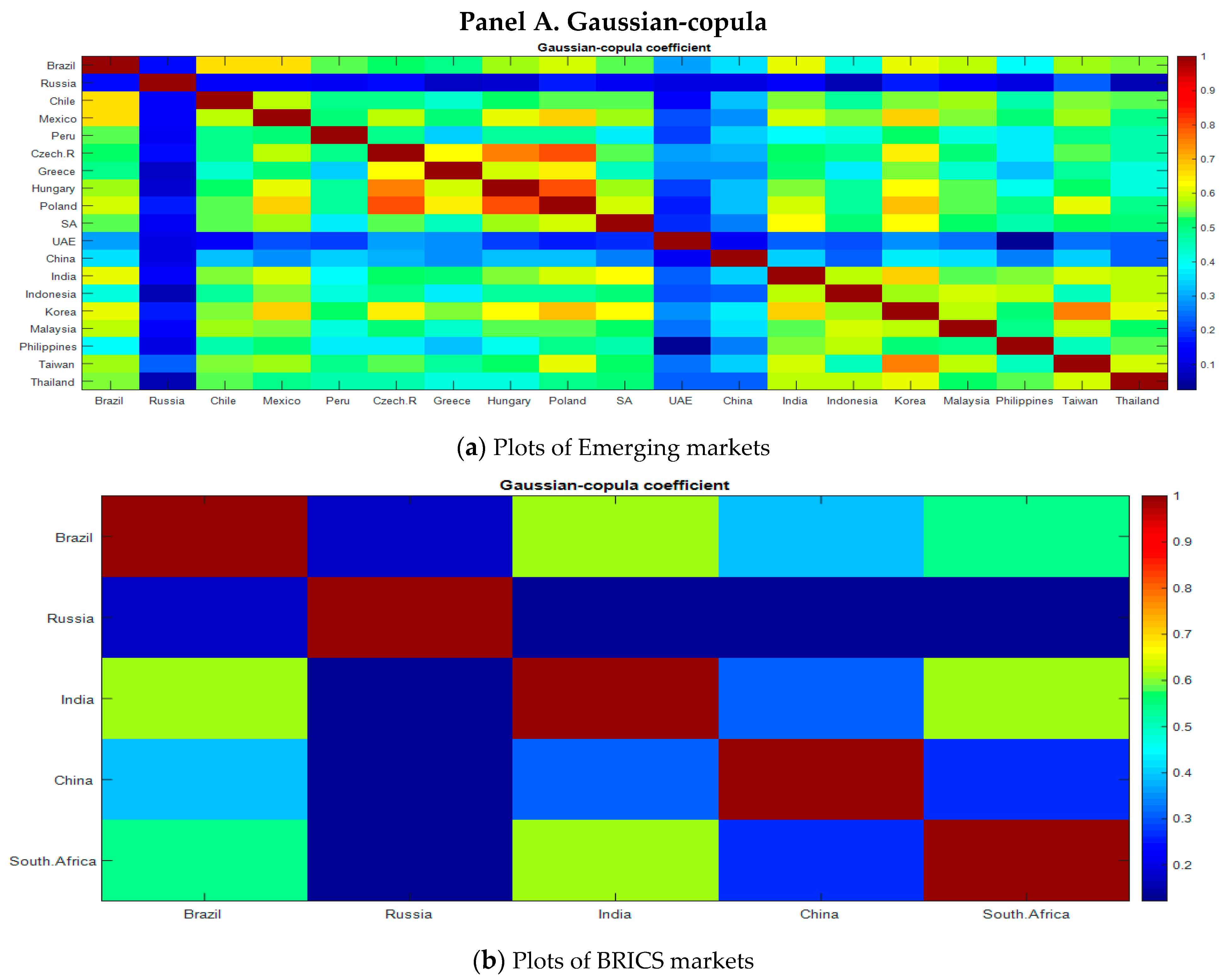
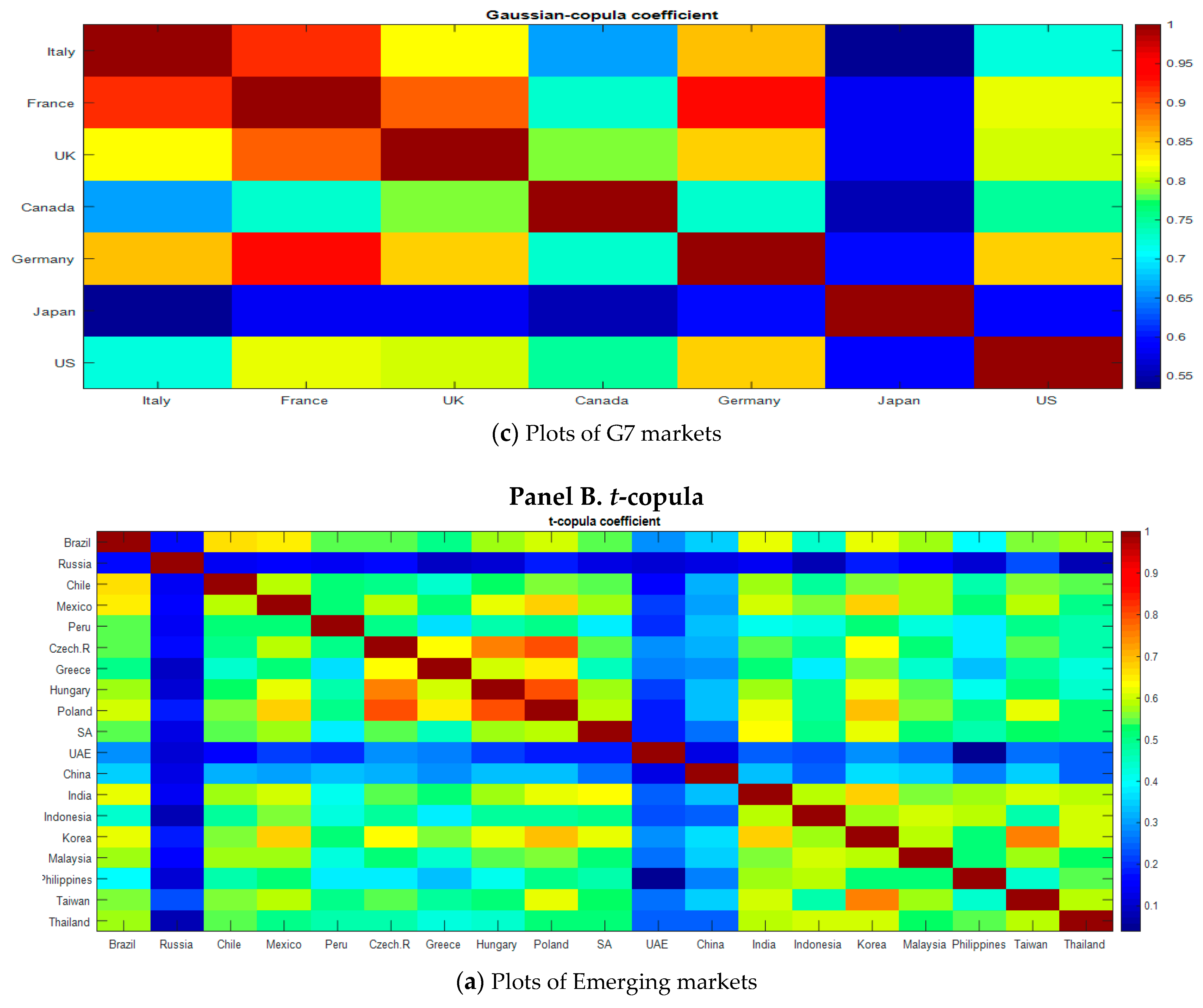
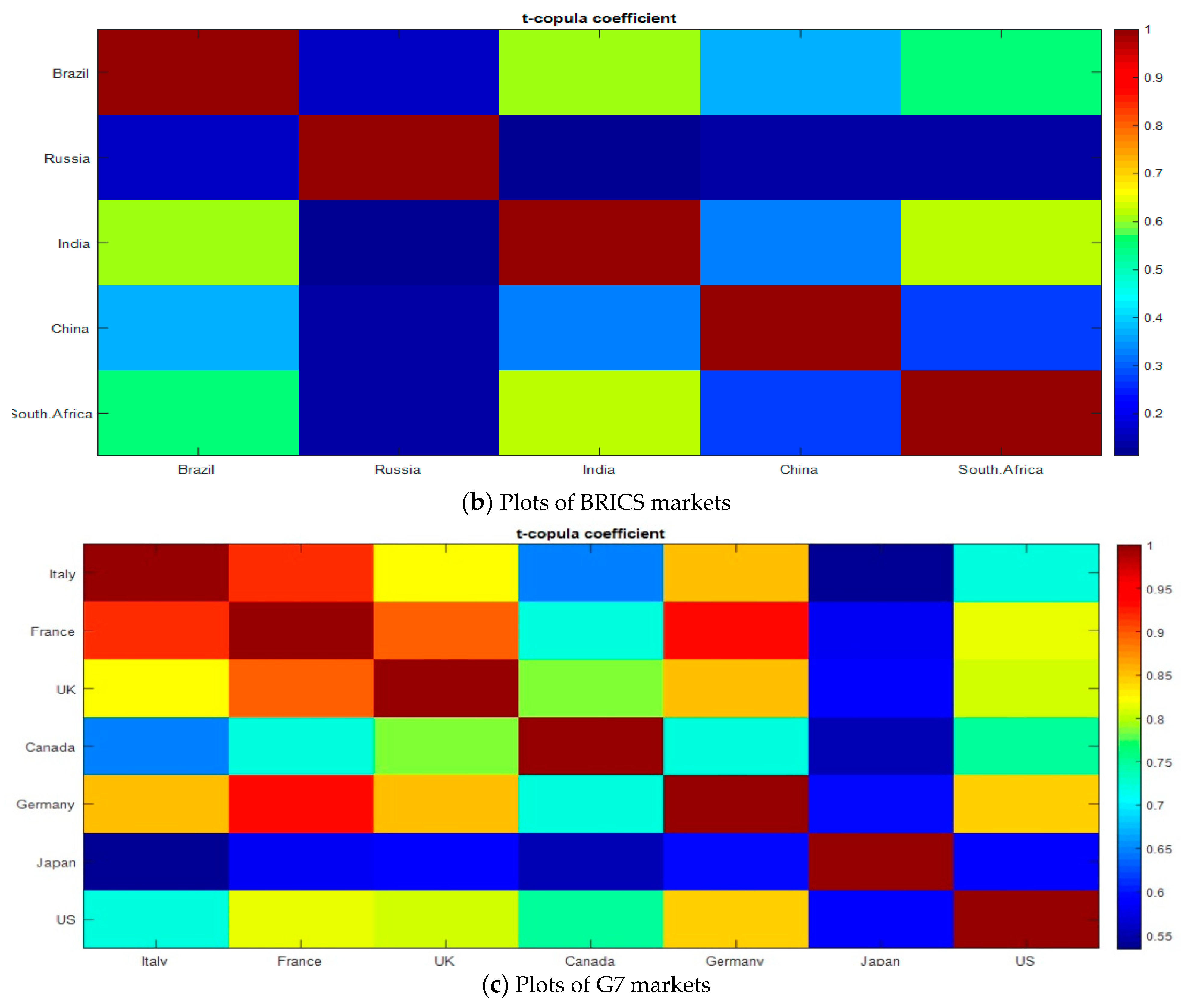
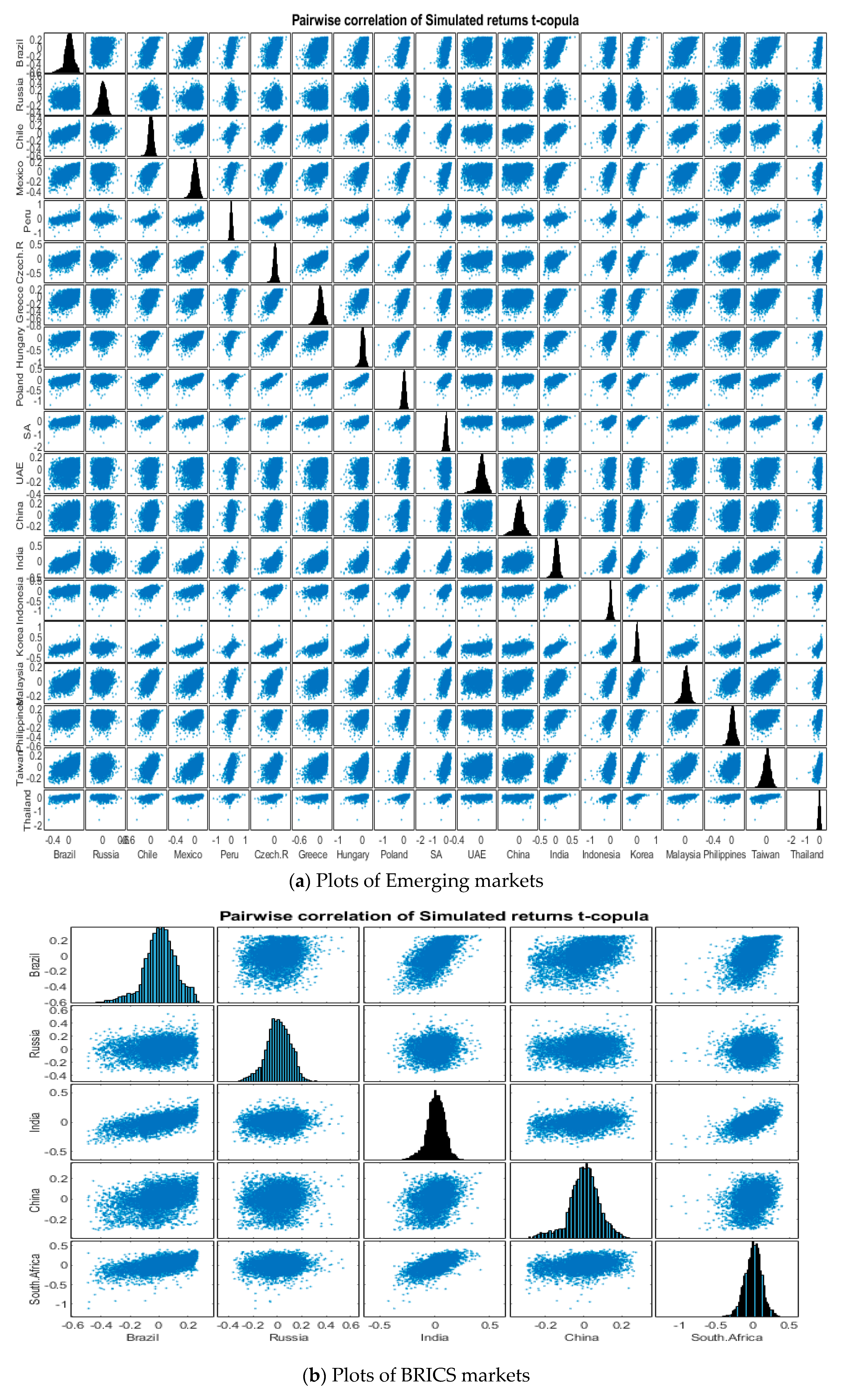
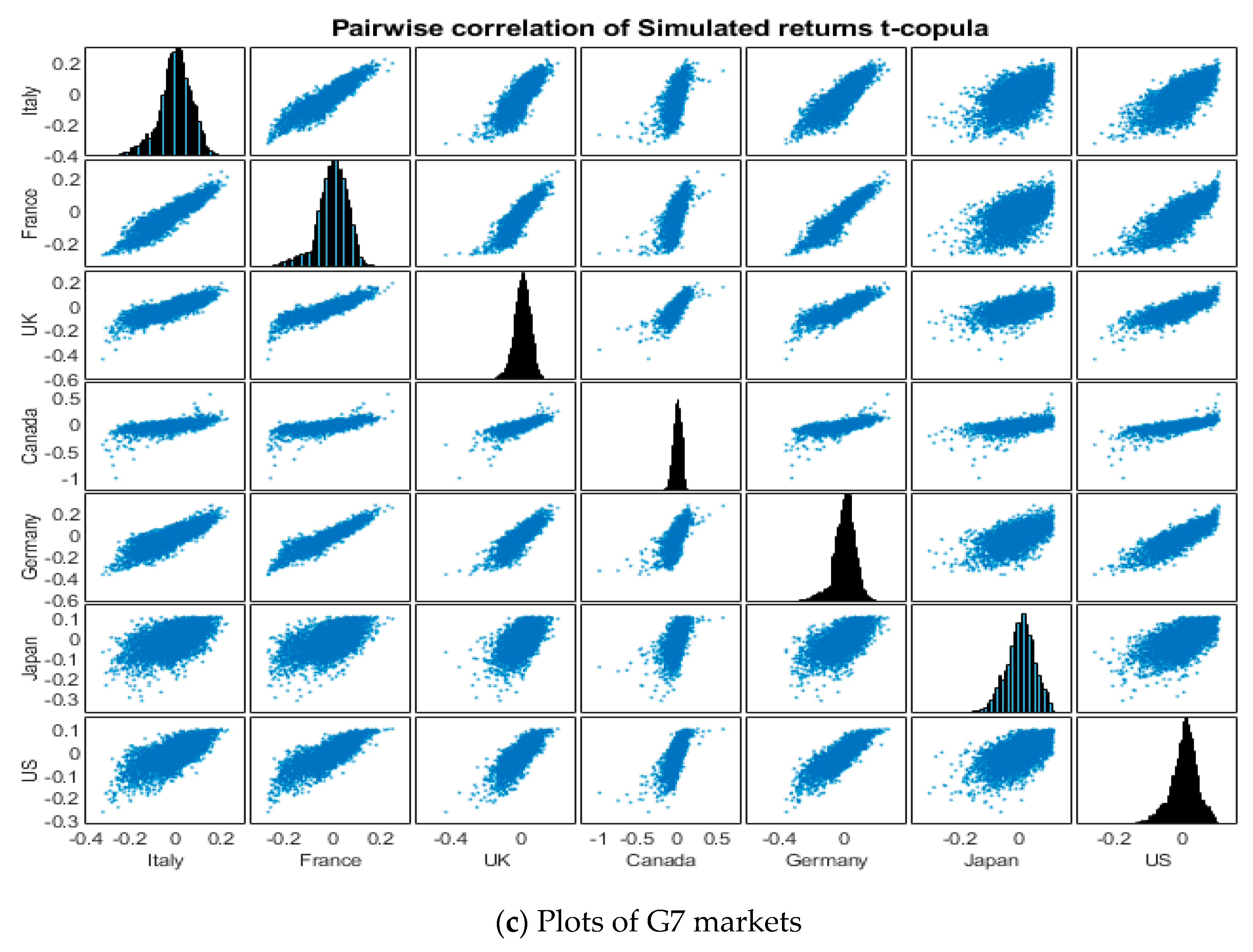

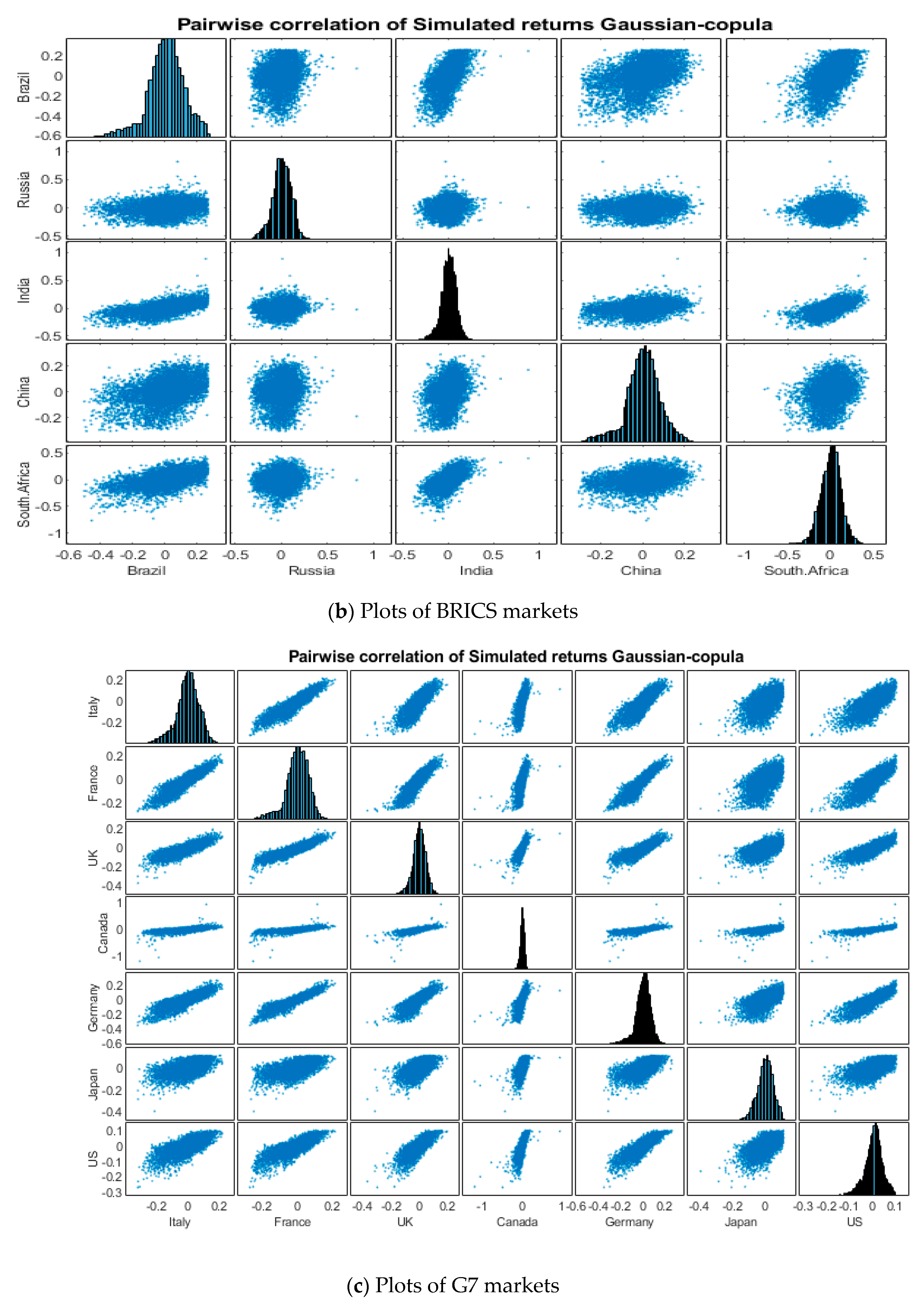
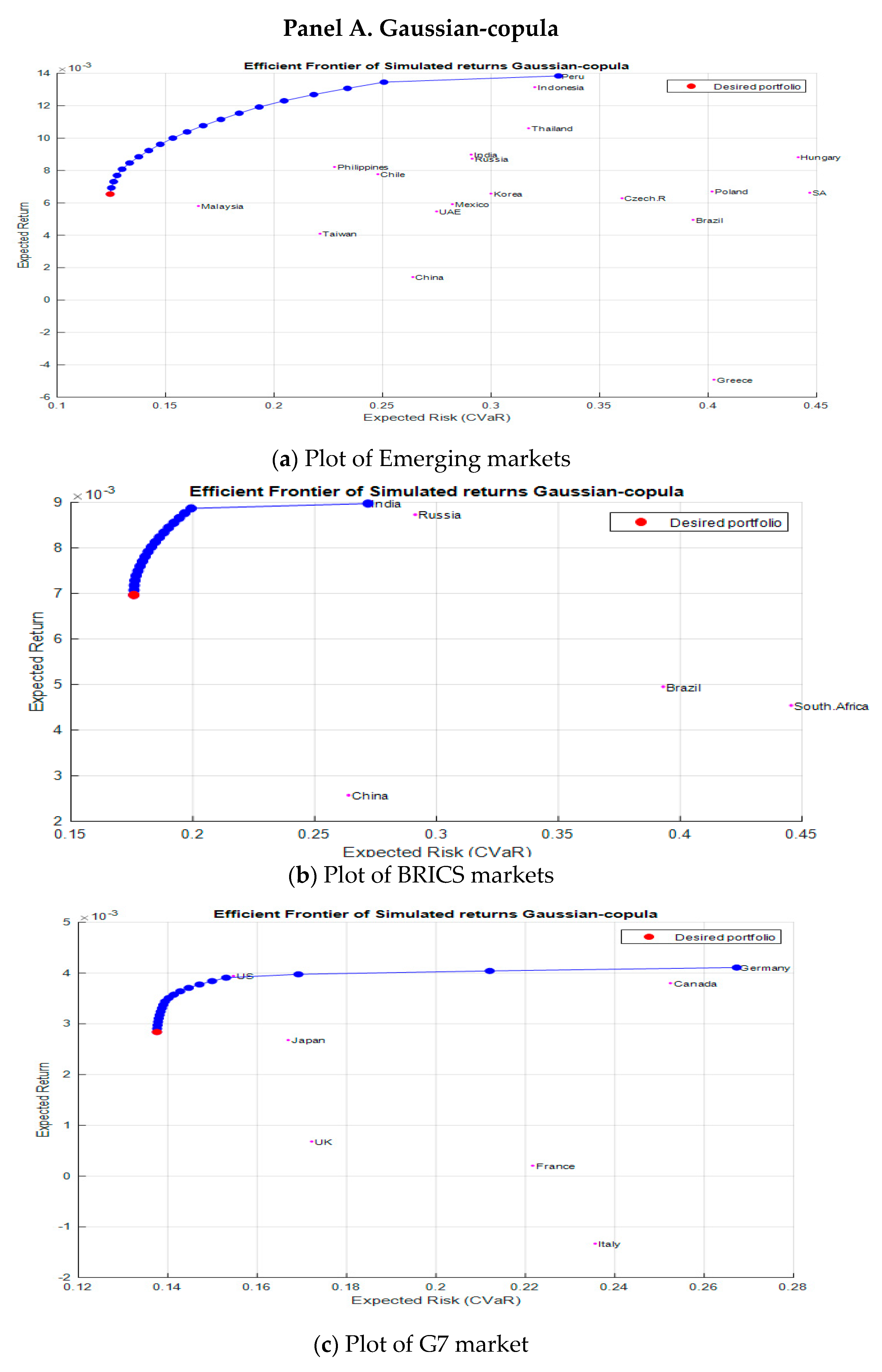
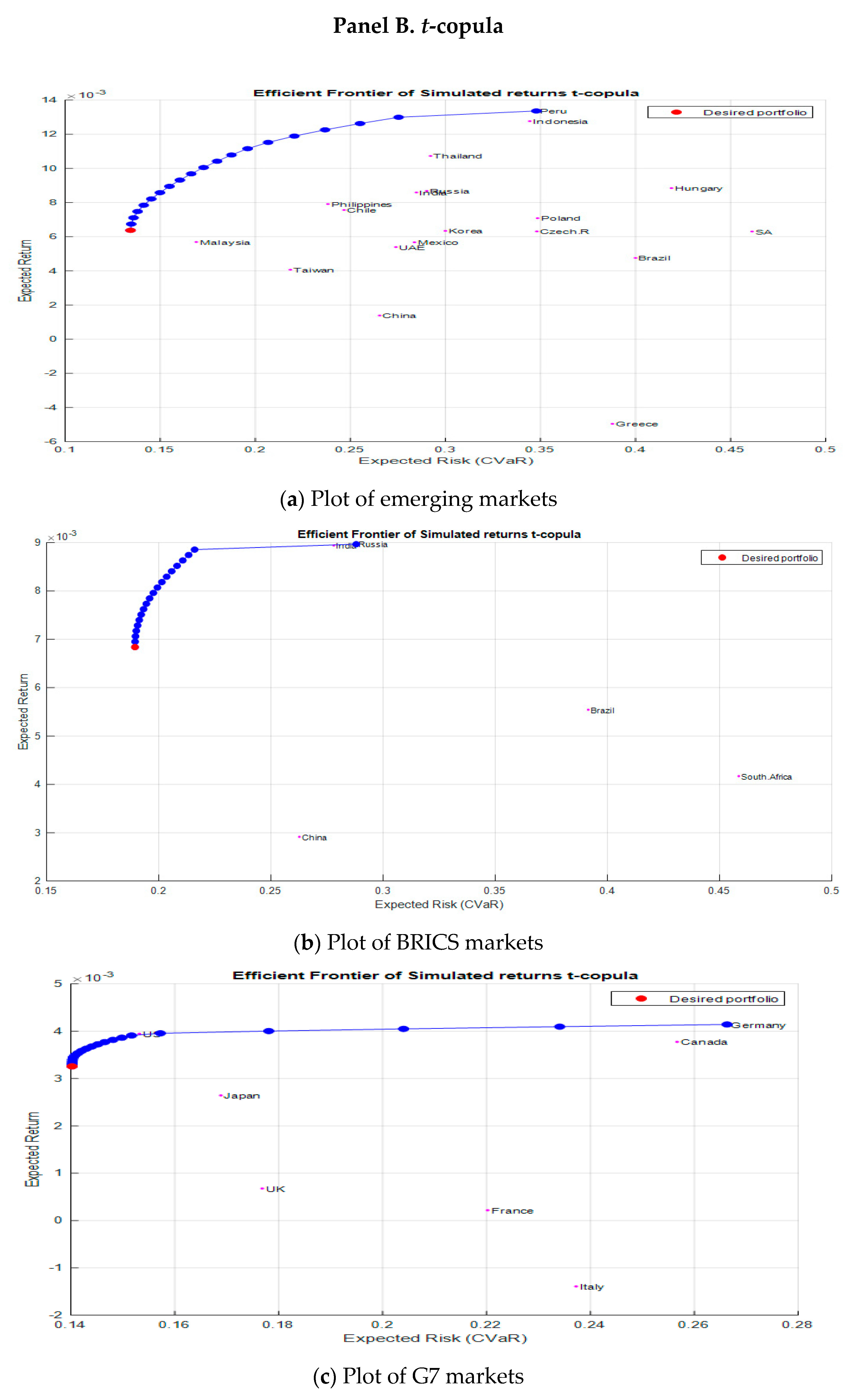
| Panel A. G7 Economies | ||||
|---|---|---|---|---|
| Lower Tail | Upper Tail | |||
| US | −Inf < x < −0.05 | −0.04 (0.03) | 0.05 < x < Inf | −0.50 (0.02) |
| Canada | −Inf < x < −0.06 | 0.36 (0.02) | 0.07 < x < Inf | 0.40 (0.01) |
| UK | −Inf < x < −0.07 | 0.26 (0.04) | 0.08 < x < Inf | 0.08 (0.02) |
| France | −Inf < x < −0.07 | −0.47 (0.09) | 0.07 < x < Inf | 0.00 (0.02) |
| Italy | −Inf < x < −0.09 | −0.25 (0.06) | 0.09 < x < Inf | −0.09 (0.02) |
| Germany | −Inf < x < −0.07 | −0.30 (0.09) | 0.08 < x < Inf | −0.01 (0.01) |
| Japan | −Inf < x < −0.06 | 0.06 (0.02) | 0.06 < x < Inf | −0.57 (0.05) |
| Panel B. BRICS Economies | ||||
| Brazil | −Inf < x < −0.12 | −0.36 (0.14) | 0.14 < x < Inf | −0.68 (0.08) |
| Russia | −Inf < x < −0.11 | −0.37 (0.09) | 0.14 < x < Inf | 0.16 (0.06) |
| India | −Inf < x < −0.10 | −0.21 (0.08) | 0.10 < x < Inf | 0.10 (0.04) |
| China | −Inf < x < −0.09 | −0.54 (0.11) | 0.10 < x < Inf | −0.24 (0.05) |
| South Africa | −Inf < x < −0.15 | 0.16 (0.06) | 0.15 < x < Inf | −0.23 (0.07) |
| Panel C. Emerging Economies | ||||
| Brazil | −Inf < x < −0.12 | −0.36 (0.14) | 0.14 < x < Inf | −0.68 (0.08) |
| Russia | −Inf < x < −0.11 | −0.37 (0.09) | 0.13 < x < Inf | 0.16 (0.03) |
| India | −Inf < x < −0.09 | 0.21 (0.08) | 0.10 < x < Inf | 0.04 (0.04) |
| China | −Inf < x < −0.09 | −0.54 (0.11) | 0.10 < x < Inf | 0.10 (0.03) |
| South Africa | −Inf < x < −0.15 | 0.16 (0.05) | 0.15 < x < Inf | −0.23 (0.07) |
| Chile | −Inf < x < −0.07 | 0.05 (0.05) | 0.08< x < Inf | −0.01 (0.03) |
| Mexico | −Inf < x < −0.07 | 0.04 (0.06) | 0.10 < x < Inf | −0.33 (0.05) |
| Peru | −Inf < x < −0.08 | 0.29 (0.03) | 0.12 < x < Inf | 0.26 (0.03) |
| Czech Republic | −Inf < x < −0.07 | 0.03 (0.07) | 0.09 < x < Inf | 0.06 (0.03) |
| Greece | −Inf < x < −0.14 | 0.13 (0.05) | 0.12 < x < Inf | −0.64 (0.07) |
| Hungary | −Inf < x < −0.09 | 0.12 (0.07) | 0.11 < x < Inf | −0.11 (0.04) |
| Poland | −Inf < x < −0.10 | 0.39 (0.03) | 0.11 < x < Inf | −0.24 (0.04) |
| UAE | −Inf < x < −0.08 | −0.45 (0.11) | 0.09 < x < Inf | −0.46 (0.04) |
| Indonesia | −Inf < x < −0.08 | 0.31 (0.04) | 0.10 < x < Inf | −0.13 (0.07) |
| Korea | −Inf < x < −0.08 | 0.01 (0.05) | 0.10 < x < Inf | −0.34 (0.02) |
| Malaysia | −Inf < x < −0.05 | −0.16 (0.04) | 0.06 < x < Inf | −0.20 (0.03) |
| Philippines | −Inf < x < −0.07 | 0.10 (0.05) | 0.09 < x < Inf | −0.53 (0.04) |
| Taiwan | −Inf < x < −0.09 | −0.00 (0.05) | 0.09 < x < Inf | −0.15 (0.04) |
| Thailand | −Inf < x < −0.07 | 0.37 (0.02) | 0.10 < x < Inf | −0.23 (0.03) |
| Multivariate Normal VaR | t-Copula VaR | Gaussian Copula VaR | |
|---|---|---|---|
| Panel A. G7 Stock Markets | |||
| 99% VaR | 11.81% | 14.67% | 14.65% |
| 99%CVaR | 13.48% | 18.35% | 18.01% |
| Panel B. BRICS Markets | |||
| 99% VaR | 15.10% | 19.33% | 18.53% |
| 99%CVaR | 17.30% | 23.09% | 21.77% |
| Panel C. Emerging Markets | |||
| 99% VaR | 12.77% | 15.21% | 14.90% |
| 99%CVaR | 14.59% | 19.71% | 19.06% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trabelsi, N.; Tiwari, A.K. Market-Risk Optimization among the Developed and Emerging Markets with CVaR Measure and Copula Simulation. Risks 2019, 7, 78. https://doi.org/10.3390/risks7030078
Trabelsi N, Tiwari AK. Market-Risk Optimization among the Developed and Emerging Markets with CVaR Measure and Copula Simulation. Risks. 2019; 7(3):78. https://doi.org/10.3390/risks7030078
Chicago/Turabian StyleTrabelsi, Nader, and Aviral Kumar Tiwari. 2019. "Market-Risk Optimization among the Developed and Emerging Markets with CVaR Measure and Copula Simulation" Risks 7, no. 3: 78. https://doi.org/10.3390/risks7030078
APA StyleTrabelsi, N., & Tiwari, A. K. (2019). Market-Risk Optimization among the Developed and Emerging Markets with CVaR Measure and Copula Simulation. Risks, 7(3), 78. https://doi.org/10.3390/risks7030078






