Quantile Regression with Telematics Information to Assess the Risk of Driving above the Posted Speed Limit

Abstract

We analyzed real telematics information for a sample of drivers with usage-based insurance policies. We examined the statistical distribution of distance driven above the posted speed limit—which presents a strong positive asymmetry—using quantile regression models. We found that, at different percentile levels, the distance driven at speeds above the posted limit depends on total distance driven and, more generally, on factors such as the percentage of urban and nighttime driving and on the driver’s gender. However, the impact of these covariates differs according to the percentile level. We stress the importance of understanding telematics information, which should not be limited to simply characterizing average drivers, but can be useful for signaling dangerous driving by predicting quantiles associated with specific driver characteristics. We conclude that the risk of driving for long distances above the speed limit is heterogeneous and, moreover, we show that prevention campaigns should target primarily male non-urban drivers, especially if they present a high percentage of nighttime driving.

1. Objective

Every kilometer driven above the posted speed limit increases the risk of accident. This is the hazard to which the driver, the passengers in the vehicle, and those in vehicles on the same stretch of road expose themselves. The main objective of this paper is to analyze, in a real case telematics data set, the distribution of the distance traveled at speeds above posted limits and to show that it is dependent on the total distance driven and other factors, which include the percentages of urban and nighttime driving and the driver’s gender. If we only model the mathematical expectation, i.e., the average distance driven at speeds above the posted limits, significant relationships are likely to be found with a number of telematics covariates. However, here, we consider quantile regression to determine whether the impact of certain factors might differ depending on the percentile being analyzed.

When quantile regression slopes differ depending on the level, the risk of driving above the posted speed limit is not homogeneous across all drivers, begging the question as to how this risk might be predicted or measured. Thus, in this paper, we also seek to show how specific driver characteristics can help predict a driver’s expected ranking; that is, not in relation to the whole population, but to similar drivers.

The rest of this paper is organized as follows. In Section 2, we present the background to this study. In Section 3, the theory of quantile regression modelling and the data set used in this study are presented. In Section 4, the results are discussed and, finally, in Section 5, we outline the conclusions that can be drawn.

2. Background

There is much evidence pointing to the relationship between elevated vehicle speeds and the risk of collision (see Ossiander and Cummings 2002; Vernon et al. 2004, among others) in the literature. Likewise, the effectiveness of speed cameras in the reduction of road traffic collisions and related casualties has been extensively demonstrated (see Pilkington and Kinra 2005; Wilson et al. 2006, among others), which would seem to confirm that high speeds increase the risk of collision. Speeding, moreover, has been shown to be directly related to the severity of accidents (see, among others, Dissanayake and Lu 2002; Jun et al. 2007, 2011), while Yu and Abdel-Aty (2014) report that marked variations in speed prior to a crash increase the likelihood of severe accidents.

Not all drivers present the same tendency to exceed the posted speed limit. More specifically, evidence of gender differences in driving patterns has been reported in many articles (see Ayuso et al. 2014, 2016a, 2016b). It has been shown that, compared to women, men present riskier driving behavior, driving more kilometers per day, during the night, and at speeds above the limit. All these factors have been shown to be related to a greater number of accidents (Gao et al. 2019a; Gao and Wüthrich 2019; Guillen et al. 2019). For example, Paefgen et al. (2014) found that the risk of accident is higher at nightfall, during the weekends on urban roads, and at low-range (0–30 km/h) or high-range speeds (90–120 km/h).

Speed control has recently come under investigation in connection with advanced driver assistance systems (ADAS) and semi-autonomous vehicles. Pérez-Marín and Guillen (2019), for example, analyzed the contribution of telematics information and usage-based insurance (UBI) research in identifying the effect of driving patterns—above all, speeding—on the risk of accident. The authors used a predictive model of the number of claims in a portfolio of insureds as their starting point for addressing risk quantification in relation to vehicles exceeding the speed limit. They concluded that if excess speeds could be eliminated, the expected number of accident claims could be reduced by half, in the average conditions prevailing in their real UBI dataset. Pérez-Marín et al. (2019) show that young drivers tend to reduce posted speed limit violations after an accident.

It has also been demonstrated that both the mean speed and the coefficient of variation of speed are relevant risk factors (Taylor et al. 2002). Moreover, interest has been expressed in the percentile assessment of the speed distribution, as opposed to just the mean. In this regard, Hewson (2008) claims that controlling the 85th percentile speed is common when designing road safety interventions. The same author also examined the role of quantile regression for modelling this percentile and specifically demonstrated its potential benefits when evaluating whether or not an intervention is able to significantly modify the 85th percentile speed.

Hewson (2008) based his analysis on a data set of observations on approximately 100 vehicle speeds at each of 14 pairs of sites recorded before, right after, and some time after the intervention (the installation of warning signs, in this instance). However, here, we apply quantile regression to an analysis of the effects of telematics information on a range of percentiles of the distance travelled at speeds above the limit, rather than to the speed measured at one specific moment in time.

We should stress that the objective of our paper is not the same as Hewson’s (2008), inasmuch as we do not seek to evaluate a particular safety intervention. Our aim is to understand conditional quantiles of distance traveled, possibly at different moments, rather than an instant speed measurement. To do so, our analysis was based on real telematics information from a sample of drivers covered by a UBI policy. This means that, in addition to speed, we analyzed other telematics variables, such as the location and time of driving and the total distance travelled by each driver in the sample.

3. Methods

3.1. Quantile Regression

Our quantile regression model follows the same notation as that used in Koenker and Hallock (2001). Thus, in the classical multiple linear regression model, the response y is modeled as follows:

$$y_i=x_i^T\beta +{ϵ}_i,$$

where $x_i=\left(1,x_{i1},\dots ,x_{ip}\right),$ in which p is the number of explanatory variables, β is the vector of coefficients such that $\beta =\left({\beta }_0,{\beta }_1,\dots ,{\beta }_p\right)$, and ϵ is the random term with distribution N(0, σ²). When we model the conditional mean response, the Gaussian likelihood function is given by the following:

$$L\left(\beta \right)\propto exp\left\{-\frac{1}{2{\sigma }^2}{{\displaystyle \sum }}_{i=1}^n{\left(y_i-x_i^T\beta \right)}^2\right\}.$$

The least squares estimation of β is obtained by maximizing L(β) over β. Fitting a regression model to an asymmetric dependent variable, that is also conditionally asymmetric on the explanatory variables, is fine if one is interested in the mean, but the point here is to analyze asymmetry.

As we aim to estimate a conditional quantile function 100α%, rather than a conditional mean, we need to use a quantile regression model (see Koenker and Hallock 2001; Yu et al. 2003; Hewson 2008, among others). The objective function to be minimized in this case equals the following:

$$L_{\alpha }\left(\beta \right)={{\displaystyle \sum }}_{i=1}^n{\rho }_{\alpha }\left(y_i-x_i^T\beta \right)\left\{\right\},$$

(1)

where the expression contains an asymmetric loss function, ${\rho }_{\alpha }$. To explain just what this asymmetric loss function is, we need to introduce some notation. We consider that the 100α% quantile of the residual ϵ is the 100α% largest value (that is, it has 100α% of values smaller than it and 100(1 − α)% of values larger than it). Quantile regression, therefore, involves finding estimates $\widehat{\beta }$, where 100α% of the residuals are below zero and 100(1 − α)% are above zero. We use an indicator function, $I_A$, on the set A, as follows:

$$I_A\left(\delta \right)=\{\begin{array}{cc}1& \delta \in A\\ 0& \delta \notin A\end{array}.$$

The loss function ${\rho }_{\alpha }$ can then be defined as follows:

$${\rho }_{\alpha }\left(\delta \right)=\alpha \delta I_{\delta \ge 0}\left(\delta \right)-\left(1-\alpha \right)\delta I_{\delta <0}\left(\delta \right),$$

for any value of α between 0 and 1. Finding the values of $\widehat{\beta }$ that maximize the likelihood of the quantile regression model is the same as finding the values of $\widehat{\beta }$ that minimize this loss function. The objective Function (1) can be minimized by using linear programming techniques. As noted by Koenker and Hallock (2001), for minimizing a sum of asymmetrically weighted absolute residuals, simply giving differing weights to positive and negative residuals would yield the quantiles. The function qr of the quantreg R package (Koenker et al. 2018) can be used to fit a quantile regression model. Koenker and Machado (1999) proposed a goodness-of-fit criterion for quantile regression analogous to the R² statistic in linear regression, which we have also implemented here. The criterion is calculated as 1 − $\widehat{L_{\alpha }\left(\beta \right)}/\widetilde{L_{\alpha }\left(\beta \right)},$ where $\widehat{L_{\alpha }\left(\beta \right)}$ is the value of objective Function (1) where all covariates are included in the model specification (unrestricted model), whereas $\widetilde{L_{\alpha }\left(\beta \right)}$ is the value of the objective function when only an intercept is considered (restricted model).

3.2. The Data

The data set comprises a sample of 9614 drivers with UBI coverage, which targets drivers between the ages of 18 and 35, for the whole of 2010. The variables are presented in

Table 1. Variable description.

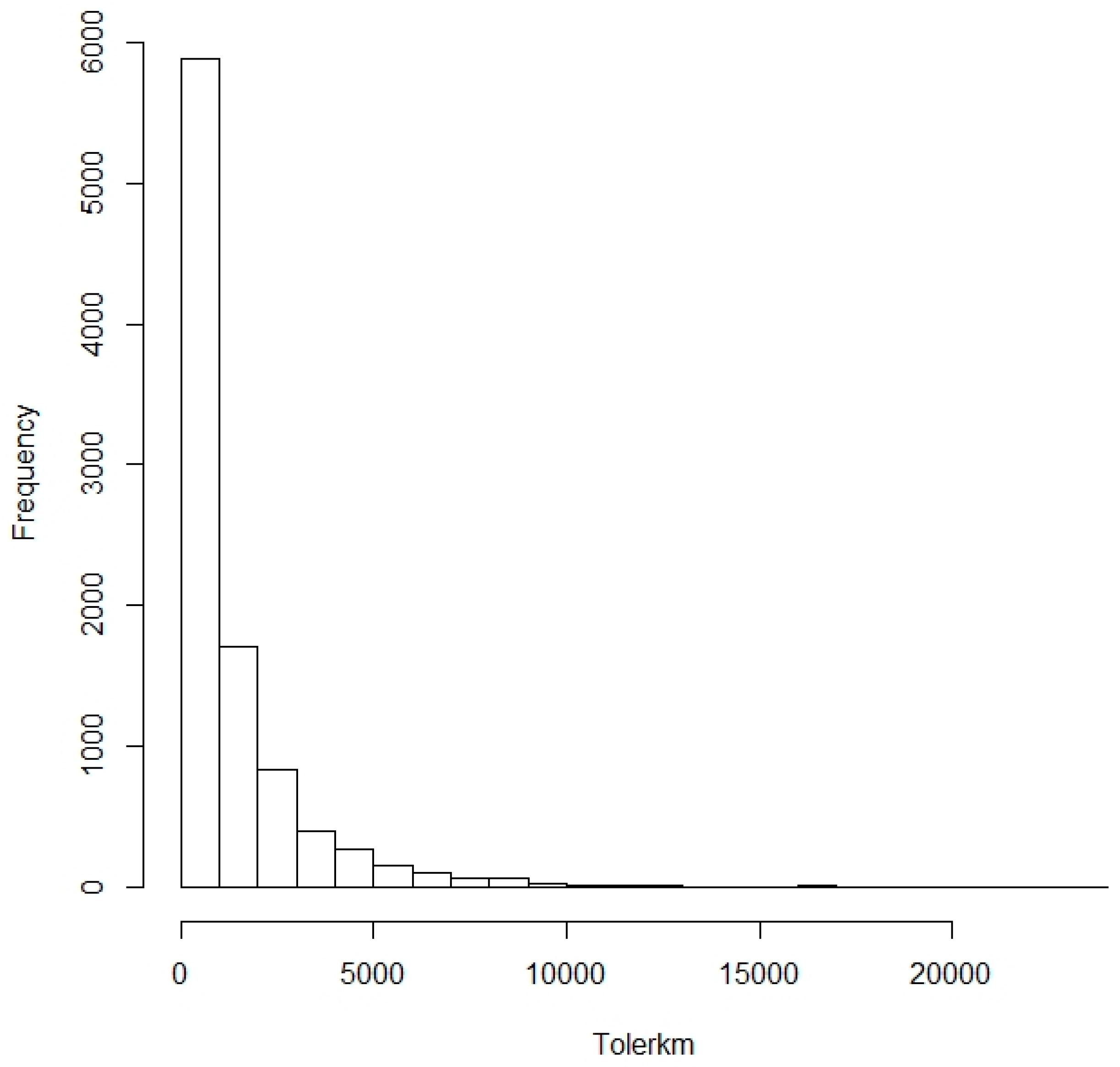
Variable	Description
Tolerkm	Number of kilometers driven at speeds above the posted limit during 2010.
Km	Total number of kilometers driven during 2010.
Lnkm	Logarithm of the total number of kilometers driven during 2010.
Pkdr_vurba	% of kilometers driven on urban roads during 2010.
Pkdr_nocturn	% of kilometers driven at night (between midnight and 6 am.) during 2010.
Age	Age of the driver at the beginning of 2010.
Gender	1 = Male, 0 = Female

. Age is the age of the driver at the beginning of 2010. We also have information on gender (Gender), total number of kilometers (km) driven during 2010 (km), and its natural logarithm (Lnkm). We also have information on the number of kilometers driven at speeds above the posted limit (Tolerkm, which is the dependent variable), the percentage of kilometers driven on urban roads (Pkdr_vurba) and, finally, percentage of kilometers driven at night (Pkdr_nocturn). All the drivers had UBI coverage throughout the whole of 2010 and all the telematics variables refer to this year. Note that we considered the natural logarithm of km, Lnkm, as it has been shown that distance travelled has a nonlinear effect on the risk of an accident (see Boucher et al. 2013). In the Appendix A, we also present the results of the model and the examples where we have removed Lnkm and, instead, we introduce km and km squared.

The gender distribution of the sample is 49% women and 51% men.

Table 2. Descriptive statistics.

Variable	Min	1st Qu	Median	Mean	3rd Qu	Max	St. Dev.	Skewness
Tolerkm	0.00	282.40	689.20	1398.20	1701.60	23,500.20	1995.37	3.64
Km	0.69	7530.56	11,697.82	13,063.71	17,337.00	57,756.98	7715.80	1.08
Lnkm	−0.37	8.93	9.37	9.27	9.76	10.96	0.75	−1.87
Pkdr_vurba	0.00	15.60	23.39	26.29	34.32	100.00	14.18	1.03
Pkdr_nocturn	0.00	2.48	5.31	7.02	9.84	78.56	6.13	1.67
Age	18.11	22.66	24.63	24.78	26.88	35.00	2.82	0.11

shows that the average age of drivers in the sample is 24.78 years. The average number of kilometers travelled during the year was 13,063.71 (standard deviation of 7715.80). We also observed that, on average, drivers travel 26.29% of kilometers on urban roads and 7.02% of kilometers at night. The mean kilometers travelled at speeds above the limit (Tolerkm, dependent variable) is 1,398.20, while its median is 689.20. Tolerkm has positive asymmetry (skewness coefficient equals 3.64); the distribution has a long tail, as can be observed in Figure 1. The rest of the variables also present some degree of skewness, but not as high as Tolerkm.

4. Results

We fitted a multiple linear regression model to the variable Tolerkm, although we consider it unsuitable insofar as the dependent variable is highly asymmetric. The variable km was included in the model as its natural logarithm (variable Lnkm), as it produced a better fit. Parameter estimates are shown in

Table 3. Parameter estimates of the linear regression model.

	Parameter Estimate (p-Value)
Intercept	−8082.506 (<0.0001)
Lnkm	1064.506 (<0.0001)
Pkdr_vurba	−21.868 (<0.0001)
Pkdr_nocturn	7.536 (0.0101)
Age	−1.131 (0.8565)
Gender	328.009 (<0.0001)
R2	25.96%

. The R-squared goodness-of-fit statistic equals 0.26.

All the explanatory variables have a significant effect except for Age, which is attributable to the fact that UBI policies were sold primarily to young drivers and, so, the age range in the sample is not wide. Note that most of drivers (see Table 1) are under 25 years of age, so we may either have not too many older drivers or, really, this factor may have no effect. Lnkm and Pkdr_nocturn present positive parameter estimates, indicating that increases in the total number of kilometers driven and in the percentage of km driven at night contribute to increasing the expected number of kilometers driven at speeds above the posted limits. Pkdr_vurba, in contrast, has the opposite effect, the higher the percentage of kilometers driven on urban roads, the lower the expected number of kilometers driven at speeds above the posted limit. Finally, gender (indicating males) has a positive parameter estimate, meaning that, on average, men drive more kilometers at speeds above the posted limit than women.

To fulfil the objectives identified in the first section and, at the same time, to address the strong positive asymmetry, a grid of quantile regressions with different percentiles were fitted to the data. The results of the quantile regression models are presented in

Table 4. Parameter estimates of the quantile regression model for different percentiles.

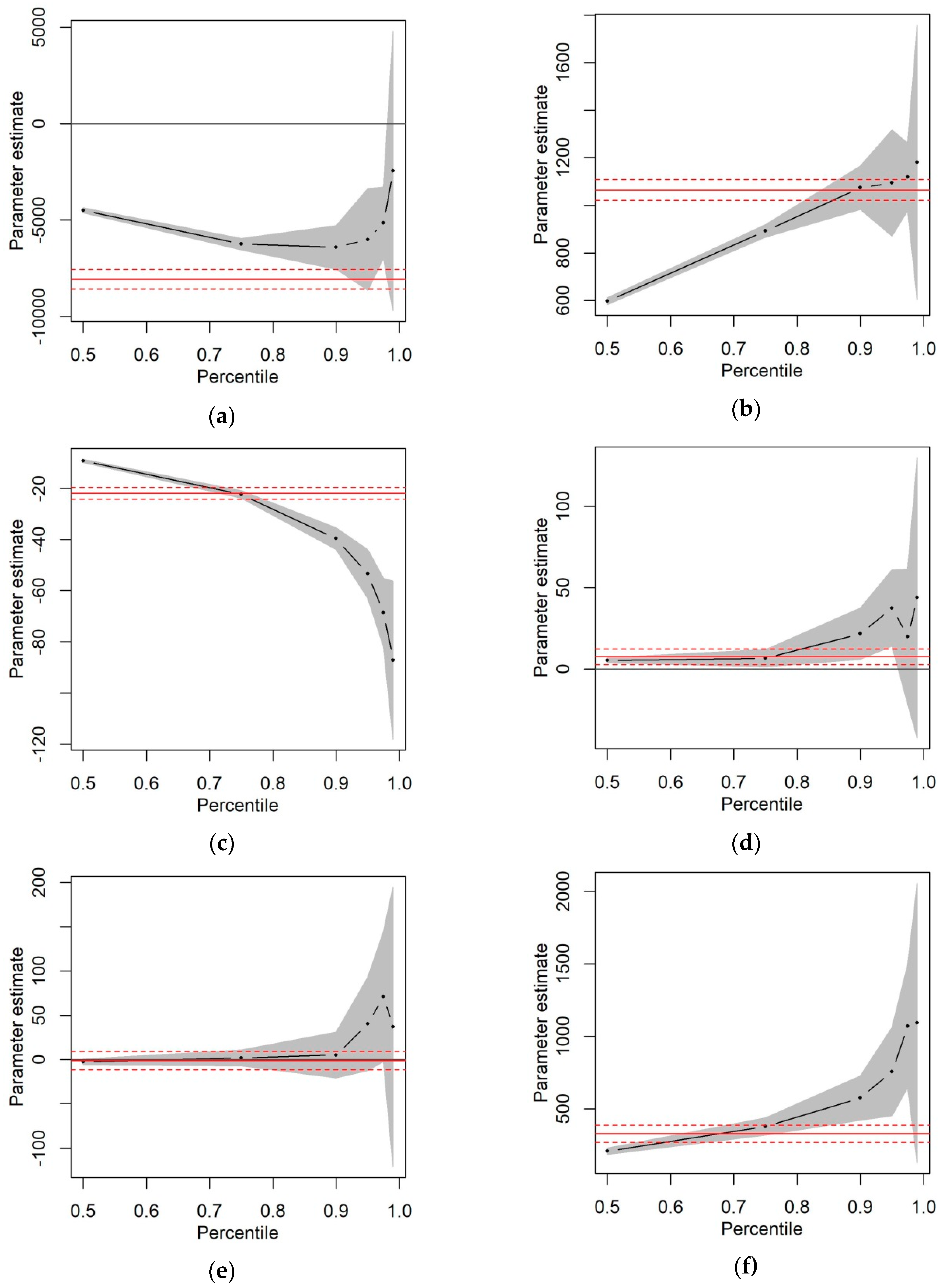
	50th Percentile (p-Value)	75th Percentile (p-Value)	90th Percentile (p-Value)	95th Percentile (p-Value)	97.5th Percentile (p-Value)	99th Percentile (p-Value)
Intercept	−4496.53 (<0.0001)	−6250.34 (<0.0001)	−6418.11 (<0.0001)	−6009.63 (<0.001)	−5137.24 (<0.0001)	−2451.17 0.5780
Lnkm	597.60 (<0.0001)	892.80 (<0.0001)	1074.66 (<0.0001)	1094.57 (<0.0001)	1119.94 (<0.0001)	1180.21 (<0.001)
Pkdr_vurba	−9.19 (<0.0001)	−22.26 (<0.0001)	−39.59 (<0.0001)	−53.44 (<0.0001)	−68.58 (<0.0001)	−87.12 (<0.0001)
Pkdr_nocturn	5.41 (<0.0001)	6.71 (0.0363)	21.76 (0.0226)	37.49 (0.0086)	20.01 (0.4266)	43.86 (0.4014)
Age	−2.56 (0.1632)	1.84 (0.7298)	5.16 (0.7419)	40.29 (0.2086)	71.28 (0.1094)	36.87 (0.7009)
Gender	206.76 (<0.0001)	377.94 (<0.0001)	574.08 (<0.0001)	755.87 (<0.0001)	1070.06 (<0.0001)	1091.38 (0.0624)
Goodness-of-fit criterion	14.19%	18.26%	20.23%	20.27%	20.56%	20.06%

. Each column shows the parameter estimates of the quantile regression at the following percentiles: 50th, 75th, 90th, 95th, 97.5th, and 99th. In general, significant parameter estimates are the same as those found in the multiple linear regression model shown in Table 3. However, the results in Table 4 show that the covariates have different marginal effects on conditional quantiles, depending on the estimated percentile. These changes in the parameters, depending on the quantile level at which the model is specified, are clearly illustrated in Figure 2 and are discussed in detail below.

First, Table 4 shows that the percentage of kilometers driven at night presents a highly significant effect when we estimate the 50th percentile and that it remains significant—at the 5% level—but with a larger p-value, when we estimate the 75th, 90th, and 95th percentiles. Likewise, the effect of gender is positive and significant at the 5% significance level for all quantiles, except for the 99th percentile. In the case of the 99th percentile, only Lnkm and Pkdr_vurba present a significant effect, while the rest of the parameters are no longer significant at the 5% level, including the model intercept. The lack of significance may be explained by the wider confidence intervals at a 5% level of significance, observed in Figure 2 for the 99th percentile. Table 4 also shows the values of the goodness-of-fit criterion and we observe that the contribution to explain the quantiles of the model with covariates with respect to the model without covariates is higher for extreme percentiles.

Second, Table 4 and Figure 2 also show that the magnitude of the marginal effects of variables with significant parameters in the models differs depending on the level of the estimated quantile. Specifically, the marginal effect of Lnkm increases as the level of the estimated quantile increases (being equal to 597.6 and 1180.2 for the 50th and 99th percentiles, respectively). The same pattern, albeit less pronounced, is observed for the marginal effect of Pkdr_nocturn, which increases as the level of the estimated quantile increases (being equal to 5.41 and 37.49 for the 50th and 95th percentiles, respectively). In the case of Pkdr_vurba, the marginal effect is always negative, but in absolute terms it increases with the level of the estimated quantile (being equal to −9.19 and −87.12 for the 50th and 99th percentiles, respectively). Finally, the marginal effect of gender is always positive and increases with the level of the estimated quantile (being equal to 206.76 and 1070.06 for the 50th and 97.5th, respectively).

It is interesting to compare the results of the quantile regression for the 75th and 95th percentiles. Thus, the model intercept is quite similar in both models. A comparison of the marginal effect of Lnkm shows that a one-unit increase in Lnkm (equivalent to multiplying km by 2.718), increases the 75th percentile of the number of kilometers driven at speeds above the posted limit by 892.80 km, while the 95th percentile increases by 1094.57 km, ceteris paribus. In the case of Pkdr_vurba, increasing the percentage of kilometers driven in urban areas by one percentage unit reduces the 75th percentile of the number of kilometers driven at speeds above the posted limit by 22.26 km and by 53.44 km at the 95th percentile, ceteris paribus. On the other hand, being a man increases the 75th percentile of the number of kilometers driven at speeds above the posted limit by 377.94 km and by 755.87 km at the 95th percentile, ceteris paribus. Finally, increasing the percentage of kilometers driven at night by one percentage unit increases the 75th percentile of the number of kilometers driven at speeds above the limit by 6.71 km and by 37.49 km at the 95th percentile, ceteris paribus.

Finally,

Table 5. Estimates of the conditional percentiles for drivers with different characteristics, each of whom has driven 600 km above the posted speed limit.

	Driver 1	Driver 2	Driver 3
Km	12,000	8000	5500
Pkdr_vurba	80	75	80
Pkdr_noctur	14	11	10.5
Age	25	25	25
Gender	1	1	1
Estimated conditional percentile 1	50th	75th	90th

¹ The estimated conditional percentile is found by locating the quantile level that produces a response equal to 600 km, given the exogenous characteristics (total kilometers driven, percent urban driving, percent nighttime driving, age, and gender) in the three example columns.

illustrates how the model can be implemented for predictive purposes. Let us consider three drivers with different characteristics, each of whom has driven exactly 600 km above the posted speed limit. Compared to the general population, and without conditioning on specific characteristics, these three drivers present a distance driven at excess speeds below the median (689.20 km) and, as such, can be considered relatively safe drivers. However, the key is to calculate the percentile risk level of the response variable given the specific characteristics of each driver. Indeed, it seems obvious that a distance of 600 km driven above the posted speed limit does not denote the same level of risk for an urban driver (who probably does a lot of driving in congested areas), as it does for a driver who drives largely outside the city limits. Most notably, the risk depends on the total distance driven. If we use the grid of different percentiles (Table 4) to make our predictions, it can be seen that, for a distance of 600 km driven above the speed limit, driver 1 lies at the 50th percentile, indicative of median risk. In contrast, driver 2 lies at the 75th percentile and, so, has a higher risk score when taking his driving characteristics into account. Finally, driver 3 lies at the 90th percentile, indicative of a very high risk.

5. Conclusions

We have shown that the distribution of the distance driven above the posted speed limit is not homogeneous with respect to certain driver characteristics. As such, quantile regression is an interesting tool for analyzing risk when telematics information is available. On the assumption that quantiles of distance driven above the speed limit represent a valuable risk measure, our model allows us to identify the factors associated with higher quantile values and, therefore, with risky drivers. This information is valuable in terms of providing preventive early warnings.

We also find that the impact of each additional kilometer driven is much greater in higher quantiles than in lower quantiles. Note that we specify a log-linear relationship between total distance driven and distance driven above the posted speed limits, which means there is a decreasing marginal effect on the latter as total distance increases.

One limitation of our analysis is that the degree to which drivers exceeded the posted limit was not recorded by the telematics equipment. Thus, we are unable to examine the magnitude of the speed violation.

We believe that UBI will soon develop into a scheme that can improve aspects of both service and protection in the sector. As insurance services are reinvented, risk scores and the identification of potential niches of drivers with risky patterns provide new ways of keeping drivers better informed and for promoting safe driving. Models such as those presented in this paper should enable insurers to design predictive models of driver risk and fix personalized indicators. In the application presented here, it could be argued that excess speed is the only feature a driver can modify, given that all other factors, including age, gender, total distance driven, and percentages of nighttime and urban driving, are dictated by external circumstances, such as distance from home to work place and by personal or professional obligations. This means the quantile regression model would predict the total distance driven above the posted speed limit percentile, given that particular set of external circumstances and, thus, it would allow the percentile risk score of the driver to be calculated by controlling for those circumstances and not for the whole population of drivers. Estimating a driver’s rank with regard to distance driven above the posted speed limit is personalized information that should constitute interesting feedback for policy holders. Indeed, safety measures and even telematics-based insurance should segment the population of drivers accordingly. Guillen et al. (2019) confirm that speed limit violations and driving in urban areas increase the expected number of accident claims. Gao et al. (2019b) analyzed the driving characteristics at different speeds and their predictive power for claims frequency modeling. Given that speed is the primary cause of severe accidents, these results should translate into lower insurance premiums for those who present a lower risk. In other words, if quantile-based behavior is considered rather than mathematical expectations of accident severity, the calculation of the premium to be paid should be improved. However, we leave questions as to how this rank might be converted into an insurance price and how information of a driver’s behavior might impact careful driving for further research.