On the Validation of Claims with Excess Zeros in Liability Insurance: A Comparative Study
Abstract
1. Introduction
2. Methodology and Notation
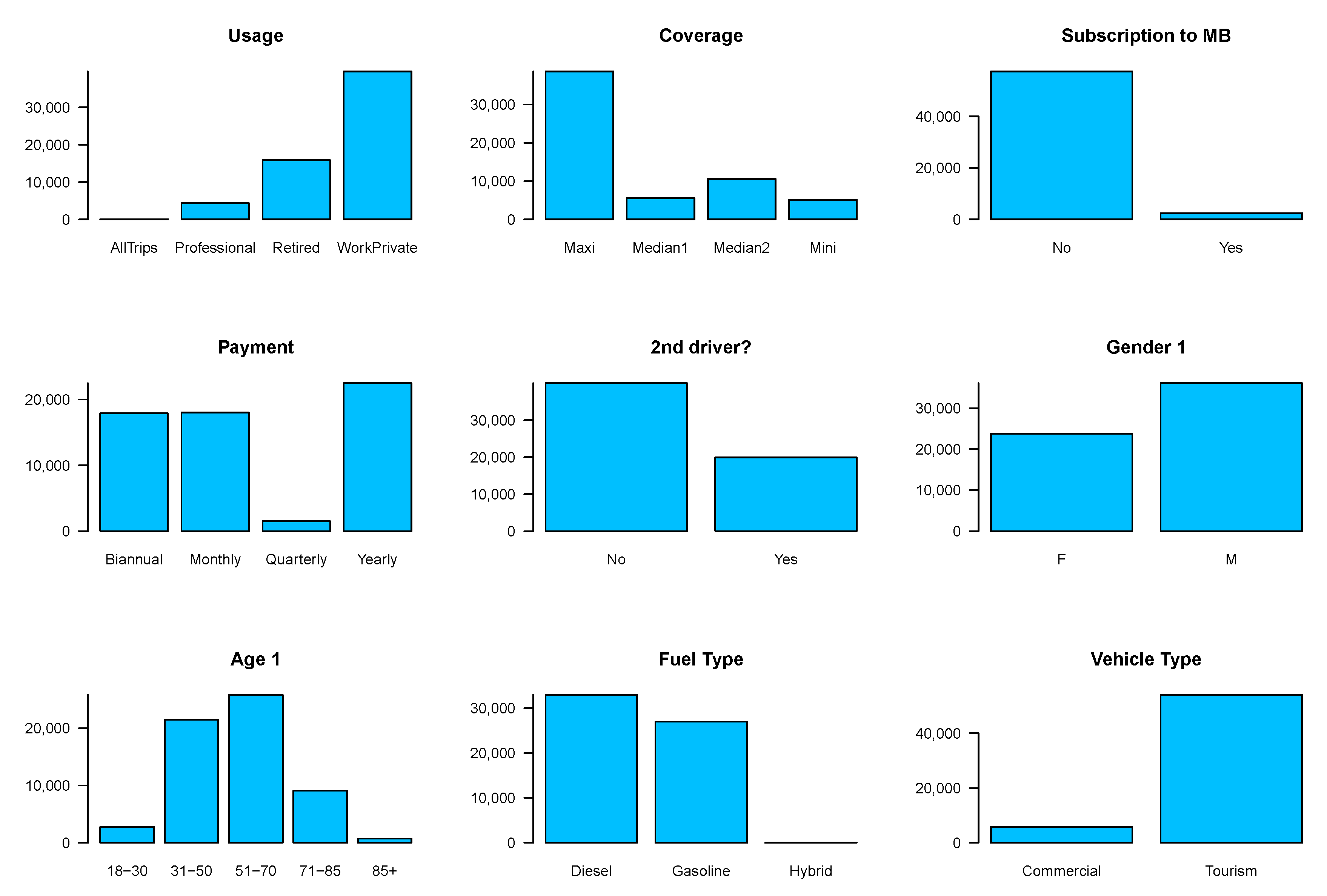
3. Data
4. Results
5. Validation
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
# Loading the prepared data
Data <- read.csv("Year0.csv", header = TRUE)
# Creating training and validation datasets
set.seed(123567)
random <- runif(dim(Data)[1])
# Training set is our data <<0.6
train <- random < 0.6
DataTrain <- cbind(Data, random, train)
# Validation set is everything not included in training set
valid <- !(train) ; DataValid <- cbind(Data, random, valid)
# Exporting our sets
write.csv(DataTrain[train == TRUE,], "DataTrain.csv")
write.csv(DataValid[valid == TRUE,], "DataValid.csv")
# Codes to produce Table~\ref{tab.2}:
DataTrain <- read.csv("DataTrain.csv", header = TRUE)
# Remove negative claim amounts
DataTrain$claim_amount[DataTrain$claim_amount < 30] <- 0
# Adjusting claim numbers
DataTrain$claim_nb <- DataTrain$claim_nb ∗ (DataTrain$claim_amount > 0)
# Removing zeros
DataTrain$drv_age2[DataTrain$drv_age2==0] <- NA
DataTrain$vh_value[DataTrain$vh_value==0] <- NA
DataTrain$vh_cyl[DataTrain$vh_cyl==0] <- NA
DataTrain$vh_weight[DataTrain$vh_weight==0] <- NA
DataTrain$drv_drv2[DataTrain$drv_drv2==0] <- NA
# Separating the training set into two sets of policies with and without claims
NClaim <- subset(DataTrain, DataTrain$claim_nb == 0)
Claim <- subset(DataTrain, DataTrain$claim_nb > 0)
# Calculations for all policies
Mydata <- data.frame(cbind(DataTrain$claim_nb, DataTrain$pol_duration,
DataTrain$pol_sit_duration, DataTrain$drv_age1, DataTrain$drv_age2,
DataTrain$vh_value, DataTrain$vh_age, DataTrain$vh_cyl,
DataTrain$vh_speed, DataTrain$vh_weight, DataTrain$vh_din))
Mean <- sapply(Mydata, mean, na.rm = TRUE)
SD <- sapply(Mydata, sd, na.rm = TRUE)
# Calculations for policies without claims
NMydata <- data.frame(cbind(NClaim$claim_nb, NClaim$pol_duration,
NClaim$pol_sit_duration, NClaim$drv_age1, NClaim$drv_age2,
NClaim$vh_value, NClaim$vh_age, NClaim$vh_cyl, NClaim$vh_speed,
NClaim$vh_weight,NClaim$vh_din))
NMean <- with(NClaim, sapply(NMydata, mean, na.rm = TRUE))
NSD <- with(NClaim, sapply(NMydata, sd, na.rm = TRUE))
# Calculations for policies with claims
CMydata <- data.frame(cbind(Claim$claim_nb, Claim$pol_duration,
Claim$pol_sit_duration, Claim$drv_age1, Claim$drv_age2,
Claim$vh_value, Claim$vh_age, Claim$vh_cyl, Claim$vh_speed,
Claim$vh_weight, Claim$vh_din))
CMean <- with(Claim, sapply(CMydata, mean, na.rm = TRUE))
CSD <- with(Claim, sapply(CMydata, sd, na.rm = TRUE))
# Modelling
DataTrain <- read.csv("DataTrain.csv", header = TRUE)
DataTrain$claim_amount[DataTrain$claim_amount < 30] <- 0
DataTrain$claim_nb <- DataTrain$claim_nb ∗ (DataTrain$claim_amount > 0)
# Re-leveling categorical variables:
DataTrain$drv_sex1_r <- relevel(factor(DataTrain$drv_sex1), ref = "M")
DataTrain$pol_coverage_r <- relevel(factor(DataTrain$pol_coverage), ref = "Maxi")
DataTrain$pol_pay_freq_r <- relevel(factor(DataTrain$pol_pay_freq), ref = "Yearly")
DataTrain$pol_payd_r <- relevel(factor(DataTrain$pol_payd), ref = "No")
DataTrain$pol_usage_r <- relevel(factor(DataTrain$pol_usage), ref = "WorkPrivate")
DataTrain$vh_fuel_r <- relevel(factor(DataTrain$vh_fuel), ref = "Diesel")
DataTrain$vh_type_r <- relevel(factor(DataTrain$vh_type), ref = "Tourism")
DataTrain$drv_drv2_r <- relevel(factor(DataTrain$drv_drv2), ref = "No")# Poisson regression
Model.poi <- glm(claim_nb ~ drv_age1 + drv_age2 + drv_sex1_r + drv_drv2_r + pol_sit_duration
+ pol_bonus + pol_coverage_r + pol_pay_freq_r + pol_payd_r + pol_usage_r
+ pol_duration + vh_fuel_r + vh_type_r + vh_din + vh_age + vh_speed,
data = DataTrain,
family = poisson(link = "log"), offset = log(Exposures), na.action = na.omit)
# Logistic regression
# y=1 represents claim and y=0 no claim
DataTrain$y[DataTrain$claim_nb==0] <- 0
DataTrain$y[DataTrain$claim_nb > 0] <- 1
# Model:
Model.log <- glm(y ~ drv_age1 + drv_age2 + drv_sex1_r + drv_drv2_r + pol_sit_duration
+ pol_bonus + pol_coverage_r + pol_pay_freq_r + pol_payd_r + pol_usage_r
+ pol_duration + vh_fuel_r + vh_type_r + vh_din + vh_age + vh_speed,
data = DataTrain,
family = binomial(link = "logit"), na.action = na.omit)# ZIP regression
library("pscl")
Model.zeropoi <- zeroinfl(claim_nb ~ drv_age1 + drv_age2 + drv_sex1_r + drv_drv2_r
+ pol_sit_duration + pol_bonus + pol_coverage_r + pol_pay_freq_r
+ pol_payd_r + pol_usage_r
+ pol_duration + vh_fuel_r + vh_type_r + vh_din + vh_age + vh_speed,
data = DataTrain, na.action = na.omit,
dist = "poisson", link = "logit")
# Validation:
# loading validation set
DataValid <- read.csv("DataValid.csv", header = TRUE)
DataValid$claim_amount[DataValid$claim_amount < 30] <- 0
DataValid$claim_nb <- DataValid$claim_nb ∗ (DataValid$claim_amount > 0)
#
DataValid$pol_coverage_r <- DataValid$pol_coverage
DataValid$vh_fuel_r <- DataValid$vh_fuel
DataValid$vh_type_r <- DataValid$vh_type
DataValid$pol_pay_freq_r <- DataValid$pol_pay_freq
DataValid$pol_payd_r <- DataValid$pol_payd
DataValid$drv_drv2_r <- DataValid$drv_drv2
DataValid$pol_usage_r <- DataValid$pol_usage
DataValid$drv_sex1_r <- DataValid$drv_sex1
DataValid$y[DataValid$claim_nb==0] <- 0
DataValid$y[DataValid$claim_nb > 0] <- 1
# Prediction:
predict.poi <- predict(Model.poi, DataValid, type = "response")
#
predict.log <- predict(Model.log, DataValid, type = "response")
#
predict.zeropoi <- cbind( DataValid, Mean = predict(Model.zeropoi,
DataValid, type = "response"),Probab = predict(Model.zeropoi,
DataValid, type = "prob"))
# Test for dispersion
library("AER")
dispersiontest(Model.poi,trafo=1)
Model.neg <- MASS::glm.nb(claim_nb ~ drv_age1 + drv_age2 + drv_drv2_r + pol_sit_duration
+ pol_bonus + pol_coverage_r + pol_payd_r + pol_usage_r
+ vh_fuel_r + vh_din + vh_age , data = DataTrain,
link = "log", na.action = na.omit)
odTest(Model.neg)
# Codes to predict zero claims:
sum(exp(-predict(Model.poi, DataValid, type = "response")))
sum(1-predict(Model.log, DataValid, type = "response"))
sum(predict(Model.zeropoi, DataValid, type = "prob")[,1])
References
- Ayuso, Mercedes, Montserrat Guillen, and Jens Perch Nielsen. 2019. Improving automobile insurance ratemaking using telematics: incorporating mileage and driver behaviour data. Transportation 46: 735–52. [Google Scholar] [CrossRef]
- Boucher, Jean-Philippe, Michel Denuit, and Montserrat Guillén. 2007. Risk classification for claim counts. North American Actuarial Journal 11: 110–31. [Google Scholar] [CrossRef]
- Boucher, Jean-Philippe, Michel Denuit, and Montserrat Guillen. 2009. Number of accidents or number of claims? An approach with zero-inflated Poisson models for panel data. The Journal of Risk and Insurance 76: 821–46. [Google Scholar] [CrossRef]
- Boucher, Jean-Philippe, Steven Côté, and Montserrat Guillen. 2017. Exposure as duration and distance in telematics motor insurance using generalized additive models. Risks 5: 54. [Google Scholar] [CrossRef]
- Cantoni, Eva, and Marie Auda. 2018. Stochastic variable selection strategies for zero-inflated models. Statistical Modelling 18: 3–23. [Google Scholar] [CrossRef]
- Chen, Kun, Rui Huang, Ngai Hang Chan, and Chun Yip Yau. 2019. Subgroup analysis of zero-inflated Poisson regression model with applications to insurance data. Insurance: Mathematics and Economics 86: 8–18. [Google Scholar] [CrossRef]
- Chowdhury, Shrabanti, Saptarshi Chatterjee, Himel Mallick, Prithish Banerjee, and Broti Garai. 2019. Group regularization for zero-inflated poisson regression models with an application to insurance ratemaking. Journal of Applied Statistics 46: 1567–81. [Google Scholar] [CrossRef]
- Dutang, Christophe, and Arthur Charpentier. 2019. CASdatasets: Insurance Datasets. Available online: http://dutangc.free.fr/pub/RRepos/web/CASdatasets-index.html (accessed on 15 March 2019).
- Fauzan, Muhammad Arief, and Hendri Murfi. 2018. The accuracy of XGBoost for insurance claim prediction. International Journal of Advances in Soft Computing and Its Applications 10: 159–71. [Google Scholar]
- Ferreira, Joseph, and Eric Minikel. 2012. Measuring per mile risk for pay-as-you-drive automobile insurance. Transportation Research Record: Journal of the Transportation Research Board 2297: 97–103. [Google Scholar] [CrossRef]
- Frees, Edward W., Richard A. Derrig, and Glenn Meyers. 2014. Predictive Modeling Applications in Actuarial Science, Volume I: Predictive Modeling Techniques. New York: Cambridge University Press. [Google Scholar]
- Frees, Edward W., Richard A. Derrig, and Glenn Meyers. 2016. Predictive Modeling Applications in Actuarial Science, Volume II: Case Studies in Insurance. New York: Cambridge University Press. [Google Scholar]
- Gao, Guangyuan, Shengwang Meng, and Mario V. Wüthrich. 2019. Claims frequency modeling using telematics car driving data. Scandinavian Actuarial Journal 2019: 143–62. [Google Scholar] [CrossRef]
- Guillen, Montserrat, Jens Perch Nielsen, Mercedes Ayuso, and Ana M. Pérez-Marín. 2019. The use of telematics devices to improve automobile insurance rates. Risk Analysis 39: 662–762. [Google Scholar] [CrossRef] [PubMed]
- Haberman, Steven, and Arthur E. Renshaw. 1996. Generalized linear models and actuarial science. The Statistician 45: 407–36. [Google Scholar] [CrossRef]
- Lambert, Diane. 1992. Zero-inflated Poisson regression, with an application to defects in manufacturing. Technometrics 34: 1–14. [Google Scholar] [CrossRef]
- Lee, Andy H., Mark R. Stevenson, Kui Wang, and Kelvin K. W. Yau. 2002. Modeling young driver motor vehicle crashes: Data with extra zeros. Accident Analysis and Prevention 34: 515–21. [Google Scholar] [CrossRef]
- Lemaire, Jean, Sojung Carol Park, and Kili C. Wang. 2015. The use of annual mileage as a rating variables. Astin Bulletin 46: 39–69. [Google Scholar] [CrossRef]
- Liu, Feng, and David Pitt. 2017. Application of bivariate negative binomial regression model in analysing insurance count data. Annals of Actuarial Science 11: 390–411. [Google Scholar] [CrossRef][Green Version]
- McCullagh, Peter, and John A. Nelder. 1998. Generalized Linear Models. London: Chapman and Hall. [Google Scholar]
- Murphy, Kevin P. 2012. Machine Learning—A Probabilistic Perspective. Cambridge: The MIT Press. [Google Scholar]
- Perumean-Chaney, Suzanne E., Charity Morgan, David McDowall, and Inmaculada Aban. 2013. Zero-inflated and overdispersed: What’s one to do? Journal of Statistical Computation and Simulation 83: 1671–83. [Google Scholar] [CrossRef]
- Spedicato, Giorgio Alfredo, Christophe Dutang, and Leonardo Petrini. 2018. Machine learning methods to perform pricing optimization. A comparison with standard GLMs. Variance, Casualty Actuarial Society 12: 69–89. [Google Scholar]
- Tang, Yanlin, Liya Xiang, and Zhongyi Zhu. 2014. Risk factor selection in rate making EM adaptive LASSO for zero-inflated Poisson regression models. Risk Analysis 34: 1112–27. [Google Scholar] [CrossRef]
- Tselentis, Dimitrios I., George Yannis, and Eleni I. Vlahogianni. 2017. Innovative motor insurance schemes: A review of current practices and emerging challenges. Accident Analysis and Prevention 98: 139–48. [Google Scholar] [CrossRef]
- Verbelen, Roel, Katrien Antonio, and Gerda Claeskens. 2018. Unraveling the predictive power of telematics data in car insurance pricing. Journal of the Royal Statistical Society: Series C (Applied Statistics) 67: 1275–304. [Google Scholar] [CrossRef]
- Weerasinghe, K. P. M. L. P., and M. C. Wijegunasekara. 2016. A comparative study of data mining algorithms in the prediction of auto insurance claims. European International Journal of Science and Technology 5: 47–54. [Google Scholar]
- Wilson, Paul, and Jochen Einbeck. 2018. A new and intuitive test for zero modification. Statistical Modelling. [Google Scholar] [CrossRef]
- Yip, Karen C. H., and Kelvin K. W. Yau. 2005. On modeling claim frequency data in general insurance with extra zeros. Insurance: Mathematics and Economics 36: 153–63. [Google Scholar] [CrossRef]
- Zeileis, Achim, Christian Kleiber, and Simon Jackman. 2008. Regression models for count data in R. Journal of Statistical Software 27: 1–25. [Google Scholar] [CrossRef]
| 1 | This happens due to subrogation rights of the insurer. |
| 2 | According to the game document, hybrid cars were not popular at the time of collecting this dataset. |


| Control | Policy | Driver (1 and 2) | Vehicle | Response |
|---|---|---|---|---|
| policy ID | bonus coefficient | driver 2? | age | number of claims |
| type of coverage | age | cylinder | ||
| duration | gender | din power | ||
| situation duration | fuel type | |||
| payment frequency | max speed | |||
| subscription to MB | type | |||
| usage | value | |||
| weight |
| Variables | All Policies | Policies without Claims | Policies with Claims | |||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | |
| Policy duration | ||||||
| Policy duration since the last change | ||||||
| Driver age 1 | ||||||
| Driver age 2 | ||||||
| Vehicle value | 18,086 | 8677.92 | 17,858 | 8618.47 | 19,894 | 8677.92 |
| Vehicle age | ||||||
| Engine cylinder | 1645 | 1,639 | 1,696 | |||
| Speed | ||||||
| Weight | 1164.36 | |||||
| Motor power (din) | ||||||
| Variables | Categories | Claim Frequency | Total | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |||
| Policy usage | WorkPrivate | 35,248 | 450 | 49 | 7 | 0 | 1 | 39,632 | |
| Retired | 14,193 | 191 | 20 | 3 | 0 | 0 | 15,869 | ||
| Professional | 544 | 76 | 10 | 0 | 0 | 0 | |||
| All trips | 41 | 10 | 1 | 0 | 0 | 0 | 0 | 52 | |
| Policy coverage | Maxis | 33,459 | 4,489 | 600 | 70 | 9 | 0 | 1 | 38,628 |
| Median 2 | 9,628 | 862 | 82 | 7 | 1 | 0 | 0 | 10,580 | |
| Median 1 | 412 | 32 | 2 | 0 | 0 | 0 | |||
| Mini | 130 | 4 | 0 | 0 | 0 | 0 | |||
| Subscription to MB | No | 50,946 | 693 | 76 | 10 | 0 | 1 | 57,440 | |
| Yes | 179 | 25 | 3 | 0 | 0 | 0 | |||
| Payment | Yearly | 20,094 | 263 | 25 | 3 | 0 | 1 | 22,492 | |
| Biannual | 15,930 | 1,746 | 199 | 29 | 3 | 0 | 0 | 17,907 | |
| Monthly | 15,880 | 234 | 23 | 4 | 0 | 0 | 18,016 | ||
| Quarterly | 166 | 22 | 2 | 0 | 0 | 0 | |||
| Policy with 2 drivers | No | 35,675 | 457 | 47 | 6 | 0 | 0 | 39,999 | |
| Yes | 17,536 | 2,079 | 261 | 32 | 4 | 0 | 1 | 19,913 | |
| Gender 1 | Male | 32,118 | 433 | 52 | 4 | 0 | 0 | 36,108 | |
| Female | 21,093 | 285 | 27 | 6 | 0 | 1 | 23,804 | ||
| Age 1 | 18–30 | 299 | 29 | 4 | 0 | 0 | 1 | ||
| 31–50 | 18,961 | 256 | 24 | 4 | 0 | 0 | 21,473 | ||
| 51–70 | 22,978 | 322 | 40 | 3 | 0 | 0 | 25,822 | ||
| 71–85 | 8,154 | 822 | 105 | 9 | 3 | 0 | 0 | ||
| 647 | 65 | 6 | 2 | 0 | 0 | 0 | 720 | ||
| Vehicle fuel | Diesel | 28,605 | 475 | 54 | 7 | 0 | 1 | 32,925 | |
| Gasoline | 24,565 | 241 | 25 | 3 | 0 | 0 | 26,938 | ||
| Hybrid | 41 | 6 | 2 | 0 | 0 | 0 | 0 | 49 | |
| Vehicle type | Tourism | 47,891 | 668 | 73 | 10 | 0 | 1 | 54,030 | |
| Commercial | 506 | 50 | 6 | 0 | 0 | 0 | |||
| Total | 53,211 | 5,893 | 718 | 79 | 10 | 0 | 1 | 59,912 | |
| Coefficients | Model 1: All Variables | Model 2: Stepwise Selection | Model 3: Only Significant | |||
|---|---|---|---|---|---|---|
| Estimate | p-Value | Estimate | p-Value | Estimate | p-Value | |
| Intercept | < | < | < | |||
| Age 1 | ||||||
| Age 2 | ||||||
| Female 1 | ||||||
| Driver2? | ||||||
| Situation duration | ||||||
| Bonus | < | < | < | |||
| Coverage(Med2) | < | < | < | |||
| Coverage(Med1) | < | < | < | |||
| Coverage(Mini) | < | < | < | |||
| Payment(biannual) | ||||||
| Payment(quarterly) | ||||||
| Payment(monthly) | ||||||
| Subscription to MB | ||||||
| Usage(retired) | ||||||
| Usage(professional) | ||||||
| Usage(all trips) | ||||||
| Duration | ||||||
| Fuel(gasoline) | < | < | < | |||
| Fuel(hybrid) | ||||||
| Type(commercial) | ||||||
| Din(power) | < | < | ||||
| Vehicle age | < | < | < | |||
| Vehicle speed | ||||||
| Log-likelihood | −23,207 | −23,207 | −23,216 | |||
| Degrees of freedom | 24 | 22 | 17 | |||
| AIC | 46,462 | 46,458 | 46,466 | |||
| BIC | 46,678 | 46,656 | 46,619 | |||
| Running time (s) | ||||||
| Coefficients | Model 1: All variables | Model 2: Stepwise Selection | Model 3: Only Significant | |||
|---|---|---|---|---|---|---|
| Estimate | p-Value | Estimate | p-Value | Estimate | p-Value | |
| Intercept | < | < | < | |||
| Age 1 | ||||||
| Age 2 | ||||||
| Female 1 | ||||||
| Driver2? | ||||||
| Situation duration | ||||||
| Bonus | < | < | < | |||
| Coverage(Med2) | < | < | < | |||
| Coverage(Med1) | ||||||
| Coverage(Mini) | < | < | < | |||
| Payment(biannual) | ||||||
| Payment(quarterly) | ||||||
| Payment(monthly) | ||||||
| Subscription to MB | ||||||
| Usage(retired) | ||||||
| Usage(professional) | ||||||
| Usage(all trips) | ||||||
| Duration | ||||||
| Fuel(gasoline) | < | < | < | |||
| Fuel(hybrid) | ||||||
| Type(commercial) | ||||||
| Din(power) | < | < | ||||
| Vehicle age | < | < | < | |||
| Vehicle speed | ||||||
| Log-likelihood | −20,292 | −20,293 | −20,299 | |||
| Degrees of freedom | 24 | 21 | 17 | |||
| AIC | 40,632 | 40,628 | 40,633 | |||
| BIC | 40,848 | 40,817 | 40,785 | |||
| Running time (s) | ||||||
| Coefficients | Model 1 * | Model 2 * | Model 3 * | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | p-Value | Estimate | p-Value | Estimate | p-Value | ||||
| Poisson (count) part | |||||||||
| Intercept | −2.2750 | < | −2.1404 | < | −2.0736 | < | |||
| Age 1 | 0.0066 | 0.0513 | 0.0063 | 0.0542 | 0.0046 | 0.1347 | |||
| Age 2 | 0.0012 | 0.6647 | 0.0013 | 0.6290 | 0.0019 | 0.4998 | |||
| Female 1 | −0.0448 | 0.4746 | −0.0479 | 0.4324 | |||||
| Driver2? | −0.0473 | 0.7366 | −0.0536 | 0.6972 | −0.0809 | 0.5584 | |||
| Situation duration | −0.0009 | 0.0194 | −0.0017 | 0.9282 | −0.0011 | 0.9558 | |||
| Bonus | 0.5787 | 0.2021 | 0.5953 | 0.2068 | 0.5433 | 0.2026 | |||
| Coverage(Med2) | −0.3670 | 0.0006 | −0.3734 | 0.0004 | −0.3646 | 0.0006 | |||
| Coverage(Med1) | −0.4294 | 0.0022 | −0.4231 | 0.0022 | −0.4269 | 0.0024 | |||
| Coverage(Mini) | −1.0487 | 0.0017 | −1.0599 | 0.0016 | −1.1031 | 0.0007 | |||
| Payment(biannual) | −0.0691 | 0.3318 | −0.0668 | 0.3472 | |||||
| Payment(quarterly) | -0.0569 | 0.7525 | −0.0452 | 0.8002 | |||||
| Payment(monthly) | 0.0091 | 0.8961 | 0.0137 | 0.8427 | |||||
| Subscription to MB | 0.0596 | 0.7580 | 0.0462 | 0.8099 | 0.0126 | 0.9486 | |||
| Usage(retired) | −0.0623 | 0.5523 | −0.0623 | 0.5455 | −0.0538 | 0.6006 | |||
| Usage(professional) | 0.0723 | 0.5491 | 0.0710 | 0.5063 | 0.0952 | 0.3725 | |||
| Usage(all trips) | 0.2543 | 0.6523 | 0.2375 | 0.6765 | −0.0332 | 0.9544 | |||
| Duration | −0.0043 | 0.2948 | −0.0025 | 0.1145 | |||||
| Fuel(gasoline) | −0.0346 | 0.6549 | −0.0387 | 0.6228 | −0.0759 | 0.3854 | |||
| Fuel(hybrid) | 0.6976 | 0.2553 | 0.7050 | 0.2500 | 0.6366 | 0.3302 | |||
| Type(commercial) | 0.0284 | 0.8457 | |||||||
| Din(power) | 0.0023 | 0.3055 | 0.0026 | 0.1207 | 0.0024 | 0.3063 | |||
| Vehicle age | 0.0024 | 0.7925 | 0.0032 | 0.1207 | 0.0063 | 0.4799 | |||
| Vehicle speed | 0.0010 | 0.7557 | |||||||
| Zero-inflation part | |||||||||
| Intercept | −0.5544 | 0.6449 | −0.4634 | 0.6883 | −0.4819 | 0.6826 | |||
| Age 1 | 0.0040 | 0.5922 | 0.0032 | 0.6558 | 0.0020 | 0.7736 | |||
| Age 2 | 0.0108 | 0.0653 | 0.0111 | 0.0546 | 0.0121 | 0.0356 | |||
| Female 1 | −0.1962 | 0.1572 | −0.2020 | 0.1358 | |||||
| Driver2? | −0.5491 | 0.0892 | −0.5633 | 0.0748 | −0.6165 | 0.0522 | |||
| Situation duration | 0.0331 | 0.3289 | 0.0309 | 0.3575 | 0.0387 | 0.2442 | |||
| Bonus | −0.8651 | 0.4958 | −0.8200 | 0.5308 | −1.0637 | 0.3802 | |||
| Coverage(Med2) | −0.3798 | 0.1014 | −0.3932 | 0.0848 | −0.3595 | 0.1139 | |||
| Coverage(Med1) | −0.4030 | 0.1541 | −0.3871 | 0.1601 | −0.3847 | 0.1645 | |||
| Coverage(Mini) | 0.2803 | 0.5949 | 0.2610 | 0.6222 | 0.2052 | 0.6923 | |||
| Payment(biannual) | −0.2596 | 0.0910 | −0.2547 | 0.0963 | |||||
| Payment(quarterly) | −0.5661 | 0.2637 | −0.5354 | 0.2798 | |||||
| Payment(monthly) | −0.1721 | 0.2518 | −0.1615 | 0.2751 | |||||
| Subscription to MB | 0.4226 | 0.2041 | 0.3978 | 0.2310 | 0.3560 | 0.3030 | |||
| Usage(retired) | −0.0775 | 0.7250 | −0.0783 | 0.7177 | −0.0533 | 0.8043 | |||
| Usage(professional) | −0.2215 | 0.4672 | −0.2273 | 0.4063 | −0.1510 | 0.5703 | |||
| Usage(all trips) | −0.3050 | 0.8550 | −0.3668 | 0.8345 | −1.8681 | 0.7405 | |||
| Duration | −0.0040 | 0.6448 | |||||||
| Fuel(gasoline) | 0.5066 | 0.0017 | 0.5002 | 0.0021 | 0.4090 | 0.0236 | |||
| Fuel(hybrid) | 114.80 | 0.1984 | 116.60 | 0.1890 | 1.0632 | 0.2829 | |||
| Type(commercial) | 0.0041 | 0.9901 | |||||||
| Din(power) | 0.0000 | 0.9944 | -0.0000 | 0.9959 | −0.0002 | 0.9627 | |||
| Vehicle age | 0.0696 | < | 0.0712 | < | 0.0756 | < | |||
| Vehicle speed | 0.0006 | 0.9258 | |||||||
| Log-likelihood | −23,044 | −23,045 | −23,054 | ||||||
| Degrees of freedom | 48 | 43 | 34 | ||||||
| AIC | 46,184 | 46,175 | 46,177 | ||||||
| BIC | 46,616 | 46,563 | 46,482 | ||||||
| Running time (s) | 16.719 | ||||||||
| Prob Zero Claims: Individual 1 ** | Prob Zero Claims: Individual 2 *** | Total No. of Zero Claims | Total No. of Non-Zero Claims | |||
|---|---|---|---|---|---|---|
| Observed value | 0 | 1 | 35,772 | 4316 | ||
| Poisson | Full model | 0.9016 | 0.8358 | 35,361.44 | 4726.56 | |
| Stepwise | 0.9019 | 0.8350 | 35,361.27 | 4726.73 | ||
| Significant | 0.9019 | 0.8410 | 35,360.50 | 4727.50 | ||
| Logistic | Full model | 0.9097 | 0.8475 | 35,606.88 | 4481.12 | |
| Stepwise | 0.9091 | 0.8480 | 35,606.95 | 4481.05 | ||
| Significant | 0.9102 | 0.8512 | 35,606.62 | 4481.38 | ||
| ZIP | Model 1 * | Count | 0.1024 | 0.1778 | 35,602 | 4486 |
| Zero | 0.9104 | 0.8446 | ||||
| Model 2 * | Count | 0.1016 | 0.1785 | 35,601.27 | 4486.74 | |
| Zero | 0.9113 | 0.8440 | ||||
| Model 3 * | Count | 0.1020 | 0.1710 | 35,601.06 | 4486.94 | |
| Zero | 0.9113 | 0.8495 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qazvini, M. On the Validation of Claims with Excess Zeros in Liability Insurance: A Comparative Study. Risks 2019, 7, 71. https://doi.org/10.3390/risks7030071
Qazvini M. On the Validation of Claims with Excess Zeros in Liability Insurance: A Comparative Study. Risks. 2019; 7(3):71. https://doi.org/10.3390/risks7030071
Chicago/Turabian StyleQazvini, Marjan. 2019. "On the Validation of Claims with Excess Zeros in Liability Insurance: A Comparative Study" Risks 7, no. 3: 71. https://doi.org/10.3390/risks7030071
APA StyleQazvini, M. (2019). On the Validation of Claims with Excess Zeros in Liability Insurance: A Comparative Study. Risks, 7(3), 71. https://doi.org/10.3390/risks7030071




