Abstract
In this paper, we apply machine learning to forecast the conditional variance of long-term stock returns measured in excess of different benchmarks, considering the short- and long-term interest rate, the earnings-by-price ratio, and the inflation rate. In particular, we apply in a two-step procedure a fully nonparametric local-linear smoother and choose the set of covariates as well as the smoothing parameters via cross-validation. We find that volatility forecastability is much less important at longer horizons regardless of the chosen model and that the homoscedastic historical average of the squared return prediction errors gives an adequate approximation of the unobserved realised conditional variance for both the one-year and five-year horizon.
Keywords:
benchmark; cross-validation; prediction; stock return volatility; long-term forecasts; overlapping returns; autocorrelation JEL Classification:
C14; C53; C58; G17; G22
1. Introduction
The volatility of financial assets has important implications for the theory and practice of asset pricing, portfolio selection, risk management, and market-timing strategies. Therefore, it is of fundamental interest to measure ex ante, or forecast successfully, the conditional variance of returns. Of course, the evaluation of the latter and the forecasting itself have been complicated by the unobservability of the realised conditional variance (Galbraith and Kisinbay 2005). An extensive amount of research is engaged in analysing the distributional and dynamic properties of stock market volatility; see, for example, Andersen et al. (2001) and citations therein. The standard approaches applied include parametric (G)ARCH-type or stochastic volatility models and estimate the underlying returns based on specific distributional assumptions. Alternatives, especially for data of higher frequency, are based on constructing model-free estimates of ex-post realized volatilities by adding up the squares and cross-products of intraday high-frequency returns (Andersen et al. 2001).
The present paper instead uses annual U.S. stock market data to construct excess stock returns at the one-year and five-year horizon and to examine their model-based variance forecasts. Note that the risk depends on the investment horizon considered and that different horizons are relevant for different applications (Christoffersen and Diebold 2000). Little is known about the forecastability of variance at horizons beyond a year. Here, we take the long-term actuarial view and extend the work of Kyriakou et al. (2019a, 2019b). In a two-step procedure, we first apply machine learning (ML) to predict stock returns in excess of different benchmarks, considering the short- and long-term interest rate, the earnings-by-price ratio, and the inflation rate. Second, the squared residuals are used to analyse model-based volatility forecastability. Here, we compare these forecasts with the forecast implicit in the unconditional residual variance, as proposed, for example, by Galbraith and Kisinbay (2005). We find that volatility forecastability is much less important at longer horizons regardless of the chosen model and that the homoscedastic historical average of the squared return prediction errors gives an adequate approximation of the unobserved realised conditional variance for both the one-year and five-year horizon.
Our preferred ML technique applied in this paper is local-linear smoothing in combination with a leave-k-out cross-validation for the following reasons.1 First, we are interested in longer-horizon stock returns based on annual observations and their volatility. Thus, we are not in the high-frequency context where the number of observations is huge and the set of possible predictive variable combinations is enormous (and, thus, dimension reduction or shrinkage are indispensable). Our data set is, instead, sparse and a careful imposition of structure to the statistical modelling process is much more promising, as shown, for example, by Nielsen and Sperlich (2003) and Scholz et al. (2015, 2016). Second, the evidence of stock return predictability is much stronger once one allows for nonlinear functions as documented, for example, in Lettau and Van Nieuwerburgh (2008); Chen and Hong (2010), or Cheng et al. (2019). Thus, the local-linear smoother is ideally suited as it can estimate a linear function—the classical benchmark in this context—without any bias. Finally, our procedures are analytically well studied, i.e., sound and rigorous, statistical tools which let us operate in a glasshouse, not in a black box—in contrast to other fancier but less clear ML methods.2
Note further that longer horizons are important to long-term investors, such as pension funds or market participants saving for distant payoffs. These investors are generally willing to take on more risk for higher rewards and, thus, volatility forecastability is for them of fundamental interest. Rapach and Zhou (2013) show that longer horizons tend to produce better estimates than shorter horizons, while Munk and Rangvid (2018) point out that major finance houses today use longer horizons—up to ten years—to stabilise and improve future predictions. In our paper, we exemplarily concentrate on the one-year and five-year view.3 However, shorter horizons based on monthly, weekly, or even daily data do not seem to provide the pension saver with good information about future income as a pensioner. Therefore, these type of short-term predictions—sometimes called investment robots—are not suitable when a pensioner should define his or her risk appetite.
The remaining of this paper is organized as follows. Section 2 presents our framework for the purpose of conditional variance prediction. We define the underlying financial model, introduce our two-step procedure, and present our validation criterion for model selection. In addition, we review different ways of estimating the conditional variance and discuss bootstrap-tests for the null hypothesis of no predictability. In Section 3, we provide a description of our data set and of our empirical findings from different validated scenarios: (i) a single benchmarking approach that uses the dependent variable transformed with the benchmark, and (ii) the case where both the independent and dependent variables are transformed with the benchmark (full benchmarking approach). Finally, we take the long-term view and comment on real income pension prediction. Section 4 summarizes the key points of our analysis and concludes the paper.
2. A Framework for Conditional Variance Prediction
In this section, we focus on nonlinear predictive relationships between squared residuals of model-based predicted stock returns over the next T years in excess of a benchmark and a set of explanatory variables. Our aim is the investigation of different benchmark models and their volatility predictability over return horizons of one year and five years. We consider four different benchmarks: the short- and the long-term interest rate, the earnings-by-price ratio, and the inflation rate.
2.1. One-Year Predictions
Let denote the (nominal) stock price at the end of year t and the (nominal) dividends paid during year t. We investigate stock returns in excess (log-scale) of a given benchmark :
where with, respectively,
using the short-term interest rate, , the long-term interest rate, , the earnings accruing to the index in year t, , and the consumer price index for year t, . The predictive and fully nonparametric regression model for a one-year horizon is then given by the location-scale model
where
are unknown smooth functions for the conditional mean and variance, resp., are serially uncorrelated zero-conditional-mean random error terms, given the past, with the conditional variance of one, and is a q-dimensional vector of available explanatory variables.4
Our aim is to forecast the conditional variance of excess stock returns based on model (2) and popular explanatory variables with predictive power reported in the literature, for example, the dividend-by-price ratio, , the earnings-by-price ratio, , the short-term interest rate, , the long-term interest rate, , inflation, , the term spread, , and lagged excess stock return, .
Based on (2), in a two-step procedure, we first estimate as in Kyriakou et al. (2019b), and, in a second step, we estimate from
using the squared residuals as the dependent variable and a local-linear smoother in both steps. The estimates and depend on smoothing parameters (bandwidths) h and g, respectively. As we are interested in predictions, we take the values which minimize the out-of-sample prediction error using cross-validation. More details are provided in Section 2.4.5
2.2. Longer-Horizon Predictions
For longer horizons T, we consider the sum of annual continuously compounded returns:
Note that we use here overlapping returns , which require a careful econometric modelling. For illustrative purposes, assume a linear relationship in (2) between and , as well as the persistence of the forecasting variable (treating the variables as deviations from their means):
with similar to the error term in (2) and a parametric specification for the conditional variance , and being white noise. The T-year regression problem that is implied by this pair of one-year regressions is now
i.e., the excess stock return for the year t over the next T years can be decomposed in a predictive part depending on the variable and an unpredictable error term . In estimating the conditional mean and variance functions for the T-year returns , we use nonparametric models because they can capture possible misspecification due to violation of the linear models assumed above. Thus, we set up our predictive nonparametric regression model in the same fashion as in (2)
where
are the unknown smooth conditional mean- and variance-function. The predictive variables X under consideration are the same as for the one-year horizon. The important difference between Equations (2) and (5) is now that the error process in Equation (5) will be serially correlated by construction.6,7 For a discussion on asymptotic properties of our nonparametric estimators of model (5) and (6), see Section 2.3 in Kyriakou et al. (2019b).
Based on (5), our two-step procedure consists now of, first, estimating , and second, estimating from
using the squared residuals as the dependent variable and a local-linear smoother again in both steps.
2.3. Alternative Ways in Estimating the Conditional Variance Function
For the estimation of the conditional variance or volatility function of a response variable Y in a location-scale model similar to (2) or (5), four different approaches are mainly proposed in the literature: the direct, the residual-based, the likelihood-based, and the difference-sequence method.
(i) The direct method uses the variance expressed as the difference of the first two conditional moments (see, for example, Härdle and Tsybakov 1997): Both parts of the right-hand side are separately estimated and, thus, the result is not necessarily nonnegative and also not fully adaptive to the mean function.8
(ii) The residual-based method consists of two stages—first, estimating the conditional mean function and calculating the squared residuals . Second, estimating the conditional variance function by regressing on a set of explanatory variables X. There exist different variants of residual based methods for the second step.9
(iii) The preferred estimators of Yu and Jones (2004) build on a localised normal likelihood and use a standard local-linear form for estimating the mean, a local log-linear form for estimating the variance, and allow for separating bandwidths for mean and variance estimation.
(iv) Finally, examples for the difference-sequence method in a fixed design can be found for the homoscedastic case in Wang and Yu (2017) and citations therein. Wang et al. (2008) analyse for the heteroscedastic case the effect of the unknown (smooth) mean function on the estimation of the variance function. They also compare the performance of the residual-based estimators to a first-order-difference-based estimator. Their results indicate that it is not desirable to estimate the variance function based on the residuals from an optimal estimator of the mean in case the mean function is not smooth. Wang et al. (2008) recommend instead an estimator for the mean with minimal bias.
In the empirical part of this paper in Section 3, we show the results of the residual-based method applying a local-linear kernel smoother in both stages. As a robustness check, we have implemented in the second step the local-exponential estimator (Ziegelmann 2002) and the combined estimator (Mishra et al. 2010) getting almost always very similar results.10 We do not consider: (i) the direct method, since it is not fully adaptive to the mean function, (ii) the re-weighted local constant estimator (Xu and Phillips 2011) due to its asymptotic similarity to the local-linear method, (iii) the method based on the assumption of normal error terms (Yu and Jones 2004), since skewness and excess kurtosis are common properties of stock returns, and (iv) the difference-sequence method, since it was not convincingly performing in a small sample study, the mean functions are rather smooth in our problem, and bias reduction is key due to sparsity.11
2.4. The Validation Criterion for the Choice of Smoothing Parameters and Model Selection
For the nonparametric technique applied in this study, we require an adequate measure of predictive power. In-sample measures, such as the classical or the adjusted , are not appropriate because they either prefer the most complex model or need a degrees of freedom adjustment which is an unclear concept in nonparametric estimation. Furthermore, our focus lies on prediction. Thus, we are interested in the out-of-sample performance of a model and not in how well it explains the variation inside the sample. Therefore, our preferred measure estimates the prediction error directly.
For the purpose of model selection and optimal bandwidth choice, we use the validated introduced in the actuarial literature by Nielsen and Sperlich (2003) and based on a leave-k-out cross-validation. Note that this criterion is very similar to the forecast content function of Galbraith (2003) and Galbraith and Kisinbay (2005) defined as the proportionate reduction in the mean square forecast error achievable relative to the unconditional mean forecast.
Our validation criteria for the first and second step are defined as
Note that leave-k-out estimators are used: and for the nonparametric functions m and , resp., and for the unconditional mean of and , resp. These are computed by removing observations: before the tth time point, t itself, and after t. We need to exclude data points due to the construction of the dependent variable over a horizon of T years, i.e., we use for the one-year horizon the classical leave-one-out estimator, while, for example, for the five-year horizon the leave-nine-out estimator. Note that the validated measures the predictive power of a model in comparison to the predictive power of the cross-validated historical mean. Thus, positive values imply that the regression model based on explanatory variables outperforms the corresponding historical average over T years. Negative values in the first step of our approach suggest that the historical mean return should be preferred over a model-based approach, while negative values in the second step indicate a constant homoscedastic conditional variance forecast. Note further that the numerator in the ratio of and corresponds to the classical cross-validation criterion. Thus, choosing the bandwidth which minimizes this criterion for a given set of explanatory variables is equivalent in maximizing the validated . This means that we can use the validated as a single criterion for both purposes: model and bandwidth selection.12
It is well known from the literature that cross-validation often requires to omit more than one observation and, possibly, additional correction when the omitted fraction of data are considerable (see, for example, Burman et al. 1994). In addition, when serial correlation arises, as in our longer- horizon application, and the structure of the error terms is ignored, De Brabanter et al. (2011) show that automatic methods for the choice of smoothing parameters, such as cross-validation or plug-in, fail. The problem is that the chosen bandwidths become smaller for increasing correlations (Opsomer et al. 2001), and the corresponding model fits become progressively more under-smoothed. The bias of the predictor reduces this way and, as it contributes in a squared fashion to the prediction mean squared error—the numerator of the ratio in (8), increases (not because the fit is good but due to the ignored correlation structure). A misleading decision on the bandwidth or model specification, as well the set of preferred covariates is the consequence. To overcome those problems, Chu and Marron (1991) propose the use of bimodal kernel functions. Such functions are known to remove the correlation structure very effectively, but the estimator suffers from increased mean squared error, as discussed in De Brabanter et al. (2011). They also propose correlation-corrected cross-validation that consists of, first, finding the amount of data k to be left out in the estimation process when a bimodal kernel function is used; and, second, applying the actual choice of the smoothing parameter using leave-k-out cross-validation with a unimodal kernel function. In our application, we can skip the first step because k is known by construction. For example, in the five-year case, we have . Now, we want to exclude the complete information included at time t, i.e., skip all that include any of ; it is easy to see that this amounts to a leave-nine-out set of (see, for example, Kyriakou et al. 2019b, Figure 1).
2.5. A Bootstrap-Test: No Predictability vs. Predictability of the Conditional Variance
We test the null of no predictability of the conditional variance applying the tests proposed by Kreiss et al. (2008) (hereafter KNY-test) and Scholz et al. (2015) (hereafter SNS-test). Formally, this is equivalent to say that, under the null, is a constant function, which essentially corresponds to the historical average of the squared residuals, i.e., constant volatility. In particular, let be the true volatility function as in (2) or (5) for some specified set of regressors , i.e., (4) or (7) holds. Let be the sample mean of the squared residuals from step one in our approach. The KNY-test is based on the distance
for some weighting function w, which has been studied by several authors and statistics have been derived from the above, for example, in Härdle and Mammen (1993) or Kreiss et al. (2008). We use the statistic derived in Equation 2.3 of Kreiss et al. (2008)
where is a symmetric kernel smoother with bandwidth h. The bandwidth is selected using for the Nadaraya–Watson kernel estimator rather than a local-linear one. We choose w to be proportional to the uniform density with support in the range of the sample data and replace integration by the mean over uniform independent observations in the range of the data:
Then, the error in the integral is (Geweke 1996). Under the null, the above test statistic is small. This choice could lead to a statistic whose power is lower than the one in Härdle and Mammen (1993) due to some implicit over-smoothing resulting in the weight function w (see comment in Kreiss et al. 2008, just after their Equation 2.5). Power may also improve by using a local-linear smoother in the test. However, the theory for this has not been developed yet, so we refrain from such extension.
Critical values for are best derived via wild bootstrap (Härdle and Mammen 1993). For the bootstrap critical values to be consistent, the procedure needs to be independent of whether the null is true or not. Hence, in correspondence with Equation 2.10 in Kreiss et al. (2008), for ,
where the ’s are independent and identically distributed random variables with a mean of zero and a variance of one, for example, . To decide if we reject or not, we use as critical values the corresponding quantiles of the empirical distribution13,
The consistency of the procedure for stationary sequences is given in Kreiss et al. (2008).
An alternative version for a wild bootstrap test is the SNS-test proposed in Scholz et al. (2015). There the B bootstrap samples are constructed using the residuals under the null, , and ’s as above, such that
Then, in each bootstrap repetition b, the cross-validated mean is calculated of the , , as well the estimates of the predictor-based model in order to get like in (8). Critical values are chosen from corresponding quantiles of the empirical distribution function similar to (13).
Both tests have their own merits. We expect the KNY-test to be more conservative and potentially with less power in comparison to the SNS-test but with clear and well-established asymptotic theory. For more discussion on standard smoothing based tests and other examples for tests of the variance function, see, for example, the survey of Gonzales-Manteiga and Crujeiras (2013).
3. Empirical Application: Conditional Variance Prediction for Stock Returns in Excess of Different Benchmarks
3.1. The Data
In this paper, we extend the analysis of Kyriakou et al. (2019b), who considered the forecasting of long-term stock returns, to conditional variance predictions. Thus, we base our predictions on the same annual US data set which is provided by Robert Shiller and can be downloaded from http://www.econ.yale.edu/~shiller/data.htm. It includes, among other variables, the Standard and Poor’s (S&P) Composite Stock Price Index, the consumer price index, and interest rate data from 1872 to 2019. We use here an updated and revised version of Shiller (1989, chp. 26), which provides a detailed description of the data. Note that the risk-free rate in this data set (based on the six-month commercial paper rate until 1997 and afterwards on the six-month certificate of deposit rate, secondary market) was discontinued in 2013. We follow the strategy of Welch and Goyal (2008) and replace it by an annual yield that is based on the six-month Treasury-bill rate, secondary market, from https://fred.stlouisfed.org/series/TB6MS. This new series is only available from 1958 to 2019. In the absence of information prior to 1958, we had to estimate it. To this end, we regressed the Treasury-bill rate on the risk-free rate from Shiller’s data for the overlapping period 1958 to 2013, which yielded
with an of 98.6%. Therefore, we instrumented the risk-free rate from 1872 to 1957 with the predicted regression equation. The correlation between the actual Treasury-bill rate and the predictions for the estimation period is 99.3%. Table 1 displays standard descriptive statistics for one-year and five-year returns as well as the available covariates.

Table 1.
US market data (1872–2019).
3.2. Single Benchmarking Approach
In this section, we consider a single benchmarking approach as in Kyriakou et al. (2019a, 2019b), i.e., only the dependent variable is benchmark adjusted, as shown in (1), while the independent variable(s) is (are) measured on the original (nominal) scale. The models (2) and (5) are estimated in both steps with a local-linear kernel smoother using the quartic kernel. The optimal bandwidths are chosen by cross-validation, i.e., by maximizing the corresponding validation measure given by (8). Given that we apply a local-linear smoother, it should be kept in mind that the nonparametric method can estimate linear functions without any bias. Thus, the linear model is automatically embedded in our approach. This is an important observation as the linear model is the usual benchmark in financial applications. In addition, in case that the true (but in advance) unknown function is really linear, our approach would exactly pick the line against all other functional alternatives. We study the values based on different validated scenarios shown for the one-year horizon in Table 2 and the five-year horizon in Table 3. Here, the same predictive variables are used in both steps of our approach. Note that we have only about 150 observations in our records. The small sample size clearly limits the complexity of our analysis in the sense of using higher dimensional vectors of explanatory variables. In what follows, we consider only one- and two-dimensional models. For a discussion on sparsely distributed annual observations in higher dimensions and ways to circumvent the curse-of-dimensionality, see, for example, Kyriakou et al. (2019a).

Table 2.
Predictive power for the variance of one-year excess stock returns : the single benchmarking approach. The prediction problem is defined in (2). The same predictive variables are used in the predictions for the conditional mean and variance function. The predictive power (%) is measured by as defined in (8). The benchmarks considered are based on the short-term interest rate (), long-term interest rate (), earnings-by-price ratio (), and consumer price index (). The predictive variables used are , given by the dividend-by-price ratio , earnings-by-price ratio , short-term interest rate , long-term interest rate , inflation , term spread , excess stock return , or the possible different pairwise combinations as indicated.

Overall, we find for the one-year horizon that only a few variables have small positive validated ’s and thus possibly some low explanatory power. For example, for the benchmarks , , and , the excess stock return has the largest validated values for one-dimensional models (2.2%, 2.4%, and 1.5%). This finding would support an ARCH-type variance structure. For the inflation benchmark , the model with the long-term interest rate produces the largest validated of 0.5%. When we apply the bootstrap tests introduced in Section 2.5, the KNY-test does not reject the null of no predictability for all cases at the 5%-level. The SNS-test rejects the null only for the covariate under the benchmarks , and at the 5%-level.14 Note that the two-dimensional models do not add predictive power as the validated values remain in the same low range.
Contrary to the mean prediction, where Kyriakou et al. (2019b) find that five-year predictability improves over the one-year case, we observe that the majority of predictor based volatility models do not surpass the constant volatility alternative for the five-year horizon. Even though some models produce small positive values, this time both the SNS- and the KNY-test do not reject the null of no predictability. Note that our results are in line with Christoffersen and Diebold (2000) who conclude that volatility forecastability may be much less important at longer horizons.
3.3. Full Benchmarking Approach
In the next step, we consider the double benchmarking approach of Kyriakou et al. (2019a, 2019b) to analyze now whether transforming the explanatory variables can improve the predictions for the volatility function. Recall that fully nonparametric models suffer in general by the curse of dimensionality. Problems with sparsely distributed annual observations in higher dimensions, as in our framework, could be reduced or circumvented by importing more structure in the estimation process.
Here, we extend the study presented in Section 3.2 transforming both the dependent and independent variables according to the same benchmark. To this end, in our full (double) benchmarking approach, the prediction problems are reformulated as
where we use transformed predictive variables
This approach can be interpreted as a simple way of reducing the dimensionality of the estimation procedure. The adjusted variable includes now an additional predictive variable, the benchmark itself. Results of this empirical study are presented for the one-year horizon in Table 4 and for the five-year horizon in Table 5.

Table 4.
Predictive power for the variance of one-year excess stock returns : the double benchmarking approach. The prediction problem is defined in (14). The same predictive variables are used in the predictions for the conditional mean and variance. The predictive power (%) is measured by as defined in (8). The benchmarks considered are based on the short-term interest rate (), long-term interest rate (), earnings-by-price ratio (), and consumer price index (). The predictive variables used are using the indicated benchmark as shown in (16). are given by the dividend-by-price ratio , earnings-by-price ratio , short-term interest rate , long-term interest rate , inflation , term spread , excess stock return , or the possible different pairwise combinations as indicated. “–” are not applicable cases of matched covariate with benchmark. Note: and (and their combinations with ) have the same by construction of the transformed spread according to (16). For example, and . The case of and is similar.

Table 5.
Predictive power for the variance of five-year excess stock returns : the double benchmarking approach. The prediction problem is defined in (15). The same predictive variables are used in the predictions for the conditional mean and variance. Additional notes: see Table 4.
We find that, in comparison to the single-benchmarking approach in the one-year case, the double benchmarking improves in 15 out of 82 models (in the sense of producing a positive and higher as before). However, predictability is still questionable. The best model under the long-term interest rate benchmark uses the pair and yields , while the best model under uses the pair and yields . The SNS-test rejects for both the null of no predictability, while the KNY-test does not. For the rest of the new combinations of predictive variables in all benchmarks, both tests again do not reject.
For the five-year case, we find that in comparison to the single-benchmarking the double benchmarking improves in 11 out of 82 models. The best model under uses and yields , while under the covariates and both yield . Nevertheless, we do not find any combination of covariates with statistically significant predictive power.
3.4. Real-Income Long-Term Pension Prediction
In long-term pension planning or other asset allocation problems optimized with regard to real-income protection (Gerrard et al. (2019a, 2019b); (Merton 2014)), the econometric models should reflect those needs and use covariates net-of-inflation. Therefore, we take the inflation benchmark and analyse in more detail the best model found by Kyriakou et al. (2019b), which uses the earnings-by-price variable for the mean prediction and produced a for the one-year horizon and for the five-year horizon (see Kyriakou et al. 2019b, Tables 4 and 5) in the double benchmarking case. For this specific model, we are now interested in finding the set of covariates that best predicts the conditional variance.15,16 The empirical findings in terms of are shown for the one-year horizon in Table 6 and the five-year horizon in Table 7. For the one-year horizon, we find in the double benchmarking approach when inflation is the benchmark, that the dividend-by-price together with the short-term interest-rate or the long-term interest-rate are chosen as best predictive variables in terms of (2.9% and 2.0%). Note that these values are rather low and that the SNS-test does reject the null of no predictability for both models, while the KNY-test does not reject. For all other combinations and also the five-year case, we do not find evidence for statistical significant predictability of the conditional variance. Therefore, we conclude that the constant volatility model is appropriate for practical purposes.

Table 6.
Predictive power for the variance of one-year excess stock returns : the double benchmarking approach for the conditional mean model with earnings-by price as single covariate. The prediction problem is defined in (14). The predictive power (%) is measured by as defined in (8). The benchmarks considered are based on the short-term interest rate (), long-term interest rate (), and consumer price index (). The predictive variables used are using the indicated benchmark as shown in (16). are given by the dividend-by-price ratio , earnings-by-price ratio , short-term interest rate , long-term interest rate , inflation , term spread , excess stock return , or the possible different pairwise combinations as indicated. “–” are not applicable cases of matched covariate with benchmark. Note: and (and their combinations with ) have the same by construction of the transformed spread according to (16). For example, and . Similar is the case of and .

Table 7.
Predictive power for the variance of five-year excess stock returns : the double benchmarking approach for the conditional mean model with earnings-by price as single covariate. The prediction problem is defined in (15). Additional notes: see Table 6.
Note further that the ratio in our validation criterion for the mean prediction, , in (8) compares the sample variance of the estimated residuals from our model based on earnings-by-price (the numerator) with the sample variance of the benchmarked stock returns (the denominator). For the one-year case, we find from Table 1 the latter to be equal to . A simple calculation using the corresponding leads then to or a standard deviation of 16.91% for returns based on the earnings-model. This means that the linear expression of real stock returns in terms of real earnings-by-price presented in Kyriakou et al. (2019b) as
gives on average 2.4% higher returns at the same risk as the historical mean .17 Similarly, for the five-year case, we get from Table 1 that . From the , we obtain then or a standard deviation of 34.08% for returns based on the earnings-model. Thus, the linear expression of real stock returns in terms of real earnings-by-price presented in Kyriakou et al. (2019b) as
gives on average 6.1% higher returns at the same risk as the historical mean .18 Figure 1 shows the estimated nonparametric function (red solid line) for the one-year horizon (left) and the five-year horizon (right) under the double inflation benchmark for the earnings-by-price covariate together with the corresponding historical mean (dashed green line). Figure 2 depicts histograms and a kernel density estimate (red solid line) of the standardized predicted returns for the one-year horizon (left) and the five-year horizon (right). The similarity for both horizons is striking and driven by the fact that the ratio of the slope of the regression lines in (17) and (18) with the corresponding standard deviation given above yields almost the same value of 6.63.
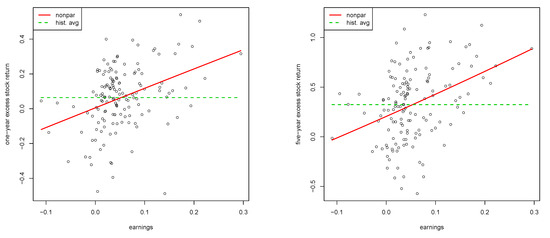
Figure 1.
Double inflation benchmark. Relation between real stock returns and real earnings-by-price. Estimated nonparametric function (red solid line) and historical average (dashed green line). Left: one-year horizon. Right: five-year horizon. Period: 1872–2019. Data: annual S&P 500.
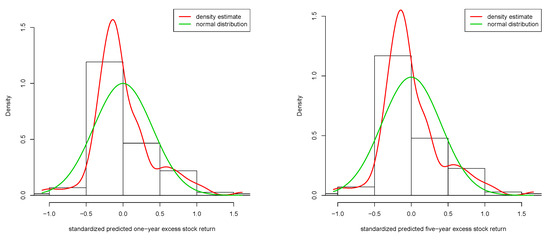
Figure 2.
Standardized predicted stock returns in excess of the inflation benchmark (based on the model using earnings-by-price as covariate for mean-prediction; double benchmarking). Histogram, kernel density estimate (red), and fitted normal distribution (green). Left: one-year horizon. Right: five-year horizon. Period: 1872–2019. Data: annual S&P 500.
Finally, we consider a simple mean-reverting autoregressive model of order one for the real earnings-by-price—the main drivers of real returns in Equations (17) and (18)—and estimate it with ordinary least squares (OLS) 19:
Note that, for the whole sample period (1872–2019), the mean and standard deviation of real earnings-by-price are 0.0524 and 0.0595, resp. Moreover, using the current (30/09/2019) value of real earnings-by-price of 0.0278, model (19) predicts a change in real earnings-by-price of 0.0176, i.e., an expected value of real earnings-by-price of 0.0454 for 2020Q3, which is still below the long-term average.20
We subsequently calculate the correlation between the estimated residuals of models (17) and (19) to be −0.014. A standard stationary block-bootstrap (Politis and Romano 1994) based on 10,000 repetitions and a block-length of 12 suggests that this correlation is not statistically significantly different from zero. The correlation structure between returns and their drivers is important while searching for optimal investment strategies in a dynamic market, see Kim and Omberg (1996). Gerrard et al. (2019c) follow the approach of Kim and Omberg (1996) in a long-term return setting and show that the above correlation is very hard to estimate with precision. Sometimes, it is negative and, with a slight change of data, it is positive, and a test would almost always provide that zero correlation cannot be rejected. When this added insight is provided that zero correlation significantly simplifies that technical calculation of the optimal dynamic strategy while significantly reducing parameter uncertainty, the conclusion seems clear: we should work with zero correlation unless there is a strong argument not to do that. In our case—which is a discrete analogue to the continuous models considered in Gerrard et al. (2019c) and Kim and Omberg (1996)—it is, therefore, comforting that we can provide a simple zero-correlation econometric model to guide the market dynamics. In further work, we expect the simple econometric model of this paper to be used while generalizing the non-dynamic new approach to pension products of Gerrard et al. (2019a, 2019b).
4. Conclusions
In this paper, we extend the original working framework of Kyriakou et al. (2019a, 2019b) of forecasting stock returns to modelling their conditional variance and test for predictability in this context. We consider returns of one-year and five-year horizons in excess of different benchmarks, considering the short- and long-term rate, the earnings-by-price ratio, and the inflation rate. We use popular explanatory variables with predictive power such as the dividend-by-price ratio, the earnings- by-price ratio, the short- and long-term interest rates, the term spread, the inflation rate, as well as the lagged excess stock return, in one- and two-dimensional settings, with the returns benchmarked or also the covariates used to predict them.
In our analysis, we find only little to no evidence of model-based volatility predictability for the one-year and five-year horizon. Only for a few of the models considered under different benchmarks, we get validation measures that are positive and significantly different from zero but of a rather small magnitude. We thus conclude that volatility forecastability is much less important at longer horizons regardless of the chosen combination of explanatory variables. The homoscedastic historical average of the squared return prediction errors gives an adequate approximation of the unobserved realised conditional variance for both the one-year and five-year horizon.
In the practically important double inflation benchmarking case, we find that the model with the largest predictive power is not only of linear functional form based on real earnings-by-price but also has a constant variance for both horizons. A simple mean-reverting linear AR1-model for the real-earnings-by-price allows then to analyse the correlation structure between returns and their main drivers. We find zero correlation which significantly simplifies the econometric modelling to guide market dynamics. This is an important observation and a relatively simple starting point when constructing forecasting models for real-value pension prognoses for long-term saving strategies.
Author Contributions
All authors contributed equally to this work.
Funding
The authors thank: (i) the Institute and Faculty of Actuaries in the UK for funding this research through the grant “Minimizing Longevity and Investment Risk while Optimizing Future Pension Plans”, and (ii) the University of Graz for the Open Access Funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Heiko Ebens. 2001. The distribution of realized stock return volatility. Journal of Finacial Economics 61: 43–76. [Google Scholar] [CrossRef]
- Burman, Prabir, Edmond Chow, and Deborah Nolan. 1994. A cross-validatory method for dependent data. Biometrika 81: 351–58. [Google Scholar] [CrossRef]
- Chen, Qingqing, and Yongmiao Hong. 2010. Predictability of Equity Returns Over Different Time Horizons: A Nonparametric Approach. Working Paper. Ithaca: Cornell University/Department of Economics. [Google Scholar]
- Cheng, Tingting, Jiti Gao, and Oliver Linton. 2019. Nonparametric Predictive Regressions for Stock Return Predictions. Cambridge Working Papers in Economics: 1932. Cambridge: Faculty of Economics, University of Cambridge. [Google Scholar]
- Christoffersen, Peter F., and Francis X. Diebold. 2000. How relevant is volatility forecasting for financial risk management? Review of Economics and Statistics 82: 12–22. [Google Scholar] [CrossRef]
- Chu, C. K., and J. S. Marron. 1991. Comparison of two bandwidth selectors with dependent errors. The Annals of Statistics 19: 1906–18. [Google Scholar] [CrossRef]
- De Brabanter, Kris, Jos De Brabanter, Johan A.K. Suykens, and Bart De Moor. 2011. Kernel regression in the presence of correlated errors. Journal of Machine Learning Research 12: 1955–76. [Google Scholar]
- Fan, Jianqing, and Qiwei Yao. 1998. Efficient estimation of conditional variance functions in stochastic regression. Biometrika 85: 645–60. [Google Scholar] [CrossRef]
- Galbraith, John W. 2003. Content horizons for univariate time-series forecasts. International Journal of Forecasting 19: 43–55. [Google Scholar] [CrossRef]
- Galbraith, John W., and Turgut Kisinbay. 2005. Content horizons for conditional variance forecasts. International Journal of Forecasting 21: 249–60. [Google Scholar] [CrossRef]
- Geller, Juliane, and Michael H. Neumann. 2018. Improved local polynomial estimation in time series regression. Journal of Nonparametric Statistics 30: 1–27. [Google Scholar] [CrossRef]
- Gerrard, Russell, Munir Hiabu, Ioannis Kyriakou, and Jens Perch Nielsen. 2019a. Communication and personal selection of pension saver’s financial risk. European Journal of Operational Research 274: 1102–11. [Google Scholar] [CrossRef]
- Gerrard, Russell, Munir Hiabu, Ioannis Kyriakou, and Jens Perch Nielsen. 2019b. Self-selection and risk sharing in a modern world of life-long annuities. British Actuarial Journal 23: e30. [Google Scholar] [CrossRef]
- Gerrard, Russell, Munir Hiabu, Jens Perch Nielsen, and Peter Vodicka. 2019c. Long-Term Real Dynamic Investment Planning. Working Paper. London: Cass Business School. [Google Scholar]
- Geweke, John F. 1996. Monte carlo simulation and numerical integration. In Handbook of Computational Economics. Edited by Hans M. Amman, David A. Kendrick and John Rust. Amsterdam: Elsevier, vol. I, pp. 731–800. [Google Scholar]
- Glad, Ingrid K. 1998. Parametrically guided non-parametric regression. Scandinavian Journal of Statistics 25: 649–68. [Google Scholar] [CrossRef]
- Gonzales-Manteiga, Wenceslao, and Rosa M. Crujeiras. 2013. An updated review of goodness-of-fit tests for regression models. Test 22: 361–411. [Google Scholar] [CrossRef]
- Härdle, Wolfgang K., and Enno Mammen. 1993. Comparing nonparametric versus parametric regression fits. Annals of Statistics 21: 1926–47. [Google Scholar] [CrossRef]
- Härdle, Wolfgang K., and Alexandre B. Tsybakov. 1997. Local polynomial estimators of the volatility function in nonparametric autoregression. Journal of Econometrics 81: 223–42. [Google Scholar] [CrossRef]
- Kim, Tong Suk, and Edward Omberg. 1996. Dynamic nonmyopic portfolio behavior. The Review of Financial Studies 9: 141–61. [Google Scholar] [CrossRef]
- Kothari, S. P., Jonathan Lewellen, and Jerold B. Warner. 2006. Stock returns, aggregate earnings surprises, and behavioral finance. Journal of Financial Economics 79: 537–68. [Google Scholar] [CrossRef]
- Kreiss, Jens-Peter, Michael H. Neumann, and Qiwei Yao. 2008. Bootstrap tests for simple structures in nonparametric time series regression. Statistics and Its Interfaces 1: 367–80. [Google Scholar] [CrossRef]
- Kyriakou, Ioannis, Parastoo Mousavi, Jens Perch Nielsen, and Michael Scholz. 2019a. Forecasting benchmarks of long-term stock returns via machine learning. Annals of Operations Research. [Google Scholar] [CrossRef]
- Kyriakou, Ioannis, Parastoo Mousavi, Jens Perch Nielsen, and Michael Scholz. 2019b. Machine Learning for Forecasting Excess Stock Returns—The Five-year View. Graz Economics Papers 2019-06. Graz: University of Graz, Departmemt of Economics. [Google Scholar]
- Lettau, Martin, and Stijn Van Nieuwerburgh. 2008. Reconciling the return predictability evidence. Review of Financial Studies 21: 1607–52. [Google Scholar] [CrossRef]
- Linton, Oliver, and Benoit Perron. 2003. The shape of the risk premium: Evidence from a semiparametric generalized autoregressive conditional heteroscedasticity model. Journal of Business & Economic Statistics 21: 354–67. [Google Scholar]
- Linton, Oliver B., and Yang Yan. 2011. Semi- and nonparametric arch processes. Journal of Probability and Statistics 2011: 906212. [Google Scholar] [CrossRef]
- Linton, Oliver B., and Enno Mammen. 2008. Nonparametric transformation to white noise. Journal of Econometrics 142: 241–64. [Google Scholar] [CrossRef]
- Merton, Robert C. 1973. An intertemporal capital asset pricing model. Econometrica 41: 867–87. [Google Scholar] [CrossRef]
- Merton, Robert C. 2014. The crisis in retirement planning. Harvard Business Review 92: 43–50. [Google Scholar]
- Mishra, Santosh, Liangjun Su, and Aman Ullah. 2010. Semiparametric estimator of time series conditional variance. Journal of Business & Economic Statistics 28: 256–74. [Google Scholar]
- Munk, Claus, and Jesper Rangvid. 2018. New assumptions of a pension forecast model: Background, level and consequences for individuals forecasted pension. Finans/Invest 6: 6–14. [Google Scholar]
- Nielsen, Jens Perch, and Stefan Sperlich. 2003. Prediction of stock returns: A new way to look at it. ASTIN Bulletin 33: 399–417. [Google Scholar] [CrossRef]
- Opsomer, Jean, Yuedong Wang, and Yuhong Yang. 2001. Nonparametric regression with correlated errors. Statistical Science 16: 134–53. [Google Scholar]
- Pagan, Adrian R., and Yong-Sik Hong. 1991. Nonparametric estimation and the risk premium. In Nonparametric and Semiparametric Methods in Econometrics and Statistics. Edited by William A. Barnett, James Powell and George E. Tauchen. Cambridge: Cambridge University Press, pp. 51–76. [Google Scholar]
- Pagan, Adrian R., and Aman Ullah. 1988. The econometric analysis of models with risk terms. Journal of Applied Econometrics 3: 87–105. [Google Scholar] [CrossRef]
- Politis, Dimitris N., and Joseph P. Romano. 1994. The stationary bootstrap. Journal of the American Statistical Association 89: 1303–13. [Google Scholar] [CrossRef]
- Rapach, David, and Guofu Zhou. 2013. Forecasting stock returns. In Handbook of Economic Forecasting. Edited by Graham Elliott and Allan Timmerman. Amsterdam: Elsevier, vol. 2A, pp. 328–83. [Google Scholar]
- Scholz, Michael, Jens Perch Nielsen, and Stefan Sperlich. 2015. Nonparametric prediction of stock returns based on yearly data: The long-term view. Insurance: Mathematics and Economics 65: 143–55. [Google Scholar] [CrossRef]
- Scholz, Michael, Stefan Sperlich, and Jens Perch Nielsen. 2016. Nonparametric long term prediction of stock returns with generated bond yields. Insurance: Mathematics and Economics 69: 82–96. [Google Scholar] [CrossRef]
- Shiller, Robert J. 1989. Market Volatility. Cambridge: MIT Press. [Google Scholar]
- Su, Liangjun, and Aman Ullah. 2006. More efficient estimation in nonparametric regression with nonparametric autocorrelated errors. Econometric Theory 22: 98–126. [Google Scholar] [CrossRef]
- Wang, Lie, Lawrence D. Brown, T. Tony Cai, and Michael Levine. 2008. Effect of mean on variance function estimation in nonparametric regression. The Annals of Statistics 36: 646–64. [Google Scholar] [CrossRef]
- Wang, WenWu, and Ping Yu. 2017. Asymptotically optimal differenced estimators of error variance in nonparametric regression. Computational Statistics and Data Analysis 105: 125–43. [Google Scholar] [CrossRef]
- Welch, Ivo, and Amit Goyal. 2008. A comprehensive look at the empirical performance of equity premium prediction. Review of Financial Studies 21: 1455–508. [Google Scholar] [CrossRef]
- Xiao, Zhijie, Oliver B. Linton, Raymond J. Carroll, and Enno Mammen. 2003. More efficient local polynomial estimation in nonparametric regression with autocorrelated errors. Journal of the American Statistical Association 98: 980–92. [Google Scholar] [CrossRef]
- Xu, Ke Li, and Peter C. B. Phillips. 2011. Tilted nonparametric estimation of volatility functions with empirical applications. Journal of Business & Economic Statistics 29: 518–28. [Google Scholar]
- Yu, Keming, and M.C. Jones. 2004. Likelihood-based local linear estimation of the conditional variance function. Journal of the American Statistical Association 99: 139–44. [Google Scholar] [CrossRef]
- Ziegelmann, Flavio A. 2002. Nonparametric estimation of volatility functions: The local exponential estimator. Econometric Theory 18: 985–91. [Google Scholar] [CrossRef]
| 1 | Our methodology of validating a fully nonparametric structure can be viewed as one of the simplest and therefore also most transparent version of machine learning; see Section 2 of Kyriakou et al. (2019a) for more details justifying the label machine learning for our approach. |
| 2 | Note that the use of a different ML method would come with the cost of losing interpretability, smoothness, or flexibility due to restrictions on the functional form. A comparison of different ML techniques in finding that one which gives the best predictions, wins an investment horse-race out-of-sample, or being the most robust method over different periods is out of the scope of our work. |
| 3 | The choice of the one-year horizon is related to the frequency of the data. In contrast, the five-year horizon is arbitrary but is intended to be a starting point for actuarial long-term models for real-income savings. Other horizons and related questions remain for future research. |
| 4 | Note that the set of explanatory variables in (2) could be different or overlapping for the mean and variance function. |
| 5 | For a description and statistical properties of the local-linear smoother, see, for example, Section 2.3 in Kyriakou et al. (2019b). Note further that the smoothing parameters h and g are separately chosen in each step. |
| 6 | Our flexible location-scale model in (5), could be easily extended to time-lags of higher order. However, in the empirical application in Section 3, we see that, for example, for real-earnings—the main driver of real-returns—an AR1-type model is ideally suited. This is in line with findings from Kothari et al. (2006). Note further that one might expect risk and return to be somehow related (see, for example, Merton 1973). The parametric GARCH-in-Mean process captures this idea (Linton and Yan 2011). However, the inclusion of an interaction of mean and variance in a fully nonparametric fashion is out of the scope of this paper. To our knowledge, only semiparametric versions where either the mean or variance function is modeled parametrically can be found in the literature, see, for example, Pagan and Hong (1991); Pagan and Ullah (1988); Linton and Perron (2003). |
| 7 | For possible solutions to the problem of autocorrelation, see, for example, Xiao et al. (2003); Su and Ullah (2006); Linton and Mammen (2008), or more recently Geller and Neumann (2018). The implementation and analysis of these techniques remain for future research. In our approach, we account for autocorrelation in the validation criterion with a leave-k-out strategy, where ; see Section 2.4. |
| 8 | It does not estimate the volatility function as efficiently as if the true mean were known. |
| 9 | Examples of these variants are: (i) Applying a local-linear kernel smoother in both stages (Fan and Yao 1998). The result is again not necessarily nonnegative but asymptotically fully adaptive to the unknown mean function. (ii) Using the local exponential estimator to ensure nonnegativity (Ziegelmann 2002). (iii) Implementing a combined estimator (a multiplicative bias reduction technique), where a parametric guide captures some roughness features of the unknown variance function (Glad 1998; Mishra et al. 2010). (iv) Utilising a re-weighted local constant estimator maximising the empirical likelihood such that it becomes a bias-reducing moment restriction (Xu and Phillips 2011). |
| 10 | Those results are available upon request by the authors. |
| 11 | There is also a lack of studies using the difference-sequence method in a random design and in multivariate problems as in our case. |
| 12 | Model selection in the sense of composition of the set of explanatory variables. |
| 13 | The symbol denotes the indicator function of an appropriate condition A, i.e., it is one when A is true and zero otherwise. |
| 14 | The tests were conducted with 1000 repetitions at the 5% significance level for a selected number of cases. We do not present the p-values of the tests to save space. The results are available upon request by the authors. |
| 15 | Note that until now we have used the same set of covariates in both steps of our analysis to reduce the overwhelming number of models. It is also clear that not all combinations of variables are practically relevant. Now, we relax this restriction for the model with the highest predictive power for the returns. |
| 16 | Table 6 and Table 7 also present the results for the short- and long-term interest benchmarks and . However, it is again hard to find predictability at all in these cases. Note that the benchmark using the earnings-by-price variable is not applicable since it matches the covariate and the benchmark in the first step. |
| 17 | Here, we use the Sharpe-ratio for the comparison. From Table 1, we get and divide it either by 18.05% or by 16.91%. We obtain 0.355 and 0.379, which corresponds to a difference of 2.4% points. |
| 18 | Here, we use again the Sharpe-ratio for the comparison. From Table 1, we get and divide it either by 36.42% or by 34.08%. We obtain 0.888 and 0.949, which corresponds to a difference of 6.1% points. |
| 19 | The estimated coefficient is significant at the 0.1%-level (with a corresponding standard error of 0.08), the residual standard error of the regression is 0.0572, and its has a value of 0.357. |
| 20 | The following values are used for the calculation of the current real earnings-by-price: , , . |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).