Predicting Motor Insurance Claims Using Telematics Data—XGBoost versus Logistic Regression
Abstract
1. Introduction
2. Methodology Description
2.1. Logistic Regression
2.2. XGBoost
2.2.1. A Closer Look at the XGBoost Minimization Algorithm
2.2.2. Implementation
3. Data and Descriptive Statistics
4. Results
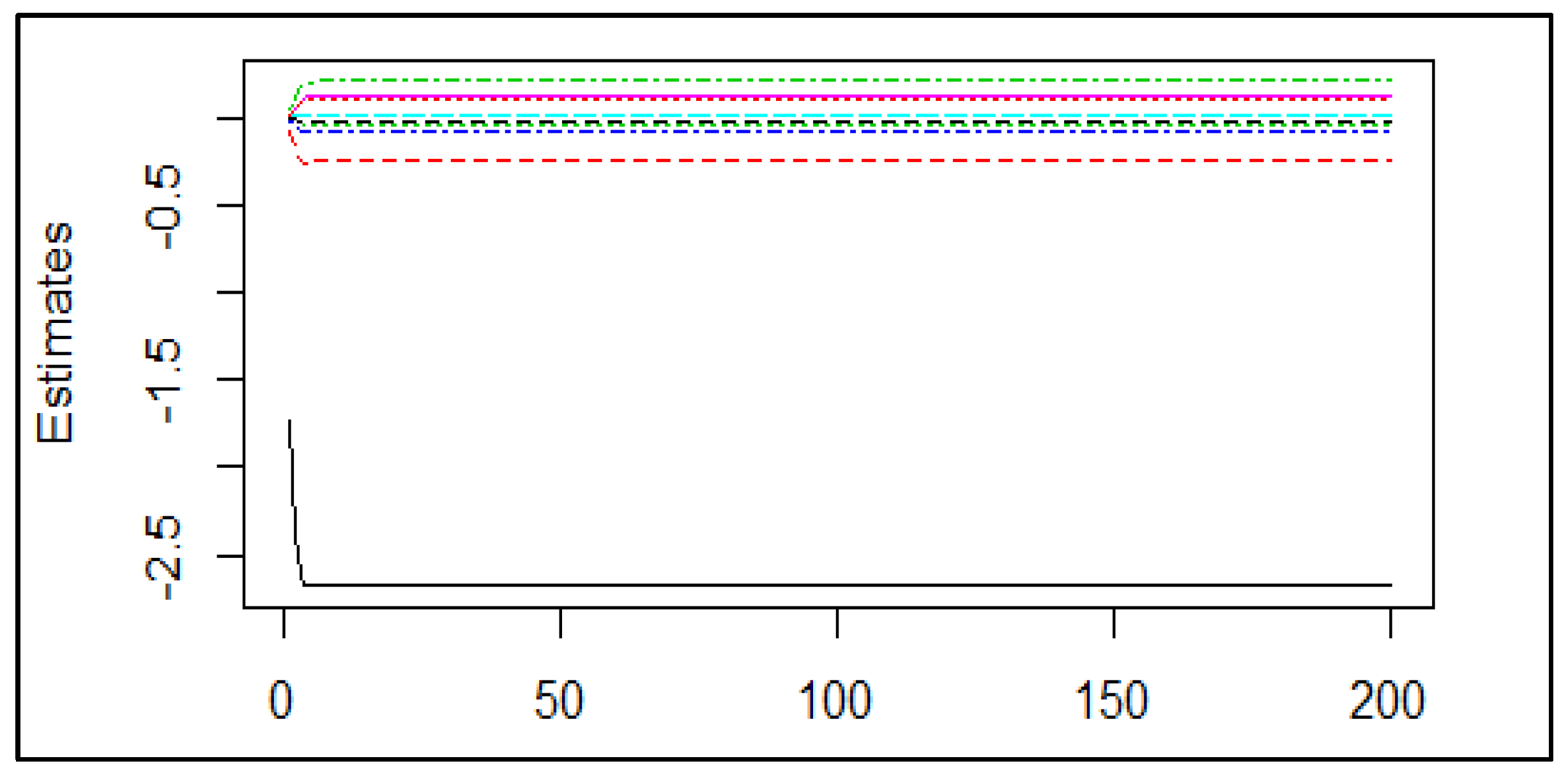
4.1. Coefficient Estimates
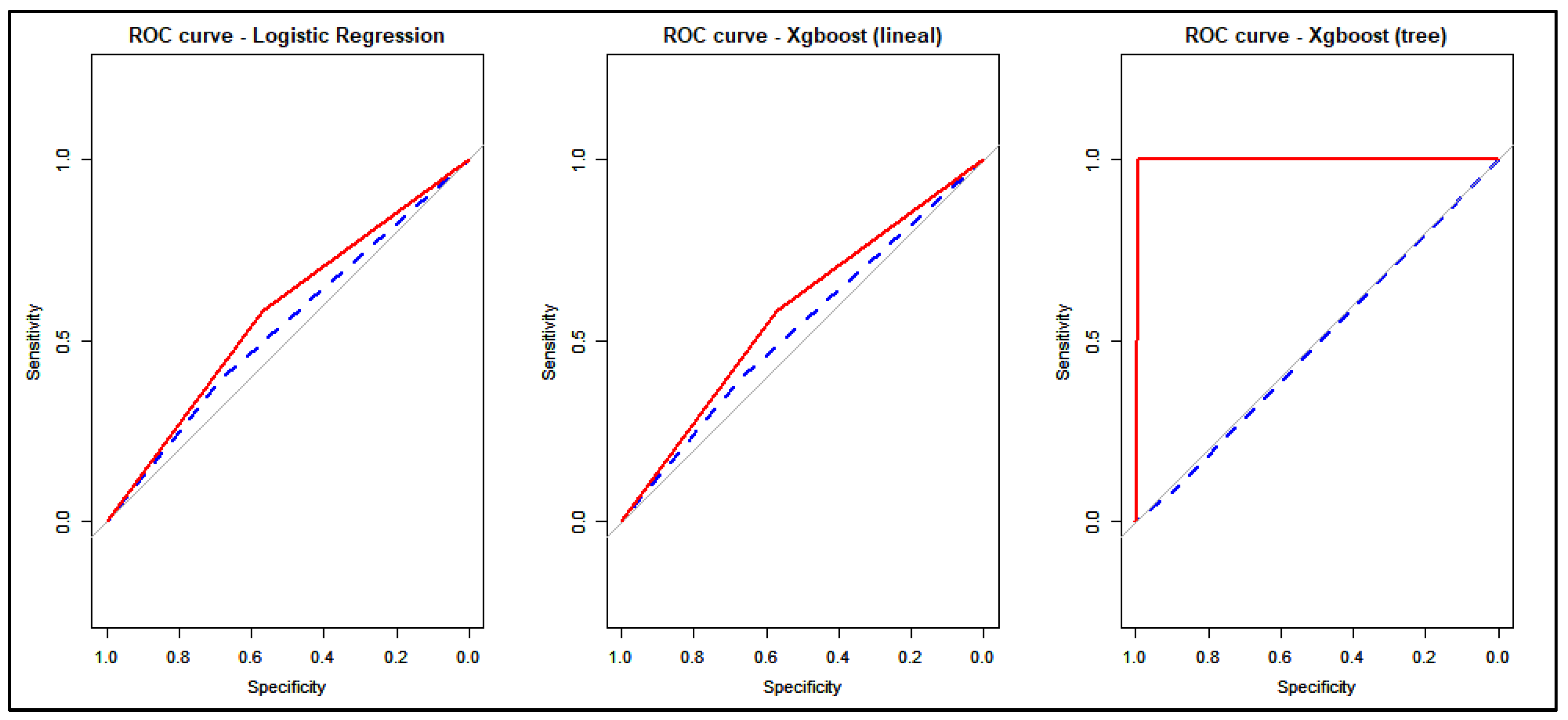
4.2. Prediction Performance
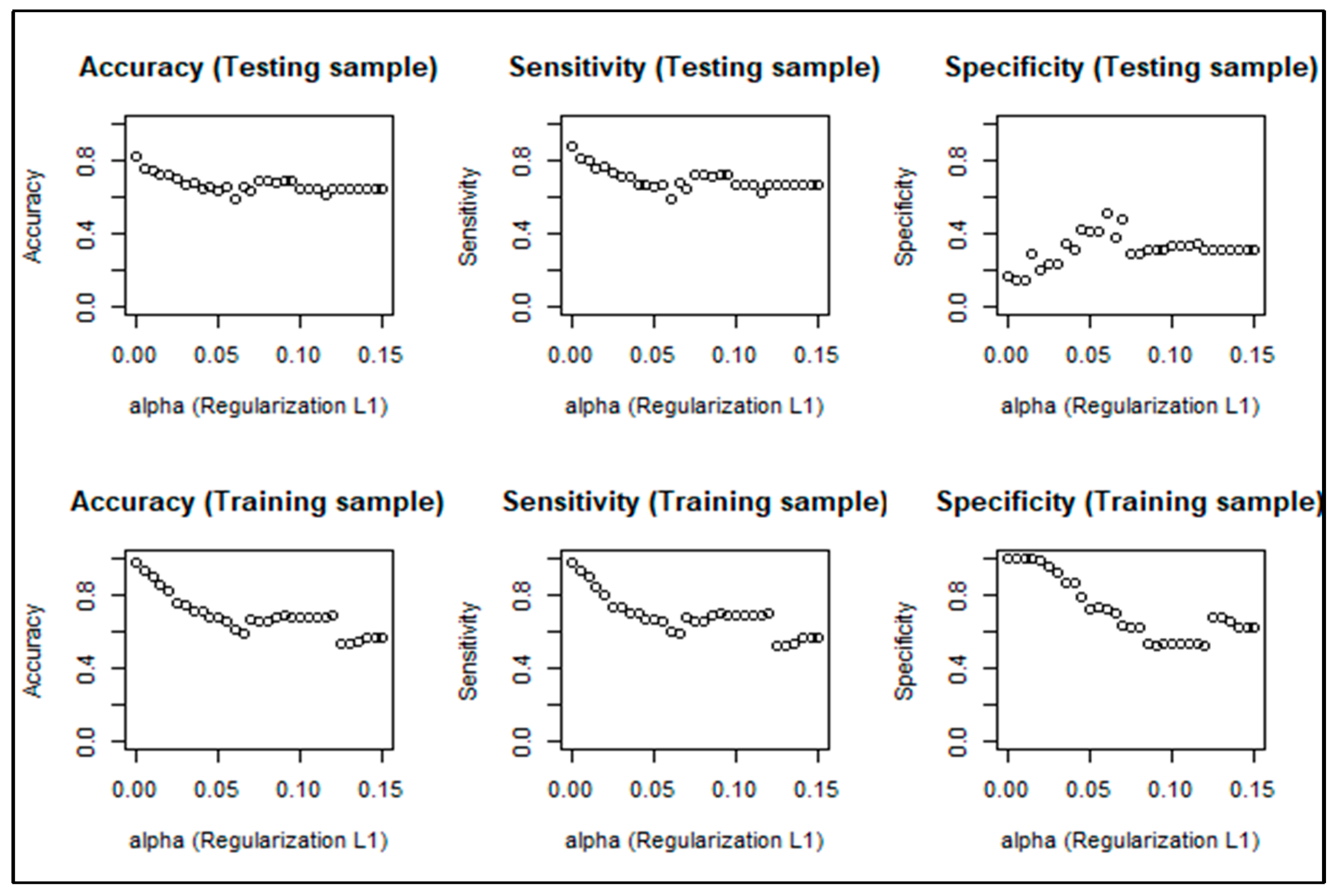
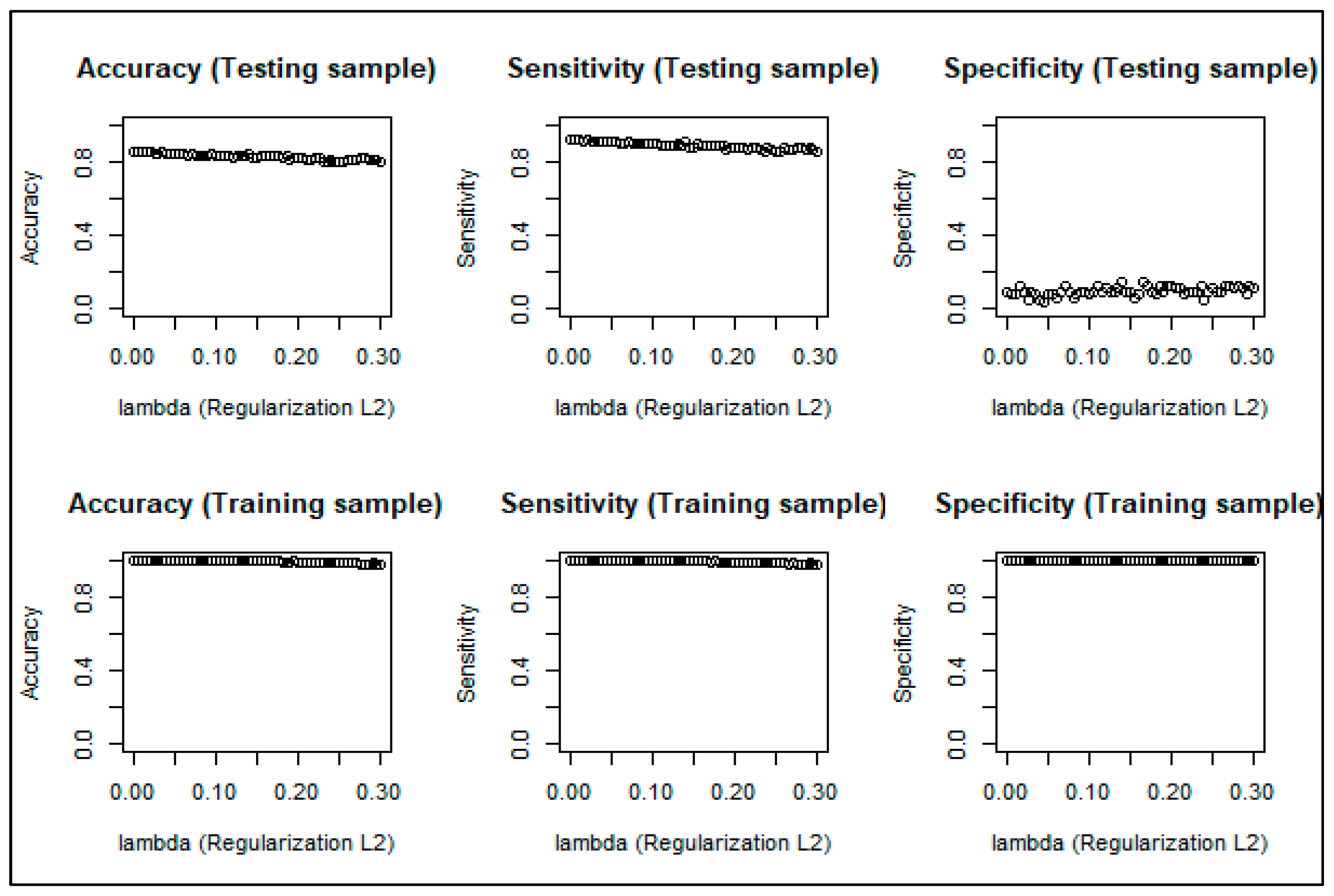
4.3. Correcting the Overfitting
4.4. Variable Importance
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| R Code |
| # Loading data |
| load(“data.Rdata”) |
| x<-data |
| # Training and test data sets |
| # We divide 70% of the data set as training, and 30% as testing |
| library(caret) |
| part<-createDataPartition(x$Y,p = 0.70, list = F) |
| train.set<-x[part,] # training data set |
| train.set<-train.set()[−1] |
| testing.set<- x[-part,] # testing data set |
| testing.set<-testing.set()[−1] |
| ## First Method: Logistic Regression |
| logistic1 <- glm(factor(train.set$Y) ~ x2+I(x2^2)+x3+x4+factor(x1)+x5+x6+x7+x8, |
| data = train.set,family = binomial(link = ‘logit’)) |
| summary(logistic1) |
| # Predicting the output with the testing data set |
| predicted.log.test <- predict(logistic1,testing.set, type = ‘response’) |
| # Predicting the output with the training data set |
| predicted.log1.train<- predict(logistic1,train.set, type = ‘response’) |
| # Variable Importance |
| varImp(logistic1) |
| ## Second Method: XGBoost (tree booster) |
| library(xgboost) |
| library(Matrix) |
| # Function xgboost requires sparsing data first |
| sparse_xx.tr<- sparse.model.matrix(Y ~ x2+I(x2^2)+x3+x4+factor(x1)+x5+x6+x7+x8, data = train.set) |
| sparse_xx.te<- sparse.model.matrix(Y ~ x2+I(x2^2)+x3+x4+factor(x1)+x5+x6+x7+x8, |
| data = testing.set) |
| xgboost_reg <- xgboost(data = sparse_xx.tr, label = train.set$Y, objective = “binary:logistic”, |
| nrounds = 100, verbose = 1) |
| # Predicting the output with testing data set |
| pred.xgboost.test<- predict(xgboost_reg,sparse_xx.te, outputmargin = F) |
| # Predicting the output with training data set |
| pred.xgboost.train<-predict(xgboost_reg,sparse_xx.tr, outputmargin = F) |
| # Variable Importance |
| importance <- xgb.importance(feature_names = sparse_xx.tr@Dimnames[(2)], |
| model = xgboost_reg) |
References
- Ayuso, Mercedes, Montserrat Guillén, and Ana María Pérez-Marín. 2014. Time and distance to first accident and driving patterns of young drivers with pay-as-you-drive insurance. Accident Analysis and Prevention 73: 125–31. [Google Scholar] [CrossRef] [PubMed]
- Ayuso, Mercedes, Montserrat Guillén, and Ana María Pérez-Marín. 2016a. Using GPS data to analyse the distance travelled to the first accident at fault in pay-as-you-drive insurance. Transportation Research Part C 68: 160–67. [Google Scholar] [CrossRef]
- Ayuso, Mercedes, Montserrat Guillén, and Ana María Pérez-Marín. 2016b. Telematics and gender discrimination: some usage-based evidence on whether men’s risk of accident differs from women’s. Risks 4: 10. [Google Scholar] [CrossRef]
- Bishop, Christopher M. 2007. Pattern recognition and machine learning. Journal of Electronic Imaging 16: 049901. [Google Scholar] [CrossRef]
- Boucher, Jean-Philippe, Steven Côté, and Montserrat Guillen. 2017. Exposure as duration and distance in telematics motor insurance using generalized additive models. Risks 5: 54. [Google Scholar] [CrossRef]
- Chen, Tianqi, and Carlos Guestrin. 2016. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, pp. 785–94. [Google Scholar] [CrossRef]
- De Boer, Pieter-Tjerk, Dirk P. Kroese, Shie Mannor, and Reuven Y. Rubinstein. 2005. A tutorial on the Cross Entropy Method. Annals of Operations Research 134: 19–67. [Google Scholar] [CrossRef]
- Dietterich, Thomas G., Pedro Domingos, Lise Getoor, Stephen Muggleton, and Prasad Tadepalli. 2008. Structured machine learning: The next ten years. Machine Learning 73: 3–23. [Google Scholar] [CrossRef]
- Elliott, Graham, and Allan Timmermann. 2003. Handbook of Economic Forecasting. Amsterdam: Elsevier. [Google Scholar]
- Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. 2001. The Elements of Statistical Learning. New York: Springer. [Google Scholar]
- Gao, Guangyuan, and Mario V. Wüthrich. 2018. Feature extraction from telematics car driving heatmaps. European Actuarial Journal 8: 383–406. [Google Scholar] [CrossRef]
- Gao, Guangyuan, and Mario V. Wüthrich. 2019. Convolutional neural network classification of telematics car driving data. Risks 7: 6. [Google Scholar] [CrossRef]
- Gao, Guangyuan, Shengwang Meng, and Mario V. Wüthrich. 2019. Claims frequency modeling using telematics car driving data. Scandinavian Actuarial Journal 2019: 143–62. [Google Scholar] [CrossRef]
- Gomez-Verdejo, Vanessa, Jeronimo Arenas-Garcia, Manuel Ortega-Moral, and Anıbal R. Figueiras-Vidal. 2005. Designing RBF classifiers for weighted boosting. IEEE International Joint Conference on Neural Networks 2: 1057–62. [Google Scholar] [CrossRef]
- Goodfellow, Ian, Bengio Yoshua, and Courville Aaron. 2016. Deep Learning. Chenai: MIT Press. [Google Scholar]
- Greene, William. 2002. Econometric Analysis, 2nd ed. New York: Chapman and Hall. [Google Scholar]
- Guillen, Montserrat, Jens Perch Nielsen, Mercedes Ayuso, and Ana M. Pérez-Marín. 2019. The use of telematics devices to improve automobile insurance rates. Risk Analysis 39: 662–72. [Google Scholar] [CrossRef] [PubMed]
- Hastie, Trevor, Rob Tibshirani, and Jerome Friedman. 2009. The Elements of Statistical Learning: Prediction, Inference and Data Mining. New York: Springer. [Google Scholar]
- He, Haibo, and Edwardo A. Garcia. 2008. Learning from imbalanced data. IEEE Transactions on Knowledge & Data Engineering 9: 1263–84. [Google Scholar] [CrossRef]
- Huang, Jianhua Z., and Lijian Yang. 2004. Identification of non-linear additive autoregressive models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 66: 463–77. [Google Scholar] [CrossRef]
- Hultkrantz, Lars, Jan-Eric Nilsson, and Sara Arvidsson. 2012. Voluntary internalization of speeding externalities with vehicle insurance. Transportation Research Part A: Policy and Practice 46: 926–37. [Google Scholar] [CrossRef]
- Ivanov, Valentin K., Vladimir V. Vasin, and Vitalii P. Tanana. 2013. Theory of Linear Ill-Posed Problems and Its Applications. Zeist: VSP. [Google Scholar]
- James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning. New York: Springer, vol. 112, p. 18. [Google Scholar]
- Kuhn, Max, and Kjell Johnson. 2013. Applied Predictive Modeling. New York: Springer, vol. 26. [Google Scholar]
- Lee, Simon, and Katrien Antonio. 2015. Why High Dimensional Modeling in Actuarial Science? Paper presented at Actuaries Institute ASTIN, AFIR/ERM and IACA Colloquia, Sydney, Australia, August 23–27; Available online: https://pdfs.semanticscholar.org/ad42/c5a42642e75d1a02b48c6eb84bab87874a1b.pdf (accessed on 8 May 2019).
- Lee, Simon CK, and Sheldon Lin. 2018. Delta boosting machine with application to general insurance. North American Actuarial Journal 22: 405–25. [Google Scholar] [CrossRef]
- Natekin, Alexey, and Alois Knoll. 2013. Gradient boosting machines, a tutorial. Frontiers in Neurorobotics 7: 21. [Google Scholar] [CrossRef] [PubMed]
- McCullagh, Peter, and John Nelder. 1989. Generalized Linear Models, 2nd ed. New York: Chapman and Hall. [Google Scholar]
- Pérez-Marín, Ana M., and Montserrat Guillén. 2019. Semi-autonomous vehicles: Usage-based data evidences of what could be expected from eliminating speed limit violations. Accident Analysis and Prevention 123: 99–106. [Google Scholar] [CrossRef] [PubMed]
- Schapire, Robert E., and Yoav Freund. 2012. Boosting: Foundations and Algorithms. Cambridge: MIT Press. [Google Scholar]
- Steinwart, Ingo, and Andreas Christmann. 2008. Support Vector Machines. New York: Springer Science & Business Media. [Google Scholar]
- Tikhonov, Andrej-Nikolaevich, and Vasiliy-Yakovlevich Arsenin. 1977. Solutions of Ill-Posed Problems. New York: Wiley. [Google Scholar]
- Verbelen, Roel, Katrien Antonio, and Gerda Claeskens. 2018. Unraveling the predictive power of telematics data in car insurance pricing. Journal of the Royal Statistical Society: Series C (Applied Statistics) 67: 1275–304. [Google Scholar] [CrossRef]
- Wüthrich, Mario V. 2017. Covariate selection from telematics car driving data. European Actuarial Journal 7: 89–108. [Google Scholar] [CrossRef]
| 1 | Note we have opted to refer here to coefficients as opposed to parameters to avoid confusion with the values defined below when describing the XGBoost method. |
| 2 | Natekin and Knoll (2013) explain that the ensemble model can be understood as a committee formed by a group of base learners or weak learners. Thus, any weak learner can be introduced as a boosting framework. Various boosting methods have been proposed, including: (B/P-) splines (Huang and Yang 2004); linear and penalized models (Hastie et al. 2009); decision trees (James et al. 2013); radial basis functions (Gomez-Verdejo et al. 2005); and Markov random fields (Dietterich et al. 2008). Although Chen and Guestrin (2016) state as a CART model, the R package xgboost currently performs three boosters: linear, tree and dart. |
| 3 | The XGBoost works in a function space rather than in a parameter space. This framework allows the objective function to be customized accordingly. |
| 4 | In general, this is only partially true. The relation of the variable age is typically non-linear, U-shaped, as (very) young drivers also cause a lot of accidents. The maximum age in this sample is 30 and so, even if models with age and age2 were estimated, the results did not change substantially. |
| 5 | This is not surprising because XGBoost (linear) is a combination of linear probability models. |
| Variables | Non-Occurrence of Accident Claims (Y = 0) | Occurrence of Accident Claims (Y = 1) | Total | |
|---|---|---|---|---|
| Age (years) | 25.10 | 24.55 | 25.06 | |
| Gender | Female | 1263 (93.21%) | 92 (6.79%) | 1355 |
| Male | 1309 (92.71%) | 103 (7.29%) | 1412 | |
| Driving experience (years) | 4.98 | 4.46 | 4.94 | |
| Age of vehicle (years) | 6.37 | 6.17 | 6.35 | |
| Total kilometers travelled | 7094.63 | 7634.97 | 7132.71 | |
| Percentage of total kilometers travelled in urban areas | 24.60 | 26.34 | 24.72 | |
| Percentage of total kilometers above the mandatory speed limit | 6.72 | 7.24 | 6.75 | |
| Percentage of total kilometers travelled at night | 6.88 | 6.66 | 6.86 | |
| Total number of cases | 2572 (92.95%) | 195 (7.05%) | 2767 |
| Training Data Set | |||||||
|---|---|---|---|---|---|---|---|
| Parameter Estimates | Logistic Regression | XGBoost (Linear Booster) | |||||
| Lower Bound | Estimate | Upper Bound | p-Value | Minimum | Mean | Maximum | |
| Constant | −2.8891 | −0.5442 | 1.8583 | 0.6526 | −2.6760 | −2.6690 | −1.7270 |
| * age | −0.2059 | −0.0994 | 0.0011 | 0.0591 | −0.2573 | −0.2416 | −0.0757 |
| drivexp | −0.1285 | −0.0210 | 0.0906 | 0.7060 | −0.0523 | −0.0517 | −0.0069 |
| ageveh | −0.0786 | −0.0249 | 0.0257 | 0.3481 | −0.0897 | −0.0885 | −0.0220 |
| male | −0.3672 | 0.0039 | 0.3751 | 0.9837 | 0.0019 | 0.0020 | 0.0070 |
| kmtotal | −0.0203 | 0.0266 | 0.2505 | 0.0137 | 0.1164 | 0.1176 | |
| pkmnig | −0.0354 | −0.0046 | 0.0239 | 0.7625 | −0.0292 | −0.0290 | −0.0061 |
| pkmexc | −0.0122 | 0.0144 | 0.0385 | 0.2650 | 0.0180 | 0.1007 | 0.1016 |
| * pkmurb | 0.0002 | 0.0146 | 0.0286 | 0.0425 | 0.0436 | 0.2008 | 0.2023 |
| Testing Data Set | |||
| Predictive Measures | Logistic Regression | XGBoost (Tree Booster) | XGBoost (Linear Booster) |
| 524 | 692 | 516 | |
| 38 | 58 | 38 | |
| 243 | 75 | 251 | |
| 25 | 5 | 25 | |
| Sensitivity | 0.3968 | 0.0790 | 0.3968 |
| Specificity | 0.6831 | 0.9022 | 0.6728 |
| Accuracy | 0.6614 | 0.8397 | 0.6518 |
| RMSE | 0.2651 | 0.2825 | 0.2651 |
| Training Data Set | |||
| Predictive Measures | Logistic Regression | XGBoost (Tree Booster) | XGBoost (Linear Booster) |
| 1030 | 1794 | 1030 | |
| 55 | 0 | 55 | |
| 775 | 11 | 775 | |
| 77 | 132 | 77 | |
| Sensitivity | 0.5833 | 1.0000 | 0.5833 |
| Specificity | 0.5706 | 0.9939 | 0.5706 |
| Accuracy | 0.5715 | 0.9943 | 0.5715 |
| RMSE | 0.2508 | 0.0373 | 0.2508 |
| Level of Importance | Logistic Regression | XGBoost (Tree Booster) |
|---|---|---|
| First | percentage of total kilometers travelled in urban areas | percentage of kilometers above the mandatory speed limits |
| Second | age | percentage of total kilometers travelled in urban areas |
| Third | total kilometers | percentage of total kilometers travelled at night |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pesantez-Narvaez, J.; Guillen, M.; Alcañiz, M. Predicting Motor Insurance Claims Using Telematics Data—XGBoost versus Logistic Regression. Risks 2019, 7, 70. https://doi.org/10.3390/risks7020070
Pesantez-Narvaez J, Guillen M, Alcañiz M. Predicting Motor Insurance Claims Using Telematics Data—XGBoost versus Logistic Regression. Risks. 2019; 7(2):70. https://doi.org/10.3390/risks7020070
Chicago/Turabian StylePesantez-Narvaez, Jessica, Montserrat Guillen, and Manuela Alcañiz. 2019. "Predicting Motor Insurance Claims Using Telematics Data—XGBoost versus Logistic Regression" Risks 7, no. 2: 70. https://doi.org/10.3390/risks7020070
APA StylePesantez-Narvaez, J., Guillen, M., & Alcañiz, M. (2019). Predicting Motor Insurance Claims Using Telematics Data—XGBoost versus Logistic Regression. Risks, 7(2), 70. https://doi.org/10.3390/risks7020070






