Treatment Level and Store Level Analyses of Healthcare Data
Abstract
:1. Introduction
2. Literature
2.1. Frequency-Severity Modeling
2.2. Longitudinal Modeling
2.3. Medical Data Analysis
3. Lognormal Regression
3.1. Model
3.2. Specific Example
4. GLMs
4.1. Motivation
- GLMs are able to model both the claim frequency and the claim severity in a unified language similar to that used in linear regression modeling.
- Standardized routines are readily available for software packages such as R, SAS, SPSS, and JMP, allowing the analyst to avoid writing complex maximum likelihood code and scripts.
- GLMs have flexibility in incorporating covariates into the modeling framework.
4.2. Poisson Regression for Count Data
4.3. Other GLM Models
4.4. The Frequency-Severity Model
- N, the number of claims (events),
- the amount of each claim (expense).
5. Treatment-Level Analysis
5.1. Model
- number of treatments in Department 1 (the department of interest)
- number of treatments in Department 2 (a department being compared with Department 1)
- number of treatments in Department 3 (all other departments)
5.1.1. Modeling Using GLMs
5.1.2. Modeling Using GLMs
5.1.3. Modeling Using GLMs
5.1.4. Modeling the Conditional Expenditure Severity
5.2. Treatment Categories
5.3. Patient Treatment Data
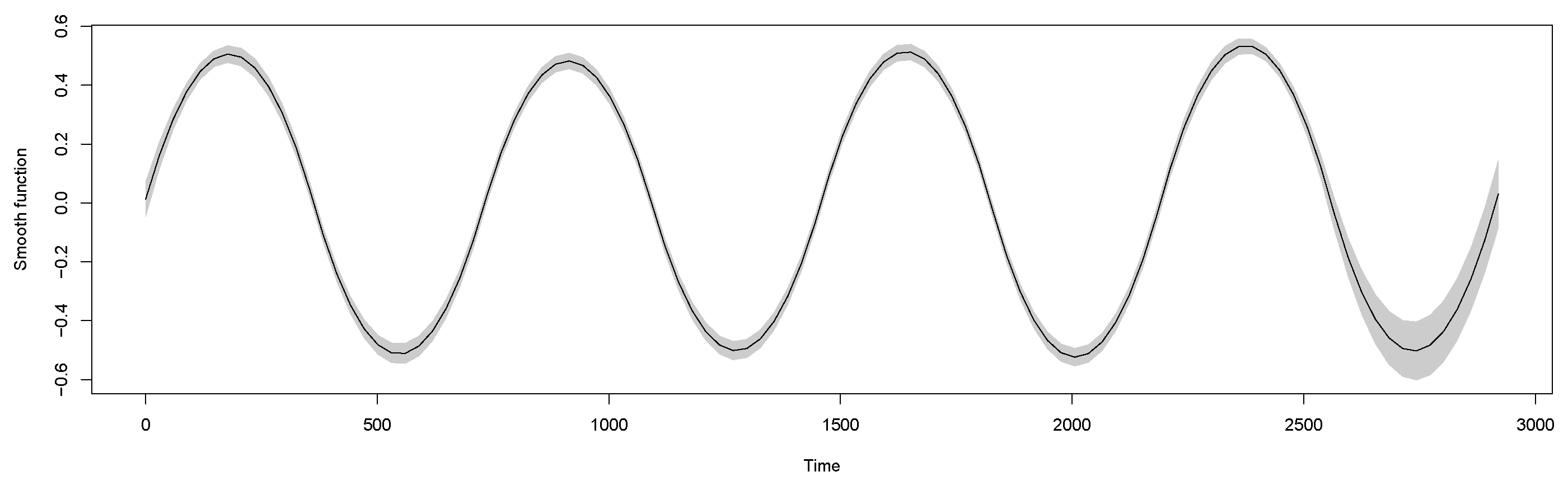
6. GAMs
7. Results
7.1. Simulation Study
- For each t, randomly generate the total number of patients from a Poisson distribution, so that , where t is the number of days elapsed since 1 January 2010, with the maximum t corresponding to 1 January 2019.
- Each patient i receives one treatment, whose ICD-10 code chapter is randomly generated from a multinomial distribution with the probability of each category following , for , sampled from a Dirichlet distribution.
- Department 1 opens at time 1 January 2017.
- Each treatment is assigned to either Department 1, 2, or 3 using a multinomial distribution with probability , sampled from a Dirichlet distribution. We fixed before the opening of Department 1, because the probability that a treatment is assigned to Department 1 should be zero before its opening. We used a different set of probabilities , also sampled from a Dirichlet distribution, after Department 1 opens.
- Each treatment results in a positive charge with probability 0.95.
- Given that a charge in ICD-10 code chapter k is positive, it results in a charge amount sampled from a gamma distribution with its scale parameter sampled from an exponential distribution with rate 0.001 and shape parameters fixed to one.
- The total number of days in the synthetic data is 3287, with a total of 67,983 patients.
7.2. Real Data Analysis
7.3. Model Validation
7.4. Dependence Modeling
8. Conclusions
9. Disclaimer
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boucher, Jean-Philippe. 2014. Regression with count dependent variables. In Predictive Modeling Applications in Actuarial Science. Cambridge: Cambridge University Press. [Google Scholar]
- De Jong, Piet, and Gillian Z. Heller. 2008. Generalized Linear Models for Insurance Data. Cambridge: Cambridge University Press. [Google Scholar]
- Dobson, Annette J., and Barnett Adrian G. 2008. An Introduction to Generalized Linear Models. Boca Raton: Chapman and Hall/CRC, Taylor & Francis Group. [Google Scholar]
- Frees, Edward W. 2004. Longitudinal and Panel Data: Analysis and Applications in the Social Sciences. Cambridge: Cambridge University Press. [Google Scholar]
- Frees, Edward W. 2009. Regression Modeling with Actuarial and Financial Applications. Cambridge: Cambridge University Press. [Google Scholar]
- Frees, Edward W. 2014. Frequency and severity models. In Predictive Modeling Applications in Actuarial Science. Cambridge: Cambridge University Press. [Google Scholar]
- Frees, Edward W. 2015. Analytics of insurance markets. Annual Review of Finacial Economics 7: 253–77. [Google Scholar] [CrossRef]
- Frees, Edward W., Jie Gao, and Marjorie A Rosenberg. 2011. Predicting the frequency and amount of health care expenditures. North American Actuarial Journal 15: 377–92. [Google Scholar] [CrossRef]
- Frees, Edward W., and Gee Lee. 2016. Rating endorsements using generalized linear models. Variance 10: 51–74. [Google Scholar]
- Frees, Edward W., Gee Y. Lee, and Lu Yang. 2016. Multivariate frequency-severity regression models in insurance. Risks 4: 4. [Google Scholar] [CrossRef]
- Frees, Edward W., Glenn Meyers, and A. David Cummings. 2011. Summarizing insurance scores using a gini index. Journal of the American Statistical Association 106: 495. [Google Scholar] [CrossRef]
- Frees, Edward W., and Emiliano A. Valdez. 2008. Hierarchical insurance claims modeling. Journal of the American Statistical Association 103: 1457–69. [Google Scholar] [CrossRef]
- Guillén, Montserrat. 2014. Regression with categorical dependent variables. In Predictive Modeling Applications in Actuarial Science. Cambridge: Cambridge University Press. [Google Scholar]
- Joe, Harry. 2014. Dependence Modeling with Copulas. Boca Raton: CRC Press. [Google Scholar]
- Keeler, Emmett B., and John E. Rolph. 1988. The demand for episodes of treatment in the health insurance experiment. Journal of Health Economics 7: 337–67. [Google Scholar] [CrossRef]
- Klugman, Stuart A., Harry H. Panjer, and Gordon E. Willmot. 2012. Loss Models: From Data to Decisions. Hoboken: John Wiley & Sons, Inc. [Google Scholar]
- Mildenhall, Stephen J. 1999. A systematic relationship between minimum bias and generalized linear models. Proceedings of the Casualty Actuarial Society 86: 393–487. [Google Scholar]
- Myers, Raymond, Douglas C. Montgomery, G. Geoffrey Vining, and Timothy J. Robinson. 2002. Generlized Linear Models with Applications in Engineering and the Sciences. New York: John Wiley & Sons, Inc. [Google Scholar]
- Nelder, John, and Robert Wedderburn. 1972. Generalized linear models. Journal of the Royal Statistical Society. Series A (General) 135: 370–84. [Google Scholar] [CrossRef]
- Nelsen, Roger B. 1999. An Introduction to Copulas. New York: Springer Science & Business Media, Inc. [Google Scholar]
- Ohlsson, Esbjörn, and Björn Johansson. 2010. Non-Life Insurance Pricing with Generalized Linear Models. Berlin Heidelberg: Springer Verlag. [Google Scholar]
- Rosenberg, Marjorie A., and Phillip M. Farrell. 2008. Predictive modeling of costs for a chronic disease with acute high-cost episodes. North American Actuarial Journal 12: 1–19. [Google Scholar] [CrossRef]
- Ruscone, Marta Nai, and Silvia Angela Osmetti. 2016. Modelling the Dependence in Multivariate Longitudinal Data by Pair Copula Decomposition. Basel: Springer International Publishing Switzerland. [Google Scholar]
- Shi, Peng. 2012. Multivariate longitudinal modeling of insurance company expenses. Insurance: Mathematics and Economics 51: 204–15. [Google Scholar] [CrossRef]
- Shi, Peng. 2014. Fat-tailed regression models. In Predictive Modeling Applications in Actuarial Science. Cambridge: Cambridge University Press. [Google Scholar]
- Shi, Peng, and Emiliano Valdez. 2014. Longitudinal modeling of insurance claim counts using jitters. Scandinavian Actuarial Journal 2014: 159–79. [Google Scholar] [CrossRef]
- Smith, Michael, Aleksey Min, Carlos Almeida, and Claudia Czado. 2010. Modeling longitudinal data using a pair-copula decomposition of serial dependence. Journal of the American Statistical Association 105: 1467–79. [Google Scholar] [CrossRef]
- Sun, Jiafeng, Edward W. Frees, and Marjorie A. Rosenberg. 2008. Heavy-tailed longitudinal data modeling using copulas. Insurance: Mathematics and Economics 42: 817–30. [Google Scholar] [CrossRef]
- Wood, Simon N. 2017. Generalized Additive Models: An Introduction with R, Second Edition. Boca Raon: CRC Press. [Google Scholar]
- Yang, Xipei. 2011. Multivariate Long-Tailed Regression With New Copulas. Ph.D. thesis, University of Wisconsin-Madison, Madison, WI, USA. [Google Scholar]

| Chapter | Block | Description |
|---|---|---|
| 1 | A00–B99 | Certain infectious and parasitic diseases |
| 2 | C00–D48 | Neoplasms |
| 3 | D50–D89 | Diseases of the blood and blood-forming organs and certain disorders |
| involving the immune mechanism | ||
| 4 | E00–E90 | Endocrine, nutritional and metabolic diseases |
| 5 | F00–F99 | Mental and behavioral disorders |
| 6 | G00–G99 | Diseases of the nervous system |
| 7 | H00–H59 | Diseases of the eye and adnexa |
| 8 | H60–H95 | Diseases of the ear and mastoid process |
| 9 | I00–I99 | Diseases of the circulatory system |
| 10 | J00–J99 | Diseases of the respiratory system |
| 11 | K00–K93 | Diseases of the digestive system |
| 12 | L00–L99 | Diseases of the skin and subcutaneous tissue |
| 13 | M00–M99 | Diseases of the musculoskeletal system and connective tissue |
| 14 | N00–N99 | Diseases of the genitourinary system |
| 15 | O00–O99 | Pregnancy, childbirth and the puerperium |
| 16 | P00–P96 | Certain conditions originating in the perinatal period |
| 17 | Q00–Q99 | Congenital malformations, deformations and chromosomal |
| abnormalities | ||
| 18 | R00–R99 | Symptoms, signs and abnormal clinical and laboratory findings, |
| not elsewhere classified | ||
| 19 | S00–T98 | Injury, poisoning and certain other consequences of external causes |
| 20 | V01–Y98 | External causes of morbidity and mortality |
| 21 | Z00–Z99 | Factors influencing health status and contact with health services |
| 22 | U00–U99 | Codes for special purposes |
| Variable Name | Description |
|---|---|
| ClinicOpen | Indicator variable of whether Department 1 is open |
| WDay | A categorical variable of the weekday. |
| (Categories: Sun, Mon, Tue, Wed, Thr, Fri, Sat) | |
| Month | A categorical variable of the month. |
| (Categories: Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec) | |
| Chapter | A categorical variable of the treatment category. |
| (Categories: shown in Table 1) | |
| Time | Numeric variable corresponding to the current day relative to a reference time |
| point. In our study, the reference time point is the first day in which data are available. |
| Model for Number of Patients | |||
|---|---|---|---|
| Estimate | Std. Err. | ||
| (Intercept) | −0.034 | 0.026 | |
| ClinicOpen | 0.017 | 0.050 | |
| Month:2 | 0.131 | 0.019 | *** |
| Month:3 | 0.196 | 0.018 | *** |
| Month:4 | 0.180 | 0.018 | *** |
| Month:5 | 0.079 | 0.019 | *** |
| Month:6 | −0.136 | 0.020 | *** |
| Month:7 | −0.405 | 0.021 | *** |
| Month:8 | −0.666 | 0.023 | *** |
| Month:9 | −0.895 | 0.025 | *** |
| Month:10 | −0.821 | 0.025 | *** |
| Month:11 | −0.550 | 0.024 | *** |
| Month:12 | −0.294 | 0.022 | *** |
| Chapter:2 | 0.824 | 0.024 | *** |
| Chapter:3 | −1.869 | 0.055 | *** |
| Chapter:4 | −0.278 | 0.031 | *** |
| Chapter:5 | 0.234 | 0.027 | *** |
| Chapter:6 | −0.176 | 0.030 | *** |
| Chapter:7 | 0.531 | 0.025 | *** |
| Chapter:8 | 1.501 | 0.022 | *** |
| Chapter:9 | 0.357 | 0.026 | *** |
| Chapter:10 | −1.801 | 0.053 | *** |
| Chapter:11 | −1.217 | 0.042 | *** |
| Chapter:12 | −1.288 | 0.043 | *** |
| Chapter:13 | −0.800 | 0.036 | *** |
| Chapter:14 | 0.191 | 0.027 | *** |
| Chapter:15 | −0.493 | 0.033 | *** |
| Chapter:16 | 0.269 | 0.027 | *** |
| Chapter:17 | −0.494 | 0.033 | *** |
| Chapter:18 | −1.584 | 0.049 | *** |
| Chapter:19 | −2.909 | 0.088 | *** |
| Chapter:20 | 1.174 | 0.023 | *** |
| Chapter:21 | −2.052 | 0.060 | *** |
| Chapter:22 | 0.078 | 0.028 | ** |
| Number of Treatments (Department 1) | |||
| Estimate | Std. Err. | ||
| (Intercept) | −1.550 | 0.030 | ** |
| Probability of Positive Charge (Department 1) | |||
| Estimate | Std. Err. | ||
| (Intercept) | 0.952 | 0.004 | *** |
| Charge Severity Model (Department 1) | |||
| Estimate | Std. Err. | ||
| (Intercept) | 5.902 | 0.115 | *** |
| Chapter:2 | −0.223 | 0.153 | |
| Chapter:3 | 1.168 | 0.491 | * |
| Chapter:4 | 1.309 | 0.216 | *** |
| Chapter:5 | 1.033 | 0.175 | *** |
| Chapter:6 | 0.936 | 0.223 | *** |
| Chapter:7 | 0.648 | 0.166 | *** |
| Chapter:8 | −1.584 | 0.140 | *** |
| Chapter:9 | −0.133 | 0.179 | |
| Chapter:10 | −1.271 | 0.394 | ** |
| Estimate | Std. Err. | ||
| Chapter:11 | 0.712 | 0.298 | * |
| Chapter:12 | 0.282 | 0.419 | |
| Chapter:13 | 0.917 | 0.232 | *** |
| Chapter:14 | 0.963 | 0.193 | *** |
| Chapter:15 | −0.246 | 0.229 | |
| Chapter:17 | 0.741 | 0.223 | *** |
| Chapter:18 | 1.197 | 0.419 | ** |
| Chapter:19 | 1.710 | 1.073 | |
| Chapter:20 | 1.399 | 0.145 | *** |
| Chapter:21 | 1.097 | 0.491 | * |
| Chapter:22 | −0.266 | 0.201 | |
| Number of treatments (Department 2) | |||
|---|---|---|---|
| Estimate | Std. Err. | ||
| (Intercept) | −0.370 | 0.005 | *** |
| ClinicOpen | −0.451 | 0.022 | ** |
| Probability of Positive Charge (Department 2) | |||
| Estimate | Std. Err. | ||
| (Intercept) | 0.949 | 0.001 | ** |
| Charge Severity Model (Department 2) | |||
| Estimate | Std. Err. | ||
| (Intercept) | 6.826 | 0.020 | *** |
| Chapter:2 | −1.121 | 0.026 | *** |
| Chapter:3 | 0.199 | 0.067 | ** |
| Chapter:4 | 0.436 | 0.035 | *** |
| Chapter:5 | 0.049 | 0.030 | |
| Chapter:6 | 0.233 | 0.034 | *** |
| Chapter:7 | −0.392 | 0.028 | *** |
| Chapter:8 | −2.479 | 0.023 | *** |
| Chapter:9 | −1.212 | 0.029 | *** |
| Chapter:10 | −1.759 | 0.067 | *** |
| Chapter:11 | −0.236 | 0.050 | *** |
| Chapter:12 | −0.835 | 0.052 | *** |
| Chapter:13 | −0.433 | 0.043 | *** |
| Chapter:14 | 0.004 | 0.031 | |
| Chapter:15 | −1.411 | 0.038 | *** |
| Chapter:16 | −2.991 | 0.030 | *** |
| Chapter:18 | 0.436 | 0.059 | *** |
| Chapter:19 | 0.184 | 0.110 | . |
| Chapter:20 | 0.491 | 0.024 | *** |
| Chapter:21 | −0.014 | 0.071 | |
| Chapter:22 | −1.393 | 0.031 | *** |
| Estimate | Std. Err. | ||
| (Intercept) | −1.094 | 0.007 | *** |
| ClinicOpen | 0.079 | 0.024 | ** |
| Probability of Positive Charge (Department 3) | |||
| Estimate | Std. Err. | ||
| (Intercept) | 0.948 | 0.002 | *** |
| Charge Severity Model (Department 3) | |||
| Estimate | Std. Err. | ||
| (Intercept) | 6.625 | 0.036 | *** |
| Chapter:2 | −0.928 | 0.043 | *** |
| Chapter:3 | 0.456 | 0.101 | *** |
| Chapter:4 | 0.636 | 0.054 | *** |
| Chapter:5 | 0.244 | 0.048 | *** |
| Chapter:6 | 0.374 | 0.053 | *** |
| Chapter:7 | −0.186 | 0.045 | *** |
| Chapter:8 | −2.267 | 0.039 | *** |
| Chapter:9 | −0.978 | 0.047 | *** |
| Chapter:10 | −1.469 | 0.092 | *** |
| Chapter:11 | −0.019 | 0.075 | |
| Chapter:12 | −0.532 | 0.077 | *** |
| Chapter:13 | −0.069 | 0.063 | |
| Chapter:14 | 0.206 | 0.048 | *** |
| Chapter:15 | −1.152 | 0.058 | *** |
| Chapter:16 | −2.827 | 0.048 | *** |
| Chapter:17 | 0.404 | 0.058 | *** |
| Chapter:18 | 0.671 | 0.087 | *** |
| Chapter:19 | 0.373 | 0.157 | * |
| Chapter:20 | 0.682 | 0.041 | *** |
| Chapter:21 | −0.124 | 0.113 | |
| Chapter:22 | −1.150 | 0.050 | *** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Ding, J.; Lidwell, K.R.; Manski, S.; Lee, G.Y.; Esposito, E.X. Treatment Level and Store Level Analyses of Healthcare Data. Risks 2019, 7, 43. https://doi.org/10.3390/risks7020043
Wang K, Ding J, Lidwell KR, Manski S, Lee GY, Esposito EX. Treatment Level and Store Level Analyses of Healthcare Data. Risks. 2019; 7(2):43. https://doi.org/10.3390/risks7020043
Chicago/Turabian StyleWang, Kaiwen, Jiehui Ding, Kristen R. Lidwell, Scott Manski, Gee Y. Lee, and Emilio Xavier Esposito. 2019. "Treatment Level and Store Level Analyses of Healthcare Data" Risks 7, no. 2: 43. https://doi.org/10.3390/risks7020043
APA StyleWang, K., Ding, J., Lidwell, K. R., Manski, S., Lee, G. Y., & Esposito, E. X. (2019). Treatment Level and Store Level Analyses of Healthcare Data. Risks, 7(2), 43. https://doi.org/10.3390/risks7020043





