Target Matrix Estimators in Risk-Based Portfolios
Abstract
1. Introduction
2. Risk-Based Portfolios
3. Shrinkage Estimator
3.1. Target Matrix Literature Review
3.2. Estimators for the Target Matrix
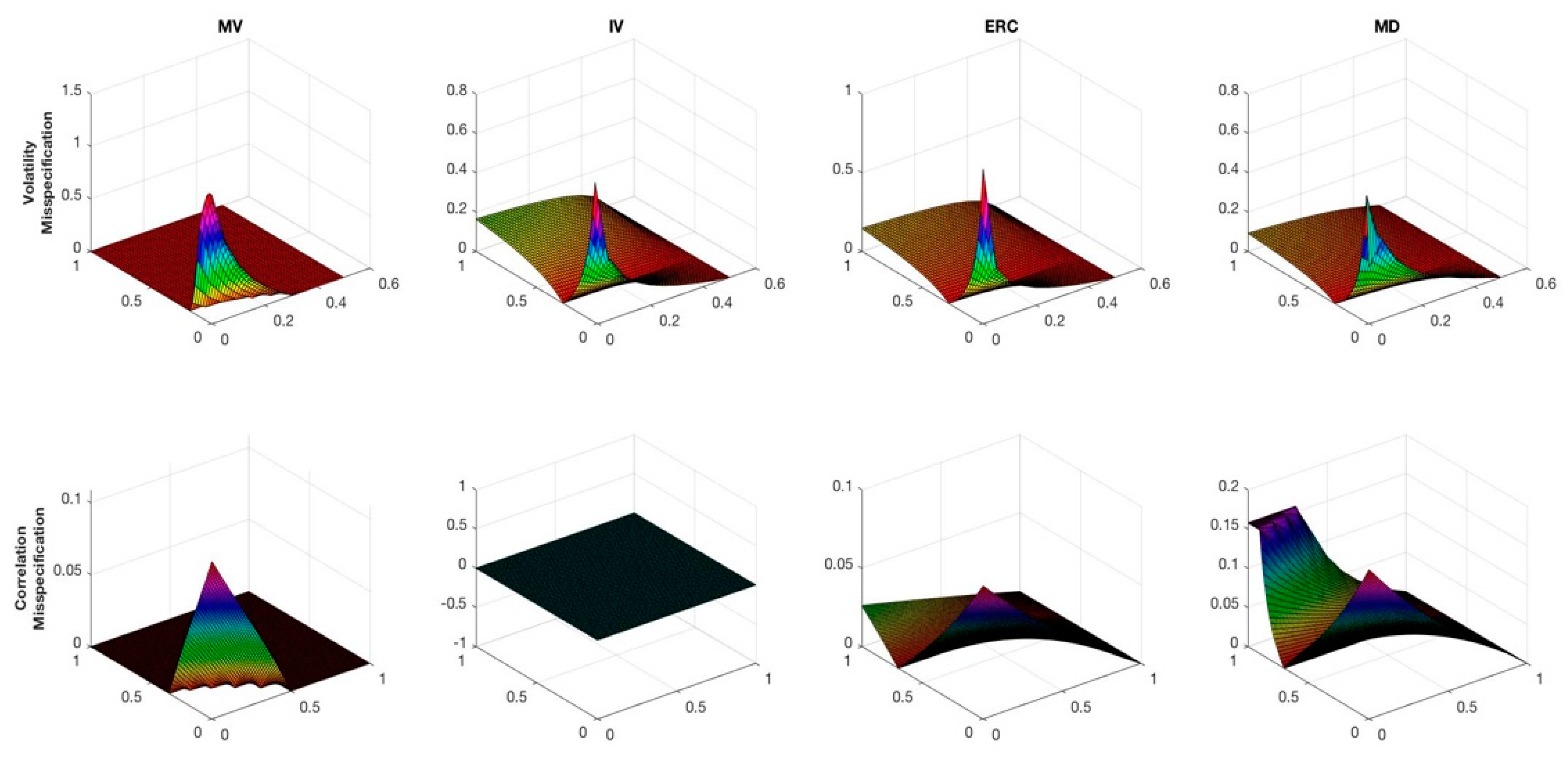
3.3. The Impact of Misspecification in the Target Matrix
4. Case Study—Monte Carlo Analysis
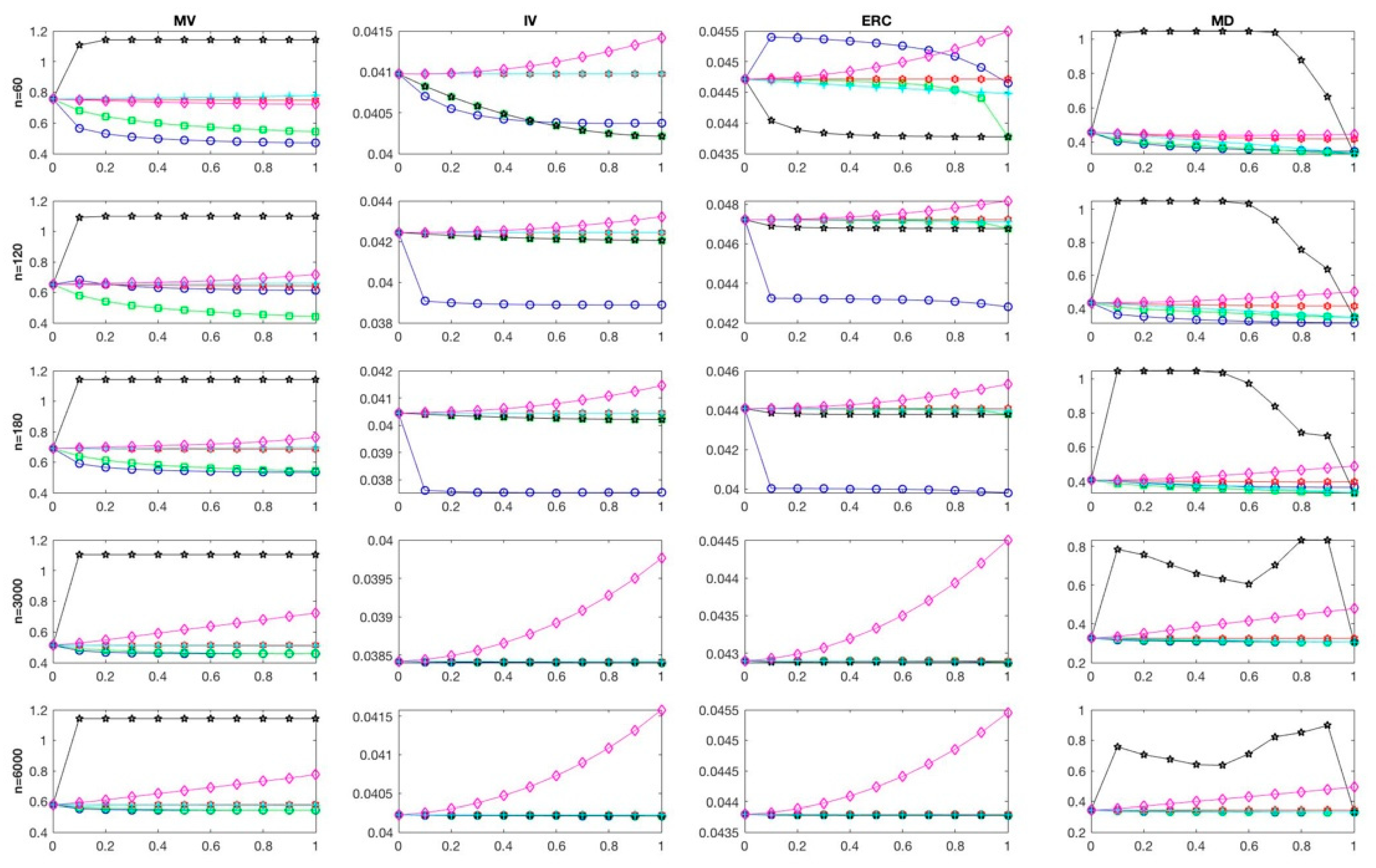
4.1. Main Results
4.1.1. Results on Portfolio Weights
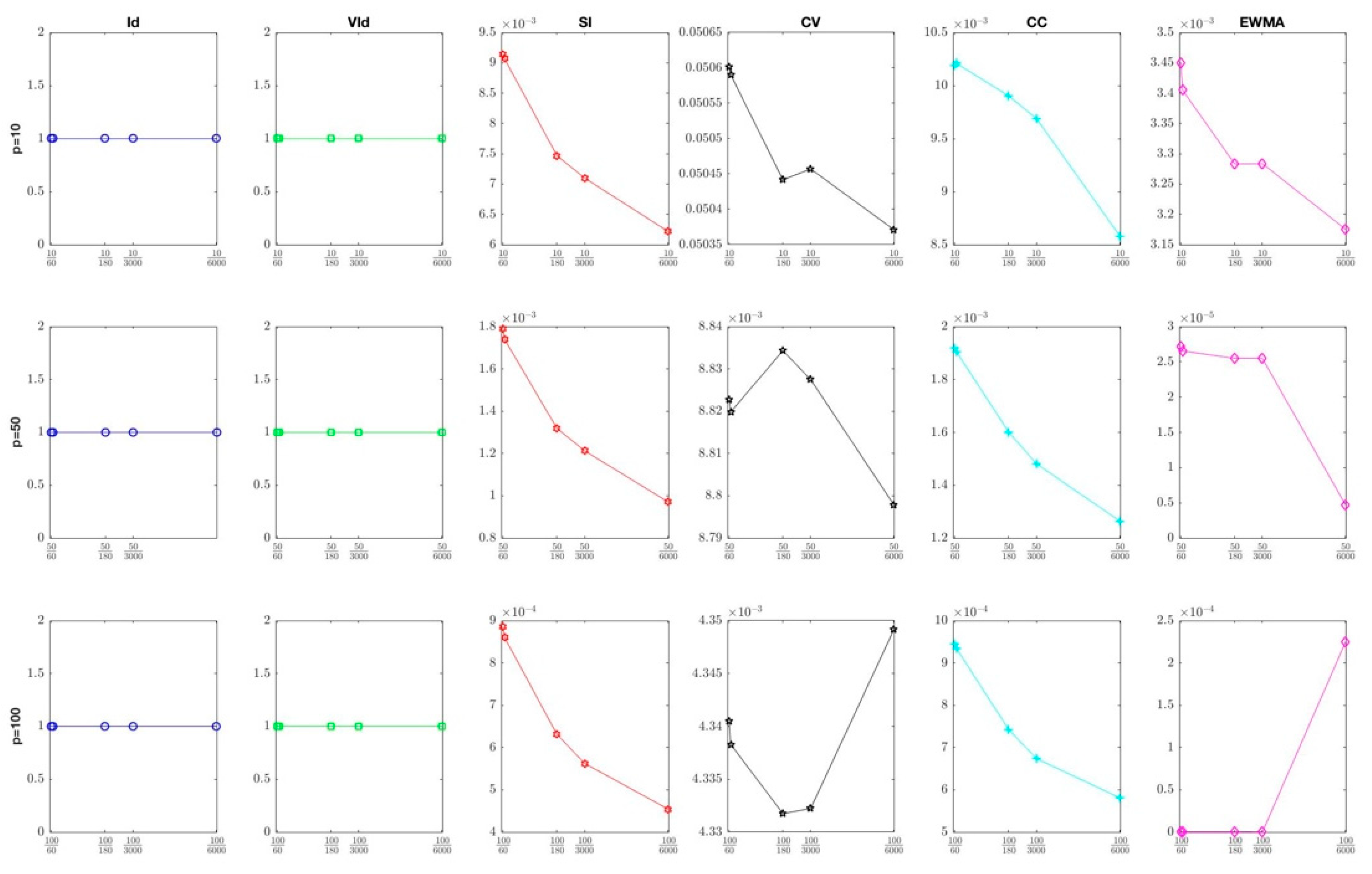
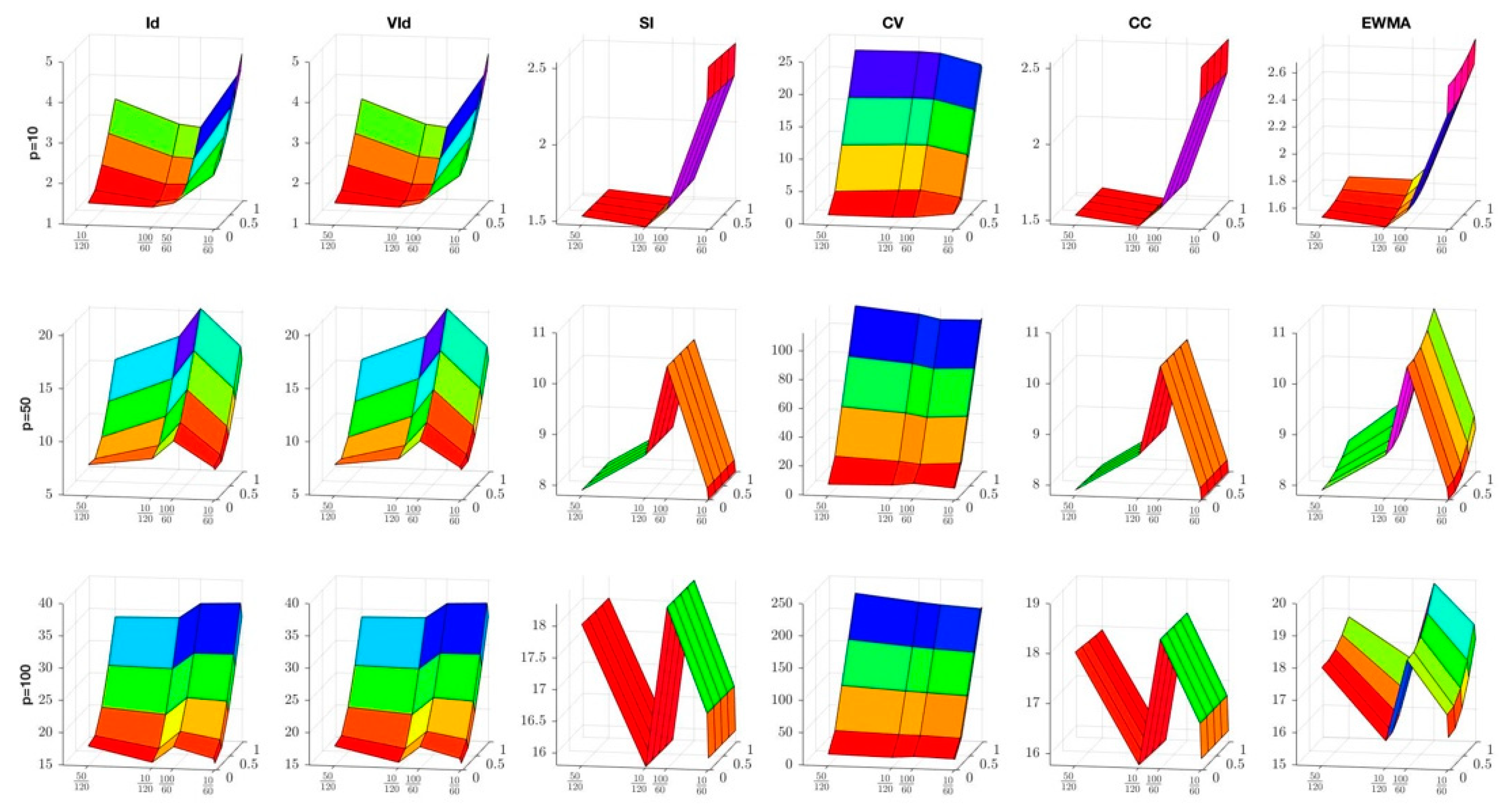
4.1.2. Sensitivity to Shrinkage Intensity
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Ardia, David, Guido Bolliger, Kris Boudt, and Jean Philippe Gagnon-Fleury. 2017. The Impact of Covariance Misspecification in Risk-Based Portfolios. Annals of Operations Research 254: 1–16. [Google Scholar] [CrossRef]
- Black, Fischer, and Robert Litterman. 1992. Global Portfolio Optimization. Financial Analysts Journal 48: 28–43. [Google Scholar] [CrossRef]
- Briner, Beat G., and Gregory Connor. 2008. How Much Structure Is Best? A Comparison of Market Model, Factor Model and Unstructured Equity Covariance Matrices. Journal of Risk 10: 3–30. [Google Scholar] [CrossRef]
- Candelon, Bertrand, Christophe Hurlin, and Sessi Tokpavi. 2012. Sampling Error and Double Shrinkage Estimation of Minimum Variance Portfolios. Journal of Empirical Finance 19: 511–27. [Google Scholar] [CrossRef]
- Chopra, Vijay Kumar, and William T. Ziemba. 1993. The Effect of Errors in Means, Variances, and Covariances on Optimal Portfolio Choice. The Journal of Portfolio Management 19: 6–11. [Google Scholar] [CrossRef]
- Choueifaty, Yves, and Yves Coignard. 2008. Toward Maximum Diversification. The Journal of Portfolio Management 35: 40–51. [Google Scholar] [CrossRef]
- De Miguel, Victor, Lorenzo Garlappi, and Raman Uppal. 2009. Optimal versus Naive Diversification: How Inefficient Is the 1/N Portfolio Strategy? Review of Financial Studies 22: 1915–53. [Google Scholar] [CrossRef]
- De Miguel, Victor, Alberto Martin-Utrera, and Francisco J. Nogales. 2013. Size Matters: Optimal Calibration of Shrinkage Estimators for Portfolio Selection. Journal of Banking and Finance 37: 3018–34. [Google Scholar] [CrossRef]
- J., P. Morgan, and Reuters Ltd. 1996. Risk Metrics—Technical Document, 4th ed. New York: Morgan Guaranty Trust. [Google Scholar]
- Jagannathan, Ravi, and Tongshu Ma. 2003. Risk Reduction in Large Portfolios: Why Imposing the Wrong Constraints Helps. Journal of Finance 58: 1651–84. [Google Scholar] [CrossRef]
- James, W., and Charles Stein. 1961. Estimation with Quadratic Loss. Proceedings of the 4th Berkeley Symposium on Probability and Statistics, Volume 1. Paper presented at Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, June 20–July 30. [Google Scholar]
- Jorion, Philippe. 1986. Bayes-Stein Estimation for Portfolio Analysis. The Journal of Financial and Quantitative Analysis 21: 279–92. [Google Scholar] [CrossRef]
- Ledoit, Olivier, and Michael Wolf. 2003. Improved Estimation of the Covariance Matrix of Stock Returns with an Application to Portfolio Selection. Journal of Empirical Finance 10: 603–21. [Google Scholar] [CrossRef]
- Ledoit, Olivier, and Michael Wolf. 2004a. A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices. Journal of Multivariate Analysis 88: 365–411. [Google Scholar] [CrossRef]
- Ledoit, Olivier, and Michael Wolf. 2004b. Honey, I Shrunk the Sample Covariance Matrix—Problems in Mean-Variance Optimization. Journal of Portfolio Management 30: 110–19. [Google Scholar] [CrossRef]
- Leote de Carvalho, Raul, Xiao Lu, and Pierre Moulin. 2012. Demystifying Equity Risk–Based Strategies: A Simple Alpha plus Beta Description. The Journal of Portfolio Management 38: 56–70. [Google Scholar] [CrossRef]
- MacKinlay, A. Craig, and Lubos Pastor. 2000. Asset Pricing Models: Implications for Expected Returns and Portfolio Selection. Review of Financial Studies 13: 883–916. [Google Scholar] [CrossRef]
- Maillard, Sébastien, Thierry Roncalli, and Jérôme Teïletche. 2010. The Properties of Equally Weighted Risk Contribution Portfolios. The Journal of Portfolio Management 36: 60–70. [Google Scholar] [CrossRef]
- Marčenko, Vladimir Alexandrovich, and Leonid Andreevich Pastur. 1967. Distribution of Eigenvalues for Some Sets of Random Matrices. Mathematics of the USSR-Sbornik 1: 507–36. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio Selection. The Journal of Finance 7: 77–91. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1956. The Optimization of a Quadratic Function Subject to Linear Constraints. Naval Research Logistics Quarterly 3: 111–33. [Google Scholar] [CrossRef]
- Merton, Robert C. 1980. On Estimating the Expected Return on the Market: An Exploratory Investigation. Topics in Catalysis 8: 323–61. [Google Scholar]
- Michaud, Richard O. 1989. The Markowitz Optimization Enigma: Is Optimized Optimal? Financial Analysts Journal 45: 31–42. [Google Scholar] [CrossRef]
- Pantaleo, Ester, Michele Tumminello, Fabrizio Lillo, and Rosario N. Mantegna. 2011. When Do Improved Covariance Matrix Estimators Enhance Portfolio Optimization? An Empirical Comparative Study of Nine Estimators. Quantitative Finance 11: 1067–80. [Google Scholar] [CrossRef]
- Qian, Edward. 2006. On the Financial Interpretation of Risk Contribution: Risk Budgets Do Add Up. Journal of Investment Management 4: 41–51. [Google Scholar] [CrossRef]
- Schäfer, Juliane, and Korbinian Strimmer. 2005. A Shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Applications in Genetics and Molecular Biology 4: 1175–89. [Google Scholar] [CrossRef] [PubMed]
- Sharpe, William F. 1963. A simplified model for portfolio analysis. Management Science 9: 277–93. [Google Scholar] [CrossRef]
| 1 | The majority of papers on risk-based portfolios are published in journal aimed at practitioners, as the Journal of Portfolio Management. |
| 2 | With this we refer to the population covariance matrix, which by definition is not observable and then unfeasible. Hence, is estimated taking into account the observations stored in X: we will deeply treat this in the next section. |
| 3 | The sample covariance matrix is the Maximum Likelihood Estimator (MLE) under Normality, therefore it lets data speaks without imposing any structure. |
| 4 | In reality, we exclude the Scaled Identity of De Miguel et al. (2013) because of its great similarity with the Identity and Variance Identity implemented in our study. |
| 5 | Ardia et al. (2017) imposes Asset-1 and Asset-2 to have 10% annual volatility; Asset-3 to have 20% annual volatility; correlations between Asset-1/Asset-2 and Asset-1/Asset-3 are set as negative and correlation between corporate bonds and equities (Asset-2/Asset-3) is set as positive. However, to better resemble real data, specifically the S&P500, the US corporate index and the US Treasury Index total returns, we assume all three correlation parameters to be positive. |
| 6 | |
| 7 | Simulations were done in MATLAB setting the random seed generator at its default value, thus ensuring the full reproducibility of the analysis. Related code available at the GitHub page of the author: https://github.com/marconeffelli/Risk-Based-Portfolios. |

| Reference | Matrix to Shrink | Target Matrix | Shrinkage Intensity | Portfolio Selection Rule | Research Question |
|---|---|---|---|---|---|
| (Ledoit and Wolf 2003) | SCVm | Market Model and Variance Identity | Risk-function minimisation | Classical Markowitz problem | Portfolio Performance comparison |
| (Ledoit and Wolf 2004a) | SCVm | Identity | Risk-function minimisation | N.A. | Theoretical paper to gauge the shrinkage asymptotic properties |
| (Ledoit and Wolf 2004b) | SCVm | Constant Correlation Model | Optimal shrinkage constant | Classical Markowitz problem | Portfolio Performance comparison |
| (Briner and Connor 2008) | Demeaned SCVm | Market Model | Same as (Ledoit and Wolf 2004b) | N.A. | Analysis of the trade-off estimation error and model specification error |
| (Pantaleo et al. 2011) | SCVm | Market Model, Common Covariance and Constant Correlation Model | Unbiased estimator of (Schäfer and Strimmer 2005) | Classical Markowitz problem | Portfolio Performance comparison |
| (Candelon et al. 2012) | SCVm | Market Model and Identity | Same as (Ledoit and Wolf 2003, 2004b) | Black-Litterman GMVP | Portfolio Performance comparison |
| (De Miguel et al. 2013) | SCVm | Scaled Identity | Expected quadratic loss and bootstrapping approach | Classical Markowitz problem | Comprehensive investigation of shrinkage estimators |
| (Ardia et al. 2017) | SCVm | Market Model | Same as (Ledoit and Wolf 2003) | Risk-based portfolios | Theoretical paper to assess effect on risk-based weights |
| Asset | Minimum Variance (MV) | Inverse Volatility (IV) | Equal-Risk-Contribution (ERC) | Maximum Diversification (MD) |
|---|---|---|---|---|
| Asset-1 | 0.500 | 0.400 | 0.448 | 0.506 |
| Asset-2 | 0.500 | 0.400 | 0.374 | 0.385 |
| Asset-3 | 0.000 | 0.200 | 0.177 | 0.108 |
| P = 10 | P = 50 | P = 100 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MV | IV | ERC | MD | MV | IV | ERC | MD | MV | IV | ERC | MD | |
| Panel A: n = 60 | ||||||||||||
| S | 0.834 | 0.1585 | 0.1736 | 0.5842 | 0.7721 | 0.0573 | 0.0637 | 0.4933 | 0.7555 | 0.0409 | 0.0447 | 0.4565 |
| Id | 0.6863 | 0.1425 | 0.1528 | 0.5045 | 0.6215 | 0.0559 | 0.0631 | 0.3873 | 0.4967 | 0.0404 | 0.0451 | 0.3652 |
| VId | 0.6935 | 0.1583 | 0.1732 | 0.5176 | 0.5999 | 0.0567 | 0.0634 | 0.4092 | 0.5901 | 0.0404 | 0.0445 | 0.3686 |
| SI | 0.838 | 0.1585 | 0.1736 | 0.5678 | 0.7685 | 0.0573 | 0.0637 | 0.4709 | 0.75 | 0.0409 | 0.0447 | 0.4288 |
| CV | 1.2438 | 0.1583 | 0.1731 | 1.011 | 1.1484 | 0.0567 | 0.0628 | 0.9381 | 1.1386 | 0.0404 | 0.0438 | 0.9185 |
| CC | 0.8353 | 0.1585 | 0.1733 | 0.5361 | 0.7808 | 0.0573 | 0.0635 | 0.4328 | 0.7663 | 0.0409 | 0.0445 | 0.3922 |
| EWMA | 0.8473 | 0.1593 | 0.1745 | 0.595 | 0.7811 | 0.0575 | 0.064 | 0.5142 | 0.7325 | 0.0411 | 0.045 | 0.4431 |
| Panel B: n = 120 | ||||||||||||
| S | 0.9064 | 0.0877 | 0.0989 | 0.4649 | 0.7814 | 0.059 | 0.0656 | 0.5065 | 0.6519 | 0.0424 | 0.0472 | 0.4332 |
| Id | 0.8157 | 0.087 | 0.0983 | 0.4256 | 0.6259 | 0.0613 | 0.0688 | 0.4354 | 0.6307 | 0.0389 | 0.0431 | 0.328 |
| VId | 0.8235 | 0.0871 | 0.0985 | 0.4284 | 0.6259 | 0.0613 | 0.0688 | 0.4354 | 0.489 | 0.0421 | 0.0471 | 0.3712 |
| SI | 0.9097 | 0.0877 | 0.0989 | 0.4563 | 0.7777 | 0.059 | 0.0656 | 0.4925 | 0.6458 | 0.0424 | 0.0472 | 0.419 |
| CV | 1.3269 | 0.0871 | 0.0982 | 0.9667 | 1.1806 | 0.0587 | 0.0651 | 1.0138 | 1.0974 | 0.0421 | 0.0467 | 0.8951 |
| CC | 0.905 | 0.0877 | 0.0988 | 0.4357 | 0.7822 | 0.059 | 0.0655 | 0.4636 | 0.6566 | 0.0424 | 0.0471 | 0.3856 |
| EWMA | 0.9281 | 0.0883 | 0.0996 | 0.4859 | 0.7994 | 0.0592 | 0.0658 | 0.5246 | 0.6788 | 0.0427 | 0.0475 | 0.4601 |
| Panel C: n = 180 | ||||||||||||
| S | 0.7989 | 0.1311 | 0.1423 | 0.5007 | 0.7932 | 0.0564 | 0.0627 | 0.4631 | 0.6905 | 0.0404 | 0.044 | 0.4065 |
| Id | 0.7206 | 0.1308 | 0.142 | 0.4736 | 0.6705 | 0.0562 | 0.0625 | 0.405 | 0.5477 | 0.0375 | 0.0399 | 0.3748 |
| VId | 0.7273 | 0.1308 | 0.1421 | 0.4757 | 0.6838 | 0.0562 | 0.0626 | 0.4127 | 0.5754 | 0.0402 | 0.044 | 0.3556 |
| SI | 0.8001 | 0.1311 | 0.1423 | 0.4954 | 0.7904 | 0.0564 | 0.0627 | 0.4545 | 0.6873 | 0.0404 | 0.044 | 0.3982 |
| CV | 1.2715 | 0.1308 | 0.1419 | 0.9961 | 1.2073 | 0.0562 | 0.0624 | 0.9988 | 1.1422 | 0.0402 | 0.0437 | 0.8705 |
| CC | 0.7957 | 0.1311 | 0.1423 | 0.4803 | 0.792 | 0.0564 | 0.0626 | 0.4259 | 0.692 | 0.0404 | 0.044 | 0.3672 |
| EWMA | 0.8415 | 0.1322 | 0.1435 | 0.526 | 0.8284 | 0.0567 | 0.0631 | 0.5005 | 0.7206 | 0.0408 | 0.0445 | 0.4429 |
| Panel D: n = 3000 | ||||||||||||
| S | 0.7504 | 0.1476 | 0.1596 | 0.3957 | 0.734 | 0.049 | 0.0539 | 0.3988 | 0.513 | 0.0384 | 0.0428 | 0.3259 |
| Id | 0.7441 | 0.1477 | 0.1597 | 0.3946 | 0.7009 | 0.049 | 0.0539 | 0.3872 | 0.4615 | 0.0384 | 0.0428 | 0.3096 |
| VId | 0.7437 | 0.1477 | 0.1596 | 0.3945 | 0.7043 | 0.049 | 0.0539 | 0.3886 | 0.4673 | 0.0384 | 0.0428 | 0.312 |
| SI | 0.7516 | 0.1476 | 0.1596 | 0.3955 | 0.7339 | 0.049 | 0.0539 | 0.3984 | 0.5123 | 0.0384 | 0.0428 | 0.3252 |
| CV | 1.2864 | 0.1477 | 0.1597 | 0.963 | 1.2281 | 0.049 | 0.0538 | 0.9954 | 1.1041 | 0.0384 | 0.0428 | 0.6822 |
| CC | 0.7488 | 0.1476 | 0.1596 | 0.3949 | 0.7316 | 0.049 | 0.0539 | 0.3904 | 0.5096 | 0.0384 | 0.0428 | 0.3143 |
| EWMA | 0.8563 | 0.1489 | 0.1611 | 0.4452 | 0.8161 | 0.0497 | 0.0547 | 0.4652 | 0.6244 | 0.0389 | 0.0435 | 0.4076 |
| Panel E: n = 6000 | ||||||||||||
| S | 0.9672 | 0.1302 | 0.1409 | 0.4821 | 0.5737 | 0.0539 | 0.0589 | 0.3481 | 0.5772 | 0.0402 | 0.0437 | 0.3436 |
| Id | 0.9496 | 0.1301 | 0.1408 | 0.4813 | 0.6095 | 0.0575 | 0.0639 | 0.4076 | 0.5449 | 0.0402 | 0.0437 | 0.3342 |
| VId | 0.951 | 0.1301 | 0.1409 | 0.4815 | 0.5419 | 0.054 | 0.0589 | 0.3401 | 0.5483 | 0.0402 | 0.0437 | 0.3354 |
| SI | 0.9688 | 0.1302 | 0.1409 | 0.482 | 0.574 | 0.0539 | 0.0589 | 0.3479 | 0.5772 | 0.0402 | 0.0437 | 0.3434 |
| CV | 1.4142 | 0.1301 | 0.1408 | 1.0034 | 1.1436 | 0.054 | 0.0589 | 0.9706 | 1.1422 | 0.0402 | 0.0437 | 0.7031 |
| CC | 0.9656 | 0.1302 | 0.1409 | 0.4814 | 0.5709 | 0.0539 | 0.0589 | 0.3415 | 0.575 | 0.0402 | 0.0437 | 0.3368 |
| EWMA | 1.0432 | 0.1312 | 0.1422 | 0.5232 | 0.6946 | 0.0547 | 0.0599 | 0.4319 | 0.681 | 0.0407 | 0.0444 | 0.4229 |
| P = 10 | P = 50 | P = 100 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MV | IV | ERC | MD | MV | IV | ERC | MD | MV | IV | ERC | MD | |
| Panel A: n = 60 | ||||||||||||
| S | 0.8340 | 0.1585 | 0.1736 | 0.5842 | 0.7721 | 0.0573 | 0.0637 | 0.4933 | 0.7555 | 0.0409 | 0.0447 | 0.4565 |
| Id | 0.6778 | 0.1424 | 0.1525 | 0.501 | 0.5997 | 0.0558 | 0.0624 | 0.3704 | 0.471 | 0.0403 | 0.0446 | 0.3462 |
| VId | 0.6689 | 0.1581 | 0.173 | 0.5084 | 0.5539 | 0.0565 | 0.0627 | 0.3795 | 0.5428 | 0.0402 | 0.0437 | 0.3331 |
| SI | 0.8345 | 0.1585 | 0.1735 | 0.558 | 0.7666 | 0.0573 | 0.0637 | 0.4633 | 0.7479 | 0.0409 | 0.0447 | 0.4195 |
| CV | 1.2392 | 0.1581 | 0.1729 | 0.509 | 1.117 | 0.0565 | 0.0627 | 0.3795 | 1.1068 | 0.0402 | 0.0437 | 0.3331 |
| CC | 0.8335 | 0.1585 | 0.1731 | 0.5081 | 0.7733 | 0.0573 | 0.0634 | 0.3795 | 0.757 | 0.0409 | 0.0444 | 0.3332 |
| EWMA | 0.8331 | 0.1586 | 0.1737 | 0.5852 | 0.7706 | 0.0573 | 0.0637 | 0.4953 | 0.7213 | 0.0409 | 0.0447 | 0.4395 |
| Panel B: n = 120 | ||||||||||||
| S | 0.9064 | 0.0877 | 0.0989 | 0.4649 | 0.7814 | 0.059 | 0.0656 | 0.5065 | 0.6519 | 0.0424 | 0.0472 | 0.4332 |
| Id | 0.8121 | 0.087 | 0.0981 | 0.4241 | 0.6119 | 0.0613 | 0.0685 | 0.4255 | 0.613 | 0.0388 | 0.0428 | 0.3111 |
| VId | 0.8121 | 0.087 | 0.0982 | 0.4242 | 0.6119 | 0.0613 | 0.0685 | 0.4255 | 0.4425 | 0.042 | 0.0467 | 0.3445 |
| SI | 0.907 | 0.0877 | 0.0989 | 0.4526 | 0.776 | 0.059 | 0.0656 | 0.4872 | 0.6431 | 0.0424 | 0.0472 | 0.414 |
| CV | 1.3269 | 0.087 | 0.0981 | 0.4245 | 1.1756 | 0.0586 | 0.0651 | 0.4302 | 1.0916 | 0.042 | 0.0467 | 0.3445 |
| CC | 0.9043 | 0.0877 | 0.0987 | 0.4241 | 0.781 | 0.059 | 0.0654 | 0.4302 | 0.6527 | 0.0424 | 0.0471 | 0.3446 |
| EWMA | 0.9052 | 0.0876 | 0.0988 | 0.4651 | 0.7797 | 0.0589 | 0.0655 | 0.5056 | 0.6554 | 0.0424 | 0.0472 | 0.4331 |
| Panel C: n = 180 | ||||||||||||
| S | 0.7989 | 0.1311 | 0.1423 | 0.5007 | 0.7932 | 0.0564 | 0.0627 | 0.4631 | 0.6905 | 0.0404 | 0.044 | 0.4065 |
| Id | 0.7177 | 0.1307 | 0.1419 | 0.4724 | 0.6613 | 0.0562 | 0.0624 | 0.3977 | 0.534 | 0.0375 | 0.0398 | 0.3645 |
| VId | 0.718 | 0.1307 | 0.1419 | 0.4724 | 0.6614 | 0.0562 | 0.0624 | 0.3979 | 0.5428 | 0.0402 | 0.0437 | 0.3331 |
| SI | 0.799 | 0.1311 | 0.1423 | 0.4929 | 0.7897 | 0.0564 | 0.0627 | 0.4515 | 0.6863 | 0.0404 | 0.044 | 0.3955 |
| CV | 1.2715 | 0.1307 | 0.1418 | 0.4724 | 1.2073 | 0.0562 | 0.0624 | 0.3979 | 1.1422 | 0.0402 | 0.0437 | 0.3331 |
| CC | 0.7942 | 0.1311 | 0.1422 | 0.4725 | 0.7912 | 0.0564 | 0.0626 | 0.3977 | 0.6904 | 0.0404 | 0.0439 | 0.3331 |
| EWMA | 0.8035 | 0.1312 | 0.1424 | 0.5008 | 0.7951 | 0.0564 | 0.0626 | 0.4653 | 0.6938 | 0.0404 | 0.044 | 0.4074 |
| Panel D: n = 3000 | ||||||||||||
| S | 0.7504 | 0.1476 | 0.1596 | 0.3957 | 0.734 | 0.049 | 0.0539 | 0.3988 | 0.513 | 0.0384 | 0.0428 | 0.3259 |
| Id | 0.7425 | 0.1477 | 0.1596 | 0.3941 | 0.6988 | 0.049 | 0.0538 | 0.3859 | 0.4573 | 0.0384 | 0.0428 | 0.3072 |
| VId | 0.7426 | 0.1476 | 0.1596 | 0.3941 | 0.6988 | 0.049 | 0.0538 | 0.3859 | 0.4573 | 0.0384 | 0.0428 | 0.3072 |
| SI | 0.7506 | 0.1476 | 0.1596 | 0.3953 | 0.7339 | 0.049 | 0.0539 | 0.3983 | 0.512 | 0.0384 | 0.0428 | 0.325 |
| CV | 1.2864 | 0.1476 | 0.1596 | 0.3951 | 1.2281 | 0.049 | 0.0538 | 0.3859 | 1.1041 | 0.0384 | 0.0428 | 0.3072 |
| CC | 0.7477 | 0.1476 | 0.1596 | 0.3946 | 0.7299 | 0.049 | 0.0539 | 0.386 | 0.5073 | 0.0384 | 0.0428 | 0.3072 |
| EWMA | 0.7615 | 0.1477 | 0.1597 | 0.3981 | 0.7439 | 0.0491 | 0.0539 | 0.4043 | 0.5263 | 0.0384 | 0.0429 | 0.3346 |
| Panel E: n = 6000 | ||||||||||||
| S | 0.9672 | 0.1302 | 0.1409 | 0.4821 | 0.5737 | 0.0539 | 0.0589 | 0.3481 | 0.5772 | 0.0402 | 0.0437 | 0.3436 |
| Id | 0.9486 | 0.13 | 0.1408 | 0.4811 | 0.6085 | 0.0575 | 0.0639 | 0.4072 | 0.5428 | 0.0402 | 0.0437 | 0.3331 |
| VId | 0.9486 | 0.13 | 0.1408 | 0.4811 | 0.5365 | 0.054 | 0.0589 | 0.3381 | 0.5428 | 0.0402 | 0.0437 | 0.3331 |
| SI | 0.9675 | 0.1302 | 0.1409 | 0.482 | 0.5738 | 0.0539 | 0.0589 | 0.3478 | 0.5772 | 0.0402 | 0.0437 | 0.3433 |
| CV | 1.4142 | 0.13 | 0.1408 | 0.4811 | 1.1436 | 0.054 | 0.0589 | 0.3381 | 1.1422 | 0.0402 | 0.0437 | 0.3331 |
| CC | 0.9644 | 0.1302 | 0.1409 | 0.4812 | 0.5687 | 0.0539 | 0.0589 | 0.3381 | 0.5733 | 0.0402 | 0.0437 | 0.3331 |
| EWMA | 0.9765 | 0.1302 | 0.1409 | 0.4832 | 0.5901 | 0.054 | 0.059 | 0.3561 | 0.59 | 0.0402 | 0.0438 | 0.3524 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neffelli, M. Target Matrix Estimators in Risk-Based Portfolios. Risks 2018, 6, 125. https://doi.org/10.3390/risks6040125
Neffelli M. Target Matrix Estimators in Risk-Based Portfolios. Risks. 2018; 6(4):125. https://doi.org/10.3390/risks6040125
Chicago/Turabian StyleNeffelli, Marco. 2018. "Target Matrix Estimators in Risk-Based Portfolios" Risks 6, no. 4: 125. https://doi.org/10.3390/risks6040125
APA StyleNeffelli, M. (2018). Target Matrix Estimators in Risk-Based Portfolios. Risks, 6(4), 125. https://doi.org/10.3390/risks6040125





