Country Risk Ratings and Stock Market Returns in Brazil, Russia, India, and China (BRICS) Countries: A Nonlinear Dynamic Approach
Abstract
:1. Introduction
2. Literature Review
3. Methodology
4. Data and Empirical Results
4.1. Data
4.2. Empirical Results from the NARDL Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Specification of the NARDL Models Estimated
The NARDL Models
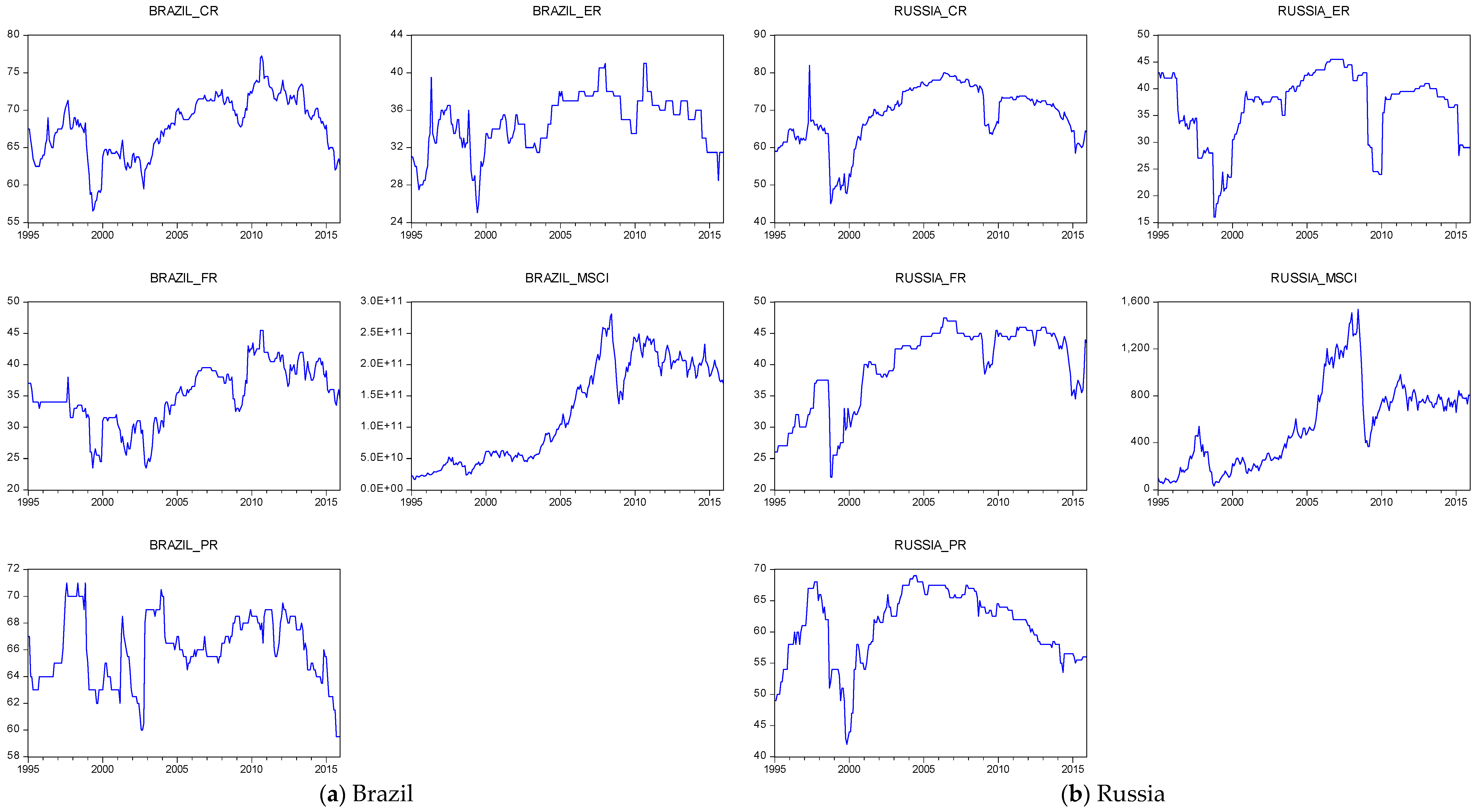
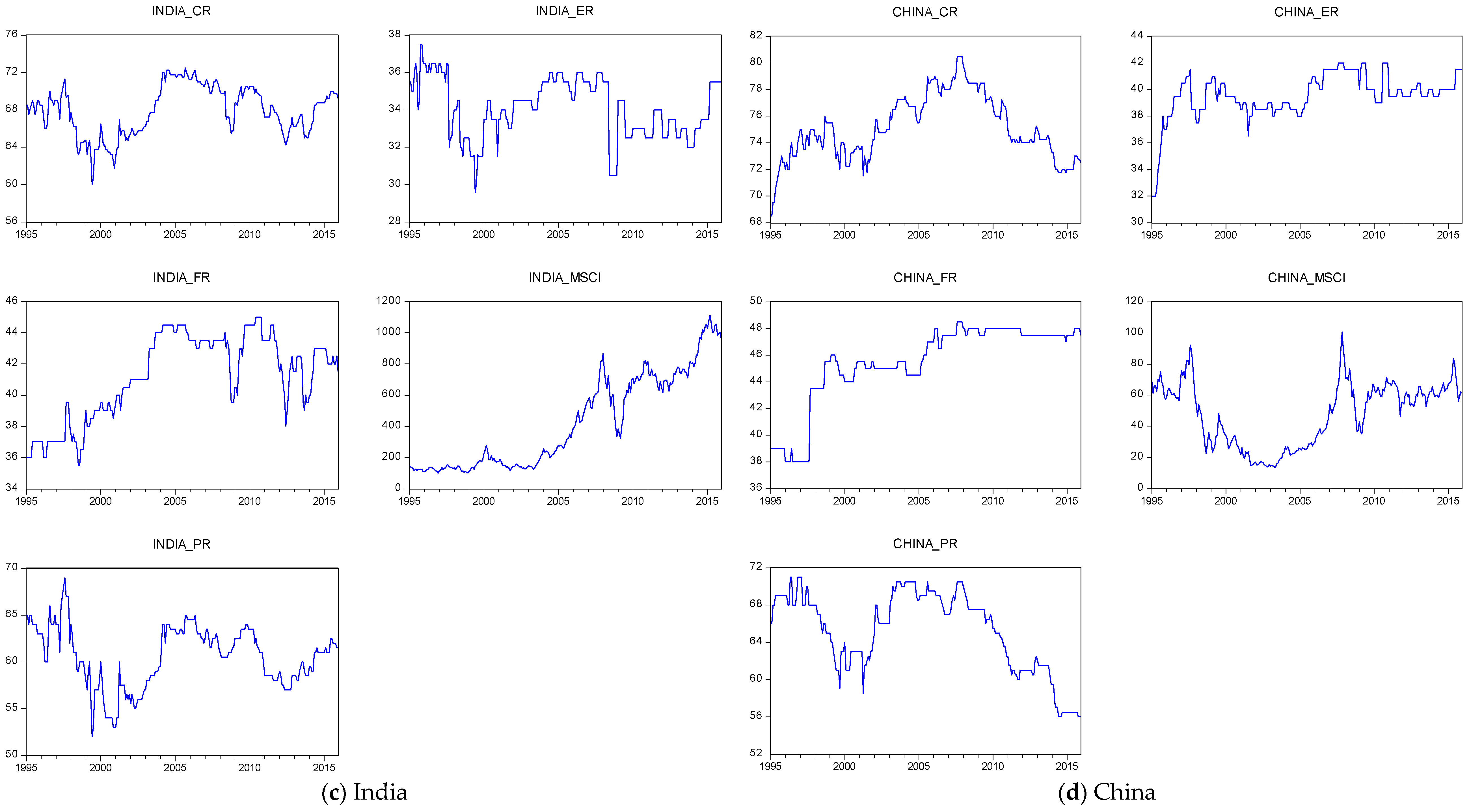
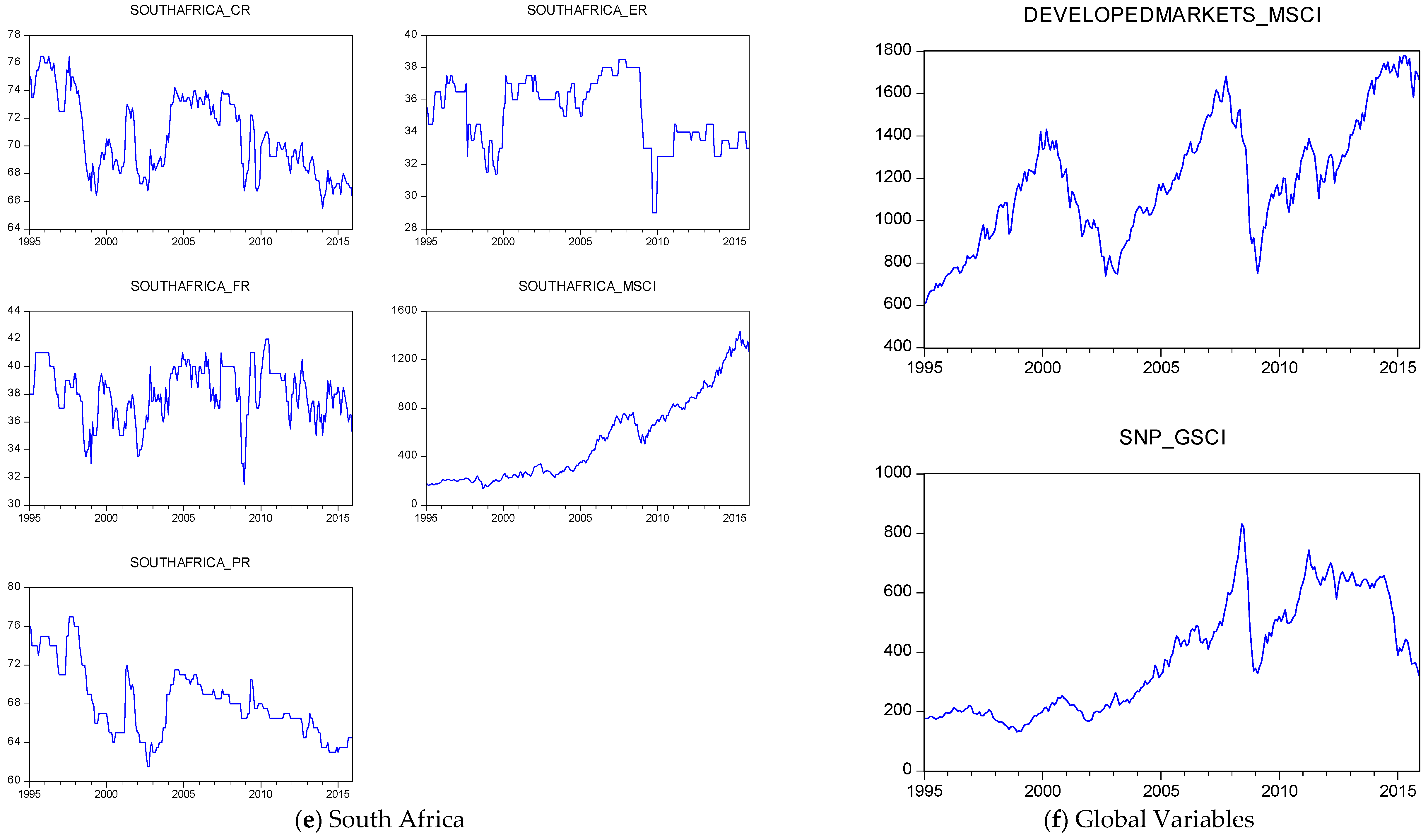
| Variables | Mean | Median | Maximum | Minimum | Standard Deviation | CV | Skewness | Kurtosis | Jarque-Bera | Probability |
|---|---|---|---|---|---|---|---|---|---|---|
| Brazil_CR | 67.855 | 68.250 | 77.250 | 56.540 | 4.061 | 0.060 | −0.375 | 2.624 | 7.382 | 0.025 |
| Brazil_ER | 34.655 | 35.000 | 41.000 | 25.060 | 2.988 | 0.086 | −0.487 | 3.139 | 10.179 | 0.006 |
| Brazil−FR | 35.050 | 35.000 | 45.500 | 23.500 | 4.849 | 0.138 | −0.318 | 2.583 | 6.085 | 0.048 |
| Brazil_PR | 66.000 | 66.000 | 71.000 | 59.500 | 2.546 | 0.039 | −0.246 | 2.475 | 5.438 | 0.066 |
| Brazil_MSCI | 1.25 × 1011 | 1.12 × 1011 | 2.81 × 1011 | 1.66 × 1010 | 8 × 1010 | 0.640 | 0.142 | 1.425 | 26.910 | 0.000 |
| Russia_CR | 68.717 | 70.000 | 82.000 | 45.000 | 7.820 | 0.114 | −0.829 | 3.342 | 30.101 | 0.000 |
| Russia_ER | 36.830 | 38.500 | 45.500 | 16.000 | 6.639 | 0.180 | −1.048 | 3.410 | 47.848 | 0.000 |
| Russia_FR | 39.579 | 42.500 | 47.500 | 22.000 | 6.439 | 0.163 | −0.871 | 2.554 | 33.934 | 0.000 |
| Russia_PR | 60.893 | 62.000 | 69.000 | 42.000 | 5.768 | 0.095 | −0.818 | 3.329 | 29.258 | 0.000 |
| Russia_MSCI | 554.690 | 520.846 | 1539.354 | 31.221 | 362.081 | 0.653 | 0.486 | 2.445 | 13.141 | 0.001 |
| India_CR | 67.909 | 68.500 | 72.500 | 60.030 | 2.622 | 0.039 | −0.301 | 2.329 | 8.514 | 0.014 |
| India_ER | 34.091 | 34.000 | 37.500 | 29.560 | 1.600 | 0.047 | −0.318 | 2.417 | 7.828 | 0.020 |
| India_FR | 41.161 | 41.500 | 45.000 | 35.500 | 2.722 | 0.066 | −0.434 | 1.898 | 20.667 | 0.000 |
| India_PR | 60.536 | 61.000 | 69.000 | 52.000 | 3.252 | 0.054 | −0.274 | 2.580 | 5.007 | 0.082 |
| India_MSCI | 424.631 | 287.242 | 1111.045 | 100.851 | 300.412 | 0.707 | 0.535 | 1.892 | 24.942 | 0.000 |
| China_CR | 75.087 | 74.625 | 80.500 | 68.500 | 2.414 | 0.032 | 0.136 | 2.501 | 3.396 | 0.183 |
| China_ER | 39.541 | 39.500 | 42.000 | 32.000 | 1.713 | 0.043 | −1.714 | 8.717 | 466.571 | 0.000 |
| China_FR | 45.435 | 46.000 | 48.500 | 38.000 | 3.040 | 0.067 | −1.402 | 3.947 | 91.973 | 0.000 |
| China_PR | 65.177 | 66.000 | 71.000 | 56.000 | 4.254 | 0.065 | −0.575 | 2.274 | 19.434 | 0.000 |
| China_MSCI | 47.751 | 54.250 | 100.662 | 13.752 | 20.537 | 0.430 | −0.084 | 1.894 | 13.147 | 0.001 |
| South Africa_CR | 70.699 | 70.000 | 76.500 | 65.500 | 2.834 | 0.040 | 0.262 | 1.866 | 16.401 | 0.000 |
| South Africa_ER | 35.141 | 35.500 | 38.500 | 29.000 | 2.047 | 0.058 | −0.373 | 2.606 | 7.476 | 0.024 |
| South Africa_FR | 38.069 | 38.000 | 42.000 | 31.500 | 1.996 | 0.052 | −0.493 | 2.955 | 10.236 | 0.006 |
| South Africa_PR | 68.139 | 67.500 | 77.000 | 61.500 | 3.640 | 0.053 | 0.558 | 2.585 | 14.861 | 0.001 |
| South Africa_MSCI | 538.146 | 375.284 | 1432.465 | 137.224 | 355.219 | 0.660 | 0.789 | 2.501 | 28.738 | 0.000 |
| Developed Markets_MSCI | 1184.746 | 1178.420 | 1779.307 | 608.263 | 294.215 | 0.248 | 0.173 | 2.225 | 7.559 | 0.023 |
| S&P GSCI Commodity Spot Price Index | 379.791 | 348.328 | 832.304 | 131.751 | 188.518 | 0.060 | 0.422 | 1.801 | 22.587 | 0.000 |
| (a) | ||||||
|---|---|---|---|---|---|---|
| Level | ||||||
| Variable | ADF | PP | NP | |||
| Constant | Constant + Trend | Constant | Constant + Trend | Constant | Constant + Trend | |
| Brazil_CR | −1.635 | −1.545 | −1.911 | −1.934 | −6.016 * | −6.334 |
| Brazil_ER | −2.936 ** | −2.905 | −2.928 ** | −2.956 | −7.940 * | −16.03 * |
| Brazil−FR | −2.188 | −2.875 | −2.241 | −2.982 | −8.000 * | −8.716 |
| Brazil_PR | −2.412 | −2.355 | −2.412 | −2.355 | −12.28 ** | −13.283 |
| Brazil_MSCI | −1.637 | −1.519 | −1.637 | −1.577 | 0.335 | −6.310 |
| Russia_CR | −2.214 | −2.104 | −2.141 | −2.017 | −4.184 | −8.738 |
| Russia_ER | −2.445 | −2.481 | −2.512 | −2.555 | −7.393 * | −9.486 |
| Russia_FR | −2.480 | −2.570 | −2.523 | −2.803 | −0.632 | −7.984 |
| Russia_PR | −2.476 | −2.290 | −2.666 | −2.484 | −1.742 | −4.058 |
| Russia_MSCI | −2.243 | −2.842 | −1.940 | −2.692 | −1.225 | −14.669 * |
| India_CR | −2.417 | −2.545 | −2.364 | −2.495 | −10.926 ** | −11.185 |
| India_ER | −3.783 ** | −3.795 ** | −3.804 ** | −3.822 ** | −17.008 *** | −25.341 *** |
| India_FR | −2.243 | −2.527 | −2.316 | −2.381 | −1.110 | −10.360 |
| India_PR | −2.860 * | −2.832 | −2.682 * | −2.642 | −6.229 * | −10.682 |
| India_MSCI | −0.468 | −2.762 | −0.538 | −2.971 | 0.710 | −6.805 |
| China_CR | −2.794 * | −2.458 | −2.795 * | −2.414 | −0.849 | −2.081 |
| China_ER | −4.749 *** | −4.722 *** | −4.749 *** | −4.715 *** | −0.050 | −3.565 |
| China_FR | −2.071 | −2.070 | −2.064 | −2.054 | −0.019 | −5.740 |
| China_PR | −0.746 | −1.678 | −0.514 | −1.529 | −1.993 | −4.984 |
| China_MSCI | −1.530 | −1.913 | −1.629 | −1.983 | −2.706 | −3.213 |
| South Africa_CR | −2.619 * | −3.141 * | −2.523 | −3.042 | −2.726 | −18.075 ** |
| South Africa_ER | −2.701 * | −2.966 | −2.688 * | −3.007 | −13.943 *** | −16.045 * |
| South Africa_FR | −4.291 *** | −4.280 *** | −4.426 *** | −4.414 *** | −33.194 *** | −32.647 *** |
| South Africa_PR | −2.308 | −2.538 | −2.424 | −2.766 | −0.797 | −8.168 |
| South Africa_MSCI | −0.330 | −3.067 | −0.242 | −3.079 | 1.254 | −10.501 |
| Developed Markets_MSCI | −2.122 | −2.383 | −2.261 | −2.719 | 0.425 | −4.964 |
| S&P GSCI Commodity Spot Price Index | −1.513 | −1.280 | −1.484 | −1.280 | −1.277 | −8.470 |
| (b) | ||||||
|---|---|---|---|---|---|---|
| First Difference | ||||||
| Variable | ADF | PP | NP | |||
| Constant | Constant + Trend | Constant | Constant + Trend | Constant | Constant + Trend | |
| Brazil_CR | −13.954 *** | −13.945 *** | −13.954 *** | −13.945 *** | −123.228 *** | −123.077 *** |
| Brazil_ER | −10.699 *** | −10.739 *** | −16.416 *** | −16.420 *** | −265.278 *** | −267.574 *** |
| Brazil−FR | −15.371 *** | −15.341 *** | −15.371 *** | −15.341 *** | −124.937 *** | −124.842 *** |
| Brazil_PR | −14.366 *** | −14.360 *** | −14.334 *** | −14.315 *** | −123.935 *** | −123.979 *** |
| Brazil_MSCI | −15.810 *** | −15.874 *** | −15.810 *** | −15.875 *** | −40.119 *** | −124.007 *** |
| Russia_CR | −16.831 *** | −16.835 *** | −16.874 *** | −16.852 *** | −124.450 *** | −124.437 *** |
| Russia_ER | −16.339 *** | −16.306 *** | −16.351 *** | −16.318 *** | −124.834 *** | −124.831 *** |
| Russia_FR | −12.357 *** | −12.390 *** | −13.274 *** | −13.267 *** | −183.011 *** | −183.631 *** |
| Russia_PR | −15.790 *** | −15.868 *** | −15.866 *** | −15.911 *** | −124.999 *** | −124.997 *** |
| Russia_MSCI | −13.629 *** | −13.630 *** | −13.590 *** | −13.588 *** | −7.48776 * | −19.8712 ** |
| India_CR | −15.429 *** | −15.402 *** | −15.527 *** | −15.498 *** | −124.950 *** | −124.927 *** |
| India_ER | −16.408 *** | −16.387 *** | −16.924 *** | −17.230 *** | −124.790 *** | −124.786 *** |
| India_FR | −13.688 *** | −13.706 *** | −13.564 *** | −13.571 *** | −122.614 *** | −121.793 *** |
| India_PR | −13.109 *** | −13.102 *** | −16.686 *** | −16.715 *** | −170.486 *** | −170.648 *** |
| India_MSCI | −14.741 *** | −14.719 *** | −14.747 *** | −14.725 *** | −29.557 *** | −122.479 *** |
| China_CR | −16.489 *** | −16.718 *** | −16.482 *** | −16.758 *** | −124.748 *** | −124.688 *** |
| China_ER | −16.083 *** | −16.155 *** | −16.083 *** | −16.155 *** | −124.963 *** | −124.952 *** |
| China_FR | −16.172 *** | −16.215 *** | −16.174 *** | −16.225 *** | −124.944 *** | −124.966 *** |
| China_PR | −17.253 *** | −17.316 *** | −17.379 *** | −17.545 *** | −124.009 *** | −123.866 *** |
| China_MSCI | −14.061 *** | −14.066 *** | −14.015 *** | −14.008 *** | −5.917 * | −116.973 *** |
| South Africa_CR | −13.822 *** | −13.793 *** | −13.723 *** | −13.689 *** | −122.948 *** | −122.651 *** |
| South Africa_ER | −16.529 *** | −16.501 *** | −16.770 *** | −16.741 *** | −124.709 *** | −124.705 *** |
| South Africa_FR | −16.228 *** | −16.201 *** | −16.837 *** | −16.801 *** | −124.859 *** | −124.986 *** |
| South Africa_PR | −14.068 *** | −14.054 *** | −14.070 *** | −14.056 *** | −123.372 *** | −123.397 *** |
| South Africa_MSCI | −15.824 *** | −15.792 *** | −15.896 *** | −15.899 *** | −1.851 | −36.2192 *** |
| Developed Markets_MSCI | −13.925 *** | −13.917 *** | −14.032 *** | −14.022 *** | −122.520 *** | −123.040 *** |
| S&P GSCI Commodity Spot Price Index | −11.018 *** | −11.066 *** | −11.069 *** | −11.079 *** | −110.133 *** | −109.161 *** |
References
- Ang, Andrew, and Geert Bekaert. 2004. How do regimes affect asset allocation? Financial Analyst Journal 60: 86–98. [Google Scholar] [CrossRef]
- Bekaert, Geert, and Campbell Harvey. 1997. Emerging equity market volatility. Journal of Financial Economics 43: 29–77. [Google Scholar] [CrossRef]
- Balcilar, Mehmet, Matteo Bonato, Riza Demirer, and Rangan Gupta. 2017. Geopolitical Risks and Stock Market Dynamics of the BRICS. Economic Systems 42: 295–306. [Google Scholar] [CrossRef]
- Banerjee, Anindya, Juan Dolado, and Ricardo Mestre. 1998. Error-correction mechanism tests for cointegration in a single-equation framework. Journal of Time Series Analysis 19: 267–83. [Google Scholar] [CrossRef] [Green Version]
- Bilson, Christopher M., Timothy J. Brailsford, and Vincent C. Hooper. 2002. The explanatory power of political risk in emerging markets. International Review of Financial Analysis 11: 1–27. [Google Scholar] [CrossRef]
- Caldara, Dario, and Matteo Iacoviello. 2016. Measuring Geopolitical Risk; Working Paper. Washington: Board of Governors of the Federal Reserve Board.
- De Santis, Giorgio, and Bruno Gérard. 1997. International asset pricing and portfolio diversification with time varying risk. Journal of Finance 52: 1881–912. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive times series with a unit root. Journal of the American Statistical Society 75: 427–31. [Google Scholar]
- Engle, Robert, and Clive Granger. 1987. Co-integration and error correction: Representation, estimation and testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- Erb, Claude B., Campbell R. Harvey, and Tadas E. Viskanta. 1994. National risk in global fixed-income allocation. Journal of Fixed Income 4: 17–26. [Google Scholar] [CrossRef]
- Erb, Claude B., Campbell R. Harvey, and Tadas E. Viskanta. 1995. Country risk and global equity selection. The Journal of Portfolio Management 21: 74–83. [Google Scholar] [CrossRef]
- Erb, Claude B., Campbell R. Harvey, and Tadas E. Viskanta. 1996. Political risk, economic risk, and financial risk. Financial Analysts Journal 52: 29–46. [Google Scholar] [CrossRef]
- Errunza, Vihang, and Etienne Losq. 1985. International asset pricing under mild segmentation: Theory and test. Journal of Finance 40: 105–24. [Google Scholar] [CrossRef]
- Forbes, Kristin, and Roberto Rigobon. 2002. No contagion, only interdependence: Measuring stock market comovements. The Journal of Finance 57: 2223–61. [Google Scholar] [CrossRef]
- Girard, Eric, and Mohamed Omran. 2007. What are the risks when investing in thin emerging equity markets: Evidence from the Arab world. Journal of International Financial Markets, Institutions and Money 17: 102–23. [Google Scholar] [CrossRef]
- Godfrey, Leslie. 1978. Testing for multiplicative heteroskedasticity. Journal of Econometrics 8: 227–36. [Google Scholar] [CrossRef]
- Granger, Clive W., and Gawon Yoon. 2002. Hidden Cointegration. 2002-02. San Diego: University of California. [Google Scholar]
- Greenwood-Nimmo, Matthew, Tae-Hwan Kim, Yongcheol Shin, and Till Van Treeck. 2013. Fundamental Asymmetries in US Monetary Policymaking: Evidence from a Nonlinear Autoregressive Distributed Lag Quantile Regression Model. Mimeo: University of Melbourne. [Google Scholar]
- Grubel, Herbert. 1968. Internationally diversified portfolios: Welfare gains and capital flows. American Economic Review 58: 1299–314. [Google Scholar]
- Hamilton, James D. 1983. Oil and the macroeconomy since WWII. Journal of Political Economy 91: 228–48. [Google Scholar] [CrossRef]
- Hammoudeh, Shawkat, Ramazan Sari, Mehmet Uzunkaya, and Tengdong Liu. 2013. The dynamics of BRICS’s country risk ratings and domestic stock markets, U.S. stock market and oil price. Mathematics and Computers in Simulation 94: 277–94. [Google Scholar] [CrossRef]
- Harms, Philipp. 2002. Political risk and equity investment in developing countries. Applied Economics Letters 9: 377–80. [Google Scholar] [CrossRef]
- Harvey, Campbell R. 1995a. Predictable risk and returns in emerging markets. Review of Financial Studies 8: 773–816. [Google Scholar] [CrossRef]
- Harvey, Campbell R. 1995b. The risk exposure of emerging equity markets. The World Bank Economic Review 9: 19–50. [Google Scholar] [CrossRef]
- Harvey, Campbell R. 2012. Allocation to Emerging Markets in a Globally Diversified Portfolio. Durham: Duke University. [Google Scholar]
- Hatemi-J, Abdulnasser. 2012. Asymmetric causality tests with an application. Empirical Economics 43: 447–56. [Google Scholar] [CrossRef]
- Jarque, Carlos M., and Anil K. Bera. 1980. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Economics Letters 6: 255–59. [Google Scholar] [CrossRef]
- Johansen, Søren, and Katarina Juselius. 1990. Maximum likelihood estimation and inference on cointegration—With applications to the demand for money. Oxford Bulletin of Economics and Statistics 52: 169–210. [Google Scholar] [CrossRef]
- Kaminsky, Graciela, and Sergio L. Schmukler. 2001. Emerging Markets Instability: Do Sovereign Ratings Affect Country Risk and Stock Returns? Policy Research Working Paper Series 2678; Washington: The World Bank. [Google Scholar]
- Kang, Wensheng, and Ronald A. Ratti. 2013. Oil shocks, policy uncertainty and stock market returns. Journal of International Financial Markets, Institutions and Money 26: 305–18. [Google Scholar] [CrossRef]
- Lehkonen, Heikki, and Kari Heimonen. 2015. Democracy, political risk and stock market performance. Journal of International Money and Finance 59: 77–99. [Google Scholar] [CrossRef]
- Lintner, John. 1965. The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. The Review of Economics and Statistics 47: 13–37. [Google Scholar] [CrossRef]
- Liu, Tengdong, Shawkat Hammoudeh, and Mark A. Thompson. 2013. A momentum threshold model of stock prices and country risk ratings: Evidence from BRICS countries. Journal of International Financial Markets, Institutions and Money 27: 99–112. [Google Scholar] [CrossRef]
- Longin, Franҫois, and Bruno Solnik. 1995. Is the correlation in international equity returns constant: 1960–90? Journal of International Money and Finance 14: 3–26. [Google Scholar] [CrossRef]
- Longin, Franҫois, and Bruno Solnik. 2001. Extreme correlation of international equity markets. The Journal of Finance 61: 649–76. [Google Scholar] [CrossRef]
- Mensi, Walid, Shawkat Hammoudeh, Seong-Min Yoon, and M. Mehmet Balcilar. 2017. Impact of macroeconomic factors and country risk ratings on GCC stock markets: Evidence from a dynamic panel threshold model with regime switching. Applied Economics 49: 1255–72. [Google Scholar] [CrossRef]
- Mensi, Walid, Shawkat Hammoudeh, Juan Carlos Reboredo, and Duc Khuong Nguyen. 2014. Do global factors impact BRICS stock markets? A quantile regression approach. Emerging Markets Review 19: 1–17. [Google Scholar] [CrossRef]
- Mensi, Walid, Shawkat Hammoudeh, Seong-Min Yoon, and Duc Khuong Nguyen. 2016. Asymmetric linkages between BRICS stock returns and country risk ratings: Evidence from dynamic panel threshold models. Review of International Economics 24: 1–19. [Google Scholar] [CrossRef]
- Ng, Serena, and Pierre Perron. 2001. Lag length selection and the construction of unit root tests with good size and power. Econometrica 69: 1519–54. [Google Scholar] [CrossRef]
- Pesaran, Hashem M., Yongcheol Shin, and Richard J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef] [Green Version]
- Phillips, Peter C., and Pierro Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Ramcharran, Harri. 2003. Estimating the impact of risks on emerging equity market performance: Further evidence on data from rating agencies. Multinational Business Review 11: 77–90. [Google Scholar] [CrossRef]
- Ramsey, J.B. 1969. Tests for specification errors in classical linear least squares regression analysis. Journal of the Royal Statistical Society: Series B 31: 350–71. [Google Scholar]
- Romilly, Peter, Song Haiyan, and Xiaming Liu. 2001. Car ownership and use in Britain: A comparison of the empirical results of alternative cointegration estimation methods and forecasts. Applied Economics 33: 1803–18. [Google Scholar] [CrossRef]
- Sari, Ramazan, Mehmet Uzunkaya, and Shawtak Hammoudeh. 2013. The Relationship between Disaggregated Country Risk Ratings and Stock Market Movements: An ARDL Approach. Emerging Markets Finance and Trade 49: 4–16. [Google Scholar] [CrossRef]
- Scholes, Myron S. 2000. Crisis and Risk Management. American Economic Review 90: 17–21. [Google Scholar] [CrossRef] [Green Version]
- Schorderet, Yann. 2001. Revisiting Okun’s Law: An Hysteretic Perspective. San Diego: University of California, Mimeo. [Google Scholar]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. The Journal of Finance 19: 425–42. [Google Scholar]
- Shin, Yongcheol, Byungchul Yu, and Matthew Greenwood-Nimmo. 2014. Modelling asymmetric cointegration and dynamic multipliers in an ARDL framework. In Festschrift in Honor of Peter Schmidt. Edited by William C. Horrace and Robin C. Sickles. New York: Springer Science & Business Media. [Google Scholar]
- Sousa, Ricardo M., Andrew Vivian, and Mark E. Wohar. 2016. Predicting asset returns in the BRICs: The role of macroeconomic and fundamental predictors. International Review of Economics and Finance 41: 122–43. [Google Scholar] [CrossRef] [Green Version]
- World Bank. 2015. World Development INDICATORS. Washington: The World Bank. [Google Scholar]
| 1 | In 2010, South Africa joined this group of countries and formed the BRICS. |
| 2 | Mensi et al. (2017) also used this approach to carry out a similar analysis for Gulf Cooperation Council (GCC) countries. |
| 3 | Sari et al. (2013) have also used the autoregressive distributed lag (ARDL) model to study the impact of country risk ratings on the Turkish stock market. |
| 4 | The parameter ρ is assumed to be negative in order to have a cointegration relationship among the variables. |
| 5 | According to Granger and Yoon (2002), two times series are hidden cointegrated if their positive and negative components are cointegrated with each other. |
| 6 | For the bounds testing procedure, two sets of critical values are provided. The upper critical bound assumes that there is a cointegration relationship among the variables, while the lower critical bound assumes that no cointegration relationship exists between the variables. If the F-statistic is greater than the upper level critical value, then the null hypothesis of no-cointegration is rejected (i.e., all variables are cointegrated). Conversely, if the computed F-statistic falls below the lower bound critical value, then the null hypothesis cannot be rejected (i.e., no cointegration). Finally, if the F-statistic falls between the bounds, the test is inconclusive. |
| 7 | Results of the BDM test for all equations are available upon request. |
| 8 | Based on the suggestions of an anonymous referee, in order to account for bearish and bullish stock markets, we also estimated a quantiles-based version of the NARDL model, i.e., a QNARDL model as developed by Greenwood-Nimmo et al. (2013). Our results, which are available upon request, however. suggested that estimates of the parameters of model are not statistically different across the various quantiles. This result is an indication of the fact that our NARDL model is not misspecified across bear and bull markets and the QNARDL model does not necessarily bring in new information in our context. Having said this, we must also be cautious of the fact that this result could purely be driven by our relatively small sample size, which is not large enough to handle the overparameterized QNARDL model. |
| Brazil | China | India | Russia | South Africa | |
|---|---|---|---|---|---|
| Model 1 | 4.097 ** | 5.247 *** | 3.292 | 5.192 *** | 2.772 |
| Model 2 | 3.384 * | 6.581 *** | 1.734 | 5.495 *** | 2.747 |
| Model 3 | 4.935 *** | 2.973 | 5.664 *** | 9.238 *** | 2.902 |
| Model 4 | 8.381 *** | 3.288 | 5.146 *** | 3.523 * | 6.833 *** |
| Model 5 | 4.113 ** | 3.283 | 4.816 *** | 8.649 *** | 5.230 *** |
| Model 6 | 3.310 | 4.326 ** | 2.098 | 2.040 | 4.573 ** |
| Brazil | China | India | ||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Coeff. | S.E. | Variable | Coeff. | S.E. | Variable | Coeff. | S.E. |
| 0.464 | 0.511 | −0.095 | 0.252 | −0.370 | 0.239 | |||
| −0.020 | 0.024 | −0.089 *** | 0.020 | −0.055 ** | 0.027 | |||
| 0.044 * | 0.026 | 0.128 *** | 0.032 | 0.038 * | 0.023 | |||
| −0.033 | 0.026 | −0.055 | 0.042 | 0.067 * | 0.039 | |||
| −0.192 | 0.175 | −0.222 | 0.135 | 0.091 | 0.111 | |||
| −0.134 ** | 0.054 | −0.339 * | 0.173 | 0.339 * | 0.179 | |||
| −0.027 | 0.077 | 0.563 * | 0.287 | −0.235 | 0.202 | |||
| −0.359 * | 0.202 | −0.590 ** | 0.269 | 0.090 | 0.131 | |||
| −0.075 | 0.102 | −0.651 | 0.649 | 0.225 | 0.137 | |||
| −0.062 | 0.088 | 1.230 *** | 0.251 | −0.123 | 0.114 | |||
| −0.120 ** | 0.048 | 0.318 *** | 0.089 | −0.125 ** | 0.050 | |||
| −0.111 ** | 0.049 | −0.378 *** | 0.091 | −0.124 ** | 0.048 | |||
| 0.179 ** | 0.071 | −0.243 ** | 0.093 | 0.227 *** | 0.075 | |||
| 1.144 *** | 0.092 | −0.250 *** | 0.090 | −0.218 *** | 0.075 | |||
| −0.838 ** | 0.353 | 1.142 *** | 0.114 | 0.726 *** | 0.091 | |||
| 0.844 ** | 0.349 | 0.324 *** | 0.114 | 0.190 ** | 0.088 | |||
| 1.000 *** | 0.375 | 0.338 *** | 0.114 | −0.235 *** | 0.088 | |||
| −0.712 ** | 0.349 | 1.410 ** | 0.552 | 0.202 ** | 0.089 | |||
| 0.373 ** | 0.159 | 1.415 *** | 0.480 | −0.687 ** | 0.295 | |||
| −0.391 *** | 0.149 | 1.098 ** | 0.483 | 0.732 ** | 0.293 | |||
| 0.407 ** | 0.177 | 2.632 ** | 1.185 | −0.792 *** | 0.296 | |||
| 0.574 *** | 0.204 | 0.936 ** | 0.442 | |||||
| 0.969 ** | 0.484 | 0.821 ** | 0.401 | |||||
| 0.430 *** | 0.162 | −1.049 *** | 0.386 | |||||
| 0.860 *** | 0.185 | 1.106 *** | 0.337 | |||||
| 0.447 ** | 0.188 | 1.180 *** | 0.453 | |||||
| 0.496 ** | 0.196 | 0.519 ** | 0.241 | |||||
| 1.090 *** | 0.246 | |||||||
| −0.633 *** | 0.234 | |||||||
| Long−run effects | −0.716 *** | 0.243 | ||||||
| 2.214 | 2.436 | 1.434 *** | 0.391 | 0.688 ** | 0.297 | |||
| −1.660 | 2.726 | −0.611 | 0.537 | 1.234 ** | 0.501 | |||
| −9.626 | 16.577 | −2.484 * | 1.357 | 1.656 | 1.995 | |||
| −6.705 | 9.345 | −3.803 ** | 1.705 | 6.201 | 4.793 | |||
| −1.364 | 4.728 | 6.313 ** | 2.983 | −4.301 | 5.027 | |||
| −18.026 | 25.062 | −6.618 * | 3.775 | 1.655 | 1.971 | |||
| −3.755 | 7.658 | −7.303 | 6.644 | 4.116 | 3.246 | |||
| −3.120 | 6.054 | 13.790 *** | 4.067 | −2.244 | 2.079 | |||
| Statistics and Diagnostics | ||||||||
| −0.818 | −4.537 ** | −2.040 | ||||||
| 0.247 | [0.620] | 1.275 | [0.260] | 0.000 | [0.999] | |||
| 0.304 | [0.582] | 0.292 | [0.589] | 0.779 | [0.379] | |||
| 0.350 | [0.555] | 2.963 | [0.087] | 0.194 | [0.660] | |||
| 0.548 | [0.460] | 6.518 | [0.011] | 9.183 | [0.003] | |||
| 16.788 | [0.000] | 0.919 | [0.339] | 0.350 | [0.555] | |||
| 0.011 | [0.916] | 5.161 | [0.024] | 0.237 | [0.627] | |||
| 0.524 | 0.466 | 0.518 | ||||||
| 13.373 | [0.342] | 15.598 | [0.210] | 8.053 | [0.781] | |||
| 5.155 | [0.023] | 0.020 | [0.886] | 0.267 | [0.605] | |||
| 4.644 | [0.098] | 31.498 | [0.000] | 0.239 | [0.887] | |||
| 43.365 | [0.000] | 0.122 | [0.727] | 0.010 | [0.921] | |||
| Russia | South Africa | ||||
|---|---|---|---|---|---|
| Variable | Coeff. | S.E. | Variable | Coeff. | S.E. |
| −0.208 | 0.346 | 0.260 * | 0.143 | ||
| −0.103 *** | 0.029 | −0.119 *** | 0.027 | ||
| 0.132 *** | 0.038 | 0.028 * | 0.015 | ||
| 0.017 | 0.055 | 0.032 * | 0.019 | ||
| 0.089 | 0.151 | 0.072 | 0.095 | ||
| 0.134 | 0.183 | 0.017 | 0.072 | ||
| −0.226 ** | 0.091 | 0.164 * | 0.088 | ||
| 0.196 | 0.228 | 0.206 * | 0.117 | ||
| −0.340 ** | 0.138 | −0.122 * | 0.072 | ||
| 0.062 | 0.059 | 0.171 ** | 0.072 | ||
| 0.105 ** | 0.049 | 0.146 *** | 0.052 | ||
| 0.110 ** | 0.044 | 0.611 *** | 0.071 | ||
| 0.242 ** | 0.119 | −0.708 ** | 0.294 | ||
| 1.355 *** | 0.155 | −0.660 ** | 0.292 | ||
| −0.950 ** | 0.422 | 0.970 *** | 0.296 | ||
| −0.869 *** | 0.328 | −1.029 ** | 0.416 | ||
| −0.860 *** | 0.326 | −1.083 ** | 0.419 | ||
| 0.382 ** | 0.177 | −0.386 ** | 0.162 | ||
| 2.624 *** | 0.433 | 0.353 ** | 0.155 | ||
| 1.271 *** | 0.258 | 0.655 *** | 0.189 | ||
| 0.989 *** | 0.246 | ||||
| −1.049 *** | 0.302 | ||||
| −0.521 ** | 0.234 | ||||
| −0.735 *** | 0.274 | ||||
| −0.519 *** | 0.137 | ||||
| 0.424 *** | 0.127 | ||||
| 0.557 *** | 0.163 | ||||
| 0.288 ** | 0.134 | ||||
| Long−run effects | |||||
| 1.289 *** | 0.351 | 0.236 ** | 0.115 | ||
| 0.168 | 0.509 | 0.269 * | 0.143 | ||
| 0.869 | 1.356 | 0.606 | 0.809 | ||
| 1.305 | 1.701 | 0.141 | 0.599 | ||
| −2.194 ** | 0.983 | 1.374 * | 0.768 | ||
| 1.908 | 2.003 | 1.730 * | 0.992 | ||
| −3.304 * | 1.727 | −1.024 * | 0.584 | ||
| 0.600 | 0.610 | 1.434 *** | 0.533 | ||
| Statistics and Diagnostics | |||||
| 5.495 *** | 2.747 | ||||
| −3.598 | −4.488 ** | ||||
| 0.242 | [0.623] | 1.997 | [0.159] | ||
| 4.252 | [0.040] | 34.555 | [0.000] | ||
| 5.881 | [0.016] | 0.007 | [0.932] | ||
| 31.652 | [0.000] | 4.941 | [0.027] | ||
| 4.434 | [0.036] | 0.020 | [0.887] | ||
| 1.053 | [0.306] | 12.053 | [0.001] | ||
| 0.617 | 0.487 | ||||
| 12.230 | [0.427] | 9.651 | [0.647] | ||
| 2.735 | [0.098] | 3.550 | [0.060] | ||
| 5.720 | [0.057] | 3.491 | [0.175] | ||
| 0.334 | [0.564] | 30.155 | [0.000] | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Nasr, A.; Cunado, J.; Demirer, R.; Gupta, R. Country Risk Ratings and Stock Market Returns in Brazil, Russia, India, and China (BRICS) Countries: A Nonlinear Dynamic Approach. Risks 2018, 6, 94. https://doi.org/10.3390/risks6030094
Ben Nasr A, Cunado J, Demirer R, Gupta R. Country Risk Ratings and Stock Market Returns in Brazil, Russia, India, and China (BRICS) Countries: A Nonlinear Dynamic Approach. Risks. 2018; 6(3):94. https://doi.org/10.3390/risks6030094
Chicago/Turabian StyleBen Nasr, Adnen, Juncal Cunado, Rıza Demirer, and Rangan Gupta. 2018. "Country Risk Ratings and Stock Market Returns in Brazil, Russia, India, and China (BRICS) Countries: A Nonlinear Dynamic Approach" Risks 6, no. 3: 94. https://doi.org/10.3390/risks6030094
APA StyleBen Nasr, A., Cunado, J., Demirer, R., & Gupta, R. (2018). Country Risk Ratings and Stock Market Returns in Brazil, Russia, India, and China (BRICS) Countries: A Nonlinear Dynamic Approach. Risks, 6(3), 94. https://doi.org/10.3390/risks6030094







