On Exactitude in Financial Regulation: Value-at-Risk, Expected Shortfall, and Expectiles
Abstract
1. Introduction
2. Value-at-Risk and Coherence
2.1. Value-at-Risk
2.2. Subadditivity, Coherence, and Comonotonicity
- Translation (drift) invariance: Adding a constant return c to total return will reduce risk by that amount: .
- (Linear) homogeneity: Multiplying any position by positive factor λ results in a corresponding, linear increase in risk: .
- Monotonicity: If position Y1 is first-order stochastically dominant to position Y2, in that Y1 offers higher returns than Y2 in every conceivable economic state (Levy 1992, 2015), then the risk associated with Y1 cannot exceed the risk associated with Y2: . Y1 dominates Y2 in the sense that —i.e., the cumulative distribution function of losses for Y1 is less than or equal to the cdf for Y2 for all x. Therefore, .
- Subadditivity: The risk associated with two combined positions cannot exceed the total risk associated with either position, considered alone: .
3. Expected Shortfall and Elicitability
3.1. Expected Shortfall as a Response to VaR
3.2. Elicitability
- “Let the interval I be the potential range of the outcomes, … and let the probability distribution F be concentrated on I.”
- “Then a scoring function is any mapping S: I × I → [0, ∞).”
- “A functional is a potentially set valued mapping .”
- “A scoring function S is consistent for the functional T if for all F, all t ∈ T(F) and all x ∈ I.”
- The scoring function S “is strictly consistent if it is consistent and equality of the expectations implies that x ∈ T(F).”
- Therefore, “a functional is elicitable if there exists a scoring function that is strictly consistent for it.”
3.3. The Nonelicitability of Expected Shortfall
4. Backtesting
4.1. Traditional Backtesting
4.2. Comparative Backtesting
- : The internal model predicts at least as well as the standard model.
- : The internal model predicts at most as well as the standard model.
5. Robustness: Realism and Tradeoffs in the Choice of a Risk Measure
6. Expectiles
6.1. The Appealing Properties of Expectiles
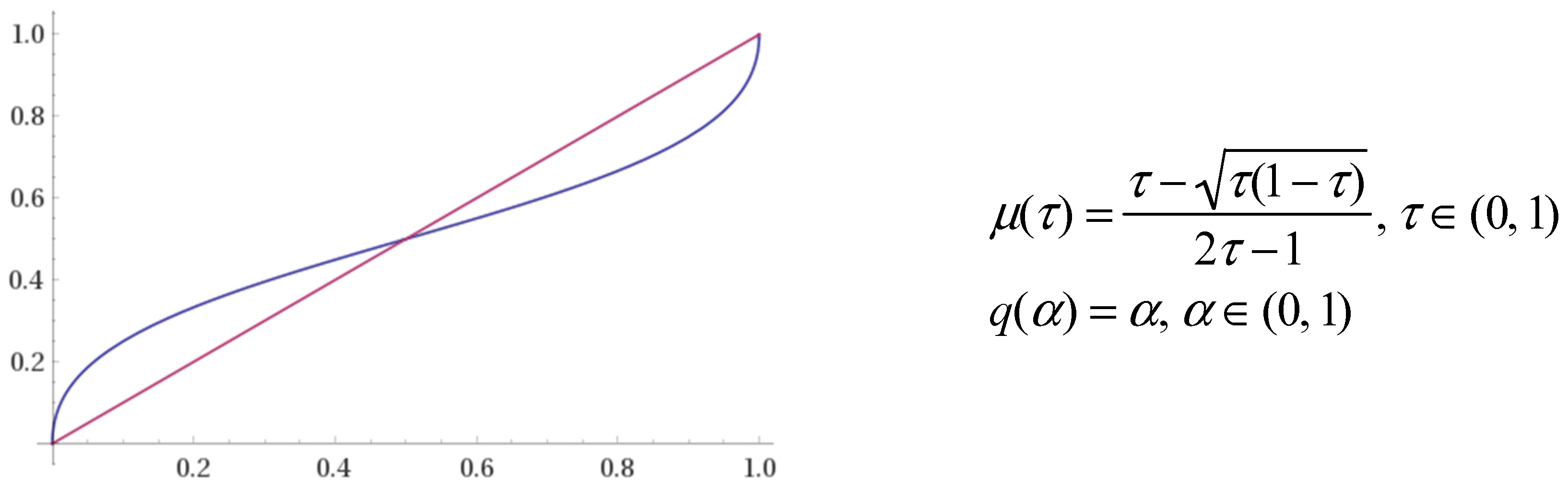
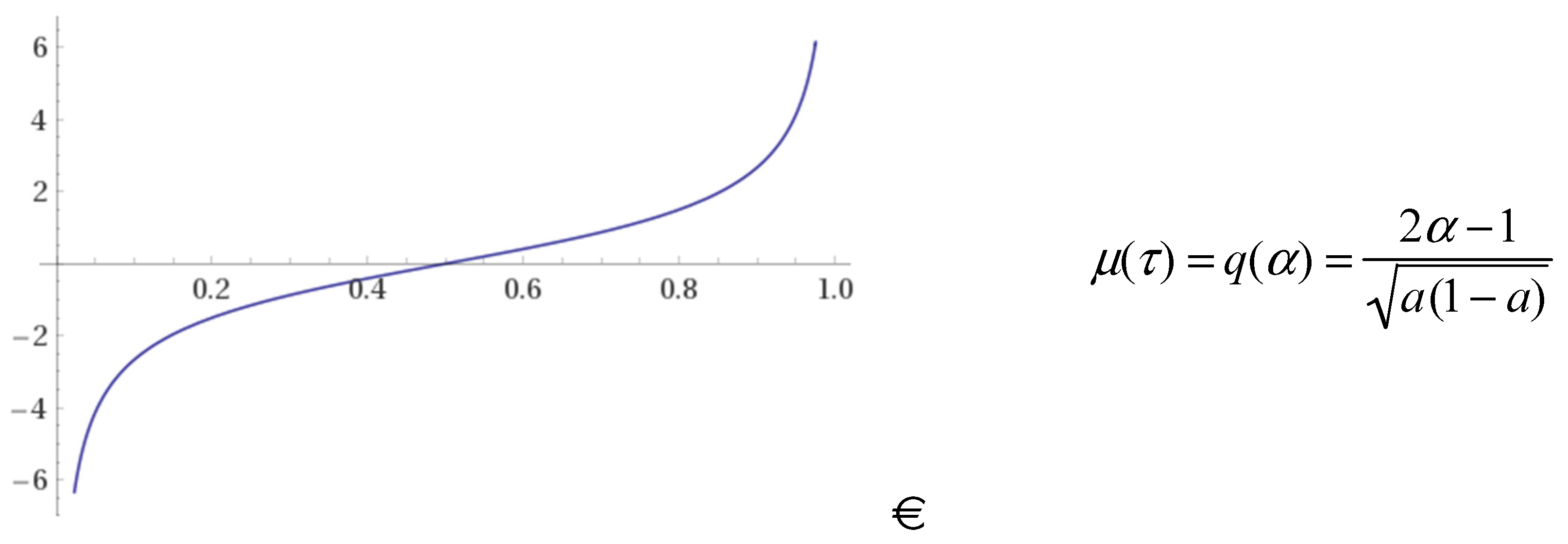
6.2. Expectiles as Quantiles
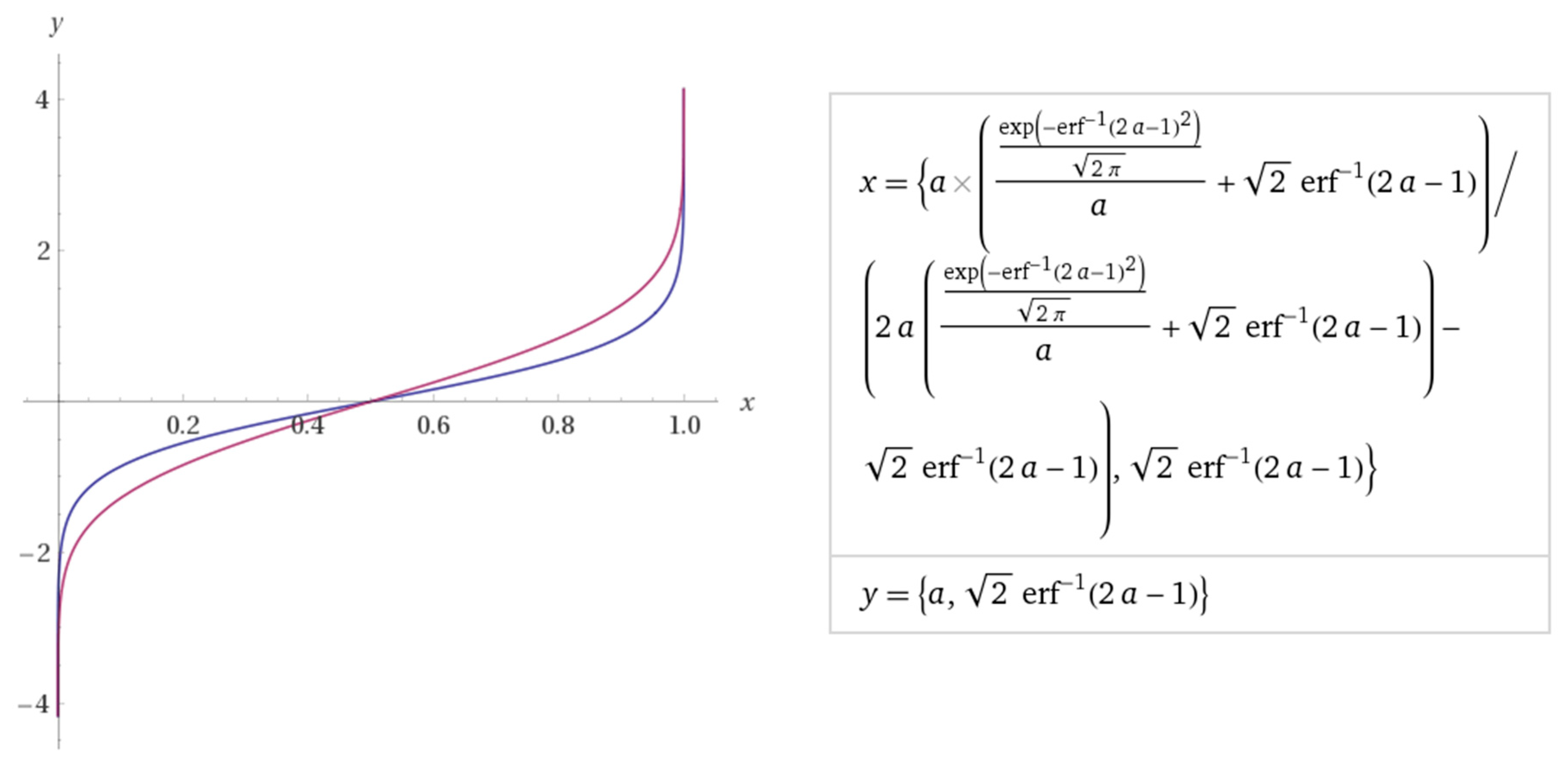
6.3. Visual Comparisons of Expectiles and Quantiles
7. Expressing the Expectile Function μ(τ) in Terms of α, VaR, and Expected Shortfall
7.1. Expectiles as a Function of VaR and Expected Shortfall
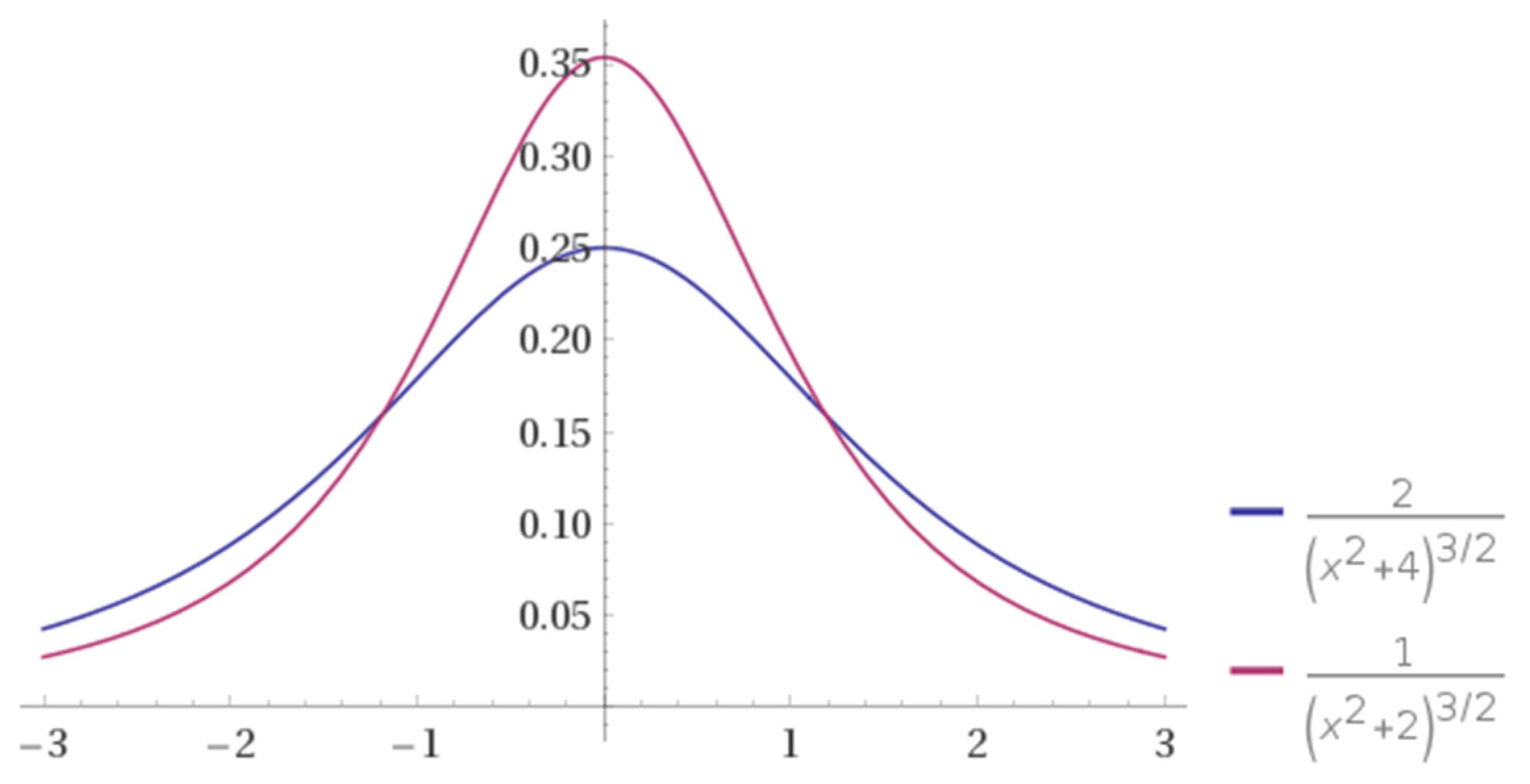
7.2. VaR, Expected Shortfall, and Expectile Values for Normally Distributed Risk
8. Expectiles as Gain/Loss Ratios
9. Conclusions
Acknowledgments
Conflicts of Interest
References
- Abdous, Belkacem, and Bruno Rémillard. 1995. Relaing quantiles and expectiles under weighted-symmetry. Annals of the Institute of Statistical Mathematics 47: 371–84. [Google Scholar] [CrossRef]
- Acerbi, Carlo. 2002. Spectral measures of risk: A coherent representation of subjective risk aversion. Journal of Banking and Finance 26: 1505–18. [Google Scholar] [CrossRef]
- Acerbi, Carlo, and Balász Székely. 2014. Back-testing expected shortfall. Risk 27: 76–81. [Google Scholar]
- Acerbi, Carlo, and Dirk Tasche. 2002. On the coherence of expected shortfall. Journal of Banking and Finance 26: 1487–503. [Google Scholar] [CrossRef]
- Adam, Alexandre, Mohamed Houkari, and Jean-Paul Laurent. 2008. Spectral risk measures and portfolio selection. Journal of Banking and Finance 32: 1870–82. [Google Scholar] [CrossRef]
- Arnold, Barry C. 2015. Pareto Distributions, 2nd ed. Boca Raton: Chapman and Hall/CRC. [Google Scholar]
- Artzner, Phillipe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Aumann, Robert J., and Roberto Serrano. 2008. An economic index of riskiness. Journal of Political Economy 116: 810–36. [Google Scholar] [CrossRef]
- Balakrishnan, N., and V. B. Nevzorov. 2003. A Primer on Statistical Distributions. Hoboken: John Wiley and Sons. [Google Scholar]
- Bao, Yong, Tae-Hwy Lee, and Burak Saltoğlu. 2006. Evaluating predictive performance of value-at-risk models in emerging markets: A reality check. Journal of Forecasting 25: 101–28. [Google Scholar] [CrossRef]
- Barrieu, Pauline, and Giacomo Scandolo. 2015. Assessing financial model risk. European Journal of Operational Research 242: 546–56. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. 1996. Supervisory Framework for the Use of "Backtesting" in Conjunction with the Internal Models Approach to Market Risk Capital Requirements. Available online: https://www.bis.org/publ/bcbs22.pdf (accessed on 8 April 2018).
- Basel Committee on Banking Supervision. 1999. Credit Risk Modeling: Current Practices and Applications. Available online: http://www.bis.org/publ/bcbs49.pdf (accessed on 8 April 2018).
- Basel Committee on Banking Supervision. 2004. Basel II: International Convergence of Capital Measurement and Capital Standards: A Revised Framework. Available online: http://www.bis.org/publ/bcbs107.pdf and http://www.bis.org/publ/bcbs107b.pdf (accessed on 8 April 2018).
- Basel Committee on Banking Supervision. 2011a. Interpretive Issues with Respect to the Revisions to the Market Risk Framework. Available online: http://www.bis.org/publ/bcbs193a.pdf (accessed on 8 April 2018).
- Basel Committee on Banking Supervision. 2011b. Messages from the Academic Literature on Risk Measurement for the Trading Book. Available online: http://www.bis.org/publ/bcbs_wp19.pdf (accessed on 8 April 2018).
- Basel Committee on Banking Supervision. 2012. Consultative Document: Fundamental Review of the Trading Book. Available online: http://www.bis.org/publ/bcbs219.pdf (accessed on 8 April 2018).
- Basel Committee on Banking Supervision. 2013. Consultative Document: Fundamental Review of the Trading Book: A Revised Market Risk Framework. Available online: http://www.bis.org/publ/bcbs265.pdf (accessed on 8 April 2018).
- Basel Committee on Banking Supervision. 2014. Consultative Document: Fundamental Review of the Trading Book: Outstanding Issues. Available online: http://www.bis.org/bcbs/publ/d305.pdf (accessed on 8 April 2018).
- Bellini, Fabio, and Valeria Bignozzi. 2015. On elicitable risk measures. Quantitative Finance 15: 725–33. [Google Scholar] [CrossRef]
- Bellini, Fabio, and Elena Di Bernardino. 2017. Risk management with expectiles. European Journal of Finance 23: 487–506. [Google Scholar] [CrossRef]
- Bellini, Fabio, Bernhard Klar, Alfred Müller, and Emanuela Rosazza Gianin. 2014. Generalized quantiles as risk measures. Insurance: Mathematics and Economics 54: 41–48. [Google Scholar] [CrossRef]
- Bellini, Fabio, Bernhard Klar, and Alfred Müller. 2017. Expectiles, Omega ratios, and stochastic ordering. In Methodology and Computing in Applied Probability. Berlin: Springer. [Google Scholar]
- Berkowitz, Jeremy, and James O’Brien. 2002. How accurate are value-at-risk models at commercial banks? Journal of Finance 57: 1093–111. [Google Scholar] [CrossRef]
- Berkowitz, Jeremy, Peter F. Christofferson, and Denis Pelletier. 2011. Evaluating value-at-risk models with desk-level data. Management Science 57: 2213–27. [Google Scholar] [CrossRef]
- Bernardo, Antonio E., and Olivier Ledoit. 2000. Gain, loss, and asset pricing. Journal of Political Economy 108: 144–72. [Google Scholar] [CrossRef]
- Bingham, Nicholas H., Charles M. Goldie, and Jef L. Teugels. 1987. Regular Variation. Cambridge: Cambridge University Press. [Google Scholar]
- Blundell-Wignall, Adrian, and Paul Atkinson. 2010. Thinking beyond Basel III: Necessary solutions for capital and liquidity. OECD Journal: Financial Market Trends 2010: 9–33. [Google Scholar] [CrossRef]
- Borges, Jorge Luis. 1979. On exactitude in science. In A Universal History of Infamy. New York: E.P. Dutton & Co, p. 139. First published in 1946. [Google Scholar]
- Brummer, Chris. 2012. Soft Law and the Global Financial System: Rule Making in the 21st Century. Cambridge: Cambridge University Press. [Google Scholar]
- Buraschi, Andrea, and Francesco Corielle. 2005. Risk management of time-inconsistency: Model updating and recalibration of no-arbitrage models. Journal of Banking and Finance 29: 2883–907. [Google Scholar] [CrossRef]
- Busse, Marc, Michel M. Dacorogna, and Marie Kratz. 2014. The impact of systemic risk on the diversification benefits of a risk portfolio. Risks 2: 260–76. [Google Scholar] [CrossRef]
- Camus, Albert. 1955. The myth of Sisyphus. In The Myth of Sisyphus and Other Essays. Translated by Justin O’Brien. New York: Alfred A. Knopf, pp. 1–138. First published in 1942. [Google Scholar]
- Carroll, Lewis. 1897. Through the Looking-Glass, and What Alice Found There. Philadelphia: Henry Altemus Co. First published in 1872. [Google Scholar]
- Carroll, Lewis. 1895. Sylvie and Bruno Concluded. London: Macmillan. [Google Scholar]
- Chang, Chia-Lin, Michel McAleer, Juan-Ángel Jiménez-Martín, and Teodosio Pérez-Amaral. 2011. Risk management under the Basel accord: Forecasting value-at-risk of VIX futures. Managerial Finance 37: 1088–106. [Google Scholar] [CrossRef]
- Chang, Chia-Lin, Juan-Ángel Jiménez-Martín, Esfandiar Maasoumi, and Teodosio Pérez-Amaral. 2017. Choosing expected shortfall over VaR in Basel III using stochastic dominance. Advances in Economics, Business and Management Research 26: 133–56. [Google Scholar]
- Chen, James Ming. 2014. Measuring market risk under the Basel Accords: VaR, stressed VaR, and expected shortfall. Aestimatio 8: 184–201. [Google Scholar]
- Chen, Zhiping, and Qianhui Hu. 2017. On coherent risk measures induced by convex risk measures. Methodology and Computing in Applied Probability 1: 1–26. [Google Scholar] [CrossRef]
- Chen, Li, Simai He, and Shuzhong Zhang. 2011. Tight bounds for some risk measures, with applications to robust portfolio selection. Operations Research 59: 847–65. [Google Scholar] [CrossRef]
- Christoffersen, Peter F. 2011. Elements of Financial Risk Management, 2nd ed. Amsterdam: Academic Press. [Google Scholar]
- Colson, Benoît, Patrice Marcotte, and Gilles Savard. 2007. An overview of bilevel optimization. Annals of Operational Research 153: 235–56. [Google Scholar] [CrossRef]
- Cont, Rama, Romain DeGuest, and Giacomo Scandolo. 2010. Robustness and sensitivity of risk measurement procedures. Quantitative Finance 10: 593–606. [Google Scholar] [CrossRef]
- Costanzino, Nick, and Mike Curran. 2015. Backtesting general spectral risk measures with application to expected shortfall. Risk Model Validation 6: 1–11. [Google Scholar] [CrossRef]
- Costanzino, Nick, and Michael Curran. 2018. A simple traffic light approach to backtesting expected shortfall. Risks 2: 6. [Google Scholar] [CrossRef]
- Cotter, John, and Kevin Dowd. 2006. Extreme spectral risk measures: An application to futures clearinghouse margin requirements. Journal of Banking and Finance 30: 3469–85. [Google Scholar] [CrossRef]
- Daníelsson, Jón. 2004. The emperor has no clothes: Limits to risk modelling. In Risk Measures for the 21st Century. Edited by Giorgio Szegö. Chichester: John Wiley & Sons, pp. 13–32. [Google Scholar]
- Daníelsson, Jón. 2011. Financial Risk Forecasting: The Theory and Practice of Forecasting Market Risk with Implementation in R and Matlab. Chichester: John Wiley & Sons. [Google Scholar]
- Daníelsson, Jón, and Jean-Pierre Zigrand. 2006. On time scaling of risk and the square-root-of-time rule. Journal of Banking and Finance 30: 2701–13. [Google Scholar] [CrossRef]
- Daníelsson, Jón, Bjørn N. Jorgensen, Gennady Samorodnitsky, Mandira Sarma, and Casper G. de Vries. 2013. Fat tails, VaR and subadditivity. Journal of Econometrics 172: 283–91. [Google Scholar] [CrossRef]
- Daníelsson, Jón, Kevin R. James, Marcela Valenzuela, and Ilknur Zer. 2016. Model risk of risk models. Journal of Financial Stability 23: 79–91. [Google Scholar] [CrossRef]
- Daouia, Abdelaati, Stéphane Girard, and Gilles Stupfler. 2018. Estimation of tail risk based on extreme expectiles. Journal of the Royal Statistical Society, Series B 80: 263–92. [Google Scholar] [CrossRef]
- Dawkins, Richard, and John R. Krebs. 1979. Arms races between and within species. Proceedings of the Royal Society of London, Series B 205: 489–511. [Google Scholar] [CrossRef]
- De Rossi, Giuliano, and Andrew Harvey. 2009. Quantiles, expectiles and splines. Journal of Econometrics 152: 179–85. [Google Scholar] [CrossRef]
- Derman, Emanuel. 1996. Model Risk. Goldman Sachs Quantitative Strategies Research Notes. April. Available online: http://www.emanuelderman.com/media/gs-model_risk.pdf (accessed on 8 April 2018).
- Dhaene, J., R. J. A. Laeven, S. Vanduffel, G. Darkiewicz, and M. J. Goovaerts. 2008. Can a coherent risk measure be too subadditive? Journal of Risk and Insurance 75: 365–86. [Google Scholar] [CrossRef]
- Dowd, Kevin, and David Blake. 2006. After VaR: The theory, estimation, and insurance applications of quantile-based risk measures. The Journal of Risk and Insurance 73: 193–229. [Google Scholar] [CrossRef]
- Dowd, Kevin, John Cotter, and Ghulam Sorwar. 2008. Spectral risk measures: Properties and limitations. Journal of Financial Services Research 34: 61–75. [Google Scholar] [CrossRef]
- Du, Zaichao, and Juan Carlos Escanciano. 2017. Backtesting expected shortfall: Accounting for tail risk. Management Science 63: 940–58. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Jun Pan. 1997. An overview of value at risk. Journal of Derivatives 4: 7–49. [Google Scholar] [CrossRef]
- Eco, Umberto. 1995. On the impossibility of drawing a map of the empire on a scale of 1 to 1. In How to Travel with a Salmon, and Other Essays. San Diego: Harcourt. [Google Scholar]
- Efron, B. 1991. Regression percentiles using asymmetric squared error loss. Statistica Sinica 1: 93–125. [Google Scholar]
- Ehm, Werner, Tilmann Gneiting, Alexander Jordan, and Fabian Krüger. 2016. Of quantiles and expectiles: consistent scoring functions, Choquet representations and forecast rankings. Journal of the Royal Statistical Society, Series B 78: 505–62. [Google Scholar] [CrossRef]
- Eilers, Paul H.C. 2013. Discussion: The beauty of expectiles. Statistical Modelling 13: 317–22. [Google Scholar] [CrossRef]
- El Ghaoui, Laurent, Maksim Oks, and François Oustry. 2003. Worst-case value-at-risk and robust portfolio optimization: A conic programming approach. Operations Research 51: 543–56. [Google Scholar] [CrossRef]
- Embrechts, Paul, Alexander McNeil, and Daniel Straumann. 2002. Correlation and dependence in risk management: Properties and pitfalls. In Risk Management: Value at Risk and Beyond. Edited by M. A. H. Dempster. Cambridge: Cambridge University Press, pp. 176–223. [Google Scholar]
- Embrechts, Paul, Giovanni Puccetti, Ludger Rüschendorf, Ruodo Wang, and Antonela Beleraj. 2014. An academic response to Basel 3.5. Risks 2: 25–48. [Google Scholar] [CrossRef]
- Embrechts, Paul, Bin Wang, and Ruodu Wang. 2015. Aggregation-robustness and model uncertainty of regulatory risk measures. Finance and Stochastics 19: 763–90. [Google Scholar] [CrossRef]
- Emmer, Susanne, Marie Kratz, and Dirk Tasche. 2015. What is the best risk measure in practice? Journal of Risk 18: 31–60. [Google Scholar] [CrossRef]
- Engelberg, Joseph, Charles F. Manski, and Jared Williams. 2009. Comparing the point predictions and subjective probability distributions of professional forecasters. Journal of Business and Economic Statistics 27: 30–41. [Google Scholar] [CrossRef]
- Escanciano, J. Carlos, and José Olmo. 2011. Robust backtesting tests for value-at-risk models. Journal of Financial Econometrics 9: 132–61. [Google Scholar] [CrossRef]
- Escanciano, Juan Carlos, and Pei Pei. 2012. Pitfalls in backtesting Historical Simulation VaR models. Journal of Banking and Finance 36: 2233–44. [Google Scholar] [CrossRef]
- Fildes, R., K. Nikolopoulos, S. F. Crone, and A. A. Syntetos. 2008. Forecasting and operational research: A review. Journal of the Operational Research Society 59: 1150–72. [Google Scholar] [CrossRef]
- Fisher, R. A. 1925. Applications of “Student’s” distribution. Metron 5: 90–104. [Google Scholar]
- Fissler, Tobias, and Johanna F. Ziegel. 2016. Higher order elicitability and Osband’s principle. Annals of Statistics 44: 1680–707. [Google Scholar] [CrossRef]
- Fissler, Tobias, Johanna F. Ziegel, and Tilmann Gneiting. 2016. Expected shortfall is jointly elicitable with value at risk—Implications for backtesting. Risk 29: 58–61. [Google Scholar]
- Fuchs, Sebastian, Ruben Schlotter, and Klaus D. Schmidt. 2017. A review and some complements on quantile risk measures and their domain. Risks 5: 59. [Google Scholar] [CrossRef]
- Giacomini, Raffaella, and Ivana Komunjer. 2005. Evaluation and combination of conditional quantile forecasts. Journal of Business and Economic Statistics 23: 416–31. [Google Scholar] [CrossRef]
- Gneiting, Tilmann. 2008. Probabilistic forecasting. Journal of the Royal Statistical Society, Series A 171: 319–321. [Google Scholar] [CrossRef]
- Gneiting, Tilmann. 2011. Making and evaluating point forecasts. Journal of the American Statistical Association 106: 746–62. [Google Scholar] [CrossRef]
- Gneiting, Tilmann, and Matthias Katzfuss. 2014. Probabilistic forecasting. Annual Review of Statistics and Its Application 1: 125–51. [Google Scholar] [CrossRef]
- Goodhart, Charles. 1981. Problems of monetary management: The U.K. experience. In Inflation, Depression, and Economic Policy in the West. Edited by Anthony S. Courakis. Lanham: Rowman and Littlefield, pp. 111–46. [Google Scholar]
- Gourieroux, C., J. P. Laurent, and O. Scaillet. 2000. Sensitivity analysis of values at risk. Journal of Empirical Finance 7: 225–45. [Google Scholar] [CrossRef]
- Gschöpf, Philipp, Wolfgang Karl Härdle, and Andrija Mihoci. 2015. Tail Event Risk Expectile Based Shortfall. SFB 649 Discussion Paper 2015-047. Available online: http://sfb649.wiwi.hu-berlin.de/papers/pdf/SFB649DP2015-047.pdf (accessed on 8 April 2018).
- Guo, Xu, Xuejun Jiang, and Wing-Keung Wong. 2017. Stochastic dominance and Omega ratio: Measures to examine market efficiency, arbitrage opportunity, and anomaly. Economies 5: 38. [Google Scholar] [CrossRef]
- Hanif, Muhammad, and Mohammad Zafar Yab. 1990. Quantile analogues: An evaluation of expectiles and M-quantiles as measures of distributional tendency. Pakistan Journal of Statistics, Series B 16: 21–37. [Google Scholar]
- Heyde, Chris C., and Steven G. Kou. 2004. On the controversy over tailweight of distributions. Operations Research Letters 32: 399–408. [Google Scholar] [CrossRef]
- Holzmann, Hajo, and Bernhard Klar. 2016. Weighted scoring rules and hypothesis testing. Available online: https://arxiv.org/abs/1611.07345 (accessed on 8 April 2018).
- Hull, John. 2015. Risk Management and Financial Institutions, 4th ed. Hoboken: John Wiley & Sons. [Google Scholar]
- Inui, Koji, and Masaaki Kijima. 2005. On the significance of expected shortfall as a coherent risk measure. Journal of Banking and Finance 29: 853–64. [Google Scholar] [CrossRef]
- Jones, M.C. 1994. Expectiles and m-quantiles are quantiles. Statistics and Probability Letters 20: 149–53. [Google Scholar] [CrossRef]
- Jorion, Philippe. 2006. Value at Risk: The New Benchmark for Managing Financial Risk, 3rd ed. New York: McGraw-Hill. [Google Scholar]
- Kellner, Ralf, and Daniel Rösch. 2016. Quantifying market risk with value-at-risk or expected shortfall? Consequences for capital requirements and model risk. Journal of Economic Dynamics & Control 68: 56–61. [Google Scholar]
- Kerkhof, Jeroen, and Bertrand Melenberg. 2004. Backtesting for risk-based regulatory capital. Journal of Banking and Finance 28: 1845–65. [Google Scholar] [CrossRef]
- Kneib, Thomas. 2013. Beyond mean regression. Statistical Modelling 1: 275–303. [Google Scholar] [CrossRef]
- Koenker, Roger. 1992. When are expectiles percentiles? Econometric Theory 8: 423–24. [Google Scholar] [CrossRef]
- Koenker, Roger. 1993. When are expectiles percentiles? Econometric Theory 9: 526–27. [Google Scholar] [CrossRef]
- Koenker, Roger. 2005. Quantile Regression. Cambridge: Cambridge University Press. [Google Scholar]
- Koenker, Roger. 2013. Living beyond our means. Statistical Modelling 13: 323–33. [Google Scholar] [CrossRef]
- Koenker, Roger, and Kevin F. Hallock. 2001. Quantile regression. Journal of Economic Perspectives 15: 143–56. [Google Scholar] [CrossRef]
- Kou, Steven, Xianhua Peng, and Chris C. Heyde. 2013. External risk measures and Basel accords. Mathematics of Operations Research 38: 393–417. [Google Scholar] [CrossRef]
- Krätschmer, Volker, and Henryk Zähle. 2017. Statistical inference for expectile-based risk measures. Scandinavian Journal of Statistics 44: 425–54. [Google Scholar] [CrossRef]
- Krätschmer, Volker, Alexander Schied, and Henryk Zähle. 2012. Qualitative and infinitesimal robustness of tail-dependent statistical functionals. Journal of Multivariate Analysis 103: 35–47. [Google Scholar] [CrossRef]
- Krätschmer, Volker, Alexander Schied, and Henryk Zähle. 2014. Comparative and qualitative robustness for law-invariant risk measures. Finance and Stochastics 18: 271–95. [Google Scholar] [CrossRef]
- Kratz, Marie. 2017. Discussion of “Elicitability and backtesting: Perspectives for banking regulation”. Annals of Applied Statistics 11: 1894–900. [Google Scholar]
- Kratz, Marie, Yen H. Lok, and Alexander J. McNeil. 2018. Multinomial VaR backtests: A simple implicit approach to backtesting expected shortfall. Journal of Banking and Finance 88: 393–407. [Google Scholar] [CrossRef]
- Kuan, Chung-Ming, Jin-Huei Yeh, and Yu-Chin Hsu. 2009. Assessing value at risk with CARE, the conditional autoregressive expectile models. Journal of Econometrics 150: 261–70. [Google Scholar] [CrossRef]
- Kuester, Keith, Stefan Mittnick, and Marc S. Paolella. 2006. Value-at-risk prediction: A comparison of alternative strategies. Journal of Financial Econometrics 4: 53–89. [Google Scholar] [CrossRef]
- Kupiec, Paul H. 1995. Techniques for verifying the accuracy of risk measurement models. Journal of Derivatives 3: 73–84. [Google Scholar] [CrossRef]
- Kusuoka, Shigeo. 2001. On law-invariant coherent risk measures. In Advances in Mathematical Economics. Edited by Shigeo Kusuoka and Toru Maruyama. Tokyo: Springer, vol. 3, pp. 83–95. [Google Scholar]
- Levy, Haim. 1992. Stochastic dominance and expected utility: Survey and Analysis. Management Science 38: 555–93. [Google Scholar] [CrossRef]
- Levy, Haim. 2015. Stochastic Dominance: Investment Decision Making Under Uncertainty, 3rd ed. New York: Springer. [Google Scholar]
- Li, Jonathan Yu-Meng. 2017. Closed-form Solutions for Worst-Case Law Invariant Risk Measures with Application to Robust Portfolio Optimization. Available online: http://www.optimization-online.org/DB_FILE/2016/09/5637.pdf (accessed on 8 April 2018).
- Mabrouk, Samir, and Samir Saadi. 2012. Parametric value-at-risk analysis: Evidence from stock indices. Quarterly Review of Economics and Finance 52: 305–21. [Google Scholar] [CrossRef]
- Małecka, Marta. 2017. Testing VaR under Basel III with application to no-failure setting. In Contemporary Trends and Challenges in Finance: Proceedings from the 2nd Wroclaw International Conference in Finance. Edited by Krzysztof Jajuga, Lucjan T. Orlowski and Karsten Staehr. Cham: Springer, pp. 95–102. [Google Scholar]
- Manganelli, Simone, and Robert F. Engle. 2004. A comparison of value-at-risk models in finance. In Risk Measures for the 21st Century. Edited by Giorgio Szegö. Chichester: John Wiley & Sons, pp. 123–44. [Google Scholar]
- Mausser, Helmut, David Saunders, and Luis Seco. 2006. Optimising omega. Risk 19: 88–94. [Google Scholar]
- McAleer, Michel, Juan-Ángel Jiménez-Martín, and Teodosio Pérez-Amaral. 2009. A decision rule to minimize daily capital charges in forecasting value-at-risk. Journal of Forecasting 29: 617–34. [Google Scholar] [CrossRef]
- McAleer, Michel, Juan-Ángel Jiménez-Martín, and Teodosio Pérez-Amaral. 2013a. Has the Basel II accord improved risk management during the global financial crisis? North American Journal of Economics and Finance 26: 250–56. [Google Scholar] [CrossRef]
- McAleer, Michel, Juan-Ángel Jiménez-Martín, and Teodosio Pérez-Amaral. 2013b. Intenational evidence on GFC-robust risk management strategies under the Basel accord. Journal of Forecasting 32: 267–88. [Google Scholar] [CrossRef]
- McNeil, Alexander J., and Rüdiger Frey. 2000. Estimation of tail-related risk measures for heteroscedastic financial time series: An extreme value approach. Journal of Empirical Finance 7: 271–300. [Google Scholar] [CrossRef]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2005. Quantitative Risk Management: Concepts, Techniques, Tools. Princeton: Princeton University Press. [Google Scholar]
- Mina, Jorge, and Jerry Yi Xiao. 2001. Return to RiskMetrics: The Evolution of a Standard. New York: RiskMetrics Group, Inc. [Google Scholar]
- Murphy, Allan H., and Robert L. Winkler. 1987. A general framework for forecast verification. Monthly Weather Review 115: 1330–38. [Google Scholar] [CrossRef]
- Natarajan, Karthik, Melvyn Sim, and Joline Uichanco. 2010. Tractable robust expected utility and risk models for portfolio optimization. Mathematical Finance 20: 695–731. [Google Scholar] [CrossRef]
- Newey, Whitney K., and James L. Powell. 1987. Asymmetric least squares estimation and testing. Econometrica 55: 819–847. [Google Scholar] [CrossRef]
- Nolde, Natalia, and Johanna F. Ziegel. 2017a. Elicitability and backtesting: Perspectives for banking regulation. Annals of Applied Statistics 11: 1833–74. [Google Scholar] [CrossRef]
- Nolde, Natalia, and Johanna F. Ziegel. 2017b. Rejoinder: “Elicitability and backtesting: Perspectives for banking regulation”. Annals of Applied Statistics 11: 1901–11. [Google Scholar]
- Osband, Kent. 2011. Pandora’s Risk: Uncertainty at the Core of Finance. New York: Columbia Business School Publishing. [Google Scholar]
- Pafka, Szilárd, and Imre Kondor. 2001. Evaluating the RiskMetrics methodology in measuring volatility and value-at-risk in financial markets. Physica A 299: 305–10. [Google Scholar] [CrossRef]
- Patton, Andrew J. 2011. Volatility forecast comparison using imperfect volatility proxies. Journal of Econometrics 160: 246–56. [Google Scholar] [CrossRef]
- Righi, Marcello Bratti, and Paulo Sergio Ceretta. 2013. Individual and flexible expected shortfall backtesting. Journal of Risk Model Validation 7: 3–20. [Google Scholar] [CrossRef]
- Righi, Marcello Bratti, and Paulo Sergio Ceretta. 2015. A comparison of Expected Shortfall estimation models. Journal of Economics and Business 78: 14–47. [Google Scholar] [CrossRef]
- Rockafellar, R. Tyrrell, and Stanislav Uryasev. 2000. Optimization of conditional value-at-risk. Journal of Risk 2: 21–42. [Google Scholar] [CrossRef]
- Rockafellar, R. Tyrrell, and Stanislav Uryasev. 2002. Conditional value-at-risk for general loss distributions. Journal of Banking and Finance 26: 1443–71. [Google Scholar] [CrossRef]
- Rossignolo, Adrian F., Meryem Duygun Fethi, and Mohamed Shaban. 2012. Value-at-risk models and Basel capital charges: Evidence from emerging and frontier stock markets. Journal of Financial Stability 8: 303–19. [Google Scholar] [CrossRef]
- Shadwick, William F., and Con Keating. 2002. A universal performance measure. Journal of Performance Measurement 6: 59–84. [Google Scholar]
- Shapiro, Alexander. 2013. On Kusuoka representation of law invariant risk measures. Mathematics of Operations Research 38: 142–52. [Google Scholar] [CrossRef]
- Sharma, Amita, Sebastian Utz, and Aparna Mehra. 2017. Omega-CVaR portfolio optimization and its worst case analysis. OR Spectrum 39: 505–39. [Google Scholar] [CrossRef]
- So, Mike K.P., and Chi-Ming Wong. 2012. Estimation of multiple period expected shortfall and median shortfall for risk management. Quantitative Finance 12: 739–54. [Google Scholar] [CrossRef]
- Student (William Sealy Gosset). 1908. The probable error of a mean. Biometrika 6: 1–25. [Google Scholar]
- Taylor, James W. 2008. Estimating value at risk and expected shortfall using expectiles. Journal of Financial Econometrics 6: 231–52. [Google Scholar] [CrossRef]
- Taylor, James W. 2017. Forecasting value at risk and expected shortfall using a semiparametric approach based on the asymmetric Laplace distribution. Journal of Business and Economic Statistics. [Google Scholar] [CrossRef]
- Van Valen, Leigh. 1973. A new evolutionary law. Evolutionary Theory 1: 1–30. [Google Scholar]
- Waltrup, Linda Schulze, Fabian Sobotka, Thomas Kneib, and Göran Kauermann. 2015. Expectile and quantile regression—David and Goliath? Statistical Modelling 15: 433–56. [Google Scholar] [CrossRef]
- Weber, Stefan. 2006. Distribution-invariant risk measures, information, and dynamic consistency. Mathematical Finance 16: 419–41. [Google Scholar] [CrossRef]
- Wong, Woon K. 2008. Backtesting trading risk of commercial banks using expected shortfall. Journal of Banking and Finance 32: 1404–15. [Google Scholar] [CrossRef]
- Wong, Woon K. 2010. Backtesting value-at-risk based on tail losses. Journal of Empirical Finance 17: 526–38. [Google Scholar] [CrossRef]
- Yamai, Yasuhiro, and Toshinao Yoshiba. 2002. On the validity of value-at-risk: Comparative analyses with expected shortfall. Monetary and Economic Studies 20: 57–85. [Google Scholar]
- Yamai, Yasuhiro, and Toshinao Yoshiba. 2005. Value-at-risk versus expected shortfall: A practical perspective. Journal of Banking and Finance 29: 997–1015. [Google Scholar] [CrossRef]
- Yao, Qiwei, and Howell Tong. 1996. Asymmetric least squares regression estimation: A nonparametric approach. Nonparametric Statistics 6: 273–92. [Google Scholar] [CrossRef]
- Ye, Kai, Panos Parpas, and Berç Rustem. 2012. Robust portfolio optimization: A conic programming approach. Computational Optimization and Applications 52: 403–48. [Google Scholar] [CrossRef]
- Zakamouline, Valeri, and Steen Koekebakker. 2009. Portfolio performance with generalized Sharpe ratios: Beyond the mean and variance. Journal of Banking and Finance 33: 1242–54. [Google Scholar] [CrossRef]
- Ziegel, Johanna F. 2016. Coherence and elicitability. Mathematical Finance 26: 901–18. [Google Scholar] [CrossRef]
- Zou, Hui. 2014. Generalizing Koenker’s distribution. Journal of Statistical Planning and Inference 148: 123–27. [Google Scholar] [CrossRef]
| Zone | Exceedances | Plus Factor k | Cumulative Probability (in %) |
|---|---|---|---|
| ■ | 0 | 0.00 | 08.11 |
| ■ | 1 | 0.00 | 28.58 |
| ■ | 2 | 0.00 | 54.32 |
| ■ | 3 | 0.00 | 75.81 |
| ■ | 4 | 0.00 | 89.22 |
| ■ | 5 | 0.40 | 95.88 |
| ■ | 6 | 0.50 | 98.63 |
| ■ | 7 | 0.65 | 99.60 |
| ■ | 8 | 0.75 | 99.89 |
| ■ | 9 | 0.85 | 99.97 |
| ■ | 10+ | 1.00 | 99.99 |
| Zone | Traditional | Comparative |
|---|---|---|
| VaR (BCBS 2013): | Nolde and Ziegel (2017a): : The internal model predicts at least as well as the standard model. : The internal model predicts at most as well as the standard model. Some choice of significance level . E.g., = 0.05. | |
| Expected shortfall (Costanzino and Curran 2018): | ||
| ■ | is rejected at = 0.05. | |
| ■ | Neither nor is rejected | |
| ■ | is rejected at = 0.05. |
| α | VaRα | ESα | τ(α) |
|---|---|---|---|
| 0.00135000 | –2.99998 | –3.28308 | 0.000127364 |
| 0.00353299 | –2.69372 | –3.00000 | 0.000401386 |
| 0.010000 | –2.32648 | –2.66521 | 0.00145241 |
| 0.025000 | –1.95996 | –2.33780 | 0.00477345 |
| 0.050000 | –1.64485 | –2.06271 | 0.0123873 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.M. On Exactitude in Financial Regulation: Value-at-Risk, Expected Shortfall, and Expectiles. Risks 2018, 6, 61. https://doi.org/10.3390/risks6020061
Chen JM. On Exactitude in Financial Regulation: Value-at-Risk, Expected Shortfall, and Expectiles. Risks. 2018; 6(2):61. https://doi.org/10.3390/risks6020061
Chicago/Turabian StyleChen, James Ming. 2018. "On Exactitude in Financial Regulation: Value-at-Risk, Expected Shortfall, and Expectiles" Risks 6, no. 2: 61. https://doi.org/10.3390/risks6020061
APA StyleChen, J. M. (2018). On Exactitude in Financial Regulation: Value-at-Risk, Expected Shortfall, and Expectiles. Risks, 6(2), 61. https://doi.org/10.3390/risks6020061





