Stochastic Modeling of Wind Derivatives in Energy Markets
Abstract
:1. Introduction
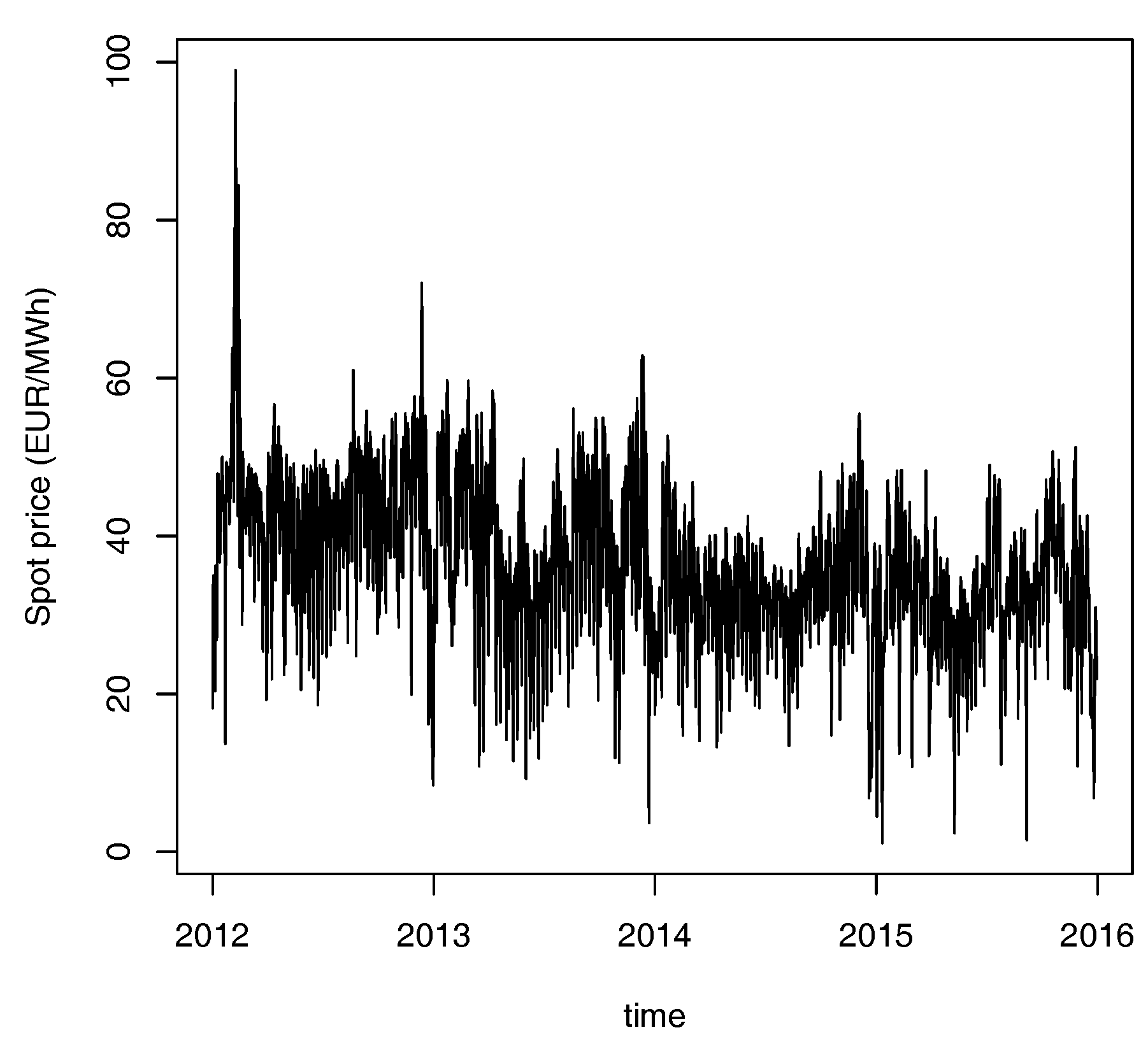
2. Spot Price Model
Calibration
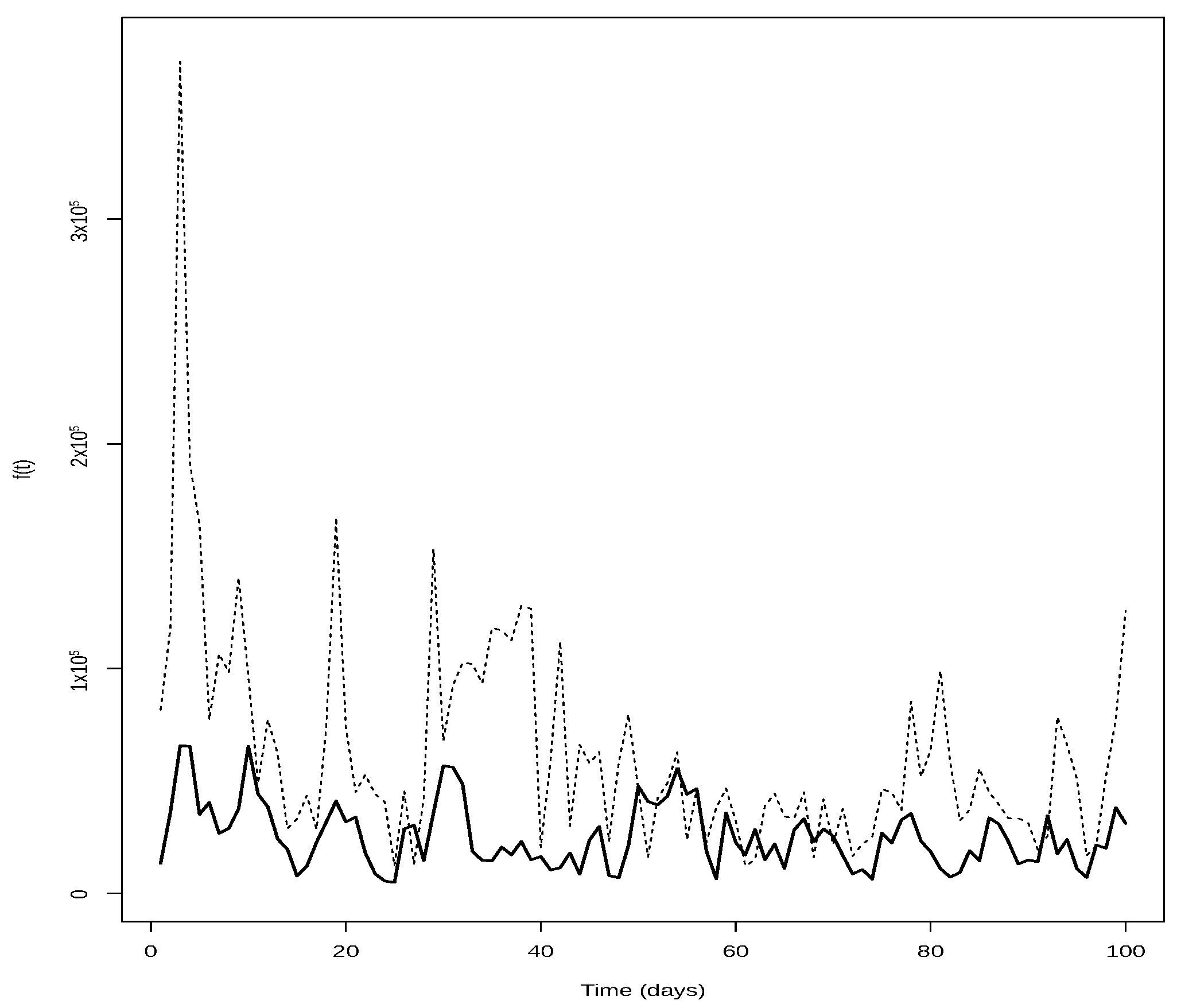
3. Models for Wind
Calibration
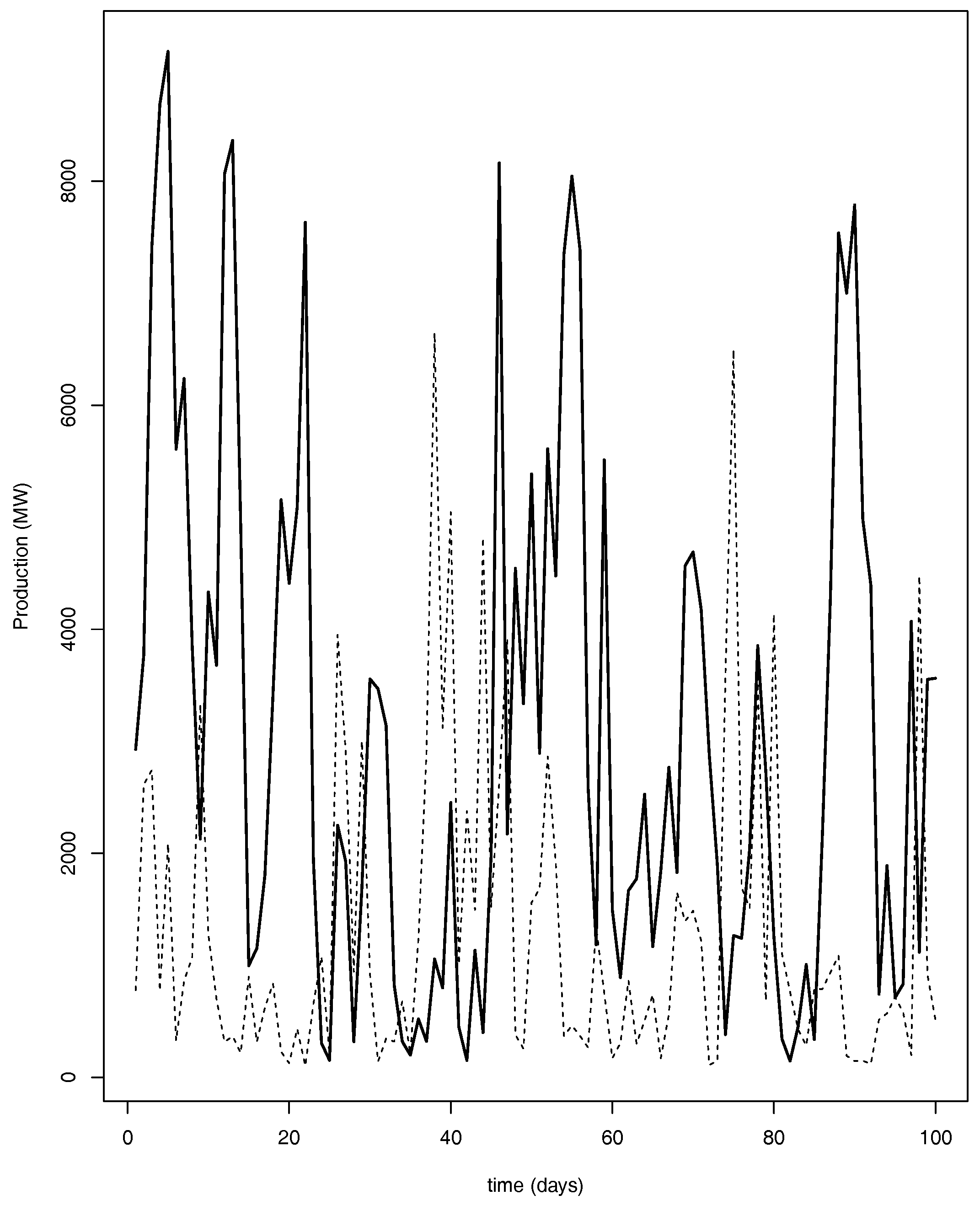
4. Income for a Wind Energy Company
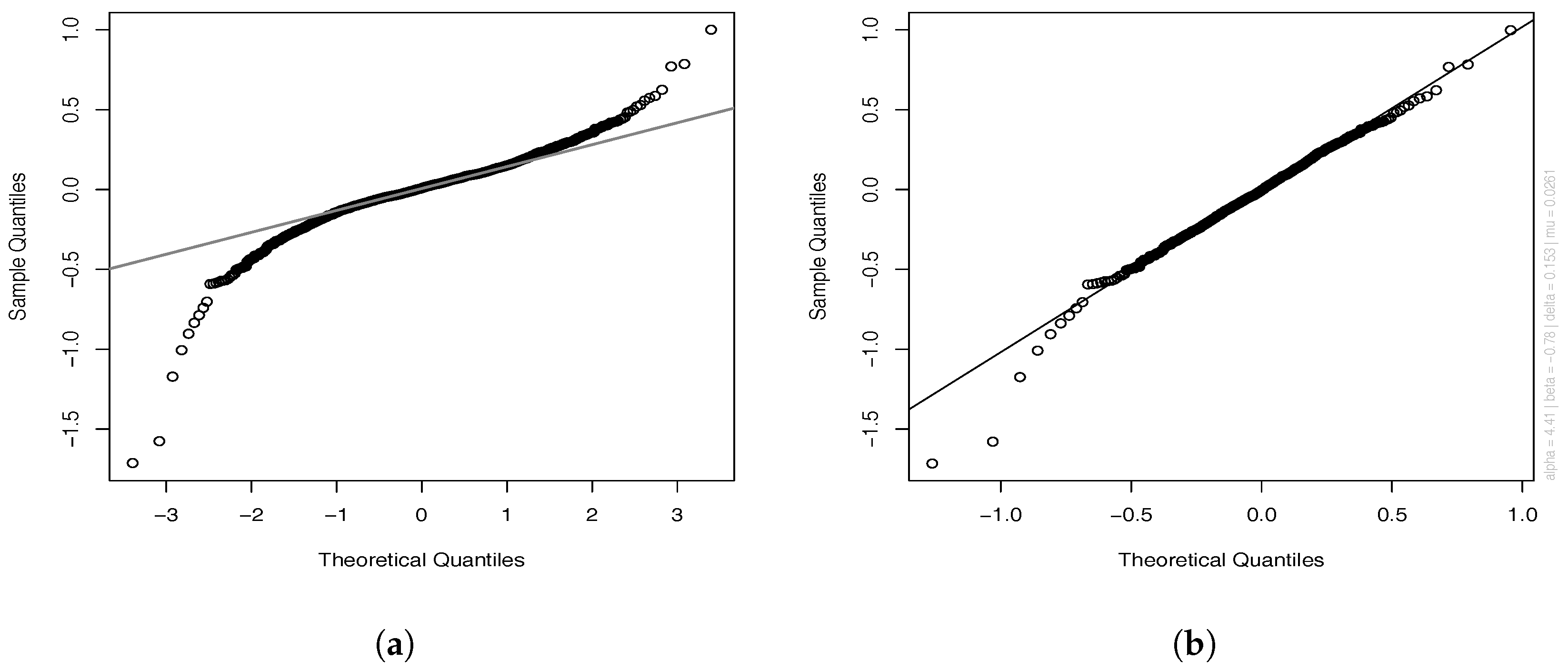
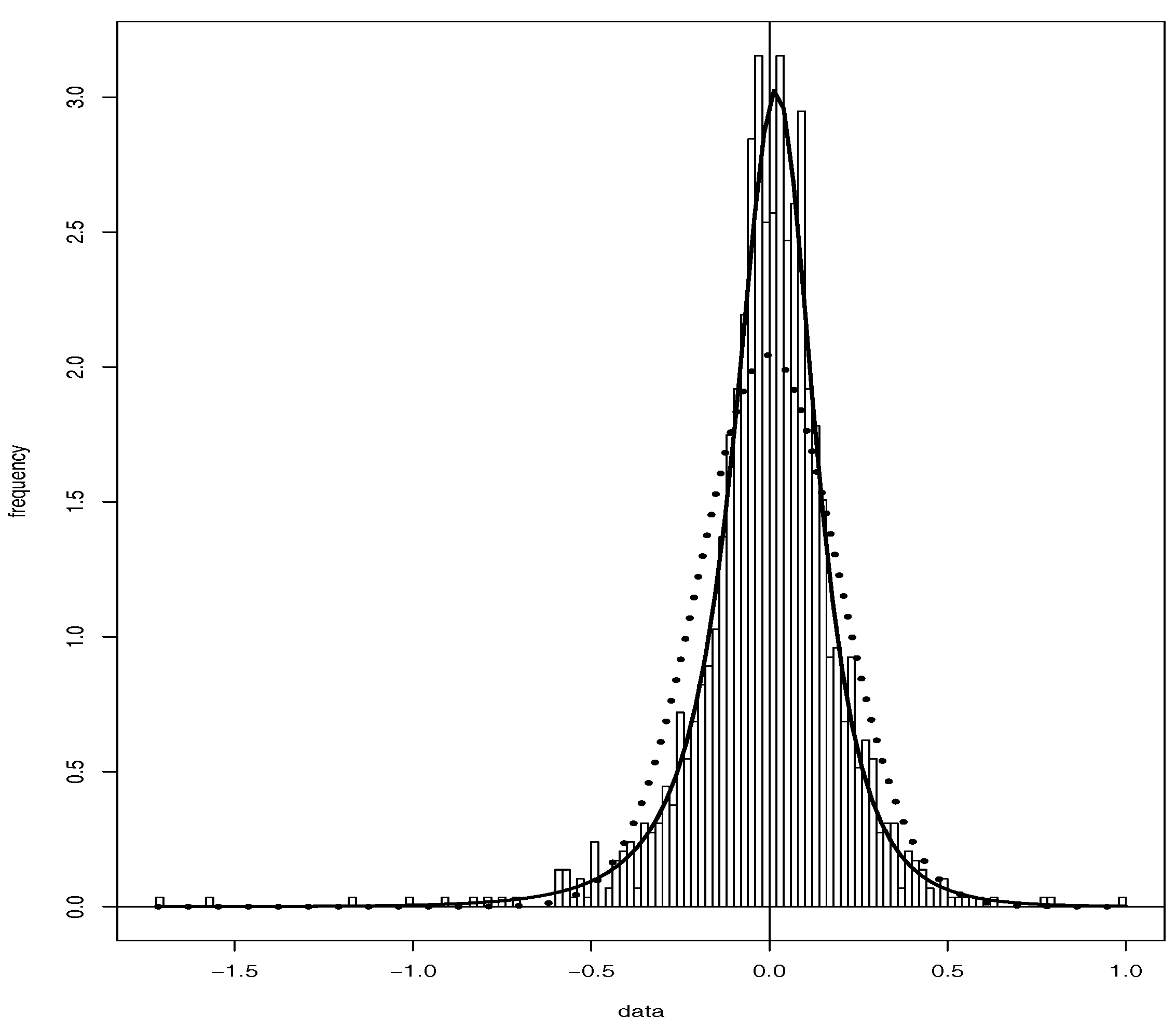
4.1. Normal Inverse Gaussian Approximation
4.2. Income Formulas
5. Quanto Options
5.1. Contract Structure
5.2. Futures Dynamics
5.3. Option Price
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of fZ
References
- Applebaum, David. 2009. Lévy Processes and Stochastic Calculus. Cambridge Studies in Advanced Mathematics. Cambridge: Cambridge University Press. [Google Scholar] [CrossRef]
- Asmussen, Søren, and Jan Rosiński. 2011. Approximations of Small Jumps of LéVy Processes with a View towards Simulation. Journal of Applied Probability 38: 432–93. [Google Scholar]
- Benth, Fred E., and Jūratė Š. Benth. 2004. The Normal Inverse Gaussian distribution and spot price modeling in energy markets. International Journal of Theoretical and Applied Finance 7: 177–92. [Google Scholar] [CrossRef]
- Benth, Fred E., and Jūratė Š. Benth. 2012. Modeling and Pricing in Financial Markets for Weather Derivatives. Singapore: World Scientific. [Google Scholar]
- Benth, Fred E., Jūratė Š. Benth, and Steen Koekebakker. 2008. Stochastic Modelling of Electricity and Related Markets. Singapore: World Scientific. [Google Scholar]
- Benth, Fred E., Nina Lange, and Tor Åge Myklebust. 2013. Pricing and hedging quanto options in energy markets. Journal of Energy Markets 8: 1–35. [Google Scholar] [CrossRef]
- Betz, Albert. 1966. Introduction to the Theory of Flow Machines. Oxford: Pergamon Press. [Google Scholar]
- Burton, Tony. 2011. Wind Energy: Handbook. Hoboken: John Wiley & Sons. [Google Scholar]
- Folland, Gerald B. 2007. Real Analysis: Modern Techniques and Their Applications, 2nd ed. Hoboken: Wiley. [Google Scholar]
- Jørgensen, Bent. 1982. Statistical Properties of the Generalised Inverse Gaussian Distribution. Lecture Notes in Statistics. New York: Springer, vol. 9. [Google Scholar]
- Schwartz, Eduardo S. 1997. The stochastic behavior of commodity prices: Implication for valuation and hedging. The Journal of Finance 52: 923–73. [Google Scholar] [CrossRef]
- Tankov, Peter, and Rama Cont. 2004. Financial Modeling with Jump Processes. CRC Financial Mathematics Series; Boca Raton: CRC Press. [Google Scholar]
- Villanueva, Daniel, and Feijoó Andrés. 2010. Wind power distributions: A review of their applications. Renewable and Sustainable Energy Reviews 14: 1490–95. [Google Scholar] [CrossRef]
- Wystup, Uwe. 2010. Quanto Options. In Encyclopedia of Quantitative Finance. Hoboken: Wiley. [Google Scholar] [CrossRef]
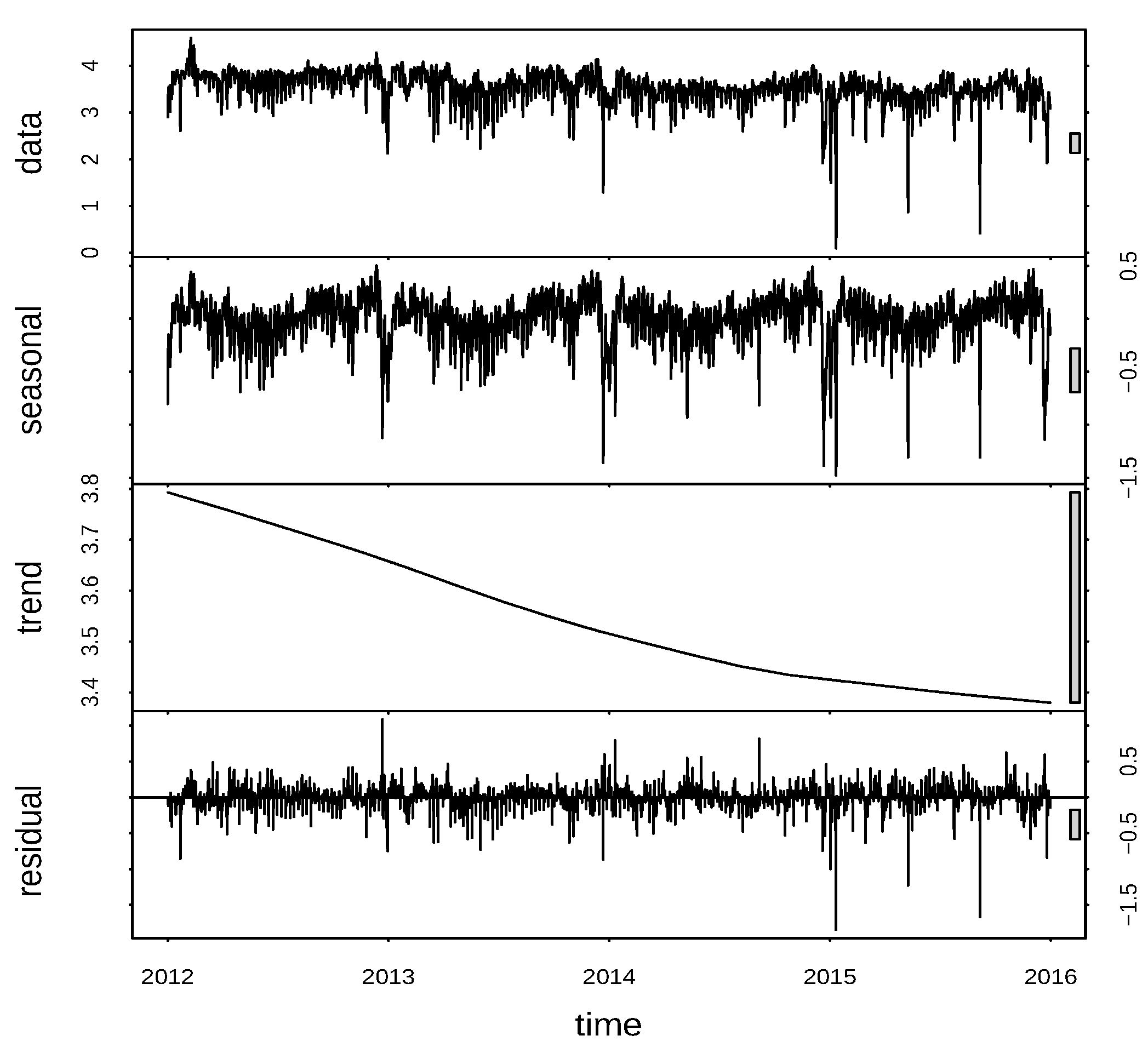
| 1 | We use the R function stl from package stats. |
| 2 | We use the R function arima from package stats. |
| 3 | We use the R function nigFit from package fBasics. |
| 4 | We use the R function boot from the package boot. |
| 5 | We use the R function lm from package stats. |
| 6 | We use the R function stl from package stats. |
| 7 | We use the R function arima from package stats. |
| 8 | We use the R function integrate from package stats, together with besselK from package base. |
| Estimate | Confidence interval (95%) | Estimate | Confidence interval (95%) | ||
|---|---|---|---|---|---|
| Estimate | Confidence Interval (95%) | Estimate | Confidence Interval (95%) | ||
|---|---|---|---|---|---|
| : | 31/12/2014 |
| : | 01/01/2015 |
| : | 31/12/2015 |
| Three-Year Calibration | Two-Year Calibration | One-Year Calibration | ||||
|---|---|---|---|---|---|---|
| 0 | ||||||
| Three-Year Calibration | Two-Year Calibration | One-Year Calibration |
|---|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benth, F.E.; Di Persio, L.; Lavagnini, S. Stochastic Modeling of Wind Derivatives in Energy Markets. Risks 2018, 6, 56. https://doi.org/10.3390/risks6020056
Benth FE, Di Persio L, Lavagnini S. Stochastic Modeling of Wind Derivatives in Energy Markets. Risks. 2018; 6(2):56. https://doi.org/10.3390/risks6020056
Chicago/Turabian StyleBenth, Fred Espen, Luca Di Persio, and Silvia Lavagnini. 2018. "Stochastic Modeling of Wind Derivatives in Energy Markets" Risks 6, no. 2: 56. https://doi.org/10.3390/risks6020056
APA StyleBenth, F. E., Di Persio, L., & Lavagnini, S. (2018). Stochastic Modeling of Wind Derivatives in Energy Markets. Risks, 6(2), 56. https://doi.org/10.3390/risks6020056





