Using Cutting-Edge Tree-Based Stochastic Models to Predict Credit Risk

Abstract

Credit risk is a critical issue that affects banks and companies on a global scale. Possessing the ability to accurately predict the level of credit risk has the potential to help the lender and borrower. This is achieved by alleviating the number of loans provided to borrowers with poor financial health, thereby reducing the number of failed businesses, and, in effect, preventing economies from collapsing. This paper uses state-of-the-art stochastic models, namely: Decision trees, random forests, and stochastic gradient boosting to add to the current literature on credit-risk modelling. The Australian mining industry has been selected to test our methodology. Mining in Australia generates around $138 billion annually, making up more than half of the total goods and services. This paper uses publicly-available financial data from 750 risky and not risky Australian mining companies as variables in our models. Our results indicate that stochastic gradient boosting was the superior model at correctly classifying the good and bad credit-rated companies within the mining sector. Our model showed that ‘Property, Plant, & Equipment (PPE) turnover’, ‘Invested Capital Turnover’, and ‘Price over Earnings Ratio (PER)’ were the variables with the best explanatory power pertaining to predicting credit risk in the Australian mining sector.

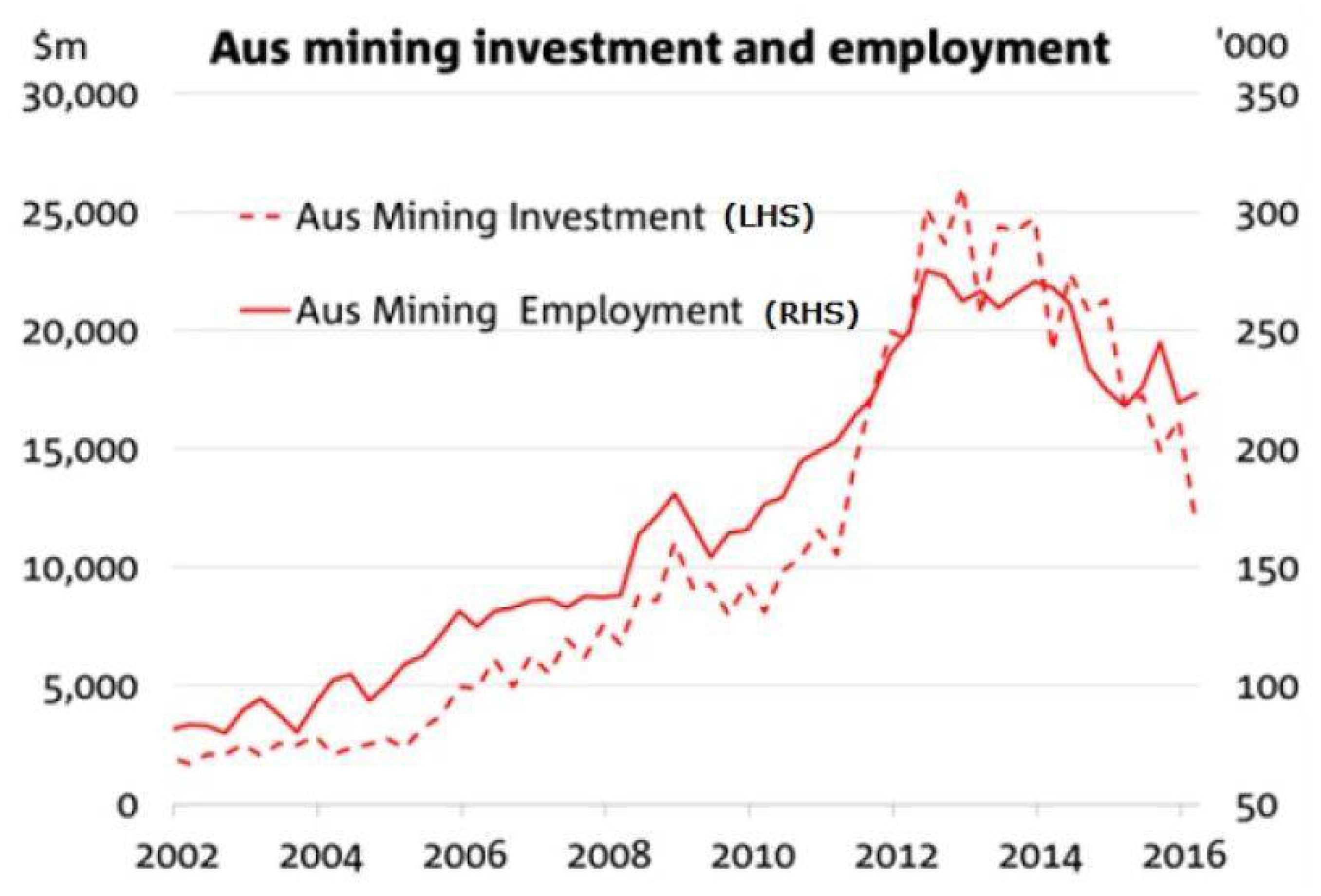
1. Introduction

It is vital to have an understanding of a company’s credit risks, as they can provide an invaluable insight into its financial state. If a company’s high credit risk goes on untreated, this will not only affect its financial health, but may eventually lead to insolvency. There are a number of factors that can lead to a high credit risk, including, but not limited to: Financial, economic, disaster, neglect, and fraud/clandestine activities (Anderson 2006). Credit Risk Modelling is interchangeably used in the literature by many other names, including: Financial Distress Prediction, Bankruptcy Prediction, Firm Failure Prediction, Insolvency Prediction, Financial Risk Prediction, and Credit Default (Prediction Gepp and Kumar 2012). From this point forward, this paper will use them term Credit Risk Modelling to refer to the above-mentioned substitute terms and will be frequently denoted by its acronym CRM.

CRM involves developing statistical models that can predict the level of financial risk of companies based on information, such as publicly available financial ratios from financial statements (Gepp and Kumar 2012). The predictive statistical models have wide applications, including for the company itself, creditors, and other stakeholders. These models can assist financial institutions in determining whether to provide credit. They can also be used to develop proactive and preventive financial and managerial decisions in order to avoid business failure (Jaikengit 2004). Due to the models’ wide applicability and important implications, the literature is quickly becoming filled with studies across various disciplines, such as finance, accounting, statistics, and actuary, that attempt to accurately forecast the financial risk levels of companies (Cybinski 2001; Yu et al. 2014). There is a lot of variety in the researchers’ choice of statistical models used to achieve the maximum level of forecasting accuracies, including: Multivariate discriminant analysis, logistic regression, random forests, and many others.

According to Gepp and Kumar 2012, CRM has many advantages, including: Enabling banks and other creditors to predict companies’ level of credit risk before establishing the suitability of providing a loan; existing and potential stockholders can use CRM to make more informed investment decisions for best Return On Investment (ROI) opportunities; various stakeholders can use these models to gain information that will allow them to establish whether engaging with the modelled companies will result in gains or losses; and governments and regulatory bodies can use the models to determine which companies have high credit risk or are in danger of becoming insolvent, and installing appropriate corrective measures to get the company back on track financially.

CRM can be applied to any industry; however, in this paper, we have chosen the Australian mining sector to illustrate the application of CRM. According to the Australian Securities and Investments Commission, 2960 businesses became insolvent in the September quarter in 2015. This equates to almost 1000 bankrupt businesses per month (ASIC 2015). Such a high statistic is troubling for the Australian economy in general. This paper will proceed to explain the importance of the mining sector in Australia.

The Australian mining sector enjoyed a boom after 2007 which helped cushion the economy from the 2008 Global Financial Crisis (GFC) (Shah 2014). During 2007–2012, the mining sector set the highest employment growth nationwide, increasing by a record-breaking 94.3% to reach almost 270,000 workers, a record high according to the Australian Bureau of Statistics (Shah 2014). During the mining boom, mining investment accounted for approximately 67% of economic growth in Australia between 2011 and 2012, when it made up about 8% of the Gross Domestic Product (GDP). Compared to 4.25% presently, this is forecasted to fall to 1.25%, returning to a pre-boom historical low (Letts 2016). According to the National Australia Bank (NAB), the mining boom has come to an end; falling commodity prices, coupled with a 70% fall in forecasted investment from the current level over the next three years in the mining industry will result in a loss of 50,000 more jobs (Letts 2016). Figure 1 shows the Australian mining sector’s investment and employment rates for the time-period 2002−2016. As is evident from the graph, both the employment and investment in the mining sector spiked during the boom period but are now starting to plummet. This creates an atmosphere of uncertainty and ambiguity. This paper aims to tackle this issue by mitigating the adverse effects of credit risk through CRM.

2. Literature Review

Numerous statistical models have been developed over the years that deal with CRM. They vary in the method used to achieve their result. However, their core aim is the same, that is, to get as accurate models as possible. Refer to

Table 1. Percentage comparison of different credit risk modelling (CRM) methods used in the literature.

Method	Percentage in Literature
MDA	27.45%
LR	25.49%
DT	7.84%
RF	5.88%
SGB	5.88%

for a percentage comparison of various CRM models used in prior studies. The results were calculated by reviewing in excess of 100 papers from the field of CRM and manually classifying them as per the model(s) used in each paper.

Fitzpatrick (FitzPatrick 1932) pioneered the modelling of credit risk for financial businesses in 1932, followed by (Winakor and Smith 1935). Their researches were furthered by (Beaver 1966) through establishing the first modern statistical model—the Univariate Model, which used financial ratios individually for CRM. He used 30 financial ratios that were commonly used and performed well in the literature. He tested his model on 158 businesses, half of which were successful and the other half were failed. His model’s error was approximately 22% for Type I Error and 5% for Type II Error. In the literature, Type I Error refers to misclassifying a risky business as not risky, whereas Type II Error refers to misclassifying a not risky business as a risky one (Gepp and Kumar 2012). However, this was not time-constant, that is, the margin of error increased as the length of prediction increased, which was problematic for long-term predictions. Another issue faced by Beaver’s model was that various ratios resulted in conflicting predictions in some circumstances, and therefore ceased to be a feasible model (Gepp and Kumar 2012).

After Beaver’s univariate analysis, Altman founded the first multivariate approach pertaining to CRM—Discriminant Analysis (Altman 1968). His model was designed to address the main issue faced by Beaver’s model, specifically various ratios that resulted in conflicting predictions. Altman devised a single weighted score (Z) for each business based on five ratios, namely: Working capital divided by total assets, retained earnings divided by total assets, earnings before interest and tax divided by total assets, market value of equity divided by book value of total debt, and sales over total assets, which was calculated in the following equation:

$$Z={\alpha }_1{x}_1+{\alpha }_2{x}_2+{\alpha }_3{x}_3+{\alpha }_4{x}_4+{\alpha }_5{x}_5+c$$

○

Z = Discriminant Score of Company;

○

$\alpha$_i & c = Estimated Parameters;

○

x_i = Independent Variables (the five ratios previously mentioned).

Altman 1968 used financial ratios as the independent variables because cash flow ratios were found to be insignificant, which contrasted Beaver’s Univariate Model. Based on the results, cut-off scores were then generated to classify the business. A Z-Score of less than 1.8, predicts a failed business; more than 2.7 predicts a successful business; and between 1.8 and 2.7 results in an inconclusive prediction. Altman’s Multivariate Discriminant Analysis (MDA) model outperformed that of Beaver’s. The chief benefit of the MDA model for predicting credit risk is its ability to alleviate a multidimensionality problem to a sole score with high accuracy level. However, the time correlation issues persisted, that is, it was better for short-term predictions (Gepp and Kumar 2012). The short-term accuracy of the model was 95%, however, this drops down to 72% when it is for two or more years prior to bankruptcy (Altman 1968). MDA has been used in innumerable CRM studies, for example: (Chung et al. 2008; Lee and Choi 2013; Mensah 1984; Altman et al. 2014; Perez 2006).

Logit Regression (LR) devises a score for each company analogous with MDA, but unlike MDA, there are no assumptions of normality and equal covariance (Kumar and Tan 2005). Ohlson (1980) pioneered applying LR to CRM. He devised a study that looks into the probabilistic prediction of businesses’ financial risk using LR. Comparable to Altman’s Z-score, Ohlson’s O-score can be regarded as a financial risk pointer fashioned from a predefined set of variables. Ohlson used 14 independent variables, comprising financial ratios and balance sheet dummy variables. LR has been used in numerous papers that deal with CRM, for example: (Chen 2011; Daniel and Ionut 2013; Hua et al. 2007; Laitinen and Laitinen 2001). LR’s main advantage over MDA is that it is not as affected when elementary statistical assumptions are infringed, like the multivariate normality of the variables. However, as in the case of MDA, its predictive power remains better for short-term predictions (Altman 1993). LR computes log-odds, where $\log \left(\frac{P}{2-P}\right)={\alpha }_1{x}_1+{\alpha }_2{x}_2+\dots {\alpha }_5{x}_5+c$. This results in a model that can be easily interpreted in terms of the changing odds of financial credit risk, as will be demonstrated later in the paper.

Recursive partitioning models are often a superior substitute to parametric regression models (Zhang and Singer 2010). Recursive partitioning refers to a group of statistical models for multivariate analysis. They are nonparametric models that are designed to eliminate the distribution assumptions related to parametric models, like LR and MDA (Breiman 1984). These models are more versatile and have a wider scope than traditional models since they can handle nominal variables, outliers, nonlinear variables, interactions, missing values, and qualitative variables. However, recursive partitioning does not provide precise probabilities of group membership, that is, credit risk—except for a whole node (group of businesses), nor is there a formal test for assessing the statistical significance of variables (Altman 1993). Examples of recursive partitioning models include: Decision Trees (DT), Stochastic Gradient Boosting (SGB), and Random Forests (RF). Due to their recent invention—relative to parametric models—they are naturally less occurrent in the literature, however, they are slowly gaining traction due to their superior predictive capabilities (Gepp 2015).

DTs assign input objects to a group from a pre-established set of classification groups. When applied to CRM, DTs assign companies to either the risky or not risky group. Therefore, the tree is generated in a recursive process that splits the data from a higher level to a lower level of the tree, ending with leaf nodes that characterise classification groups (risky or not risky). The splitting at each node is determined by comparing an expression that is assessed for each company with a cut-off point. There are two main tasks for the algorithms that generate DTs. First, to choose the optimal splitting rule at each non-leaf node to differentiate between risky and not risky companies, and secondly, to determine the number of nodes in the DT (Gepp and Kumar 2012).

DTs are beneficial for many reasons, including invariance to monotonic alterations of input variables, handling outliers in the data effectively as well as mixed variables, and being able to deal with a data set that contains missing data. There are different algorithms that can be used to generate DTs. These algorithms all create similar tree structures, but selecting the correct algorithm for a particular circumstance can have a huge impact on the predictive power of the generated model. Popular implementations of decision trees include Classification and Regression Trees (CART) and See5 (Gepp et al. 2010). In a 2005 study, a pioneering study compared the accuracy of CART and See5 pertaining to CRM. The results showed CART to be empirically superior to See5 (Huarng et al. 2005). This claim was further solidified by another study in 2010 (Gepp et al. 2010). DTs have not been used extensively in the literature, relative to parametric models. Some of the other studies that apply DTs to CRM include: (Chen 2011; Gepp et al. 2010; Hung and Chen 2009). In the CRM literature, DTs generally acquire a more accurate predicting power compared to parametric models (Chen 2011; Gepp et al. 2010; Huarng et al. 2005; Geng et al. 2015; Sun and Li 2008).

Random Forests (RF) are an ensemble learning method for classification and regression that generate numerous decision trees. In classification, the output is the mode of the classifications of the individual trees. In regression, the output is the mean from every individual tree. As part of their intrinsic nature, RF models bring about a dissimilarity measure amongst the observations. One can also define an RF dissimilarity measure between unlabelled data. The idea is to build an RF predictor that distinguishes the observed data from suitably created synthetic data (Chandra et al. 2009). RF has similar advantages to single trees but is also shown to be more accurate in many cases, because of multiple models being used. RF is also easily capable of handling many variables due to its inherent variable selection (Chandra et al. 2009). Relative to studies that use parametric models, there are only a few studies that apply RF to CRM. Some of these papers are: (Chandra et al. 2009; Fantazzini and Figini 2009; Nanni and Lumini 2009).

Stochastic Gradient Boosting (SGB) is a dynamic and adaptable data mining tool that creates numerous small decision trees in an incremental error–correcting process. SGB’s versatility enables it to deal with data contaminated with erroneous target labels. Such data are usually extremely problematic for conventional boosting and are a challenge to handle using conventional data-mining tools; au contraire, SGB is less affected by such errors (Mukkamala et al. 2006). As with RF, only a few studies applied SGB to CRM. These papers empirically showcase the superior predictive power of SGB over other parametric and nonparametric models—some of these papers are: (Mukkamala et al. 2006; Kumar and Ravi 2007; Ravi et al. 2007).

3. Data

Archival data was extracted from the MorningStar database pertaining to the Australian mining companies used in the research. Archival data is readily-available and therefore easily reproducible, and provides a quick way to extract financial data that would otherwise be onerous to collect and collate (Shultz et al. 2005). The MorningStar database contains raw data of approximately half-a-million investment offerings, in addition to real-time international market data on millions of commodities, foreign exchange, indices, and numerous others (MorningStar 2015). The MorningStar database has been used widely in the literature across many disciplines (Halteh 2015; Shah 2014; Smith 2011).

This research used all available data from the database for listed and delisted mining companies. The company status variable in MorningStar was used to determine the listed or delisted status. According to the Australian Securities Exchange (ASX), the source of much of the data from MorningStar, an Australian company is ‘listed’ if it is currently operational, whereas a company is ‘delisted’ for a number of reasons, including insolvency, merger, or take-over. All of these collectively imply an element of credit risk leading to the delisting of the company (MorningStar 2016). This study will refer to listed companies as not risky, and delisted companies as risky.

Financial data was collected for both not risky and risky Australian mining companies for the years 2011–2015. Twenty-nine explanatory variables were chosen for the study—refer to

Table 2. Complete list of variables—variables highlighted in red were later omitted due to missing values.

Variable	Description
Net Profit Margin	Net Profit/Revenue
EBIT Margin	Earnings Before Interest and Tax/Net Revenue
Return on Equity (ROE)	Net Profit After Tax/(Shareholders Equity − Outside Equity Interests)
Return on Assets (ROA)	Earnings before interest/(Total Assets Less Outside Equity Interests)
Return on Invested Capital (ROIC)	Net Operating Profit Less Adjusted Tax/Operating Invested Capital
NOPLAT Margin	Net Operating Profit Less Adjusted Tax/Revenue
Inventory Turnover	Net Sales/Inventory
Asset Turnover	Operating Revenue/Total Assets
PPE Turnover	Revenue/(Property, Plant & Equipment − Accumulated Depreciation)
Depreciation/PP&E	Depreciation/Gross PPE
Depreciation/Revenue	Depreciation/Revenue
Working Cap/Revenue	Working Capital/Revenue
Working Cap Turnover	Operating Revenue/Operating Working Capital
Gross Gearing (D/E)	(Short-Term Debt + Long-Term Debt)/Shareholders Equity
Financial Leverage	Total Debt/Total Equity
Current Ratio	Current Assets/Current Liabilities
Quick Ratio	(Current Assets − Current Inventory)/Current Liabilities
Gross Debt/CF	(Short-Term Debt + Long-Term Debt)/Gross Cash Flow
Cash per Share ($)	Cash Flow/Shares Outstanding
Invested Capital Turnover	Operating Revenue/Operating Invested Capital Before Goodwill
Net Gearing	(Short-Term Debt + Long-Term Debt − Cash)/Shareholders Equity
NTA per Share ($)	Net Tangible Assets (NTA)/Number of Shares on Issue
BV per Share ($)	(Total Shareholder Equity − Preferred Equity)/Total Outstanding Shares
Receivables/Op. Rev.	Debtors/Operating Revenue
Inventory/Trading Rev.	Inventory/Trading Revenue
Creditors/Op. Rev.	Creditors/Operating Revenue
Sales per Share ($)	Total Revenue/Weighted Average of Shares Outstanding
EV/EBITDA	Enterprise Value/Earnings Before Interest, Tax, Depreciation & Amortisation
PER	Price/Earnings Ratio = {(Market Value of Share)/(Earnings per Share)}

Note: Cells with red background indicate that they were the omitted variables in the model.

for a complete list of the variables used. The variables were chosen based upon several factors, including standard accounting and financial variables, use in prior empirical research and literature, endorsement by theorists, and as per availability of data.

4. Methodology

The data collected for the companies within the Australian mining sector were extracted from the official portal of MorningStar by selecting ‘listed’ and ‘delisted’ companies from the ‘Search Scope’ list. Time-series data was then chosen for the years 2011–2015. Following that, the Australian mining sector was selected from the ‘Global Industry Classification Standard’ (GICS) field. The results yielded 632 listed companies and 118 delisted companies. The data were then downloaded to a spreadsheet for cleaning. The initial count was 590 rows (118 companies multiplied by 5 years) for delisted companies and 3160 rows (632 companies multiplied by 5 years) for listed companies, a total of 3750 rows incorporating data for 29 explanatory variables. After examining the data, some company rows needed to be deleted due to insufficient data. Company rows that had 50% or more missing data were deleted, along with omitting 10 variables due to 50% or more missing data. The final sample contained 19 variables with 3375 rows; 339 rows for delisted companies and 3036 for listed companies. All 29 variables are shown in Table 2, with the ones omitted highlighted in red.

Following this, a dichotomous binary variable was used to refer to the status of each company—coded ‘1’ if the company is listed (not risky) and ‘0’ if the company is delisted (risky). The data was then partitioned by randomly selecting 80% not risky and 80% risky companies for a training set used to develop statistical models, with the remaining 20% of the not risky and risky companies being used for testing and evaluating models. Having a separate data set is necessary to obtain representative estimates of real-world performance for fair comparisons between models. This process and the resulting data sets are summarised in

Table 3. Data overview.

Sample Partition	Number of Rows	Percentage	Not Risky Companies	Risky Companies	Class Imbalance %
Train	2700	80.00%	2419	281	89.59% Not Risky − 10.41% Risky
Test	675	20.00%	617	58	91.41% Not Risky − 8.59% Risky
Total	3375	100.00%	3036	339	89.96% − 10.04% Risky

.

As is evident in Table 3, we have class-imbalance in our data set, meaning that there are a lot more not risky companies than risky. When splitting the data for the training and testing sets, the class imbalance percentage has been kept very similar to enable a representative test sample for model evaluation.

The class-imbalance is particularly problematic when the difference is extreme, as the models will tend to automatically overlook the minority class and predict everything as the majority class. In this case, the overall results will appear good overall, but they will be unusable as all predictions are the same.

The model building methods that are used in the study are logistic regression (as a well-established benchmark), decision trees, random forests, and stochastic gradient boosting. We hypothesize that the results of the state-of-the-art recursive partitioning models will outperform the parametric logistic regression model. This would provide confirmatory evidence from a larger data set of similar results in the limited existing literature.

4.1. Logistic Regression (LR)

The logistic regression model was estimated using only the train dataset with all 19 variables used as covariates to explain the status (not risky or risky). SPSS statistical software was used to develop the model, but as the model is deterministic, the same results would be obtained using other software packages

4.2. Decision Trees (DT)

Classification and Regression Trees (CART) using Salford Predictive Modeller (SPM) have been used to generate the CRM tree. All 19 variables were selected as predictors in the model. The Gini splitting rule was used because of its popularity and widespread use. The minimum data points in a non-leaf node was set to 10 to avoid the tree becoming too large. This setting assists in avoiding over-fitting, that is, looking for patterns in very small subsamples that are likely not to generalise.

4.3. Random Forests (RF)

SPM has again been used and all 19 variables were used as predictors. There are two main parameters to set for a RF model: The number of trees to be generated, and the number of variables to be considered at each node. A model was developed for each of 200, 500, and 1000 trees to empirically determine the best choice for this parameter. The number of variables considered at each node was set to the square root of the total number of predictors: $\sqrt{19}\approx 4.36\approx 4$. The square root heuristic was chosen as it has been recommended by and used in prior literature (Bhattacharyya et al. 2011; Whiting et al. 2012).

4.4. Stochastic Gradient Boosting (SGB)

Once again, SPM has been used and all 19 variables were used as predictors. Models were developed based on 200, 500, and 1000 trees, to empirically determine the best choice for this parameter. As mentioned in the literature review, SGB relies on incremental improvements and therefore, it is important that no individual tree is too complex (large). Consequently, individual trees are kept small by setting the maximum nodes per tree to 6 (a standard setting) with a minimum number of data points of 10 in each node. The criterion to determine the optimal number of trees, that is, how much incremental improvement to perform, was chosen based on the default of cross entropy.

4.5. Cut-Off Values for Classification

All four models can estimate the probability of being not risky (1). Often, a default value of 0.5 is used such that if a company has a value greater than 0.5 it will be classified as not risky, else as risky. However, this is commonly unsuitable when there is a substantial class imbalance, as will be demonstrated, in this case, in the Results section. Consequently, the cut-off values will be empirically optimised using the training sample—this approach has been used successfully in the literature (Beneish 1997; Bayley and Taylor 2007; Perols 2011). Because this optimisation will be completed for each model, it is possible that the cut-off values will vary between the models. The cut-off value must be between zero and one, as they are the limits of any probability figure. The optimised cut-off value is chosen as the value that produces the most balanced accuracy on the train sample. The most balanced is defined by minimising the difference between prediction accuracy for not risky companies and prediction accuracy for risky companies. It is important to highlight that the cut-off values were optimised exclusively on the train sample, so that model evaluation on the test sample still represents performance on data that is completely new to the model.

5. Results

The following subsections explore and analyse, in detail, the results achieved and performances of the various models used in the study. Specificity represents the accuracy at classifying not risky companies, while sensitivity represents the accuracy at classifying risky companies.

5.1. LR Model

As shown in

Table 4. Logistic regression classification table for default 0.5 cut-off value.

Classification Table
Observed			Predicted
			Training			Testing
			Status		Percentage Correct	Status		Percentage Correct
			Risky	Not Risky		Risky	Not Risky
Step 1	Status	Risky (0)	2	279	0.7	0	58	0.0
		Not Risky (1)	2	2417	99.9	2	615	99.7
	Overall Percentage				89.6			91.1

, the default logistic regression model yielded an average accuracy of 91.41% on the test sample. However, as mentioned in the Methodology section above, this model is not practically useful because of class-imbalance. When using the default 0.5 cut-off value, the model predicts almost all the companies as not risky (1), which results in a mirage of high predictive accuracy. Even though their overall accuracy is high, the model is useless because it cannot successfully predict risky companies: 0.7% on the training data and 0% on the testing data.

To remedy this class-imbalance problem, we empirically optimise the cut-off values in the training sample to give the most accurate balanced rates, as explained in the Methodology section. Results for both the training and testing samples are shown in

Table 5. (a) Optimised LR-train sample; (b) optimised LR-test sample; (c) LR model accuracy (test sample) with optimised cut-off values.

(a)				(b)
Train Sample				Test Sample
Class	Cases	Misclassified	% Error	Class	Cases	Misclassified		% Error
Risky (0)	281	111	39.50%	Risky (0)	58	16		27.59%
Not Risky (1)	2419	1422	58.78%	Not Risky (1)	617	364		59.00%
(c)
Accuracy at Predicting Not Risky Companies (Specificity)							41.00%
Accuracy at Predicting Risky Companies (Sensitivity)							72.41%
Simple Average							56.71%

a,b. As shown in Table 5c, the overall model’s accuracy dropped to an average of 56.71%. However, the accuracy is now more balanced between risky (0) and not risky (1) companies. Therefore, this model is of more practical use and its assessment is more indicative of a logistic regression model. As for the variable importance, ‘PER’, ‘sales per share’, and ‘gross debt/CF’ were found to be the most statistically significant variables, all having p-values less than 10%.

5.2. Decision Tree Model

The empirical optimisation of the cut-off value on the training sample resulted in a cut-off value of 0.9. As shown in

Table 6. (a) DT-train sample; (b) DT-test sample; (c) DT model accuracy (test sample).

(a)				(b)
Train Sample				Test Sample
Class	Cases	Misclassified	% Error	Class	Cases	Misclassified	% Error
0	281	66	23.49%	0	58	14	24.14%
1	2419	788	32.58%	1	617	200	32.41%
(c)
Accuracy at Predicting Not Risky Companies (Specificity)							67.59%
Accuracy at Predicting Risky Companies (Sensitivity)							75.86%
Simple Average							71.72%

c, the decision tree yielded an average accuracy of 71.72% on the test sample. This is already a better outcome vis-à-vis LR, both for the specificity and sensitivity measures. This is consistent with existing literature that recursive partitioning models outperform traditional models. More detailed results for the train and test samples are shown in Table 6a,b, respectively. As for the variable importance, ‘invested capital turnover’, ‘BV per share’, and ‘NTA per share’ were found to be the most important variables for predicting credit risk in this model.

5.3. Random Forests Model

Experimentation was conducted on generating 200, 500, and 1000 trees. Using 1000 trees yielded the most accurate results, which have been reported. The empirical optimisation of the cut-off value on the training sample resulted in a value of 0.47, which was close to the default 0.5 that was chosen.

Results for both the training and testing samples are shown in

Table 7. (a) RF-train sample; (b) RF-test sample; (c) RF model accuracy (test sample).

(a)				(b)
Train Sample				Test Sample
Class	Cases	Misclassified	% Error	Class	Cases	Misclassified	% Error
0	281	81	28.83%	0	58	13	22.41%
1	2419	806	33.32%	1	617	204	33.06%
(c)
Accuracy at Predicting Not Risky Companies (Specificity)							66.94%
Accuracy at Predicting Risky Companies (Sensitivity)							77.59%
Simple Average							72.26%

a,b. As shown in Table 7c, the RF model yielded an average accuracy of 72.26% on the test data. However, compared to a single decision tree, this model is better at predicting risky companies, but slightly worse at predicting not risky companies. As for variable importance, ‘invested capital turnover, ‘BV per share’, and ‘NTA per share’ were found to be the most important variables for predicting credit risk in this model.

5.4. Stochastic Gradient Boosting Model

The empirical optimisation of the cut-off value on the training sample resulted in a value of 0.91, which was close to the 0.9 mark, hence 0.9 was chosen. Experimentation was conducted across 200, 500, and 1000 trees. The model with 1000 trees yielded the most accurate results.

Both the training and testing samples results are shown in

Table 8. (a) SGB-train sample; (b) SGB-test sample; (c) SGB model accuracy (test sample).

(a)				(b)
Train Sample				Test Sample
Class	Cases	Misclassified	% Error	Class	Cases	Misclassified	% Error
0	281	49	17.44%	0	58	15	25.86%
1	2419	596	24.64%	1	617	165	26.74%
(c)
Accuracy at Predicting Not Risky Companies (Specificity)							73.26%
Accuracy at Predicting Risky Companies (Sensitivity)							74.14%
Simple Average							73.70%

a,b. As shown in Table 8c, stochastic gradient boosting yielded an average accuracy of 73.70% on the test data. On average, and as per the specificity score, this model outperforms all other models in the study. However, DT and RF yielded slightly better sensitivity accuracy. As for the variable importance, ‘Property, Plant, & Equipment (PPE) turnover’, ‘invested capital turnover’, and ‘PER’ were found to be the most important variables for predicting credit risk in this model. ‘Invested capital turnover’ is of utmost importance when trying to work out the riskiness, because it constantly appeared in all three non-parametric recursive partitioning models.

Table 9. Model comparison table using test data.

Model	Overall Model Accuracy	Most Important Variables	AUC %
Logistic Regression	Specificity: 41.00% Sensitivity: 72.41% Average: 56.71%	PER, Sales per Share, Gross Debt/CF	59.00%
Decision Tree	Specificity: 67.59% Sensitivity: 75.86% Average: 71.72%	Invested Capital Turnover, BV per Share, NTA per Share	74.00%
Random Forest	Specificity: 66.94% Sensitivity: 77.59% Average: 72.26%	Invested Capital Turnover, BV per Share, NTA per Share	78.99%
Stochastic Gradient Boosting	Specificity: 73.26% Sensitivity: 74.14% Average: 73.70%	PPE Turnover, Invested Capital Turnover, PER	88.98%

summarises the performance of all four models. The rightmost column of the table represents the Area under the Receiver Operating Characteristic Curve (AUC)—a measure that is widely used in the literature. The AUC measure was added in order to solidify our findings as to which model has the highest predictive accuracy. The closer the percentage is to 100%, the more accurate the model is in classifying the risky and not risky companies. The presented percentages represent the AUC for the test samples. As can be seen, the Stochastic Gradient Boosting (SGB) model outperforms all others as per the “Overall Model Accuracy averages criterion” and the “AUC” measures.

6. Conclusions

To conclude, this paper has showcased a real-world problem that needs to be addressed, that is, a high number of business failures in Australia in general, and an impending financial risk of mining companies, in particular. Credit Risk Modelling (CRM) can be utilized to forecast impending risks to enable the decision makers to take the preventive measures to hold-off such risks or mitigate their effect. Recursive partitioning models were employed to test for the most accurate model at predicting credit risk. These models are not exclusive to the mining industry; they can be used in any industry worldwide. Our results indicated that ‘Invested Capital Turnover’ was the variable most occurring amongst the recursive partitioning models. In terms of the best model overall, Stochastic Gradient Boosting (SGB) yielded the most accurate results in predicting credit risk in the Australian mining industry, as per the AUC and averages of the sensitivity and specificity criteria. However, the random forests model yielded the best results at predicting the risky companies (sensitivity). All in all, our analysis has shown that tree-based models are more accurate, versatile and have a wider scope than traditional models, such as logistic regression. The main takeaway from this study is that modern models, such as the recursive partitioning models, can offer substantial accuracy improvements and should be considered in future research and in practice, especially in conjunction with qualitative measures and managerial decision-making. The models analysed in this paper can be algorithmically automated to input new data as soon as they become available, for example through interim or annual reports, thus saving time to reconstruct the models manually and ensuring up-to-date models. It is imperative to address the class-imbalance problem; in this paper, we used ‘empirically optimised cut-off scores’. There are other approaches in the literature to handle class-imbalance that can change the overall data set, such as the Synthetic Minority Oversampling Technique (SMOTE), which could be investigated in future studies.