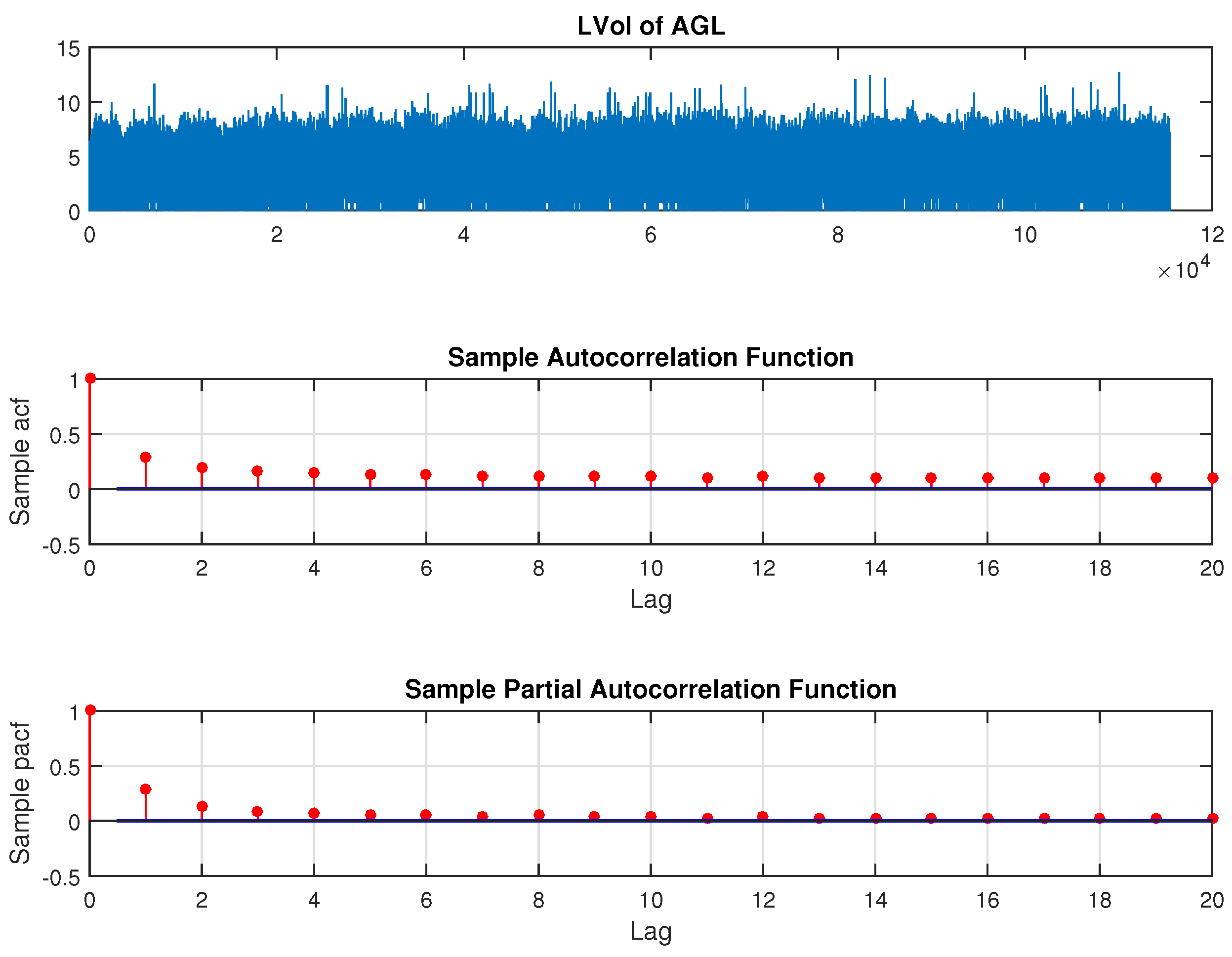
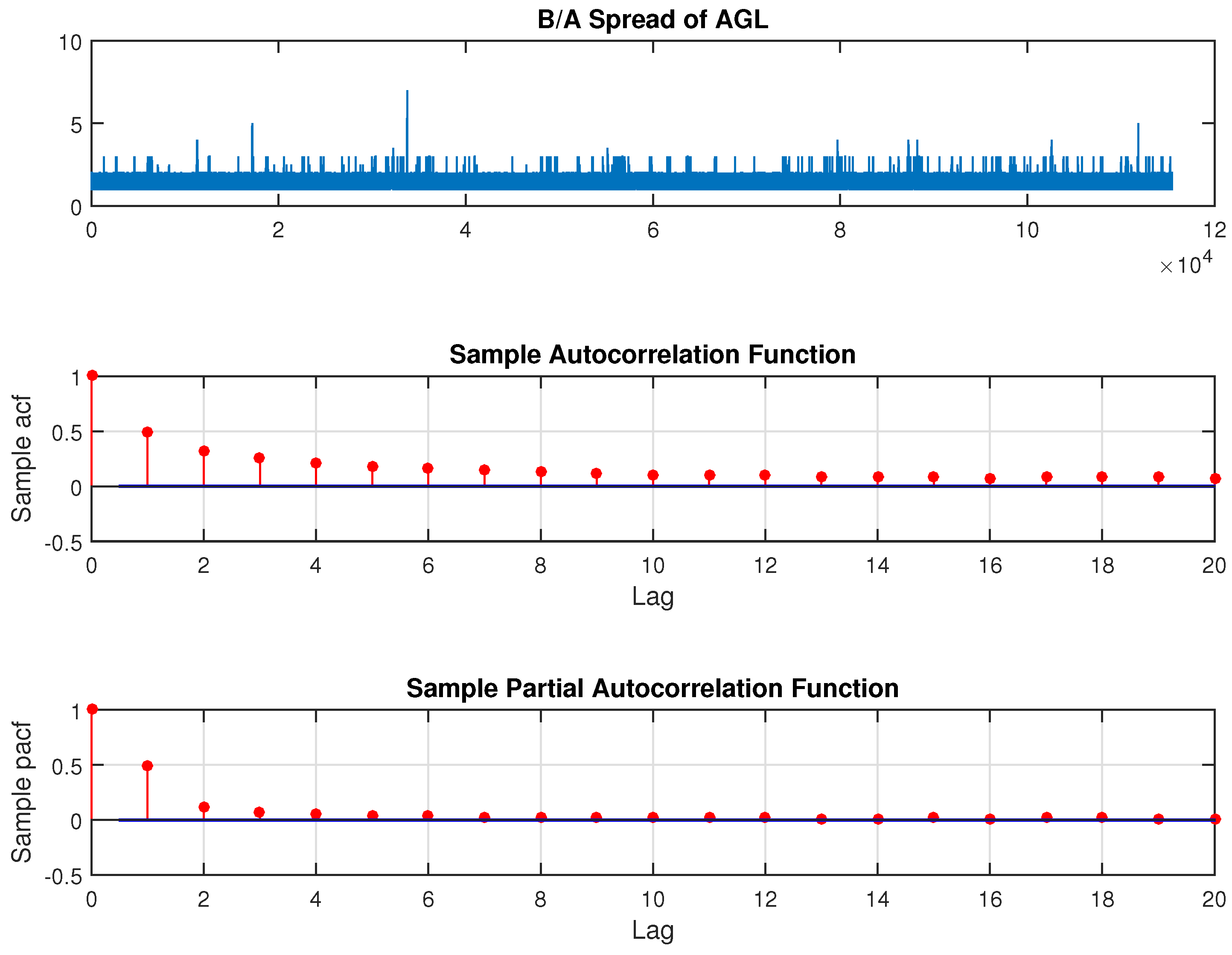
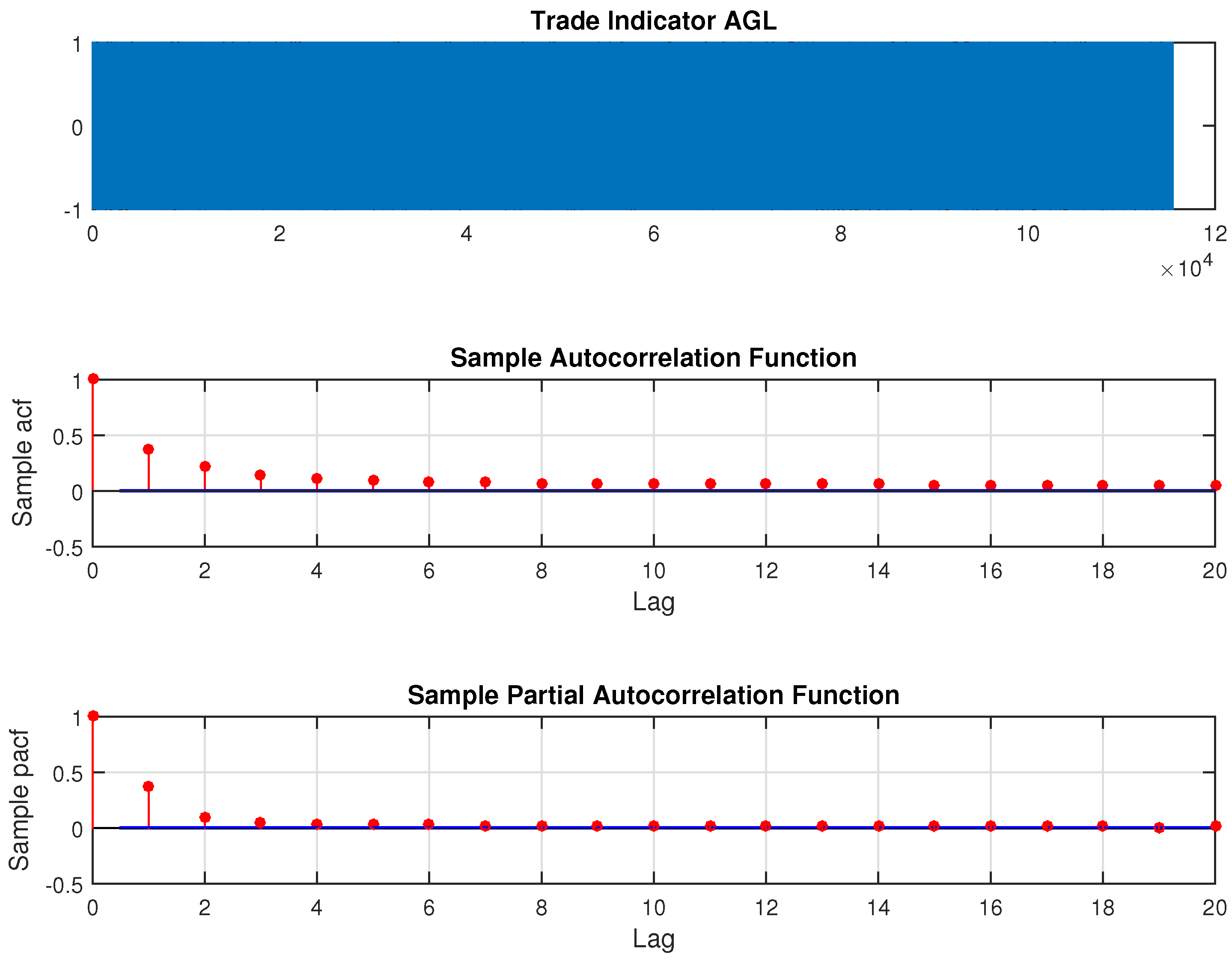
The model estimation for the direction of price change is carried out for these stocks for the period 16 January to 14 April 2014. Out of sample forecasts are generated for the last day of the sample, on 15 April 2014 from 10:30 a.m. to 15:30 p.m.
denotes the price changes between the
k and
th trades in terms of integer multiples of ticks. The price change here is representative of the change in the observed transaction prices. The number of states that could be assumed by the observed price changes
is set to 3, under the ordered probit framework. Price increases of at least 1 tick being grouped as +1, price decreases of at least 1 tick as −1, while price changes falling in (−1,1), taking the value 0. The choice of
m is based on achieving the balance between price resolution and minimising states with zero or very few observations. The decision to restrict
m to 3 was mainly influenced by the fact that the observed price changes exceeding
ticks was below
for most stocks. The distribution of observed price changes in terms of ticks, over the transactions, is presented in
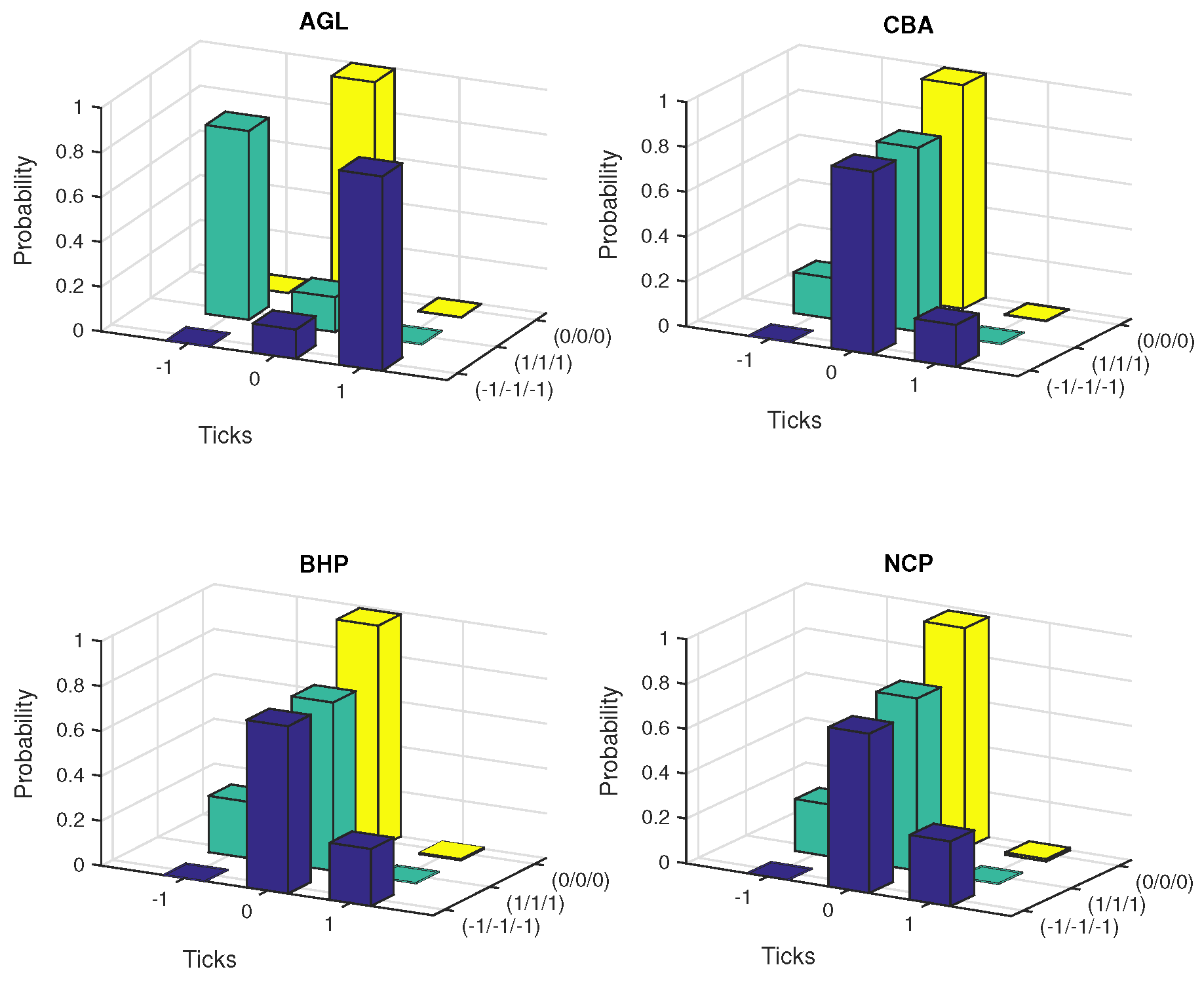
Figure 4. Prices tend to remain stable in more than 80 per cent of the transactions, in general. For the rest of the time, rises and falls are more or less equally likely.
4.1. Ordered Probit Model Estimation
Prior to model estimation, all variables considered in the analysis was tested for stationarity using an Augmented Dickey-Fuller (ADF) test, which confirmed the same, which is in agreement with previous findings. The Ordered probit model specification depends on the underlying distribution of the price series. The model can assume any suitable arbitrary multinomial distribution, by shifting the partition boundaries accordingly. However, the assumption of Gaussianity here has no major impact in deriving the state probabilities, though it is relatively easier to capture conditional heteroscedasticity.
The dependent variable in Equation (
11) below is the price change in ticks. (An explanation of the latent continuous version of the price change was given in
Section 2). The variables used in Equation (
11) were described in
Section 3. Just to recap, the first three variables on the R.H.S. of Equation (
11) are three lags of the dependent variable.
is the trade indicator; which classifies a trade as a buyer-initiated, seller-initiated or other type of trade.
is the Bid-Ask spread, measured in cents.
gives the natural logarithm of
th trade size.
and
denote the natural log of number of shares at best ask and bid prices respectively.
is the trade imbalance, based on the preceding 30 trades on the same day. Conditional duration,
and standardised transaction duration
are derived estimates by fitting an autoregressive conditional duration model (ACD (1,1)) to diurnally adjusted duration data. The ACD (1,1) model is described in the appendix.
, prevailing immediately prior to transaction
k, is calculated as the continuously compounded return on the ASX 200.
The mean equation under the ordered probit specification takes the following form:
The maximum likelihood estimates of the ordered probit model on price changes were computed based on BHHH algorithm of
Berndt et al. (
1974). The estimated coefficients of the above ordered probit system are presented in
Table 3 while the corresponding z statistics are recorded within parentheses. Most of the regressors are highly significant to the model for all seven stocks, based on the asymptotically normally distributed z statistic (
Hausman et al. 1972). The pseudo-
values given at the bottom of the table show an improvement, irrespective of the number of observations, in comparison to those of YP. A relatively higher number of significant coefficients across all stocks is another improvement.
The first three lags of the dependent variable comes under scrutiny, first. All the lags are significant with a 95% confidence level, with a negative coefficient for each stock. This inverse relationship with past price changes is consistent with the existing literature, indicating a reversal in the price compared to its past changes. Consider a one tick rise in price over the last three trades in the case of AGL, for example, keeping the other variables constant. The subsequent fall in the conditional mean () would be 3.9448, which is less than the lower threshold, resulting in −1 for . The coefficients of the traditional variables such as the bid ask spread (), trade volume (LVol) and the market index returns are significant for all stocks but one, in each case. The and has a positive impact on the price change across all stocks. The market index returns, based on the ASX200, as a measure of the overall economy, generally has a significant positive impact on price changes. Overall, this is in line with the conventional wisdom. Meanwhile, the coefficients of the trade indicator, the number of shares at the best bid price and the number of shares at the best ask price are significant for all stocks.
The trade imbalance () between buyers and sellers has a positive impact on price change and is statistically significant across all stocks. This phenomenon agrees well with the general inference that more buyer-initiated trades tend to exert pressure from the demand-side, resulting in a subsequent rise in price and vice versa. The impact of the time duration between trades is measured separately via the two constituent components of an ACD model. One is the conditional expected duration (signed), and the other isthe standardised innovations (signed), also referred to as unexpected durations, . The signed conditional expected duration is significant for all stocks while the unexpected component is significant for all but one. This highlights the informational impact of time between trades in price formation. The interpretation of these measures of duration is not straightforward as they are comprised of two components. The kind of impact those variables have on price change will depend on the significance of the trade initiation as well as on the durations. One striking feature is that either both the components have a positive impact or both have a negative impact for a given stock. Wald tests were performed to investigate the significance of duration on price changes. The tests were conducted under the null hypotheses in which either the coefficient of the conditional duration is zero or the coefficient of standardised duration is zero or both are jointly zero. The resultant F statistics suggest that both the components of duration are significant for all the stocks considered. The test results are not presented here for the sake of brevity.
The partition boundaries produced below the coefficient estimates determine the partition points of the direction of change in the latent variable. There are three possible directions the price change can take in terms of ticks, , and . By comparing these boundary values with the estimated continuous variable , values −1, 0 or +1 are assigned to the observed variable .
In parameterising the conditional variance, an ARMA specification was used following YP. Therefore, a GARCH (
) specification including up to two lags was used on the residual series of the ordered probit model across all stocks. The orders
were selected on the basis of Akaike information criterion (AIC). The selected parameter estimates of the fitted GARCH models are reported in
Table 4. Only some of the parameters appear to be significant with less persistence in conditional volatility for some stocks.
4.2. Price Impact of a Trade
Price impact measures the effect of a current trade of a given volume on the conditional distribution of the subsequent price movement. In order to derive this,
has to be conditioned on trade size and other relevant explanatory variables. The volumes, durations and the spread were kept at their median values while the index was fixed at 0.001 whereas trade indicator and trade imbalance were kept at zero to minimise any bias. It is observed that the coefficients of the three lags of
are not identical, implying path dependence of the conditional distribution of price changes (
Hausman et al. 1972). Consequently, the conditioning has to be based on a particular sequence of price changes as well, as a change in the order will affect the final result. These conditioning values of
’s specify the market conditions under which the price impact is to be evaluated.
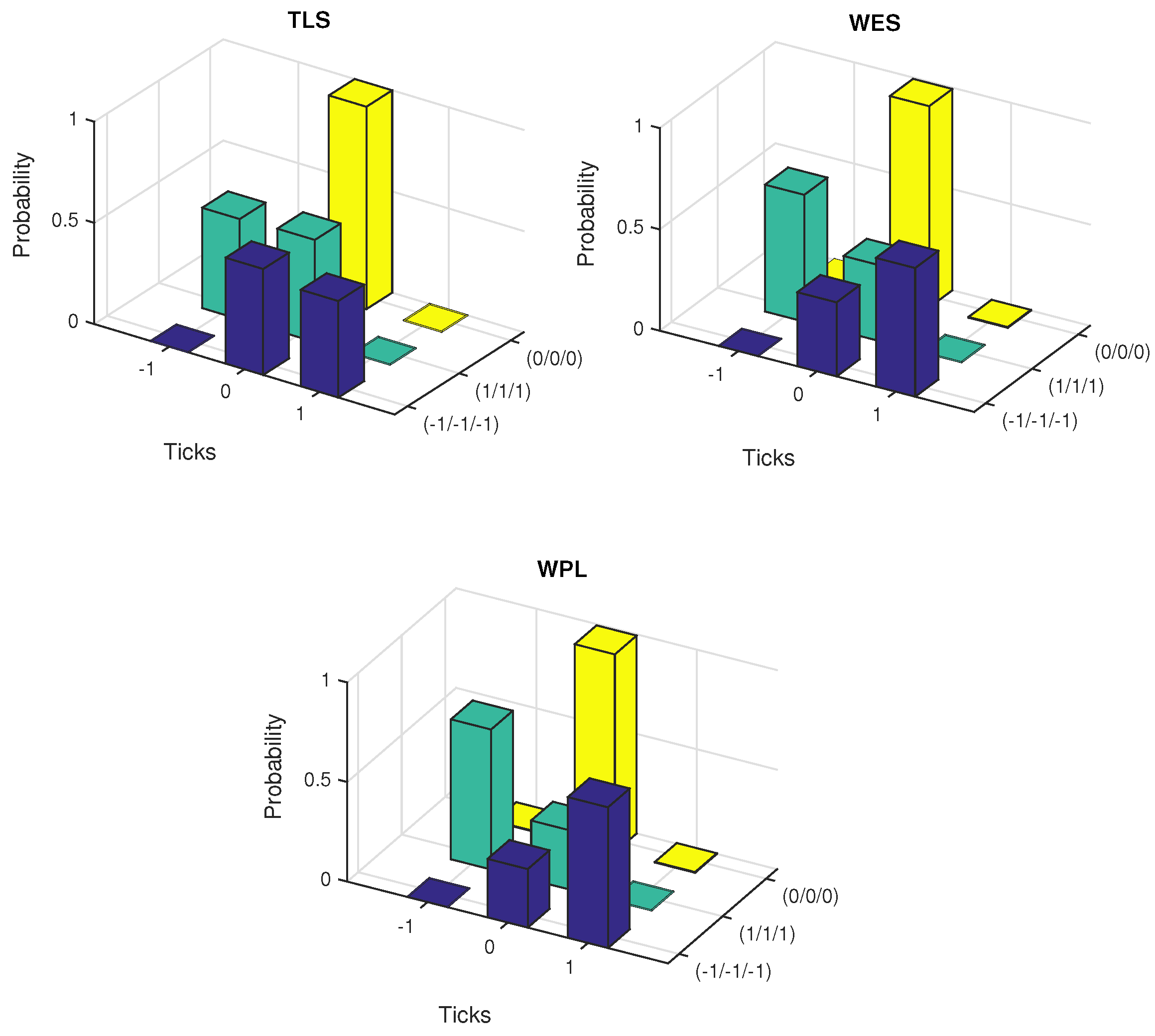
The conditional probabilities were estimated under five scenarios of path dependence keeping the other quantities at the specified values. These are falling prices (−1/−1/−1), rising prices (1/1/1), constant prices (0/0/0) and alternative price changes, (−1/+1/−1) and (+1/−1/+1).
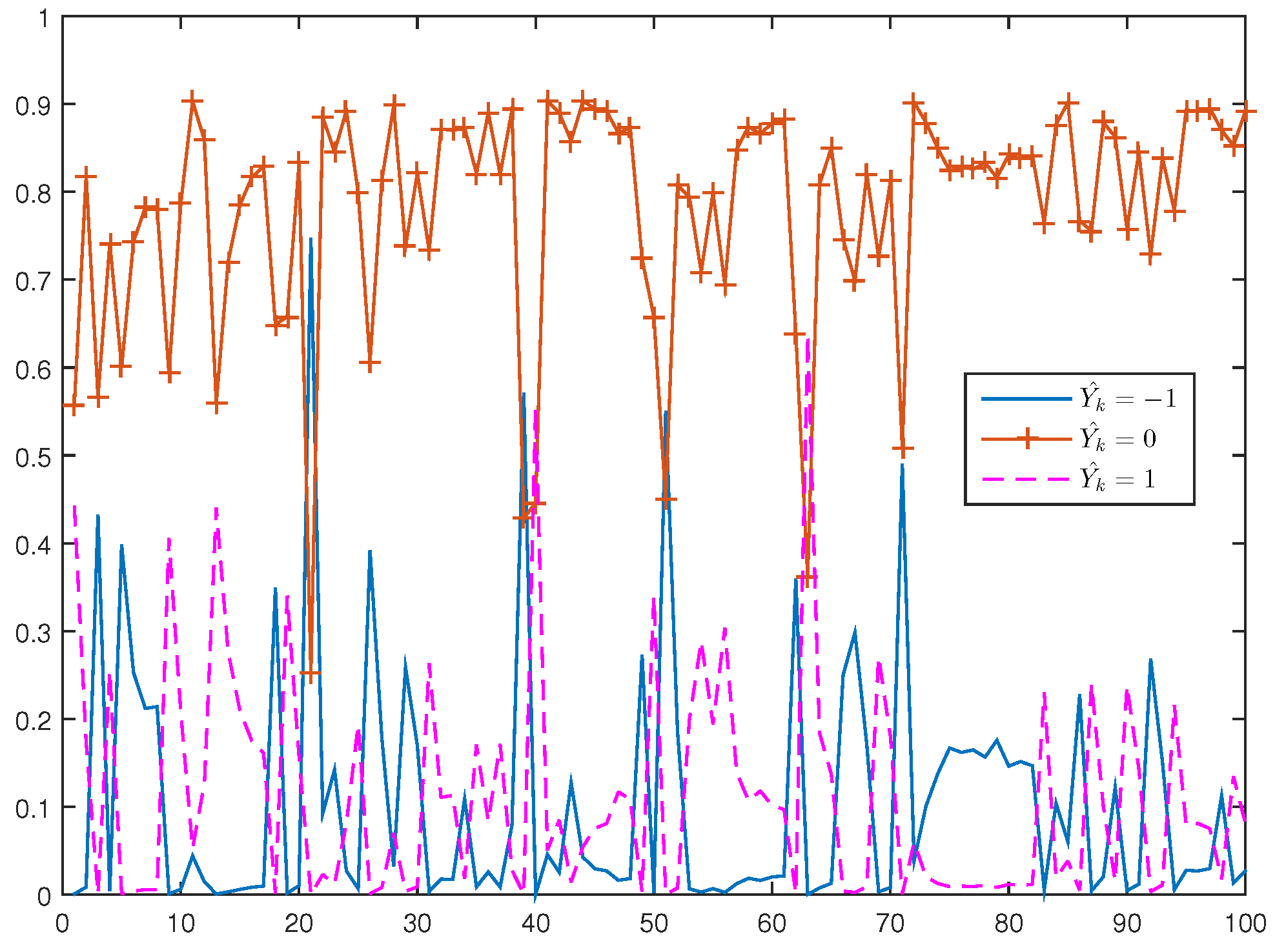
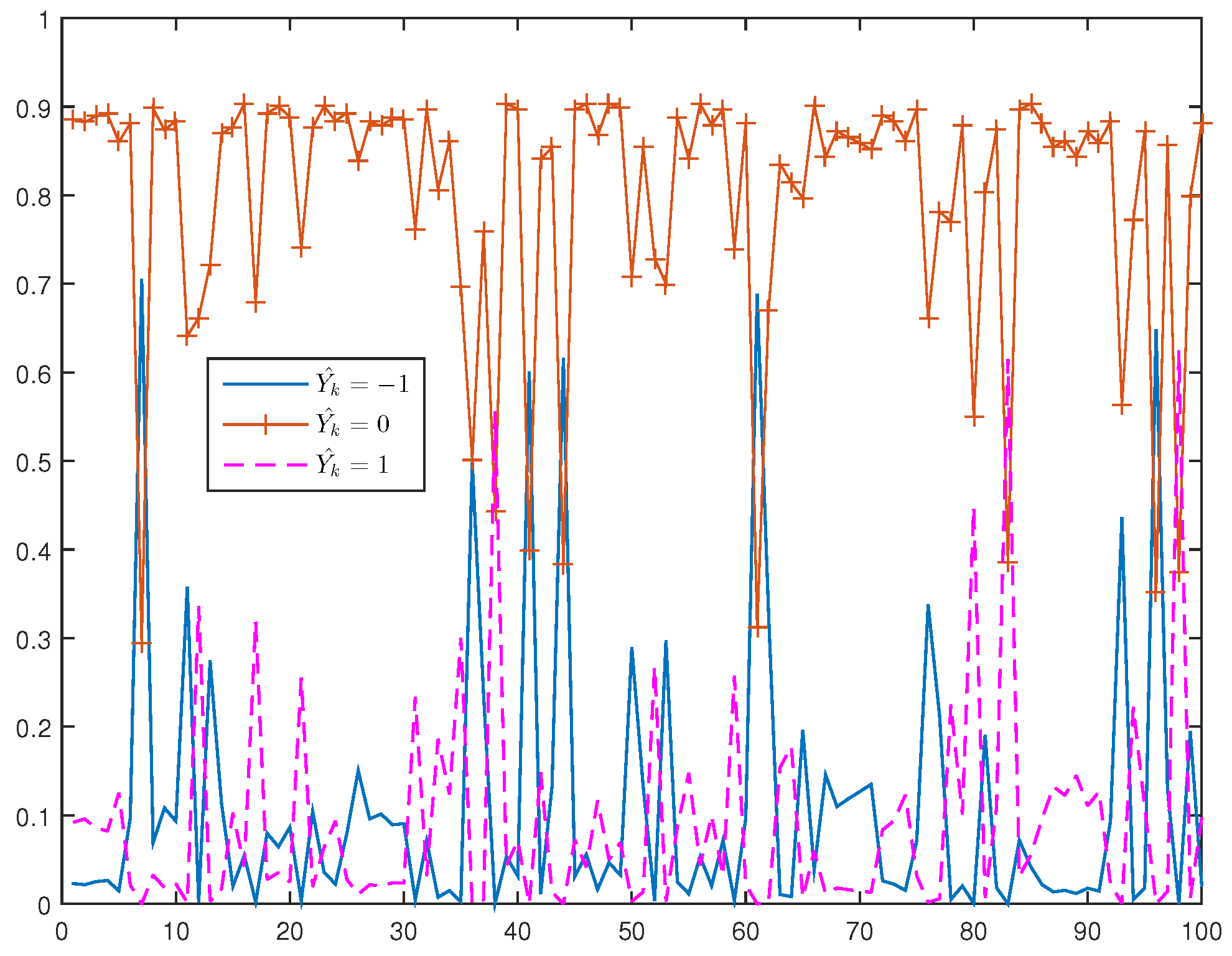
Figure 5 and
Figure 6 exhibit the plots of estimated probabilities under the first three scenarios for all the seven stocks. The shifts in the distribution are clearly evident for the first two cases as against the third case of constant prices. Under the falling price scenario, the shift is more towards the right while for the rising price scenario, it is more towards the left indicating an increased chance of price reversal after three consecutive rises or falls. In the case of alternating prices it was revealed that prices tend to remain stable in the subsequent trade.