1. Introduction
Solvency II is changing the way regulatory capital is assessed in European countries. Despite clear challenges, the new framework also offers insurers the possibility to improve business strategy and capital allocation. In this context, risk mitigation appears as a key driver.
For most companies, regulatory capital requirements have historically played a relatively small role in the decision to purchase a particular reinsurance contract. However, the main results of quantitative impact studies have showed that capital requirements under Solvency II are likely to increase substantially for most non-life insurers.
Although, at the moment, it is far from becoming the dominant factor in a reinsurance purchasing decision (see
Wills Re (
2017) for a survey on this point), the impact of the reinsurance in Solvency II capital assessment should be explored. The capital requirement being more risk-based than in the past, it will likely become, among others, an important factor in the selection of reinsurance contracts. In this regard, a growing influence of risk appetite is observed, helping insurance companies navigate reinsurance coverage options (
Wills Re (
2017)).
Under the standard formula (see
European Commission (
2015)), the capital relief for non-life underwriting risk is easily determined by multiplying by the ceded percentage for proportional reinsurance (as quota share). For non-proportional reinsurance, the capital saving effect is less immediately apparent, and it is mainly based on the evaluation of a non-proportional factor given by European Insurance and Occupational Pensions Authority (EIOPA). In particular, the standard formula defines the methodology for assessing the non-proportional factor, subject to specific limitations and criteria. This factor should quantify the mitigation of total losses’ variability given by excess of loss (XL) treaties.
This paper raises a number of key considerations and complexities in the recognition of reinsurance mitigation in the standard formula and partial internal models, including concerns surrounding the quantification of the capital reduction
1.
We show how the solution provided by Solvency II is not consistent with collective risk theory (see
Beard et al. (
1984),
Daykin et al. (
1994), and
Klugman et al. (
2008)) commonly used for premium risk evaluation. In this regard, as shown in
Daykin et al. (
1994),
Gisler (
2009), and
Savelli and Clemente (
2009), a systematic component usually affects the number of claims. We prove that both formulae provided by the Commission Delegated Regulation (or delegated acts—DA) (
European Commission (
2015)) and quantitative impact study 5 (QIS5) (
European Commission (
2010)) neglect this component, leading to an overestimation of the risk mitigating effect. This result is clearly relevant from the supervisor’s perspective. Additionally, the size of the insurers is not taken into account. As is well known, because of a different pooling risk between small and large insurers, the impact of XL reinsurance could be substantially different. Furthermore, the approach provided by the standard formula being based on a lognormal assumption (
Clark (
1996),
Coutts and Thomas (
1997a),
Coutts and Thomas (
1997b)), the shape of the distribution of net aggregate claims is proportional to the relative volatility. Focusing the XL treaty on the right tail of the claim-size distribution, it should be evaluated if the mitigation of skewness is greater than the reduction of volatility.
In order to overcome these pitfalls, we provide a fruitful solution to measure the effect of XL treaties on the variability coefficient of the aggregate claim amount. We show how the methodology is consistent with the Solvency II standard formula and how it could be a viable alternative to existing specific approaches. For the sake of brevity, we focus here only on XL treaties, but the approach can also be easily extended to other non-proportional strategies (as stop-loss).
In particular, in
Section 2, some preliminaries are given.
Section 3 and
Section 4 describe methods provided in QIS5 and DA respectively to evaluate non-proportional reinsurance. An alternative solution to this problem is given in
Section 5. Finally some numerical results are reported in
Section 6 in order to compare alternative approaches considering a multi-line non-life insurer. Furthermore, we show how main characteristics, such as the portfolio size, pooling risk, and portfolio mix can affect the results. Conclusions follow.
3. Non-Proportional Reinsurance in QIS5
The purpose of this section is to describe the main features of the QIS5 standard formula as they would apply to a property/casualty insurer. As this paper deals with non-proportional reinsurance, we focus on the premium and reserve risk sub-module. The capital charge is obtained as
where
measures the distance between the 99.5% quantile and the mean of the distribution of the r.v. derived as the ratio of total losses divided by the volume measure
V related to both premium and reserve risk for all the LoBs.
The function is set equal to , and it has been calibrated under the assumption of a lognormal distribution. V takes into account both the expected earned next-year premiums and the value of the best estimate of the claims reserve at the valuation date. Both amounts are considered the net of reinsurance.
represents instead the standard deviation of the r.v. previously defined in relation to the overall non-life portfolio. The overall is derived by obtaining the standard deviation of each risk and LoB i ( and ) and aggregating them through a two-step procedure. We have indeed an initial aggregation between the premium and reserve risk of a single LoB assuming a correlation coefficient of 0.5, and then the standard deviations of different LoBs are aggregated by using a fixed correlation matrix.
To this aim, following relation holds:
where
is the correlation matrix between different LoBs given by QIS5 (
European Commission (
2010)), and
with
n being the number of LoBs. For each LoB
i, we have
The standard deviations
and
may be derived by using alternatively a given market-wide estimate or an undertaking-specific approach based on fixed methodologies
3 applied to insurer’s data.
Only for premium risk can the market-wide estimates be reduced using a formula to reflect the extent the ceded reinsurance is non-proportional reinsurance.
is indeed equal to a fixed volatility factor (e.g., 10% for motor third-party liabilities (MTPL)) multiplied by a non-proportional factor
that allows for risk-mitigating effects of
per risk XL reinsurance. Undertakings may choose for each LoB to set the adjustment factor
to 1 or to calculate it as set out in the QIS5 technical specifications (TS) (
European Commission (
2010)).
If the XL treaty meets the requirement requested by TS
4,
may be derived as
where
and
are the mean and the standard deviation of the gross claim severity distribution
evaluated by using loss experience.
and
are instead the net (of reinsurance) values. The effect of the reinsurance retention (and limit) is evaluated by assuming a lognormal distribution of individual losses.
We note that Equation (
6) measures the net-to-gross ratio of variability coefficients of total losses. The same relation can be found by applying Equation (
2) under the assumption that the total losses are described by a pure compound Poisson process (i.e.,
and consequently
). We have that
disregards the effect of parameter uncertainty on the claim count and is instead a systematic component that cannot be reduced by XL reinsurance. We show in
Section 6 how this assumption can overestimate the effect of reinsurance treaties, leading to a significant capital relief.
Furthermore, if we restrict the analysis to premium risk of a single LoB, Equation (
3) can be rewritten as
where
and
are the net and gross coefficients of variation of the total losses under a pure compound Poisson process (as assumed in QIS5).
Other than neglecting parameter risk, it is noteworthy that Equation (
7) shows further implicit assumptions regarding reinsurance:
The standard deviation of the ratio of gross losses to gross premiums
is modified to take into account XL through the net-to-gross ratio of coefficients of variation:
. QIS5 implicitly assumes that expected losses decrease in the same proportion as the volume measure after reinsurance:
. In other words, Equation (
7) assumes that loading coefficients of the reinsurer are equal to loading coefficients of the cedent.
The size of insurers’ portfolio is not considered. Risk mitigation usually has a different effect because of a different weight of pooling and non-pooling risk (see, e.g.,
International Actuarial Association (
2004)).
Both the gross and net reinsurance distributions are assumed as lognormal. The skewness of this distribution being strictly related to the coefficient of variation
5, QIS5 assumes that skewness
reduces in a similar way to CV (
) for usual volatilities. The XL acting on the tail of the severity distribution, it should be evaluated if the mitigation of skewness is greater than the mitigation of volatility.
4. Non-Proportional Reinsurance in Commission Delegated Regulation
The evaluation of the premium and reserve sub-module was slightly modified by the Technical Specifications of the Long-Term Guarantee Assessment in 2013. Changes have been confirmed by the Commission Delegated Regulation (or DA) (
European Commission (
2015)) approved by the European Commission. This is the final version of the standard formula of Solvency II applied by the insurers for the solvency assessment in 2016 and 2017 balance sheets
6. The general approach is always based on a factor-based formula in which the standard deviation of each LoB and risk is derived by means of either a market-wide or an undertaking-specific approach. Standard deviations are then aggregated by applying Equations (
4) and (
5) on the basis of the same correlation matrices used in QIS5. The overall standard deviation is used to quantify the capital charge via the following relation:
where the function
has been replaced by a fixed multiplier equal to 3.
This assumption tends to simplify the calculations, but it does not take into account the skewness of the distribution of losses, assuming always the same ratio of the 99.5% quantile less the mean divided by the standard deviation. It gives the same result as the function used in QIS5 only when is around 14.5%. This choice tends to underestimate capital requirement for small insurers and overestimate it for larger insurers, with respect to the assumption of a lognormal distribution of total losses.
Furthermore, the market-wide estimates of the standard deviation of the premium risk are based on a gross volatility multiplied by a
adjustment factor. DA provides a different estimation of
. In particular, the undertaking-specific adjustment factor for non-proportional reinsurance is derived through the following credibility formula:
where
is a fixed value equal to 80% in MTPL, motor own damages (MOD), and property LoBs only if XL treaties are in force. It is equal to 1 for all other segments;
c is a credibility coefficient depending by the length of available time series. A minimum of 5 years is required to have a value of
c greater than zero. This is instead equal to 1 when data over at least 10 years are available. For MTPL, property, and general third-party liabilites (GTPL), at least 15 years are requested to have full credibility.
Finally
can be estimated by insurers’ data as the square root of the net-to-gross ratio of second raw moments of severity distributions:
The gross amount is estimated by data, while the net amount is derived by evaluating the effect of reinsurance retention on a lognormal distribution. The same approach is adopted in cases for which the recognizable excess of the loss reinsurance contract provides compensation only up to a specified limit.
Equation (
10) appears to be a stronger approximation than QIS5. The gross volatility factor
, which measures a relative variability, is reduced by means of the risk mitigation effect on the second raw moment of the claim size. Under a compound pure Poisson process,
measures the net-to-gross ratio of the standard deviations of the total losses. Indeed, considering only one LoB and only premium risk, DA assumes in the case of full credibility (
) that
where
and
are the net and gross standard deviations of the total losses under a pure compound Poisson process.
Furthermore, it is noteworthy that DA implicitly assumes that reinsurance does not affect the skewness of distribution. Equation (
8) obtains the distance between the 99.5% quantile and the mean as 3 times the standard deviation in both net and gross cases.
6. Some Examples of Numerical Impact
In order to compare our proposal to the capital requirements derived by QIS5 and DA, we consider a standard non-life insurer. The main figures are summed up in
Table 1, where gross characteristics are reported. The insurer’s portfolio is structured around three LoBs: MTPL, GTPL, and MOD, with a prominent weight of MTPL. As detailed in the following, next-year premiums have been estimated assuming an annual increase of 5% with respect to earned premiums of the previous year. This increase was the standard assumption on annual premiums’ growth in quantitative impact studies. No multi-year policies are present. Best estimates of claims reserves posted by the insurer at the end of year are also reported in
Table 1. We observe the significant number of claims reserves because two long-tail LoBs are considered. Furthermore, we assume that the insurer wishes to reinsure a part of his portfolio in order to reduce its volatility. To investigate the effect of non-proportional factors on the premium risk capital requirement, we consider XL treaties, varying the reinsurance limits for each LoB.
Table 2 reports the observed number of claims (
n) and average cost per claim (
m). These values, together with the assumptions on the real growth rate of the portfolio (
g) and on the claim inflation rate (
i), allow us to estimate the risk premiums for next year,
. It has to be pointed out that some key parameters, such as the safety loading coefficient (
) on the risk premium and the standard deviation of the structure variable (
), are obtained mainly by Italian market loss ratios and combined ratios for the period 1999–2013. A negative safety loading coefficient is used when the observed combined ratio is greater than 1 (e.g., in GTPL). Furthermore, expenses’ loadings (
c) have been calibrated by using the historical pattern of both management and acquisition expenses in the same period. Next-year premiums have been derived as
. For the sake of simplicity, we take into account only new business and annual contracts. Finally, in order to reflect variability of LoBs, we consider the coefficient of variation of the claim size (
), estimated by using the empirical distribution of individual losses.
These calibrations
7 allow a realistic analysis of the effect of non-proportional reinsurance on the capital requirement in order to assure a consistent comparison between alternative approaches.
We focus initially on the premium risk volatility of each LoB. Subsequently, we assess the total capital requirement in order to evaluate the risk mitigation effect also on an aggregated basis.
To assure a consistent comparison, we assume that the retention limit
of the XL treaty is equal to the sum of the average claim cost and a fixed multiplier
S of the standard deviation:
.
S is initially set equal to 15. In this scenario, the attachment point is roughly 400,000 euro for MTPL, 1.5 million euro for GTPL, and 80,000 euro for MOD. We report in
Table 3 the non-proportional factor derived by applying QIS5, DA and Equation (
12). Equation (
12) has been evaluated by assuming that the reinsurer has a safety loading coefficient either equal to (see
) or greater than the ceding company (see
). In the second case, the reinsurer’s safety loading has been derived by taking into account the reduction in the variability of the cedent. Finally, we give full credibility (
) to the undertaking-specific methodology when DA is applied (i.e.,
).
We may observe (see
Table 3) that QIS5 and DA lead to similar adjustment factors. It is noteworthy that the standard formula tends to overestimate the risk mitigation effect because non-pooling risk is ignored.
gives instead greater values because of parameter risk (i.e.,
effect). In particular, long-tail LoBs (such as GTPL and MTPL) show a significant underestimation of
under the Solvency II criteria. Additionally, the fixed value of 80% allowed by DA for MTPL and MOD also appears not to be a prudential choice. Finally, the non-proportional factor has been evaluated in order to also consider reinsurer pricing (
). A slight reduction in the factor is observed when the reinsurer applies a safety loading greater than that of the insurer.
In a similar fashion,
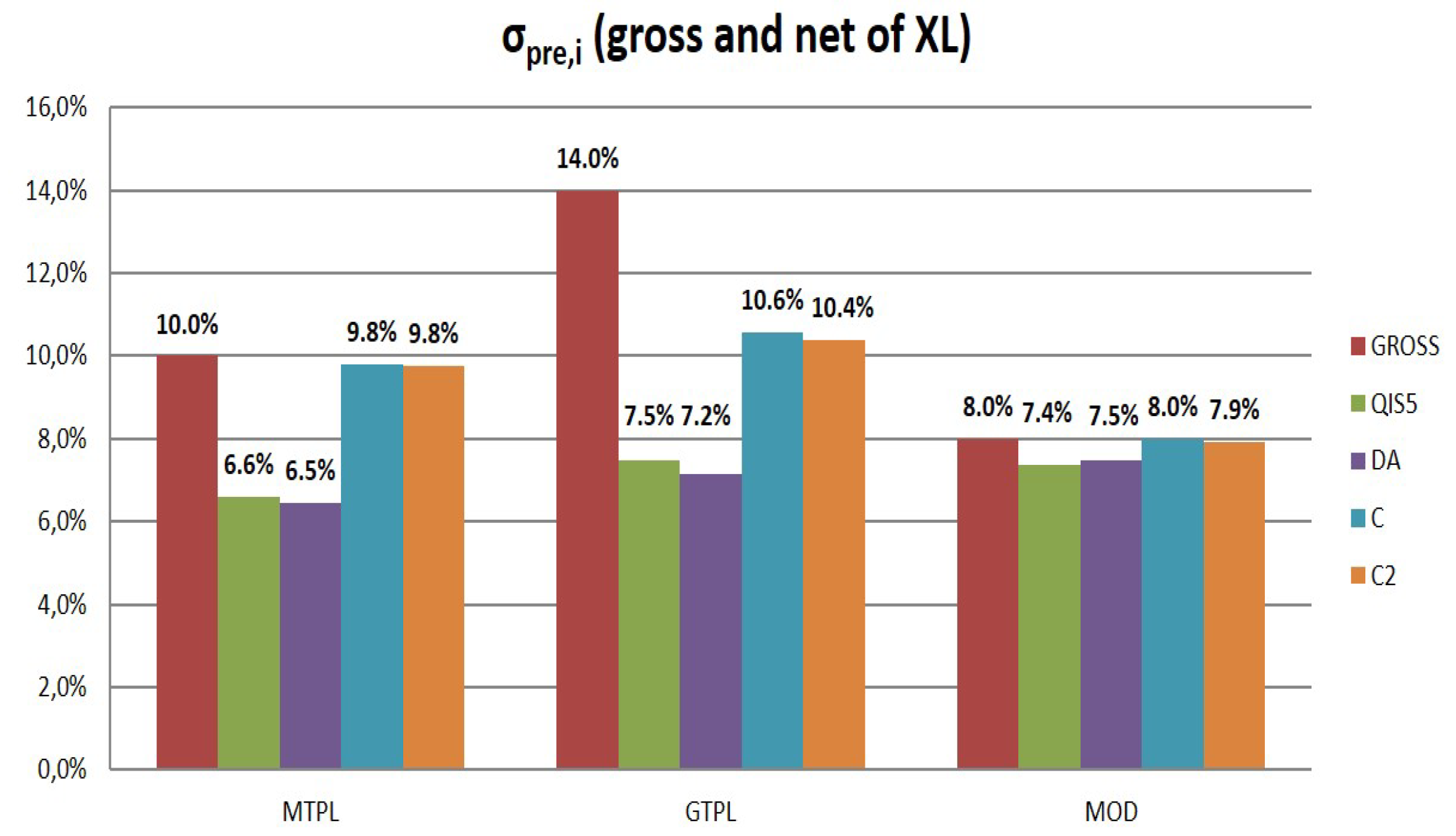
Figure 1 reports the values of the volatility factor of the premium risk for the LoBs analyzed. As expected, we observe how the methodology proposed by both QIS5 and DA leads to a significant reduction in the volatility factor.
Figure 2 reports instead the Solvency Capital Requirement (SCR) ratios (SCR divided by initial gross premiums) considering either only premium risk or both premium and reserve risk. Capital requirements have been derived using only a market-wide approach, by testing alternative formulae for the non-proportional factor and by considering both
and
versions proposed by QIS5 and DA, respectively (see Equations (
3) and (
8)).When reinsurance is not considered, the premium risk capital charge is equal to 27% of premiums under the lognormal assumption and to 29% with the DA approach. Also taking into account reserve risk, we observe ratios of 61% and 66%. It is emphasized how lower volatilities lead to higher differences between the two approaches. The gross
is indeed equal to 7.6% when both the premium and reserve are considered, while it is equal to 9% when only premium risk is present.
Considering the risk mitigation effect of XL treaties, both QIS5 and DA allow us to save roughly 40% of the capital requirement for premium risk. As is well known, the market-wide approach does not consider the effect of reinsurance on the reserve risk volatility, leading to a saving of capital cost of about 16% for the premium and reserve sub-module.
A limited effect is indeed recognized under and criteria because the systematic component of the claim count is not affected by the treaty. In this case, net-to-gross capital ratios are equal to roughly 90% and 94% when either only premium risk or also reserve risk is taken into account.
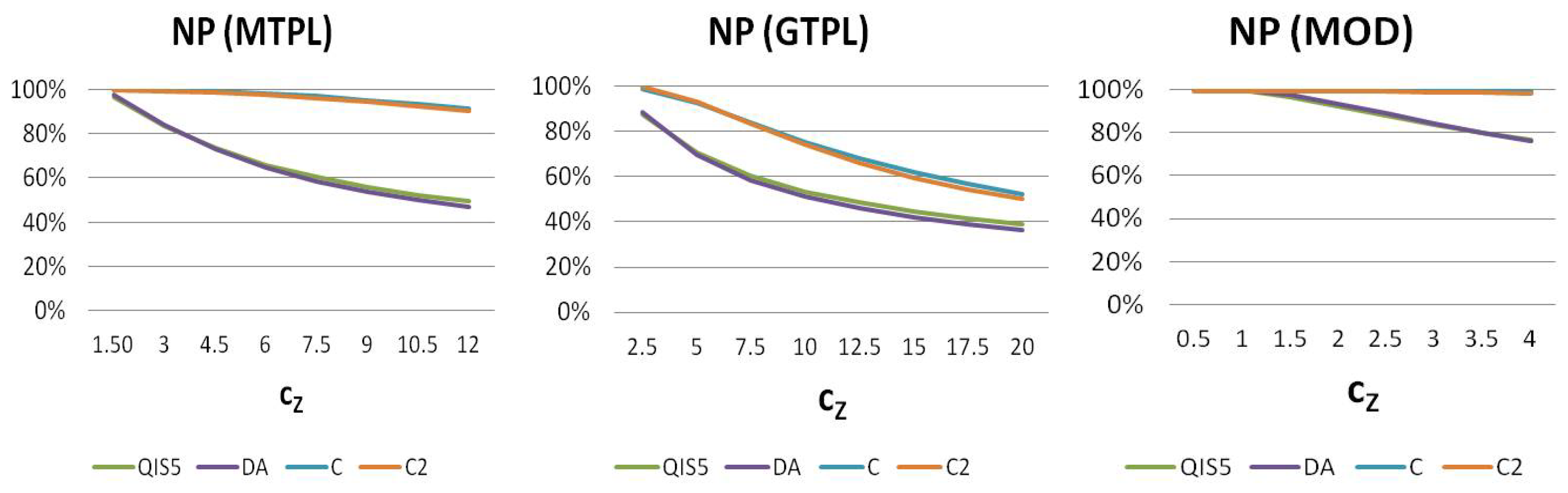
In order to better analyze the effect on the non-proportional factor of the insurer’s characteristics, we develop a sensitivity analysis suitable to identify critical parameters. In this regard,
Figure 3 shows values of
evaluated considering alternative coefficients of variation of the severity distribution. As expected, higher variabilities lead to an increasing effect of non-proportional reinsurance. Although this result is apparent, we observe how the overestimation of the risk mitigation effect recognized by the standard formula increases for higher values of
. Only when very low relative volatilities are considered do all the methodologies provide similar values of
close to 1.
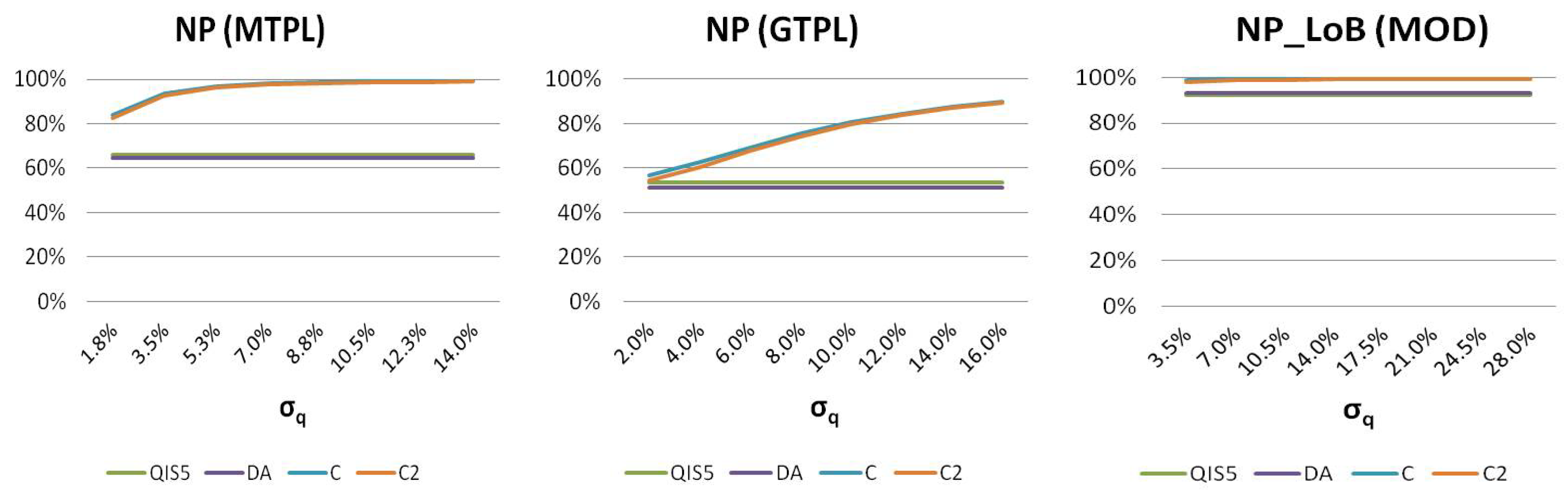
The parameter uncertainty (
) on the claims count has been tested and is shown in
Figure 4. While QIS and DA are not affected by this systematic component, the effect of XL should decrease, the pooling risk being neglectable (as shown by
and
results).
Furthermore, the portfolio size is not even considered in the standard formula, leading to the same risk mitigation for small and large companies (see
Figure 5). Generally, small companies show a higher relative saving of capital when XL treaties are in force (see, e.g., Appendix B on non-life insurance of
International Actuarial Association (
2004)). As both
and
show, this effect increases for LoB with a higher
or a lower
because of the more relevant pooling risk.
We also evaluate the effect of a different retention limit (see
Figure 6). The attachment point has been evaluated as
, where alternative values of
S have been tested (see also
De Lourdes Centeno (
1995) for an analysis of the effect of retention limit on risk reserve). As expected, a greater retention limit leads to a reduction in
. Also in this analysis, the overestimation of the risk mitigation effect when the standard formula is applied has been confirmed. In particular, it is noteworthy that the standard formula also provides, for higher retentions, a non-proportional factor significantly lower than 1. For example, when
S is equal to 100, attachment points are equal to roughly 2.5 million euro for MTPL, 10.3 million euro for GTPL, and 0.5 million euro for MOD. Although very high limits, the
evaluated by the standard formula is equal to roughly 88% for MTPL, 77% for GTPL, and 99.5% for MOD with a significant capital relief.
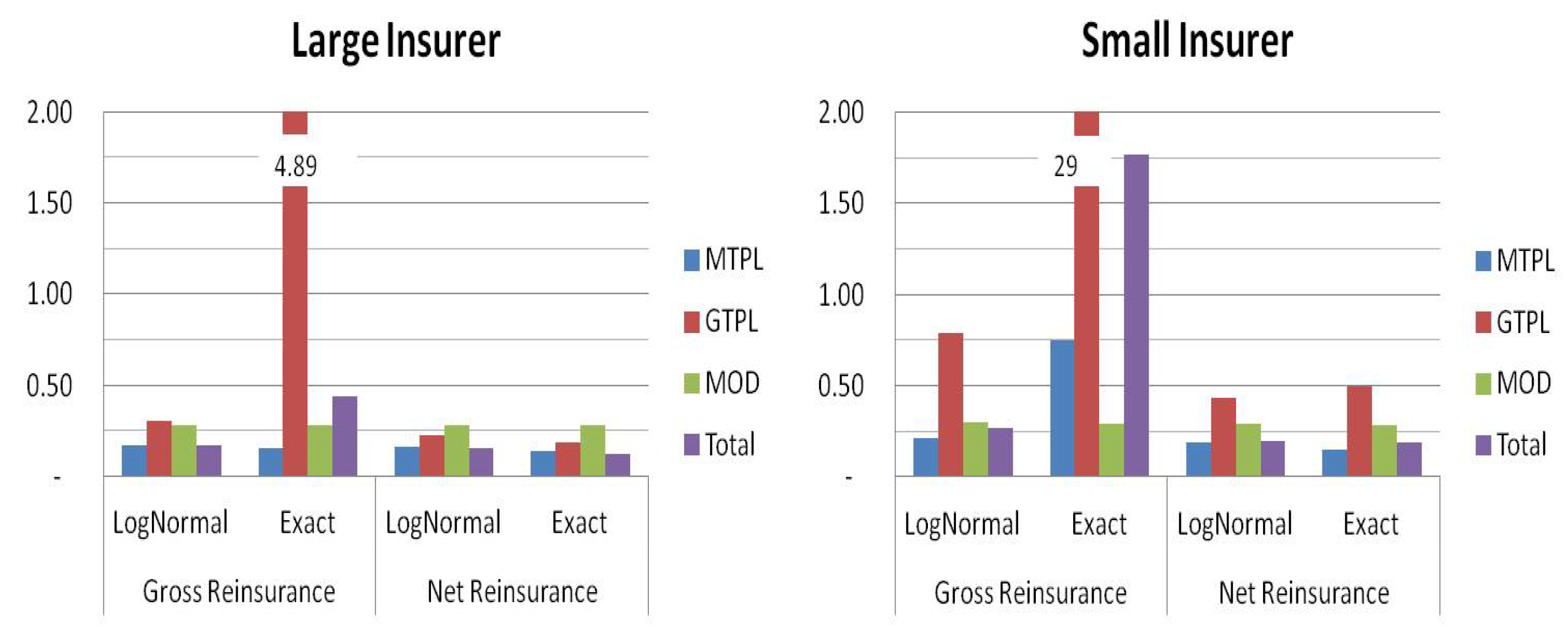
Finally, in order to test the lognormal assumption of the net total losses, we analyze the skewness of this r.v. To this end, we compare the skewness of the lognormal distribution to the exact distribution provided by Equation (
13). Furthermore, to evaluate the skewness of the total portfolio, the dependence is described by a Gaussian copula calibrated through the standard formula correlation matrix. The comparison regards both the insurer, whose characteristics are reported in
Table 1, and a smaller insurer, whose portfolio is 1/10 of the larger portfolio.
Figure 7 shows how the lognormal assumption tends to underestimate real skewness for small portfolios or highly volatile businesses (such as GTPL). However, for both companies, this assumption seems consistent when we analyze the net of the reinsurance distribution.