Bayesian Option Pricing Framework with Stochastic Volatility for FX Data
Abstract
:1. Introduction
2. Stochastic Volatility Model and Option Pricing
2.1. Problem Formulation
- It should be a simple model that enables us to apply the standard Bayesian inference via MCMC;
- It should be convenient to transform the model under to the model under , the risk-neutral probability;
- The resulting -process should generate option prices close to market prices.
- (P1)
- Equivalent probability measures: iff for any event A;
- (P2)
- Martingale property: , where r is the one-step continuously compounded interest rate;
- (P3)
- Equivalent local variance:
2.2. The SV Model with VG and t Error Distributions
2.3. Bayesian Framework
2.4. Option Pricing
- Step A: For j = 1:J where J is the number of simulated stock price paths,
- A1:
- Set ;
- A2:
- Set ;
- A3:
- Sample from ;
- A4:
- Sample from ;
- Step B: For i = 1:T,
- B1:
- Sample from ;
- B2:
- Sample from
- B3:
- Set ;
- Step C: By (16), set
3. Empirical Studies
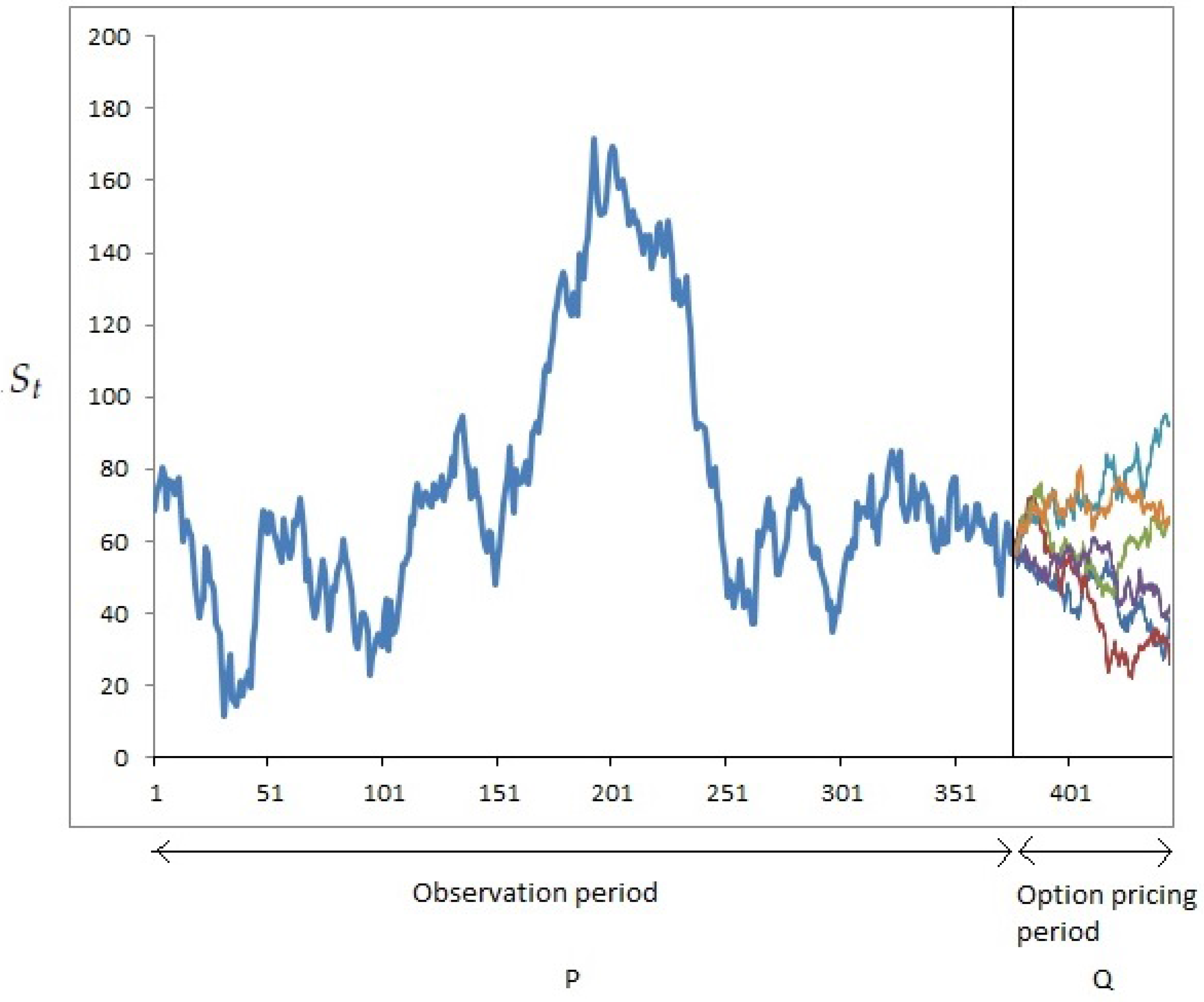
3.1. FX Market Data
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- R.F. Engle. “Autoregressive conditional heteroscedasticity with estimates of variance of United Kingdom inflation.” Econometrica 50 (1982): 987–1008. [Google Scholar] [CrossRef]
- T. Bollerslev. “Generalized autoregressive conditional heteroskedasticity.” J. Econ. 31 (1986): 307–327. [Google Scholar] [CrossRef]
- J.C. Duan. “The GARCH option pricing model.” Math. Financ. 5 (1995): 13–32. [Google Scholar] [CrossRef]
- D.B. Nelson. “Conditional heteroskedasticity in asset returns: A new approach.” Econometrica 59 (1991): 347–370. [Google Scholar] [CrossRef]
- J.C. Hull, and A. White. “The pricing of options on assets with stochastic volatilities.” J. Financ. 42 (1987): 281–300. [Google Scholar] [CrossRef]
- S.L. Heston. “A closed solution for options with stochastic volatility, with application to bond and currency options.” Rev. Financ. Stud. 6 (1993): 327–343. [Google Scholar] [CrossRef]
- A.S. Cordis, and C. Korby. “Discrete stochastic autoregressive volatility.” J. Bank. Financ. 43 (2014): 160–178. [Google Scholar] [CrossRef]
- E. Jacquier, N. Polson, and P. Rossi. “Bayesian analysis of stochastic volatility models (with discussion).” J. Bus. Econ. Stat. 12 (1994): 371–417. [Google Scholar]
- N. Shephard, and M.K. Pitt. “Likelihood analysis of non-Gaussian measurement time series.” Biometrika 84 (1997): 653–667. [Google Scholar] [CrossRef]
- C.A. Abanto-Valle, D. Bandyopadhyay, V.H. Lachos, and I. Enriquez. “Robust Bayesian analysis of heavy-tailed stochastic volatility models using scale mixtures of normal distributions.” Comput. Stat. Data Anal. 54 (2010): 2883–2898. [Google Scholar] [CrossRef] [PubMed]
- R. Meyer, and J. Yu. “BUGS for a Bayesian analysis of stochastic volatility models.” Econ. J. 3 (2000): 198–215. [Google Scholar] [CrossRef]
- J. Yu. “On leverage in a stochastic volatility model.” J. Econ. 127 (2005): 165–178. [Google Scholar] [CrossRef]
- S.T.B. Choy, W.Y. Wan, and C.M. Chan. “Bayesian Student-t stochastic volatility models via scale mixtures.” Adv. Econ. 23 (2008): 595–618. [Google Scholar] [CrossRef]
- J.J.J. Wang, S.K.J. Chan, and S.T.B. Choy. “Stochastic volatility models with leverage and heavy-tailed distributions: A Bayesian approach using scale mixtures.” Comput. Stat. Data Anal. 55 (2011): 852–862. [Google Scholar] [CrossRef]
- C.A. Abanto-Valle, H. Migon, and V.H. Lachos. “Bayesian analysis of heavy-tailed stochastic volatility in mean model using scale mixtures of normal distributions.” J. Stat. Plan. Inference 141 (2011): 1875–1887. [Google Scholar] [CrossRef]
- D.S. Bates. “Maximum likelihood estimation of latent affine processes.” Rev. Financ. Stud. 19 (2006): 909–965. [Google Scholar] [CrossRef]
- D.B. Madan, and E. Seneta. “The variance gamma (V.G.) model for share market returns.” J. Bus. 63 (1990): 511–524. [Google Scholar] [CrossRef]
- D.B. Madan, P.P. Carr, and E.C. Chang. “The variance gamma process and option pricing.” Eur. Financ. Rev. 2 (1998): 79–105. [Google Scholar] [CrossRef]
- A. Badescu, R.J. Elliott, and T.K. Siu. “Esscher transforms and consumption-based models.” Insur. Math. Econ. 45 (2009): 337–347. [Google Scholar] [CrossRef]
- S.T.B. Choy, and J.S.K. Chan. “Scale mixtures in statistics modelling.” Aust. N. Z. J. Stat. 50 (2008): 135–146. [Google Scholar] [CrossRef]
- S.F. Chung, and H.Y. Wong. “Analytical pricing of discrete arithmetic Asian options with mean reversion and jumps.” J. Bank. Financ. 44 (2014): 130–140. [Google Scholar] [CrossRef]
- J. Kanniainen, B. Lin, and H. Yang. “Estimating and using GARCH models with VIX data for option valuation.” J. Bank. Financ. 43 (2014): 200–211. [Google Scholar] [CrossRef]
| Model | N-N | t-t | t- | -t | - |
|---|---|---|---|---|---|
| DIC | 383.3 | 379.9 | 378.6 | 353.3 | 360.2 |
| BIC | 386.6 | 376.9 | 379.7 | 370.9 | 371.0 |
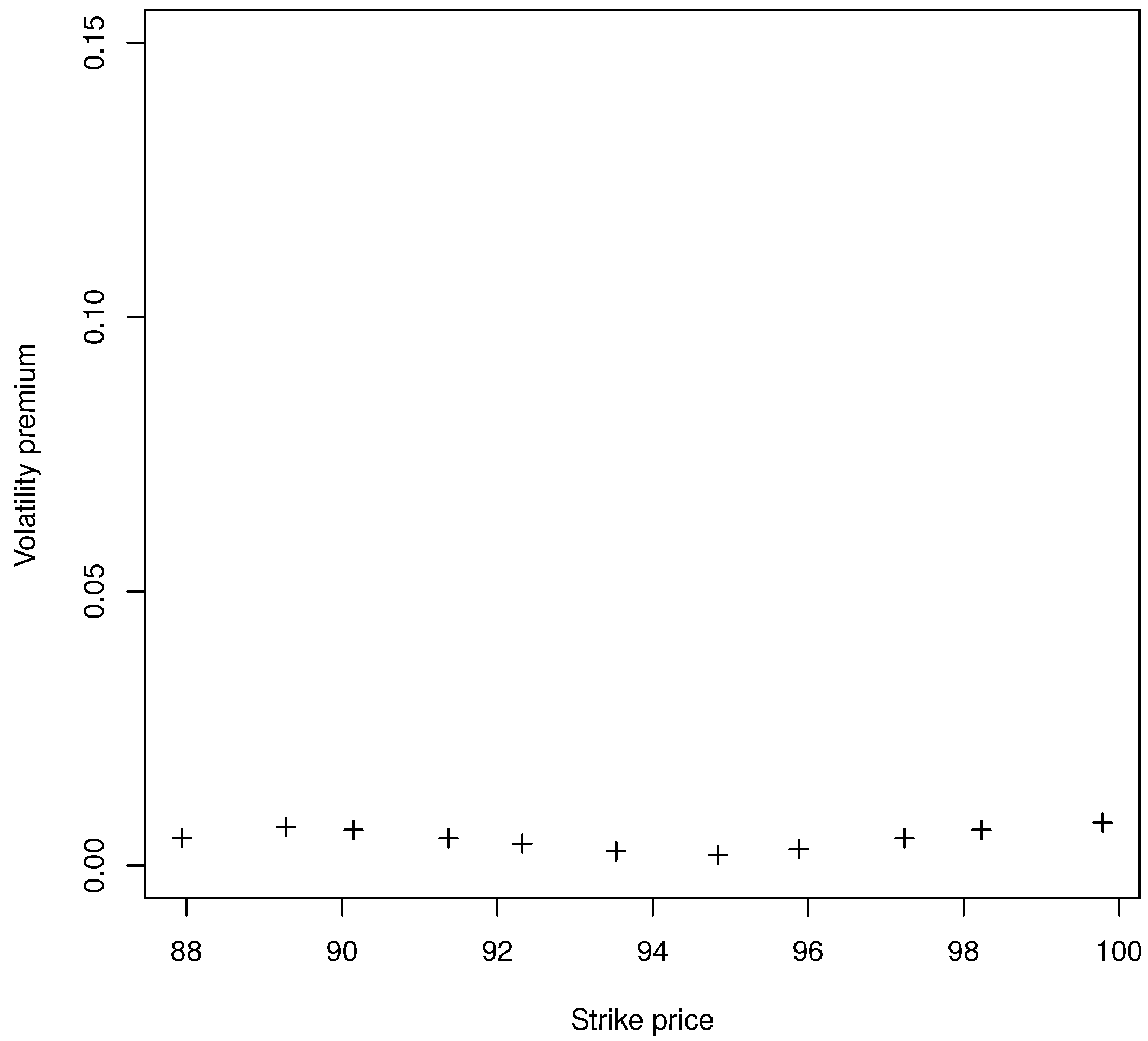
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | Sd. |
|---|---|---|---|---|---|---|
| 0.0002 | 0.0031 | 0.0310 | 0.0052 |
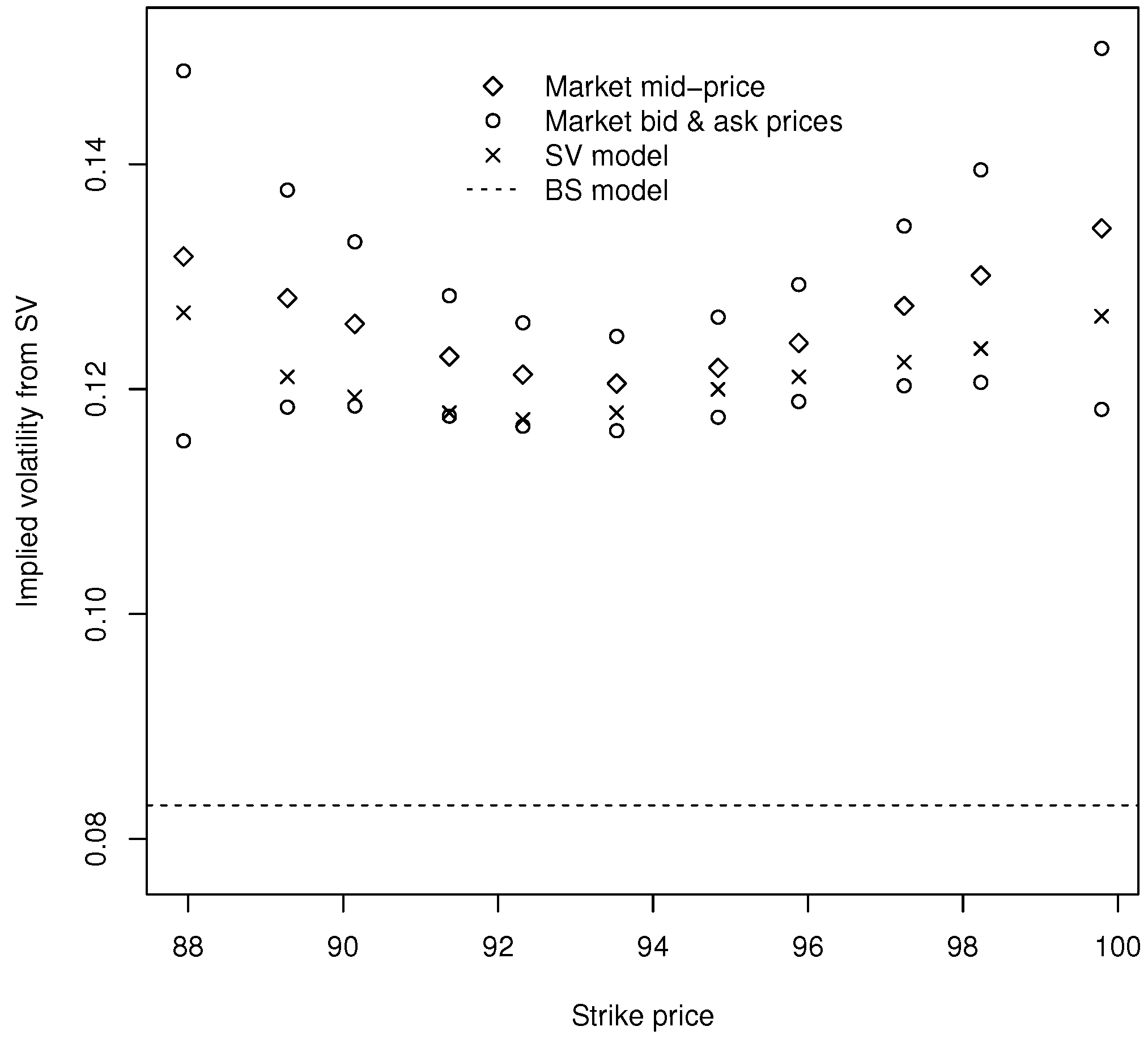
| K = 87.94 | K = 89.28 | K = 90.15 | K = 91.37 | K = 92.32 | K = 93.53 | |
| Mid | 0.1318 | 0.1281 | 0.1258 | 0.1229 | 0.1213 | 0.1205 |
| Bid | 0.1154 | 0.1184 | 0.1185 | 0.1176 | 0.1167 | 0.1163 |
| Ask | 0.1483 | 0.1377 | 0.1331 | 0.1283 | 0.1259 | 0.1247 |
| K = 93.84 | K = 95.88 | K = 97.24 | K = 98.23 | K = 99.79 | ||
| Mid | 0.1219 | 0.1241 | 0.1274 | 0.1301 | 0.1343 | |
| Bid | 0.1175 | 0.1189 | 0.1203 | 0.1206 | 0.1182 | |
| Ask | 0.1264 | 0.1293 | 0.1345 | 0.1395 | 0.1503 |
| Par. | Mean | Sd | 95% CI |
|---|---|---|---|
| β | 0.078 | 0.064 | ( , 0.203) |
| τ | 0.225 | 0.067 | (0.128 , 0.361) |
| μ | 0.351 | (, ) | |
| ϕ | 0.873 | 0.088 | (0.687 , 0.988) |
| ν | 8.176 | 4.155 | (2.531 , 18.114) |
| α | 15.622 | 8.582 | (4.290 , 34.868) |
| Model | K = 87.94 | K = 89.28 | K = 90.15 | K = 91.37 | K = 92.32 | K = 93.53 |
| Mkt | 5.728 | 4.480 | 3.711 | 2.712 | 2.040 | 1.335 |
| BS | 5.658 | 4.339 | 3.507 | 2.410 | 1.676 | 0.934 |
| SV | 5.679 | 4.372 | 3.555 | 2.480 | 1.759 | 1.020 |
| Model | K = 94.84 | K = 95.88 | K = 97.24 | K = 98.23 | K = 99.79 | |
| Mkt | 0.049 | 0.509 | 0.272 | 0.169 | 0.077 | |
| BS | 0.414 | 0.189 | 0.054 | 0.019 | 0.003 | |
| SV | 0.497 | 0.259 | 0.104 | 0.055 | 0.022 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Choy, S.T.B.; Wong, H.Y. Bayesian Option Pricing Framework with Stochastic Volatility for FX Data. Risks 2016, 4, 51. https://doi.org/10.3390/risks4040051
Wang Y, Choy STB, Wong HY. Bayesian Option Pricing Framework with Stochastic Volatility for FX Data. Risks. 2016; 4(4):51. https://doi.org/10.3390/risks4040051
Chicago/Turabian StyleWang, Ying, Sai Tsang Boris Choy, and Hoi Ying Wong. 2016. "Bayesian Option Pricing Framework with Stochastic Volatility for FX Data" Risks 4, no. 4: 51. https://doi.org/10.3390/risks4040051
APA StyleWang, Y., Choy, S. T. B., & Wong, H. Y. (2016). Bayesian Option Pricing Framework with Stochastic Volatility for FX Data. Risks, 4(4), 51. https://doi.org/10.3390/risks4040051





