1. Introduction
Many wealth management and insurance companies worldwide are offering investment products known as variable annuities (VA) with some guarantees of living and death benefits to assist investors with managing their pre-retirement and post-retirement plans. These products take advantage of market growth while providing a protection of the savings against the market downturns. Insurers started to offer these products from the 1990s in the United States. Later, these products became popular in Europe, UK and Japan and more recently in Australia. The VA contract cashflows received by the policyholder are linked to the investment portfolio choice and performance (e.g., the choice of mutual fund and its strategy) while traditional annuities provide a pre-defined income stream in exchange for the lump sum payment. According to LIMRA (Life Insurance and Market Research Association) reports, the VA market is huge: VA sales in United States were $158 billion in 2011, $147 billion in 2012 and $145 billion in 2013.
The types of VA guarantees (referred in the literature as VA riders) offered for investment portfolios are classified as guaranteed minimum withdrawal benefit (GMWB), guaranteed minimum accumulation benefit (GMAB), guaranteed minimum income benefit (GMIB) and guaranteed minimum death benefit (GMDB). These guarantees, generically denoted as GMxB, provide different types of protection against the market downturns and policyholder death. GMWB allows the withdrawing of funds from the VA account up to some pre-defined limit regardless of the investment performance during the contract; GMAB and GMIB both provide a guaranteed investment account balance at the contract maturity that can be taken as a lump sum or standard annuity respectively. Guaranteed lifelong withdrawal benefit (GLWB), a specific type of GMWB, allows withdrawing funds at the contractual rate as long as the policyholder is alive. GMDB provides a specified payment if the policyholder dies. Precise specifications of the products within each type can vary across companies and some products may include combinations of these guarantees.
A good overview of the VA products and the development of their market can be found in [
1,
2,
3]. There have been a number of papers in the academic literature considering pricing of these products. Most of these are focused on pricing VA riders under the pre-determined (
static) policyholder behaviour in withdrawal and surrender. Some studies include pricing under the active (
dynamic) strategy when the policyholder ‘
optimally’ decides the amount of withdrawal at each withdrawal date depending on the information available at that date. Standard Monte Carlo (MC) method can easily be used to estimate price in the case of pre-defined withdrawal strategy but handling the dynamic strategy requires a backward in time solution that can be done only via the partial differential equation (PDE), direct integration or regression type MC methods.
In brief, pricing under the static and dynamic withdrawal strategies via the PDE based methods has been developed in [
4,
5,
6]. The authors of [
1] develop a unified approach with numerical estimation via MC and direct integration methods. The direct integration method was developed further in [
7,
8] using the Gauss-Hermite quadrature and cubic interpolations. The authors of [
9] consider many VA riders under the stochastic interest rate and stochastic volatility if the policyholder withdraws at the pre-defined contractual rate or completely surrenders the contract. Their pricing is accomplished either by the ordinary MC or Least-Squares MC to account for the optimal surrender. Often, pricing of the VA riders is considered under the assumption of a geometric Brownian motion for the risky asset underlying the contract, though a few papers looked at extensions such as stochastic interest rate and/or stochastic volatility, see, e.g., [
9,
10,
11,
12].
The authors of [
13] prove the existence of an optimal
bang-bang control for GLWB contract when thecontract holder can maximize contract writer’s losses by only ever performing non-withdrawal, withdrawal at the contract rate or full surrender. However, they also demonstrate that the related GMWB contract does not satisfy the bang-bang principle other than in certain degenerate cases. The authors of [
11] developed a regression-based MC method for pricing GLWB under the bang-bang strategy in the case of stochastic volatility. GMWB pricing under the bang-bang strategy was studied in [
14]. The difficulty with applying the well known Least-Squares MC introduced in [
15] for pricing VA riders under the optimal strategy is due to the fact that the paths of the underlying VA wealth account are affected by the withdrawals. In principle, one can apply the
control randomization methods extending Least-Squares MC to handle optimal stochastic control problems with controlled Markov processes recently developed in [
16], but the accuracy and robustness of this method for pricing of the VA riders have not been studied yet.
One common observation in the above mentioned literature is that pricing under the optimal strategy often leads to prices significantly higher than observed on the market. These studies rely on the option pricing risk-neutral methodology in quantitative finance to find a fair fee. Here, the fundamental idea is to find the cost of a dynamic self-financing replicating portfolio which is designed to provide an amount at least equal to the payoff of the contract. The cost of establishing this hedging strategy is the no-arbitrage price of the contract. This is under the assumption that the contract holder adopts an optimal strategy (exercise strategy maximising the monetary value of the contract). If the purchaser follows any other exercise strategy, the contract writer will generate a guaranteed profit if continuous hedging is performed. Of course the strategy optimal in this sense is not related to the policyholder circumstances. In pricing VA with guarantees, it is reasonable to consider alternative assumptions regarding the investor’s withdrawal strategy. This is because an investor may follow what appears to be a sub-optimal strategy that does not maximise the monetary value of the option. This could be due to reasons such as liquidity needs, tax and other personal circumstances. Moreover, the mortality risk is diversified by the contract issuer through selling many contracts while the policyholder cannot do it. Also, there might be no liquid secondary market for VAs on which the policy could be sold (or repurchased) at its fair value. The policyholder may act optimally with respect to his preferences and circumstances but it may be different from the optimal strategy that maximises the monetary value of the contract. In this case we calculate a fair fee to be deducted in order to finance a dynamic replicating portfolio for the guarantees (options) embedded in the contract under the assumption of a particular exercise strategy. The replicating portfolio will provide sufficient funds to meet any future payouts that arise from writing the contract.
However, the fair fee obtained under the assumption that investors behave optimally to maximise the value of the guarantee does offer an important benchmark because it is a worst case scenario for the contract writer. Also, as noted in [
17], secondary markets for the equity linked insurance products (where the policyholder can sell their contracts) are growing. Thus, third parties can potentially generate a guaranteed profit through hedging strategies from the financial products such as VA riders which are not priced under the assumption of the optimal withdrawal strategy. The authors of [
18] mention several companies recently suffering large losses related to increased surrender rates, indicating that either the charged fees were not sufficiently large or that the hedging program did not perform as expected.
One way to analyze the withdrawal behavior of a VA holder and evaluate the need of these products is to solve the life-cycle utility model accounting for consumption, housing, bequest and other real life circumstances. Developing a full life-cycle model with all preferences and required parameters is challenging but there are already several contributions reporting some interesting findings in this direction: [
19,
20,
21,
22]. This topic will not be considered in this paper. It is also important to note a recent paper by [
23] considering the pricing under the optimal strategy in the presence of taxes via
subjective risk-neutral valuation methodology. They demonstrated that including taxes significantly affects the value of the VA withdrawal guarantees producing results in line with empirical market prices. This approach will be discussed in
Section 5.
Often it is assumed that insurance company can diversify the mortality risk through selling many contracts and the financial risk can be completely hedged using the underlying financial asset. Then the fair price of the product is calculated as the expected present value of the product benefits with respect to the risk-neutral process for the financial risk and the real process for the mortality. In practice, one has to account for a systemic mortality risk that cannot be diversified (often modelled through stochasticity of the death probabilities). If the assets for perfect hedging of the mortality risk would exist then one could calculate the unique fair price as expectation with respect to a risk-neutral process for mortality. However, the current status of the insurance market does not allow investment into such assets. There will be a residual risk for the contract issuer not only due to systemic mortality risk but also due to the finite size of the portfolio and imperfections of the hedging with respect to the financial risk. In this case, one can calculate extra loading to the fair price so that the issuer residual risk (quantified as, e.g., Value-at-Risk or expected shortfall at some confidence level) is no greater than zero. This can be accomplished via simulations of the hedging strategy based on the fair price valuation and quantification of the residual hedging errors. The extra loading to cover the residual risk depends on the risk management strategy for the product and was considered in [
24,
25]. This topic will be briefly discussed in
Section 3.
In this paper we review pricing of living and death benefit guarantees offered with VAs, and present an optimal stochastic control framework for pricing these contracts. The main ideas have been developed and appeared in some forms in a number of other papers. However, we believe that our presentation is easier to understand and implement. We also present a direct integration method based on computing of the expected contract values in a backward time-stepping through the high order Gauss-Hermite integration quadrature applied on the cubic spline interpolation. This method can be applied when transition density of the underlying asset between the contract cashflow event dates
or its moments are known in closed form. We have used this for pricing specific financial derivatives and some simple versions of the VA guarantees in [
7,
26]. Here, we adapt and extend the method to handle pricing VA riders in general. As a numerical example, we calculate accurate prices of GMAB with possible annual
ratchets (reset of the guaranteed capital to the investment portfolio value if the latter is larger on the contract anniversary dates) and allowing optimal withdrawals. The contract that we consider is very similar in specifications to the real product marketed in Australia, see for example [
27,
28]. Numerical difficulties encountered in pricing this VA rider are common across other VA guarantees and at the same time comprehensive numerical pricing results for this product are not available in the literature. These results (reported for a range of parameters) can serve as a numerical benchmark for practitioners and researchers developing pricing of the VA riders to assess the accuracy of their numerical implementations.
In the next section, a general specification of VA riders is given. In
Section 3 we discuss different stochastic models used for pricing these products including complete/incomplete financial market models and stochastic mortality.
Section 4 provides precise specification for some popular VA riders. In
Section 5 we present calculation of the fair price and fair fee as a solution of an optimal stochastic control problem and discuss pricing under the optimal/sub-optimal policyholder behaviour and in the presence of taxes.
Section 6 reviews the numerical methods and algorithms for pricing VA riders. In
Section 7 we present numerical results for the fair fees of GMAB rider. Concluding remarks are given in
Section 8.
2. VA Rider Contract Specification
Consider a VA contract with some guarantees for living and death benefits purchased by an
x-year old individual at time
with the up-front premium invested in a risky asset (e.g., a mutual fund), denoted as
at time
. The VA rider specification includes dates when events such as withdrawal, ratchet (
step-up), bonus (
roll-up), death benefit payment, etc. may occur. Precise definitions of these events depend on the contract and corresponding examples will be provided in
Section 4. The contract holder is allowed to take withdrawals and we assume that these can only take place on the set of the ordered
event times , where
is the contract maturity (in the case of lifelong guarantees
T corresponds to the maximum age beyond which survival is deemed impossible). Denote the withdrawal amount at time
as
. Also, the set of policy anniversaries when the ratchet event may occur is denoted as
and is assumed to be a subset of
. For simplicity of notation we assume that all other events may only occur on the withdrawal dates. The value of the contract payments at time
is determined by three state variables: wealth account
, guarantee account
and life status indicator
.
Wealth account is value of the investment account which is linked to the risky asset
. Initially,
is set equal to the upfront premium. For a given process of risky asset
,
, the value of the wealth account
evolves as
where
and
α is the annual fee continuously charged by the contract issuer for the provided guarantee. Here, we denote the values of the wealth account just before and just after
as
and
respectively, and similarly for other variables. The function
is introduced to have a generic notation covering cases of discretely charged fees discussed later in this section.
Guarantee account is the value used to calculate benefits provided by the VA rider, also referred in the literature as
benefit base. It is not changing between the event times but can be stochastic via stochasticity in
at the event times depending on the contract features. Initially,
is set equal to the upfront premium. At the event time, the benefit base may change as
where the function
is determined by the contract specifications and may also depend on the fee, penalty and other parameters. Specific cases will be provided in
Section 4. For example, if only a
ratchet is possible at
and no other contract events, then
Also, if there is only withdrawal at time
, then
In practice, several events such as withdrawal, ratchet, bonus, etc. may occur at the same time, and the contract specification determines the order of these events.
Life status indicator is a discrete random variable with the states in the set corresponding to the policyholder is being alive at , died during , or died before or at respectively. This variable is needed if there are death benefit features in the contract. It can be extended to include extra states corresponding to the policyholder partner if there is a spouse continuation feature in the contract. This case will not be considered explicitly but is easy to add. One could write the contract payoff function using the random variable τ representing lifetime of the policyholder, but instead we introduce to have a payoff written in the standard form for the optimal stochastic control framework.
An extra state variable is also required to track a tax free base to account for taxes; this will be considered in
Section 5.4. In principle, different guarantees included in VA may have different benefit base state variables. For notational simplicity and also from a practical perspective, we assume that all guarantees in VA are linked to the same benefit base account.
The contract product specification also determines:
the contractual (guaranteed) withdrawal amount for the period that may depend on the benefit base and/or ;
possible range for withdrawal ;
the payout at the contract maturity if policyholder is alive at ;
the payout to the beneficiary at in the case of the policyholder death during , ;
the cashflow received by the policyholder at the event times , , that might be different from due to penalties.
The specification details typically vary across different companies and are difficult to extract from the very long product specification documents. Moreover, results for specific GMxB riders presented in academic literature often refer to different specifications.
Denote the state variable vector at time
before the withdrawal as
and
. Then, given the withdrawal strategy
, the present value of the overall payoff of the VA contract with a guarantee can be written as
Here,
is the cashflow at the contract maturity, and
is the cashflow at time
. Also,
is the discounting factor from
to
where
is the risk-free interest rate (possibly stochastic).
In practice, the guarantee fee is charged discretely and proportional to the wealth account that requires some changes to the wealth process (1). Denoting the discretely charged fee with the annual basis as
, the wealth process becomes
Typically, the difference between continuously and discretely charged fees is not material as observed in our numerical results given in
Section 7.
Another popular fee structure corresponds to fees charged as a proportion of the benefit base, so that
Here, it is assumed that discrete fees are deducted before the withdrawal but it can be vice versa depending on the contract specifications.
Once the above conditions, i.e., functions , , , , and admissible range for withdrawal are specified by the contract design, and a specific stochastic evolution of the financial risky asset and death indicator is assumed, then pricing of the contract can be accomplished by numerical methods. In particular, if the withdrawals are optimal then pricing can be accomplished by the PDE, direct integration or regression based MC methods. If the withdrawals are pre-defined, then the standard MC along with PDE and direct integration methods can be used. The use of a particular numerical technique is determined by the complexities of the underlying stochastic model and contract details.
3. Stochastic Model
Commonly in the literature, stochastic models for the financial risky asset
underlying the VA rider assume that there is no arbitrage in the financial market which means that there is a risk-neutral measure
under which payment streams can be valued as expected discounted values. Moreover, this means that the cost of a portfolio replicating the contract is given by its expected discounted value under
. Hence, the fair price of the contract can be expressed as an expectation of the contract discounted cashflows with respect to
. Some models (such as Black-Scholes model) considered in the literature are
complete which means that the risk-neutral measure
is unique. Other models (such as extending Black-Scholes model to stochastic volatility and/or stochastic interest rate) are
incomplete implying that
is not unique. It is also assumed that the financial market has a risk-free asset that accumulates continuously at the risk-free interest rate. These are typical assumptions in the academic research literature on pricing financial derivatives, for a good textbook in this area we refer the reader to, e.g., [
29].
A benchmark model commonly considered in the literature on pricing VA riders is the well-known Black-Scholes dynamics for the reference portfolio of assets
that under the risk-neutral measure
is known to be
Here,
is the standard Wiener process,
is deterministic time dependent risk-free interest rate and
is deterministic time dependent volatility. Under this model the financial market is complete. The solution for this process is just
where
are independent and identically distributed standard Normal random variables,
and
.
Many models have been developed in the literature of pricing financial derivatives extending the Black-Scholes dynamics to the stochastic interest rate and/or stochastic volatility. These are incomplete models where the risk-neutral measure
is not unique. It is impossible to review all these models and we refer the reader to the standard textbooks in this area such as [
30] or [
31]. Some of these models have been applied for pricing VA riders that can be represented as the following risk-neutral diffusion process
where
are the model parameters, and
and
are the Wiener processes possibly correlated with
. In particular, [
9] studied the case of stochastic interest rate and stochastic volatility corresponding to
,
,
. In [
11], the authors considered the case of deterministic interest rate and stochastic volatility with
and
. In [
12], the authors developed solution for deterministic volatility and stochastic interest rate with
. An alternative way to modelling stochasticity in the interest rate and volatility via diffusion processes is to consider the Markov regime switching models. Under this approach, the interest rate and volatility are assumed to have the finite number of possible values and their evolution in time is driven by the finite state Markov chain variable representing possible regimes of the economy. In the context of pricing VA riders under the optimal withdrawal strategy, this approach was used in, e.g., [
10].
The mortality risk is assumed to be independent from the financial risk. A standard way to model mortality is to introduce the
force of mortality for a person aged
x at time
which may be stochastic or deterministic, such that the person lifetime
τ satisfies
For calculation of the VA rider payoff we need evolution of a life status indicator variable
with the states in the set
corresponding to the policyholder is being alive at
, died during
, or died before or at
correspondingly. Then the conditional transition probabilities
with
can be written as
If
is modelled as stochastic, then the transition probabilities
become stochastic due to stochasticity of
and a random variable
becomes a
doubly stochastic random variable. It is common to assume that
is a Markov process. Then the survival function (probability of surviving from time
t to
) given the knowledge of the mortality force at time
t is
There are many mortality models developed in the actuarial literature starting from the Gompertz deterministic model
introduced in 1825, for a textbook treatment of this topic see, e.g., [
32]. If
is deterministic, the mortality risk can be fully diversified via selling the contract to many policyholders, i.e., the contract price averaged over
L independent policyholders of the same age converges to the expected value of the contract as
L increases. The standard way to estimate deterministic death probabilities
is to use the official Life Tables that provide annual death probabilities for each age and gender in a given country; probabilities for time periods within a year are typically estimated assuming constant force of mortality within a year.
Stochastic modelling of
is a more recent development starting from the Lee-Carter model introduced in [
33]. Many stochastic mortality models extending the Lee-Carter model have been developed to capture the period, cohort and stochastic volatility features, see, e.g., [
34,
35,
36]. The stochasticity of
will introduce some dependence between the lifetimes of the policyholders leading to the systemic (undiversified) mortality risk. For pricing VA riders, the force of mortality is often model by a real diffusion process
where
is the Wiener process and some specific forms for the drift
and volatility
are considered in, for example, [
9,
24]. If we need to model a portfolio of the contracts, then the dependence between the policyholder deaths can be introduced via models for the number of deaths in a given population driven by some common factors as in the Lee-Carter model and its extensions reviewed in, e.g., [
34], or under the CreditRisk+ framework for mortality developed recently in [
37,
38].
Note that the current status of the insurance market does not allow to invest into the assets to hedge the systemic mortality introducing incompleteness in the model. In this case, pricing can be accomplished by either the financial mathematics no-arbitrage approach or the actuarial principle. Under the financial mathematics no-arbitrage approach, ([
29] (proposition 15.3)), we find the risk-neutral mortality process corresponding to the real process (12) to be
where
is the risk premium and
is the Wiener process under the risk-neutral measure. Then the fair price is calculated as an expectation with respect to the risk-neutral measure both for the financial asset and mortality processes. Of course, the risk premium is unknown and should be found using extra condition such as the requirement for the risk of hedging error loss (measured, e.g., as Value-at-Risk or expected shortfall at some confidence level) to be no greater than zero. This is the approach taken in, e.g., [
24]. Under the actuarial principle, the fair price is calculated as the expectation under the risk-neutral process for financial asset and under the
real process for mortality. As a result, there will be a residual risk that the issuer cannot control and the fair price can be adjusted by adding extra loading to the fair fee so that the risk of hedging error loss is no greater than zero, similarly to the estimation of the risk premium under the financial mathematics no-arbitrage approach. This procedure was considered in, e.g., [
25].
Even if the force of mortality is deterministic, there will be a residual risk due to the finite size of the portfolio. Moreover, it is important to note that even if there is no mortality risk, in practice, there will be a residual risk due to discrete hedging and other incompleteness of financial markets. To handle this, again, one should quantify the fair price hedging error distribution and adjust the price extra loading under the actuarial principle or adjust risk premium under the no-arbitrage financial mathematics approach so that the risk of hedging error loss will not exceed the required level. These adjustments depend on the risk management strategy for the product.
Remark 1. For simplicity, we do not consider management fees
charged by a mutual fund for managing the investment portfolio. If management fees
is given exogenously, then it will have an impact on the fair fee
α that should by charged by the VA guarantee issuer. This can be accomplished as described in, e.g., [
10] and can be easily incorporated in the framework outlined in our paper. Obviously,
α will be larger for given
comparing to the case
. The management fees reduce the performance of the investment account thus increasing the value of the guarantee as reported in, e.g., [
39] for GMWB or [
10] for GLWB. They commented that insurers wishing to provide the cheapest guarantee could provide the guarantee on the corresponding inexpensive exchange traded index fund rather than on a managed mutual fund account with extra fees.
5. Fair Pricing
Given the withdrawal strategy
, the present value of the contract cahsflows is given by (3) which is a function of the state vector
,
. Let
be the price of the VA contract with a guarantee at time
t, when
,
and the policyholder is alive. For simplicity of notation, if the policyholder is alive, we drop mortality state variable
in the function arguments. Then the contract fair price under the given withdrawal strategy
can be calculated as
Here,
denotes an expectation with respect to the state vector
X, conditional on information available at time
t, i.e., with respect to the financial risky asset process under the risk-neutral probability measure
and with respect to the mortality process under the probability measure
. The latter can be either real or risk-neutral probability measure depending on the pricing approach in the incomplete market as discussed in
Section 3.
The fair fee value of α to be charged for the VA guarantee corresponds to . That is, once a pricing of for a given α is developed, then a numerical root search algorithm is required to find the fair fee.
Remark 2. If volatility, interest rate or force of mortality are stochastic then these variables should be added to the state vector X for valuation of the fair price expectation (27).
5.1. Pricing as Stochastic Control Problem
The withdrawal strategy can depend on the time and state variables and is assumed to be given when the price of the contract is calculated in (27). The withdrawal strategies are classified as static, optimal, and sub-optimal.
Static strategy. Under this strategy, the policyholder decisions are deterministically determined at the beginning of the contract and do not depend on the evolution of the wealth and benefit base accounts. For example, policyholder withdraws at the contractual rate only.
Optimal strategy. Under the optimal withdrawal strategy, the decision on the withdrawal amount
depends on the information available at time
, i.e., depends on the state variable
. The optimal strategy is calculated as
where the supremum is taken over all admissible strategies
. Any other strategy
different from
is called
sub-optimal and leads to a smaller price.
Given that the state variable
is a Markov process and the contract payoff is represented by the general formula (3), calculation of the contract value (27) under the optimal withdrawal strategy (28) is a standard optimal stochastic control problem for a
controlled Markov process. Note that, the control variable
affects the transition law of the underlying wealth
process from
to
and thus the process is controlled. For a good textbook treatment of stochastic control problems in finance, see [
43]. This type of problems can be solved recursively to find the contract value
at
when
for
via the backward induction
Bellman equation
starting from the final condition
. The upperscript
in the expectation operator is used to indicate that the transition probability to reach state
at time
if the withdrawal (
action)
is applied in the state
x at time
depends on
. Obviously, the above backward induction can also be used to calculate the fair contract price in the case of a static strategy
; in this case the space of admissible strategies
contains only one pre-defined value and
becomes redundant.
For clarity, denote
and
the contract values just before and just after the event time
respectively. Then, in the case of deterministic force of mortality, after calculating the expectation with respect to the mortality state variable
in (29), the required backward recursion can be rewritten explicitly as
with the jump condition
This recursion is solved for , starting from the maturity condition .
In the case of a stochastic force of mortality , when , see (11), the contract value and the optimal value of are not only functions of and but also functions of a stochastic force of mortality . In this case, one has to add expectation with respect to process conditional on to the right side of Equation (30). Similarly, if the interest rate and/or volatility are modelled as stochastic.
Also, we would like to note that if the risk-free interest rate
is stochastic, then it can be convenient to use change of numéraire technique. In particular, changing the numéraire from the money market account
to the bond price
at time
with maturity
will simplify calculations in (30) using
Here,
is a new probability measure obtained from
using the Radon-Nikodym derivative
,
, see, e.g., [
12].
5.2. Alternative Solution
Consider the case of deterministic force of mortality
used to calculate death probabilities in (11). Given that the mortality and financial asset processes are independent, and the withdrawal decision does not affect the mortality process, one can calculate the expected value of the payoff (3) with respect to the mortality process,
, and then calculate the price under the optimal strategy as
or under the given strategy as
. It is easy to find that
where
and
for a random death time
τ, i.e.,
. Note that, previously we defined
.
The payoff (32) has the same general form as the payoff (3). Thus, the optimal stochastic control problem
can be solved using the Bellman Equation (29) leading to the following explicit recursion
for
, starting from
.
It is easy to verify that this recursion leads to the same solution
and the same optimal strategy for
as obtained from the recursion (30) and (31), noting that
. The result is somewhat obvious because
Note that,
. That is, one cannot find the price under the optimal strategy conditional on the death time and then average over random death times, that would lead to the result larger than
, see [
8].
Note that if the force of mortality is stochastic then equality (35) is not valid, the optimal withdrawal value of becomes a function of and the formulas in this section cannot be used to calculate the fair price.
5.3. Remarks on Withdrawal Strategy
The guarantee fare fee based on the optimal policyholder withdrawal is the worst case scenario for the issuer, i.e., if the guarantee is hedged then this fee will ensure no losses for the issuer (in other words full protection against the policyholder strategy and market uncertainty). Of course this is under the given assumptions about stochastic model for the underlying risky asset, and in the case of deterministic force of mortality assuming that the mortality risk is fully diversified. If the issuer hedges continuously but investors deviate from the optimal strategy, then the issuer will receive a guaranteed profit.
Any strategy different from the optimal is sup-optimal and will lead to smaller fair fees. Of course the strategy optimal in this sense is not related to the policyholder circumstances. The policyholder may act optimally with respect to his preferences and circumstances but it may be different from the optimal strategy calculated in (31). On the other hand, as noted in [
17], secondary markets for equity linked insurance products (where the policyholder can sell their contracts) are growing. Thus, financial third parties can potentially generate guaranteed profit through hedging strategies from financial products such as VA riders which are not priced according to the worst case assumption of the optimal withdrawal strategy. Thus the development of secondary markets for VA riders would lead to an increase in the fees charged by the issuing companies. [
18] undertakes an empirical study of policyholders behavior in Japanese VA market and they show that the moneyness of the guarantee has the largest explanatory power for the surrender rates.
One way to introduce a reasonable sub-optimal withdrawal model is to assume that the policyholder follows a default strategy withdrawing a contractual amount
at each event time
unless the extra value from undertaking an optimal withdrawal is greater than
,
. Setting
corresponds to the optimal strategy, while
leads to the strategy of withdrawals at the contract rate. This is the approach considered, e.g., in [
10,
39]. More complicated approach would specify a life-cycle utility model to determine the strategy optimal for the policyholder with respect to his circumstances and preferences, this is the approach studied in [
19,
20,
21,
22]. In any case, once the strategy is specified (estimated empirically or by another model), one can use Equation (31) to calculate the fair price and fair fee with the admissible strategy space
restricted to the specified strategy.
5.4. Tax Consideration
Withdrawals from the VA type contracts may attract country and individual specific government taxes. In [
23], the authors demonstrated that including taxes significantly affects the value of VA withdrawal guarantees. They developed a
subjective risk-neutral valuation methodology and produced results in line with empirical market prices. Following closely to [
23], we introduce an extra state variable
to present the
tax base which is the amount that may still be drawn tax-free, and assume that all event times
are the policy anniversary dates. The initial premium is assumed to be post-tax and taxes are applied to future investment gains (not the initial investment).
Denote a marginal income tax rate as
and a marginal capital gain tax from investment outside of VA contract as
κ. It is assumed that earnings from VA are treated as ordinary income and withdrawals are taxed on a last-in first-out basis. Thus if the wealth account
exceeds the tax base
, any withdrawal up to
will be taxed at the rate
and will not affect the tax base; larger withdraws will not be subject to tax but will reduce the tax base. Specifically, the tax base will change at the withdrawal time
as
The cashflow received by the policyholder will be reduced by taxes,
i.e., one has to make the following change in the contract specifications listed in
Section 4,
Using arguments for replicating pre-tax cashlows at
with post-tax cashflows at
, it was shown in [
23] that
should be found not as the direct expectation (30) but should be found as the solution of the following nonlinear equation
where
This is referred to as
subjective valuation from the policyholder perspective and depends on the investor current position (including possible offset tax responsibilities) and tax rates. Numerical examples in [
23] show that the VA guarantee prices accounting for taxes in the above way are lower than ignoring the taxes (not surprisingly, because it is just a sub-optimal strategy), making the prices overall more aligned with those observed in the market.
6. Numerical Valuation of VA Riders
In the case of realistic VA riders with discrete events such as ratchets and optimal withdrawals, there are no closed form solutions and the fair price has to be calculated numerically, even in the case of simple geometric Brownian motion process for the risky asset. In general, one can use the PDE, direct integration or regression type MC methods, where the backward recursion (30) and (31) is solved numerically. Of course, if the withdrawal strategy is known, then one can always use a standard MC to simulate all state variables forward in time till the contract maturity or the policyholder death and average the payoff discounted cashflows over many independent realizations. This standard procedure is well known and no further discussion is needed.
In this section, we give a brief review of different numerical methods that can be used for valuation of VA riders. Then, we provide detailed description of the direct integration method that can be very efficient and simple to implement, when the transition density of the underlying asset or it’s moments between the event times are known in closed form. Finally, in
Section 6.5 we present calculation of the hedging parameters (the so-called
Greeks).
6.1. Numerical Algorithms
Simulation based Least-Squares MC method introduced in [
15] is designed for uncontrolled Markov process problems and can be used to account for the contract early surrender, as, e.g., in [
9]. However, it cannot be used to estimate the full optimal withdrawal strategy. This is because dynamic withdrawals affect the paths of the underlying wealth account and one cannot carry out a forward simulation step required for the subsequent regression in the backward induction. However, it should be possible to apply the control randomization methods extending Least-Squares MC to handle the optimal stochastic control problems with controlled Markov processes, as was recently developed in Kharroubi et al. [
16]. The idea is to first simulate the control (withdrawals) and the state variables forward in time, where the control is simulated independently from other variables. Then, use a regression on the simulated state variables and control to estimate the expectation in (30) and find the optimal withdrawal using (31). However, the accuracy and robustness of this method for pricing withdrawal benefit type products have not been studied yet. As usual, it is expected that the choice of the basis functions for the required regression step will have significant impact on the performance. We also note that in some simple cases of the withdrawal strategy admissible space such as bang-bang (no withdrawal, withdrawal at the contractual rate, or full surrender), it is possible to develop other modifications of Least-Squares MC such as in [
11] for pricing of the GLWB rider.
The expectation in (30) can also be calculated using PDE or direct integration methods. In both cases, the modeller discretizes the space of the state variables and then calculates the contract value for each grid point. The PDE for calculation of expected value (30) under the assumed risk-neutral process for the risky asset
is easily derived using Feynman-Kac theorem; for a good textbook treatment of this topic, see, e.g., [
29]. However, the obtained PDE can be difficult or even not practical to solve in the high-dimensional case. In the case of the geometric Brownian motion process for the risky asset (9), the governing PDE in the period between the event times is the one-dimensional Black-Scholes PDE, with the jump conditions (31) at each event time to link the prices at the adjacent periods. Since the benefit base state variable
remains unchanged within the interval
, the contract value
satisfies the following PDE with no explicit dependence on
A,
This PDE can be solved numerically using, e.g., Crank-Nicholson finite difference scheme for each
A backward in time with the jump condition (31) applied at the contract event times. This has been done, e.g., in [
4,
5] for pricing GMWB with discrete optimal withdrawals. Of course, if the volatility or/and interest rate are modelled as diffusion processes, then extra dimensions will add to the PDE making it more difficult to solve. [
10] used the PDE approach to calculate VA rider prices in the case of stochastic regime-switching volatility and interest rate. In this case the required PDE to be solved is still one-dimensional that allows to develop a very efficient numerical valuation.
Under the direct integration approach, the expected value (30) is calculated as an integral approximated by summation over the space grid points, see, e.g., [
1]. More efficient quadrature methods (requiring less points to approximate the integral) exist. In particular, in the case of a geometric Brownian motion process for the risky asset, it is very efficient to use the Gauss-Hermite quadrature as developed in [
26] and applied for GMWB pricing in [
7].
Section 6.3 provides detailed description of the method for pricing VA riders in general. This method can be applied when the transition density of the underlying asset between the event times
or it’s moments are known in closed form. It is relatively easy to implement and computationally faster than PDE method because the latter requires many time steps between the event times. In [
12], this method was also used to calculate GMWB in the case of stochastic interest rate under the Vasicek model.
In both PDE and direct integration approaches, one needs some interpolation scheme to implement the jump condition (31), because state variables located at the grid points of the discretized space do not appear on the grid points after the jump event. This will be discussed in detail in
Section 6.4. Of course, if the underlying stochastic process is more complicated than geometric Brownian motion (9) and does not allow efficient calculation of the transition density or its moments, one can always resort to PDE method.
In our numerical examples of GMAB pricing in
Section 7, we adapt a direct intergation method based on the Gauss-Hermite integration quadrature applied on a cubic spline interpolation,
hereafter referred to as GHQC. For testing purposes, we also implemented Crank-Nicholson finite difference (FD) scheme solving corresponding PDE (38) with the jump condition (31).
6.2. Overall Algorithm Description
Both PDE and direct integration numerical schemes start from a final condition for the contract value at . Then, a backward time stepping using (30) or solving corresponding PDE gives solution for the contract value at . Application of the jump condition (31) to the solution at gives the solution at from which further backward in time recursion gives solution at . For simplicity assume that there are only and state variables. The numerical algorithm then takes the following key steps.
| Algorithm 1 Direct Integration or partial differential equation (PDE) method |
Step 1. Generate an auxiliary finite grid to track the benefit base balance A. Step 2. Discretize wealth account balance W space as to generate the grid for computing the expectation (30). Step 3. At , apply the final condition at each node point , , to get . Step 4. Evaluate expectation (30) for each , , to obtain either using direct integration or solving PDE. In the case of direct integration method, this involves one-dimensional interpolation in W space to find values of at the guadrature points different from the grid points. Step 5. Apply the jump condition (31) to obtain for all possible values of and find that maximizes . In general, this involves a two-dimensional interpolation in space. Step 6. Repeat Steps 4 and 5 for . Step 7. Evaluate integration (30) for the backward time step from to to obtain solution at and , or may be at several points if these are needed for calculation of some hedging sensitivities such as Delta and Gamma discussed in Section 6.5.
|
In our implementation of the direct integration method based on the Gauss-Hermite quadrature for numerical examples in
Section 7, we use a one-dimensional cubic spline interpolation required to handle integration in Step 4 and a bi-cubic spline interpolation to handle jump condition in Step 5.
If the model has other stochastic state variables (similar to W) changing stochastically between the contract event times, such as stochastic volatility and/or stochastic interest rate, then grids for these extra dimensions should be generated and the required integration or PDE to evaluate (30) will have extra dimensions. Also, extra auxiliary state variables (similar to A) unchanged between the contract event times, such as tax base and/or extra benefit base, will require extra dimensions in the grid and interpolation for the jump condition at the event times.
We have to consider the possibility of
goes to zero due to withdrawal and market movement, thus one has to use the lower bound
. The upper bound
should be set sufficiently far from the initial wealth at time zero
. A good choice of such a boundary could be based on the high quantiles of distribution of
. For example, in the case of the geometric Brownian motion process (1), one can set conservatively
Often, it is more efficient to use an equally spaced grid in space. In this case, cannot be set to zero and instead should be set to a very small value (e.g., . Also, for some VA riders, using equally spaced grid in space is also more efficient.
6.3. Direct Integration Method
To compute
, we have to evaluate the expectations in the recursion (30). Assuming the conditional probability density of
given
is known in closed form
, the required expectation (30) can be calculated as
where
The above integral can be estimated using various numerical integration (
quadrature) methods. Note that, one can always find
as a transformation of the standard normal random variable
Z as
where
is the standard normal distribution, and
and
are the distribution and its inverse of
. Then, the integral (39) can be rewritten as
This type of integrand is well suited for the Gauss-Hermite quadrature that for an arbitrary function
gives the following approximation
Here,
q is the order of the Hermite polynomial,
are the roots of the Hermite polynomial
, and the associated weights
are given by
This approximate integration works very well if function is without singularities and it calculates the integral exactly if is represented by a polynomial of degree or less.
Note that is known only at the grid points , and interpolation is required to estimate at the quadrature points. From our experience with pricing different VA guarantees, we recommend the use of the natural cubic spline interpolation which is smooth in the first derivative and continuous in the second derivative; and the second derivative is assumed zero for the extrapolation region above the upper bound.
Of course it can be difficult to find the distribution
and its inverse
in general. In the case of geometric Brownian motion process (1), the transition density
is just a lognormal density and
Then, a straightforward application of the Gauss-Hermite quadrature for the evaluation of integral (39) gives
that should be calculated for each grid point
,
. Often, a small number of quadrature points is required to achieve a very good accuracy; in our numerical examples in the next section we use
but very good results are also obtained with
.
If the transition density function from
to
is not known in closed form but one can find its moments, then the integration can also be done with similar efficiency and accuracy by the method of matching moments as described in [
7,
26]. The method also works very well in the two-dimensional case, see, e.g., [
12] where it was applied for GMWB pricing in the case of stochastic interest rate.
6.4. Jump Condition Application
Either in PDE or direct integration method, one has to apply the jump condition (31) at the event times to obtain . For the optimal strategy, we chose a value of withdrawal maximizing the value .
To apply the jump conditions, for each
, we associate a continuous solution using (42) and interpolation. In general, as can be seen from (31), the jump condition makes it impractical, if not impossible, to ensure the values of
W and
A after the jump to always fall on a grid point. Thus a two-dimensional interpolation is required. In this work we adopted the bi-cubic spline interpolation for accuracy and efficiency.
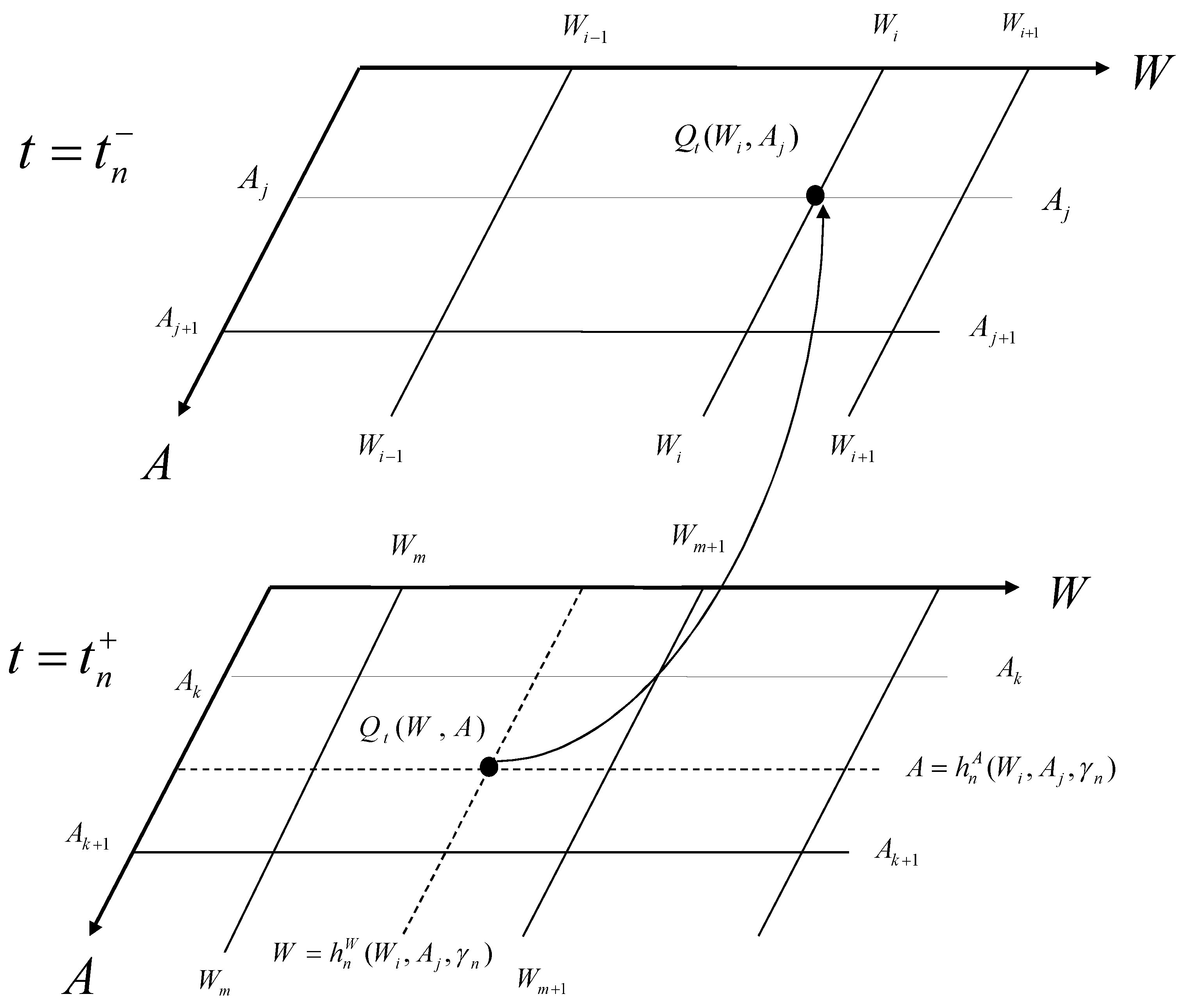
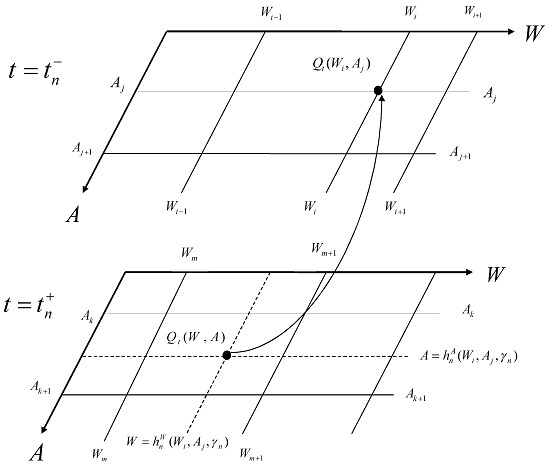
Figure 1 illustrates the application of jump conditions.
It is natural to form a uniform grid in
A so that optimal withdrawal strategies can be tested on a constant increment
, as has been done successfully in [
7] for pricing of a basic GMWB specified by (14) and (15). However, extensive numerical tests show that if a uniform grid in
A is used for pricing GMAB with ratchets and optimal withdrawals (our numerical example in
Section 7), then neither linear interpolation nor cubic interpolation in
A can achieve an efficient convergence in pricing results. A very fine mesh has to be used before we see a stable solution, which can take up to several hours to obtain a fair fee, in sharp contrast to the basic GMWB where less than one minute computer time is required. On the other hand, if we make the grid in
A uniform in
and use a linear or cubic interpolation based on variable
Y, then we obtain a very good convergence on a moderately fine grid and the CPU time for a fair fee is about 30 min (a few minutes for a fair price). The CPU used for all the calculations in this study is Intel(R) Core(TM) i5-2400 @3.1GHz.
As we have already mentioned, a two-dimensional interpolation has to be used for applying the jump condition. We suggest to use either a bi-linear interpolation or a bi-cubic spline interpolation, e.g., see (see Section 3.6 in [
44]), in both cases applied on the log-transformed state variables
and
. For numerical examples in this paper, we have adapted the more accurate bi-cubic spline interpolation for all the numerical results.
For uniform grids, the bi-cubic spline is about five times as expensive in terms of computing time as the one-dimensional cubic spline. Suppose the jump condition requires the value at the point located inside a grid: and . Equivalently, the point and is inside the grid: and . Because the grid is uniform in both X and Y variables, the second derivatives and can be accurately approximated by the three-point central difference, and consequently the one-dimensional cubic spline on a uniform grid involves only four neighboring grid points for any single interpolation. For the bi-cubic spline, we can first obtain at four points , , , by applying the one-dimensional cubic spline on the dimension for each point and then we can use these four values to obtain through a one-dimensional cubic spline in . Thus five one-dimensional cubic spline interpolations are required for a single bi-cubic spline interpolation, which involves sixteen grid points neighboring point.
6.5. Calculating Greeks for Hedging
Calculation of the contract price in (30) under the risk-neutral probability measure
means that one can find a portfolio replicating the VA guarantee (assuming mortality risk is fully diversified), i.e., perform hedging eliminating the financial risk. Finding correct hedging depends on the underlying stochastic model for the risky asset. The basic hedging is the so-called
delta hedging eliminating randomness due to stochasticity in the underlying risky asset
. Here, we use
as a tradable asset to hedge the exposure of the guarantee to the wealth account
. One can construct a portfolio consisting of the money market account and
units of
, so that
, where
is the number of units of the wealth account referred as
. Denote the value of the VA guarantee as
which is just a difference between the contract value with the guarantee
and the value of the wealth account
W, i.e.,
Then, under the delta hedging strategy, one has to select
for time
t between the contract event times. Of course if there are extra stochasticities in the model such as stochastic interest rate and/or stochastic volatility, delta hedging will not eliminate risk completely and hedging with extra assets will be required which is model specific. See, e.g., [
10], for constructing hedging in the case of regime switching stochastic volatility and interest rate. A popular active hedging strategy in the case of extra stochastic factors is the minimum variance hedging strategy, where
is selected to minimize the variance of portfolio’s instantaneous changes, e.g., applied in [
11] for hedging GLWM in the case of stochastic volatility model.
Practitioners also calculate other sensitivities (partial derivatives) of the contract with respect to the interest rate and volatility (referred to as
and
) and even second partial derivatives such as
to improve hedging strategies. Here, we refer the reader to the standard textbooks in the area of pricing financial derivatives such as [
30] or [
31].
Numerical estimation of the contract sensitivities (referred to as Greeks) is more difficult than estimation of the contract price. A general standard approach to calculate the Greeks is to perturb the relevant parameter and re-calculate the price. Then one can use a two-point central difference to estimate the first derivatives and a three-point central difference for the second derivatives. In general, the finite difference PDE (or direct integration) methods generally produce superior accuracy in calculating Greeks when compared to the Monte Carlo method (at least for low dimensions when the finite difference method is practical or direct integration is possible). For and , the finite difference method (or direct integration method) yields second order accurate values without re-calculating price using prices already calculated at the uniform grid points.
More accurate calculation of the main Greeks,
and
, can be achieved using the so-called
likelihood method as follows. The contract price at
is calculated in the last time step
in backward induction as an integral (39). Differentiating (39) with respect to
,
can be found as
Thus it can be calculated using the same direct integration method as used for
with the factor
added to the integrand. Similarly, the required derivative to calculate
can be found as
Note, the above integrations for Delta and Gamma are only required for the
time step and for a single grid point
. Here,
should be understood as the current contract valuation time rather than time when the contract was initiated. Equivalently, for the PDE approach using finite difference method, one can sometimes derive the corresponding PDEs for the Greeks and solve these PDEs for the last time step, see, e.g., [
45]. Similarly for Monte Carlo method, simulations used to calculate the price can be used to calculate
and
weighted with extra factors under the expectations in (44) and (45).
It is illustrative to show how to derive a hedging portfolio under the basic Black-Scholes model. Here, we assume that the underlying risky asset
follows
where
is the standard Brownian motion under the physical (
real) probability measure, and
is the real drift. Then the wealth account evolution is
Here, we assume a continuously charged fee proportional to the wealth account but it is not difficult to deal with the case of discretely charged fees.
To hedge, the guarantee writer takes a long position in
units of
, i.e., forms a portfolio
By Ito’s lemma, the changes of portfolio within
,
are
where the last term
is the fee amount collected over
. Setting
eliminates all the random terms in (47), making the portfolio locally riskless. This means that the portfolio earns at the risk-free interest rate
, i.e.,
, leading to the PDE
Substituting in the above gives the PDE for , the total value for the contract with the guarantee, i.e., the same as (38). Recalling Feynman-Kac theorem, it is easy to see that the stochastic process for W corresponding to this PDE is the risk-neutral process (9).
7. Numerical Example: GMAB Pricing
Numerical solutions for pricing VA riders involve many complicated numerical procedures and features. These are more involved when compared to pricing of most exotic derivatives in financial markets. It is important that these solutions are properly tested and validated. As a numerical example for illustration, using direct integration method (GHQC), we calculate accurate prices of GMAB with possible annual
ratchets, allowing optimal withdrawals and no death benefit as specified in
Section 4.3. With these features, the GMAB rider is very close to the real product marketed in Australia by, e.g., [
27,
28]. We assume geometric Brownian motion model for the risky asset (9). When applicable, we compare results with the MC and finite difference PDE methods. Numerical difficulties encountered in pricing this GMAB rider are common across other VA guarantees. Also, comprehensive numerical pricing results for this particular product are not available in the literature. These validated results (reported for a range of parameters) can serve as a numerical benchmark for practitioners and researchers developing numerical pricing of the VA with guarantees. We consider four GMAB types:
GMAB with the annual ratchets but no withdrawals. In this case, a standard MC method can be used to compare with GHQC results—this is a good validation of the implemented numerical functions related to the ratchet feature, in addition to validating the numerical integration based on the Gauss-Hermite quadrature.
GMAB with the annual ratchets and regular withdrawals of a fixed percentage of the wealth account. In this case a standard MC method can also be used to compare with GHQC results—this is a good validation of implemented numerical functions related to jump conditions due to both ratchet and withdrawal features. In addition, in order to test the numerical functions related to the application of penalties, we assume a pension account where the static withdrawal rate is set above the penalty threshold.
GMAB with the optimal quarterly withdrawals and the annual ratchets for a super account, where the penalty (24) is applied on any withdrawal when .
GMAB with the optimal quarterly withdrawals and the annual ratchets for a pension account, where the penalty (25) is applied if the withdrawal is above the penalty threshold and if .
As a comparison, results from our PDE finite difference implementation will also be shown for Case 4, the most complicated example among the four listed above. In addition, we will also calculate results for Case 4 in the case of the guarantee fee charged discretely (quarterly). All reported GHQC results are based on quadrature points. We did not observe any material difference in results if q is increased further. Results based on are also very accurate.
7.1. GMAB with Ratchet and No Withdrawal
Consider a GMAB rider with the annual ratchet and no withdrawals. In this case a standard MC method can be used to compare with GHQC results which is a good validation of implemented numerical functions related to the
ratchet feature.
Table 1 compares GHQC and MC results for the fare fee
α of GMAB with the annual ratchet for the interest rate
r ranging from
to
and the volatility
and
. The maximum relative difference between the two methods is
at the interest rate
and the volatility
. The maximum absolute difference between the two methods is one basis point at the lowest interest rate
where the fee is the highest. On average, the relative difference is
and the absolute difference is 0.5 basis point, which is 5 cents per year on a one thousand dollar account. The GHQC results are obtained with the mesh size
and
, and on the average it takes 22 s per price (calculation of the fare fee requires iterations over several prices). The MC results are obtained using 20 million simulations and it takes about 62 s per price.
The agreement between the two methods at is also very good. In absolute terms, the maximum difference between the two methods is 1.1 basis point at the lowest interest rate . In relative terms, the maximum difference between the two methods is at the highest interest rate . On average, the relative difference is which is significantly smaller than the corresponding case at .
7.2. GMAB with Ratchet and Static Withdrawal
Consider a GMAB rider with the annual ratchet and a regular quarterly withdrawals of a fixed percentage of the wealth account. In this case a standard MC method can also be used to compare with the GHQC results which is a good validation of implemented numerical functions related to jump conditions due to both ratchet and withdrawal features. Here, we consider a pension type account with the penalty given by (25). In this case, regular withdrawals at a pre-determined percentage level are allowed. In order to test the numerical functions related to the application of penalty, we also consider the static withdrawal above a pre-determined threshold level that will attract a penalty. We set the withdrawal threshold at of the wealth account per annum, and the withdrawal frequency is quarterly, i.e., the quarterly withdrawal threshold is of the wealth account.
In the first test we allow a regular quarterly withdrawal of
of the wealth account balance, i.e.,
and there is no penalty on the withdrawals.
Table 2 compares the GHQC and MC results for the fare fee
α. In relative terms, the maximum difference between the two methods is
at interest rate
. On average, the relative difference is
and the absolute difference is 0.3 basis point. The GHQC results are obtained with the mesh size
and
, and the MC results are obtained with 20 million simulations per price.
Comparing with
Table 1, the fair fee for the static withdrawal is about
higher than the corresponding no-withdrawal case at the lowest interest rate
, but it is about
lower than the corresponding no-withdrawal case at
. We have also tested static
quarterly withdrawals and obtained the same pattern: at the lower interest rate the fair fee of static withdrawal (which is also below the penalty threshold) is higher than the corresponding no-withdrawal case, and at the higher interest it is the opposite. These differences in the fair fees at relatively low and high interest rates can be broadly interpreted as follows. At the lower interest rates, where the expected capital growth is relatively slow, it is better to perform a regular withdrawal at or below the penalty threshold and take the protected capital at the maturity. However, at the higher interest rates, where the expected capital growth rate is also high, it is beneficial not to carry out a regular withdrawal and keep the capital to grow.
The above test also demonstrates that the MC and GHQC methods agree very well for pricing GMAB with a static withdrawal not exceeding the penalty threshold. This confirms the accuracy and efficiency of our numerical implementation of the jump condition using a bi-cubic interpolation in GHQC method.
In the second test of static withdrawal, we allow a regular quarterly withdrawal of
(
per annum), i.e., the annual withdrawal rate is slightly higher than the penalty threshold of
per annum and there is a penalty applied for each withdrawal. The GHQC and MC results for this test are also presented in
Table 2. In absolute terms, the maximum difference between the two methods is only 0.07 basis point at the interest rate
, which is less than 1 cent per year for a one thousand dollar account. In relative terms, the maximum difference between the two methods is
at the interest rate
. On average the relative difference is only
, which shows the two methods also agree very well in the case of excessive static withdrawals, where the penalty is applied for each withdrawal. This is a very convincing validation that our GHQC implementation of all numerical functions associated with the jump conditions, including the bi-cubic spline interpolation, is correct and accurate. The above tests are very close to validation of the entire algorithm in the case of optimal withdrawals. This is because in pricing the optimal withdrawal case, exactly the same integration and interpolation functions are used, and the only extra step required is to find the withdrawal rate maximizing the price. Nevertheless, for optimal strategy cases we will carry out some further validations by comparing results between GHQC and finite difference PDE methods.
Comparing
Table 2 with
Table 1 for the no-withdrawal case, the fair fee for the static withdrawal in excess of the penalty threshold is dramatically reduced: it is reduced by about
from the corresponding no-withdrawal case at
, and it is reduced by about
at
. Thus, a regular withdrawal above the penalty threshold is a very bad strategy regardless the interest rate level. In this instance, the penalty takes away the protected capital on a regular basis. Note that, the penalty is applied in terms of the whole withdrawal amount, not just on the exceeded part, see penalty function (25). Thus a slight excess over the penalty threshold can cause a large change in the price or in the fair fee, as observed in the second test.
The above two tests show that a regular static withdrawal is only slightly beneficial at very low interest rate and only when the withdrawal rate does not exceed the penalty threshold. In the next section, it will be demonstrated by numerical results that an optimal withdrawal is always beneficial regardless the interest rate level and penalties.
7.3. Optimal Withdrawal—Super Account
Consider a GMAB for a super account with the annual ratchet and assume that the policyholder can exercise an optimal withdrawal strategy quarterly. For a super account, any withdrawal will penalize the protected capital amount (benefit base) if the wealth account is below the benefit base according to (23) and (24).
Table 3 shows the fair fee for a super account as a function of the interest rate at
and
. The columns under
show an extra percentage value in the fee due to optimal withdrawal when compared to the static case of no withdrawal in
Table 1. The results show, the extra fee is only about one or two percent for most cases, except at the low interest rate and high volatility. This extra fee due to optimal withdrawal is insignificant for the super account in most cases, mainly due to the heavy penalties applied. As will be shown in the next section, if the penalty is less severe as in the case of pension account, the extra fee becomes much more significant. If the penalty is completely removed, then numerical experiments show that the extra fee will be several times, e.g.,
, larger than the static case, demonstrating the full value of the optimal strategy.
7.4. Optimal Withdrawal—Pension Account
Consider a GMAB for a pension account with the annual ratchet and assume that the policyholder can exercise an optimal withdrawal strategy quarterly. For a pension account, any withdrawal above a pre-defined withdrawal level will penalize the protected capital amount if the wealth account is below according to (23) and (25). Here, we set the annual withdrawal limit at of the wealth account, i.e., is quarterly withdrawal threshold.
Table 4 shows the fair fee of GMAB for a pension account as a function of the interest rate
r when
and
. The columns under
show an extra percentage value in the fee due to optimal withdrawal when compared to the static case of no withdrawal in
Table 1. The results show, the extra fee ranges from about
at the highest interest rate
to about
at the lowest interest rate
. This extra fee is much more significant than in the case of super account, see
Table 3, apparently due to reduced penalties. At
, the extra fee ranges from about
at the highest interest rate
to about
at the lowest interest rate
. This extra fee is higher than in the case of lower volatility
, in both percentage and absolute terms.
Also, in
Table 4, the numbers in the parentheses next to the continuous fair fee values
α are the GHQC results for the discretely charged fair fee
, where at the end of each quarter
, the policyholder wealth account is charged a fee proportional to the account value
, see the wealth process (7). Results show only little difference between the continuous fee
α and the discrete fee
. On average, the relative difference is
. Of course, at a higher frequency of charging fee (e.g., a monthly fee), the difference will be even less.
The last column in
Table 4 shows the continuous fee calculated using our PDE finite difference (FD) method. The agreement between the GHQC (quadrature method) and FD method is very good. The average relative difference in the fair fees between the two methods is
.
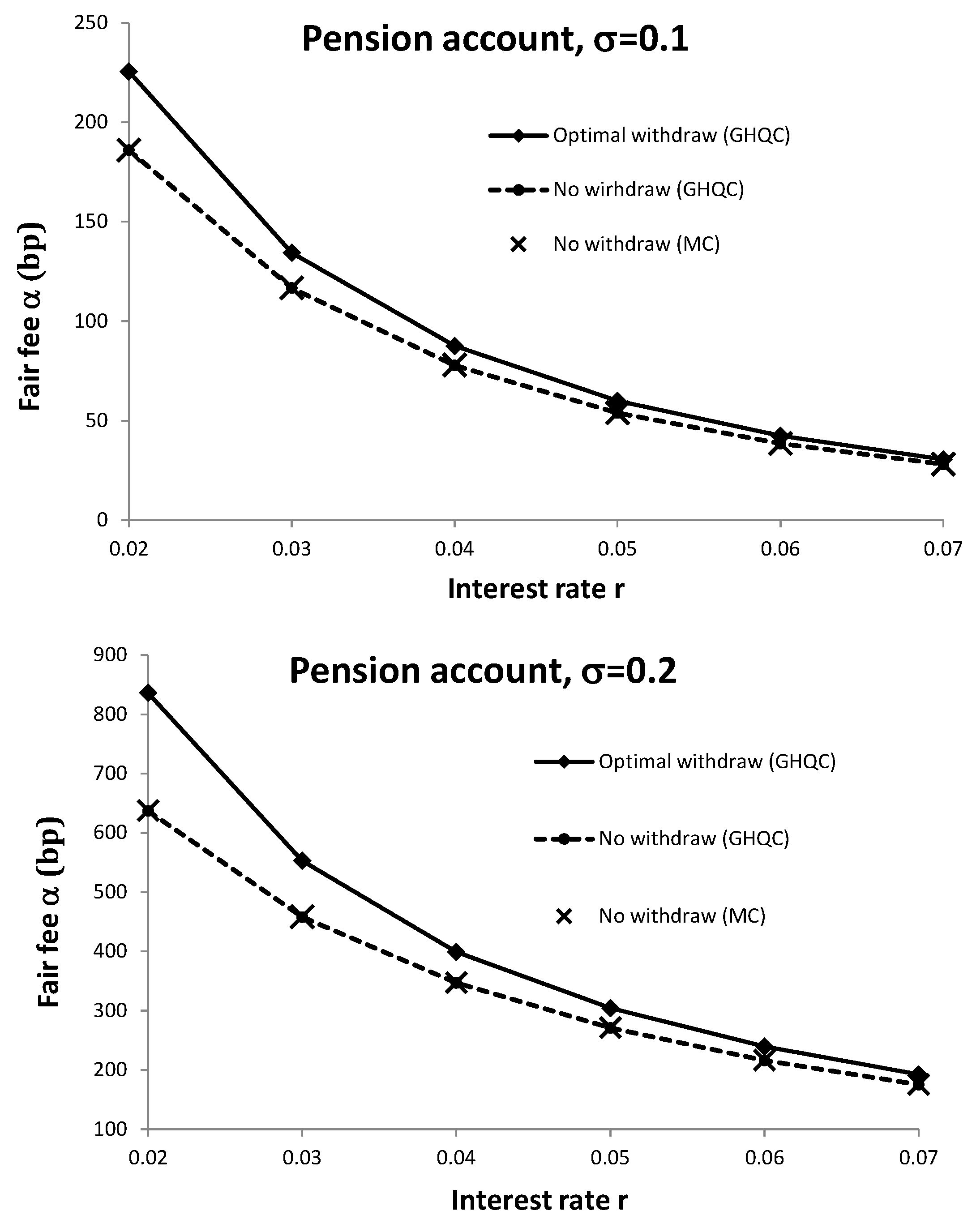
Figure 2 show the curves of the fair fee for a pension account as a function of interest rate
r using results from
Table 4, in comparison with the static case (no withdrawal) from
Table 1.
For some comparison, the market fees offered by [
28] are 1.75% for a 10 year capital protection of a “balanced portfolio” and 0.95% for a “conservative growth portfolio”; and fees offered by [
27] are 1.3% for a 10 year capital protection of a “balanced strategy” portfolio and 0.95% for a “moderately defensive strategy” portfolio. Though the values of volatility are not known for these market portfolios, it seems that market prices are significantly lower than the
fair fee, which is also observed in the literature before; e.g., see [
1,
6,
39].
For results in
Table 4, the average CPU time per price is 108 s for GHQC and 138 s for FD. Since all the cases have the same maturity and withdrawal frequency, the variation of CPU time among the cases under the same method is negligible. Note the speed advantage of GHQC over FD, although still significant, is not as great as in the case of the basic GMWB reported in [
7], where GHQC is several times faster than FD. This is because a much higher proportion of CPU time is spent on the two-dimensional cubic spline interpolation for applying the jump condition in the case of GMAB, and GHQC and FD use identical interpolation functions.
8. Conclusions
In this paper we have reviewed the pricing VA riders and presented a unified pricing approach via an optimal stochastic control framework. We discussed different models and numerical procedures applicable in general to most of the VA riders with various contractual specifications. To price these VA riders under the geometric Brownian motion model for the risky asset, often assumed in practice, we have extended and generalized the direct integration method based on the Gauss-Hermite quadrature, introduced earlier in [
7] for some specific and simpler product specifications.
As an example, we presented a numerical valuation of capital protection guarantees (GMAB riders), with specifications matching closely the real market products offered in Australia by, e.g., [
27,
28]. Numerical valuation of this guarantee involves all the main numerical difficulties encountered in pricing other VA riders, such as ratchets and optimal withdrawals. Numerical results have been validated by MC and finite difference PDE methods and can serve as a numerical benchmark for practitioners and researchers developing numerical pricing of VA riders to assess the accuracy of numerical implementations. As expected, we observed that the extra fee that has to be charged to counter the optimal policyholder behavior is most significant at lower interest rates and higher volatility levels, and it is very sensitive to the penalty withdrawal threshold.
As we have already discussed in
Section 5.3, the fee based on the optimal policyholder withdrawal is the worst case scenario for the issuer. That is, if the guarantee is hedged perfectly to eliminate the financial risk and mortality risk is fully diversified then this fee will
ensure no losses for the issuer (in other words a full protection against the policyholder strategy and the market uncertainty). If the issuer hedges continuously but investors deviate from the optimal strategy, then the issuer will receive a guaranteed profit. Any strategy different from the optimal is sup-optimal and will lead to smaller fair fees. Of course the strategy optimal in this sense is not related to the policyholder circumstances. The policyholder may act optimally with respect to his preferences and circumstances which may be different from the optimal strategy maximizing losses for the policy issuer. Life-cycle modelling can be undertaken to analyze and estimate sub-optimality of policyholder behaviors. However, development of the secondary markets for insurance products may expose the policy issuers to some significant risk if a fee for the guarantees is not charged to cover the worst case scenario.
It is important to note that the guarantee could be written on more than one asset (e.g., on several mutual funds). In this case it is still common for practitioners to use a single-asset proxi model to calculate the price and hedging parameters. Obviously such approach has significant drawbacks (e.g., the sum of geometric Brownian motions is not a geometric Brownian motion). The PDE and direct integration methods are not practical in high-dimensions and thus one has to rely on the MC methods to treat multi-asset case accurately. In the case of static withdrawals, it is not difficult to consider a full multi-asset model and calculate the price using a standard MC as in [
46]. However, in the case of optimal withdrawal strategies, numerical valuation in the multi-asset case will require the development of a regression type MC solving the backward recursion for processes affected by the withdrawals. One could apply
control randomization methods extending the Least-Squares MC developed in [
16], but the accuracy and robustness of this method for pricing VA riders have not been studied yet.
The specification details of VA riders typically vary across different companies and are difficult to extract and compare from the very long product specification documents. Moreover, results for specific GMxB riders presented in the academic literature often refer to different specifications. As a result, cross-validation and benchmark research studies are rare. Given that numerical solutions used for pricing of VA riders are complex, it is important that these solutions are properly tested and validated. Moreover, new products are appearing in the VA market regularly with increasing complexity that raises an important question, as discussed in [
47] and mentioned in [
23], whether new complex products are designed to suite the policyholder needs better or introduced for the purpose of
obfuscation.