Abstract
This paper features an analysis of major currency exchange rate movements in relation to the US dollar, as constituted in US dollar terms. Euro, British pound, Chinese yuan, and Japanese yen are modelled using a variety of non-linear models, including smooth transition regression models, logistic smooth transition regressions models, threshold autoregressive models, nonlinear autoregressive models, and additive nonlinear autoregressive models, plus Neural Network models. The models are evaluated on the basis of error metrics for twenty day out-of-sample forecasts using the mean average percentage errors (MAPE). The results suggest that there is no dominating class of time series models, and the different currency pairs relationships with the US dollar are captured best by neural net regression models, over the ten year sample of daily exchange rate returns data, from August 2005 to August 2015.
Keywords:
non linear models; time series; non-parametric; smooth-transition regression models; neural networks; GMDH shell JEL:
C45; C53; F3; G15
1. Introduction
The Global Financial Crisis (GFC) had a major and sustained impact on the world’s financial markets. This paper examines whether the exchange rate behaviour of four major currencies; namely the Euro, British pound, Chinese Yuan, and Japanese yen, in the context of their paired relationships with the US dollar, is better captured using a variety of nonlinear autoregressive models or by a machine learning approach. The models examined include the following nonlinear regression models: smooth transition regression model (STAR), Logistic smooth transition regressions models (LSTAR), self-exciting threshold autoregressive models (SETAR), neural network nonlinear autoregressive model (NNET), and additive nonlinear autoregressive model (AAR), and further models based on the application of various regression specifications of neural network models. The relative performance of the various models is evaluated via the use of twenty day out of sample forecasts.
Franses and van Dijk (2000) [1] mention that nonlinear time series models have become fashionable tools to describe and forecast economic time series. They have been applied to macro-economic and financial variables such as unemployment, industrial production, and exchange rates. Economic and financial systems are known to frequently exhibit both structural and behavioral changes, it follows that it may be neccessary to adopt different time series models to explain the empirical data at different points in time. This is apparent in modelling exchange rate behaviour. To model nonlinear behavior in economic and financial time series, it seems natural to allow for the existence of different states of the world or regimes and to allow the dynamics to be different in different regimes.
A popular set of models assumed to apply in different regimes used to capture the dynamic behavior of the time series are autoregressive (AR) models. These might be threshold AR, self-exciting threshold AR and smooth transition AR models. This is because simple AR models are arguably the most popular time series model and are easily estimated using regression methods. By extending AR models to allow for nonlinear behavior, the resulting nonlinear models are easy to understand and interpret.
A stationary time series model is called a linear time series model if it is equivalent (for example in the mean-square sense) to:
where is a white noise andd the summation is assumed to exist in some sense. Simple linear models do not appear to be successful in capturing the complexities of exchange rate movements. This might be because of the possible existence of regimes within which returns and volatility display different dynamic behaviour.
The modelling and forecasting of exchange rate behaviour remains a troublesome issue. Rogoff (1996) [2] chronicled some of the difficulties, particularly in relation to purchasing power parity (PPP). This embodies the simple empirical proposition that once converted to a single currency; national price levels should be equal. He mentions the paradoxical contrast between the extremely slow rate at which currencies appear to converge to long-run equilibrium, and the enormous volatility of short-run real exchange rate movements.
The general difficulties encountered in exchange rate modelling are discussed in Taylor and Sarno (2003) [3], and more specifically, nonlinear modelling dynamics in Taylor et al. (2001) [4] and Sarno et al. (2004) [5]. Baillie and Bollerslev (1989) [6], suggest that foreign currency rates are best characterized as pure unit-root (random walk or martingale) processes, which implies it is impossible to predict exchange rate movements. Engel and Hamilton (1990) [7] applied a Markov switching model for exchange rate changes, while Diebold and Nason (1990) [8] and Meese and Rose (1990) [9] used variants of local regression. Morana and Beltratti (2004) [10] examine long memory and structural breaks in the realized variance process for the DM/US$ and Yen/US$ exchange rates. Chang et al. (2012) [11] have analysed the hedging of major currencies using fututres contracts in a multivariate GARCH framework.
The use of neural networks to forecast exchange rate movements was initiated by studies such as Kuan and Liu (1995) [12], who used feedforward and recurrent artificial neural networks (ANN) to produce conditional mean forecasts. In recent years the argument in favour of the martingale hypothesis has been queried because of the possibility of long memory (fractional) dynamic behaviour in the foreign currency market, an approach which is adopted in this paper. Other applications of the non-linear time series models applied in this paper include Matias et al. (2012) [13] and Reboredo et al. (2012) [14], who model the behaviour of high frequency returns on the S&P 500 index using intra-day data. Gradojevic and Yang (2006) [15] compare high frequency US dollar Canadian dollar exchange rate behaviour and report that ANN models outperform linear time series models. The current paper can be viewed as an extension of the models used to non-linear time series models applied across a wider range of currency pairs. We similarly confine ourselvs to the application of ANNs and do not consider other types of machine learning techniques, such as support vector machines, in this paper.
2. Research Methods
2.1. Data Set and Econometric Models
Data Sets
The data set includes daily data for each currency, in US dollar terms, of the exchange rates paired with the Euro, British pound, Chinese yuan, and Japanese yen, taken from a ten-year period drawn from 29 August 2005 to 28 August 2015. These daily US dollar-denominated exchange rate series are sourced from the FRED database (Federal Reserve Bank of St. Louis Economic Data). Unit root tests, based on KPSS tests, and fractional integration tests, indicated that the levels series of these exchange rates are non-stationary, as shown in Table 1. Therefore we chose to work with the logarithms of the first difference, that is, log differences, of our base series, for the purposes of the modelling of these exchange rate movements and forecasts, as shown below:
where indicates the US dollar denominated exchange rate and i indexes the four series, on day t. We scaled the returns by 100 to make them easier to manage for the purposes of statistical analysis. Thus, the results are in percentage terms.

Table 1.
Tests of Stationarity
The data sets used are shown in Table 2. The tests of stationarity, featuring KPSS tests, with null hypothesis of stationarity, and tests of fractional integration, using a local Whittle approximation, are reported in Table 1. The KPSS tests strongly reject the null hypothesis of stationarity for the levels series of all four exchange rates, and the fractional integration tests all suggest values above 1. Hence, we use the logarithm of first differences of our base series.

Table 2.
List of countries and exchange rates.
A set of graphs of the base series are shown in Figure 1.
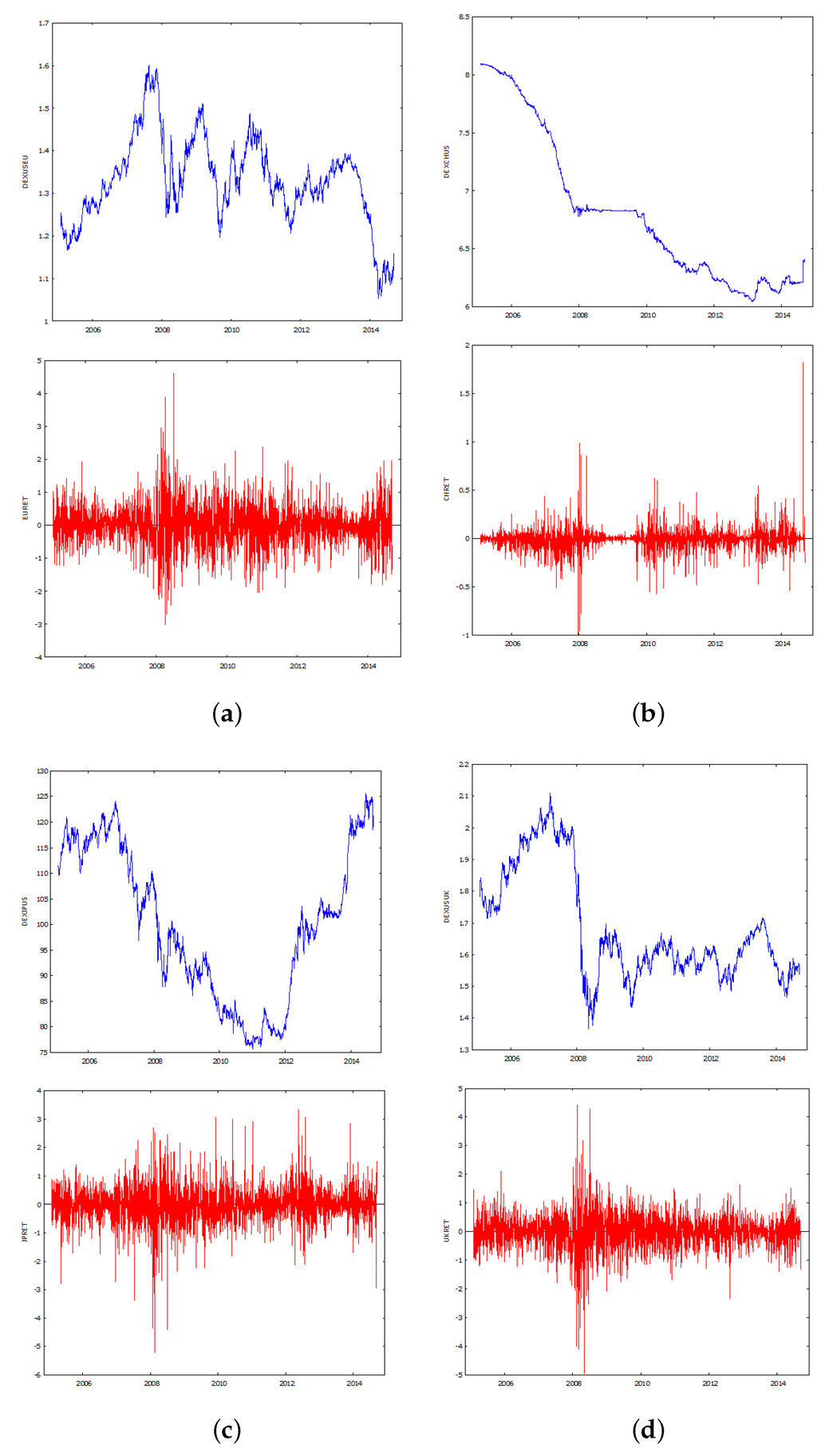
Figure 1.
Time series plots of the base series and their logarithmic differences. (a) US -EURO; (b) US-CHINA; (c) US-JAPAN; (d) US-UK.
2.2. Data Characteristics
The characteristics of the basic index series used in our data set presented in Table 3 suggest substantial departures from normal distributions.

Table 3.
Descriptive statistics
The summary statistics presented in Table 3 show that these exchange rate return series, have means and medians that are close to zero, and they are not particularly skewed. All series have excess kurtosis, which is very evident in the cases of China, and to a lesser degree in the other three.
The QQ plots, as shown in Figure 2, show that all the exchange rate return series have too many extreme observations in their tails to conform to normal distributions.
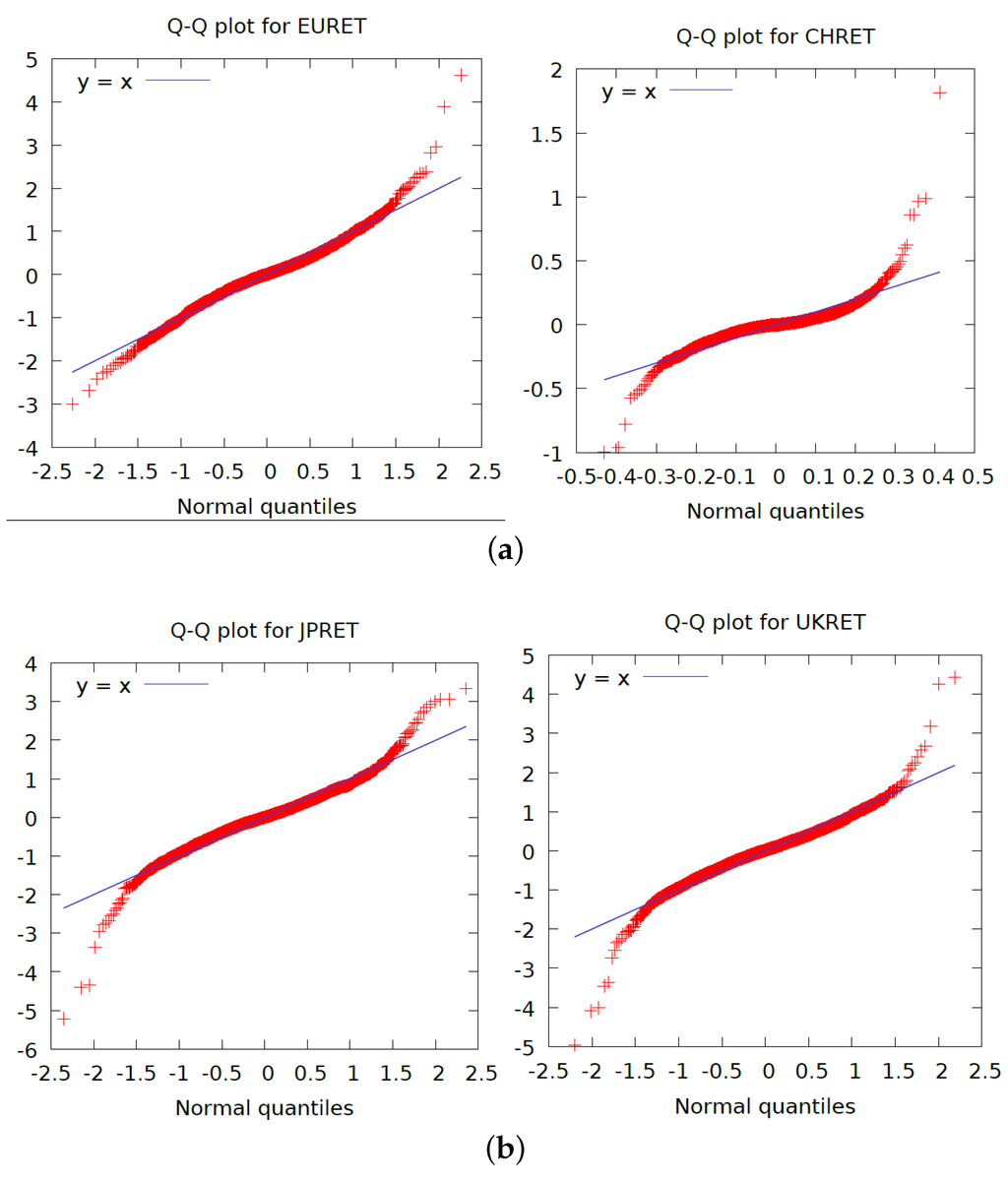
Figure 2.
QQ Plots. (a) EEU and China; (b) Japan and UK.
2.3. Econometric Methods
We use nonlinear autoregressive time series models in the analysis. Consider a discrete time stochastic process that is generated by:
with white noise, independent with respect and with f a generic function from to R. This class of models is frequently referred to as being nonlinear autoregressive of order
In Equation (2) there is an implicit definition of the embedding dimension the time delay and the forecasting steps The generic vector, indicates the vector of parameters determining the shape of which will be estimated on the basis of empirical evidence in the form of an observed time series.
A classical model can be written as:
The model in equation (3) can be estimated using conditional least squares.
A Self-Exciting Threshold Autoregressive Model (SETAR) can be written as:
with being a threshold variable. This can be variously defined for estimation purposes (see the discussion in the R package tsDyn available on Cran, https://cran.r-project.org/). A Logistic Smooth Transition Autoregressive Model (LSTAR) can be viewed as a generalisation of a SETAR model [16], and can be written as:
with G the logistic function, and the threshold variable.
A non-parametric generalised additive autoregressive model (GAM) can be written as:
where are smooth functions represented by penalized cubic regression splines.
In the empirical analysis, we used two approaches to the empirical estimation of neural network models. One was a linear approach, which is available in the R package TsDyn. A neural network model with linear input, D hidden units and activation function can be written as:
We also apply some nonlinear neural net modelling, using the GMDH shell program (http:www.gmdhshell.com). This program is built around an approximation called the “Group Method of Data Handling”. This approach is used in such fields as data mining, prediction, complex systems modelling, optimization and pattern recognition. The algorithms feature an inductive procedure that performs a sifting and ordering of gradually complicated polynomial models, and the selection of the best solution by external criterion.
A GMDH model with multiple inputs and one output is a subset of components of the base function:
where f are elementary functions dependent on different inputs, a are unknown coefficients, and m is the number of base function components.
In general, the connection between input-output variables can be approximated by Volterra functional series, the discrete analague of which is the Kolmogorov-Gabor polynomial:
where, , the input variables vector, and the vector of weights. The Kolmogorov-Gabor polynomial can approximate any stationary random sequence of observations, and can be computed by either adaptive methods or a system of Gaussian normal equations. Ivakhnenko (1968) [17] developed a new algorithm, ’The Group Method of Data Handling (GMDH)’ by using a heuristic and peceptron type of approach. He demonstrated that a second-order polynomial (Ivakhnenko polynomial: can reconstruct the entire Kolmorogorov-Gabor polynomial using an iterative peceptron-type procedure. This approach is featured in the second stage of the empirical analysis, as given below, which uses the GMDH shell software.
3. Empirical Results
3.1. Nonlinear Time Series Analysis
A summary of the results of applying the various nonlinear models to the US dollar to Euro exchange rate returns is shown in Table 4. It can be seen that none of the models is particularly effective. The additive autoregressive model for the US dollar Euro exchange rate returns, the results for which are shown in the top row of Table 4, produced an AIC value of −2444, a Mean Average Percentage error (MAPE) of 104.5% and an adjusted R-squared value of less than 1%. The MAPE values are based on 20 day out of sample forecasts.

Table 4.
Non-linear models-Euro
The two-regime SETAR model for the Euro fared slightly better in terms of AIC, with a value of −2258, but had a worse MAPE of 106.1%. Two coefficients in the high regime, which accounted for 15.6% of the total values were significant. The neural net 2-3-1 network with 13 weights faired the best with an AIC of −2317, and the lowest MAPE of 102.9%. The LSTAR model for the Euro also performed relatively poorly, with an AIC of −2259 and a MAPE of 106%.
We also report the results of running the forecast of the exchange rate change as a strict simple random walk with no drift. In this model, the prediction of the next return is the current return, which produces a MAPE for the EURO of 118% when using a one-step ahead forecast. When it was fitted as a simple linear regression, the coefficients are insignificant, and the adjusted R squared is zero. However, the time series models were used to make 20-period forecasts, which based on the random walk model, produces a MAPE of 108%, which is worse than for the time series models.
We examined various graphical analyses. Some of the results relating to the SETAR model are shown in Figure 3. In Sub-Figure 3a, we plot the original US$ Euro exchange rate return series and the residuals from the SETAR analysis, in the top of the panel, and below it in Sub-Figure 3a, we plot the autocorrelation function of the original series and that of the residuals. In Sub-Figure 3b, we plot the mutual information (MI) series and one of the lag relationships (lag −1, 0). In Sub-Figure 3c we plot lag (−1,1) plus a regime switching plot.
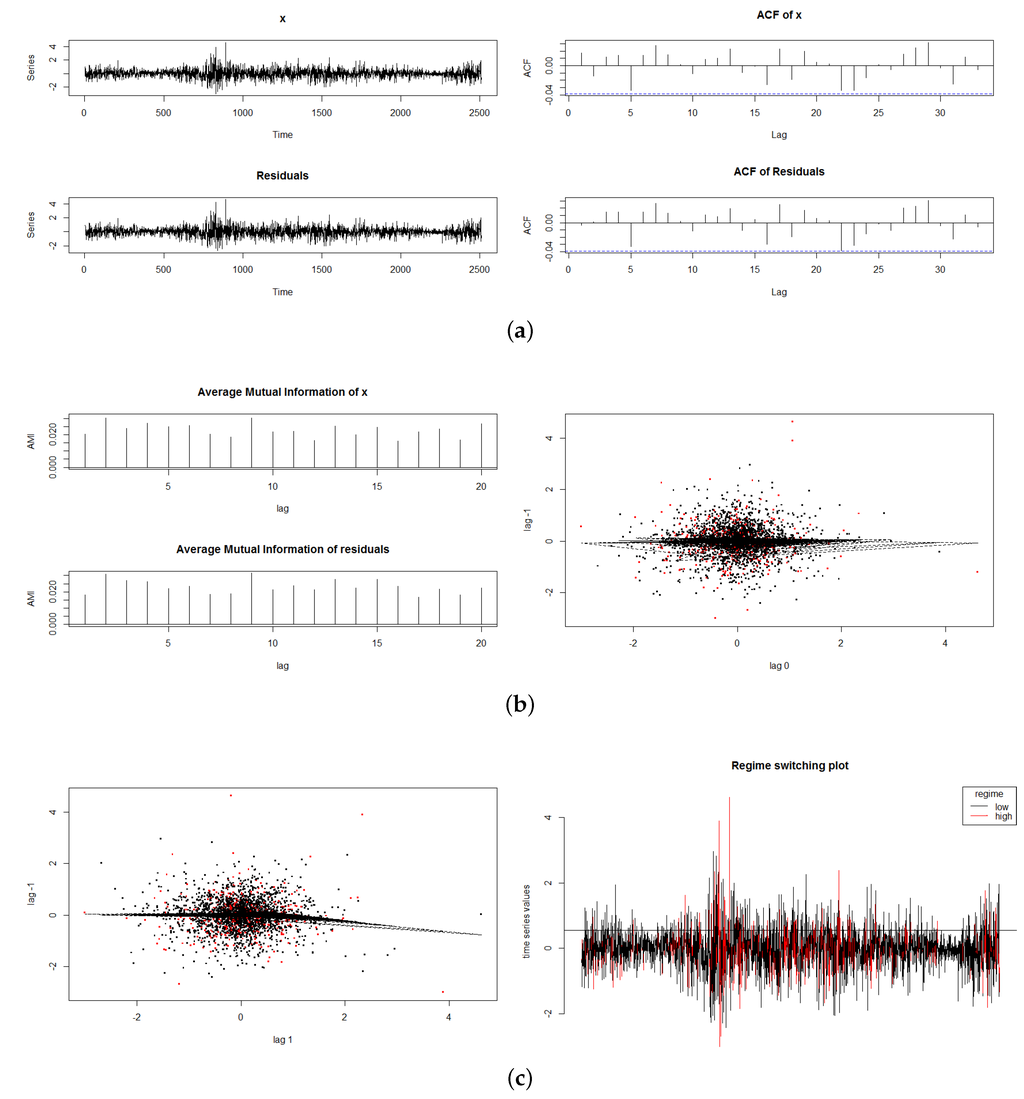
Figure 3.
SETAR analysis of US$ - Euro returns; (a) Euro SETAR Residuals and ACF; (b) MI Euro and lag −1, 0; (c) lag 1 −1 SETAR Euro and Regime Switching.
The results for the Chinese exchange rate with the US $ returns are shown in Table 5. The plots of the exchange rate series in Figure 1, Sub-Figure 1b, reveal that the Chinese exchange rate with the US $ behaves differently, is smoother, and shows evidence of exchange rate management.

Table 5.
Non-linear models-China.
However, this has not translated into a greater ease of forecasting Chinese currency exchange rate return changes. The Mean Average Percentage Errors (MAPE) range from 116% to 122%. The AIC again suggests the NNET approach is preferred, though this approach has a relatively high MAPE of 121.8%. A regression of the current return on the previous return, as discussed above, produces a statistically significant slope coefficent. However, the use of a strict random walk model to forecast the series, in a one-step ahead process, produces the lowest MAPE of 100.2%, but a 20-period forecast has a MAPE of 121.38%, which is worse than some of the time series models, for 20-period forecasts.
The results for Japan are quite clear cut. The NNET model has the highest AIC score (in absolute) terms, and the lowest MAPE, shown in Table 6, of the nonlinear methods. The results of the random walk regression are insignificant, but use of the random walk model for forecasting purposes, with one lag, produces the lowest MAPE of 88.92%, but 20 lags produce a MAPE of 104.44%. This is comparable with the time series models.

Table 6.
Non-linear models-JAPAN.
The UK results, shown in Table 7, are similar. The NNET model produces the highest absolute value of AIC, but its MAPE is 106.2%. All the other nonlinear models produce inferior results. The UK random walk regression is insignificant, with a slope coefficient close to zero, but use of a strict random walk model, or naive no change model, for forecasting purposes, for one lag, yields the lowest MAPE of 89.29%. In order to be strictly comparable with the time series models, which used 20 period forecasts, the MAPE is 110.28%, which is inferior to the time series results.

Table 7.
Non-linear models-UK.
Given that neural network analysis seemed to perform relatively well in these analyses, it was decided to extend the analysis applying non-linear neural net estimation procedures in a regression context.
3.2. Further Analysis Using Neural Nets
Regression analyses using higher order polynomials produced the models shown in Table 8. In all cases where one individul currency exchange rate return was the dependent variable in the regression analysis, only lagged terms of the other exchange rates were used. The neural network analysis produced quite complex models, with higher order terms and new variables that were complex weights of existing variables. For example, in Euro model 2, the new variable N9 is a combination of lagged observations of the Euro exchange rate return, combined with lagged observations of the Chinese exchange rate return. The neural nets were trained on 80% of the available time series observations, and the forecasts were run on the remaining 20% of observations.

Table 8.
Neural Network Regression Analysis.
Plots of the neural net model forecasts are shown in Figure 4. It is apparent that the neural net based regression models capture only a small proportion of the volatile changes in currency rate of return movements. The results for fluctuations in China appear to be better than for the other three currencies.
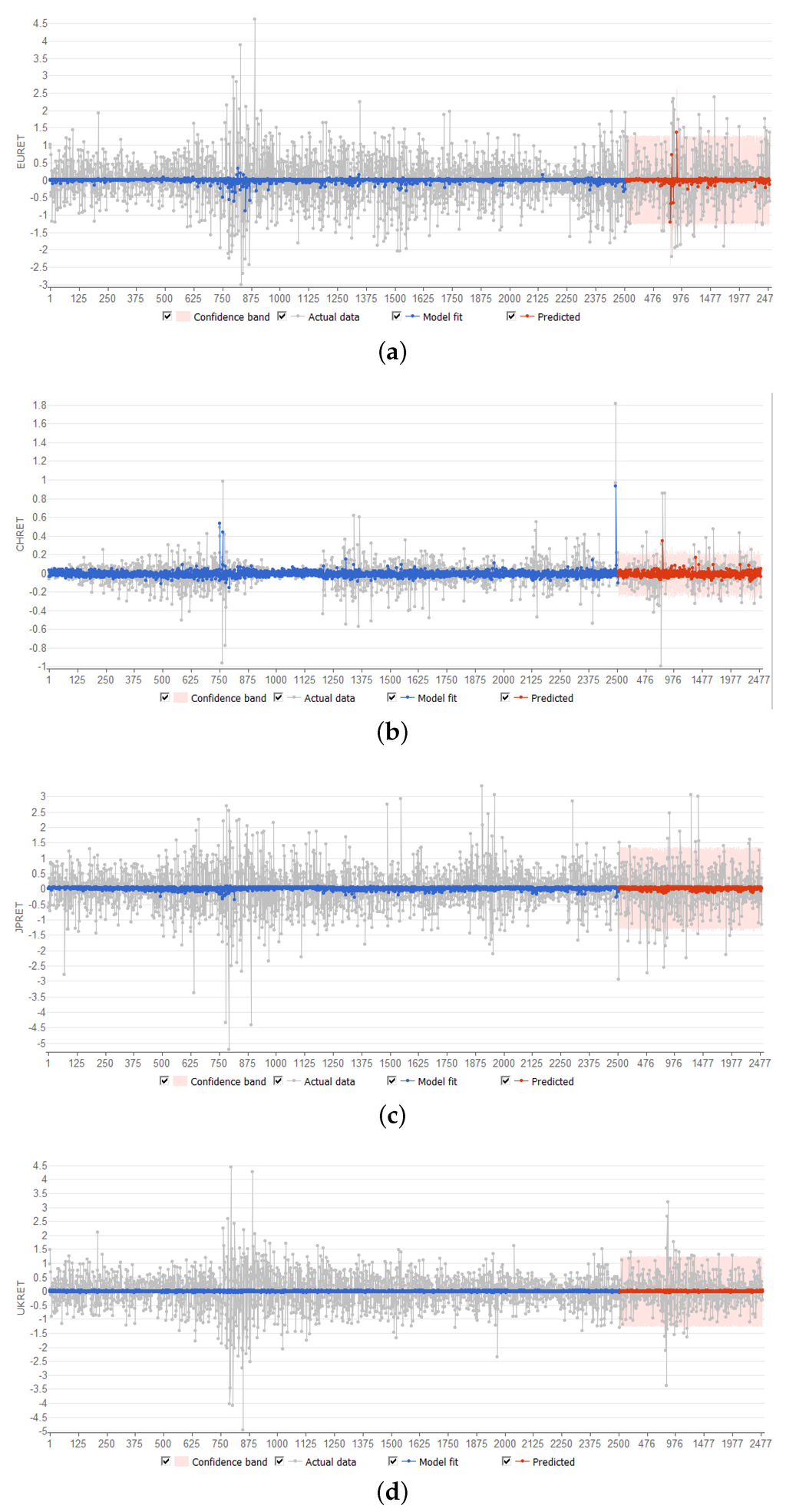
Figure 4.
Model forecasts; (a) Euro; (b) China; (c) Japan; (d) UK.
Plots of the residuals are shown in Figure 5. These reveal that the models behave reasonably well, in that the autocorrelation of residuals is of a low order, and the histograms of the residuals are unimodal. There is a clustering of observations in excess of two standard errors from the model fit, in the case of both the training and forecast periods.This is consistent with the existence of volatility clustering, and will be explored further in a subsequent paper.
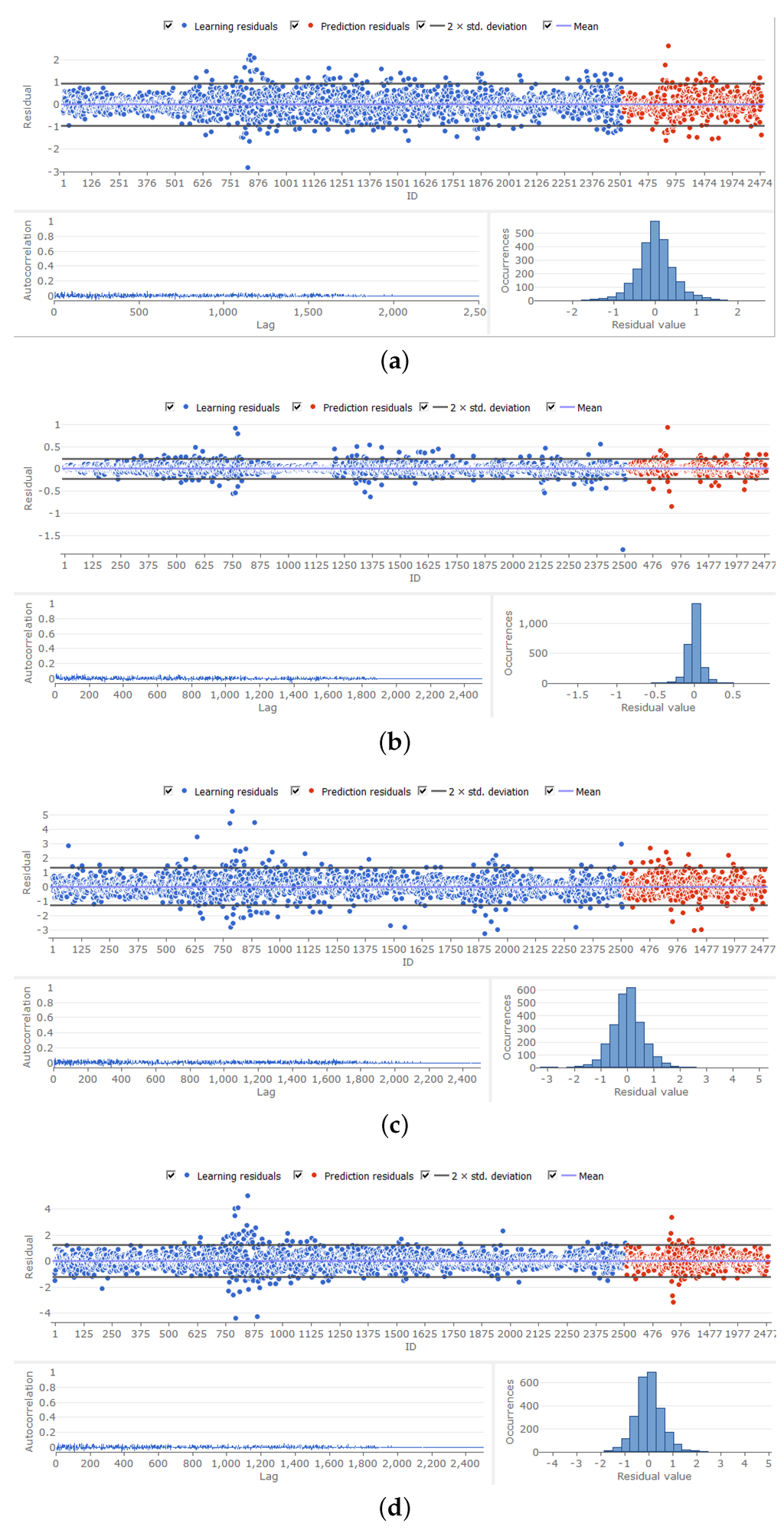
Figure 5.
Residual plots Neural Network Regression Analysis; (a) Euro; (b) China; (c) Japan; (d) UK.
The error metrics from the neural net regressions are shown in Table 9. The most successful model is for China, which has the lowest mean absolute errors of 0.067 and 0.07 for model fit and predictions, respectively, and similarly root mean square errors of 0.11 and 0.11 for model fit and predictions. The coefficient of determination is 0.10 for model fit and 0.11 for predictions, respectively. The next best model is that for the UK, with a mean absolute error of 0.44, a root mean square error of 0.62, and a coefficient of determination of 0.0011 for model fit. Its errors are lower than those for the Euro, but its coefficient of determination for model fit is lower than for the Euro 0.0068. However, the metrics for the UK predictions are better than those for the Euro. The metrics for Japan for both model fit and for predictions are relatively weak. Clearly, the managed nature of the Chinese currency makes it much easier to forecast than the other three more freely floating currencies. It appears that the neural network regression techniques, particularly in the case of China, work better than the non-linear time series regression models.

Table 9.
Neural network regression error metrics.
4. Conclusions
In this paper we have modelled exchange rate return series for four currencies, namely the Euro, Chinese Yuan, Japanese Yen, and UK pound, when paired with the US dollar, in US dollar terms. We used a variety of non-linear time series models which included the following: smooth transition regression models, logistic smooth transition regressions models, threshold autoregressive models, nonlinear autoregressive models, and additive nonlinear autoregressive models, plus linear and nonlinear Neural Network based regression models. We used the various models to produce 20 period out of sample forecasts. The resultant error metrics were then compared across models. These models were also contrasted with a random walk model with no drift, used for both one and twenty lags, to provide a naive, no-change benchmark model for purposes of comparison.
The neural network based models clearly dominated, and the non-linear regression Neural Network models appeared to be the most effective, in terms of error metrics, for forecasting purposes. The Chinese yuan exchange rate return series appeared to be the most amenable to prediction, but all series produced large errors and low coefficients of determination.
Acknowledgments
We thank the two anonymous reviewers for their helpful comments. For financial support, the first author acknowledges the Australian Research Council, and the second author is most grateful to the Australian Research Council, National Science Council, Taiwan, and the Japan Society for the Promotion of Science.
Author Contributions
Allen and McAleer conceived and designed the research methods and econometric analysis; Allen performed the analysis and obtained the data; Allen, McAleer, Peiris and Singh wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- P.H. Franses, and D. van Dijk. Nonlinear Time Series Models in Empirical Finance. Cambridge, UK: Cambridge University Press, 2000. [Google Scholar]
- K. Rogoff. “The purchasing power parity puzzle.” J. Econ. Lit. 34 (1996): 647–668. [Google Scholar]
- M.P. Taylor, and L. Sarno. The Economics of Exchange Rates. Cambridge, UK: Cambridge University Press, 2003. [Google Scholar]
- M.P. Taylor, D.A. Peel, and L. Sarno. “Nonlinear mean-revision in real exchange rates: Towards a solution of the purchasing power parity puzzles.” Int. Econ. Rev. 42 (2001): 1015–1042. [Google Scholar] [CrossRef]
- L. Sarno, M. Taylor, and L. Chowdhury. “Nonlinear Dynamics in Deviations from the Law of One Price: A Broad-Based Empirical Study.” J. Int. Money Financ. 23 (2004): 1–25. [Google Scholar]
- R.T. Baillie, and T. Bollerslev. “Common stochastic trends in a system of exchange rates.” J. Financ. 44 (1989): 167–181. [Google Scholar] [CrossRef]
- C. Engel, and J.D. Hamilton. “Long swings in the dollar: Are they in the data and do markets know it? ” Am. Econ. Rev. 80 (1990): 689–713. [Google Scholar]
- F. Diebold, and J. Nason. “Nonparametric exchange rate prediction? ” J. Int. Econ. 28 (1990): 315–332. [Google Scholar] [CrossRef]
- R.A. Meese, and A.K. Rose. “Nonlinear, nonparametric, nonessential exchange rate estimation.” Am. Econ. Rev. Pap. Proc. 80 (1990): 192–196. [Google Scholar]
- C. Morana, and A. Beltratti. “Structural change and long range dependence in volatility of exchange rates, either, neither or both? ” J. Empir. Financ. 11 (2004): 629–658. [Google Scholar] [CrossRef]
- C. Chang, L. Gonzalez-Serrano, and J.-A. Jimenez-Martin. “Currency Hedging Strategies Using Dynamic Multivariate GARCH.” Working Paper, Madrid, Spain: Department of Quantitative Economics, Complutense University Madrid, 2012. [Google Scholar]
- C.M. Kuan, and T. Liu. “Forecasting exchange rates using feedforward and recurrent neural networks.” J. Appl. Econ. 10 (1995): 347–364. [Google Scholar] [CrossRef]
- J.M. Matias, and J.C. Reboredo. “Forceasting performance of non-linear models for intra-day stock returns.” J. Forecast. 31 (2012): 172–188. [Google Scholar] [CrossRef]
- J.C. Reboredo, J.M. Matias, and R. Garcia-Rubio. “Non-linearity in forecasting of high frequency stock returns.” Comput. Econ. 40 (2012): 245–264. [Google Scholar] [CrossRef]
- N. Gradojevic, and J. Yang. “Non linear, non-parametric, non-fundamental exchange rate forecasting.” J. Forecast. 25 (2006): 227–245. [Google Scholar] [CrossRef]
- F.D. Antonio, J.L. Narzo, and A.M. Stigler. “tsDyn: Time Series Analysis Based on Dynamical Systems Theory 2009.” Available online: http://stat.ethz.ch/CRAN/web/packages/tsDyn/vignettes/tsDyn.pdf (accessed on 30 September 2016).
- A.G. Ivakhnenko. “The group method of data handling – a rival of the method of stochastic approximation.” Sov. Autom. Control Avtom. 1 (1968): 43–55. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).