1. Introduction and Motivation
Many insurance data sets feature information about how often claims arise, the frequency, in addition to the claim size, the severity. Observable responses can include:
N, the number of claims (events),
the amount of each claim (loss), and
the aggregate claim amount.
By convention, the set
is empty when
.
Importance of Modeling Frequency. The aggregate claim amount
S is the key element for an insurer’s balance sheet, as it represents the amount of money paid on claims. So, why do insurance companies regularly track the frequency of claims as well as the claim amounts? As in an earlier review [
1], we can segment these reasons into four categories: (i) features of contracts; (ii) policyholder behavior and risk mitigation; (iii) databases that insurers maintain; and (iv) regulatory requirements.
Contractually, it is common for insurers to impose deductibles and policy limits on a per occurrence and on a per contract basis. Knowing only the aggregate claim amount for each policy limits any insights one can get into the impact of these contract features.
Covariates that help explain insurance outcomes can differ dramatically between frequency and severity. For example, in healthcare, the decision to utilize healthcare by individuals (the frequency) is related primarily to personal characteristics whereas the cost per user (the severity) may be more related to characteristics of the healthcare provider (such as the physician). Covariates may also be used to represent risk mitigation activities whose impact varies by frequency and severity. For example, in fire insurance, lightning rods help to prevent an accident (frequency) whereas fire extinguishers help to reduce the impact of damage (severity).
Many insurers keep data files that suggest developing separate frequency and severity models. For example, insurers maintain a “policyholder” file that is established when a policy is written. A separate file, often known as the “claims” file, records details of the claim against the insurer, including the amount. These separate databases facilitate separate modeling of frequency and severity.
Insurance is a closely monitored industry sector. Regulators routinely require the reporting of claims numbers as well as amounts. Moreover, insurers often utilize different administrative systems for handling small, frequently occurring, reimbursable losses, e.g., prescription drugs, versus rare occurrence, high impact events, e.g., inland marine. Every insurance claim means that the insurer incurs additional expenses suggesting that claims frequency is an important determinant of expenses.
Importance of Including Covariates. In this work, we assume that the interest is in the joint modeling of frequency and severity of claims. In actuarial science, there is a long history of studying frequency, severity and the aggregate claim for homogeneous portfolios; that is, identically and independently distributed realizations of random variables. See any introductory actuarial text, such as [
2], for an introduction to this rich literature.
In contrast, the focus of this review is to assume that explanatory variables (covariates, predictors) are available to the analyst. Historically, this additional information has been available from a policyholder’s application form, where various characteristics of the policyholder were supplied to the insurer. For example, in motor vehicle insurance, classic rating variables include the age and sex of the driver, type of the vehicle, region in which the vehicle was driven, and so forth. The current industry trend is towards taking advantage of “big data”, with attempts being made to capture additional information about policyholders not available from traditional underwriting sources. An important example is the inclusion of personal credit scores, developed and used in the industry to assess the quality of personal loans, that turn out to also be important predictors of motor vehicle claims experience. Moreover, many insurers are now experimenting with global positioning systems combined with wireless communication to yield real-time policyholder usage data and much more. Through such systems, they gather micro data such as the time of day that the car is driven, sudden changes in acceleration, and so forth. This foray into detailed information is known as “telematics”. See, for example, [
3] for further discussion.
Importance of Multivariate Modeling. To summarize reasons for examining insurance outcomes on a multivariate basis, we utilize an earlier review in [
4]. In that paper, frequencies were restricted to binary outcomes, corresponding to a claim or no claim, known as “two-part” modeling. In contrast, this paper describes more general frequency modeling, although the motivation for examining multivariate outcomes are similar. Analysts and managers gain useful insights by studying the joint behavior of insurance risks,
i.e., a multivariate approach:
For some products, insurers must track payments separately by component to meet contractual obligations. For example, in motor vehicle coverage, deductibles and limits depend on the coverage type, e.g., bodily injury, damage to one’s own vehicle, or damage to another party; is natural for the insurer to track claims by coverage type.
For other products, there may be no contractual reasons to decompose an obligation by components and yet the insurer does so to help better understand the overall risk. For example, many insurers interested in pricing homeowners insurance are now decomposing the risk by “peril”, or cause of loss. Homeowners is typically sold as an all-risk policy, which covers all causes of loss except those specifically excluded. By decomposing losses into homogenous categories of risk, actuaries seek to get a better understanding of the determinants of each component, resulting in a better overall predictor of losses.
It is natural to follow the experience of a policyholder over time, resulting in a vector of observations for each policyholder. This special case of multivariate analysis is known as “panel data”, see, for example, [
5].
In the same fashion, policy experience can be organized through other hierarchies. For example, it is common to organize experience geographically and analyze spatial relationships.
Multivariate models in insurance need not be restricted to only insurance losses. For example, a study of term and whole life insurance ownership is in [
6]. As an example in customer retention, both [
7,
8] advocate for putting the customer at the center of the analysis, meaning that we need to think about the several products that a customer owns simultaneously.
An insurer has a collection of multivariate risks and the interest is managing the distribution of outcomes. Typically, insurers have a collection of tools that can then be used for portfolio management including deductibles, coinsurance, policy limits, renewal underwriting, and reinsurance arrangements. Although pricing of risks can often focus on the mean, with allowances for expenses, profit, and “risk loadings”, understanding capital requirements and firm solvency requires understanding of the portfolio distribution. For this purpose, it is important to treat risks as multivariate in order to get an accurate picture of their dependencies.
Dependence and Contagion. We have seen in the above discussion that dependencies arise naturally when modeling insurance data. As a first approximation, we typically think about risks in a portfolio as being independent from one another and rely upon risk pooling to diversify portfolio risk. However, in some cases, risks share common elements such as an epidemic in a population, a natural disaster such as a hurricane that affects many policyholders simultaneously, or an interest rate environment shared by policies with investment elements. These common (pandemic) elements, often known as “contagion”, induce dependencies that can affect a portfolio’s distribution significantly.
Thus, one approach is to model risks as univariate outcomes but to incorporate dependencies through unobserved “latent” risk factors that are common to risks within a portfolio. This approach is viable in some applications of interest. However, one can also incorporate contagion effects into a more general multivariate approach that we adopt this view in this paper. We will also consider situations where data are available to identify models and so we will be able to use the data to guide our decisions when formulating dependence models.
Modeling dependencies is important for many reasons. These include:
Dependencies may impact the statistical significance of parameter estimates.
When we examine the distribution of one variable conditional on another, dependencies are important.
For prediction, the degree of dependency affects the degree of reliability of our predictions.
Insurers want to construct products that do not expose them to extreme variation. They want to understand the distribution of a product that has many identifiable components; to understand the distribution of the overall product, one strategy is to describe the distribution of each product and a relationship among the distributions.
A recent review paper [
3] provides additional discussion.
Plan for the Paper. The following is a plan to introduce readers further to the topic.
Section 2 gives a brief overview of univariate models, that is, regression models with a single outcome for a response. This section sets the tone and notation for the rest of the paper.
Section 3 provides an overview of multivariate modeling, focusing on the “copula” regression approach described here. This section discusses continuous, discrete, and mixed (Tweedie) outcomes. For our regression applications, the focus is mainly on a family of copulas known as “elliptical”, because of their flexibility of modeling pairwise dependence and wide usages in multivariate analysis.
Section 3 also summarizes a modeling strategy for the empirical approach of copula regression.
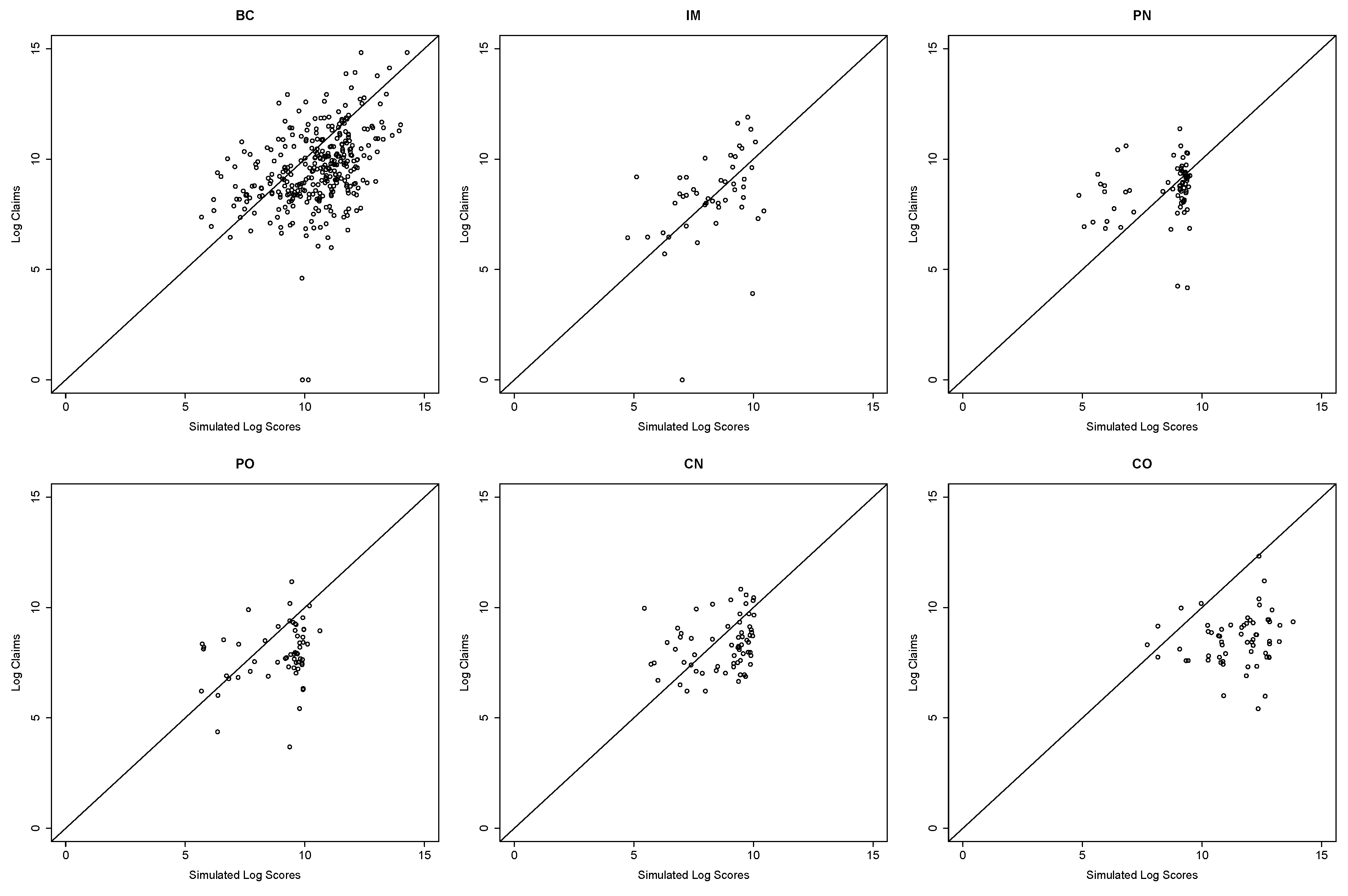
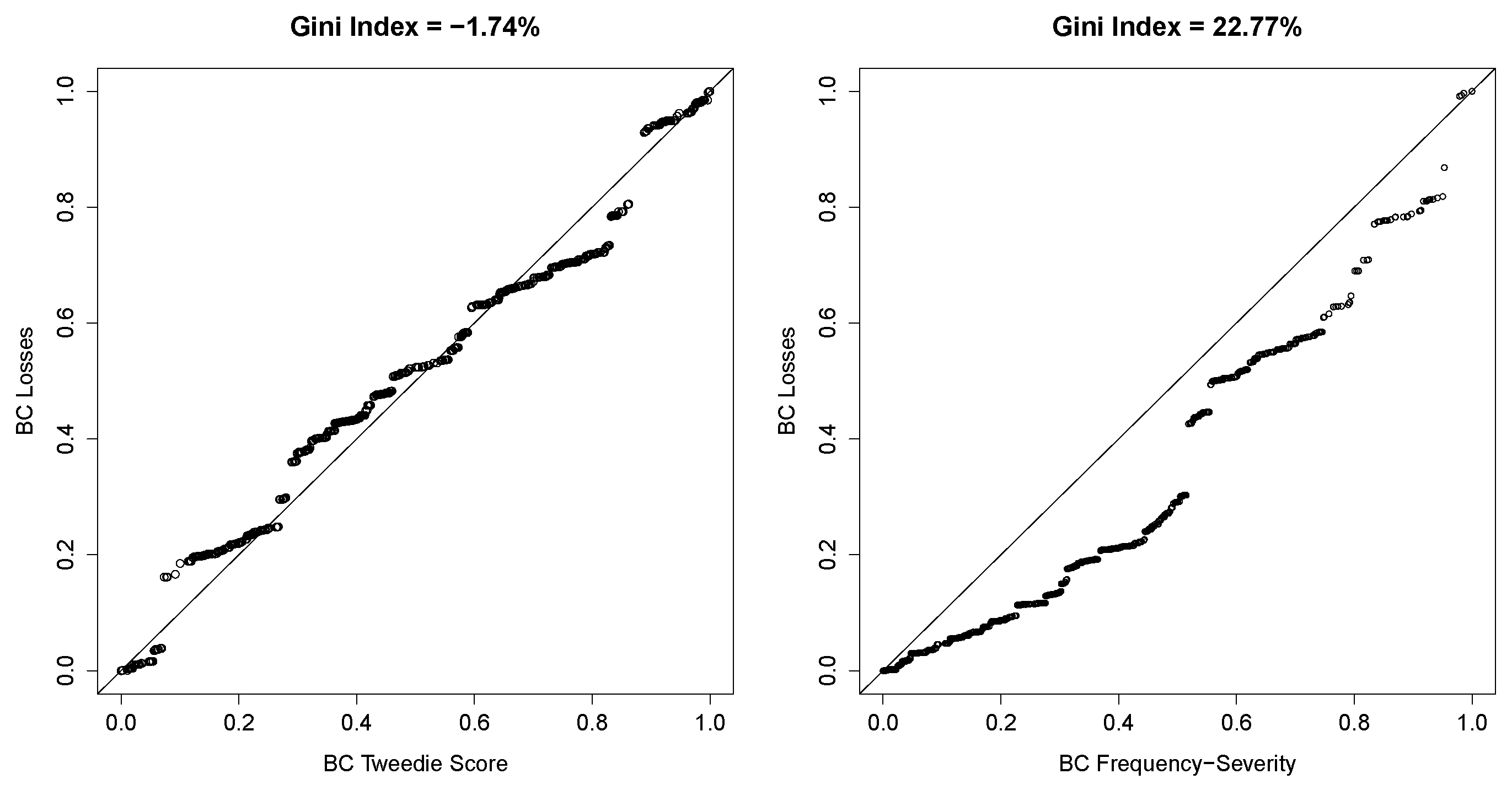
Section 4 reviews other recent work on multivariate frequency-severity model and describes the benefits of diversification, particularly important in an insurance context. To illustrate our ideas and approach,
Section 5 and
Section 6 provide our analysis using data from the Wisconsin Local Government Property Insurance Fund.
Section 7 concludes with a few closing remarks.
2. Univariate Foundations
For notation, define N for the random number of claims, S for the aggregate claim amount, and for the average claim amount (defined to be 0 when ). To model these outcomes, we use a collection of covariates , some of which may be useful for frequency modeling whereas others will be useful for severity modeling. The dependent variables and as well as covariates vary by the risk . For each risk, we also are interested in multivariate outcomes indexed by . So, for example, represents the vector of p claim outcomes from the ith risk.
This section summarizes modeling approaches for a single outcome (
). A more detailed review can be found in [
1].
2.1. Frequency-Severity
For modeling the joint outcome
(or equivalently,
), it is customary to first condition on the frequency and then modeling the severity. Suppressing the
subscript, we decompose the distribution of the dependent variables as:
where
denotes the joint distribution of
. Through this decomposition, we do
not require independence of the frequency and severity components.
There are many ways to model dependence when considering the joint distribution
in Equation (
1). For example, one may use a latent variable that affects both frequency
N and loss amounts
S, thus inducing a positive association. Copulas are another tool used regularly by actuaries to model non-linear associations and will be described in subsequent
Section 4. The conditional probability framework is a natural method of allowing for potential dependencies and provides a good starting platform for empirical work.
2.2. Modeling Frequency Using GLMs
It has become routine for actuarial analysts to model the frequency
based on covariates
using generalized linear models, GLMs,
cf., [
9]. For binary outcomes, logit and probit forms are most commonly used,
cf., [
10]. For count outcomes, one begins with a Poisson or negative binomial distribution. Moreover, to handle the excessive number of zeros relative to that implied by these distributions, analysts routinely examine zero-inflated models, as described in [
11].
A strength of GLMs relative to other non-linear models is that one can express the mean as a simple function of linear combinations of the covariates. In insurance, it is common to use a “logarithmic link” for this function and so express the mean as
, where
β is a vector of parameters associated with the covariates. This function is used because it yields desirable parameter interpretations, seems to fit data reasonably well, and ties well with other approaches traditionally used in actuarial ratemaking applications [
12].
It is also common to identify one of the covariates as an “exposure” that is used to calibrate the size of a potential outcome variable. In frequency modeling, the mean is assumed to vary proportionally with
, for exposure. To incorporate exposures, we specify one of the explanatory variables to be
and restrict the corresponding regression coefficient to be 1; this term is known as an
offset. With this convention, we have
Since there are inflated numbers of 0 s and 1 s in our data, a "zero-one-inflated" model is introduced. As an extension of the zero-inflated method, a zero-one-inflated model employs two generating processes. The first process is governed by a multinomial distribution that generates structural zeros and ones. The second process is governed by a Poisson or negative binomial distribution that generates counts, some of which may be zero or one.
Denote the latent variable in the first process as
, which follows a multinomial distribution with possible values 0, 1 and 2 with corresponding probabilities
. Here,
is frequency.
Here,
may be a Poisson or negative binomial distribution. With this, the probability mass function of
is
A logit specification is used to parameterize the probabilities for the latent variable
. Denote the covariates associated with
as
. A logit specification is used to parameterize the probabilities for the latent variable
. Using level 2 as a reference, the specification is
Maximum likelihood estimation is used to fit the parameters.
2.3. Modeling Severity
Modeling Severity Using GLMs. For insurance analysts, one strength of the GLM approach is that the same set of routines can be used for continuous as well as discrete outcomes. For severities, it is common to use a gamma or inverse Gaussian distribution, often with a logarithmic link (primarily for parameter interpretability).
One strength of the linear exponential family that forms the basis of GLMs is that a sample average of outcomes comes from the same distribution as the outcomes. Specifically, suppose that we have
m independent variables from the same distribution with location parameter
θ and scale parameter
. Then, the sample average comes from the same distributional family with location parameter
θ and scale parameter
. This result is helpful as insurance analysts regularly face grouped data as well as individual data. For example, [
1] provides a demonstration of this basic property.
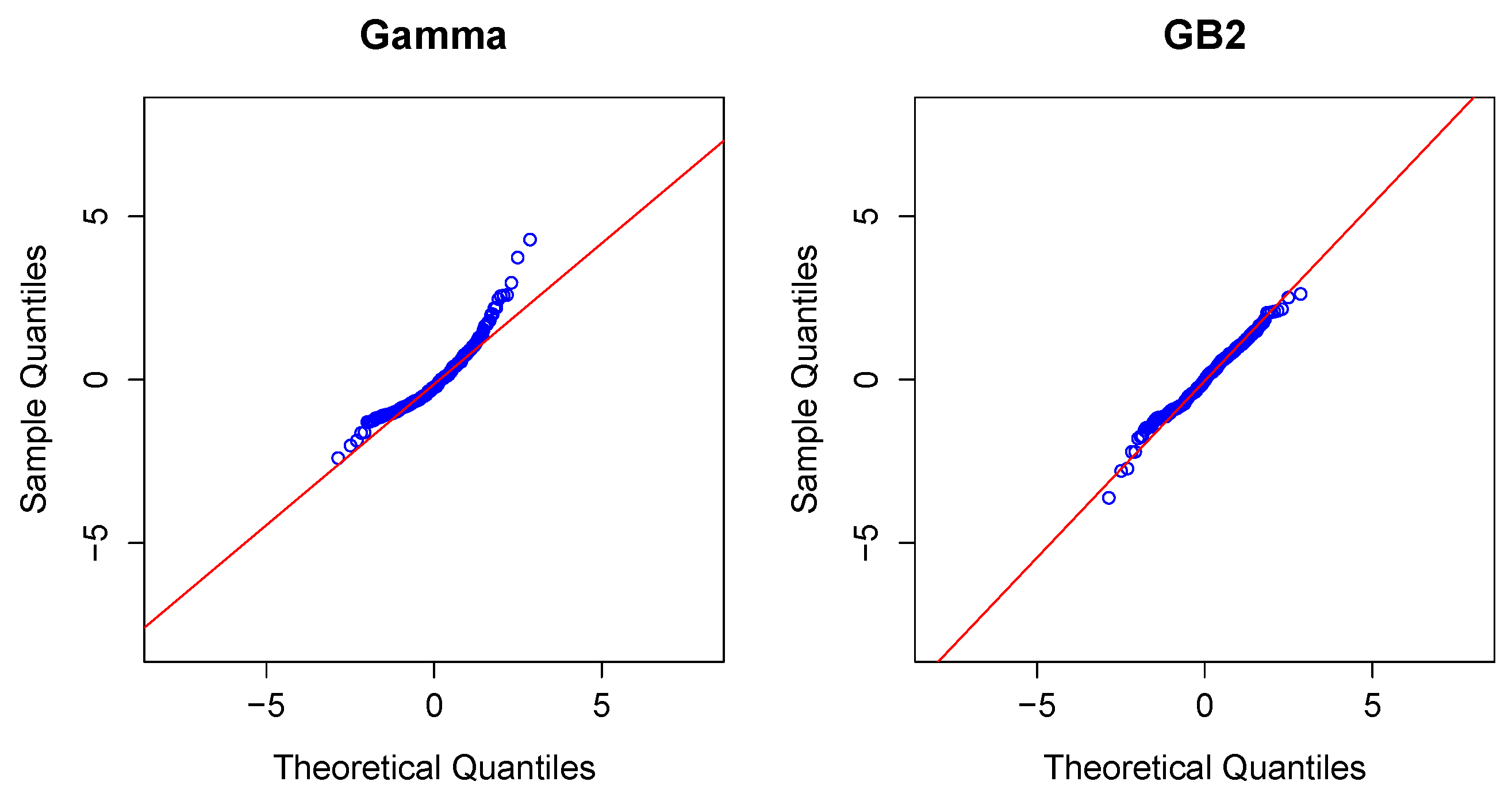
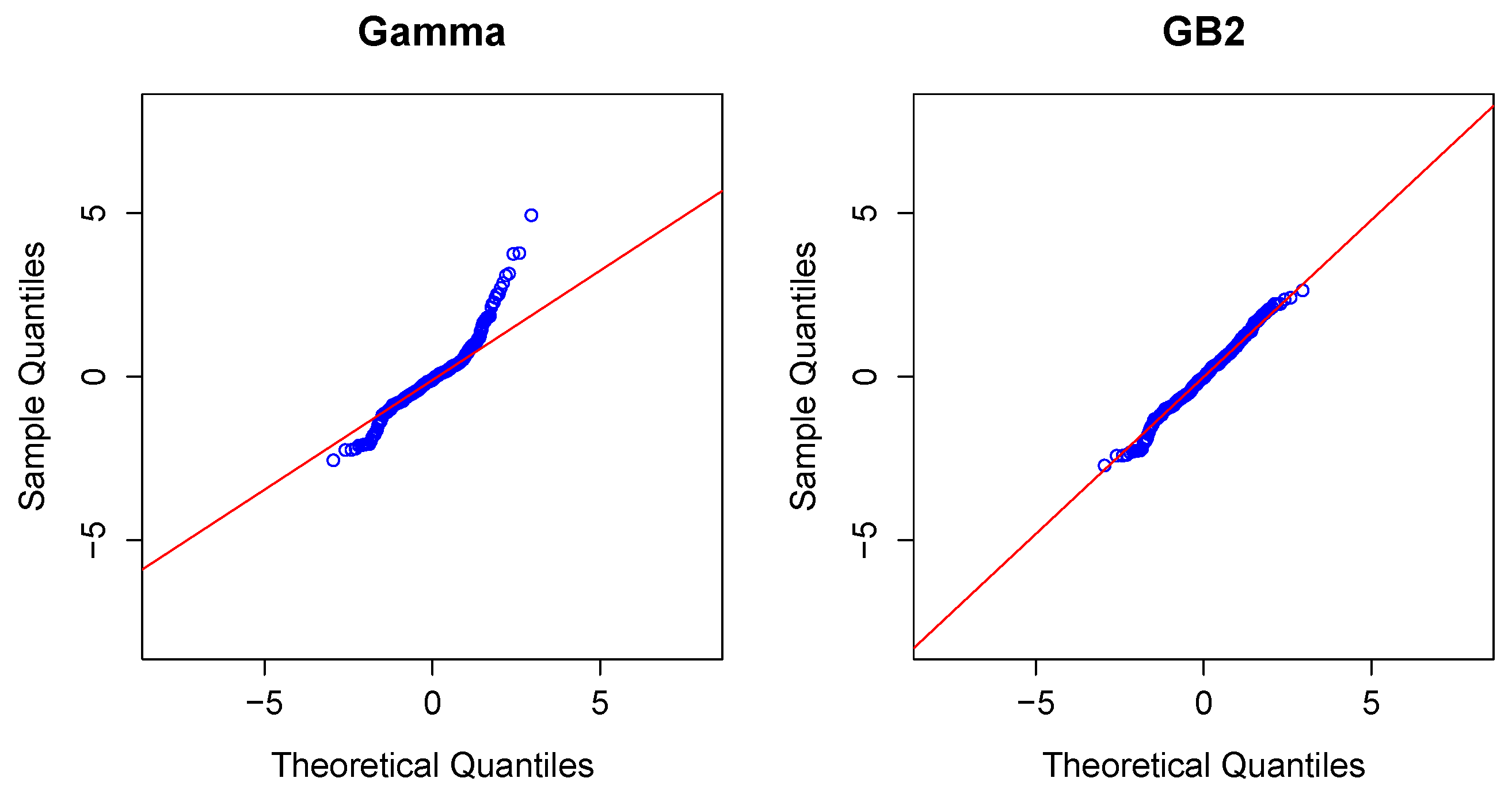
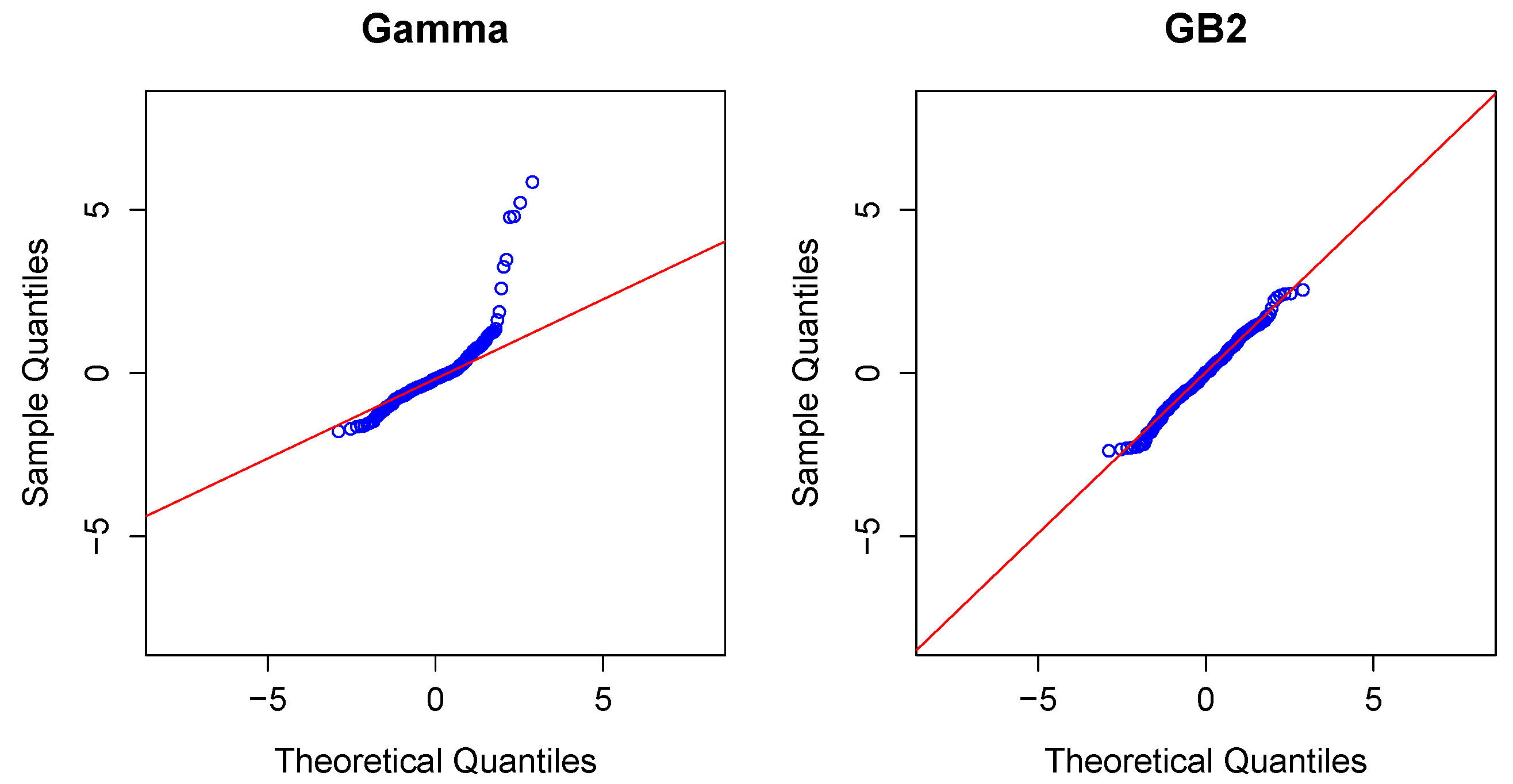
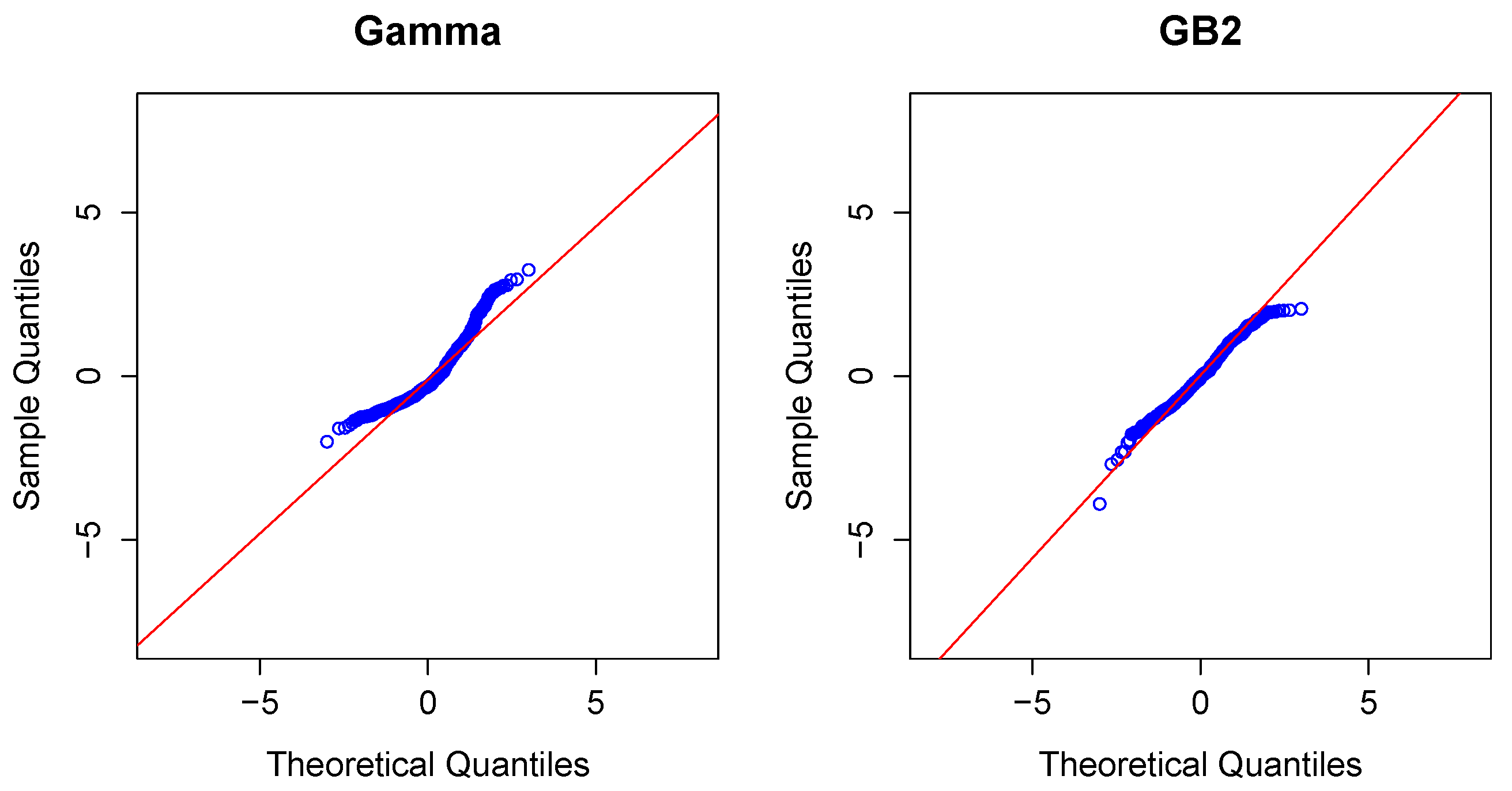
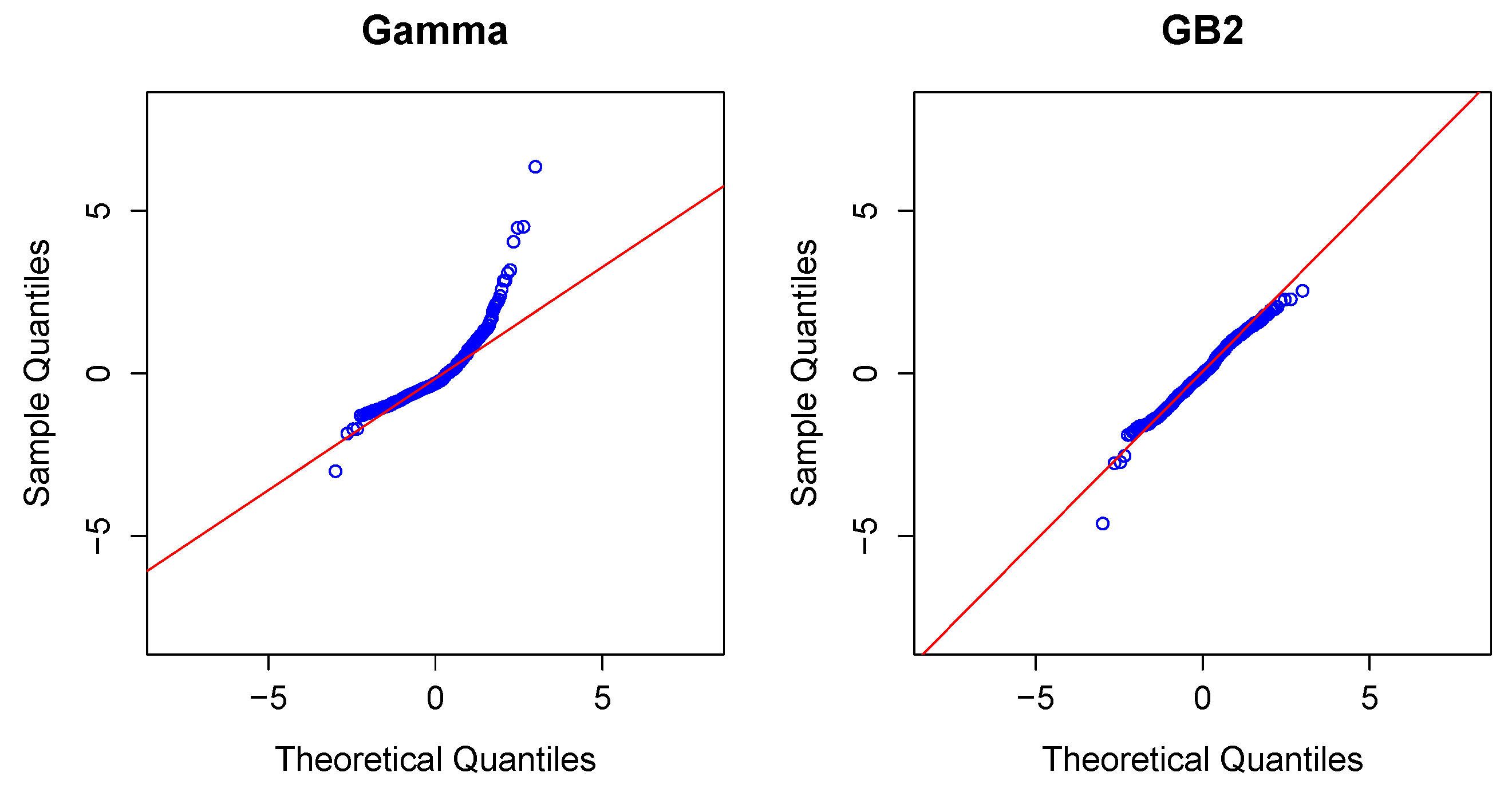
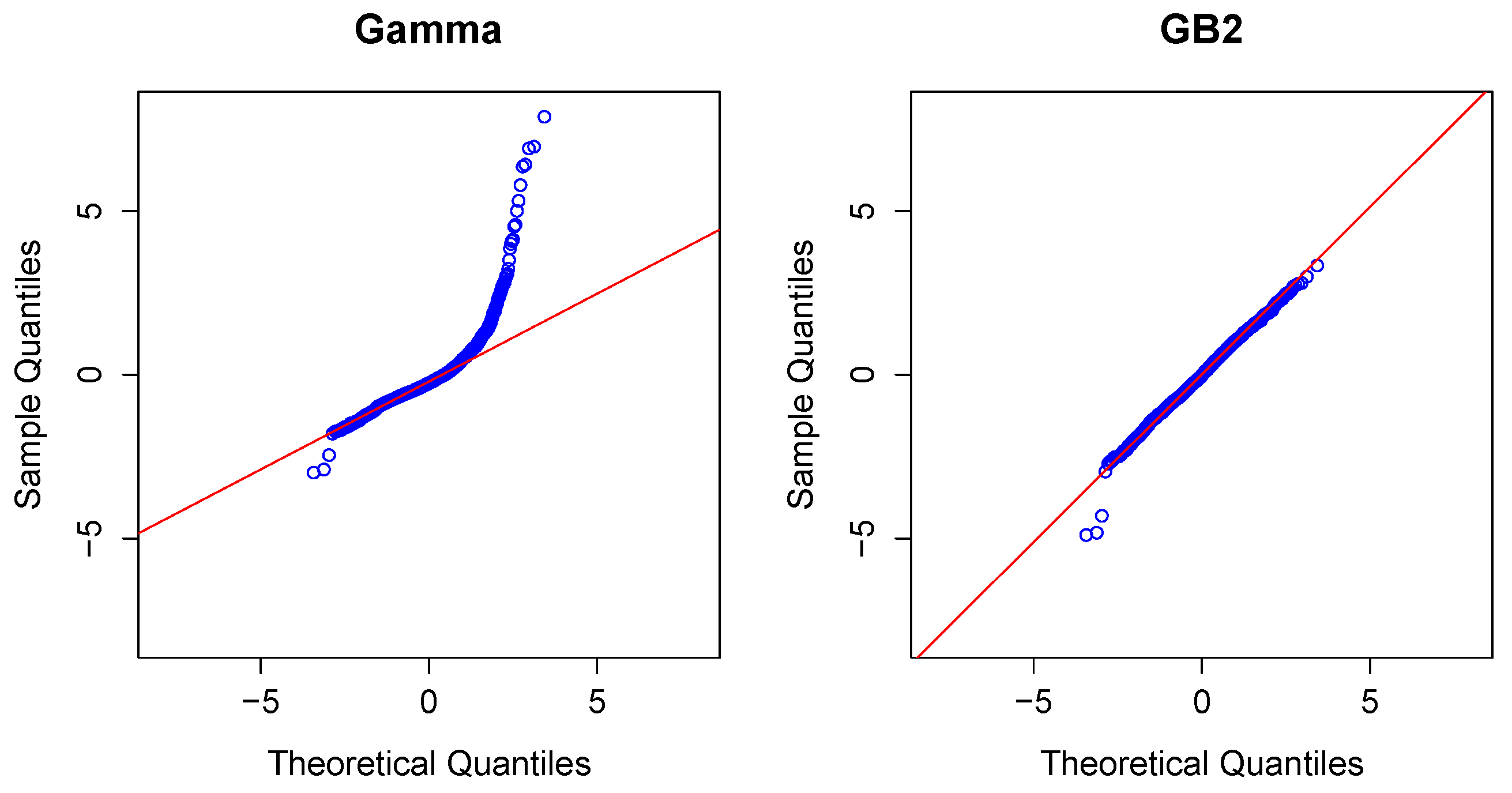
To illustrate, in the aggregate claims model, if individual losses have a gamma distribution with mean and scale parameter , then, conditional on observing losses, the average aggregate loss has a gamma distribution with mean and scale parameter .
Modeling Severity Using GB2. The GLM is the workhorse for industry analysts interested in analyzing the severity of claims. Naturally, because of the importance of claims severity, a number of alternative approaches have been explored,
cf., [
13] for an introduction. In this review, we focus on a specific alternative, using a distribution family known as the “generalized beta of the second kind”, or
GB2, for short.
A random variable with a
GB2 distribution can be written as
where the constant
,
and
are independent gamma random variables with scale parameter 1 and shape parameters
and
, respectively. Further, the random variable
F has an
F-distribution with degrees of freedom
and
, and the random variable
Z has a beta distribution with parameters
and
.
Thus, the
GB2 family has four parameters (
,
,
μ and
σ), where
μ is the location parameter. Including limiting distributions, the
GB2 encompasses the “generalized gamma” (by allowing
and hence the exponential, Weibull, and so forth. It also encompasses the “Burr Type 12” (by allowing
), as well as other families of interest, including the Pareto distributions. The
GB2 is a flexible distribution that accommodates positive or negative skewness, as well as heavy tails. See, for example, [
2] for an introduction to these distributions.
For incorporating covariates, it is straightforward to show that the regression function is of the form
where the constant
can be calculated with other (non-location) model parameters. Under the most commonly used way of parametrization for the GB2, where
μ is associated with covariates, if
, then we have
where
.
Thus, one can interpret the regression coefficients in terms of a proportional change. That is,
In principle, one could allow for any distribution parameter to be a function of the covariates. However, following this principle would lead to a large number of parameters; this typically yields computational difficulties as well as problems of interpretations, [
14]. In this paper,
μ is used to incorporate covariates. An alternative parametrization, as described in
Appendix A.1, is introduced as an extension of the GLM framework.
2.4. Tweedie Model
Frequency-severity modeling is widely used in insurance applications. However, for simplicity, it is also common to use only the aggregate loss S as a dependent variable in a regression. Because the distribution of S typically contains a positive mass at zero representing no claims, and a continuous component for positive values representing the amount of a claim, a widely used mixture is the Tweedie (1984) distribution. The Tweedie distribution is defined as a Poisson sum of gamma random variables. Specifically, suppose that N has a Poisson distribution with mean λ, representing the number of claims. Let be an i.i.d. sequence, independent of N, with each having a gamma distribution with parameters α and β, representing the amount of a claim. Note, β is standard notation for this parameter used in loss-model textbooks, and the reader should understand it is different from the bold-faced β, as the latter is a symbol we will use for the coefficients corresponding to explanatory variables. Then, is a Poisson sum of gammas.
To understand the mixture aspect of the Tweedie distribution, first note that it is straightforward to compute the probability of zero claims as
. The distribution function can be computed using conditional expectations,
Because the sum of i.i.d. gammas is a gamma,
(not
S) has a gamma distribution with parameters
and
β. For
, the density of the Tweedie distribution is
From this, straight-forward calculations show that the Tweedie distribution is a member of the linear exponential family. Now, define a new set of parameters
through the relations
Easy calculations show that
where
. The Tweedie distribution can also be viewed as a choice that is intermediate between the Poisson and the gamma distributions.
In the basic form of the Tweedie regression model, the scale (or dispersion) parameter
is constant. However, if one begins with the frequency-severity structure, calculations show that
depends on the risk characteristics (
i,
cf., [
1]). Because of this and the varying dispersion (heteroscedasticity) displayed by many data sets, researchers have devised ways of accommodating and/or estimating this structure. The most common way is the so-called “double GLM” procedure proposed in [
15] that models the dispersion as a known function of a linear combination of covariates (as for the mean, hence the name “double GLM”).
4. Frequency Severity Dependency Models
In traditional models of insurance data, the claim frequency is assumed to be independent of claim severity. We emphasize in
Appendix A.4 that the average severity may depend on frequency, even when this classical assumption holds.
One way of modeling the dependence is through the conditioning argument developed in
Section 2.1. An advantage of this approach is that the frequency can be used as a covariate to model the average severity. See [
51] for a healthcare application of this approach. For another application, a Bayesian approach for modeling claim frequency and size was proposed in [
52], with both covariates as well as spatial random effects taken into account. The frequency was incorporated into the severity model as covariate. In addition, they checked both individual and average claim modeling and found the results were similar in their application.
As an alternative approach, copulas are widely used for frequency severity dependence modeling. In [
46], Czado
et al. fit Gaussian copula on Poisson frequency and gamma severity and used an optimization by parts method from [
53] to do the estimation. They derived the conditional distribution of frequency given severity. In [
54], the distribution of policy loss is derived without the independence assumption between frequency and severity. They also showed that the ignoring of dependence can lead to underestimation of loss. A Vuong test was adopted to select the copula.
To see how the copula approach works, recall that
represents average severity of claims and
N denotes frequency. Using a copula, we can express the likelihood as
This yields the following expression for the likelihood
For another approach, Shi
et al. also built a dependence model between frequency and severity in [
55]. They used an extra indicator variable for occurrence of claim to deal with the zero-inflated part, and built a dependence model between frequency and severity conditional on positive claim. The two approaches described previously were compared; one approach using frequency as a covariate for the severity model, and the other using copulas. They used a zero-truncated negative binomial for positive frequency and the
GG model for severity. In [
56], a mixed copula regression based on
GGS copula (see [
25] for an explanation of this copula) was applied on a medical expenditure panel survey (MEPS) dataset. In this way, the negative tail dependence between frequency and average severity can be captured.
Brechmann
et al. applied the idea of the dependence between frequency and severity to the modeling of losses from operational risks in [
57]. For each risk class, they considered the dependence between aggregate loss and the presence of loss. Another application of this methodology in operational risk aggregation can be found in [
58]. Li
et al. focused on two dependence models; one for the dependence of frequencies across different business lines, and another for the aggregate losses. They applied the method on Chinese banking data and found significant difference between these two methods.