A Two-Account Life Insurance Model for Scenario-Based Valuation Including Event Risk

Abstract

Using a two-account model with event risk, we model life insurance contracts taking into account both guaranteed and non-guaranteed payments in participating life insurance as well as in unit-linked insurance. Here, event risk is used as a generic term for life insurance events, such as death, disability, etc. In our treatment of participating life insurance, we have special focus on the bonus schemes “consolidation” and “additional benefits”, and one goal is to formalize how these work and interact. Another goal is to describe similarities and differences between participating life insurance and unit-linked insurance. By use of a two-account model, we are able to illustrate general concepts without making the model too abstract. To allow for complicated financial markets without dramatically increasing the mathematical complexity, we focus on economic scenarios. We illustrate the use of our model by conducting scenario analysis based on Monte Carlo simulation, but the model applies to scenarios in general and to worst-case and best-estimate scenarios in particular. In addition to easy computations, our model offers a common framework for the valuation of life insurance payments across product types. This enables comparison of participating life insurance products and unit-linked insurance products, thus building a bridge between the two different ways of formalizing life insurance products. Finally, our model distinguishes itself from the existing literature by taking into account the Markov model for the state of the policyholder and, hereby, facilitating event risk.

1. Introduction

Classical life insurance mathematics deals with the computation of reserves and cash flows for guaranteed payments in participating life insurance. Non-guaranteed payments in participating life insurance and guaranteed and non-guaranteed payments in unit-linked insurance depend on the evolution of the financial market, and this makes them difficult to model, in particular on top of the state model of the policyholder. Note that by non-guaranteed payments, we mean all future payments that are not guaranteed, with bonus in participating life insurance as the leading example. The paper [1] offers examples of this advanced combined modeling in the case of a Black–Scholes financial market. To lower the mathematical complexity and allow for more complicated financial markets while maintaining a general biometric state model, we focus on economic scenarios. An economic scenario could, for example, consist of a sample path for the short interest rate and/or a stock index. The scenarios may be worst-case scenarios, stress scenarios from Solvency II, scenarios generated via Monte Carlo simulation or best-estimate scenarios. For a given scenario, the balance of the policy is projected into the future. For scenarios generated via Monte Carlo simulation, one obtains a valid approximation of the expected future payments, guaranteed as well as non-guaranteed, by averaging over sufficiently many projections (as is common practice with Monte Carlo simulation). For worst-case or best-estimate scenarios, a single projection is enough to obtain the corresponding worst-case or best-estimate approximation of the future payments. We will not go into details about the generation of stochastic scenarios; we simply take them as financial input to our model. For Monte Carlo simulation, we refer to [2]. For the generation of worst-case scenarios, we refer to [3]. Scenario-based calculations have the advantage that the overall projection approach does not change with the financial model, because the stochastic scenarios are the only financial input. Economic scenarios are widely used in the insurance industry; see, for example, [4] and Chapter 10 “A Simulation-Based ALM Model in Practical Use by a Norwegian Life Insurance Company” in [5].

Considering non-guaranteed payments when valuing the liabilities has many applications, such as risk management, product development and solvency. In [6], Paragraph 79, it is stated that the value of financial guarantees and contractual options should take into account non-guaranteed as well as guaranteed payments. Scenario-based calculations allow for market valuation, solvency calculations, hedging and pricing of guaranteed and non-guaranteed payments in participating life and unit-linked insurance. Hence, scenario-based calculations, which is exactly what we propose, are useful for complying with current Solvency II regulation.

We model life insurance contracts using two interacting accounts described by stochastic differential equations. One account measures the assets, and the other account is a technical account. For each scenario, the stochastic differential equations simplify to deterministic differential equations that can be solved numerically. A numerical solution can, for example, be obtained by applying a simple numerical discretization. Thereby, our model is simple to implement. Furthermore, our model allows us to model participating life and unit-linked insurance in the same framework. By doing so, we are able to compare the two. In their nature, unit-linked and participating life insurance seem different, but they are really not. The products may vary in riskiness, but projection-wise, they are almost the same. The main difference lies in the specification of how non-guaranteed payments arise, stated in the contract from the beginning (unit-linked) or determined fairly by the company along the way (participating life).

By use of a two-account model, we are able to illustrate general concepts without making the model too abstract. Our two-account model is based on the two-account model in [7], and both models offer a common framework for the valuation of guaranteed and non-guaranteed payments in participating life and unit-linked insurance. Our model distinguishes itself from the model in [7] by taking into account the Markov model for the state of the policyholder, thereby including event risk. Here, event risk is used as a generic term for life insurance events, such as death, disability, etc. The existing literature considers the valuation of guaranteed and non-guaranteed payments in participating life insurance or unit-linked insurance without event risk, whereas a common framework and inclusion of event risk are rare. The papers [8,9,10,11] are examples of recent literature that considers valuation in participating life insurance without (or with very limited) event risk. The papers [12,13,14] are other examples within the same area, but their focus is more risk-related. On the other hand, [15] models participating life insurance, taking into account the Markov model for the state of the policyholder, but the model is only tractable for a very simple financial environment, and it does not apply to unit-linked insurance. The work in [1] and, more specifically, [16] cover participating life and unit-linked insurance with broad event risk, but only in a Black–Scholes market, and the results involve non-trivial partial differential equations.

In our treatment of participating life insurance, we have special focus on bonus allocation and on the bonus schemes “consolidation” and “additional benefits”. These bonus schemes are the most common in the Danish life insurance and pensions industry, but to our knowledge, consolidation is barely mentioned in the literature. An important goal of this paper is to formalize exactly how these bonus schemes work and interact. Other papers with a similar focus on bonus include [17,18,19,20], but again, none of them include event risk. In our treatment of unit-linked insurance, we have special focus on the implementation of guarantees and on the similarities and differences in relation to participating life insurance. For both product types, we include numerical examples to demonstrate the possible applications of our two-account model.

In Section 2, we discuss scenario-based projection in general. Our main focus is on projection level and which measure to project under (physical or pricing measure). In Section 3, we discuss valuation bases in life insurance and formalize a common model for the state-wise evolution of the policies under consideration. In Section 4, we consider participating life insurance. We briefly touch upon different bonus schemes, and we present our two-account model for a general participating life insurance policy, although not allowing for policyholder behavior options. We include simple survival model examples to illustrate formulas and provide intuition. We end the section with a numerical example building on the survival model. The example illustrates a fair bonus strategy and the risk of unfair redistribution between policies in a portfolio. It also highlights some of the many possible applications of scenario-based calculations. In Section 5, we consider unit-linked insurance. We touch upon different aspects of unit-linked insurance, and we present our two-account model for a general unit-linked insurance policy. Again, we include simple and illustrative survival model examples. We end the section with a numerical example that is a unit-linked version of the numerical example in the previous section. The example illustrates a fair guarantee fee strategy, and we compare the unit-linked insurance policy to its participating life insurance counterpart, making good use of our common modeling framework.

2. Projection in General

In participating life insurance, we introduce stochastic scenarios to allow for market valuation of non-guaranteed payments, pricing and hedging of guarantees, bonus and benefit prognoses and solvency calculations. In unit-linked insurance, we introduce stochastic scenarios to utilize retirement savings and benefit prognoses, solvency calculations and hedging and pricing of unit-linked guarantees. In both cases, each scenario consists of two sample paths: one for the short interest rate, r, and one for the return on the fund that the policyholder and/or the insurance company has chosen to invest in, $R_X$. We assume that the stochastic scenarios arise from a financial model equipped with a physical measure P and a risk-neutral pricing measure Q. For each scenario, we project the accounts that determine the financial progress of a given policy. When making the projections in participating life insurance, as well as in unit-linked insurance, it is important to bear in mind the requested outcome.

For pricing, hedging, market valuation and solvency assessments of guaranteed and non-guaranteed payments (in participating life) or of a provided guarantee (in unit-linked) or for examining a bonus allocation strategy (in participating life), it is the expected evolution of the policy, both financially and across states, that is relevant. Hence, the evolution of the policy is considered on an average “portfolio level”. For pricing, hedging and market valuation, the projections are carried out under the pricing measure (Q), since the focus is on pricing and valuation. For solvency assessments, the projections are carried out under the physical measure (P) up to some relevant time point, and from then on, they are carried out under the pricing measure (Q). For examining a bonus allocation strategy and quantifying the total expected future bonus, the projections are carried out under the physical measure (P), since the focus is on the actual outcome.

For retirement savings, benefit and bonus prognoses, it is the expected financial evolution of the policy that is relevant. The policyholder wants to know what to expect in each state, not the average expectation. Hence, the evolution of the policy is considered on an individual “policy level”. However, in participating life insurance, the amount of bonus allocated to the policy depends on the financial evolution and the average evolution of the policy. Hence, for the purpose of prognoses in participating life insurance, the assets and the reserves must, first, be projected on portfolio level to produce a sample path for the bonus allocation. Second, the sample path for the bonus allocation is used to project the reserves on an individual path-wise “policy level”. In either case, the projections are carried out under the physical measure (P), since the focus is on the actual bonus, retirement savings and benefits.

In this paper, we limit our focus to projection on portfolio level and leave projection on policy level for future research.

3. Valuation Bases and Insurance Model

A cornerstone in life insurance mathematics is the principle of equivalence, which states that the expected present values of premiums and benefits should be equal. The principle relies on the law of large numbers that will, then, on average, make premiums and benefits balance in a large insurance portfolio. To apply the equivalence principle, one needs assumptions about interest, mortality and other relevant economic-demographic elements. The uncertain development of these elements subjects the insurance company to a risk that is independent of the size of the portfolio. In participating life insurance, the insurance company can neither raise the premiums nor reduce the benefits along the way, so the only way for the insurance company to mitigate this risk is to build a safety loading into the premiums. This is done by performing the equivalence principle under conservative assumptions about interest, mortality, etc. These assumptions make up the so-called technical basis, and it represents a provisional worst-case scenario for its elements. Below, we mark elements of the technical basis by superscript “*”. For market-consistent valuation of future payments, the technical basis does not apply due to its worst-case nature. Instead, valuation is performed under the so-called market basis, which is made up of best-estimate assumptions about the various elements. Below, we mark elements of the market basis by superscript “m”. In unit-linked insurance, the benefits are typically allowed to fluctuate with the market, hereby making the technical basis superfluous.

In participating life insurance, as well as in unit-linked insurance, we consider a policy whose state-wise evolution is governed by a continuous-time Markov process Z with a finite state space J, starting at zero. For a detailed description of the Markov model, see [21] or [22]. For $k,j\in J,j\ne k$, we define the counting process $N_{jk}$ and the indicator process $I_k$ by

$$\begin{array}{cc}\hfill N_{jk}\left(t\right)& =\#\left\{s\le t:Z\left(s-\right)=j,Z\left(s\right)=k\right\},\hfill \end{array}$$

$$\begin{array}{cc}\hfill I_k\left(t\right)& =1_{\left\{Z\left(t\right)=k\right\}}.\hfill \end{array}$$

With this definition, $N_{jk}\left(t\right)$ counts the number of jumps from state j to state k until time t, and $I_k\left(t\right)$ indicates a sojourn in state k at time t. Under the technical basis, we model the evolution of Z by the transition intensities $t\mapsto {\mu }_{jk}^{*}\left(t\right)$, $j,k\in J,j\ne k$, and under the market basis, we model the evolution of Z by the transition intensities $t\mapsto {\mu }_{jk}^m\left(t\right)$, $j,k\in J,j\ne k$. The corresponding technical and market transition probabilities from state j to state k over the time interval $\left[t,s\right]$ are denoted by $p_{jk}^{*}\left(t,s\right)$ and $p_{jk}^m\left(t,s\right)$, and with $○=*,m$ indicating the basis, we have

$${\mu }_{jk}^{○}\left(t\right)=\underset{h\downarrow 0}{lim}\frac{p_{jk}^{○}\left(t,t+h\right)}{h}.$$

The transition probabilities can be calculated numerically from the transition intensities by use of the Kolmogorov equations; see, for example, [21]. We assume that the process Z governing the state of the policy is independent of the financial market, and under both P and Q, the evolution of Z is described by the transition intensities from the market basis.

In addition to the market transition intensities, the market basis consists of a market interest rate. The market basis has no more elements, as we do not take expenses or any other economic-demographic elements into account. Similarly, the technical basis consists of the technical transition intensities and a technical interest rate. In unit-linked insurance, only the market basis comes into play.

4. Participating Life Insurance

In this section, we consider participating life insurance. We touch upon different bonus schemes, and we present our two-account model for a general participating life insurance policy. We include simple survival model examples to illustrate formulas and provide intuition. We end the section with a numerical example building on the survival model.

4.1. Non-Guaranteed Payments (Bonus)

In participating life insurance, the guaranteed payments are based on the technical basis. The conservative technical basis gives rise to a systematic surplus that is to be paid back to the policyholders in terms of bonus. There are many possible ways to do so. For a short survey, see [1]. We consider a bonus scheme consisting of two steps: first, consolidation, and then, when the policy is consolidated on a sufficiently low technical interest rate (if ever), additional benefits. The bonus scheme consolidation (in Danish “styrkelse”) is much used in the Danish market, but it can easily be skipped below, heading straight for the bonus scheme additional benefits.

The bonus scheme consolidation is primarily used for policies with a technical interest rate that is “too high” compared to the market interest rate. Bonus is used to consolidate the policy on a lower technical interest rate. By consolidate, we mean that the technical interest rate is lowered without changing the guaranteed payments. This may seem to be less favorable for the policyholder, but since the guaranteed payments are not changed, the policyholder is not worse off. When a sufficiently low technical interest rate has been reached, the remaining bonus is used for additional benefits. Hence, consolidation does not benefit the policyholder in terms of more favorable payments immediately after bonus payments, but it helps to ensure that the liabilities of the policy can be met. Furthermore, the lower technical interest rate gives rise to a higher systematic surplus in the future, which will eventually be redistributed and reflected in the payments.

The bonus scheme additional benefits is primarily used for policies with a low technical interest rate compared to the market interest rate. Bonus is used to increase parts of the guaranteed benefits proportionally, whereas the remaining benefits, the premiums and the technical interest rate are maintained. It is usually the retirement part of the benefits (such as a pure endowment or a life annuity) that is increased and the insurance part of the benefits (such as a term insurance or disability coverage) that is not. There is good reason to increase the retirement part of the benefits instead of decreasing the premiums or increasing all of the benefits, since the retirement benefits are typically set according to which premiums the policyholder can afford and which insurance coverage he/she needs, and not the other way around. Furthermore, there is good reason to increase the retirement benefits proportionally, as the benefit profile reflects the policyholder's preferences.

4.2. Product Specification

We consider a participating life insurance policy with guaranteed payments based on a technical basis whose elements are marked by superscript “*”. The state-wise evolution of the policy is described in Section 3. We let $r^{*\left(0\right)}$ denote the technical interest rate at time 0. By $B^u$, $B^f$ and C, we denote the guaranteed payment streams at time 0. Here, C is the premium stream (“C” for contributions), $B^u$ is the benefit stream for the benefits that are increased (“B” for benefits and superscript “u” for upscaled) and $B^f$ is the benefit stream for the benefits that are kept fixed (superscript “f” for fixed). The payments streams are given by

$$\begin{array}{cc}\hfill \mathrm{d}C& =\sum _{j\in J}{I}_j\mathrm{d}{c}_j,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathrm{d}{B}^i& =\sum _{j\in J}{I}_j\mathrm{d}{b}_j^i+\sum _{j,k\in J:k\ne j}{b}_{jk}^i\mathrm{d}{N}_{jk},i=f,u,\hfill \end{array}$$

where $c_j$, $b_j^f$ and $b_j^u$ are deterministic, state-wise payment streams and $b_{jk}^f$ and $b_{jk}^u$ are deterministic lump sum payments upon jumps. We note that we, hereby, exclude policyholder behavior options, such as surrender and free policy, since they imply non-deterministic payments. However, for surrender modeling, see the remark on Page 197. Examples of deterministic lump sum payments upon jumps include insurance coverage, such as a death sum, a disability sum or a sum upon critical illness. The policy terminates at time T. Thereafter, there are no payments.

4.3. Two-Account Model

We denote by X the assets of the policy, including its share of the collective bonus potential, and by Y, we denote the market expected technical reserve for the policy. By market expected technical reserve, we mean the expectation of future state-wise technical reserves where the expectation across states is taken under the market basis. Thus, the market expected technical reserve is not a state-wise reserve, but a probability weighted sum of state-wise reserves. The accounts X and Y are the backbone of our two-account model. The policy is issued before or at time 0, and the two accounts amount to $X\left(0-\right)=x_0$ and $Y\left(0-\right)=y_0$ just before time 0. For a policy issued at time 0, $y_0$ and $x_0$ are both zero. For a policy issued before time 0, $y_0$ is equal to the technical reserve for the policy just before time 0, and $x_0$ is equal to the assets of the policy just before time 0. Both are assumed to be known when initiating the projection.

The assets X are invested in a fund with stochastic return $R_X$. The market expected technical reserve Y accumulates according to the technical interest rate. In good times, the return rate on the assets exceeds the technical interest rate. Parts of the excess return are allocated to the policy in terms of bonus, which adds to the market expected technical reserve, but parts are saved for times where the return rate on the assets is less favorable. In really bad times, the assets may be insufficient to cover the guaranteed payments of the policy. In that case, the equity holders of the insurance company step in with a capital injection taken from the company's equity. We speak of the possible capital injection as a guarantee injection, and its role is to raise the assets in case of unfavorable developments in the financial market. The policyholder pays for the company's risk taking by having a guarantee fee deducted from the assets and paid to the equity holders of the insurance company in good times. We assume that the insurance company's equity is always sufficient to cover the guarantee injections and that all guarantee injections and guarantee fees are settled via the equity. In Denmark, the guarantee fee used to be known as the “driftsherretillæg” (translates to “technical yield”). All of the above does not happen continuously, but at pre-specified, deterministic time points $0<t_1<...<t_n=T$ (for example, once a year) where the two accounts X and Y are updated. We let

$$\begin{array}{c}\hfill ϵ\left(t\right)=\#\left\{i=1,...,n:t_i\le t\right\}\end{array}$$

count the number of updates prior to time t. The updates consist of bonus allocation d (if funds are sufficient), guarantee injection g from the equity holders of the insurance company (if needed) and deduction of the guarantee fee ${\pi }_g$ in return for the possible guarantee injection. All three are non-negative. For technical convenience, we assume that the stochastic return on the assets, $R_X$, does not jump at the time points $0<t_1<...<t_n=T$ with account updates. Furthermore, for all t with $\mathrm{d}ϵ\left(t\right)=1$, i.e., for all time points with an account update, we assume that $d\left(t\right)$ and ${\pi }_g\left(t\right)$ are known at time $t-$ and that $g\left(t\right)$ is calculated at time $t-$. This is to ensure predictability and, thereby, stochastic integrability.

4.4. Bonus Mechanisms

As mentioned, we consider a bonus scheme where bonus allocated to the policy is, first, used to lower the technical interest rate until it hits a pre-described level $r^{*}$. Typically, this level coincides with the technical interest rate for new policies. Thereafter, bonus is used to increase the benefits $B^u$. The additional benefits are priced using the technical transition intensities ${\mu }_{jk}^{*}$ and the technical interest rate $r^{*}$. This means that the minimum technical interest rate for consolidation and the pricing interest rate for additional benefits are assumed to coincide. One could have chosen another technical interest rate for the pricing of additional benefits, but that would require a division of the technical reserve on two different technical bases, so we insist on using $r^{*}$. We let $r^{*\left(n\right)}$ denote the technical interest rate after the n-th bonus accrual and $k^{\left(n\right)}$ denote the upscaling of the benefits $B^u$ after the n-th bonus accrual. We note that the upscaling factor starts at one, i.e., $k^{\left(0\right)}=1$. After the n-th bonus accrual, the guaranteed benefit stream for the policy is given by

$$\begin{array}{c}\hfill B^{\left(n\right)}=k^{\left(n\right)}{B}^u+B^f.\end{array}$$

We point out that $r^{*\left(n\right)}$ and $k^{\left(n\right)}$ depend on the development of the financial market and are therefore stochastic. However, for each economic scenario, we have a procedure for calculating them according to the equivalence principle. The procedure is presented in Section 4.8. We note that we have $k^{\left(n\right)}=1$ for all n with $r^{*\left(n\right)}>r^{*}$, and if $k^{\left(n\right)}>1$, then necessarily $r^{*\left(n\right)}=r^{*}$. This is because we do not increase the guaranteed benefits until the technical interest rate has been lowered to $r^{*}$. Finally, we note that the technical interest rate and the upscaling factor amount to $r^{*\left(ϵ\left(t\right)\right)}$ and $k^{\left(ϵ\left(t\right)\right)}$ at time t, since there has been $ϵ\left(t\right)$ account updates at time t.

For all t with $\mathrm{d}ϵ\left(t\right)=1$, that is for all time points with an account update, we assume that the technical interest rate $r^{*\left(ϵ\left(t\right)\right)}$ and the upscaling factor $k^{\left(ϵ\left(t\right)\right)}$ are calculated at time $t-$. Again, this is to ensure predictability. Furthermore, additional benefits are in effect from time $t-$, such that benefits paid out at time t include the upscaling $k^{\left(ϵ\left(t\right)\right)}$. The latter ensures that a policyholder with a final lump sum payment actually benefits from the last bonus update.

4.5. Technical Reserves

We denote by $V_j^{f,*,+}\left(·,\rho \right)$ and $V_j^{u,*,+}\left(·,\rho \right)$ the state-wise technical benefit reserves for the benefit streams $B^f$ and $B^u$ given that the policy is in state j and that the technical interest rate is ρ. Similarly, we denote by $V_j^{*,-}\left(·,\rho \right)$ the state-wise technical premium reserves for the premium stream C. Note that we use superscript “+” to indicate the benefit reserves and superscript “−” to indicate the premium reserve. Furthermore, we use superscript “*” to indicate that the reserve is evaluated under the technical basis. Finally, we use the generic constant ρ in place of the technical interest rate, because we need to evaluate the technical reserves for different technical interest rates in connection with the bonus scheme consolidation. We have

$$\begin{array}{cc}\hfill V_j^{*,-}\left(t,\rho \right)& ={\text{𝔼}}^{*}\left[{\int }_t^T{e}^{-\rho \left(s-t\right)}\mathrm{d}C\left(s\right)|Z\left(t\right)=j\right]\hfill \\ & ={\int }_t^T{e}^{-\rho \left(s-t\right)}\sum _{l\in J}{p}_{jl}^{*}\left(t,s\right)\mathrm{d}{c}_l\left(s\right),\hfill \\ \hfill V_j^{i,*,+}\left(t,\rho \right)& ={\text{𝔼}}^{*}\left[{\int }_t^T{e}^{-\rho \left(s-t\right)}\mathrm{d}{B}^i\left(s\right)|Z\left(t\right)=j\right]\hfill \\ & ={\int }_t^T{e}^{-\rho \left(s-t\right)}\sum _{l\in J}{p}_{jl}^{*}\left(t,s\right)\left\{\mathrm{d}{b}_l^i\left(s\right)+\sum _{k\in J:k\ne l}{\mu }_{lk}^{*}\left(s\right)b_{lk}^i\left(s\right)\mathrm{d}s\right\}\hfill \end{array}$$

(1)

for $i=f,u$. Here, ${\text{𝔼}}^{*}$ denotes technical expectation and $p_{jl}^{*}$ is the technical probability of transition from state 0 to j. Both are determined by the transition intensities from the technical basis. The state-wise technical reserves can be calculated numerically by use of Thiele's differential equations; see [23].

We denote by $V_i^{*}\left(·,\rho ,k\right)$ the state-wise technical reserve for the (partly upscaled by k) payment stream $B^f+k{B}^u-C$, given that the policy is in state i and that the technical interest rate is ρ, i.e.,

$$\begin{array}{c}\hfill V_i^{*}\left(t,\rho ,k\right)=k{V}_i^{u,*,+}\left(t,\rho \right)+V_i^{f,*,+}\left(t,\rho \right)-V_i^{*,-}\left(t,\rho \right),i\in J.\end{array}$$

(2)

Here, $V_j^{f,*,+}$, $V_j^{u,*,+}$, and $V_j^{*,-}$ are the state-wise technical benefit and premium reserves defined in Equation (1). With the introduction of $V_i^{*}$, we can write the market expected technical reserve as

$$\begin{array}{cc}\hfill Y\left(t\right)& =\sum _{j\in J}{p}_{0j}^m\left(0,t\right)V_j^{*}\left(t,r^{*\left(ϵ\left(t\right)\right)},k^{\left(ϵ\left(t\right)\right)}\right).\hfill \end{array}$$

We recall that $p_{0j}^m$ is the market probability of transition from state 0 to j, which is determined by the transition intensities from the market basis. We note that the stochasticity in $Y\left(t\right)$ comes from the stochastic development of the technical interest rate $r^{*\left(ϵ\left(t\right)\right)}$ and the upscaling factor $k^{\left(ϵ\left(t\right)\right)}$. However, for each t, the technical interest rate $r^{*\left(ϵ\left(t\right)\right)}$ is determined as a constant interest rate over $\left[t,T\right]$, so we never plug a non-constant technical interest rate into the reserves in Equation (1) when calculating $V_j^{*}\left(t,r^{*\left(ϵ\left(t\right)\right)},k^{\left(ϵ\left(t\right)\right)}\right)$.

Example 1 (Survival model). We consider a simple example that provides the basis for numerical illustrations later on. The state of the policy is described by the classical survival model with two states, 0 (alive) and 1 (dead). The payments of the policy consist of a constant continuous premium payment π while alive, a term insurance sum $b^{ad}$ upon death before expiration T and a pure endowment sum $b^a$ upon survival until expiration T. Under the bonus scheme “additional benefits”, bonus is used to increase the endowment sum. There are no payments in the death state. For simplicity, we write $I=I_1$, $N=N_{01}$, ${\mu }^{○}={\mu }_{01}^{○}$ and $p^{○}=p_{00}^{○}$ for $○=*,m$, and we have

$$\begin{array}{c}\hfill p^{○}\left(s,t\right)=e^{-{\int }_s^t{\mu }^{○}\left(v\right)\mathrm{d}v},s\le t.\end{array}$$

The payment streams of the policy read

$$\begin{array}{cc}\hfill \mathrm{d}C\left(t\right)& =\pi I\mathrm{d}t,t\le T,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathrm{d}{B}^f\left(t\right)& =b^{ad}\mathrm{d}N\left(t\right),t\le T,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \mathrm{d}{B}^u\left(t\right)& =b^{a}I\left(t\right)\mathrm{d}{ϵ}_T\left(t\right),t\le T,\hfill \end{array}$$

where ${ϵ}_T$ is the Dirac measure in T, i.e., for a measurable set $A\subseteq \text{ℝ}$

$$\begin{array}{c}\hfill {ϵ}_T\left(A\right)=1_{\left\{T\right\}}\left(A\right)=\left\{\begin{array}{cc}1\hfill & forT\in A,\hfill \\ 0\hfill & \text{for}T\notin A.\hfill \end{array}\right.\end{array}$$

We note that

$$\begin{array}{c}\hfill {\int }_0^T\mathrm{d}{B}^u\left(t\right)=b^{a}I\left(T\right).\end{array}$$

The technical premium and benefit reserves are zero in the state “dead”, and in the state “alive”, they read

$$\begin{array}{cc}\hfill V^{*,-}\left(t,\rho \right)& ={\int }_t^T{e}^{-\rho \left(s-t\right)}{p}^{*}\left(t,s\right)\pi \mathrm{d}s\hfill \\ & =\pi {\int }_t^T{e}^{-\rho \left(s-t\right)}{e}^{-{\int }_t^s{\mu }^{*}\left(v\right)\mathrm{d}v}\mathrm{d}s,t\le T,\hfill \\ \hfill V^{f,*,+}\left(t,\rho \right)& ={\int }_t^T{e}^{-\rho \left(s-t\right)}{p}^{*}\left(t,s\right)b^{ad}{\mu }^{*}\left(s\right)\mathrm{d}s\hfill \\ & =b^{ad}{\int }_t^T{e}^{-\rho \left(s-t\right)}{e}^{-{\int }_t^s{\mu }^{*}\left(v\right)\mathrm{d}v}{\mu }^{*}\left(s\right)\mathrm{d}s,t\le T,\hfill \\ \hfill V^{u,*,+}\left(t,\rho \right)& ={\int }_t^T{e}^{-\rho \left(s-t\right)}{p}^{*}\left(t,s\right)b^a\mathrm{d}{ϵ}_T\left(s\right)\hfill \\ & =b^a{e}^{-\rho \left(T-t\right)}{e}^{-{\int }_t^T{\mu }^{*}\left(v\right)\mathrm{d}v},t\le T.\hfill \end{array}$$

4.6. Cash Flows

For projection on portfolio level, it it useful to consider market cash flows of the policy. Here, we use the term market cash flows for the expectation of the stochastic payment streams taken under the market basis. By ς, ${\beta }^f$ and ${\beta }^u$, we denote the time 0 market cash flows for the premium stream C and the benefit streams $B^f$ and $B^u$, i.e.,

$$\begin{array}{cc}\hfill \varsigma \left(t\right)& ={\text{𝔼}}^m\left[{\int }_0^t\mathrm{d}C\left(s\right)\right]\hfill \\ & =\sum _{j\in J}{\int }_0^t{p}_{0j}^m\left(0,s\right)\mathrm{d}{c}_j\left(s\right),\hfill \\ \hfill {\beta }^i\left(t\right)& ={\text{𝔼}}^m\left[{\int }_0^t\mathrm{d}{B}^i\left(s\right)\right]\hfill \\ & =\sum _{j\in J}{\int }_0^t{p}_{0j}^m\left(0,s\right)\left\{\mathrm{d}{b}_j^i\left(s\right)+\sum _{k\in J:k\ne j}{\mu }_{jk}^m\left(s\right)b_{jk}^i\left(s\right)\mathrm{d}s\right\},i=f,u,\hfill \end{array}$$

where the expectation ${\text{𝔼}}^m$ is taken under the market basis. Furthermore, we need the market expected market reserve. By $V\left(t\right)$, we denote the market expected market reserve at time t for the most recently guaranteed payment stream $B^{\left(ϵ\left(t\right)\right)}-C=B^f+k^{\left(ϵ\left(t\right)\right)}{B}^u-C$, i.e.,

$$\begin{array}{cc}\hfill V\left(t\right)& ={\text{𝔼}}_{k^{\left(ϵ\left(t\right)\right)}}^m\left[{\text{𝔼}}_{k^{\left(ϵ\left(t\right)\right)}}^m\left[{\int }_t^T{e}^{-{\int }_t^{s}r\left(v\right)\mathrm{d}v}\mathrm{d}\left(B^{\left(ϵ\left(t\right)\right)}-C\right)\left(s\right)|Z\left(t\right)\right]\right]\hfill \\ & ={\int }_t^T{e}^{-{\int }_t^s{r}_t\left(v\right)\mathrm{d}v}\left(k^{\left(ϵ\left(t\right)\right)}\mathrm{d}{\beta }^u\left(s\right)+\mathrm{d}{\beta }^f\left(s\right)-\mathrm{d}\varsigma \left(s\right)\right).\hfill \end{array}$$

(3)

Here, ${\text{𝔼}}_{k^{\left(ϵ\left(t\right)\right)}}^m$ denotes market expectation given $k^{\left(ϵ\left(t\right)\right)}$, r is the stochastic short interest rate and $r_t$ is the yield curve seen from time t. Similar to the market expected technical reserve, the market expected market reserve is not a state-wise reserve, but a market probability weighted sum of state-wise market reserves. This is not evident from the formula above, since the reserve simplifies due to the tower property. We emphasize that only additional benefits, and not consolidation, raise the guarantee. However, consolidation has an effect on the non-guaranteed benefits as the technical reserve increases.

Example 2 (Survival model continued). For the simple policy in Example 1, the time 0 market premium and benefit cash flows read

$$\begin{array}{cc}\hfill \varsigma \left(t\right)& ={\int }_0^t{p}^m\left(0,s\right)\pi \mathrm{d}s=\pi {\int }_0^t{e}^{-{\int }_0^s{\mu }^m\left(v\right)\mathrm{d}v}\mathrm{d}s,t\le T,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\beta }^f\left(t\right)& ={\int }_0^t{p}^m\left(0,s\right)b^{ad}{\mu }^m\left(s\right)\mathrm{d}s=b^{ad}{\int }_0^t{e}^{-{\int }_0^s{\mu }^m\left(v\right)\mathrm{d}v}{\mu }^m\left(s\right)\mathrm{d}s,t\le T,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\beta }^u\left(t\right)& ={\int }_0^t{p}^m\left(0,s\right)b^a\mathrm{d}{ϵ}_T\left(s\right)=b^a{e}^{-{\int }_0^T{\mu }^m\left(v\right)\mathrm{d}v}{I}_{\left\{t\ge T\right\}},t\le T.\hfill \end{array}$$

The market expected market reserve V reads

$$\begin{array}{cc}\hfill V\left(t\right)& =e^{-{\int }_t^T{r}_t\left(v\right)\mathrm{d}v}{e}^{-{\int }_0^T{\mu }^m\left(v\right)\mathrm{d}v}{k}^{\left(ϵ\left(t\right)\right)}{b}^a\hfill \\ & \phantom{==}+{\int }_t^T{e}^{-{\int }_t^s{r}_t\left(v\right)\mathrm{d}v}{e}^{-{\int }_0^s{\mu }^m\left(v\right)\mathrm{d}v}\left(b^{ad}{\mu }^m\left(s\right)-\pi \right)\mathrm{d}s.\hfill \end{array}$$

4.7. Two-Account Projection

On portfolio level, the assets X and the market expected technical reserve Y of the policy evolve according to the stochastic differential equations (SDEs)

$$\begin{array}{cc}\hfill \mathrm{d}X\left(t\right)& =X\left(t-\right)\mathrm{d}{R}_X\left(t\right)-\mathrm{d}{\beta }^f\left(t\right)-k^{\left(ϵ\left(t\right)\right)}\mathrm{d}{\beta }^u\left(t\right)+\mathrm{d}\varsigma \left(t\right)\hfill \\ & \phantom{==}+\left[g\left(t\right)-{\pi }_g\left(t\right)\right]\mathrm{d}ϵ\left(t\right),t\le T,\hfill \\ \hfill X\left(0-\right)& =x_0,\hfill \\ \hfill \mathrm{d}Y\left(t\right)& =Y\left(t\right)r^{*\left(ϵ\left(t\right)\right)}\mathrm{d}t-\mathrm{d}{\beta }^f\left(t\right)-k^{\left(ϵ\left(t\right)\right)}\mathrm{d}{\beta }^u\left(t\right)+\mathrm{d}\varsigma \left(t\right)\hfill \\ & \phantom{==}+d\left(t\right)\mathrm{d}ϵ\left(t\right)+\alpha \left(t,r^{*\left(ϵ\left(t\right)\right)},k^{\left(ϵ\left(t\right)\right)}\right)\mathrm{d}t,t\le T,\hfill \\ \hfill Y\left(0-\right)& =y_0.\hfill \end{array}$$

(4)

Here, α is an adjustment term given by

$$\begin{array}{cc}\hfill \alpha \left(t,\rho ,k\right)& =\sum _{j\in J}\sum _{l\in J:l\ne j}{p}_{0j}^m\left(0,t\right)\left({\mu }_{jl}^{*}\left(t\right)-{\mu }_{jl}^m\left(t\right)\right)\hfill \\ & \phantom{=======}\times \left(V_j^{*}\left(t,\rho ,k\right)-k{b}_{jl}^u\left(t\right)-b_{jl}^f\left(t\right)-V_l^{*}\left(t,\rho ,k\right)\right),\hfill \end{array}$$

where $V_i^{*}\left(t,\rho ,k\right)$ are the state-wise technical reserves defined in Equation (2). The adjustment term accounts for the market expected surplus arising from the conservative technical transition intensities. See, for example, [15].

We recall that $R_X$ is the stochastic return on the assets, g is the guarantee injection provided by the equity holders of the insurance company, ${\pi }_g$ is the guarantee fee deducted from the assets and paid to the equity holders, d is the allocated bonus and ϵ counts the number of updates of guarantee injection, guarantee fee and bonus (typically annual). The bonus d and the guarantee fee ${\pi }_g$ are specified by the company, whereas the guarantee injection g is designed to ensure that the assets are at least equal to the guaranteed liabilities. We define the guaranteed liabilities L as the maximum of the market expected market reserve and the market expected technical reserve for the guaranteed payments, i.e.,

$$L\left(t\right)=max\left\{V\left(t\right),Y\left(t\right)\right\}.$$

(5)

This definition has been common practice in Denmark since the introduction of market values. However, the guaranteed liabilities can easily be defined differently, for example $L=V$. The guarantee injection $g\left(t\right)$ is calculated according to the formula

$$g\left(t\right)={\left(L\left(t-\right)-\left(X\left(t-\right)-{\pi }_g\left(t\right)\right)\right)}^{+}.$$

(6)

This guarantee design ensures that the assets X are sufficient to cover the guaranteed liabilities L after the guarantee fee ${\pi }_g$ has been paid to the equity holders of the insurance company. The guaranteed liabilities L represent the lowest amount that the insurance company can set aside for the guaranteed payments. Hence, the assets should always exceed the guaranteed liabilities, and by design of the guarantee injection, this will always be the case after adding the guarantee injection. The inclusion of the guarantee fee is a technicality that ensures that the assets are not drained by guarantee fee payments to the equity holders of the insurance company in bad times where the liabilities exceed the assets. By the design of the guarantee injection, no guarantee fee is deducted from the assets in those times. In Section 4.9, we get into details about how the bonus allocation and guarantee fee are determined.

The stochastic element $R_X$ enters via a sample path for the asset returns. Furthermore, the size of the guarantee injection g depends on the sample path for the short interest rate. In practice, one will often work with a discretized version of the stochastic differential equations in Equation (4). For an example, see Section 4.11.

Example 3 (Survival model continued). For the simple policy in Example 1–2, the adjustment term α reads

$$\alpha \left(t,\rho ,k\right)=p^m\left(0,t\right)\left({\mu }^{*}\left(t\right)-{\mu }^m\left(t\right)\right)\left(V^{*}\left(t,\rho ,k\right)-b^{ad}\right),$$

where the total technical reserve $V^{*}$ in the state “alive” is given by

$$\begin{array}{cc}\hfill V^{*}\left(t,\rho ,k\right)& =k{V}^{u,*,+}\left(t,\rho \right)+V^{f,*,+}\left(t,\rho \right)-V^{*,-}\left(t,\rho \right)\hfill \\ & =k{b}^a{e}^{-\rho \left(T-t\right)}{e}^{-{\int }_t^T{\mu }^{*}\left(v\right)\mathrm{d}v}\hfill \\ & +{\int }_t^T{e}^{-\rho \left(s-t\right)}{e}^{-{\int }_t^s{\mu }^{*}\left(v\right)\mathrm{d}v}\left(b^{ad}{\mu }^{*}\left(s\right)-\pi \right)\mathrm{d}s,t\le T.\hfill \end{array}$$

4.8. Procedure for Determining the Technical Interest Rate and the Upscaling Factor

Assume that $\mathrm{d}ϵ\left(t\right)=1$, meaning that there is an update at time t. In determining the technical interest rate $r^{*\left(ϵ\left(t\right)\right)}$ and the upscaling factor $k^{\left(ϵ\left(t\right)\right)}$, the distribution of the policy across states at time t enters. The distribution depends on the choice of basis; in our case, the technical basis or the market basis. The market basis reflects the true distribution of the policy across states. Therefore, we strongly suggest to work under the market basis. Working under the technical basis has the advantage that the tower property applies (see below), which limits the number of computations. However, taking the short cut and using the artificial technical basis leads to a twisted picture of the evolution of the policy, so we discourage it. For completeness, we include both options and model them by ○ below.

Assume that $r^{*\left(ϵ\left(t-\right)\right)}>r^{*}$, so that the policy is still in the consolidation phase of the bonus scheme. Then, necessarily, $k^{\left(ϵ\left(t-\right)\right)}=1$ (since we consolidate first), and the technical interest rate $r^{*\left(ϵ\left(t\right)\right)}$ is determined as the solution to the equation

$$\begin{array}{cc}\hfill Y\left(t-\right)+d\left(t\right)& =V^{*,○}\left(t-,r^{*\left(ϵ\left(t\right)\right)}\right),\hfill \end{array}$$

(7)

where $V^{*,○}\left(·,\rho \right)$ is the market or technical (indicated by the ○) expected technical reserve for the payment stream $B^{\left(0\right)}-C=B^f+B^u-C$, given that the technical interest rate is ρ. That is

$$\begin{array}{cc}\hfill V^{*,○}\left(t,\rho \right)& ={\text{𝔼}}^{○}\left[{\text{𝔼}}^{*}\left[{\int }_t^T{e}^{-\rho \left(s-t\right)}\mathrm{d}\left(B^f+B^u-C\right)\left(s\right)|Z\left(t\right)\right]\right]\hfill \\ & ={\text{𝔼}}^{○}\left[V_{Z\left(t\right)}^{*}\left(t,\rho ,1\right)\right],\hfill \end{array}$$

where the state-wise technical reserves $V_j^{*}$, $j\in J$, are given in Equation (2), and ${\text{𝔼}}^{○}$ denotes market or technical expectation. Hence, $r^{*\left(ϵ\left(t\right)\right)}$ is the technical interest rate that complies with the equivalence principle on portfolio level. Under the technical basis, the tower property applies, and the reserve simplifies to

$$\begin{array}{cc}\hfill V^{*,*}\left(t,\rho \right)& =\sum _{j\in J}{p}_{0j}^{*}\left(0,t\right)V_j^{*}\left(t,\rho ,1\right)\hfill \\ & ={\int }_t^T{e}^{-\rho \left(s-t\right)}\mathrm{d}\left({\beta }^{f,*}+{\beta }^{u,*}-{\varsigma }^{*}\right)\left(s\right),\hfill \end{array}$$

where ${\varsigma }^{*}$, ${\beta }^{f,*}$ and ${\beta }^{u,*}$ are the time 0 technical cash flows for the premium stream C and the benefit streams $B^f$ and $B^u$. This means that the reserve can be calculated using only the technical cash flows. Under the market basis, the reserve reads

$$V^{*,m}\left(t,\rho \right)=\sum _{j\in J}{p}_{0j}^m\left(0,t\right)V_j^{*}\left(t,\rho ,1\right).$$

Hence, using the market basis, both transition probabilities and state-wise technical reserves are needed in order to solve Equation (7). This is a drawback, but in our opinion, it is not enough to switch to the artificial technical basis. If the solution $r^{*\left(ϵ\left(t\right)\right)}$ is strictly smaller than $r^{*}$, then $r^{*\left(ϵ\left(t\right)\right)}$ is set to $r^{*}$, and the remaining bonus

$$Y\left(t-\right)+d\left(t\right)-V^{*,○}\left(t-,r^{*}\right)$$

is used to raise the upscaling factor $k^{\left(ϵ\left(t\right)\right)}$ as below. Otherwise, we set $k^{\left(ϵ\left(t\right)\right)}=1$.

Now, assume that $r^{*\left(ϵ\left(t-\right)\right)}=r^{*}$. Then, the policy is in the additional benefits phase of the bonus scheme, and we set $r^{*\left(ϵ\left(t\right)\right)}=r^{*}$. The upscaling factor $k^{\left(ϵ\left(t\right)\right)}$ is determined as the solution to the equation

$$d\left(t\right)=\left(k^{\left(ϵ\left(t\right)\right)}-k^{\left(ϵ\left(t-\right)\right)}\right)V^{u,*,○,+}\left(t-\right),$$

i.e.,

$$k^{\left(ϵ\left(t\right)\right)}=k^{\left(ϵ\left(t-\right)\right)}+\frac{d\left(t\right)}{V^{u,*,○,+}\left(t-\right)}.$$

Here, $V^{u,*,○,+}$ is the market or technical (indicated by the ○) expected technical reserve for the benefit stream $B^u$, given that the interest rate is $r^{*}$, i.e.,

$$\begin{array}{cc}\hfill V^{u,*,○,+}\left(t\right)& ={\text{𝔼}}^{○}\left[{\text{𝔼}}^{*}\left[{\int }_t^T{e}^{-r^{*}\left(s-t\right)}\mathrm{d}{B}^u\left(s\right)|Z\left(t\right)\right]\right]\hfill \\ & ={\text{𝔼}}^{○}\left[V_{Z\left(t\right)}^{u,*,+}\left(t,r^{*}\right)\right],\hfill \end{array}$$

where the state-wise technical benefit reserves $V_j^{u,*,+}$, $j\in J$, are given in Equation (1), and ${\text{𝔼}}^{○}$ denotes market or technical expectation. Hence, $k^{\left(ϵ\left(t\right)\right)}$ is the upscaling factor that satisfies the equivalence principle on portfolio level. Under the technical basis, the tower property applies, and the reserve simplifies to

$$\begin{array}{cc}\hfill V^{u,*,*,+}\left(t\right)& =\sum _{j\in J}{p}_{0j}^{*}\left(0,t\right)V_j^{u,*,+}\left(t,r^{*}\right)\hfill \\ & ={\int }_t^T{e}^{-r^{*}\left(s-t\right)}\mathrm{d}{\beta }^{u,*}\left(s\right).\hfill \end{array}$$

Under the market basis, it reads

$$\begin{array}{c}\hfill V^{u,*,m,+}\left(t\right)=\sum _{j\in J}{p}_{0j}^m\left(0,t\right)V_j^{u,*,+}\left(t,r^{*}\right).\end{array}$$

Again, we see that, using the market basis, both transition probabilities and state-wise technical reserves are needed.

We emphasize that there is no reason to consider the case $r^{*\left(ϵ\left(t-\right)\right)}<r^{*}$. For the explanation, recall that consolidation serves to lower the technical interest rate, so if the technical interest rate is already low, there is no need for consolidation. If the initial technical interest rate $r^{*\left(ϵ\left(0\right)\right)}$ is high compared to the pre-described level $r^{*}$, the allocated bonus is used for consolidation until $r^{*\left(ϵ\left(t\right)\right)}=r^{*}$ for some t. Thereafter, the bonus is used for additional benefits, and the technical interest rate is kept fixed. If the initial technical interest rate $r^{*\left(ϵ\left(0\right)\right)}$ is equal to $r^{*}$, the consolidation phase is skipped, the allocated bonus is used for additional benefits and the technical interest rate is kept fixed from the beginning. In neither case, we arrive at $r^{*\left(ϵ\left(t-\right)\right)}<r^{*}$. In the third and last case where the initial technical interest rate $r^{*\left(ϵ\left(0\right)\right)}$ is low compared to $r^{*}$, there is clearly no need for consolidation. Now, one has two options. Either, one can lower $r^{*}$ to $r^{*\left(ϵ\left(0\right)\right)}$ and proceed as in the case where $r^{*\left(ϵ\left(0\right)\right)}$ is equal to $r^{*}$; or, one can raise $r^{*\left(ϵ\left(0\right)\right)}$ to $r^{*}$, use the decline in the technical reserve for additional benefits and then proceed as in the case where $r^{*\left(ϵ\left(0\right)\right)}$ is equal to $r^{*}$. Both solutions will avert the case $r^{*\left(ϵ\left(t-\right)\right)}<r^{*}$. We note that the case $r^{*\left(ϵ\left(0\right)\right)}<r^{*}$ represents a situation with increasing technical interest rate. This has not been observed in Denmark in recent years, which is why we exclude the case from our paper. However, as argued above, our model can easily handle the case.

Example 4 (Survival model continued). For the simple policy in Example 1–3, the expected technical reserve $V^{*,○}\left(·,\rho \right)$ reads

$$\begin{array}{cc}\hfill V^{*,○}\left(t,\rho \right)& =e^{-{\int }_0^t{\mu }^{○}\left(v\right)\mathrm{d}v}\left({\int }_t^T{e}^{-\rho \left(s-t\right)}{e}^{-{\int }_t^s{\mu }^{*}\left(v\right)\mathrm{d}v}\left(b^{ad}{\mu }^{*}\left(s\right)-\pi \right)\mathrm{d}s\right.\hfill \\ & +\left.b^a{e}^{-\rho \left(T-t\right)}{e}^{-{\int }_t^T{\mu }^{*}\left(v\right)\mathrm{d}v}\right),t\le T.\hfill \end{array}$$

The expected technical benefit reserve $V^{u,*,○,+}\left(·\right)$ reads

$$\begin{array}{c}\hfill V^{u,*,○,+}\left(t\right)=b^a{e}^{-{\int }_0^t{\mu }^{○}\left(v\right)\mathrm{d}v}{e}^{-r^{*}\left(T-t\right)}{e}^{-{\int }_t^T{\mu }^{*}\left(v\right)\mathrm{d}v}.\end{array}$$

Remark 1. In Section 4.2, we mentioned that our setup does not allow for policyholder behavior options, such as surrender or free policy. However, it is not particularly complicated to include surrender, since it is an absorbing state. For the sake of clarity, we will not go into details on how. We just mention that, under the bonus scheme “additional benefits”, the surrender cash flow needs to be split into an upscaled and non-upscaled part. Furthermore, under the bonus scheme “consolidation”, the bonus suddenly raises the guarantee through a higher surrender value (typically equal to the technical reserve), and the market cash flows need to be recalculated every time the policy is consolidated to account for the higher surrender value.

4.9. Bonus Allocation and Guarantee Fee

In Section 4.7, we took the bonus d and the guarantee fee ${\pi }_g$ as exogenously given. This is imprecise for at least three reasons. Firstly, the total bonus allocated to the policies in a (homogeneous) portfolio typically depends on the collective bonus potential of the portfolio. The collective bonus potential K is defined as the maximum of zero and assets less guaranteed liabilities, i.e.,

$$K\left(t\right)={\left(X\left(t\right)-L\left(t\right)\right)}^{+},$$

where the assets X and the guaranteed liabilities L are calculated on portfolio level. With this definition, the balance sheet can be represented as in Figure 1.

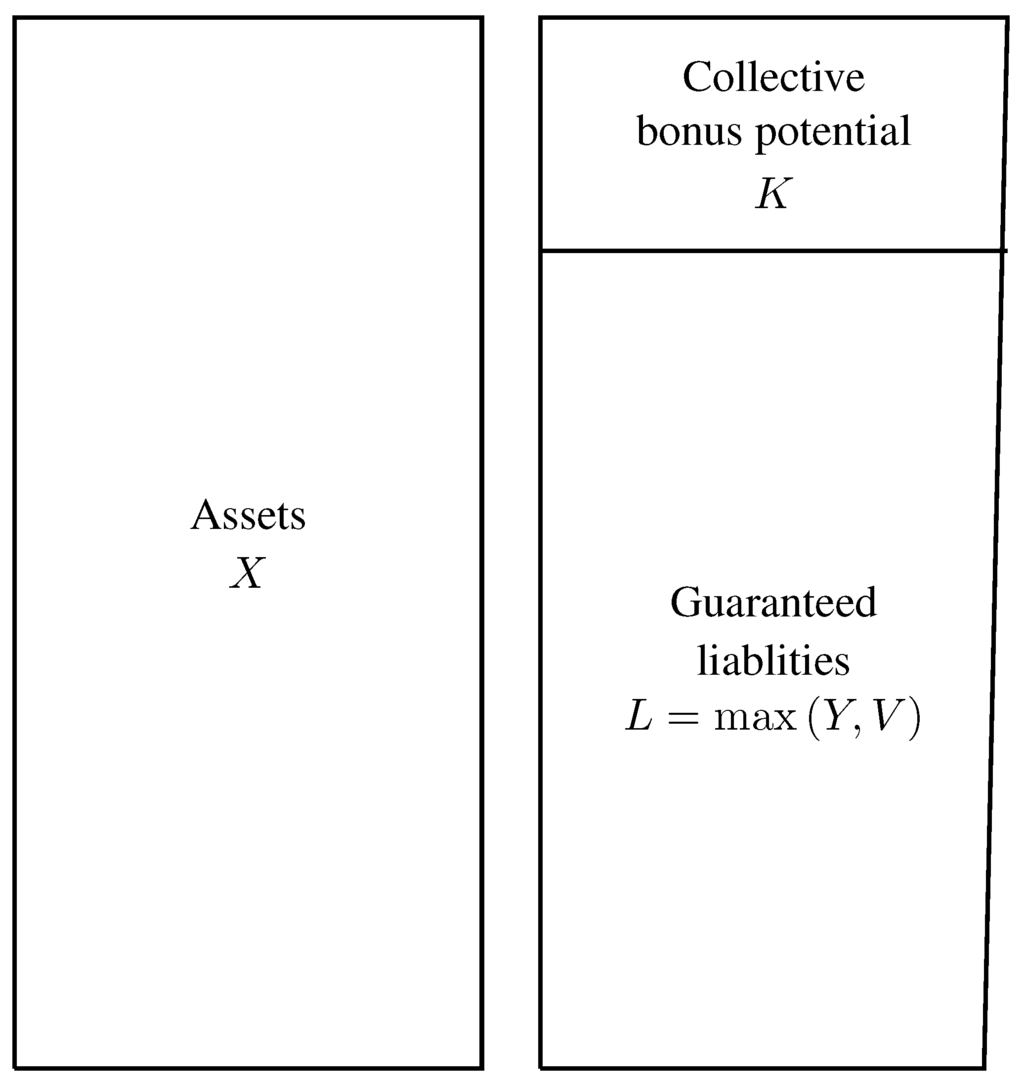
Figure 1. Portfolio balance sheet.

Figure 1. Portfolio balance sheet.

The collective bonus potential is a result of the systematic surplus to which the conservative technical basis gives rise. The systematic surplus of the policy is to be paid back to the policyholder in terms of bonus, but the collective bonus potential serves as a buffer in years with poor financial returns and/or poor risk results, so most often, the systematic surplus is not paid out right away. Therefore, to avoid redistribution across policies via the collective bonus potential, the portfolio must be homogeneous with respect to interest rate and risk (and costs, but in this paper, we leave that out). Furthermore, in order to avoid redistribution across generations, the systematic surplus should be paid out as soon as possible.

Secondly, the policy's share of the portfolio bonus depends on how much the policy has contributed to the portfolio's systematic surplus. As mentioned, the adjustment term α in the projection SDEs in Equation (4) is the market expected surplus arising from the conservative technical transition intensities. We choose to pay out the adjustment term immediately as risk bonus, such that the collective bonus potential collects surplus from capital gains only. The surplus collected in the collective bonus potential is then paid out, but not immediately, as interest rate bonus, i.e., proportional to the market expected technical reserve Y. If the technical transition intensities are not chosen carefully enough (which can be difficult for varying products), the adjustment term can be negative for some ages. In that case, no risk bonus is paid out.

Thirdly, for the contract to be fair, the bonus d and the guarantee fee ${\pi }_g$ must be chosen in such a way that the equivalence principle is satisfied for the total payments under the market basis, i.e.,

$$\begin{array}{c}\hfill {\text{𝔼}}^Q\left[{\int }_0^T{e}^{-{\int }_0^{s}r\left(v\right)\mathrm{d}v}\mathrm{d}\left(B^{\left(ϵ\left(s\right)\right)}-C\right)\left(s\right)\right]=x_0.\end{array}$$

(8)

In a multi-policy portfolio, the fairness constraint can be difficult to honor. It is possible to have fairness on portfolio level, but not on policy level, implying an unfair redistribution of systematic surplus across policies.

Often, the guarantee fee is a fraction of either the assets or the asset returns. The bonus allocation takes on more forms, but is ultimately a function of the collective bonus potential, the market reserve and the technical reserve. In Section 4.11, we present a numerical example with a one-policy and a two-policy portfolio. We show how to find a fair bonus and guarantee fee strategy, and we exemplify the challenges of fairness in a two-policy portfolio.

4.10. Application of Projections

We recall that the state process Z is independent of the financial market, and that, under both P and Q, the evolution of Z is described by the market basis. Most importantly, the projections of X and Y can be used to calculate the total time 0 market cash flow $CF$ and market value W for the guaranteed and non-guaranteed payments, i.e., to calculate

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{d}CF\left(t\right)& ={\text{𝔼}}^Q\left[k^{\left(ϵ\left(t\right)\right)}\mathrm{d}{B}^u\left(t\right)+\mathrm{d}{B}^f\left(t\right)-\mathrm{d}C\left(t\right)\right]\hfill \\ & ={\text{𝔼}}^Q\left[k^{\left(ϵ\left(t\right)\right)}\right]\mathrm{d}{\beta }^u\left(t\right)+\mathrm{d}{\beta }^f\left(t\right)-\mathrm{d}\varsigma \left(t\right)\hfill \end{array}\end{array}$$

(9)

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill W\left(0\right)& ={\text{𝔼}}^Q\left[{\int }_0^T{e}^{-{\int }_0^{s}r\left(v\right)\mathrm{d}v}\mathrm{d}\left(B^{\left(ϵ\left(s\right)\right)}-C\right)\left(s\right)\right]\hfill \\ & ={\text{𝔼}}^Q\left[{\int }_0^T{e}^{-{\int }_0^{s}r\left(v\right)\mathrm{d}v}\left(k^{\left(ϵ\left(s\right)\right)}\mathrm{d}{\beta }^u\left(s\right)+\mathrm{d}{\beta }^f\left(s\right)-\mathrm{d}\varsigma \left(s\right)\right)\right].\hfill \end{array}\end{array}$$

(10)

Here, r is the stochastic short interest rate. We emphasize that the cash flow and market value distinguish themselves from the usual cash flows and market values by including non-guaranteed payments as well as guaranteed payments. In particular, we have

$$\begin{array}{cc}\hfill W\left(0\right)& =V\left(0\right)+{\text{𝔼}}^Q\left[{\int }_0^T{e}^{-{\int }_0^{s}r\left(v\right)\mathrm{d}v}\left(k^{\left(ϵ\left(s\right)\right)}-1\right)\mathrm{d}{\beta }^u\left(s\right)\right],\hfill \end{array}$$

where V is the usual market value from Equation (3). The additional term is the market value of the non-guaranteed benefits. If the projections are based on scenarios generated via Monte Carlo simulation, then for each t, the expectation ${\text{𝔼}}^Q\left[k^{\left(ϵ\left(t\right)\right)}\right]$ in Equation (9) is approximated by averaging over a sufficient number of Q-projections up to time t. If, instead, the projections are of the worst-case or best-estimate type (and, hence, singular), then ${\text{𝔼}}^Q\left[k^{\left(ϵ\left(t\right)\right)}\right]$ is approximated by the single projected value. If the short interest rate is deterministic, then Equation (10) simplifies to

$$W\left(0\right)={\int }_0^T{e}^{-{\int }_0^{s}r\left(v\right)\mathrm{d}v}\mathrm{d}CF\left(s\right).$$

Otherwise, Equation (10) is approximated by averaging over a sufficient number of integrated sample paths $t\mapsto k^{\left(ϵ\left(t\right)\right)}\mathrm{d}{\beta }^u\left(t\right)+\mathrm{d}{\beta }^f\left(t\right)-\mathrm{d}\varsigma \left(t\right)$, discounted by the short interest rate.

The market value is useful for determining the bonus allocation d and guarantee fee ${\pi }_g$ according to the fairness criterion in Equation (8), which can be written as

$$W\left(0\right)=x_0.$$

So far, we have suppressed the influence of the investment strategy, but it enters through the stochastic return on the assets. Hence, the task of determining d and ${\pi }_g$ is the classical trade-off between the aggressiveness of dividend allocation (expressed by d) and the option price (expressed by ${\pi }_g$) given the aggressiveness of the investment strategy (typically expressed by the volatility).

The projections of X and Y are also useful for calculating the time 0 P-expected cash flow for the guaranteed and non-guaranteed payments, i.e., for calculating

$$\begin{array}{cc}\hfill \mathrm{d}C{F}^P\left(t\right)& ={\text{𝔼}}^P\left[k^{\left(ϵ\left(t\right)\right)}\mathrm{d}{B}^u\left(t\right)+\mathrm{d}{B}^f\left(t\right)-\mathrm{d}C\left(t\right)\right]\hfill \\ & ={\text{𝔼}}^P\left[k^{\left(ϵ\left(t\right)\right)}\right]\mathrm{d}{\beta }^u\left(t\right)+\mathrm{d}{\beta }^f\left(t\right)-\mathrm{d}\varsigma \left(t\right).\hfill \end{array}$$

If the projections are based on scenarios generated via Monte Carlo simulation, then for each t, the expectation ${\text{𝔼}}^P\left[k^{\left(ϵ\left(t\right)\right)}\right]$ is approximated by averaging over a sufficient number of P-projections up to time t. If instead, the projections are of the worst-case or best-estimate type (and, hence, singular), then ${\text{𝔼}}^P\left[k^{\left(ϵ\left(t\right)\right)}\right]$ is approximated by the single projected value. The P-expected cash flow is an estimate of the money out flow from the insurance company at future time points, and it is, therefore, useful for liquidity considerations. Again, the cash flow distinguishes itself by including non-guaranteed payments as well as guaranteed payments, thereby, providing a more complete picture.

Finally, for solvency purposes, one can use scenarios generated via Monte Carlo simulation to calculate P-quantiles for the capital requirement at time $T_1$.

$$\begin{array}{cc}& {\text{𝔼}}^Q\left[{\int }_0^{T\vee T_1}{e}^{-{\int }_{T_1}^{s}r\left(v\right)\mathrm{d}v}\mathrm{d}\left(B^{\left(ϵ\left(s\right)\right)}-C\right)\left(s\right)|{\left(k^{\left(ϵ\left(s\right)\right)},r\left(s\right)\right)}_{s\le T_1}\right]=\hfill \\ & \phantom{}{\int }_0^{T_1}{e}^{-{\int }_{T_1}^{s}r\left(v\right)\mathrm{d}v}\left(k^{\left(ϵ\left(s\right)\right)}\mathrm{d}{\beta }^u\left(s\right)+\mathrm{d}{\beta }^f\left(s\right)-\mathrm{d}\varsigma \left(s\right)\right)+\hfill \\ & \phantom{}{\text{𝔼}}^Q\left[{\int }_{T_1}^{T\vee T_1}{e}^{-{\int }_{T_1}^{s}r\left(v\right)\mathrm{d}v}\left(k^{\left(ϵ\left(s\right)\right)}\mathrm{d}{\beta }^u\left(s\right)+\mathrm{d}{\beta }^f\left(s\right)-\mathrm{d}\varsigma \left(s\right)\right)|k^{\left(ϵ\left(T_1\right)\right)},r\left(T_1\right)\right].\hfill \end{array}$$

The capital requirement is expressed in terms of the capital needed up to time $T_1$ plus the market value of future liabilities at time $T_1$. The conditional Q-expectation appears in the capital requirement, because the capital requirement concerns future payments and balance sheets. The quantiles are obtained by projecting up to time $T_1$ under the physical measure P. However, for each projection, the Q-expectation is approximated by projecting from time $T_1$ to time T under the pricing measure Q. Hence, if N sample paths are needed for approximating cash flows and market values, then $N^2$ paths are needed for the quantiles. The quantiles can be used for solvency assessments of the provided guarantee.

4.11. Numerical Examples

In this section, we go through two numerical examples with a one-policy portfolio and a two-policy portfolio. A larger portfolio would, of course, be more realistic, but a large number of policies could easily drown the key insights from the examples. Going from one to two policies is by far the biggest step, and conceptually, there is no impediment to extending the theory to larger portfolios. Working in a discrete projection setup, we show how to find a fair bonus and guarantee fee strategy for the one-policy portfolio, and we exemplify the fairness challenges in a two-policy portfolio. The examples are based on 5000 scenarios generated via Monte Carlo simulation. We have made sure that the number of simulated scenarios is sufficiently high for our numerical results and graphs not to change between simulations, but we do not go into details about the robustness of the simulations, since the examples only serve to demonstrate the possible applications of our model.

4.11.1. One-Policy Portfolio

We consider a portfolio consisting of a single policy. The policy is the one from Examples 1–4. The policyholder is a female aged 25 at time 0, where the policy is issued. We fix $r^{*}=0.02$, and we assume that $r^{*\left(0\right)}=r^{*}$, which is natural for a newly-issued policy. Thereby, we only consider the bonus scheme “additional benefits”. We recall that bonus is used to increase the endowment sum and not the term insurance sum. The death of the policyholder is governed by the technical mortality intensity

$$\begin{array}{c}\hfill {\mu }^{*}\left(t\right)=5·{10}^{-4}+5.3456·{10}^{-5}·e^{0.087498\left(25+t\right)}.\end{array}$$

For the last three decades, this has served as a standard mortality intensity for adult women in Denmark. It is part of the so-called G82 technical basis that was set forth as a Danish industry standard in 1982. The market mortality intensity is given by

$$\begin{array}{c}\hfill {\mu }^m\left(t\right)=0.8{\mu }^{*}\left(t\right).\end{array}$$

With this choice of mortality intensities and with the product choices below, the technical basis is on the safe side, except for low ages, where the death sum exceeds the savings, resulting in a negative contribution from mortality risk. However, due to the low mortality for low ages, the negative contribution is insignificantly small.

The policy expires at time $T=40$ when the policyholder is 65. We fix the term insurance sum at $b^{ad}=1$ and the pure endowment sum at $b^a=3$. The equivalence premium is determined via the equivalence relation

$$V^{*,-}\left(0,r^{*}\right)=V^{f,*,+}\left(0,r^{*}\right)+V^{u,*,+}\left(0,r^{*}\right),$$

i.e.,

$$\pi =\frac{b^a{e}^{-{\int }_0^T\left(r^{*}+{\mu }^{*}\left(v\right)\right)\mathrm{d}v}+b^{ad}{\int }_0^T{e}^{-{\int }_0^s\left(r^{*}+{\mu }^{*}\left(v\right)\right)\mathrm{d}v}{\mu }^{*}\left(s\right)\mathrm{d}s}{{\int }_0^T{e}^{-{\int }_0^s\left(r^{*}+{\mu }^{*}\left(v\right)\right)\mathrm{d}v}\mathrm{d}s}.$$

Using numerical methods, we obtain $\pi =0.04614$. The bonus d is allocated and the guarantee fee ${\pi }_g$ is paid once a year. Hence, we have

$$\begin{array}{c}\hfill ϵ\left(t\right)=\#\left\{i=1,...,40:i\le t\right\}.\end{array}$$

We note that $ϵ\left(t\right)=t$ for $t=1,...,40$. We project the two accounts X and Y using steps of a size of one year by applying a discretized version of the stochastic differential equations for X and Y. For the discretization, we recall from Example 2 that ${\beta }^u$ is a pure jump function and that ς and ${\beta }^f$ are continuous functions. Hence, we get the stochastic difference equations

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill X\left(t-\right)& =X\left(t-1\right)\left(1+R_X\left(t\right)\right)-{\int }_{\left(t-1,t\right)}\left(\mathrm{d}{\beta }^f\left(s\right)-\mathrm{d}\varsigma \left(s\right)\right),\hfill \\ \hfill X\left(t\right)& =X\left(t-\right)-k^{\left(t\right)}\text{Δ}{\beta }^u\left(t\right)+g\left(t\right)-{\pi }_g\left(t\right),t=1,...,40,\hfill \\ \hfill X\left(0\right)& =0,\hfill \\ \hfill Y\left(t-\right)& =Y\left(t-1\right)e^{r^{*}}-{\int }_{\left(t-1,t\right)}\left(\mathrm{d}{\beta }^f\left(s\right)-\mathrm{d}\varsigma \left(s\right)\right)+\alpha \left(t,r^{*},k^{\left(t-1\right)}\right),\hfill \\ \hfill Y\left(t\right)& =Y\left(t-\right)-k^{\left(t\right)}\text{Δ}{\beta }^u\left(t\right)+d\left(t\right),t=1,...,40,\hfill \\ \hfill Y\left(0\right)& =0.\hfill \end{array}\end{array}$$

(12)

We assume a deterministic market interest rate $r=0.04$, and the assets of the portfolio (in this case, the assets of the policy) are invested in a fund with log-normal returns that are paid out once a year, i.e.,

$$\begin{array}{cc}\hfill R_X\left(t\right)& =\frac{S\left(t\right)-S\left(t-1\right)}{S\left(t-1\right)},t=1,...,40,\hfill \end{array}$$

where S is a geometric Brownian motion. We basically consider a simple Black–Scholes financial market. We assume that the fund size S has drift $0.07$ and volatility $0.2$ under the physical measure P (and, consequently, drift $r=0.04$ and volatility $0.2$ under the pricing measure Q).

The bonus d is determined as a fraction ${\theta }_1$ of the excess collective bonus potential K just before the bonus allocation over a threshold $\overline{K}$ if this fraction exceeds the positive part of the natural risk bonus α (see Section 4.9 for more on risk bonus), i.e.,

$$\begin{array}{cc}\hfill d\left(t\right)& =max\left\{{\left(\alpha \left(t,r^{*},k^{\left(ϵ\left(t-\right)\right)}\right)\right)}^{+},{\theta }_1{\left(K\left(t-\right)-\overline{K}\left(t-\right)\right)}^{+}\right\},\hfill \\ & t=1,...,40,\hfill \end{array}$$

where K and $\overline{K}$ are given by

$$\begin{array}{cc}\hfill K\left(t\right)& ={\left(X\left(t\right)-L\left(t\right)\right)}^{+},\hfill \\ \hfill \overline{K}\left(t\right)& ={\theta }_{2}L\left(t\right),\hfill \end{array}$$

with the guaranteed liabilities L defined in Equation (5). The threshold $\overline{K}$ can be seen as a preferred minimum collective bonus potential. We fix ${\theta }_1=0.2$ and ${\theta }_2=0.1$. As mentioned, the chosen technical transition intensity is not on the safe side for low ages. Therefore, we need to take the positive part of α in the expression above to exclude negative risk bonus. Finally, we choose the guarantee fee ${\pi }_g$ to be a fraction ${\theta }_3$ of the positive part of the returns on the assets, i.e.,

$$\begin{array}{c}\hfill {\pi }_g\left(t\right)={\theta }_3{\left(R_X\left(t\right)X\left(t-1\right)\right)}^{+}.\end{array}$$

In addition to the yearly guarantee fee, the equity holders of the insurance company receives the remaining collective bonus potential at expiration as part of the final guarantee fee. We determine the fraction ${\theta }_3$ according to the fairness criterion in Equation (8). Furthermore, using this guarantee fee, we consider:

• the expected evolution of the upscaling factor $t\mapsto {\text{𝔼}}^Q\left[k^{\left(ϵ\left(t\right)\right)}\right]$,
• the expected evolution of the assets $t\mapsto {\text{𝔼}}^Q\left[X\left(t\right)\right]$, market reserve $t\mapsto {\text{𝔼}}^Q\left[V\left(t\right)\right]$, technical reserve $t\mapsto {\text{𝔼}}^Q\left[Y\left(t\right)\right]$ and collective bonus potential $t\mapsto {\text{𝔼}}^Q\left[K\left(t\right)\right]$,
• the expected level for the guarantee injections ${\text{𝔼}}^Q\left[g\left(t\right)\right]$ and guarantee fees ${\text{𝔼}}^Q\left[{\pi }_g\left(t\right)\right]$,$t=1,...,T$.

Using standard Monte Carlo methods, we simulate 5000 sample paths for the asset returns $R_X$ under the measure Q, and for each sample path, we project X and Y for different values of ${\theta }_3$, using the difference equations in Equation (12). More specifically, we look for a ${\theta }_3$, such that we get zero when approximating the time 0 market value $W\left(0\right)$ from Equation (11). We recall that W is the market value of the guaranteed and non-guaranteed payments. We arrive at the fair guarantee fee fraction ${\theta }_3=0.31$.

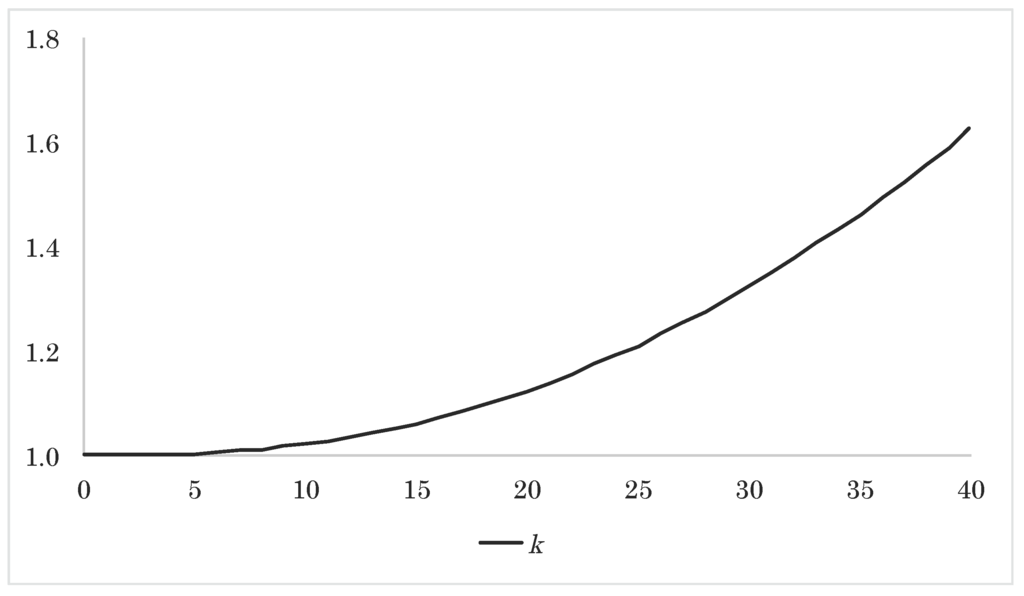
Figure 2. Approximated expected upscaling factor k as a function of time.

Figure 2. Approximated expected upscaling factor k as a function of time.

Figure 3. Approximated expected guarantee injection g and guarantee fee π_g as a function of time.

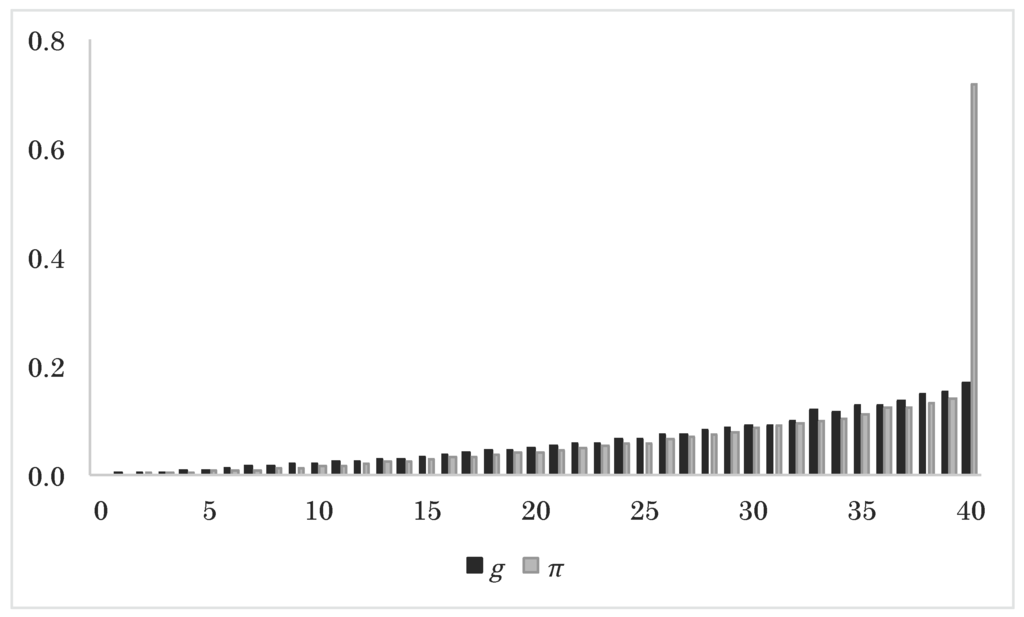
Figure 3. Approximated expected guarantee injection g and guarantee fee π_g as a function of time.

In Figure 2, Figure 3 and Figure 4, we plot the average evolution of the upscaling factor, the average level for the guarantee injection and guarantee fee, and the average evolution of the assets, reserves and collective bonus potential. From Figure 2, we see that more than 60% of the final endowment sum comes from bonus. This is primarily due to the technical interest rate being only half the size of the market interest rate. From Figure 3, we observe that the guarantee fees and the guarantee injections follow each other closely, implying that the structure of the guarantee fee is reasonable. The final guarantee fee includes the remaining collective bonus potential at expiration and is, consequently, much higher than the other guarantee fees. We note that a considerable part of the guarantee injections are paid for by giving up the remaining collective bonus potential at expiration. In a multi-generation portfolio, this is of course transferred to the other policies, leading to a higher guarantee fee throughout the period. From Figure 4, we see how the different parts of the balance in Figure 1 evolve in expectation.

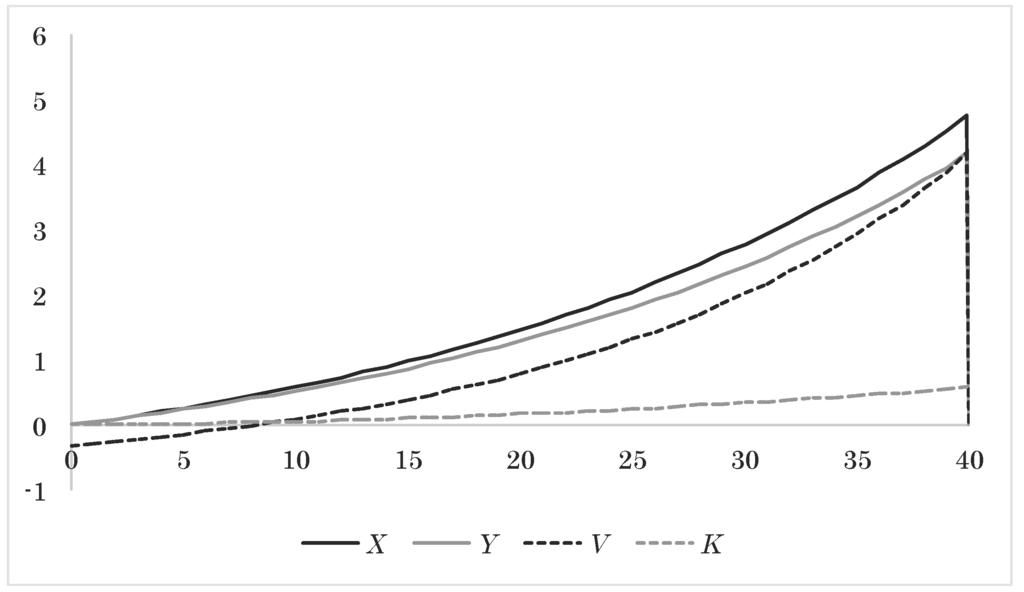
Figure 4. Approximated expected assets X, technical reserve Y, market reserve V and collective bonus potential K as a function of time.

Figure 4. Approximated expected assets X, technical reserve Y, market reserve V and collective bonus potential K as a function of time.

4.11.2. Two-Policy Portfolio

We consider a portfolio consisting of two policies, Policy 1 and 2, which are identical to the one in Section 4.11.1. However, only Policy 1 is issued at time 0; Policy 2 is not issued until time 20. Hence, from time 0 to time 20, there is one policy in the portfolio; from time 20 to time 40, there are two policies in the portfolio; and from time 40 to time 60, there is, again, one policy in the portfolio. If not careful, this overlap in time easily causes an unfair redistribution between the two policies.

We let ${\alpha }_i$, $k_i^{\left(·\right)}$ and $Y_i$ denote, respectively, the adjustment term, the upscaling factor and the market expected technical reserve for policy $i=1,2$. We work with the convention that all quantities (except the upscaling factor) are zero for Policy 2 until time 20 and zero for Policy 1 after time 40. By X, V and Y, we denote the total assets, the total market expected market reserve and the total market expected technical reserve of the portfolio.

We make the same market assumptions as in Section 4.11.1, and because of the longer time period, we now have

$$ϵ\left(t\right)=\#\left\{i=1,...,60:i\le t\right\}.$$

The guarantee injection g is calculated on portfolio level and reads

$$g\left(t\right)={\left(L\left(t-\right)+{\pi }_g\left(t\right)-X\left(t-\right)\right)}^{+},$$

where the guaranteed liabilities L are given by

$$L\left(t\right)=max\left\{V\left(t\right),Y\left(t\right)\right\}.$$

The total bonus to the policies in the portfolio is determined as a fraction ${\theta }_1$ of the excess collective bonus potential K just before the bonus allocation over a threshold $\overline{K}$ if this fraction exceeds the positive part of the total natural risk bonus α for the policies of the portfolio, i.e.,

$$\begin{array}{cc}\hfill d\left(t\right)& =max\left\{\alpha \left(t\right),{\theta }_1{\left(K\left(t-\right)-\overline{K}\left(t-\right)\right)}^{+}\right\},t\in \left\{1,2,...,60\right\},\hfill \end{array}$$

where α, K and $\overline{K}$ are given by

$$\begin{array}{cc}\hfill \alpha \left(t\right)& ={\left({\alpha }_1\left(t,r^{*},k_1^{\left(ϵ\left(t-\right)\right)}\right)\right)}^{+}+{\left({\alpha }_2\left(t,r^{*},k_2^{\left(ϵ\left(t-\right)\right)}\right)\right)}^{+},\hfill \\ \hfill K\left(t\right)& ={\left(X\left(t\right)-L\left(t\right)\right)}^{+},\hfill \\ \hfill \overline{K}\left(t\right)& ={\theta }_{2}L\left(t\right).\hfill \end{array}$$

The threshold $\overline{K}$ can again be seen as a preferred minimum collective bonus potential for the portfolio. We keep ${\theta }_1=0.2$ and ${\theta }_2=0.1$. The bonus is divided between the policies of the portfolio in the following way: First, each policy receives its natural risk bonus given by the adjustment terms ${\alpha }_1$ and ${\alpha }_2$. We, thereby, use the collective bonus potential as a financial buffer only. Second, the remaining bonus (if any) is distributed as a technical interest rate margin, i.e., proportional to the market expected technical reserves $Y_1$ and $Y_2$. In formulas, the bonus to policy $i=1,2$ is given by

$$\begin{array}{cc}\hfill d_i\left(t\right)& ={\left({\alpha }_i\left(t,r^{*},k_i^{\left(ϵ\left(t\right)\right)}\right)\right)}^{+}+\left(d\left(t\right)-\alpha \left(t\right)\right)\frac{Y_i\left(t\right)}{Y\left(t\right)},t\in \left\{1,2,...,60\right\}.\hfill \end{array}$$

4.11.3. Constant Guarantee Fee Fraction

First, we stick to a guarantee fee ${\pi }_g$ that is a constant fraction ${\theta }_3$ of the positive part of the returns on the assets, i.e.,

$${\pi }_g\left(t\right)={\theta }_3{\left(R_X\left(t\right)X\left(t-1\right)\right)}^{+}.$$

In addition to the yearly guarantee fee, the equity holders of the insurance company receive the remaining collective bonus potential at the expiration of Policy 2 as part of the final guarantee fee. We determine the fraction ${\theta }_3$ according to the fairness criterion in Equation (8) applied on portfolio level. We take the 5000 sample paths simulated in Section 4.11.1, and for each sample path, we project X, $Y_1$ and $Y_2$ for different values of ${\theta }_3$, using three difference equations almost identical to the ones in Equation (12). More specifically, we look for a ${\theta }_3$, such that we get zero when approximating the time 0 market value from Equation (11) on portfolio level. We arrive at the guarantee fee fraction ${\theta }_3=0.35$. We notice that the fraction is higher than in the one-policy case, possibly to cover increased risk associated with an extra policy and a longer time horizon. Furthermore, we calculate the average evolution of the upscaling factor, the average guarantee injection and guarantee fee levels, and the average evolution of the assets, reserves and collective bonus potential. We discover that the guarantee fee is only fair on portfolio level. Approximating the time 0 market value from Equation (11) for each of the policies individually, we get

$$\begin{array}{c}\hfill W^1\left(0\right)=-0.061,W^2\left(0\right)=0.068.\end{array}$$

Hence, a significant amount of the systematic surplus is being redistributed from Policy 1 to Policy 2. We recall that $W^1$ and $W^2$ are the market values of the guaranteed and non-guaranteed payments; and not the usual market values that only include guaranteed payments. To illustrate the redistribution, we plot the average evolution of the upscaling factors in Figure 5. From the figure, it appears that Policy 2's final upscaling factor is much larger than Policy 1's. Furthermore, comparing with Figure 2, we see that Policy 1's final upscaling factor is significantly smaller than in the one-policy case, so it is not just a matter of both policies benefiting from being part of the two-policy portfolio and Policy 2 benefiting more from it than Policy 1.

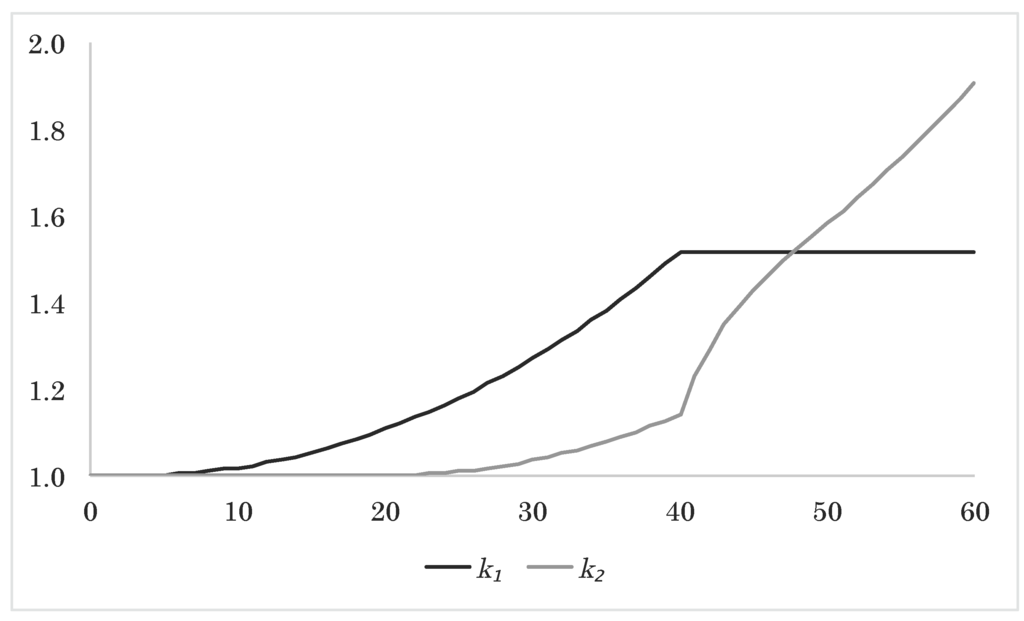
Figure 5. Approximated expected upscaling factors $k_1$ and $k_2$ as function of time.

Figure 5. Approximated expected upscaling factors $k_1$ and $k_2$ as function of time.

4.11.4. Period-Dependent Guarantee Fee Fraction

To overcome the unfairness introduced by the constant guarantee fee fraction, we allow there to be a different fraction ${\theta }_3$ determining the guarantee fee for each of the time periods $\left[0,20\right]$, $\left(20,40\right]$ and $\left(40,60\right]$, i.e.,

$${\pi }_g\left(t\right)={\theta }_3^{i\left(t\right)}{\left(R_X\left(t\right)X\left(t-1\right)\right)}^{+},$$

where

$$i\left(t\right)=\left\{\begin{array}{cc}1\hfill & t\le 20,\hfill \\ 2\hfill & 20<t\le 40,\hfill \\ 3\hfill & t>40.\hfill \end{array}\right.$$

In addition to the yearly guarantee fee, the equity holders of the insurance company still receive the remaining collective bonus potential at the expiration of Policy 2 as part of the final guarantee fee. First, we fix ${\theta }_3^1=0.31$, since this is the fair guarantee fee fraction from the one-policy portfolio. Second, we take the 5000 sample paths simulated in Section 4.11.1 and search (in the same way as before) for a value of ${\theta }_3^2$ for which $W^1\left(0\right)=0$, meaning that the guarantee fee determined by the pair $\left({\theta }_3^1,{\theta }_3^2\right)$ is fair for Policy 1. We find the fair guarantee fee fraction ${\theta }_3^2=0.29$. Third, we search for a value of ${\theta }_3^3$ for which $W^2\left(0\right)=0$, meaning that the guarantee fee determined by the triplet $\left({\theta }_3^1,{\theta }_3^2,{\theta }_3^3\right)$ is fair for Policy 2. We find the fair guarantee fee fraction ${\theta }_3^3=0.61$. We notice that the guarantee fee fraction is much higher in the last time period than in the first two time periods and that the guarantee fee fraction in the second time period is slightly smaller than in the first time period. This is best explained by the fact that Policy 2 inherits collective bonus potential from Policy 1. Policy 1 is compensated for this transfer via the lower guarantee fee fraction in the second time period, and Policy 2 pays for the transfer in terms of the high guarantee fee fraction in the last time period. This is reflected in Figure 6. Again, the final guarantee fee is much higher than the other guarantee fees, since it includes the remaining collective bonus potential at the expiration of Policy 2. In a multi-generation portfolio, this is transferred to the other policies, leading to a higher guarantee fee throughout the period.

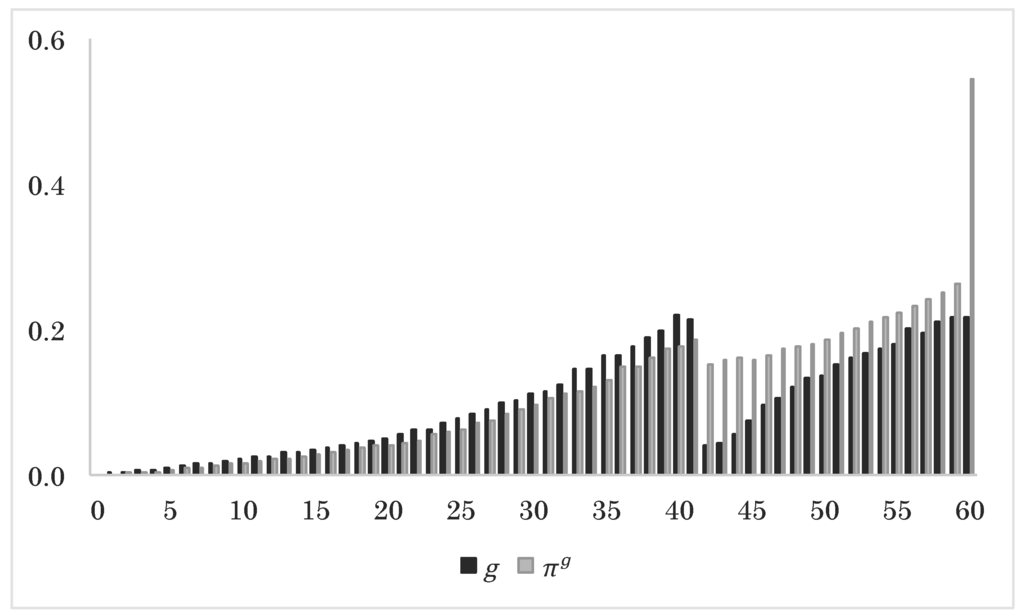
Figure 6. Approximated expected guarantee injection g and guarantee fee π_g as a function of time.

Figure 6. Approximated expected guarantee injection g and guarantee fee π_g as a function of time.

Figure 7. Approximated expected upscaling factors k₁ and k₂ as a function of time.

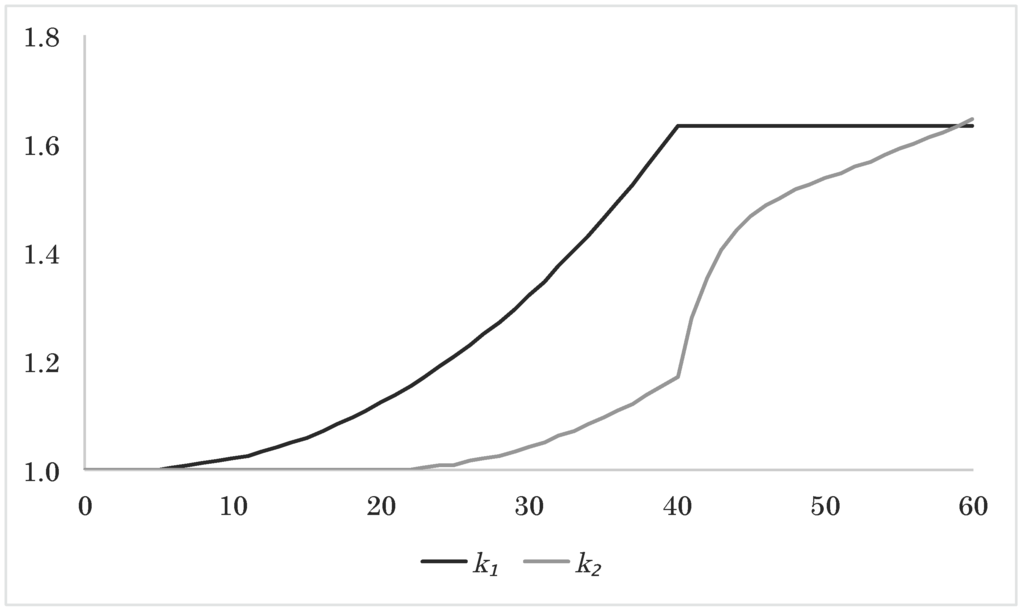
Figure 7. Approximated expected upscaling factors k₁ and k₂ as a function of time.

In Figure 6, Figure 7 and Figure 8, we plot the average evolution of the upscaling factors, the average guarantee injection and guarantee fee, and the average evolution of the assets, reserves and collective bonus potential. With the fair guarantee fee, we see from Figure 7 that the two policies' final upscaling factors are essentially equal; also to the final upscaling factor from Section 4.11.1. From Figure 8, we see how the different parts of the balance in Figure 1 evolve in expectation for the two-policy portfolio.

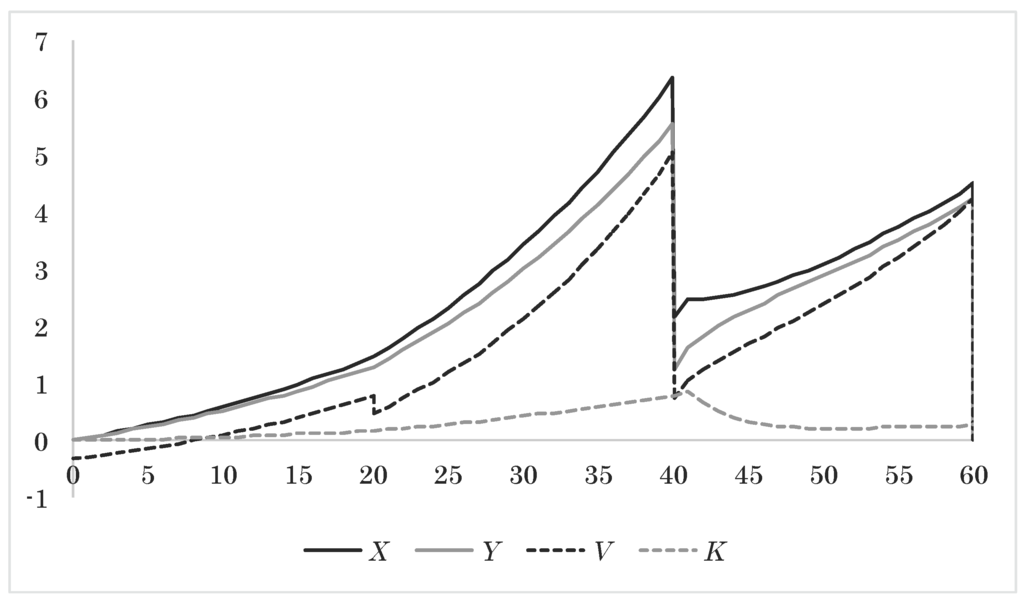
Figure 8. Approximated expected assets X, technical reserve Y, market reserve V and collective bonus potential K as a function of time.

Figure 8. Approximated expected assets X, technical reserve Y, market reserve V and collective bonus potential K as a function of time.

5. Unit-Linked Insurance

In this section, we consider unit-linked insurance. We touch upon different aspects of unit-linked insurance, and we present our two-account model for a general unit-linked insurance policy. Again, we include simple and illustrative survival model examples. We end the section with a numerical example that is a unit-linked version of the numerical example in the previous section.

5.1. Product Specification and Two-Account Model

We consider a unit-linked insurance policy. The state-wise evolution of the policy is described in Section 3. The payments of the policy consist of a state-dependent payment stream $B^f+B^u-C$ where C is a fixed state-dependent premium stream (“C” for contribution), $B^f$ is a fixed state-dependent benefit stream (“B” for benefits and superscript “f” for fixed) and $B^u$ is a state-dependent benefit stream that is linked to the financial market (superscript “u” for unit-linked). More precisely, the assets of the policy are invested in a fund, and the benefit stream $B^u$ depends on the value of the assets. The policy includes a guaranteed minimum retirement savings amount at the retirement date R, based on a guarantee account with a guaranteed interest rate $r^{*}$ (for example, $r^{*}=0$). We do not take costs into account.

We denote by X the assets of the policy and by Y the guarantee account. Again, the accounts X and Y are the backbone of our two-account model. The policy is issued before or at time 0, and the two accounts amount to $Y\left(0-\right)=x_0$ and $Y\left(0-\right)=y_0$ just before time 0. The policy terminates at time $T\ge R$. Thereafter, there are no payments.

The assets X are invested in a fund with stochastic return $R_X$. The guarantee account Y accumulates according to the guaranteed interest rate. In good times, the return rate on the assets exceeds the technical interest rate, and then, the assets outgrow the guarantee account. In that case, the guarantee account is upgraded (increased) according to the terms of the contract. For example, it may be stipulated in the contract that the guarantee account is always to make up at least 80% of the assets. Regardless of the developments in the financial market, the guarantee account is never to be downgraded (lowered), and at retirement, the maximum value of the assets and the guarantee account is paid out to the policyholder. In bad times where the guarantee account exceeds the assets at retirement, the equity holders of the insurance company step in with a capital injection taken from the company's equity. We speak of the possible capital injection

$$\begin{array}{c}\hfill g={\left(Y\left(R-\right)-X\left(R-\right)\right)}^{+}\end{array}$$

(13)

as guarantee injection, and its role is to raise the assets at retirement in case of unfavorable developments in the financial market. The policyholder pays for the company's risk taking by having a guarantee fee deducted from the assets and paid to the equity holders of the insurance company. We assume that the insurance company's equity is always sufficient to cover the guarantee injection and that the guarantee injection and guarantee fees are settled via the equity. All of the above does not happen continuously, but at pre-specified deterministic time points $0<t_1<...<t_n=R$ (for example, once a year), where the two accounts X and Y are updated. We let

$$\begin{array}{c}\hfill ϵ\left(t\right)=\#\left\{i=1,...,n:t_i\le t\right\}\end{array}$$

count the number of updates prior to time t. The updates consist of upgrades, u, of the guarantee account (if the assets exceed the guarantee account in a pre-described way) and the deduction of the guarantee fee, ${\pi }_g$, in return for the possible guarantee injection g at retirement. At retirement R, the assets are updated with the guarantee injection, g, if the guarantee account exceeds the assets. We let ${ϵ}_R\left(t\right)=1_{\left\{t\ge R\right\}}$ mark this final update. We stress the similarity with participating life insurance, although, there, the guarantee injection is settled at each update and not only at retirement. Compare for example Equation (13) to Equation (6). Again, we assume that the stochastic return on the assets, $R_X$, does not jump at time points with an account update. Furthermore, to ensure predictability, we assume that $u\left(t\right)$ and ${\pi }_g\left(t\right)$ are known at time $t-$ for all t with $\mathrm{d}ϵ\left(t\right)=1$, i.e., for all time points with an account update.

We assume that the market-linked benefit stream $B^u$ is linear in X, i.e.,

$$\begin{array}{c}\hfill \mathrm{d}{B}^u\left(t\right)=X\left(t-\right)\mathrm{d}{B}^p\left(t\right),\end{array}$$

where $B^p$ denotes a fixed state-dependent benefit stream (superscript “p” for profile). We write $X\left(t-\right)$ instead of just $X\left(t\right)$ to ensure that the asset process X is well-defined (see definition below). To ensure that, in expectation, the assets are paid out to the policyholder, we assume that $\text{Δ}{B}^f\left(T\right)=\text{Δ}C\left(T\right)=0$ and $\text{𝔼}\left[\text{Δ}{B}^p\left(T\right)\right]=1$. Here, Δ denotes the jump part of the processes.

The fixed benefit stream $B^f$ includes, for example, disability or death payments, whereas the market-linked benefit stream $B^u$ includes, for example, deposit protection, surrender payments, a variable pure endowment or a variable life annuity. We note that the setup does not cover benefits that are non-linear in X. Thus, it does not cover a deposit protection of the form

$$max\left\{X,D\right\},$$

where D is a fixed death sum. Furthermore, we exclude the policyholder behavior option “free policy”, as it introduces a duration-dependent free policy conversion factor. Formally, the payment streams of the policy are given as

$$\begin{array}{cc}\hfill \mathrm{d}C& =\sum _{j\in J}{I}_j\mathrm{d}{c}_j,\hfill \\ \hfill \mathrm{d}{B}^i& =\sum _{j\in J}{I}_j\mathrm{d}{b}_j^i+\sum _{j,k\in J:j\ne k}{b}_{jk}^i\mathrm{d}{N}_{jk},i=f,p,\hfill \end{array}$$

where $c_j$, $b_j^f$ and $b_j^p$ are deterministic, state-wise payment streams and $b_{jk}^f$ and $b_{jk}^p$ are deterministic lump sum payments upon jumps. Examples of deterministic lump sum payments upon jumps include surrender payments and insurance coverage, such as a death sum, a disability sum or a sum upon critical illness.

Example 5 (Survival model). We consider a unit-linked version of the simple participating life insurance policy in Examples 1–4. This example provides the basis for numerical illustrations later on. The state of the policy is described by the classical survival model with two states, 0 (alive) and 1 (dead). The policy expires at the retirement date, i.e., $T=R$. The payments of the policy consist of a constant continuous premium payment π while alive, a term insurance sum $b^{ad}$ upon death before expiration T and a pure endowment sum upon survival until expiration T. The size of the endowment sum is equal to the value of the assets at expiration divided by the (market) probability of surviving to expiration. There are no payments in the death state. For simplicity, we write $I=I_1$, $N=N_{01}$, ${\mu }^m={\mu }_{01}^m$ and $p^m=p_{00}^m$, and we have

$$p^m\left(s,t\right)=e^{-{\int }_s^t{\mu }^m\left(v\right)\mathrm{d}v},s\le t.$$

The payment streams of the policy read

$$\begin{array}{cc}\hfill \mathrm{d}C\left(t\right)& =\pi I\mathrm{d}t,t\le T,\hfill \\ \hfill \mathrm{d}{B}^f\left(t\right)& =b^{ad}\mathrm{d}N\left(t\right),t\le T,\hfill \\ \hfill \mathrm{d}{B}^p\left(t\right)& =\frac{I\left(t\right)}{p^m\left(0,T\right)}\mathrm{d}{ϵ}_T\left(t\right),t\le T,\hfill \end{array}$$

where ${ϵ}_T$ is the Dirac measure in T (for details, see Page 192). We divide by the probability $p^m\left(0,T\right)$ in $\mathrm{d}{B}^p\left(t\right)$ to ensure that the assets in expectation are paid out to the policyholder, i.e., to account for inheritance from those who die before time T. We note that

$$\begin{array}{c}\hfill {\int }_0^T\mathrm{d}{B}^p\left(t\right)=\frac{I\left(T\right)}{p^m\left(0,T\right)}.\end{array}$$

5.2. Cash Flows

For projection on portfolio level, it is useful to consider market cash flows of the policy. Again, we use the term market cash flows for the expectation of the stochastic payment streams taken under the market basis. By ς, ${\beta }^f$ and ${\beta }^p$, we denote the time 0 market cash flows for the premium stream C and the benefit streams $B^f$ and $B^p$, i.e.,

$$\begin{array}{cc}\hfill \varsigma \left(t\right)& ={\text{𝔼}}^m\left[{\int }_0^t\mathrm{d}C\left(s\right)\right]=\sum _{j\in J}{\int }_0^t{p}_{0j}^m\left(0,s\right)\mathrm{d}{c}_j\left(s\right),\hfill \\ \hfill {\beta }^i\left(t\right)& ={\text{𝔼}}^m\left[{\int }_0^t\mathrm{d}{B}^i\left(s\right)\right]\hfill \\ & =\sum _{j\in J}{\int }_0^t{p}_{0j}^m\left(0,s\right)\left\{\mathrm{d}{b}_j^i\left(s\right)+\sum _{k\in J:k\ne j}{\mu }_{jk}^m\left(s\right)b_{jk}^i\left(s\right)\mathrm{d}s\right\},i=f,p,\hfill \end{array}$$

where the expectation ${\text{𝔼}}^m$ is taken under the market basis and where $p_{0j}^m$ is the market probability of transition from state 0 to j, which is determined by the transition intensities from the market basis.

Example 6 (Survival model continued). For the simple policy in Example 5, the time 0 market premium and benefit cash flows read

$$\begin{array}{cc}\hfill \varsigma \left(t\right)& ={\int }_0^t{p}^m\left(0,s\right)\pi \mathrm{d}s=\pi {\int }_0^t{e}^{-{\int }_0^s{\mu }^m\left(v\right)\mathrm{d}v}\mathrm{d}s,t\le T,\hfill \\ \hfill {\beta }^f\left(t\right)& ={\int }_0^t{p}^m\left(0,s\right)b^{ad}{\mu }^m\left(s\right)\mathrm{d}s=b^{ad}{\int }_0^t{e}^{-{\int }_0^s{\mu }^m\left(v\right)\mathrm{d}v}{\mu }^m\left(s\right)\mathrm{d}s,t\le T,\hfill \\ \hfill {\beta }^p\left(t\right)& ={\int }_0^t\frac{p^m\left(0,s\right)}{p^m\left(0,T\right)}\mathrm{d}{ϵ}_T\left(s\right)=I_{\left\{t\ge T\right\}},t\le T.\hfill \end{array}$$

5.3. Two-Account Projection

On portfolio level, the assets X and the guarantee account Y evolve according to the stochastic differential equations

$$\begin{array}{cc}\hfill \mathrm{d}X\left(t\right)& =X\left(t-\right)\mathrm{d}{R}_X\left(t\right)-X\left(t-\right)\mathrm{d}{\beta }^p\left(t\right)-\mathrm{d}{\beta }^f\left(t\right)+\mathrm{d}\varsigma \left(t\right)\hfill \\ & \phantom{==}-{\pi }_g\left(t\right)\mathrm{d}ϵ\left(t\right)+g\mathrm{d}{ϵ}_R\left(t\right)\hfill \\ & \phantom{==}-1_{\left\{t=R\right\}}{\left(Y\left(R-\right)-X\left(R-\right)\right)}^{+}\mathrm{d}{\beta }^p\left(t\right),\hfill \\ \hfill X\left(0-\right)& =x_0,\hfill \\ \hfill \mathrm{d}Y\left(t\right)& =Y\left(t\right)r^{*}\left(t\right)\mathrm{d}t-X\left(t-\right)\mathrm{d}{\beta }^p\left(t\right)-\mathrm{d}{\beta }^f\left(t\right)+\mathrm{d}\varsigma \left(t\right)\hfill \\ & \phantom{==}+u\left(t\right)\mathrm{d}ϵ\left(t\right),t\le R,\hfill \\ \hfill Y\left(0-\right)& =y_0,\hfill \\ \hfill Y\left(t\right)& =0,t>R.\hfill \end{array}$$

(14)

We recall that $R_X$ is the stochastic return on the assets, g is the guarantee injection at retirement, ${\pi }_g$ is the guarantee fee deducted from the assets and paid to the equity holders of the insurance company, u is the upgrade of the guarantee account, ϵ counts the number of guarantee fee payments and guarantee upgrades (typically annual) and ${ϵ}_R$ marks the exercise of the guarantee at the retirement date. The last term in the equation for X ensures that the guarantee injection at time R is included in a possible lump sum payment at time R. The three quantities $r^{*}$, u and ${\pi }_g$ are specified in the contract. They are non-negative, and they are determined in such a way that the contract is financially fair, i.e., such that the equivalence principle is satisfied for the total payments under the market basis

$$\begin{array}{cc}\hfill x_0& ={\text{𝔼}}^Q\left[{\int }_0^T{e}^{-{\int }_0^{s}r\left(v\right)\mathrm{d}v}\mathrm{d}\left(B^u+B^f-C\right)\left(s\right)\right].\hfill \end{array}$$

(15)

Here, Q is the pricing measure and r is the stochastic short interest rate. Again, the stochastic element $R_X$ enters via a sample path for the asset returns. In practice, one will often work with a discretized version of the stochastic differential equations in Equation (14). For an example, see Section 5.5.

We assume that the total payment stream of the policy $B^f+B^u-C$ is constructed in such a way that the assets X never become negative. This is, for example, satisfied if the expected premiums are continually enough to cover the expected fixed benefits. Generally, the natural premium for unit-linked insurance payments makes up only a small part of the total insurance and savings premium. Therefore, we do not see this last assumption as a critical limitation.

It is easily seen that the projection in unit-linked insurance is equivalent to the projection in participating life insurance. The contractual difference lies in the specification of how non-guaranteed payments arise (written in the contract versus decided fairly by the company along the way). Formally, the bonus updates d in Equation (4) are replaced by guarantee upgrades u in Equation (14), and the guarantee upgrades are determined by the assets and the guarantee account only, not by some collective reserves. Furthermore, the running guarantee g in Equation (4) is replaced by the final guarantee $g={\left(Y\left(R-\right)-X\left(R-\right)\right)}^{+}$ in Equation (14). Finally, both unit-linked accounts are based on market transition intensities, so the adjustment term α from Equation (4) vanishes. Apart from that, the driving stochastic differential equation are the same in participating life insurance and unit-linked insurance. In Section 5.5.1, we compare the two product types in a simple numerical example.

A real-life product example is the Danica Link from 2001 where $r^{*}=0$, ${\pi }_g\left(t\right)=1_{\left\{t<R\right\}}\kappa X\left(t-\right)$ and $u\left(t\right)=1_{\left\{t<R\right\}}{\left(\alpha \left(X\left(t-\right)-{\pi }_g\left(t\right)\right)-Y\left(t-\right)\right)}^{+}$ for some constants $\kappa ,\alpha \in \left(0,1\right)$ (see [7]). In other words, the guarantee account bears zero interest, but each year, it is upgraded, so that it makes up at least a fraction α of the assets after the guarantee fee payment. At retirement, the difference between the guarantee account and the assets is added to the assets, if the guarantee account exceeds the assets. In return for this retirement guarantee, the policyholder pays a fraction κ of his assets to the equity holders of the insurance company each year.

5.4. Applications of Projections

Most importantly, the projections of X and Y can be used to calculate the total time 0 market cash flow $CF$ and market value W for the contract, i.e., to calculate

$$\begin{array}{cc}\hfill \mathrm{d}CF\left(t\right)& ={\text{𝔼}}^Q\left[\mathrm{d}{B}^u\left(t\right)+\mathrm{d}{B}^f\left(t\right)-\mathrm{d}C\left(t\right)\right]\hfill \\ & ={\text{𝔼}}^Q\left[X\left(t-\right)\right]\mathrm{d}{\beta }^p\left(t\right)+\mathrm{d}{\beta }^f\left(s\right)-\mathrm{d}\varsigma \left(s\right)\hfill \end{array}$$

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill W\left(0\right)& ={\text{𝔼}}^Q\left[{\int }_0^T{e}^{-{\int }_0^{s}r\left(v\right)\mathrm{d}v}\mathrm{d}\left(B^u+B^f-C\right)\left(s\right)\right]\hfill \\ & ={\text{𝔼}}^Q\left[{\int }_0^T{e}^{-{\int }_0^{s}r\left(v\right)\mathrm{d}v}\left(X\left(s-\right)\mathrm{d}{\beta }^p\left(s\right)+\mathrm{d}{\beta }^f\left(s\right)-\mathrm{d}\varsigma \left(s\right)\right)\right].\hfill \end{array}\end{array}$$

(16)

Again, r is the stochastic short interest rate. As in participating life insurance, the cash flow and market value distinguish themselves by including non-guaranteed payments as well as guaranteed payments. The Q-expectations are approximated as described in Section 4.10. If the short interest rate is deterministic, then Equation (16) simplifies to

$$\begin{array}{c}\hfill W\left(0\right)={\int }_0^T{e}^{-{\int }_0^{s}r\left(v\right)\mathrm{d}v}\mathrm{d}CF\left(s\right).\end{array}$$

(17)

The market value is useful for determining ${\pi }_g$, u and $r^{*}$ according to the fairness criterion in Equation (15), which can be written as

$$W\left(0\right)=x_0.$$

Again, the task of determining ${\pi }_g$, u and $r^{*}$ is the classical trade-off between the aggressiveness of dividend allocation (expressed by u and $r^{*}$) and the option price (expressed by ${\pi }_g$) given the aggressiveness of the investment strategy (suppressed here).

The projections are also useful for determining the time 0 market value of the guarantee injection at time R, i.e., to calculate

$${\text{𝔼}}^Q\left[e^{-{\int }_0^{R}r\left(v\right)\mathrm{d}v}{\left(Y\left(R-\right)-X\left(R-\right)\right)}^{+}\right].$$

5.5. Numerical Example

In this section, we go through a numerical example with a unit-linked version of the participating life insurance policy in Section 4.11. Working in a discrete projection setup, we show how to find a fair guarantee and guarantee fee strategy, and at the end of this section, we compare the unit-linked insurance policy with its participating life insurance counterpart. In unit-linked insurance, there is no interaction between policies as long as the insurance company has sufficient equity to meet its liabilities. In this paper, we do not model the insurance company's equity, but just assume that it is sufficient. Therefore, it is reasonable to consider just a single policy, but the example could easily be extended with more policies. The example is based on the 5000 scenarios generated via Monte Carlo simulation from Section 4.11. The number of simulated scenarios is, again, enough to ensure that our numerical results and graphs do not change between simulations.

The basics of the unit-linked policy are described in Examples 5–6. The policyholder is the 25-year-old female from Section 4.11. Her death is still governed by the market mortality intensity

$$\begin{array}{c}\hfill {\mu }^m\left(t\right)=0.8·\left(5·{10}^{-4}+5.3456·{10}^{-5}·e^{0.087498\left(25+t\right)}\right).\end{array}$$

The policy expires at time $T=R=40$ when the policyholder is 65. For comparability, we fix the term insurance sum at $b^{ad}=1$ and the premium at $\pi =0.04614$ as in Section 4.11. Furthermore, we make the same market assumptions as in Section 4.11.1. The guarantee account is upgraded and the guarantee fee paid once a year. Hence, we have

$$ϵ\left(t\right)=\#\left\{i=1,...,40:i\le t\right\}.$$

We project the two accounts X and Y using steps of a size of one year by applying a discretized version of the stochastic differential equations for X and Y. For the discretization, we recall from Example 6 that ${\beta }^p$ is a pure jump function and that ς and ${\beta }^f$ are continuous functions. Hence, we get the stochastic difference equations

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill X\left(t-\right)& =X\left(t-1\right)\left(1+R_X\left(t\right)\right)-{\int }_{\left(t-1,t\right)}\left(\mathrm{d}{\beta }^f\left(s\right)-\mathrm{d}\varsigma \left(s\right)\right),\hfill \\ \hfill X\left(t\right)& =X\left(t-\right)-X\left(t-\right)\text{Δ}{\beta }^p\left(t\right)-{\pi }_g\left(t\right)\hfill \\ & \phantom{==}+1_{\left\{t=R\right\}}g\left(1-\text{Δ}{\beta }^p\left(t\right)\right),t=1,...,40,\hfill \\ \hfill X\left(0\right)& =0,\hfill \\ \hfill Y\left(t-\right)& =Y\left(t-1\right)e^{r^{*}}-{\int }_{\left(t-1,t\right)}\left(\mathrm{d}{\beta }^f\left(s\right)-\mathrm{d}\varsigma \left(s\right)\right),\hfill \\ \hfill Y\left(t\right)& =Y\left(t-\right)-X\left(t-\right)\text{Δ}{\beta }^u\left(t\right)+u\left(t\right),t=1,...,40,\hfill \\ \hfill Y\left(0\right)& =0.\hfill \end{array}\end{array}$$

(18)

We emphasize that the discretized projection in unit-linked insurance is practically the same as the discretized projection in participating life insurance, which eases the implementation. The guarantee account Y bears interest at the rate $r^{*}=0$. The guarantee upgrade u is determined as a fraction ${\theta }_1$ of the positive part of assets X less guarantee fee ${\pi }_g$ and less guarantee account Y, all taken just before the guarantee upgrade, i.e.,

$$\begin{array}{cc}\hfill u\left(t\right)& ={\theta }_1{\left(\left(X\left(t-\right)-{\pi }_g\left(t\right)\right)-Y\left(t-\right)\right)}^{+},t=1,...,40.\hfill \end{array}$$

We fix ${\theta }_1=0.8$. At expiration, the guarantee $g={\left(Y\left(40-\right)-X\left(40-\right)\right)}^{+}$ is added to the assets to ensure that they match the guarantee account. The guarantee fee ${\pi }_g$ is a fraction ${\theta }_2$ of the positive part of the returns on the assets, i.e.,

$${\pi }_g\left(t\right)={\theta }_2{\left(R_X\left(t\right)X\left(t-1\right)\right)}^{+}.$$

We determine the fraction ${\theta }_2$ according to the fairness criterion in Equation (15). Furthermore, using this guarantee fee, we consider

• the expected evolution of the assets $t\mapsto {\text{𝔼}}^Q\left[X\left(t\right)\right]$ and the guarantee account $t\mapsto {\text{𝔼}}^Q\left[Y\left(t\right)\right]$,
• the expected level for the guarantee upgrade ${\text{𝔼}}^Q\left[u\left(t\right)\right]$, $t=1,...,40$.

We take the 5000 sample paths simulated in Section 4.11.1, and for each sample path, we project X and Y for different values of ${\theta }_2$, using the difference equations in Equation (18). More specifically, we look for a ${\theta }_2$, such that we get zero when approximating the time 0 market value $W\left(0\right)$ from Equation (17). We arrive at the fair guarantee fee fraction ${\theta }_2=0.1$. Furthermore, we calculate the average evolution of the assets and the guarantee account, the average guarantee fee and guarantee levels and the average guarantee upgrade.

In Figure 9 and Figure 10, we plot the average evolution of the assets and the guarantee account and the average level of the guarantee upgrades. From Figure 9, we see that the final guarantee injection on average raises the assets by around $30\%$, even though the guarantee account does not bear interest. This is because the final guarantee kicks in for all sample paths where the assets finish below their (previous) maximum value. From Figure 10, we see how the yearly guarantee upgrades increase over time. This is explained by the fact that the guarantee upgrades are ultimately a fraction of the excess return on the assets. On average, the assets increase over time, and so does the average excess return and, hence, the guarantee upgrades.

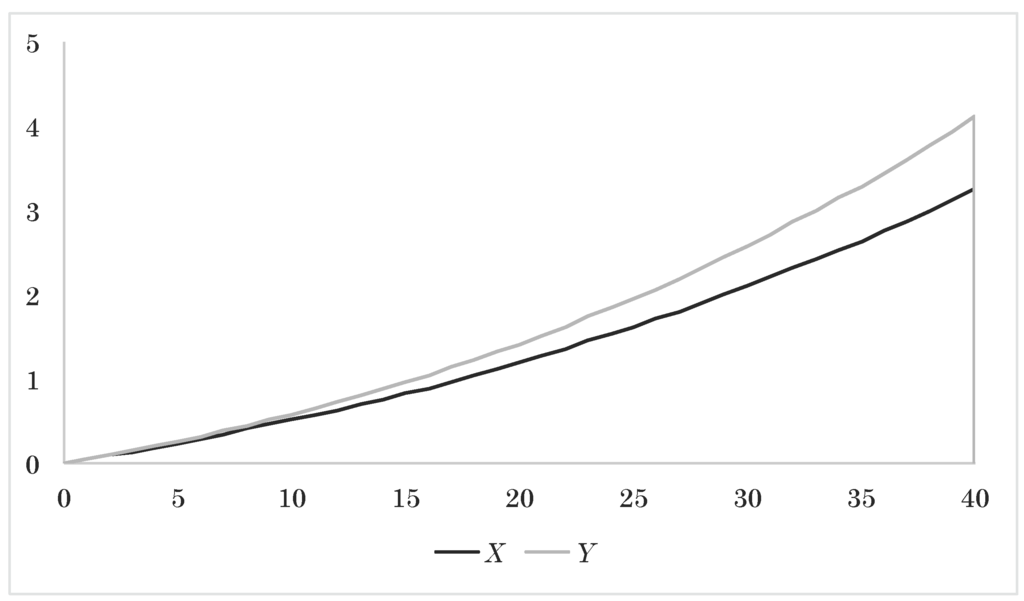
Figure 9. Approximated expected assets X and guarantee account Y as a function of time.

Figure 9. Approximated expected assets X and guarantee account Y as a function of time.

Figure 10. Approximated expected guarantee upgrade u as a function of time.

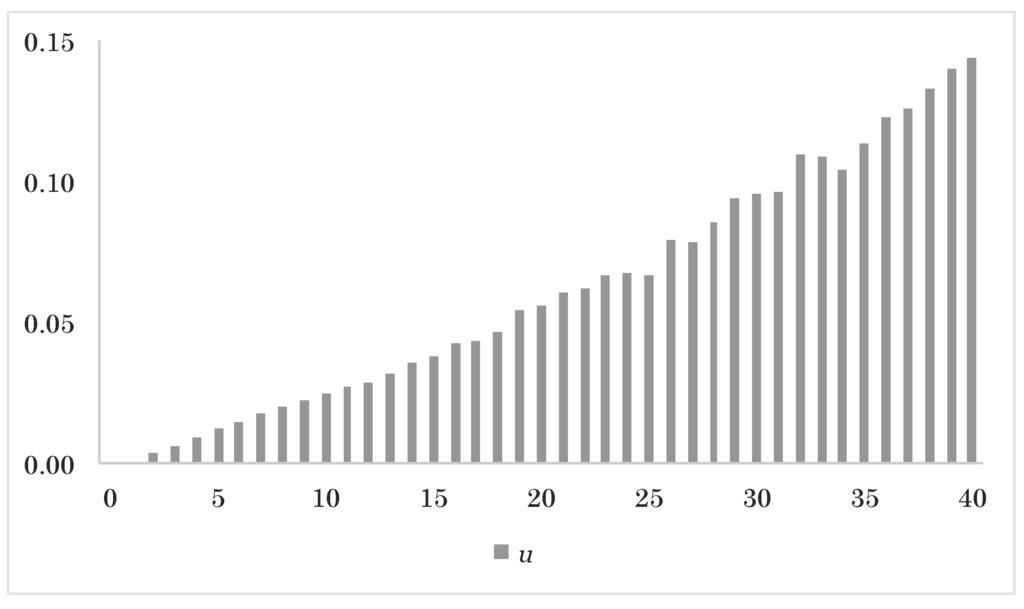
Figure 10. Approximated expected guarantee upgrade u as a function of time.

5.5.1. Unit-Linked versus Participating Life

Finally, we compare the unit-linked insurance policy with its participating life insurance counterpart from Section 4.11. The comparison is straightforward, since the two policies are modeled in the same framework. We plot the average cash flows for the two policies side-by-side in Figure 11. The two cash flows are practically the same. This was to be expected in order for the two contracts to be fair, since the premiums and death benefits are the same. To refine the picture, we plot the empirical distributions of the final payments for the two policies in Figure 12. We notice that the empirical distributions differ significantly. In particular, the unit-linked insurance policy has a bigger downside than the participating life insurance policy, and the average cash flow for the unit-linked insurance policy is held up by a few, very large, final payments and a heavier right-tale in general. This emphasizes the fact that, even though unit-linked insurance and participating life insurance are two sides of the same coin, the products may differ in riskiness. Our two-account model with event risk is a valuable tool in quantifying these differences.

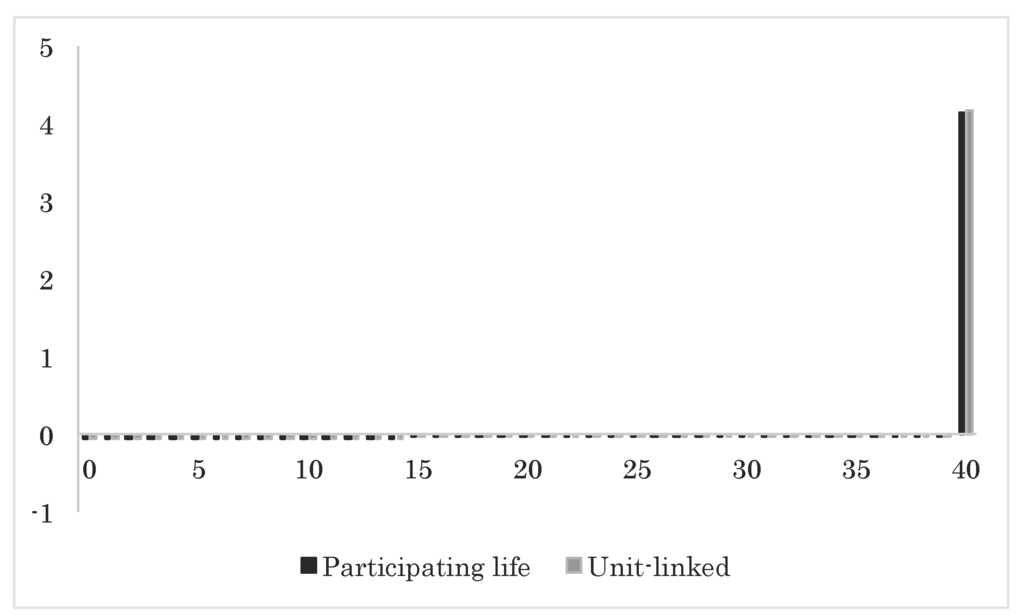
Figure 11. Approximated expected cash flows for the participating life insurance policy and the unit-linked insurance policy as a function of time.

Figure 11. Approximated expected cash flows for the participating life insurance policy and the unit-linked insurance policy as a function of time.

Figure 12. Empirical distribution of final payments for the participating life insurance policy and the unit-linked insurance policy.

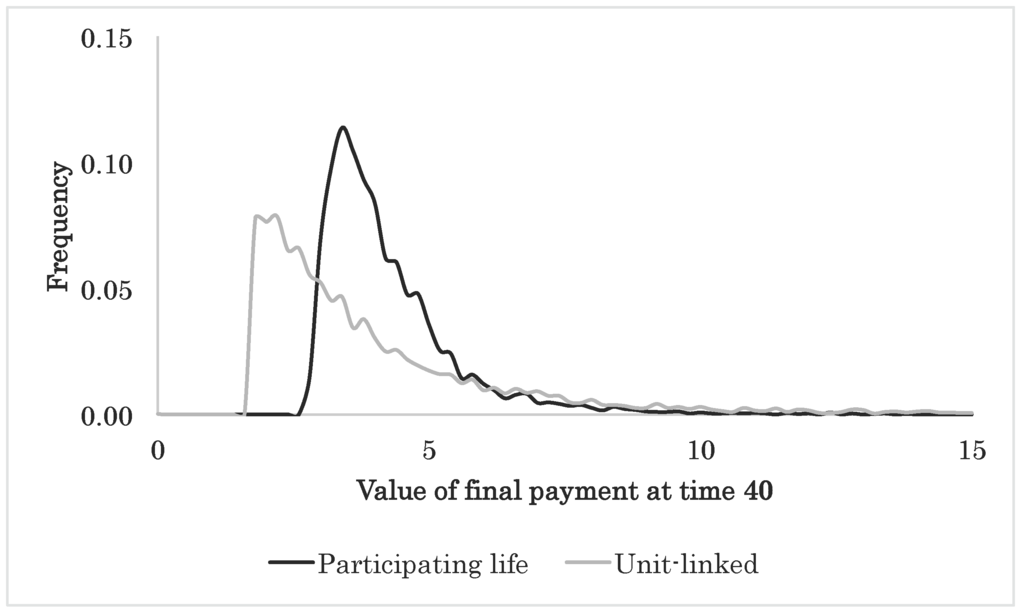
Figure 12. Empirical distribution of final payments for the participating life insurance policy and the unit-linked insurance policy.

6. Conclusions

We have introduced a two-account model with event risk, such as death and disability, for the purpose of modeling life insurance contracts taking into account both guaranteed and non-guaranteed payments in participating life insurance as well as in unit-linked insurance. We have formalized how the bonus schemes “consolidation” and “additional benefits” work and interact in participating life insurance, and we have formalized how guarantees can be implemented in unit-linked insurance. We have addressed similarities and differences between participating life insurance and unit-linked insurance, and for both product types, we have provided numerical examples to demonstrate the possible applications of our two-account model. Our numerical examples highlight the risk of unfair redistribution across policies in a seemingly homogeneous participation life insurance portfolio. Furthermore, the examples illustrate the potential difference in riskiness between a participating life insurance product and a unit-linked insurance product that are identical in expectation, but by (product) nature are different in guarantee structure. Our model is based on economic scenarios, which makes it flexible with respect to the change of financial input. We have illustrated the use of our model by conducting scenario analysis based on Monte Carlo simulation, but the model applies to scenarios in general and to worst-case and best-estimate scenarios in particular. Our work distinguishes itself from the previous literature by the inclusion of event risk and by the common framework for the valuation of guaranteed and non-guaranteed payments, in participating life and unit-linked insurance. Furthermore, the two-account structure makes it easy to illustrate general concepts, such as the interaction between realized return and bonus allocation (in participating life insurance) or the interaction between realized returns and the final guarantee (in unit-linked insurance). Finally, our paper provides a unique formalization of the most common bonus schemes in the Danish life insurance and pensions industry.