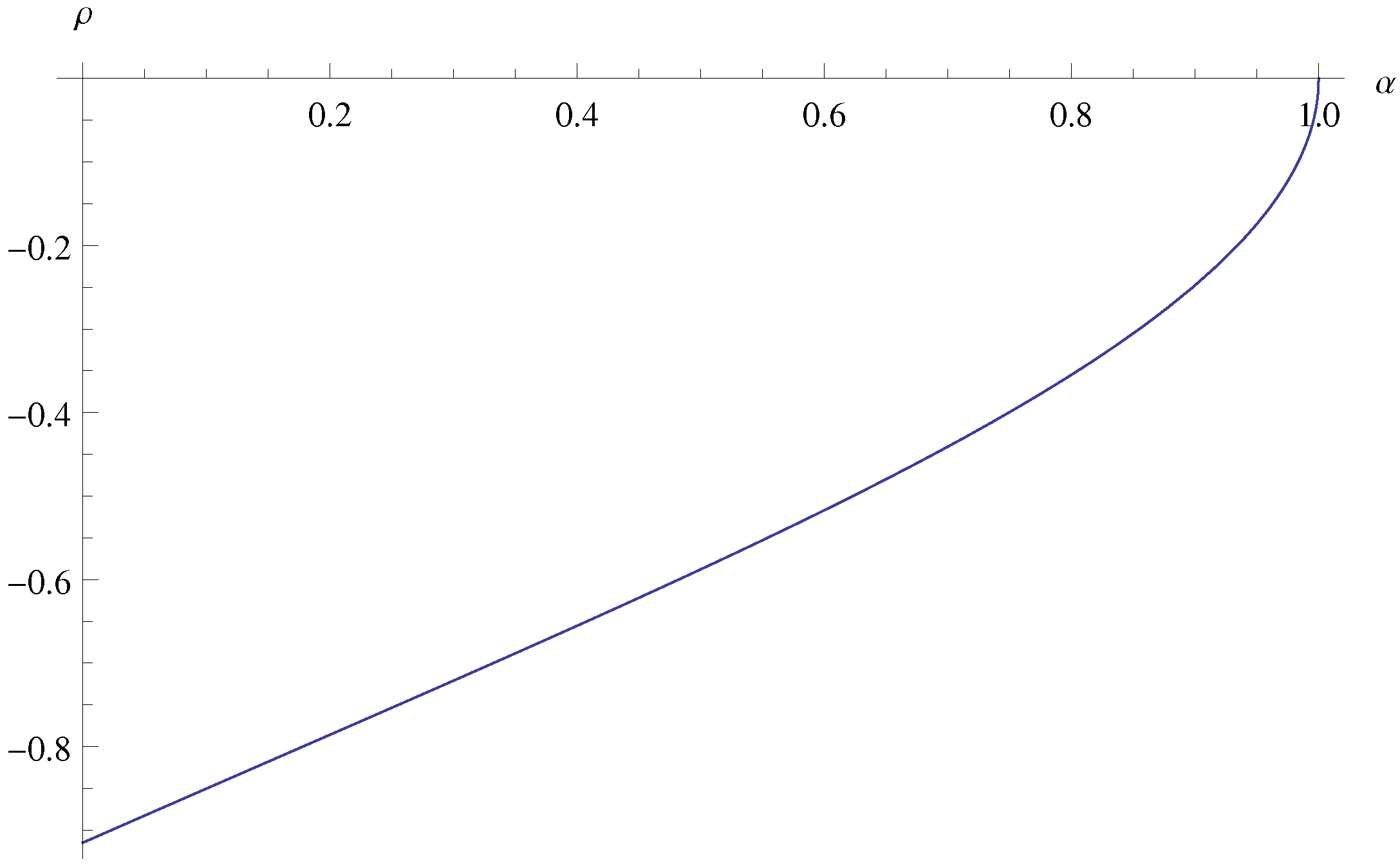1. Introduction
When dealing with heavy-tailed insurance claims, it is a classical problem to consider and quantify the influence of the largest among the claims on their total sum, see e.g., Ammeter [
1] for an early reference in the actuarial literature. This topic is particularly relevant in non-proportional reinsurance applications when a significant proportion of the sum of claims is consumed by a small number of claims. The influence of the maximum of a sample on the sum has in particular attracted considerable attention over the last fifty years (see Ladoucette and Teugels [
2] for a recent overview of existing literature on the subject). Different modes of convergence of the ratios sum over maximum or maximum over sum have been linked with conditions on additive domain of attractions of a stable law (see e.g., Darling [
3], Bobrov [
4], Chow and Teugels [
5], O’Brien [
6] and Bingham and Teugels [
7]).
It is also of interest to study the joint distribution of normalised smallest and largest claims. We will address this question in this paper under the assumption that the number of claims over time is described by a rather general counting process. These considerations may be helpful for the design of possible reinsurance strategies and risk management in general. In particular, extending the understanding of the influence of the largest claim on the aggregate sum (which is a classical topic in the theory of subexponential distributions) towards the relative influence of several large claims together, can help to assess the potential gain from reinsurance treaties of large claim reinsurance and ECOMOR type (see e.g.,
Section 1).
In this paper we consider a homogeneous insurance portfolio, where the distribution of the individual claims has a regularly varying tail. The number of claims is generated by a near mixed Poisson process. For this rather general situation we derive a number of limiting results for the joint Laplace transforms of the smallest and largest claims, as the time t tends to infinity. These turn out to be quite explicit and crucially depend on the rule of what is considered to be a large claim as well as on the value of the tail index.
Let
be a sequence of independent positive random variables (representing claims) with common distribution function
F. For
, denote by
the corresponding order statistics. We assume that the claim size distribution satisfies the condition
where
and
ℓ is a slowly varying function at infinity. The tail index is defined as
and we will typically express our results in terms of
γ. Denote by
the tail quantile function of
F where
. Under (1),
, where
is again a slowly varying function. For textbook treatments of regularly varying distributions and/or their applications in insurance modelling, see e.g., Bingham
et al. [
8], Embrechts
et al. [
9], Rolski
et al. [
10] and Asmussen and Albrecher [
11].
Denote the number of claims up to time
t by
with
. The probability generating function of
is given by
which is defined for
. Let
be its derivative of order
r with respect to
z. In this paper we assume that
is a near mixed Poisson (NMP) process,
i.e., the claim counting process satisfies the condition
for some random variable Θ, where
D denotes convergence in distribution. This condition implies that
and
Note also that, for
and
,
A simple example of an NMP process is the homogeneous Poisson process, which is very popular in claims modelling and plays a crucial role in both actuarial literature and in practice. The class of mixed Poisson processes (for which condition (2) holds not only in the limit, but for any
t) has found numerous applications in (re)insurance modelling because of its flexibility, its success in actuarial data fitting and its property of being more dispersed than the Poisson process (see Grandell [
12] for a general account and various characterisations of mixed Poisson processes). The mixing may, e.g., be interpreted as claims coming from a heterogeneity of groups of policyholders or of contract specifications. The more general class of NMP processes is used here mainly because the results hold under this more general setting as well. The NMP distributions (for fixed
t) contain the class of infinitely divisible distributions (if the component distribution has finite mean). Moreover any renewal process generated by an interclaim distribution with finite mean
ν is an NMP process (note that then by the weak law of large numbers in renewal theory,
where Θ is degenerate at the point
).
The aggregate claim up to time
t is given by
where it is assumed that
is independent of the claims
. For
and
, we define the sum of the
smallest and the sum of the
s largest claims by
so that
. Here Σ refers to
small while Λ refers to
large.
In this paper we study the limiting behaviour of the triplet with appropriate normalisation coefficients depending on γ, the tail index, and on s, the number of terms in the sum of the largest claims. We will consider three asymptotic cases, as they show a different behaviour: s is fixed, s tends to infinity but slower than the expected number of claims, and s tends to infinity and is asymptotically equal to a proportion of the number of claims.
Example 1. In large claim reinsurance for the s largest claims in a specified time interval ,
the reinsured amount is given by ,
so the interpretation of our results to the analysis of such reinsurance treaties is immediate. A variant of large claim reinsurance that also has a flavour of excess-of-loss treaties is the so-called ECOMOR (excedent du cout moyen relatif) treaty with reinsured amount
i.e.,
the deductible is itself an order statistic (or in other words, the reinsurer pays all exceedances over the s-largest claim). This treaty has some interesting properties, for instance with respect to inflation, see e.g., Ladoucette & Teugels [13]. If the reinsurer accepts to only cover a proportion β () of this amount, the cedent’s claim amount is given bywhich is a weighted sum of the quantities ,
and .
The asymptotic results above in terms of the Laplace transform can then be used to approximate the distribution of the cedent’s and reinsurer’s claim amount in such a contract, and correspondingly the design of a suitable contract (including the choice of s) will depend quite substantially on the value of the extreme value index of the underlying claim distribution.
The paper is organised as follows. We first give the joint Laplace transform of the triplet
for a fixed
t in
Section 2.
Section 3 deals with asymptotic joint Laplace transforms in the case
. We also discuss consequences for moments of ratios of the limiting quantities. The behaviour for
depends on whether
is finite or not. In the first case, the analysis for
applies, whereas in the latter one has to adapt the analysis of
Section 3 exploiting the slowly varying function
, but we refrain from treating this very special case in detail (see e.g., Albrecher and Teugels [
14] for a similar adaptation in another context).
Section 4 and
Section 5 treat the case
without and with centering, respectively. The proofs of the results in
Section 3,
Section 4 and
Section 5 are given in
Section 6.
Section 7 concludes.
2. Preliminaries
In this section, we state a versatile formula that will allow us later to derive almost all the desired asymptotic properties of the joint distributions of the triplet
. We consider the joint Laplace transform of
to study their joint distribution in an easy fashion. For a fixed
t, it is denoted by
Then the following representation holds:
Proposition 1. We haveProof. The proof is standard if we interpret
whenever
. Indeed, condition on the number of claims at the time epoch
t and subdivide the requested expression into three parts:
The conditional expectation in the first term on the right simplifies easily to the form
. For the conditional expectations in the second and third term, we condition additionally on the value
y of the order statistic
; the
order statistics
are then distributed independently and identically on the interval
yielding the factor
. A similar argument works for the
s order statistics
. Combining the two terms yields
A straightforward calculation finally shows
☐
Consequently, it is possible to easily derive the expectations of products (or ratios) of , , and by differentiating (or integrating) the joint Laplace transform. We only write down their first moment for simplicity.
Corollary 2. We haveProof. The individual Laplace transforms can be written in the following form:
where
. By taking the first derivative, we arrive at the respective expectations. ☐
3. Asymptotics for the Joint Laplace Transforms when
Before giving the asymptotic joint Laplace transform of the sum of the smallest and the sum of the largest claims, we first recall an important result about convergence in distribution of order statistics and derive a characterisation of their asymptotic distribution. All proofs of this section are deferred to
Section 6.
It is well-known that there exists a sequence
of exponential random variables with unit mean such that
where
. Let
. It may be shown that
converges in distribution to
in
, where
(see Lemma 1 in LePage
et al. [
15]). For
, the series
converges almost surely. Therefore, for a fixed
s, we deduce that, as
,
In particular, we derive by the Continuous Mapping Theorem that
Note that the first moment of
(but only the first moment) may be easily derived since
where
has a Beta
distribution. We also recall that
F belongs to the (additive) domain of attraction of a stable law with index
if and only if
(see e.g., Theorem 1 in Ladoucette and Teugels [
2]).
When
is an NMP process, we also have, as
,
and
(see e.g., Lemma 2.5.6 in Embrechts
et al. [
9]). However, note that if the triplet
is normalised by
instead of
in (6), then the asymptotic distribution will differ due to the randomness brought in by the counting process
.
The following proposition gives the asymptotic Laplace transform when the triplet is normalised by .
Proposition 3. For a fixed s ,
as ,
we have whereIf a.s., this expression simplifies to We observe that modifies the asymptotic Laplace transform by introducing into the integral (7). However, the moments of do not depend on the law of Θ:
Corollary 4. For ,
we havewhere Note that this corollary only provides the moments of
. In order to have moment convergence results for the ratios, it is necessary to assume uniform integrability of
. It is also possible to use the Laplace transform of the triplet with a fixed
t to characterise the moments of the ratios
(see Corollary 2), and then to follow the same approach as proposed by Ladoucette [
16] for the ratio of the random sum of squares to the square of the random sum under the condition that
and
for some
.
Remark 1. For , (8)
reduces again to which is (5).
Furthermore, for all Remark 2. is the ratio of the sum over .
By taking the derivative of (7),
it may be shown that, for and ,
Therefore the mean of will only be finite for sufficiently small γ. An alternative interpretation is that for given value of γ, the number s of removed maximal terms in the sum has to be sufficiently large to make the mean of the remaining sum finite. The normalisation of the sum by ,
on the other hand, ensures the existence of the moments of the ratio for all values of s and .
Remark 3. It is interesting to compare Formula (8)
with the limiting moment of the statisticFor instance,
,
and the limit of the nth moment can be expressed as an nth-order polynomial in ,
see Albrecher and Teugels [14], Ladoucette [16] and Albrecher et al.
[17]. Motivated by this similarity, let us study the link in some more detail. By using once again Lemma 1 in LePage et al.
[15], we deduce thatRecall that is the weak limit of the ratio and .
Using Equation (10)
and (which is a straightforward consequence of the fact that has regularly varying tail with tail index ), one then obtains a simple formula for the covariance between and :
Determining by exploiting Equation (8)
for ,
we then arrive at the linear correlation coefficientFigure 1 depicts as a function of .
Note that .
The correlation coefficient allows to quantify the negative linear dependence between the two ratios (the dependence becomes weaker when α increases, as the maximum term will then typically be less dominant in the sum).
Figure 1.
as a function of α.
Figure 1.
as a function of α.
Next, let us consider the case when the number of largest terms also increases as , but slower than the expected number of claims. It is now necessary to change the normalisation coefficients of and .
Proposition 5. Let for a function with and .
Then whereIf a.s. Several messages may be derived from (11). First note that the asymptotic distribution of is degenerated for , since as . Second, the asymptotic distribution of the sum of the smallest claims is the distribution of Θ up to a scaling factor, since as .
Finally, for a fixed proportion of maximum terms, it is also necessary to change the normalisation coefficients of and . We have
Proposition 6. Let for a fixed .
Then whereand .
If a.s.,
As expected, and as . If a.s. and , then has an inverse Gamma distribution with shape parameter equal to .
4. Asymptotics for the Joint Laplace Transforms when
In this section, we assume that
and hence the expectation of the claim distribution is finite. We let
. The normalisation coefficient of the sum of the smallest claims,
, will therefore be
as it is the case for
for the Law of Large Numbers. In
Section 5, we will then consider the sum of the smallest centered claims with another normalisation coefficient.
Again, consider a fixed s first. The normalisation coefficients of and are the same as for the case , but the normalisation coefficient of is now .
Proposition 7. For fixed s ,
we have whereIf a.s.,
Corollary 8. We haveand We first note that
and therefore
as
for any fixed
s . The influence of the largest claims on the sum becomes less and less important as
t is large and is asymptotically negligible. This is very different from the case
. In Theorem 1 in Downey and Wright [
18], it is moreover shown that, as
,
This result is no more true in our framework when Θ is not degenerate at 1. Assume that
. Using (3) and under a uniform integrability condition, one has
Next, we consider the case with varying number of maximum terms. The normalisation coefficients of and now differ.
Proposition 9. Let and , i.e.,
.
Then whereIf a.s.,
As for the case , as . Moreover the asymptotic distribution of the sum of the largest claim is the distribution of Θ up to a scaling factor since as . Finally note that as as for the case when s was fixed.
Finally we fix p. Only the normalisation coefficient of and its asymptotic distribution differ from the case .
Proposition 10. Let and .
Then whereand .
If a.s.,
We note that the normalisation of is the same as for and that as .
5. Asymptotics for the Joint Laplace Transform for with centered claims when s is fixed
In this section, we consider the sum of the smallest centered claims
instead of the sum of the smallest claims
. Like for the Central Limit Theorem, we have to consider two sub-cases:
and
.
For the sub-case , the normalisation coefficient of is now .
Proposition 11. For fixed s and ,
we havewhereIf a.s.,
If
, then
and we see that
and
are not independent.
This result is to compare with the one obtained by Bingham and Teugels [
7] for
(see also Ladoucette and Teugels [
2]).
For the sub-case , let . The normalisation coefficient of becomes .
Proposition 13. For s fixed and ,
we have whereIf a.s.,
If and a.s., we note that the maximum, , and the centred sum, , are independent. If and a.s., is independent of .
6. Proofs
Proof of Proposition 3. In formula (7), we first use the substitution
,
i.e.,
:
Next, the substitution
,
i.e.,
leads to
as
and also
Note that the integral is well defined since
. Moreover
and
☐
Proof of Corollary 4. From Proposition 3 we have
Hence
This gives indeed, using (3),
which extends (5) to the case of NMP processes. Next, we focus on (8) for general
k. We first consider the case
. We have
Let
By Proposition 3
and clearly
Note that
so
By the Faa di Bruno’s formula
where
Therefore
Subsequently,
with definition (9). This gives
and
so that
cf. (3), and the result follows.
For the case
, we proceed in an analogous way. Equation (12) becomes
Then
is replaced by
,
by
,
by
and, by following the same path as for
, we get
☐
Proof of Proposition 5. The proof is similar to the previous one, so we just highlight the differences here: Conditioning on
we have
We first replace
F by the substitution
,
i.e.,
:
The factor involving
v converges to
The factor containing
w behaves as
and hence for the power
Finally, for the factor containing
u, replace
F by the substitution
,
i.e.,
:
so that, as
,
For the factor with the factorials, we have by Stirling’s formula
Equivalent for the integral in
z:
By Laplace’s method, we deduce that
Altogether
☐
Proof of Proposition 6. Again, we condition on
:
For the factor containing
w, we have
For the factor involving
u one can write
The ratio with factorials behaves, by Stirling’s formula, as
For the integral in
y we have the equivalence
Let
By Laplace’s method, we deduce that
and then
Altogether
☐
Proof of Proposition 7. We first replace
F by the substitution
,
i.e.,
Then we have
Now use analogous arguments as in the proof of Proposition 3 and note that
☐
Proof of Corollary 8. By Proposition 7
Hence
and therefore
By Proposition 7
☐
Proof of Proposition 9. Condition on
to see that
Now replace
F by the substitution
,
i.e.,
Like before,
For the factor with
w, one sees that
and then
For the factor with
u, replace
F by the substitution
,
i.e.,
:
and then
The ratio of factorials coincides with (13). Also (14) applies here. Altogether
☐
Proof of Proposition 10. Given
The part involving
w coincides with the one in the proof of Proposition 6. For the factor involving
u, we have
The rest of the proof is completely analogous to the one for Proposition 6. ☐
Proof of Proposition 11. Use the substitution
,
i.e.,
:
We then replace
F by the substitution
,
i.e.,
:
Now use the same arguments as in the proof of Proposition ☐
Proof of Corollary 12. Note that
☐
Proof of Proposition 13. Use the substitution
,
i.e.,
:
Then we have
First note that
Secondly,
and it follows that
which completes the proof. Note that
☐