Catastrophe Insurance Modeled by Shot-Noise Processes
Abstract
:1. Introduction
2. Claims with Stochastic Arrival Rate
2.1. Intensity and Cumulated Intensity
2.2. Shot-Noise Processes
- (1)
- Regime switching: The shot at has a constant impact for a specified time length β and after β the impact jumps to a new level (regime) which could even be zero. For , letFor , the effect of the shot vanishes totally after a time period of length β.
- (2)
- Exponential structure: for , letHere, the effect of a shot decreases exponentially over time. As already mentioned, in this case S is Markovian. See also Figure 1 for an illustration.
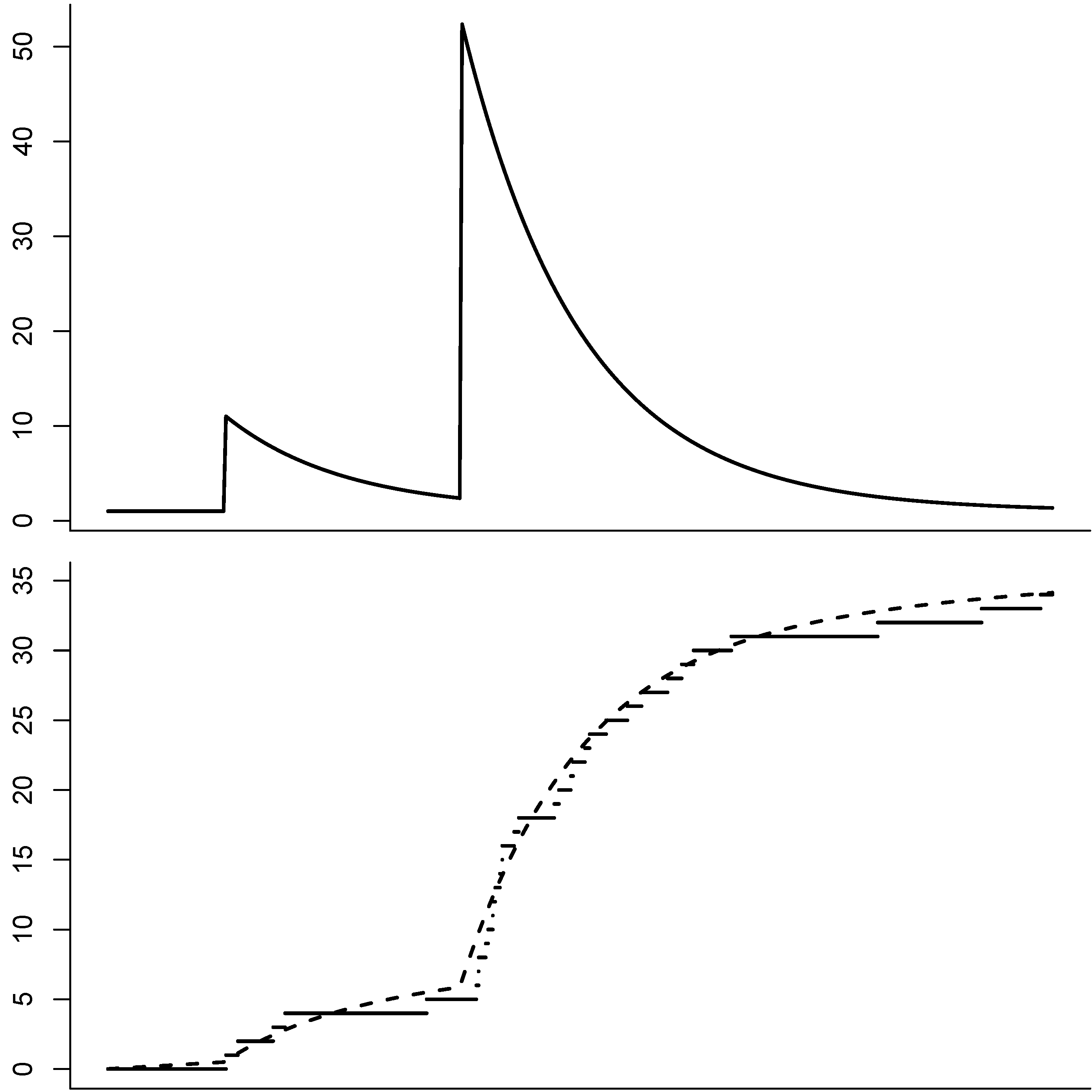
- (i)
- If we obtain that is Poisson -distributed:
- (ii)
- If then S is a compound Poisson process. We denote by the Fourier transform of and obtain
- (iii)
- If we obtain the classical Markovian shot-noise process andwith
2.3. Claims Driven by Shot-Noise Processes
- (1)
- Linear structure: for , letThis response function starts at α and increases linearly over the interval until it reaches 1. For , this function is absolutely continuous.
- (2)
- Exponential structure: for , letHere, G starts at α and increases exponentially to 1. The parameter α controls the impact of the jump size on S. If , G is differentiable. The parameter β controls the speed of the growth.
- (3)
- Rational structure: for , letThis provides an alternative specification to the exponential structure.
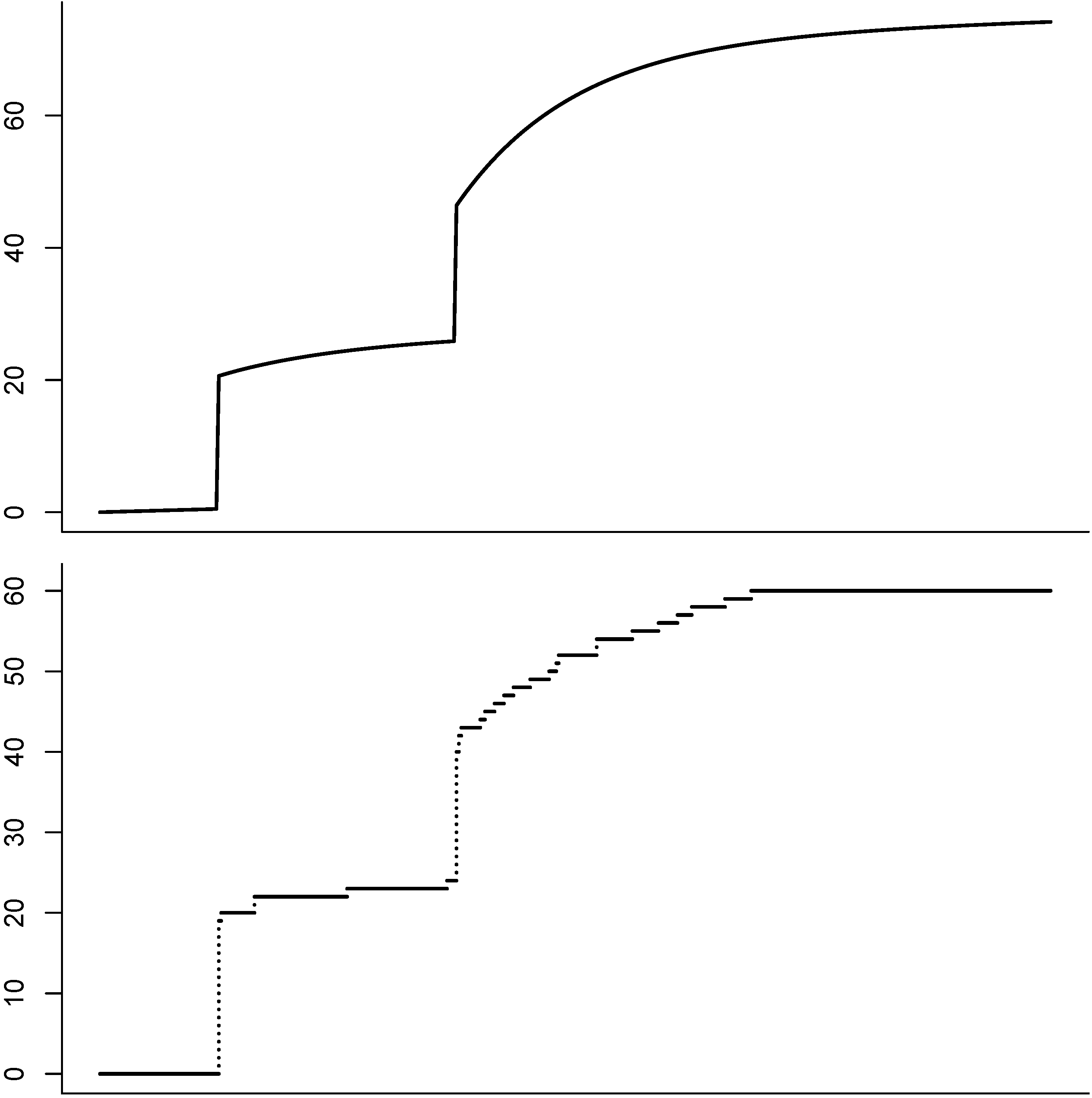
3. Catastrophe Bonds
3.1. Equivalent Measure Changes
3.1.1. Preserving Independent Increments
- 1.
- If Φ has independent increments under and , then Y is deterministic.
- 2.
- If Φ has independent and stationary increments under and , then Y is deterministic and does not depend on time.
3.2. Pricing
- (A1) We assume that under Q the marked point process Φ has i.i.d. marks and the point process is a inhomogeneous Poisson process.
4. Estimating Shot-Noise Processes
- (A2) Let be a bounded open set and suppose that for eachMoreover, the process is continuous with probability one and admits a continuous extension to .
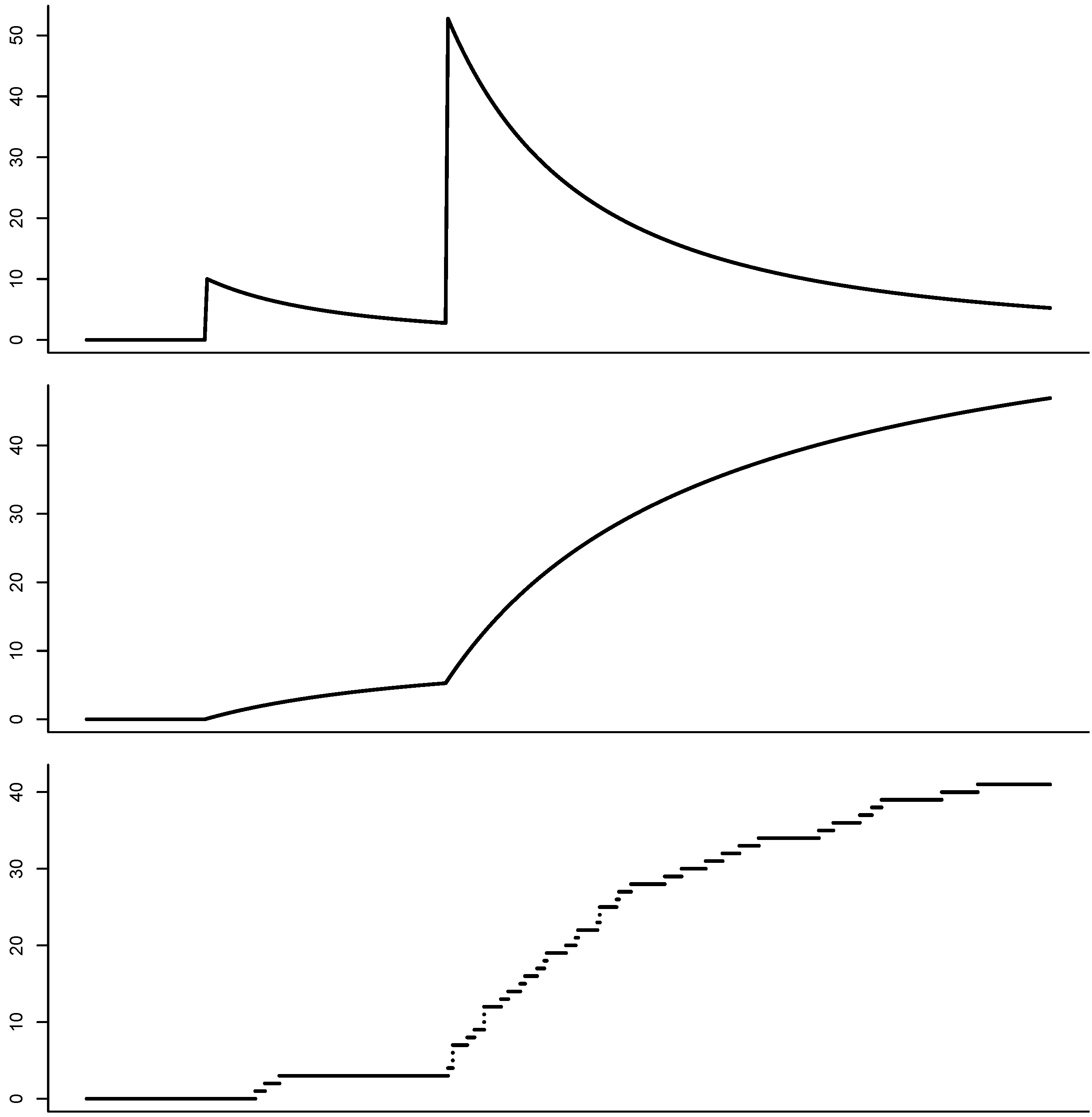
5. Simulation
- Draw the number of jumps N from a Poisson-distribution.
- Simulate N i.i.d. U random variables and set , , being the i-th order statistic.
- Simulate N i.i.d. random variables (jump heights) according to the chosen distribution .
- Compute the path .
- Simulate the claim arrival times by taking i.i.d. exponential(1)-random variables and calculating
- Simulate the claim sizes from the distribution .
Conflicts of Interest
References
- Artemis. “Catastrophe Bond Market Hits $19 billion Outstanding for First Time.” Available online: http://www.artemis.bm/blog/2013/10/08/catastrophe-bond-market-hits-19-billion-outstanding-for-first-time/ (accessed on 17 February 2013).
- Insurance Insider. “Cat Bond Market Reaches Record $18 bn Size.” Available online: http://www.insuranceinsider.com/-1244580/8 (accessed on 17 February 2013).
- W. Schottky. “Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern.” Ann. Phys. 362 (1918): 541–567. [Google Scholar] [CrossRef]
- E. Parzen. Stochastic Processes. San Francisco, CA, USA: Holden-Day, Inc., 1962. [Google Scholar]
- R.B. Lund, R.W. Butler, and R.L. Paige. “Prediction of shot noise.” J. Appl. Probab. 36 (1999): 374–388. [Google Scholar] [CrossRef]
- C. Kühn. “Shot-noise processes.” In Encyclopedia of Actuarial Science. Chichester, UK: John Wiley & Sons, 2004, pp. 1556–1558. [Google Scholar]
- T. Mikosch. Non-Life Insurance Mathematics: An Introduction with the Poisson Process, 2nd ed. Berlin, Germany: Universitext, Springer-Verlag, 2009. [Google Scholar]
- A. Dassios, and J. Jang. “Pricing of catastrophe reinsurance & derivatives using the Cox process with shot noise intensity.” Financ. Stoch. 7 (2003): 73–95. [Google Scholar] [CrossRef]
- M. Scherer, L. Schmid, and T. Schmidt. “Shot-noise multivariate default models.” Eur. Actuar. J. 2 (2010): 161–186. [Google Scholar]
- J. Jang, A. Herbertsson, and T. Schmidt. “Pricing basket default swaps in a tractable shot noise model.” Stat. Probab. Lett. 8 (2011): 1196–1207. [Google Scholar]
- D. Filipović. Term Structure Models: A Graduate Course. Berlin/Heidelberg, Germany: Springer Verlag, 2009. [Google Scholar]
- T. Bielecki, and M. Rutkowski. Credit Risk: Modeling, Valuation and Hedging. Berlin/Heidelberg, Germany; New York, NY, USA: Springer Verlag, 2002. [Google Scholar]
- P. Brémaud. Point Processes and Queues. Berlin/Heidelberg, Germany; New York, NY, USA: Springer Verlag, 1981. [Google Scholar]
- J. Jacod. “Multivariate point processes: Predictable projection, Radon-Nikodym derivatives, representation of martingales.” Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete 31 (1975): 235–253. [Google Scholar] [CrossRef]
- J. Jacod, and A. Shiryaev. Limit Theorems for Stochastic Processes, 2nd edn. Berlin/Heidelberg, Germany: Springer Verlag, 2003. [Google Scholar]
- P. Bremaud. “An insensitivity property of Lundberg’s estimate for delayed claims.” J. Appl. Probab. 37 (2000): 914–917. [Google Scholar] [CrossRef]
- T. Schmidt, and W. Stute. “General shot-noise processes and the minimal martingale measure.” Stat. Probab. Lett. 77 (2007): 1332–1338. [Google Scholar] [CrossRef]
- P. Protter. Stochastic Integration and Differential Equations, 2nd ed. Berlin/Heidelberg, Germany; New York, NY, USA: Springer Verlag, 2004. [Google Scholar]
- T. Rolski, H. Schmidli, V. Schmidt, and J. Teugels. Stochastic Processes for Insurance and Finance. New York, NY, USA: John Wiley & Sons, 1999. [Google Scholar]
- J. Rice. “On generalized shot noise.” Adv. Appl. Probab. 9 (1977): 553–565. [Google Scholar] [CrossRef]
- W. Smith. “Shot noise generated by a semi-Markov process.” J. Appl. Probab. 10 (1973): 685–690. [Google Scholar] [CrossRef]
- S. Cox, and H. Pederson. “Catastrophe risk bonds.” N. Am. Actuar. J. 4 (2000): 56–82. [Google Scholar]
- H. Louberge, E. Kellezi, and M. Gilli. “Using catastrophe-linked securities to diversify insurance risk: A financial analysis of CAT bonds.” J. Insur. Issues 22 (1999): 125–146. [Google Scholar]
- M. Lewis. “In Natures’ Casino.” New York Times, 26 August 2007. [Google Scholar]
- T. Schmidt. Shot-Noise Processes: Equivalent Measure Changes and Applications in Finance and Filtering. Working Paper; 2014. [Google Scholar]
- F. Esscher. “On the probability function in the collective theory of risk.” Skand. Aktuarietidskr. 15 (1932): 175–195. [Google Scholar]
- F. Esche, and M. Schweizer. “Minimal entropy preserves the Lévy property: How and why.” Stoch. Process. Appl. 115 (2005): 299–327. [Google Scholar] [CrossRef]
- H. Föllmer, and M. Schweizer. “Hedging of Contingent Claims under Incomplete Information.” In Applied Stochastic Analysis. Edited by M.H.A. Davis and R.J. Elliott. London, UK; New York, NY, USA: Gordon and Breach, 1990, Volume 5, pp. 389–414. [Google Scholar]
- T. Altmann, T. Schmidt, and W. Stute. “A shot noise model for financial assets.” Int. J. Theor. Appl. Financ. 11 (2008): 87–106. [Google Scholar] [CrossRef]
- A. Dassios, and J. Jang. “Kalman-Bucy filtering for linear systems driven by the Cox process with shot noise intensity and its application to the pricing of reinsurance contracts.” J. Appl. Probab. 42 (2005): 93–107. [Google Scholar] [CrossRef]
- R.J. Elliott, and D.B. Madan. “A discrete time extended Girsanov prinicple.” Math. Financ. 8 (1998): 127–152. [Google Scholar] [CrossRef]
- M. Moreno, P. Serrano, and W. Stute. “Statistical properties and economic implications of jump-diffusion processes with shot-noise effects.” Eur. J. Oper. Res. 214 (2011): 656–664. [Google Scholar] [CrossRef]
- M. Jacobsen. Statistical Analysis of Counting Processes: Lecture Notes in Statistics. New York, NY, USA: Springer-Verlag, 1982, Volume 12. [Google Scholar]
- A.F. Karr. Point Processes and Their Statistical Inference: Probability: Pure and Applied. New York, NY, USA: Marcel Dekker Inc., 1986, Volume 2. [Google Scholar]
- K. Kopperschmidt, and W. Stute. “The statistical analysis of self-exciting point processes.” Stast. Sinica 23 (2013): 1273–1298. [Google Scholar]
- D. Filipović, L. Overbeck, and T. Schmidt. “Dynamic CDO term structure modelling.” Math. Financ. 21 (2011): 53–71. [Google Scholar] [CrossRef]
© 2014 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Schmidt, T. Catastrophe Insurance Modeled by Shot-Noise Processes. Risks 2014, 2, 3-24. https://doi.org/10.3390/risks2010003
Schmidt T. Catastrophe Insurance Modeled by Shot-Noise Processes. Risks. 2014; 2(1):3-24. https://doi.org/10.3390/risks2010003
Chicago/Turabian StyleSchmidt, Thorsten. 2014. "Catastrophe Insurance Modeled by Shot-Noise Processes" Risks 2, no. 1: 3-24. https://doi.org/10.3390/risks2010003
APA StyleSchmidt, T. (2014). Catastrophe Insurance Modeled by Shot-Noise Processes. Risks, 2(1), 3-24. https://doi.org/10.3390/risks2010003



