Robust Portfolio Optimization in Crypto Markets Using Second-Order Tsallis Entropy and Liquidity-Aware Diversification
Abstract
1. Introduction
2. Materials and Methods
2.1. Mean–Second-Order Tsallis Entropy–Variance Model of Portfolio Optimization
- 1.
- For a given portfolio, this kind of entropy measures the correlation degree of the assets from the portfolio:
- 2.
- A lower entropy implies greater concentration (lower diversification), whereas a higher entropy reflects greater diversification, which may contribute positively to portfolio liquidity.
- 3.
- The standard Tsallis form converges to the Boltzmann–Gibbs/Shannon entropy as q → 1:
2.1.1. Optimization Problem Formulation
2.1.2. Solving the Portfolio Optimization Problem
2.2. Case Studies
- Case n = 2: Portfolio Optimization with Two Cryptocurrencies
- Case n = 3: Portfolio Optimization with Three Cryptocurrencies
3. Results and Discussions
3.1. Comparative Results
3.2. Liquidity Considerations
3.3. Limitations
- -
- Incorporating dynamic, forward-looking estimators for return and volatility using machine learning or regime-switching models;
- -
- Extending the entropy component to higher-order measures or adaptive entropy estimators that reflect changing market structures;
- -
- Embedding behavioral preferences and adaptive risk-aversion mechanisms into the objective function;
- -
- Exploring integration with decentralized finance (DeFi) instruments, NFT-backed assets, or hybrid portfolios combining digital and traditional securities;
- -
- Testing the model over longer time horizons or across multiple regimes to assess robustness under varying market conditions.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Closed-Form Quadratic Solution Under Covariance Risk
| Symbol | Meaning |
|---|---|
| r | Vector of expected returns |
| Σ | Variance–covariance matrix of returns |
| a, b | Parameters weighting return and risk |
| A | Matrix 2bI + 2 |
| λ | Multiplier for budget constraint |
| γ | Multiplier for variance constraint |
| x*(γ) | Optimal allocation vector |
Appendix B. Results Under Covariance-Based Risk Specification
| Asset | Equal Weights | Optimal Entropy Weights |
|---|---|---|
| BTC | 0.2500 | 0.2710 |
| ETH | 0.2500 | 0.2365 |
| SOL | 0.2500 | 0.2472 |
| BNB | 0.2500 | 0.2453 |

References
- Cheng, Tuoyuan, and Kan Chen. 2023. A general framework for portfolio construction based on generative models of asset returns. Journal of Finance and Data Science 9: 100113. [Google Scholar] [CrossRef]
- Dedu, Silvia, and Fulga Cristinca. 2011. Value-at-Risk estimation comparative approach with applications to optimization problems. Economic Computation and Economic Cybernetics Studies and Research 45: 5–20. [Google Scholar]
- Dedu, Silvia, Florentin Șerban, and Ana Tudorache. 2014. Quantitative risk management techniques using interval analysis, with applications to finance and insurance. Journal of Applied Quantitative Methods 9: 1–15. [Google Scholar]
- Hamza, Fakhri, and Jacques Janssen. 1996. Linear approach for solving large-scale portfolio optimization problems in a lognormal market. Paper presented at the 6th AFIR, Nuremberg, Germany, October 1–3, vol. II, pp. 1019–39. [Google Scholar]
- Jiang, Yuxi, Suyan He, and Xingsi Li. 2008. A maximum entropy model for large-scale portfolio optimization. Paper presented at the International Conference on Risk Management & Engineering Management (ICRMEM’08), Beijing, China, November 4–6; pp. 610–15. Available online: https://ieeexplore.ieee.org/document/4673300 (accessed on 8 September 2025).
- Ke, Jinchuan, and Can Zhang. 2008. Study on the optimization of portfolio based on entropy theory and mean-variance model. Paper presented at the IEEE International Conference on Service Operations and Logistics, and Informatics (SOLI 2008), Beijing, China, October 12–15; pp. 2668–72. Available online: https://www.researchgate.net/publication/240643459 (accessed on 5 September 2025).
- King, Alan. J. 1993. Asymmetric risk measures and tracking models for portfolio optimization under uncertainty. Annals of Operations Research 45: 165–78. [Google Scholar] [CrossRef]
- King, Alan J., and David L. Jensen. 1992. Linear-quadratic efficient frontiers for portfolio optimization. Applied Stochastic Models and Data Analysis 8: 195–207. [Google Scholar] [CrossRef]
- Konno, Hiroshi, and Hiroaki Yamazaki. 1991. A mean absolute deviation portfolio optimization model and its applications to Tokyo stock market. Management Science 37: 519–31. [Google Scholar] [CrossRef]
- Lutgens, Frank, and Peter Schotman. 2010. Robust portfolio optimisation with multiple experts. Review of Finance 14: 343–83. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio selection. The Journal of Finance 7: 77–91. [Google Scholar]
- Markowitz, Harry. 1991. Foundations of portfolio theory. The Journal of Finance 2: 469–71. [Google Scholar] [CrossRef]
- Markowitz, Harry, Peter Todd, Ganlin Xu, and Yuji Yamane. 1993. Computation of mean–semi-variance efficient sets by the critical line algorithm. Annals of Operations Research 45: 307–18. [Google Scholar] [CrossRef]
- Ou, Jen-Hao, and Yew Kam Ho. 2019. Shannon, Rényi, Tsallis Entropies and Onicescu Information Energy for Low-Lying Singly Excited States of Helium. Atoms 7: 70. [Google Scholar] [CrossRef]
- Philippatos, George C., and Charles J. Wilson. 1972. Entropy, market risk, and the selection of efficient portfolios. Applied Economics 4: 209–20. [Google Scholar] [CrossRef]
- Shannon, Claude Elwood. 1948. A mathematical theory of communication. Bell System Technical Journal 27: 379–423. [Google Scholar] [CrossRef]
- Shen, Weiwei, and Jun Wang. 2016. Portfolio Blending via Thompson Sampling. Paper presented at the IJCAI’16: Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, New York, NY, USA, July 9–15; pp. 1983–89. [Google Scholar]
- Sheraz, Muhammad, and Dedu Silvia. 2020. Bitcoin Cash: Stochastic models of fat-tail returns and risk modeling. Economic Computation and Economic Cybernetics Studies and Research 54: 43–58. [Google Scholar]
- Simonelli, Maria Rosaria. 2005. Indeterminacy in portfolio selection. European Journal of Operational Research 163: 170–76. [Google Scholar] [CrossRef]
- Speranza, M. Grazia. 1993. Linear programming models for portfolio optimization. Finance 14: 107–23. [Google Scholar]
- Yager, Ronald R. 1995. Measures of entropy and fuzziness related to aggregation operators. Information Sciences 82: 147–66. [Google Scholar] [CrossRef]
- Yoshimoto, Atsushi. 1996. The mean-variance approach to portfolio optimization subject to transaction costs. Journal of the Operations Research Society of Japan 39: 99–117. [Google Scholar] [CrossRef]
- Yu, Jing-Rung, and Wen-Yi Lee. 2011. Portfolio rebalancing model using multiple criteria. European Journal of Operational Research 209: 166–75. [Google Scholar] [CrossRef]
- Zheng, Yanan, Ming Zhou, and Gengyin Li. 2009. Information entropy-based fuzzy optimization model of electricity purchasing portfolio. Paper presented at the IEEE Power & Energy Society General Meeting (PES’09), Calgary, AB, Canada, July 26–30; pp. 1–6. [Google Scholar]
- Zhou, Rongxi, Ru Cai, and Guanqun Tong. 2013. Applications of entropy in finance: A review. Entropy 15: 4909–31. [Google Scholar] [CrossRef]
- Zopounidis, Constantin, and Michael Doumpos. 2002. Multi-criteria decision aid in financial decision making: Methodologies and literature review. Journal of Multi-Criteria Decision Analysis 11: 167–86. [Google Scholar] [CrossRef]
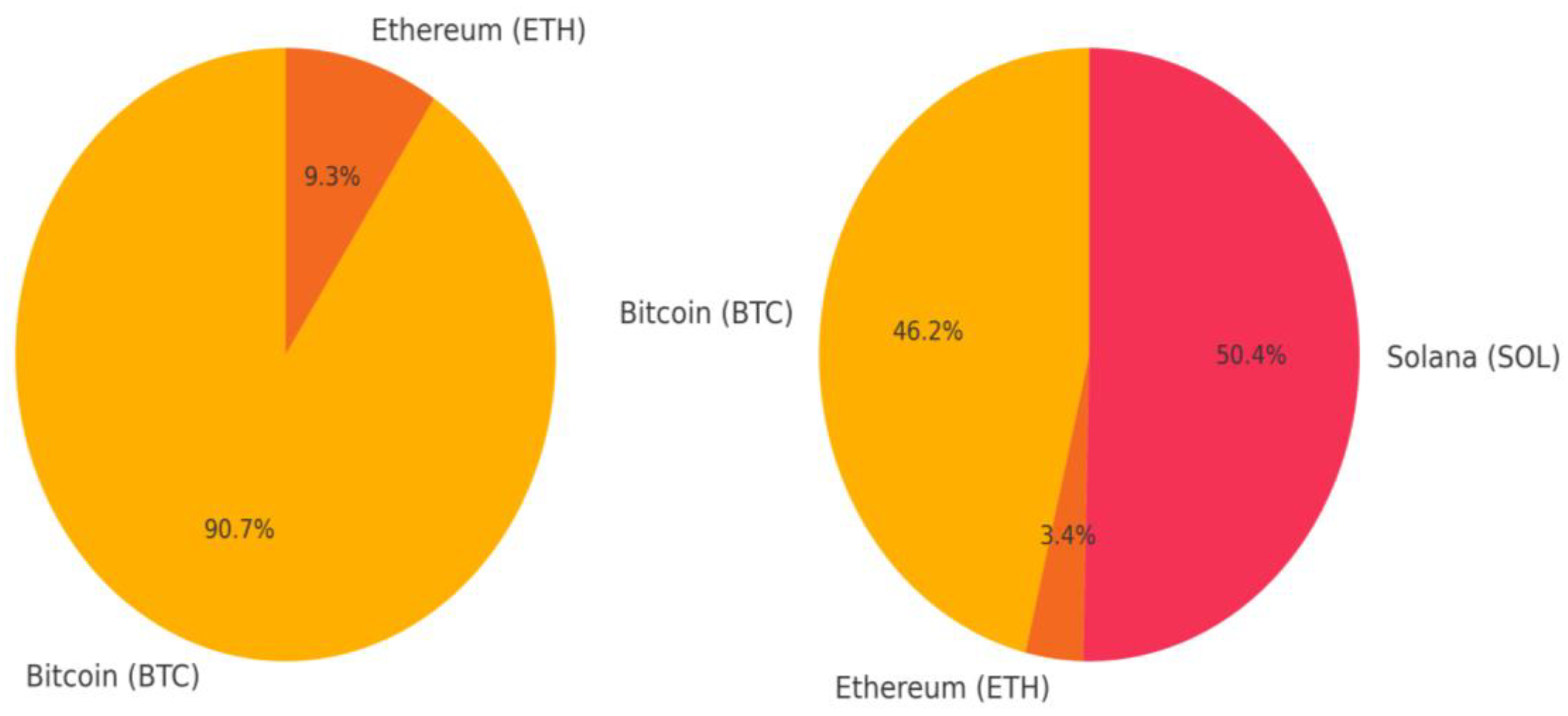


| Asset | μ (Return) | σ2 (Variance) | xᵢ (Weight) |
|---|---|---|---|
| Bitcoin (BTC) | 0.0565 | 0.033 | 0.9074 |
| Ethereum (ETH) | 0.0133 | 0.775 | 0.0926 |
| Bitcoin (BTC) | 0.0565 | 0.033 | 0.462 |
| Ethereum (ETH) | 0.0133 | 0.775 | 0.0344 |
| Solana (SOL) | 0.0755 | 0.105 | 0.5036 |
| Asset | μ (Return) | σ2 (Variance) | xᵢ (Weight) |
|---|---|---|---|
| Bitcoin (BTC) | 0.0542 | 0.031 | 0.182 |
| Ethereum (ETH) | 0.0418 | 0.045 | 0.121 |
| Solana (SOL) | 0.0674 | 0.088 | 0.153 |
| Binance Coin (BNB) | 0.0521 | 0.042 | 0.094 |
| Cardano (ADA) | 0.0387 | 0.059 | 0.066 |
| Ripple (XRP) | 0.0295 | 0.071 | 0.048 |
| Dogecoin (DOGE) | 0.0241 | 0.083 | 0.037 |
| Polkadot (DOT) | 0.0362 | 0.065 | 0.052 |
| Avalanche (AVAX) | 0.0583 | 0.091 | 0.082 |
| Polygon (MATIC) | 0.0439 | 0.072 | 0.057 |
| Litecoin (LTC) | 0.0336 | 0.077 | 0.056 |
| Tron (TRX) | 0.0311 | 0.069 | 0.052 |
| Model | Expected Return | Variance | Entropy Score | Sharpe Ratio |
|---|---|---|---|---|
| Mean–Variance | 0.148 | 0.092 | - | 1.28 |
| Shannon Entropy | 0.142 | 0.078 | 1.85 | 1.35 |
| Tsallis-2 Entropy | 0.145 | 0.08 | 2.47 | 1.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Șerban, F.; Dedu, S. Robust Portfolio Optimization in Crypto Markets Using Second-Order Tsallis Entropy and Liquidity-Aware Diversification. Risks 2025, 13, 180. https://doi.org/10.3390/risks13090180
Șerban F, Dedu S. Robust Portfolio Optimization in Crypto Markets Using Second-Order Tsallis Entropy and Liquidity-Aware Diversification. Risks. 2025; 13(9):180. https://doi.org/10.3390/risks13090180
Chicago/Turabian StyleȘerban, Florentin, and Silvia Dedu. 2025. "Robust Portfolio Optimization in Crypto Markets Using Second-Order Tsallis Entropy and Liquidity-Aware Diversification" Risks 13, no. 9: 180. https://doi.org/10.3390/risks13090180
APA StyleȘerban, F., & Dedu, S. (2025). Robust Portfolio Optimization in Crypto Markets Using Second-Order Tsallis Entropy and Liquidity-Aware Diversification. Risks, 13(9), 180. https://doi.org/10.3390/risks13090180








