Explainable Machine Learning Framework for Predicting Auto Loan Defaults

Abstract

This study develops a machine learning framework to improve the prediction of automobile loan defaults by integrating explainable feature selection with advanced resampling techniques. Using publicly available data, we compare Logistic Regression, Random Forest, eXtreme Gradient Boosting (XGBoost), and Stacked classifiers. Feature selection methods, including SHapley Additive exPlanations (SHAP) values and Mutual Information (MI), and resampling techniques such as Synthetic Minority Over-sampling TEchnique (SMOTE), SMOTE-Tomek, and SMOTE Edited Nearest Neighbor (SMOTE-ENN), are evaluated. The results show that combining SHAP-based feature selection with SMOTE-Tomek resampling and a Stacked Classifier consistently achieves superior predictive performance. These findings highlight the value of explainable AI in enhancing credit risk assessment for auto lending. This research also offers valuable insights for addressing other financial modeling challenges involving imbalanced datasets, supporting more informed and reliable decision-making.

1. Introduction

In today’s evolving economic landscape, automobile loans represent a significant component of consumer debt, underscoring the critical need for accurate and robust models to predict loan defaults. Recent economic disruptions, such as the COVID-19 pandemic and trade wars, have contributed to unprecedented increases in vehicle prices. These factors have collectively led to rising delinquency rates in auto lending, exceeding pre-pandemic levels, as highlighted in the Bank of Canada’s Monetary Policy Report https://www.autonews.com/retail/finance-insurance/anc-canadian-auto-loan-delinquency-rates-rise/ (accessed on 1 May 2024). In this context, traditional credit scoring models, which often rely on a limited set of variables and linear assumptions, are proving inadequate for capturing the dynamic risk patterns associated with modern lending, therefore creating a barrier for both consumers and financial institutions Toh (2023).

The use of machine learning and explainable AI techniques has become increasingly popular across various application domains, including financial modeling (Burkart 2021; Çelik 2023) and insurance technology (Maillart 2021; Owens 2022). Therefore, this study addresses the growing need for more sophisticated approaches by leveraging advanced machine learning (ML) techniques El Khair (2024) to improve the prediction of auto loan defaults. It explores the integration of feature selection methods, particularly SHAP (SHapley Additive exPlanations) values and Mutual Information, and resampling strategies such as Synthetic Minority Over-sampling TEchnique (SMOTE), SMOTE-Tomek, and SMOTE Edited Nearest Neighbor (SMOTE-ENN) to handle data imbalance issues and enhance predictive performance Kanaga (2024). The aim is to develop a predictive framework that not only achieves high classification accuracy but also offers interpretability and practical utility for financial institutions when handling credit risk scoring. This motivates the central research question: How can advanced machine learning models and feature selection techniques enhance the prediction of auto loan defaults relative to traditional credit scoring methods? To answer this, this study pursues several objectives: (1) to identify the most influential predictive features using SHAP and Mutual Information, (2) to evaluate the impact of different resampling techniques on class imbalance, and (3) to compare the performance of multiple classifiers, including Logistic Regression, Random Forest, XGBoost, and a Stacked ensemble, on various evaluation metrics, with particular attention to the minority class (i.e., defaulters).

The significance of this study is justified on both practical and academic grounds. For lenders, the ability to accurately identify high-risk borrowers is crucial for minimizing losses and making informed lending decisions. For the research community, this research contributes a novel perspective by integrating model-agnostic explainability and ensemble machine learning in the domain of credit risk prediction. The combination of both techniques has not been extensively explored in the literature. The use of SHAP values for feature selection, in particular, represents a significant step toward building more transparent and interpretable ML models in insurance and finance Khan (2025). Methodologically speaking, the research follows a structured machine learning framework. The study conducts data preprocessing, baseline model training, hyperparameter tuning via Randomized GridSearch, and the application of advanced resampling techniques. Special emphasis is placed on comparing feature selection strategies and their influence on model performance and interpretability, leading to a more significant contribution to the practice of credit risk modeling.

The remainder of the paper is organized as follows: Section 2 reviews the relevant literature on credit risk modeling and class imbalance in ML. Section 3 presents an exploratory analysis of the dataset and details the methodology and experimental design. Section 4 discusses the results and their implications. Finally, Section 5 offers conclusions and outlines directions for future work.

2. Literature Review

Credit risk prediction Noriega (2023) remains a key challenge in financial analytics, primarily due to issues such as data imbalance, high dimensionality, and the suboptimal performance of existing predictive models Matharaarachchi (2021). One solution to address this challenge is to leverage machine learning, particularly deep learning techniques, to achieve improved predictive performance. Recent advances in credit risk prediction have increasingly focused on integrating predictive accuracy with interpretability through explainable artificial intelligence (XAI) methods. For example, in Schmitt (2024), the use of explainable automated machine learning combined with SHAP values was proposed to enhance transparency in credit decision-making, thereby improving human–AI collaboration. Similarly, Lin (2025) investigated the stability of SHAP values in credit risk management, highlighting potential robustness issues when interpreting contributions of input features. From a methodological point of view, ensemble-based explainable models have been shown to improve both performance and interpretability, as demonstrated by Sun (2025), where XGBoost and clustering were used to enhance credit risk prediction. Beyond individual model proposals, systematic reviews have documented the rapid adoption of XAI in financial contexts. For instance, an extensive review by Cerneviciene (2024) identified key applications of XAI in finance, including credit scoring and fraud detection, which is very relevant to our work. More recently, Golec (2025) conducted a systematic review of interpretable large language models (LLMs) in the context of credit risk, underscoring their potential to emerge as transformative tools in credit risk modeling. Collectively, these studies underscore a growing recognition that effective credit risk prediction must balance predictive performance with interpretability to meet both regulatory and practical demands. While substantial progress has been made in each of these areas, the literature reveals several gaps, particularly in the integration of advanced resampling methods with interpretable, model-agnostic feature selection (Natarajan 2025; Scholbeck 2020), and in the systematic evaluation of ensemble methods under imbalanced conditions Lenka (2022).

Class imbalance (Abd Elrahman 2013; Ali 2013), where default cases constitute a minority of the dataset, is a persistent issue that degrades model performance, particularly for the minority class. Several studies have attempted to address this problem through resampling techniques. For instance, Abedin (2023) applied a weighted SMOTE (WSMOTE) ensemble method, demonstrating a 15.16% improvement in minority class accuracy, while Zhao (2024) introduced an approach called Strategic Hybrid SMOTE with Double Edited Nearest Neighbors (SH-SENN), reporting improved sensitivity on highly imbalanced datasets. Similarly, Khemakhem (2018) and Chen (2022) used SMOTE, undersampling, and weighted sampling to achieve better class balance; while these studies demonstrate the value of resampling, they often treat sampling techniques and feature selection as separate processes, overlooking the potential for interactions between irrelevant features and synthetic data to introduce noise. Moreover, most of these approaches rely on default parameter settings or focus on singular resampling strategies without systematically comparing alternatives such as SMOTE-Tomek or SMOTE-ENN, which may further refine classification decision boundaries.

Recent studies have increasingly emphasized the importance of resampling methods for addressing class imbalance in financial and insurance applications. For instance, Wang (2025) proposed a SMOTE-KMeans strategy for credit card fraud detection, achieving an AUC of 0.96 by combining clustering-based oversampling with ensemble learning. Similarly, Sakho (2025) introduced an oversampling approach tailored for mixed-type financial data, comparing its performance against SMOTE for Nominal and Continuous (SMOTE-NC) and highlighting limitations of traditional SMOTE in bank customer scoring. In the insurance domain, Noor (2025) conducted a comprehensive evaluation of SMOTE and its hybrid variants (e.g., SMOTE random undersampling (SMOTE-RUS) and SMOTE-ENN), demonstrating that hybrid resampling provides an effective trade-off between computational efficiency and predictive accuracy when applied to highly imbalanced motor insurance datasets. These works underscore the relevance of advanced SMOTE-based techniques for enhancing prediction reliability in finance and insurance. However, our study contributes by comparing multiple resampling strategies in conjunction with SHAP-based feature selection, aiming for both enhanced accuracy and reliability of the model that we used to predict the auto loan defaults.

Feature selection for high-dimensional data has traditionally been done using statistical and filter-based methods, such as chi-square tests, Cramer’s V, ANOVA, and Wilks’ Lambda, as seen in the work of Jemai (2023) and Khemakhem (2018). The work conducted by Wattanakitrungroj (2024) went a step further by employing domain-informed feature engineering to improve model performance. However, a common limitation across these studies is that many prematurely discard variables based on marginal statistical associations, without assessing their interactive effects in complex models. In contrast, this research adopts a model-agnostic feature selection method using SHAP (SHapley Additive exPlanations) values, which quantify each feature’s marginal contribution to individual predictions. SHAP offers deeper interpretability, enabling a better understanding of feature importance, especially in non-linear and ensemble-based models.

Recent advances in XAI have highlighted the growing importance of SHAP as a feature selection technique. Unlike traditional approaches that rely on distributional assumptions or embedded model-specific measures, SHAP provides a unified framework that attributes predictive power consistently across features. For example, in Wang (2025), the effectiveness of SHAP-based analysis in identifying influential predictors of corporate financialization from high-dimensional data was demonstrated. Similarly, Kraev (2024) introduced Shap-Select, a regression-based framework using SHAP values for feature selection, outperforming classical methods used in financial applications. These studies collectively emphasize the significance of adopting explainable AI-driven feature selection to enhance both interpretability and predictive performance. Despite its growing popularity, SHAP remains underexplored in the context of credit risk prediction, especially when it is coupled with resampling techniques, an important gap that this study addresses.

As a traditional approach, Logistic Regression remains a common practice in credit risk modeling Sun (2015), due to its transparency and ease of interpretation. Studies by Lim (2017) and Chen (2022) highlight the model’s continued relevance, particularly when model interpretability is required by regulatory compliance. The work conducted by Chen (2022) also demonstrates adaptability by incorporating weighted Logistic Regression with $L_2$ regularization; therefore, the class imbalance issue is improved. However, as complex patterns and non-linear relationships become more prominent in financial data, Logistic Regression often fails to capture high-order interactions, limiting its predictive power. To address this, ensemble methods such as Random Forest and XGBoost have gained attention in applications. The studies by Reddy (2022) and Xu (2021) found Random Forest effective in handling high-dimensional, imbalanced datasets. These models benefit from reduced variance and strong generalization but at the expense of model interpretability. Additionally, studies like those by Setiawan (2019) and Reddy (2022) provide comparative insights across machine learning models, but they often focus on raw accuracy and overlook critical metrics like Precision–Recall Area Under the Curve (PR-AUC) or F1-score, which are more informative and accurate under class imbalance. Furthermore, few studies assess the synergistic potential of ensemble learning and interpretable feature selection, especially when combined with advanced sampling techniques.

3. Materials and Methods

From a methodological design and application perspective, this research addresses the gap mentioned above through several key contributions. It implements and evaluates advanced resampling techniques, including SMOTE (Synthetic Minority Over-sampling Technique), SMOTE-Tomek, and SMOTE-ENN. It compares SHAP-based and Mutual Information-based feature selection methods to assess interpretability and model fit. It also conducts systematic model evaluation across multiple classifiers, such as Logistic Regression, Random Forest, XGBoost, and Stacked ensembles. To maintain focus on the main contribution of this work—the development of an explainable machine learning framework for credit risk modeling—we have not provided detailed mathematical derivations of the individual machine learning models. Instead, we direct interested readers to standard references such as James (2023), which offers comprehensive technical descriptions of Logistic Regression, Random Forest, and XGBoost. For the feature selection methods, including SHAP values and Mutual Information, we likewise refer readers to established sources such as Molnar (2020), where these methods are explained in detail with both theoretical and practical insights.

The analysis emphasizes metrics relevant for imbalanced data, such as PR-AUC and the F1-score for the minority class. From a methodological perspective, this study provides a holistic framework that emphasizes both accuracy and interpretability. It offers practical value to financial institutions aiming to optimize their risk assessment strategies. It also contributes academic value by extending the methodological toolkit for addressing imbalanced classification problems in finance. In the following section, we first introduce the dataset we use for our experiments and its key data characteristics.

3.1. Data and Their Characteristics

The data were obtained from the Kaggle platform and is titled the Automobile Loan Default Dataset https://www.kaggle.com/datasets/saurabhbagchi/dish-network-hackathon (accessed on 1 May 2024). It consists of two files: Train_Dataset.csv and Test_Dataset.csv. For model development, the Train_Dataset.csv file, containing 121,856 records, was used for initial training and validation. Final model performance was then evaluated using the Test_Dataset.csv file. Each of the training and test datasets includes 11 categorical features. Several of these features contain categories with low frequency, necessitating reclassification through cluster mapping. In particular, features such as Type of Organization, Client Income Type, Client Education, and Client Gender were identified as requiring reclassification to improve model performance.

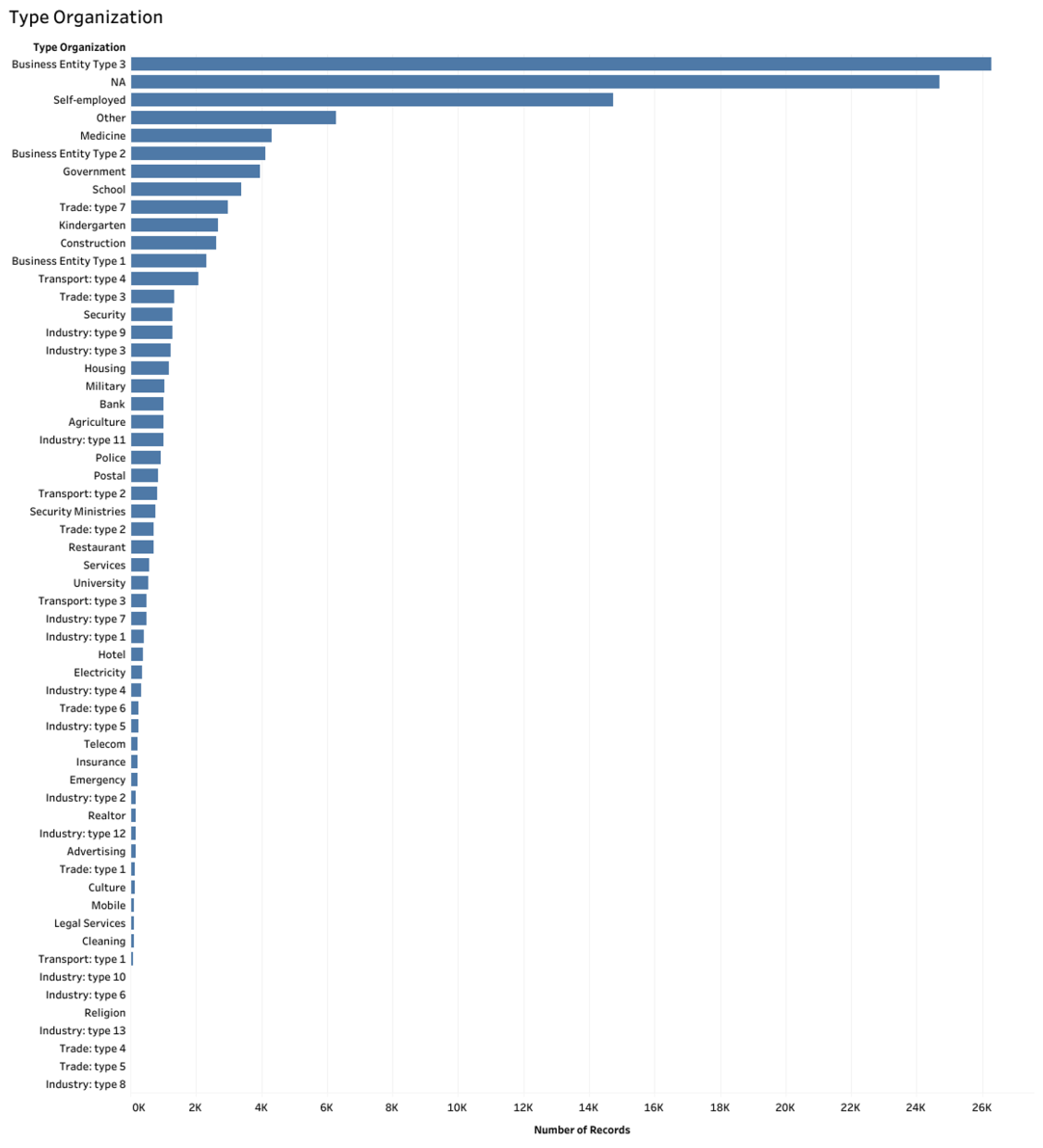
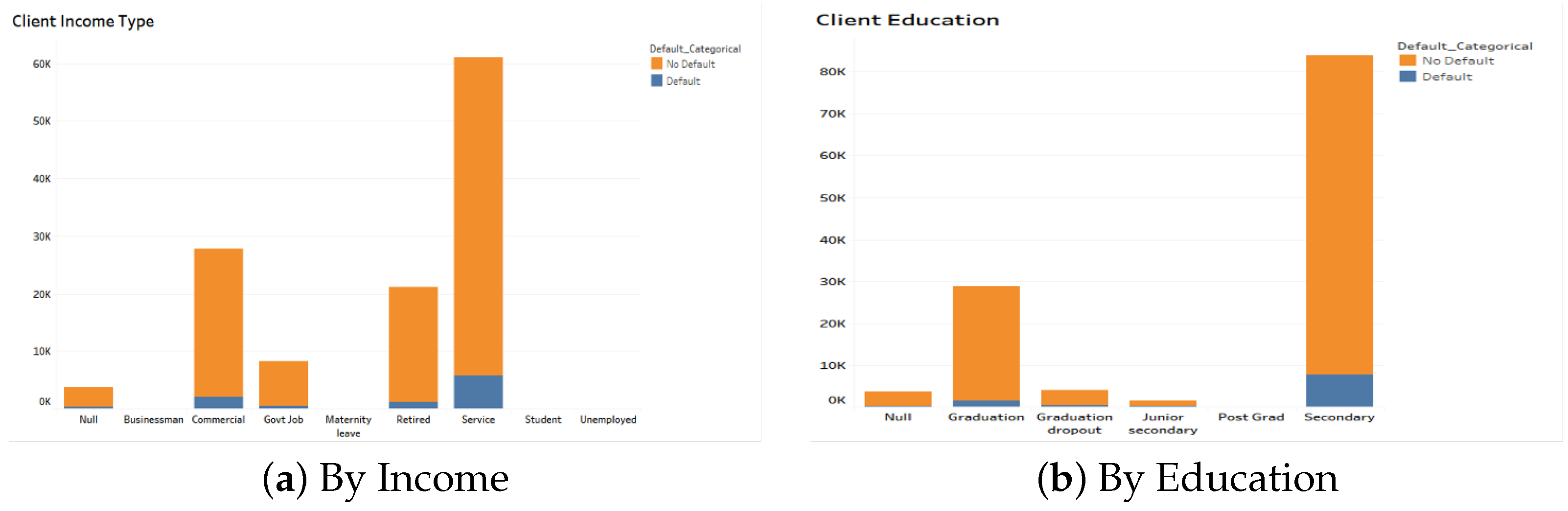
As illustrated in Figure 1, certain categories within these features, specifically those under Industry Type from Industry Type 10 to Industry Type 8, appear with such a low frequency that they can be effectively consolidated into a single ‘Other’ category. This reclassification helps to balance the distribution and reduce the impact of sparse categories on model training. Figure 2a illustrates the distribution of default and non-default cases across different income types. The majority of clients earn their income through employment in the service industry, while categories such as Businessman, Maternity Leave, Student, and Unemployed are relatively rare. Notably, clients who defaulted on their loans were primarily employed in the service or commercial sectors or were retired, suggesting potential associations between employment type and credit risk. Figure 2b presents the distribution of defaults by education level. The Post-Graduate category includes very few observations and should be considered for regrouping to improve model stability. Most clients, both in the overall population and among those who defaulted, reported secondary school as their highest level of education, followed by those with graduate-level education. These trends suggest that educational attainment may be a useful predictor of default risk.

An analysis of the target variable (loan default status) revealed a significant class imbalance. The majority of clients in the dataset did not default on their auto loans. This imbalance may adversely affect model performance, particularly in classification accuracy for the minority class. As a result, various techniques to address class imbalance (e.g., resampling or cost-sensitive learning) will be considered in the modeling phase.

Further exploratory data analysis examined the relationship between income and default frequency. Clients earning between USD 2700 and USD 50,000 accounted for the majority of default cases, as highlighted by the dark orange cluster in the income distribution plot. Notably, a peak of 1227 default cases was observed at an income level of USD 13,500, representing the highest number of defaults for a specific income band. The analysis also indicates a negative correlation between income and default frequency; as income increases, the likelihood of default decreases. These findings suggest that loan approval strategies should prioritize risk assessment for clients with lower to moderate income levels, particularly those earning between USD 2500 and USD 50,000.

The correlation matrix revealed several meaningful relationships among the variables. A strong positive correlation was observed between loan repayment and credit amount, which is expected, as the amount borrowed increases, the total repayment tends to rise accordingly. There was also a high positive correlation between the number of children and the number of family members, reflecting the intuitive relationship that larger families typically include more children. Similarly, a positive correlation between days employed and age suggests that older clients tend to have longer employment histories.

On the other hand, several negative correlations were also notable. A strong negative correlation was found between age and child count, indicating that younger clients are more likely to have children, whereas older clients are less likely to report dependent children. Additionally, the number of family members showed negative correlations with marital status, age, and employment duration. This implies that clients with fewer family members are more likely to be younger, unmarried, and have shorter employment histories. Lastly, a weak negative correlation was observed between car ownership and client gender, which may point to slight gender-related differences in vehicle ownership patterns within the dataset.

3.2. Methodology and Experiments

This section outlines the data preprocessing procedures and the key methodologies employed in this study. In addition, it provides an overview of the experimental design implemented to address the research objectives.

3.3. Data Preprocessing

Initial data preprocessing involved several key steps to ensure data quality and readiness for modeling. These steps included correcting feature data types, removing duplicate records and irrelevant features, and handling missing values using iterative imputation, which leverages the relationships between variables to estimate missing entries more accurately. To prepare the data for machine learning algorithms, numerical features were standardized using a standard scaler to ensure consistent scaling across variables. Outliers in selected numerical features were identified and removed using the Interquartile Range (IQR) method, based on insights gained during exploratory data analysis. In addition, categorical features were transformed using label encoding to convert them into a numeric format compatible with most machine learning models.

3.4. Feature Selection

Given that the dataset consists of 35 input variables, feature selection was a critical step to enhance both model performance and interpretability. In this study, we employed two complementary approaches: Mutual Information and SHAP values.

Mutual Information is an information-theoretic measure that quantifies the dependency between two random variables. Specifically, it evaluates how much knowing the value of a feature reduces uncertainty about the target variable. For feature selection, MI is computed between each input variable and the target, with higher values indicating stronger relevance. Since MI is model-agnostic and non-parametric, it is capable of capturing non-linear dependencies. However, it evaluates each feature independently, ignoring potential interactions or redundancies among features. Additionally, MI requires estimation of probability distributions, which can become unreliable in high-dimensional or continuous feature spaces. Despite these limitations, MI provides a useful initial screening mechanism for reducing the number of candidate features. In this study, features with the highest MI scores were retained for subsequent modeling (see

Table 1. Mutual Information and SHAP scores ranked by Mutual Information.

Feature	Mutual Information	SHAP Importance
Client_Contact_Work_Tag	0.016042	0.028518
Client_Education	0.015496	0.144844
Client_Permanent_Match_Tag	0.013030	0.017818
Active_Loan	0.011349	0.023240
Loan_Annuity	0.011099	0.200798
Workphone_Working	0.010468	0.047075
Employed_Days	0.010126	0.163809
Car_Owned	0.009840	0.651330
Client_Gender	0.009279	0.169230
Age_Days	0.008912	0.248645
Client_Income_Type	0.008610	0.042161
Client_Marital_Status	0.008127	0.085842
Homephone_Tag	0.007982	0.151751
Client_Housing_Type	0.007713	0.033938
Registration_Days	0.007419	0.128106
Bike_Owned	0.007253	0.017662
Child_Count	0.006785	0.055558
Client_Occupation	0.006548	0.045878
Social_Circle_Default	0.006534	0.272696
ID_Days	0.006218	0.139333
House_Own	0.005685	0.079567
Type_Organization	0.005098	0.071706
Phone_Change	0.005084	0.213914
Own_House_Age	0.004233	0.915049
Credit_Amount	0.003998	0.282806
Cleint_City_Rating	0.003758	0.220465
Client_Family_Members	0.003127	0.071070
Credit_Bureau	0.001897	0.144525
Application_Process_Day	0.001154	0.046515
Accompany_Client	0.000848	0.010186
Population_Region_Relative	0.000825	0.567377
Loan_Contract_Type	0.000401	0.032941
Application_Process_Hour	0.000000	0.082826
Mobile_Tag	0.000000	0.000000
Client_Income	0.000000	0.066395

).

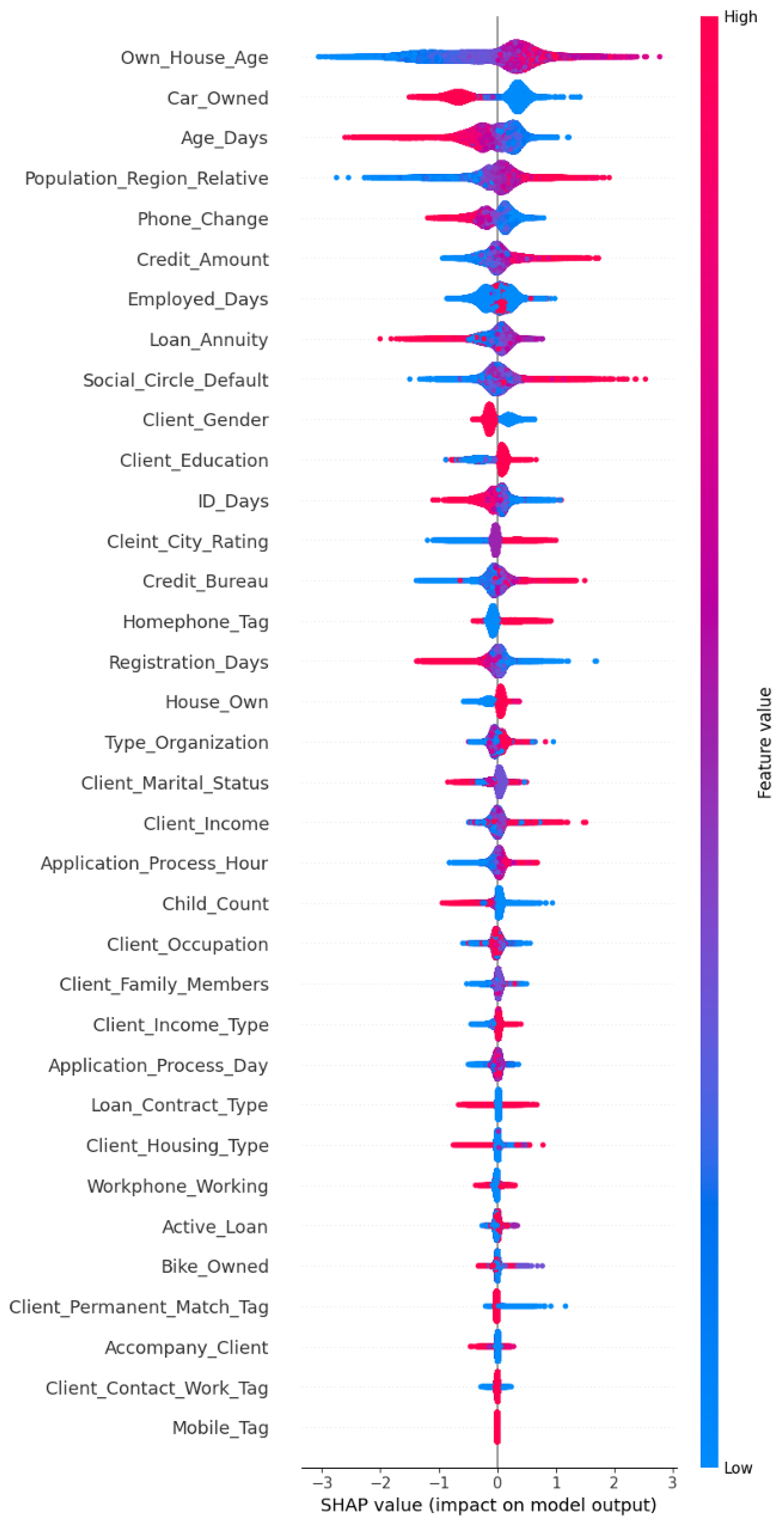
To further refine the selection process, we employed SHAP values, a model-aware approach rooted in cooperative game theory. SHAP values attribute each feature’s contribution to individual predictions by calculating its marginal effect across all possible feature combinations. Unlike MI, SHAP accounts for both main effects and interactions, offering a richer perspective on feature importance. It provides both local (instance-level) and global (dataset-level) interpretability and is especially effective in identifying redundant or weakly contributing features; while computationally more intensive and requiring a trained model, SHAP values allow for a more accurate and context-sensitive evaluation of feature relevance. The SHAP summary plot (Figure 3) visualizes and ranks features by their average contribution to the model output, offering an interpretable and data-driven view of feature impact.

By combining MI and SHAP-based evaluations, we selected a subset of features that were not only statistically informative but also predictive in the context of the trained model. This dual-method strategy reduced the dimensionality of the input space while preserving key information, resulting in enhanced model efficiency and transparency. Furthermore, the comparison between the two methods revealed useful insights into potential trade-offs or inconsistencies in feature importance, such as features ranked highly by MI but less influential in SHAP, highlighting the importance of using both statistical and model-based approaches in feature selection.

While MI provides a fast and model-agnostic filtering step, SHAP offers a more comprehensive assessment by incorporating the actual learned behavior of the model. This distinction is particularly valuable in high-dimensional or non-linear settings, where capturing feature dependencies and interaction effects is essential for robust and interpretable predictive modeling.

3.5. Resampling and Data Splitting

To address class imbalance in our dataset, three resampling techniques were employed: SMOTE, SMOTE-Tomek, and SMOTE-ENN. SMOTE generates synthetic examples for the minority class by interpolating between existing minority instances, thereby balancing the class distribution. SMOTE-Tomek extends this approach by combining SMOTE with Tomek Links, which identify pairs of nearest-neighbor instances from opposite classes; these borderline samples are removed to enhance class separability and reduce overlap. SMOTE-ENN further refines the resampled data by integrating SMOTE with Edited Nearest Neighbors, which eliminates samples misclassified by their nearest neighbors, effectively reducing noise and improving data quality. These techniques were evaluated to determine which most effectively improved model performance and the detection of the minority class. The dataset was split into an 80% training set and a 20% test set. Following the split, a standard scaler was applied to the numerical features to ensure consistency in feature scaling across all experiments.

3.6. Experiments

The experiments aimed to optimize classifier performance and enhance metrics such as accuracy, precision, recall, and AUC. The steps for each experiment are outlined as follows:

3.6.1. Experiment One

The first experiment aimed to establish a baseline for model performance using all available features. Four classifiers were trained: Logistic Regression, Random Forest, XGBoost, and a Stacked ensemble. SMOTE was applied to generate synthetic samples of the minority class to balance the dataset. After training the baseline models, Mutual Information and SHAP values were used to evaluate their impact on model accuracy. Model performance was assessed using multiple evaluation metrics, including accuracy, precision, recall, F1-score, and AUC, to ensure a comprehensive comparison across classifiers.

In the second phase, the focus shifted specifically to evaluating the effectiveness of the feature selection techniques. The MI approach involved computing MI scores to quantify the dependency between each feature and the response variable, and the top 20 features with the highest scores were selected. In contrast, the SHAP approach utilized an XGBoost model to compute SHAP values, providing a measure of feature importance based on each feature’s contribution to individual predictions. The top 20 features with the highest SHAP values were selected for further analysis. This two-step process allowed for a robust evaluation of feature selection strategies in terms of both predictive power and interpretability.

3.6.2. Experiment Two

The second experiment focused on optimizing model performance through hyperparameter tuning using Randomized GridSearch. Unlike traditional grid search, which exhaustively evaluates all parameter combinations, Randomized GridSearch randomly samples from the defined parameter space, offering a more computationally efficient approach while still effectively identifying high-performing configurations. Model performance was evaluated using two key metrics: Precision–Recall AUC (PR AUC) and Receiver Operating Characteristic AUC (ROC AUC). PR AUC is particularly well-suited for imbalanced datasets, as it emphasizes the trade-off between precision and recall, while ROC AUC assesses the model’s ability to distinguish between classes across various threshold settings.

To further improve model performance, feature selection methods mentioned previously was refined by retaining only the most influential variables identified through Mutual Information and SHAP values. Specifically, features contributing to 90% of the cumulative importance were selected, ensuring that the final models focused on the most impactful predictors. This approach maintained a balance between reducing model complexity and preserving predictive power. The optimized classifiers, trained on these reduced feature sets and fine-tuned hyperparameters, were then evaluated for their effectiveness in predicting auto loan defaults, with particular attention given to enhancing the detection of the minority class.

3.6.3. Experiment Three

In the third experiment, the focus shifted to evaluating the effectiveness of advanced resampling techniques, SMOTE-Tomek and SMOTE-ENN, in comparison to the standard SMOTE method for addressing class imbalance. These enhanced approaches were selected for their ability to not only balance class distributions but also improve class separability and reduce data noise, thereby increasing the model’s ability to accurately classify minority observations. The experiment was conducted using the optimal hyperparameters previously identified through Randomized GridSearch, applied to models using features selected by both SHAP and Mutual Information methods. This ensured that performance comparisons were consistent with previous experiments. The primary objective was to determine which resampling strategy most effectively improved model performance, particularly with respect to minority class prediction, in the context of financial risk assessment for auto loan defaults.

4. Results

4.1. Results for Experiment One

The first experiment was first conducted using baseline models for each classifier, with class imbalance addressed through SMOTE. The results are shown in

Table 2. Evaluation metrics for each base model with separate metrics for class 0.0 (non-default) and class 1.0 (default).

	LR	RF	XGBoost	Stacked
Accuracy	0.67	0.87	0.92	0.91
Precision (0.0 | 1.0)	0.96 | 0.15	0.93 | 0.18	0.92 | 0.49	0.93 | 0.37
Recall (0.0 | 1.0)	0.68 | 0.65	0.93 | 0.17	1.00 | 0.04	0.98 | 0.15
F1-score (0.0 | 1.0)	0.79 | 0.25	0.93 | 0.18	0.96 | 0.07	0.95 | 0.21

. Although higher overall accuracy was observed in the Random Forest (RF), XGBoost, and Stacked classifiers, these results were largely influenced by the models’ bias toward the majority class. This is evident in the imbalanced precision and recall scores, particularly for class 1.0 (i.e., the minority class), where both precision and recall remained low. These findings indicate that, despite achieving high overall accuracy, the models were not effectively capturing minority class instances, thus limiting their usefulness for imbalanced classification tasks.

The detailed results are presented in two tables:

Table 3. Experiment One results for models using Mutual Information (MI) feature selection, showing evaluation metrics for class 0.0 (non-default) and class 1.0 (default).

MI Selected Features
	LR	RF	XGBoost	Stacked
Accuracy	0.46	0.83	0.89	0.87
Precision (0.0 | 1.0)	0.95 | 0.11	0.93 | 0.16	0.92 | 0.16	0.92 | 0.15
Recall (0.0 | 1.0)	0.43 | 0.74	0.88 | 0.24	0.97 | 0.07	0.94 | 0.11
F1-score (0.0 | 1.0)	0.60 | 0.18	0.90 | 0.19	0.94 | 0.10	0.93 | 0.13
Precision–Recall AUC	0.13	0.13	0.12	0.12
ROC-AUC	0.63	0.64	0.63	0.62

reports the evaluation metrics for models using features selected via MI, while

Table 4. Experiment One results for models using SHAP feature selection, displaying evaluation metrics for class 0.0 (non-default) and class 1.0 (default).

SHAP Selected Features
	LR	RF	XGBoost	Stacked
Accuracy	0.53	0.80	0.90	0.895
Precision (0.0 | 1.0)	0.96 | 0.12	0.93 | 0.16	0.92 | 0.27	0.93 | 0.27
Recall (0.0 | 1.0)	0.51 | 0.74	0.84 | 0.32	0.98 | 0.10	0.96 | 0.16
F1-score (0.0 | 1.0)	0.66 | 0.21	0.88 | 0.21	0.95 | 0.15	0.94 | 0.20
Precision–Recall AUC	0.16	0.14	0.18	0.19
ROC-AUC	0.68	0.66	0.70	0.71

shows results for models using SHAP values. Overall, models utilizing SHAP-selected features consistently outperformed those based on MI, as reflected in higher scores for ROC-AUC and PR-AUC, metrics that are particularly informative in imbalanced settings. Among all classifiers, XGBoost and the Stacked ensemble demonstrated the strongest performance, especially when combined with SHAP-selected features. These models achieved the best results across multiple evaluation criteria, including accuracy using ROC-AUC and PR-AUC.

Although both feature selection approaches faced challenges in improving minority class prediction, SHAP-based selection provided a noticeable edge. This advantage was most evident in the Stacked classifier, which showed improved sensitivity to the minority class. These results highlight the importance of selecting features not only for relevance but also for their contribution to robust and equitable model performance in imbalanced classification problems.

4.2. Results for Experiment Two

The results obtained from Experiment Two are reported in

Table 5. Experiment Two results for models using MI feature selection, displaying evaluation metrics for class 0.0 (non-default) and class 1.0 (default).

MI Selected Features
	LR	RF	XGBoost	Stacked
Accuracy	0.76	0.88	0.80	0.64
Precision (0.0 | 1.0)	0.94 | 0.15	0.93 | 0.25	0.93 | 0.16	0.94 | 0.12
Recall (0.0 | 1.0)	0.79 | 0.40	0.93 | 0.25	0.85 | 0.32	0.65 | 0.54
F1-score (0.0 | 1.0)	0.86 | 0.21	0.93 | 0.25	0.89 | 0.21	0.77 | 0.20
Precision–Recall AUC	0.30	0.28	0.27	0.35
ROC-AUC	0.64	0.68	0.64	0.62

and

Table 6. Experiment Two results for models using SHAP feature selection, displaying evaluation metrics for class 0.0 (non-default) and class 1.0 (default).

SHAP Selected Features
	LR	RF	XGBoost	Stacked
Accuracy	0.80	0.85	0.86	0.87
Precision (0.0 | 1.0)	0.94 | 0.18	0.94 | 0.21	0.94 | 0.25	0.94 | 0.27
Recall (0.0 | 1.0)	0.84 | 0.40	0.89 | 0.33	0.91 | 0.35	0.93 | 0.31
F1-score (0.0 | 1.0)	0.89 | 0.25	0.91 | 0.26	0.92 | 0.29	0.93 | 0.29
Precision–Recall AUC	0.32	0.30	0.33	0.32
ROC-AUC	0.69	0.68	0.70	0.71

. For models using MI-selected features, the Random Forest classifier achieved the highest overall accuracy (0.88). However, this came at the cost of poor sensitivity to the minority class. In contrast, the Stacked classifier, while yielding a lower accuracy (0.64), achieved a notably higher recall (0.54) for the minority class, indicating an improved ability to identify default cases, along with some compromise in overall predictive accuracy. Across all models using MI-selected features, Precision–Recall AUC and ROC-AUC scores remained relatively low, suggesting persistent difficulties in distinguishing between classes.

Models built with SHAP-selected features, however, demonstrated a more balanced and effective performance. The Stacked classifier again stood out, achieving the highest accuracy (0.87), along with improved recall (0.31) and F1-score (0.29) for the minority class. Additionally, SHAP-based models recorded higher Precision–Recall AUC and ROC-AUC values, with the Stacked classifier reaching 0.33 and 0.71, respectively. These improvements suggest that SHAP-selected features capture more informative and predictive relationships, contributing to both greater model interpretability and better classification performance.

Overall, Experiment Two highlights the importance of both feature selection and decision threshold optimization in addressing class imbalance and improving the detection of minority class instances. In particular, SHAP-based feature selection, when combined with threshold tuning, provided a more robust framework for predicting auto loan defaults, balancing accuracy and recall more effectively than models based on MI features.

4.3. Results for Experiment Three

Experiment Three evaluated the effectiveness of advanced class balancing techniques, SMOTE-Tomek and SMOTE-ENN, in combination with two feature selection strategies: MI and SHAP values.

Table 7. Experiment Three results for models using MI feature selection and SMOTE-Tomek for class balancing, displaying evaluation metrics for class 0.0 (non-default) and class 1.0 (default).

MI Selected Features SMOTE-Tomek
	LR	RF	XGBoost	Stacked
Accuracy	0.78	0.78	0.74	0.73
Precision (0.0 | 1.0)	0.93 | 0.15	0.94 | 0.16	0.94 | 0.14	0.93 | 0.13
Recall (0.0 | 1.0)	0.82 | 0.36	0.81 | 0.41	0.77 | 0.41	0.76 | 0.40
F1-score (0.0 | 1.0)	0.87 | 0.21	0.87 | 0.23	0.84 | 0.21	0.84 | 0.20
Precision–Recall AUC	0.14	0.15	0.13	0.29
ROC-AUC	0.64	0.67	0.63	0.63

presents the performance of models using MI-selected features with SMOTE-Tomek. Among these, the Random Forest classifier achieved the highest ROC-AUC (0.67) and Precision–Recall AUC (0.15), indicating strong overall discriminative ability. However, the Stacked classifier, despite a slightly lower overall accuracy (0.73), exhibited the highest recall for the minority class (0.40), suggesting a better capability in identifying default cases. This trade-off implies that while Random Forest may be more balanced overall, the Stacked model provides greater sensitivity to minority class detection.

Table 8. Experiment Three results for models using SHAP feature selection and SMOTE-Tomek for class balancing, displaying evaluation metrics for class 0.0 (non-default) and class 1.0 (default).

SHAP Selected Features SMOTE-Tomek
	LR	RF	XGBoost	Stacked
Accuracy	0.80	0.81	0.82	0.85
Precision (0.0 | 1.0)	0.94 | 0.18	0.94 | 0.19	0.94 | 0.20	0.94 | 0.24
Recall (0.0 | 1.0)	0.84 | 0.40	0.85 | 0.39	0.86 | 0.38	0.89 | 0.40
F1-score (0.0 | 1.0)	0.89 | 0.25	0.89 | 0.25	0.90 | 0.26	0.91 | 0.30
Precision–Recall AUC	0.16	0.18	0.20	0.34
ROC-AUC	0.69	0.69	0.69	0.71

shows results for models using SHAP-selected features with SMOTE-Tomek. Here, the Stacked classifier clearly outperformed other models, achieving the highest accuracy (0.85), ROC-AUC (0.71), and Precision–Recall AUC (0.34). It also recorded the best recall (0.40) and F1-score (0.30) for the minority class, highlighting its effectiveness in capturing rare default instances. These findings underscore the synergy between SHAP-based feature selection, SMOTE-Tomek resampling, and model ensembling.

Table 9. Experiment Three results for models using MI feature selection and SMOTE-ENN for class balancing, displaying evaluation metrics for class 0.0 (non-default) and class 1.0 (default).

MI Selected Features SMOTE-ENN
	LR	RF	XGBoost	Stacked
Accuracy	0.78	0.81	0.74	0.78
Precision (0.0 | 1.0)	0.93 | 0.15	0.94 | 0.18	0.94 | 0.14	0.93 | 0.15
Recall (0.0 | 1.0)	0.82 | 0.36	0.85 | 0.36	0.77 | 0.42	0.82 | 0.35
F1-score (0.0 | 1.0)	0.87 | 0.21	0.89 | 0.24	0.85 | 0.21	0.87 | 0.21
Precision–Recall AUC	0.14	0.16	0.14	0.28
ROC-AUC	0.64	0.68	0.64	0.64

presents the outcomes for models using MI-selected features with SMOTE-ENN. The Random Forest model again achieved the highest accuracy (0.81), along with solid ROC-AUC (0.68) and PR AUC (0.16). However, the Stacked classifier outperformed in terms of minority class metrics, achieving a recall of 0.35 and an F1-score of 0.21. This suggests that while Random Forest offers stronger overall performance, the Stacked classifier continues to strike a better balance between detecting both classes, especially the minority.

Table 10. Experiment Three results for models using SHAP feature selection and SMOTE-ENN for class balancing, displaying evaluation metrics for class 0.0 (non-default) and class 1.0 (default).

SHAP Selected Features SMOTE-ENN
	LR	RF	XGBoost	Stacked
Accuracy	0.84	0.82	0.82	0.83
Precision (0.0 | 1.0)	0.94 | 0.20	0.94 | 0.19	0.94 | 0.20	0.94 | 0.21
Recall (0.0 | 1.0)	0.88 | 0.32	0.86 | 0.37	0.86 | 0.38	0.87 | 0.38
F1-score (0.0 | 1.0)	0.91 | 0.25	0.89 | 0.25	0.90 | 0.26	0.91 | 0.27
Precision–Recall AUC	0.16	0.17	0.19	0.32
ROC-AUC	0.68	0.69	0.69	0.71

summarizes results for models using SHAP-selected features with SMOTE-ENN. The Stacked classifier once again delivered the most consistent and well-rounded performance, achieving an ROC-AUC of 0.71 and PR-AUC of 0.32, along with a high accuracy (0.83), recall (0.38), and F1-score (0.27) for the minority class. These results confirm the effectiveness of combining SHAP-based feature selection with SMOTE-ENN to enhance both predictive accuracy and sensitivity to defaults.

Overall, the findings from Experiment Three indicate that models using SHAP-selected features consistently outperform those using MI-selected features across both SMOTE-Tomek and SMOTE-ENN resampling strategies. Among classifiers, the Stacked model demonstrated the highest and most balanced performance across evaluation metrics, reinforcing its robustness in handling imbalanced data scenarios. These results suggest that the combination of SHAP-based features, advanced resampling techniques, and ensemble modeling provides the most effective framework for predicting auto loan defaults.

4.4. Discussion

This study offers valuable insights into the predictive modeling of auto loan defaults by systematically evaluating the combined effects of machine learning algorithms, feature selection methods, and resampling strategies. The results from the three experiments emphasize the importance of integrating explainable feature selection with robust sampling techniques to significantly improve model performance in detecting default risk.

A key finding is the consistent superiority of SHAP-selected features over those chosen by Mutual Information across all experimental settings. SHAP values provided deeper interpretability by capturing complex, non-linear relationships among variables, offering a better understanding of their influence on model predictions. This outcome supports our hypothesis that model-agnostic, explainability-driven approaches are more effective in high-dimensional, imbalanced contexts, where capturing feature interactions is critical for accurate prediction. In terms of predictive performance, the Stacked classifier emerged as the most robust model, especially when combined with SHAP-based features and advanced resampling techniques like SMOTE-Tomek and SMOTE-ENN. This underscores the effectiveness of ensemble learning in managing class imbalance and enhancing the identification of minority class instances, a particularly important capability in financial risk scenarios, where false negatives can have costly consequences.

Relative to prior work in the domain of credit risk modeling, this study introduces a more holistic and interpretable framework, while earlier studies, such as Abedin (2023), employed WSMOTE-ensemble methods, and Zhao (2024) proposed the SH-SENN hybrid technique to address class imbalance, they did not investigate the role of SHAP-based feature selection or the potential of Stacked ensemble classifiers. Our findings extend this body of literature by demonstrating that coupling explainable feature selection with ensemble models and targeted resampling can yield superior predictive performance and deeper insights into feature importance.

An unexpected revealing observation was the relatively poor performance of models trained with MI-selected features, even when paired with advanced sampling techniques. This suggests that MI, while effective in capturing general feature relevance, lacks the sensitivity to capture intricate interactions and conditional dependencies in imbalanced datasets. This limitation highlights the need for more advanced, model-informed feature selection methods when working with complex financial data.

The practical implications of these findings are substantial. For financial institutions aiming to improve risk assessment and decision-making, the proposed framework, combining SHAP-based feature selection, ensemble learning, and resampling, offers a powerful, data-driven solution. By adopting such methods, lenders can more accurately predict loan defaults, allocate resources more effectively, and mitigate credit risk. Moreover, this approach is adaptable to other domains of credit risk modeling, such as mortgage or credit card default prediction, offering a foundation for broader applications in financial risk management.

Nevertheless, the study is not without limitations. First, the dataset used was relatively small and sourced from a single platform, which may limit the external validity and generalizability of the findings. Second, while SHAP-based methods improved model interpretability and performance, their computational cost may pose challenges for real-time or large-scale application. To address this trade-off, we note that approximate or model-specific variants of SHAP, such as TreeSHAP, can substantially reduce computational burden while preserving interpretability, making these methods more feasible for deployment in real-time financial risk prediction. Third, SHAP values were computed using the XGBoost model rather than the specific models to which they were applied, such as Logistic Regression and the Stacked classifier.

5. Conclusions and Future Work

This study demonstrates the value of combining advanced machine learning techniques, particularly SHAP-based feature selection, with robust resampling strategies like SMOTE-Tomek and SMOTE-ENN to improve the prediction of auto loan default risk. The consistently strong performance of the Stacked classifier across multiple experimental settings highlights its robustness in handling class imbalance and accurately identifying default risk. From an academic perspective, this research contributes a comprehensive and interpretable modeling framework that bridges feature relevance, data rebalancing, and ensemble learning to improve predictive performance. It advances the literature on credit risk modeling by demonstrating how explainable AI techniques like SHAP can enhance model transparency, offering a data-driven foundation for more accountable decision-making processes in risk analysis. From a practical standpoint, the proposed approach provides financial institutions with a scalable, data-informed methodology to enhance auto loan risk assessment. The integration of explainability and predictive precision supports more strategic lending decisions and strengthens credit evaluation pipelines. By applying these techniques, lenders can proactively identify high-risk borrowers, optimize approval processes, and mitigate potential losses.

Looking forward, future research should focus on validating these methods across varied institutional settings, geographic regions, and economic conditions. Additional exploration of combining SHAP-based feature selection methods and advanced deep learning architectures could further refine predictive accuracy and adaptability. Building on this foundation, continued work can help bridge the gap between theoretical innovation and real-world application, contributing to more resilient and equitable financial risk management systems.