Cryptocurrency Market Dynamics: Copula Analysis of Return and Volume Tails

Abstract

This paper investigates the dependence structure between returns and trading volumes for five major cryptocurrencies: Bitcoin, Cardano, Ethereum, Litecoin, and Ripple. Using a copula-based framework, we focus on a mixture of the Joe copula and its 90-degree rotation to capture asymmetric relationships, especially in the tails of the distribution. Our findings reveal significant upper and lower–upper tail dependencies, suggesting that extreme trading volumes are associated with both positive and negative return extremes. The results confirm a nonlinear and asymmetric volume–return relationship, which traditional linear models fail to capture.

1. Introduction

The rise in cryptocurrencies stands out as one of the most significant financial innovations of the past decade. Their futuristic characteristics and highly volatile price movements have garnered substantial media attention, as well as interest from regulators and researchers. Many cryptocurrencies are known for their price volatility, with notable fluctuations marked by sharp increases and dramatic crashes in recent years. The volumes of cryptocurrencies can be highly volatile, too, experiencing significant fluctuations.

A positive association between returns and volume is usually detected for many financial assets. This implies a high volume when the price is increasing (positive returns) and a low volume when the price is decreasing (negative returns). However, while cryptocurrency returns do share some similarities with traditional financial asset returns, they also exhibit unique characteristics that set them apart. A common point with traditional financial assets is the offer of potential returns as a premium for risk. Second, both cryptocurrency and traditional financial markets can be affected by investor sentiment, news, and macroeconomic factors, leading to fluctuations in asset prices. Finally, returns in both markets show volatility. However, the main difference refers to the level of volatility because cryptocurrency returns display a much higher level. Moreover, the market structure is another remarkable difference. Cryptocurrencies operate in markets without the features of centralization and regularization; traditional assets are traded in stock exchange. The unregulated nature of the markets of cryptocurrencies can lead to greater speculation and extremely erratic price movements. The occurrence of extreme returns and bubbles further distinguishes cryptocurrencies from traditional assets.

Across both traditional and cryptocurrency markets, the empirical literature demonstrates that the volume–return relationship is nonlinear, quantile-dependent, and asymmetrically structured, particularly around extreme events. Volume not only reflects trading activity but also encapsulates informational content, acting as a signal of investor sentiment, market stress, and structural shifts. As such, modern studies increasingly rely on advanced econometric techniques, such as quantile regression, copula models, extreme value theory, and threshold models, to capture these dynamics with greater precision.

In this study, we investigate the relationship between returns and trading volumes for the most widely traded cryptocurrencies. To capture the complex dependence between these variables, we employ copula functions, a flexible statistical tool well suited for modeling nonlinear associations. In particular, we utilize rotated copulas to account for both the link between low returns and high volumes, and between high returns and high volumes. Our results reveal that large trading volumes are often associated with either very low or very high returns, highlighting a nonlinear relationship that traditional statistical methods fail to capture.

Although the literature on cryptocurrency markets has expanded rapidly, most contributions rely on linear or quantile-based frameworks and rarely examine the structure of tail dependence between returns and trading volumes. In addition, cross-tail phenomena—such as the association between extreme losses and volume spikes—have received limited attention. To address this gap, we apply a mixture of the Joe copula and its 90° rotation, a framework capable of capturing both upper–upper and lower–upper dependencies. This approach enables us to quantify the probability that extreme return events coincide with abnormal trading activity. By documenting significant and asymmetric tail dependence across five major cryptocurrencies, our study advances the understanding of the nonlinear dynamics of returns and volumes, with direct implications for risk management, trading strategies, and the assessment of stability in highly volatile and weakly regulated markets.

The paper is structured as follows: Section 2 reviews the relevant literature; Section 3 describes the data and methodological framework; and Section 4 presents the empirical results. Finally, Section 5 offers concluding remarks and discusses potential directions for future research.

2. Literature

The relationship between trading volume and asset returns has been the subject of extensive empirical scrutiny in both traditional financial markets and, more recently, cryptocurrency markets. The body of research reflects a progression from classical linear models to more nuanced frameworks that incorporate nonlinearity, extreme value behavior, and distributional asymmetries. Early foundational work by Chen et al. (2001) examines the role of trading volume in forecasting negative skewness in returns, associating volume shifts with crash risk through cross-sectional regressions. This sets the stage for subsequent studies exploring the predictive content of volume beyond basic correlations. Ané and Ureche-Rangau (2008) critically assess the Bivariate Mixture of Distributions Hypothesis (BMM), which posits a common latent factor driving both volume and volatility. Their findings reveal a disconnect in the long-run dynamics of the two variables, although short-term linkages persist. Building on this, Chuang et al. (2009) introduced quantile regression to uncover how volume and returns interact across the distribution, finding a V-shaped causality: negative in lower quantiles and positive in upper quantiles, indicating that high trading volumes increase return dispersion and signal higher volatility. Similar methodologies were applied by Gebka and Wohar (2013) in Pacific Basin stock markets, confirming nonlinear causality patterns consistent with those found in developed markets. Chiang et al. (2010), by integrating realized volatility measures and nonlinear Granger tests, find no significant linear causality but robust bidirectional nonlinear dependence between volume and volatility. Research into extreme market behaviors by Longin and Pagliardi (2016) applied extreme value theory (POT and Gumbel copula) to show that price extremes are often accompanied by extreme volumes, further underscoring the need for non-Gaussian modeling approaches. Finally, Kao et al. (2024) analyzed threshold asymmetries, revealing that the effect of trading volume on both returns and volatility is contingent on whether volume crosses certain critical thresholds.

The distinctive microstructure of the cryptocurrency market and the extreme volatility of crypto assets have led to an expansion of the volume–return literature into this domain. Naeem et al. (2020) and Ning et al. (2009) (for East Asian equities) explored tail dependence via copula methods, identifying strong co-movements between extreme returns and extreme volumes. Bouri et al. (2019) confirmed that in cryptocurrency markets, volume serves as a strong predictor for both returns and volatility, particularly during periods of market stress. In line with this, Chan et al. (2022) applied extreme value theory to high-frequency crypto data, highlighting that extreme returns are tightly linked to extreme volume episodes. Hau et al. (2021) offered further evidence that transaction activity, particularly in the tails of the distribution, holds predictive power for future price movements in Bitcoin, emphasizing the information content of user behavior. Adding a temporal dimension, Yarovaya et al. (2022) investigated intraday volume–return interactions, showing that these dynamics differ not only by time of day but also by type of cryptocurrency, suggesting a heterogeneity in volume sensitivity based on asset characteristics.

While the existing literature underscores nonlinear, quantile-dependent, and asymmetric relationships between volume and returns, most of it implicitly assumes market structures similar to traditional equities. However, cryptocurrency markets differ substantially in both institutional design and behavioral dynamics. Unlike regulated stock exchanges, cryptocurrency markets operate in a largely decentralized, less transparent environment, with limited investor protection and governance structures. This institutional distinction shapes market behavior, amplifying the role of speculation, sentiment, and coordination failures (Hairudin et al. 2020). Moreover, behavioral aspects—such as herding, momentum trading, and heterogeneous user profiles—are more pronounced in cryptocurrency markets compared to traditional finance, reflecting a distinctive user base characterized by retail dominance and rapid information diffusion (Aspembitova et al. 2021).

Parallel to these institutional and behavioral factors, an expanding strand of research emphasizes the presence of systematic risk factors unique to cryptocurrencies. Liu et al. (2022) demonstrated that, beyond Bitcoin-specific shocks, common factors akin to traditional asset pricing models govern returns across the crypto universe. Extending this perspective, Lan and Frömmel (2025) identified both market-wide and idiosyncratic risk factors that shape cryptocurrency pricing, pointing to a risk–return structure that cannot be entirely captured by analogies with equities or commodities.

3. Copula Functions

To study the possibly nonlinear relationship between returns and volumes in these five cryptocurrencies, we use one of the most powerful methodologies for analyzing the dependence structure between two random variables, the copula function. Copula allows for a flexible modeling approach that accommodates both linear and nonlinear relationships.

Let X and Y be two random variables with respective marginal distribution functions $F_X\left(x\right)$ and $F_Y\left(y\right)$. Define the transformed variables as $U_X=F_X\left(X\right)$ and $U_Y=F_Y\left(Y\right)$. According to Sklar’s Theorem, the joint distribution function $H(x,y)$ of the pair $(X,Y)$ can be represented through a copula C as follows:

$$H(x,y)=C\left(F_X\left(x\right),F_Y\left(y\right)\right)=C(U_x,U_y).$$

In addition, employing specific classes of copula functions enables the evaluation of tail dependence, an important concept in the study of joint extreme events. In particular, members of the Archimedean family of copulas are widely used for this purpose.

The lower–lower tail dependence coefficient, quantifying the probability of extremely low values of variable Y, given extremely low values of variable X, is given as follows:

$${\lambda }_{LL}=\underset{u\to 1^{-}}{lim}\mathbb{P}(U_y<1-u|U_x<1-u)$$

It is easy to show that the above conditional probability can be expressed in terms of copula, that is

$${\lambda }_{LL}=\underset{u\to 1^{-}}{lim}{\displaystyle \frac{C(1-u,1-u)}{1-u}}.$$

The upper–upper tail dependence coefficient, indicating the probability of extremely high values of variable Y conditionally on extremely high values of variable X, is similarly defined as:

$${\lambda }_{UU}=\underset{u\to 1^{-}}{lim}\mathbb{P}(U_y\ge u|U_x\ge u)$$

that is

$${\lambda }_{UU}=\underset{u\to 1^{-}}{lim}{\displaystyle \frac{1-2u+C(u,u)}{1-u}}.$$

These measures play a crucial role in risk management and other fields where extreme comovements are of interest.

Nevertheless, it is essential not to disregard alternative forms of tail dependence that are empirically significant in some contexts. The lower–upper tail dependence coefficient given by

$${\lambda }_{LU}=\underset{u\to 1^{-}}{lim}\mathbb{P}(U_y>u|U_x<1-u)$$

or, in terms of copula functions, as

$${\lambda }_{LU}=\underset{u\to 1^{-}}{lim}{\displaystyle \frac{1-u-C(1-u,u)}{1-u}},$$

quantifies the probability of extremely high values of variable Y and extremely low values of variable X.

Finally, the upper–lower tail dependence coefficient,

$${\lambda }_{UL}=\underset{u\to 1^{-}}{lim}\mathbb{P}(U_y<1-u|U_x>u)$$

or

$${\lambda }_{UL}=\underset{u\to 1^{-}}{lim}{\displaystyle \frac{1-u-C(u,1-u)}{1-u}},$$

is defined analogously, by interchanging the roles of the two variables.

A popular copula function is the so-called Joe copula Joe (1997), a member of the Archimedean family of copulas. It is particularly suitable for capturing asymmetric tail dependence, especially strong upper–upper tail dependence and weak or null lower tail dependence.

As with all Archimedean copulas, the Joe copula is defined via a generator function $\varphi \left(t\right)$ that is completely monotonic in $[0,1]$. The generator for the Joe copula with parameter $\theta \ge 1$ is given as follows:

$$\varphi \left(t\right)=-ln\left[1-{(1-t)}^{\theta }\right],t\in [0,1].$$

Its pseudo-inverse (used to construct the copula) is as follows:

$${\varphi }^{-1}\left(s\right)=1-{\left(1-e^{-s}\right)}^{1/\theta },s\ge 0.$$

Using the generator, the bivariate Joe copula $C_{Joe}(u_x,u_y)$ is expressed as follows:

$$C_{Joe}(u_x,u_y)=1-{\left[{\left(1-u_x\right)}^{\theta }+{\left(1-u_y\right)}^{\theta }-{\left(1-u_x\right)}^{\theta }{\left(1-u_y\right)}^{\theta }\right]}^{1/\theta }.$$

It exhibits upper–upper tail dependence, making it suitable for applications where simultaneous extremely high values of variables are more likely. In particular, when $\theta >1$

$${\lambda }_{UU}=2-2^{1/\theta },$$

and

$${\lambda }_{LL}=0.$$

Furthermore, to have a more accurate selection process, the corresponding rotated versions can also be considered. In copula modeling, rotations are employed to generate copulas that can capture different forms of tail dependence, particularly when the original copula is asymmetric. Given a copula $C(u_x,u_y)$, one can construct its rotated versions to modify the direction of dependence.

There are three primary rotations used in the bivariate case:

• A 90-degree rotation,

  $$C^{\left(90\right)}(u_x,u_y)=u_y-C(1-u_x,u_y);$$
• A 180-degree rotation (which corresponds to the survival copula),

  $$C^{\left(180\right)}(u_x,u_y)=u_x+u_y-1+C(1-u_x,1-u_y);$$
• A 270-degree rotation,

  $$C^{\left(270\right)}(u_x,u_y)=u_x-C(u_x,1-u_y).$$

These transformations enable the modeling of negative dependence and the capturing of lower tail dependence if the original copula only has upper–upper tail dependence (or vice versa).

The Joe copula is known for exhibiting upper–upper tail dependence, and no lower–lower tail dependence and no cross-tail dependence (lower–upper or upper–lower) is allowed. Therefore, to model the lower–lower or the cross-tail dependence, one has to rotate the Joe copula. The $180$ rotation ensures a non-null lower–lower tail dependence, while the $90$ and $270$ rotations involve, respectively, non-null ${\lambda }_{LU}$ and ${\lambda }_{UL}$.

Moreover, in copula modeling, a mixture of copulas is used to capture more complex dependence structures by combining two or more copulas, which can also be different from each other. Let $C_1(u_x,u_y)$ and $C_2(u_x,u_y)$ be two bivariate copulas. A convex combination (or mixture) is defined as follows:

$$C_M(u_x,u_y)=w_1{C}_1(u_x,u_y)+w_2{C}_2(u_x,u_y)$$

with the constraint $w_1+w_2<1$. This formulation allows the resulting copula $C_M(u_x,u_y)$ to exhibit characteristics inherited from both components. Mixture copulas are particularly useful when the data exhibit asymmetric or heterogeneous dependence patterns, such as different behaviors in the upper and lower tails.

In the present application, we will use a mixture of the original Joe copula and its 90-degree rotation,

$$C_{\mathrm{Joe}}^{\left(90\right)}(u_x,u_y)=u_y-C_{\mathrm{Joe}}(1-u_x,u_y).$$

The mixture, defined as follows:

$$C_M(u_x,u_y)=w_1{C}_{\mathrm{Joe}}(u_x,u_y)+w_2{C}_{\mathrm{Joe}}^{\left(90\right)}(u_x,u_y),$$

(1)

accomodates upper–upper and lower–upper tail dependence.

4. Empirical Application

The empirical application we describe can be summarized in the following steps:

• Data collection and preprocessing
  • Downloading daily prices and volumes from Yahoo Finance (2018–2024);
  • Transformation into log-returns and log-volumes;
  • Descriptive statistics.
• Modeling returns and volumes
  • Returns: GARCH(1,1)-type models with Student-t errors;
  • Volumes: SARIMA with seasonal differencing + GARCH-type structure;
  • Filtering and residual extraction;
  • Standardized residuals checked for white noise with Ljung–Box tests.
• Copula modeling: estimate and interpretation
  • Estimation of empirical distribution functions;
  • Fitting a mixture copula combining the Joe copula and its 90° rotation;
  • Goodness-of-fit assessment with the Cramér–von Mises test;
  • Computation of ${\lambda }_{UU}$ and ${\lambda }_{LU}$ tail dependence coefficients;
  • Economic interpretation of the results.

4.1. Data Collection and Preprocessing

We focused on the five most popular cryptocurrencies: Bitcoin, Cardano, Ethereum, Litecoin, and Ripple. For each of them, we collected from Yahoo Finance daily percentage returns, computed as logarithmic differences in the prices, and volumes in the period from 1 January 2018, to 30 April 2025 for a total of 2677 observations. To reduce the variability in trading volumes, we transformed the series by taking natural logarithms and conducted the analysis using log-volumes.

Bitcoin is the first and most popular cryptocurrency, launched in 2009 by the pseudonymous developer Satoshi Nakamoto. It introduced the idea of decentralized digital currency based on blockchain technology and has a solid position as a benchmark asset in the crypto market. Ethereum, launched in 2015, revolutionized the blockchain space by introducing smart contracts. Founded by Charles Hoskinson, Cardano is a third-generation blockchain platform focusing on scalability, sustainability, and formal academic research. Created in 2011 by Charlie Lee, Litecoin offers faster block generation times and lower transaction fees. Finally, Ripple is both a digital currency (XRP) and a real-time gross settlement system designed to facilitate cross-border payments for financial institutions. Unlike most cryptocurrencies, Ripple does not use a proof-of-work or proof-of-stake system. These five cryptocurrencies represent a wide range of blockchain applications, from decentralized finance and programmable contracts (Ethereum, Cardano) to fast transactions (Litecoin), institutional use cases (Ripple), and store of value (Bitcoin). The descriptive statistics of returns and log-volumes are reported, respectively, in

Table 1. Descriptive statistics of returns: minimum, mean, median, maximum, standard deviation, skewness, and kurtosis.

Cryptocurrency	Min	Mean	Median	Max	Std. Dev.	Skewness	Kurtosis
Bitcoin	−46.47	0.07	0.08	17.18	3.53	−0.96	16.97
Cardano	−50.36	0.00	−0.03	53.84	5.49	0.29	11.83
Ethereum	−55.07	0.03	0.06	23.07	4.56	−0.93	14.11
Litecoin	−44.91	−0.04	0.03	29.06	4.87	−0.53	11.52
Ripple	−55.05	0.00	−0.05	54.86	5.51	0.39	19.33

and

Table 2. Descriptive statistics of log-volumes: minimum, mean, median, maximum, standard deviation, skewness, and kurtosis.

Cryptocurrency	Min	Mean	Median	Max	Std. Dev.	Skewness	Kurtosis
Bitcoin	21.80	23.78	23.92	26.58	0.77	−0.54	2.85
Cardano	15.94	19.68	19.65	23.68	1.49	0.04	2.52
Ethereum	20.67	23.01	23.15	25.25	0.88	−0.53	2.76
Litecoin	18.61	20.75	20.49	23.61	1.09	0.32	1.91
Ripple	18.72	21.19	21.10	24.67	0.96	0.39	3.40

.

4.2. Modeling Returns and Volumes

The selection of the copula function to be applied to the variables returns and volumes is based on different steps. First, we filter the two time series.1

For the returns time series $y_t$, we estimated a simple GARCH(1,1),

$$\begin{array}{ccc}\hfill y_t& =& \mu +{\sigma }_t{\eta }_t\hfill \\ \hfill {\sigma }_t^2& =& \omega +\alpha {(y_{t-1}-\mu )}^2+\beta {\sigma }_{t-1}^2\hfill \end{array}$$

with errors ${\eta }_t\sim iid(0,1)$ following a Student’s t distribution (only Bitcoin returns required a skew Student’s t distribution for the errors). The list of the models can be read in

Table 3. Estimated models related to cryptocurrencies’ returns.

Cryptocurrency	Returns Model
Bitcoin	GARCH(1,1)-std
Cardano	GARCH(1,1)-std
Ethereum	GARCH(1,1)-std
Litecoin	GARCH(1,1)-std
Ripple	GARCH(1,1)-std

, while

Table 4. p-value of the Ljung–Box test with $m=1$, $m=7$ and $m=14$, applied to standardized residuals (${\eta }_t$) and squared standardized residuals (${\eta }_t^2$) for the selected model.

	${\mathit{\eta }}_{\mathit{t}}$			${\mathit{\eta }}_{\mathit{t}}^2$
$\mathbf{Cryptocurrency}$	$\mathit{m}=\mathbf{1}$	$\mathit{m}=\mathbf{7}$	$\mathit{m}=\mathbf{14}$	$\mathit{m}=\mathbf{1}$	$\mathit{m}=\mathbf{7}$	$\mathit{m}=\mathbf{14}$
Bitcoin	0.41	0.20	0.32	0.85	0.82	0.97
Cardano	0.63	0.34	0.23	0.68	0.88	0.98
Ethereum	0.88	0.02	0.03	0.69	0.54	0.52
Litecoin	0.77	1.00	0.95	0.59	0.66	0.83
Ripple	0.72	0.74	0.92	0.86	1.00	1.00

reports the p-values of the Ljung–Box test,

$$Q_{LB}=T(T+2)\sum _{k=1}^m{\displaystyle \frac{{\widehat{\rho }}_k^2}{T-k}},$$

where T is the length of the time series, applied to the standardized residuals ${\eta }_t$ and squared standardized residuals ${\eta }_t^2$ with $m=1,7,14$. The high p-values generally indicate that the selected models are appropriate. The only exception is observed for Ethereum at lags 7 and 14, where the p-values fall below the 0.05 threshold, yet remain above 0.01.

Modeling the volume series $v_t$ proves to be particularly challenging due to its complex structure. As a first step, we take the logarithm of the volumes to mitigate their high variability. Next, given the evident nonstationarity of the log-transformed series, we compute first differences. An inspection of the autocorrelation function (ACF) of the differenced series reveals a nonstationary weekly seasonal pattern, which necessitates the application of seasonal differencing. Despite this, some residual seasonal structure remains, which is addressed in the modeling step. Additionally, the double-differenced series exhibits heteroskedasticity.

To accommodate all these characteristics, we adopt an ARIMA model with the seasonal component. Here, we report the SARIMA$(p,1,q)\times {(P,1,Q)}_s$,

$${\varphi }_p\left(L\right){\Phi }_P\left(L^s\right)\Delta {\Delta }_s{v}_t={\theta }_q\left(L\right){\Theta }_Q\left(L^s\right){ϵ}_t$$

where ${\varphi }_p\left(L\right)$ and ${\Phi }_P\left(L^s\right)$ are the non-seasonal and seasonal autoregressive components of orders p and P, respectively, ${\theta }_q\left(L\right)$ and ${\Theta }_Q\left(L^s\right)$ are the non-seasonal and seasonal moving average components of orders q and Q, respectively, and the innovation ${ϵ}_t$ follows a GARCH-type structure.

In light of the complexity involved, the analysis is carried out in two stages: first, we estimate a seasonal ARIMA model; then, once the residuals are confirmed to be white noise in mean, we model the conditional variance using a GARCH-type specification.

Table 5. Estimated models related to cryptocurrencies’ volumes.

Cryptocurrency	Volumes Model
Bitcoin	SARIMA(3,1,2)×(0,1,1)7-eGARCH(2,1)-sstd
Cardano	SARIMA(1,1,3)×(0,1,1)7-GARCH(1,1)-sstd
Ethereum	SARIMA(1,1,3)×(0,1,1)7-GARCH(1,2)-sstd
Litecoin	SARIMA(1,1,1)×(0,1,1)7-eGARCH(1,2)-sstd
Ripple	SARIMA(1,1,2)×(0,1,1)7-GARCH(1,1)-norm

provides a specification of the orders of the model as well as the distribution of the GARCH errors ${\eta }_t$. Despite the complexity of the adopted approach, the results are excellent, as the p-values of the Ljung–Box tests applied to ${\eta }_t$ and ${\eta }_t^2$ consistently exceed 0.05 (

Table 6. p-value of the Ljung–Box test with $m=1,7,14$ applied to standardized residuals (${\eta }_t$) and squared standardized residuals (${\eta }_t^2$) for the selected model.

	${\mathit{\eta }}_{\mathit{t}}$			${\mathit{\eta }}_{\mathit{t}}^2$
Cryptocurrency	$\mathit{m}=\mathbf{1}$	$\mathit{m}=\mathbf{7}$	$\mathit{m}=\mathbf{14}$	$\mathit{m}=\mathbf{1}$	$\mathit{m}=\mathbf{7}$	$\mathit{m}=\mathbf{14}$
Bitcoin	0.19	0.13	0.30	0.71	0.54	0.62
Cardano	0.91	0.08	0.12	0.35	0.72	0.49
Ethereum	0.37	0.20	0.32	0.08	0.22	0.51
Litecoin	0.96	0.35	0.79	0.22	0.30	0.37
Ripple	0.50	0.62	0.33	0.67	0.96	1.00

).

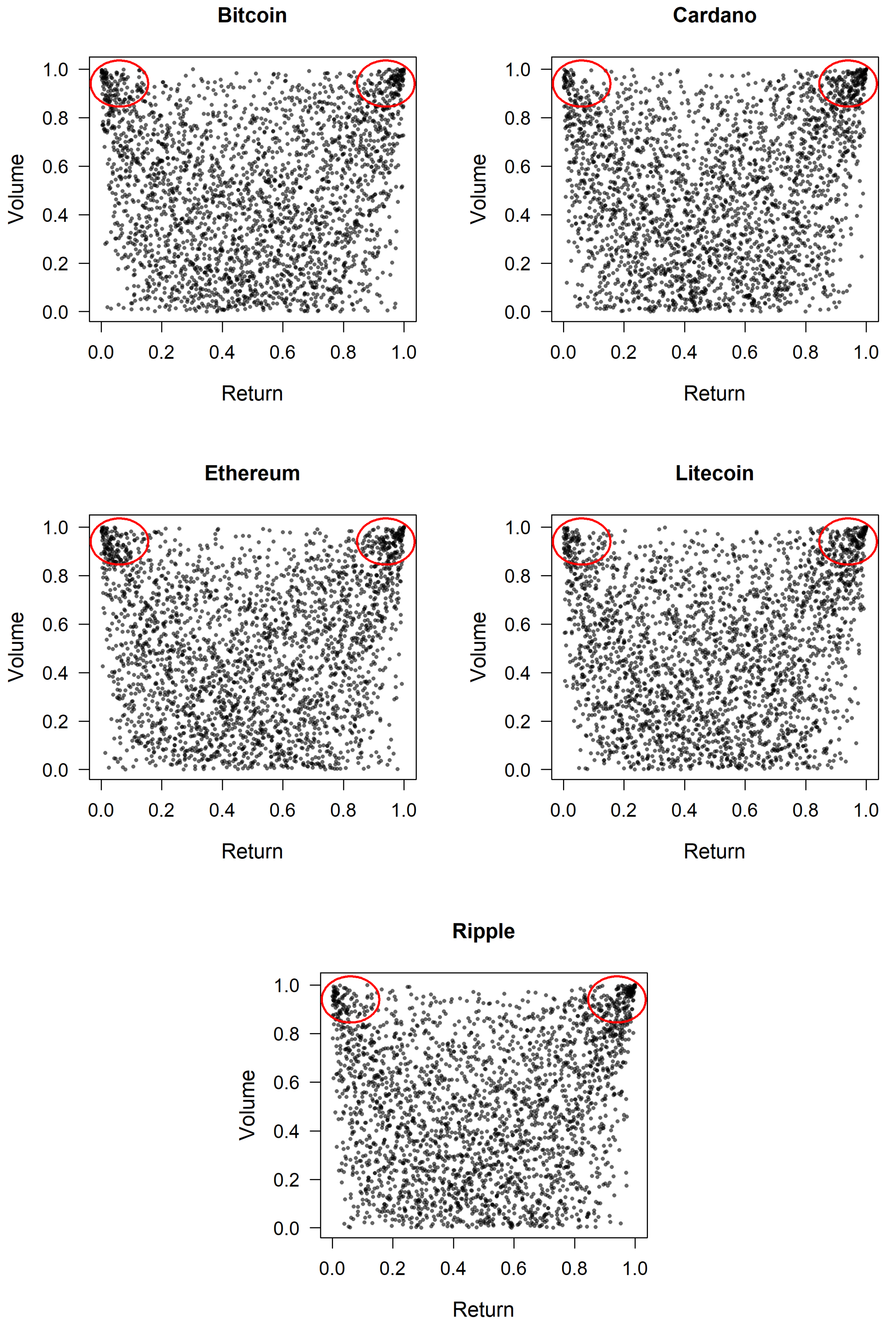
Finally, after computing the empirical distribution function $u_x$ and $u_y$ of the two filtered series, that is the residuals of the two models, we can draw the plots for the five cryptocurrencies that can be visualized in Figure 1. What we can see is a recurring pattern in the literature, that is the strong link between high trading volumes and extreme returns—both positive and negative. This relationship reflects the tendency of large price movements to occur alongside elevated trading activity (Bouri et al. 2019; Naeem et al. 2020).

4.3. Copula Modeling: Estimation and Interpretation

To model this relationship using a nonlinear approach, we employ copula functions, which allow us to capture the dependence structure between extreme returns and trading volumes. Specifically, we require a copula that can accommodate both upper–upper tail dependence—reflecting the co-occurrence of high returns and high volumes—and lower–upper tail dependence to account for the association between low returns and high volumes. For this purpose, we adopt the mixture of copulas defined in (1).

Table 7. Joe–Joe90° mixture copula: log-likelihood ($\ell \ell$), parameter estimates (${\theta }_1$, ${\theta }_2$), mixture weights ($w_1$, $w_2$), upper–upper tail dependence (${\lambda }_{UU}$), lower–upper tail dependence (${\lambda }_{LU}$), Kendall’s $\tau$, and p-value of the Cramér–von Mises (CVM) goodness-of-fit test.

Cryptocurrency	$\mathit{\ell }\mathit{\ell }$	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{w}}_1$	${\mathit{w}}_2$	${\mathit{\lambda }}_{\mathit{UU}}$	${\mathit{\lambda }}_{\mathit{LU}}$	$\mathit{\tau }$	CVM (p-Value)
Bitcoin	200.6	1.59	1.51	0.58	0.42	0.26	0.17	0.05	0.06
Cardano	241.3	1.62	1.46	0.73	0.27	0.34	0.15	0.13	0.05
Ethereum	232.0	1.70	1.56	0.56	0.44	0.28	0.19	0.05	0.07
Litecoin	242.4	1.63	1.53	0.70	0.30	0.33	0.13	0.12	0.08
Ripple	262.8	1.69	1.51	0.68	0.32	0.34	0.13	0.12	0.05

reports the estimates for the mixture of Joe and 90° rotated Joe copulas, a strategic choice for modeling the relationship in a highly flexible way and capturing extreme co-movements between returns and volumes.

The mixing weights suggest a relatively balanced contribution from both copulas in all the cryptocurrencies and the estimated parameters imply that all cryptocurrencies display non-zero upper–upper tail dependence (${\lambda }_{UU}$) and lower–upper tail dependence (${\lambda }_{LU}$). The strength of the two measures of tail dependence is generally moderate with ${\lambda }_{UU}$ ranging from 0.26 to 0.34 and ${\lambda }_{LU}$ from 0.13 to 0.19. This implies that, in roughly one-quarter to one-third of cases where an extreme return occurs, it is accompanied by an extreme trading volume episode in the same direction (put differently, the probability of observing a simultaneous high return–high volume event is around 30%). On the other hand, the probability of a low return–high volume event is closer to 15%. These magnitudes are economically meaningful when compared with traditional stock markets, where the empirical literature typically finds much weaker tail dependence (e.g., in the context of traditional equity markets, Longin and Pagliardi (2016) report that return–volume correlation decays sharply in the extreme tails, tending toward negligible levels—a finding that underscores the stronger tail dependence we observe in cryptocurrency markets). The data confirm a general asymmetry with ${\lambda }_{UU}>{\lambda }_{LU}$ in all assets, suggesting that extreme positive returns are more likely to coincide with high volumes than extreme losses. In particular, Cardano and Ripple show the highest values of ${\lambda }_{UU}$ at 0.34, indicating stronger co-movement in high return-high volume events. For the lower–upper tail dependence (${\lambda }_{LU}$), representing the co-occurrence of low returns and high volumes, Ethereum has the highest value at 0.19, while Litecoin and Ripple show the lowest (0.13), suggesting varying intensity of panic trading or sell-off volume spikes.

The measure of overall dependence between returns and volumes $\tau$ is low across all cryptocurrencies (0.05 to 0.13), indicating weak global dependence, which is expected in financial data where dependence is concentrated in the tails. All models pass the Cramér von Mises GOF test at conventional levels (p-values ≥ 0.05), confirming the adequacy of the mixture copula model.

A detailed analysis for each cryptocurrency, highlighting their specific dependence structures as captured by the estimated copula parameters, follows. With ${\lambda }_{UU}=0.26$ and ${\lambda }_{LU}=0.17$, Bitcoin displays moderate asymmetric tail dependence with mixing weights $w_1=0.58$ and $w_2=0.42$. Cardano shows the strongest upper–upper tail dependence (0.34) and notable asymmetry with the highest weight on the Joe copula ($w_1=0.73$), which aligns with speculative surges often observed in altcoins. Ethereum has moderate dependence values (${\lambda }_{UU}=0.28$), ${\lambda }_{LU}=0.19$), and relatively balanced mixing weights ($w_1=0.56$, $w_2=0.44$), suggesting both bullish and bearish volume spikes impact its dynamics. Litecoin shows similar behavior to Cardano but with a slightly lower ${\lambda }_{LU}$ (0.13) and a moderately high ${\lambda }_{UU}$ (0.33). The copula weights ($w_1=0.70$, $w_2=0.30$) indicate greater emphasis on upward tail dependence. Finally, Ripple shows strong upper–upper tail dependence (${\lambda }_{UU}=0.34$) and a modest ${\lambda }_{LU}$ of 0.13. The weights ($w_1=0.68$, $w_2=0.32$) reinforce the preference for upper–upper tail modeling.

Summarizing, the results imply that volume spikes may signal both euphoric surges and panic selloffs, but the upside tail effects are stronger. Trading strategies can exploit this by observing volume surges as potential precursors to significant market moves. The stronger upper–upper tail dependence likely reflects investor enthusiasm or fear of missing out, whereas the lower–upper tail may relate to risk aversion or panic selling. The successful application of the Joe–Joe90° mixture validates the assumption that single copulas are insufficient for modeling such asymmetric dependencies. Using rotated copulas enhances flexibility and provides a better fit to empirical data than traditional Gaussian or elliptical copulas.

The dependence structure between returns and volumes is further illustrated through contour plots of the estimated copula functions, reported in Figure 2.

5. Conclusions

This study examined the dependence between returns and trading volumes for five major cryptocurrencies—Bitcoin, Cardano, Ethereum, Litecoin, and Ripple—using copula-based modeling. The results underscore a nonlinear and asymmetric relationship, particularly characterized by strong associations between extreme returns (both positive and negative) and high trading volumes. Traditional models often fail to capture these patterns, making the use of copula functions especially valuable in this context.

We employed a mixture of the Joe copula and its 90-degree rotation to accommodate both upper–upper tail and lower–upper tail dependence structures. The estimated models successfully captured these dependencies across all cryptocurrencies, with p-values from goodness-of-fit tests indicating acceptable model adequacy. The empirical findings are consistent with existing literature, suggesting that volume acts not only as a measure of liquidity but also as a proxy for market sentiment and volatility risk.

Overall, the use of copula-based techniques offers a robust and flexible framework for analyzing complex joint behaviors in crypto-asset markets. Future research could extend this approach to dynamic copula models, or integrate high-frequency data for more granular insights. Furthermore, models focusing on the volume–return nexus in cryptocurrency markets could also incorporate the institutional incompleteness and behavioral features that differentiate these markets from traditional financial systems.

Finally, we acknowledge that future research could extend our work by incorporating structural break tests or regime-switching frameworks to assess the time invariance of the identified tail dependence patterns, as well as by analyzing cross–asset relationships and including stablecoins.