Contagion or Decoupling? Evidence from Emerging Stock Markets
Abstract
1. Introduction
2. Methodology
3. Data, Estimation, and Results
3.1. Data
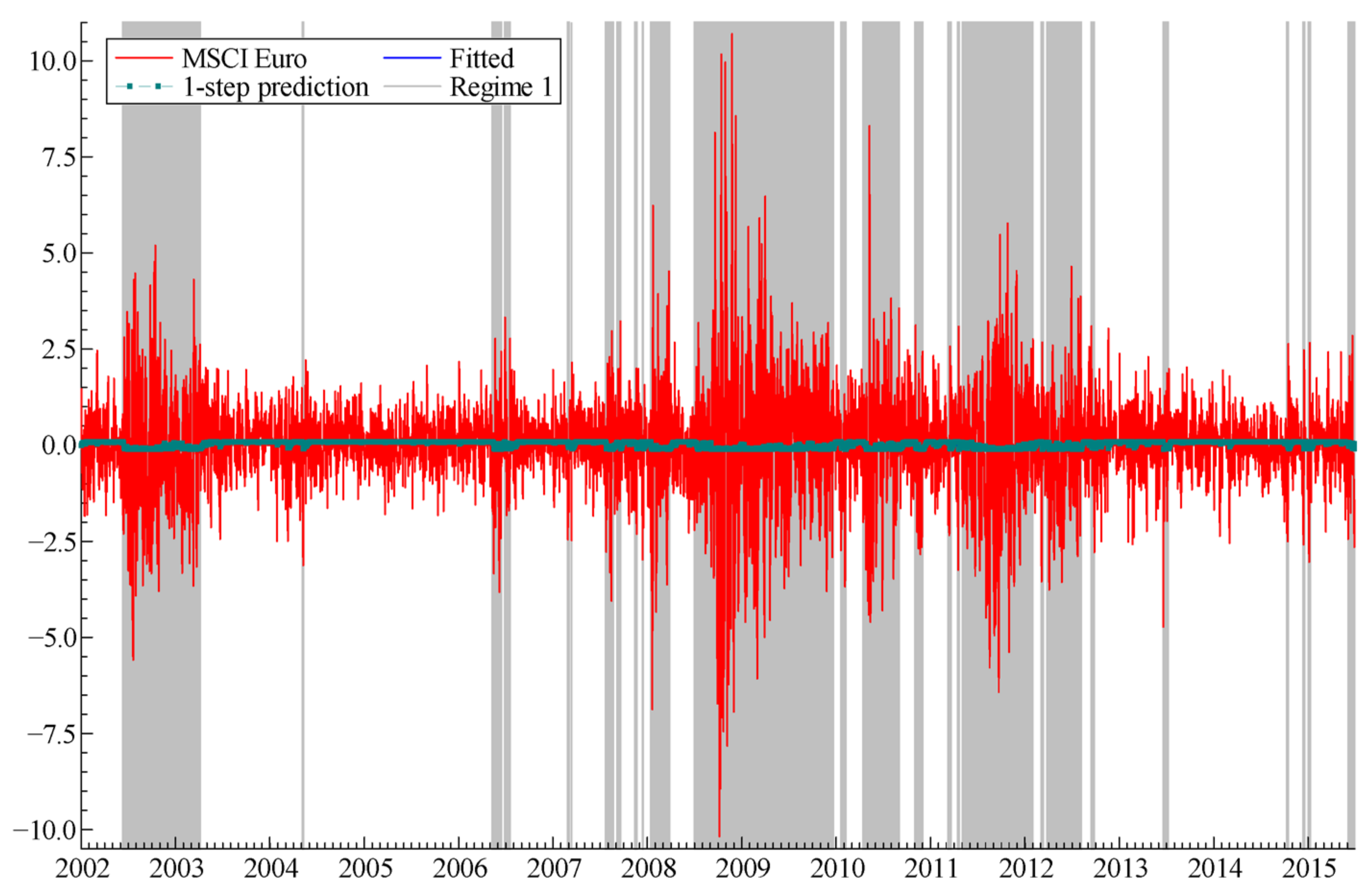
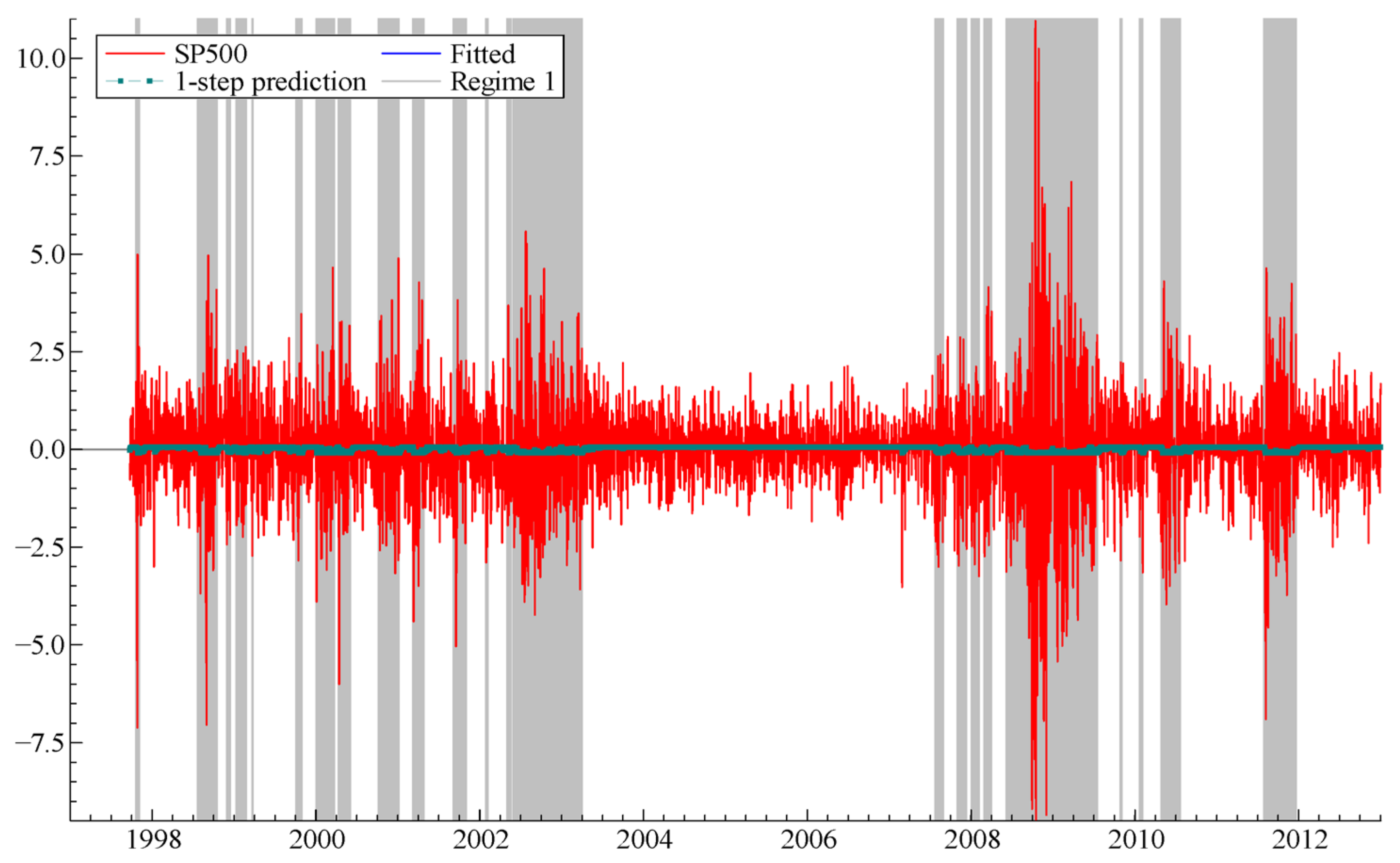
3.2. Estimations
3.3. Examination of Dynamic Conditional Correlations over Turmoil and Tranquil Periods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | Although the latest observations are available, they are not important in the context of this paper. |
| 2 | The model accounts for the change in the mean and volatility in the two regimes. Lag order and number of states selected according to AIC. |
| 3 | Their parameter estimations can be provided on request. |
References
- Acatrinei, Mădălina, Alexandru Gorun, and Nicolae Marcu. 2013. A DCC-GARCH Model to Estimate. Romanian Journal of Economic Forecasting 1: 136–48. [Google Scholar]
- Altun, Ali A., Sıtkı Çelik, and Yusuf D. Koç. 2019. Testing for Financial Contagion: New Evidence from the European Debt Crisis. Panoeconomicus 66: 611–32. [Google Scholar] [CrossRef]
- Bannigidadmath, Deepak, and Paresh Kumar Narayan. 2016. Stock Return Predictability and Determinants of Predictability and Profits. Emerging Markets Review 26: 153–73. [Google Scholar] [CrossRef]
- Baur, Dirk G. 2012. Financial Contagion and the Real Economy. Journal of Banking & Finance 36: 2680–92. [Google Scholar] [CrossRef]
- Baur, Dirk G. 2020. Decoupling and Contagion: The Special Case of the Eurozone Sovereign Debt Crisis. International Review of Finance 20: 133–54. [Google Scholar] [CrossRef]
- Bekiros, Stelios D. 2014. Contagion, Decoupling and the Spillover Effects of the US Financial Crisis: Evidence from the BRIC Markets. International Review of Financial Analysis 33: 58–69. [Google Scholar] [CrossRef]
- Benkraiem, Ramzi, Faouzi Lakhal, Ramzi Garfatta, and Imen Zorgati. 2022. Financial Contagion Intensity during the COVID-19 Outbreak: A Copula Approach. International Review of Financial Analysis 81: 102136. [Google Scholar] [CrossRef]
- Bonga-Bonga, Lumengo. 2018. Uncovering Equity Market Contagion among BRICS Countries: An Application of the Multivariate GARCH Model. The Quarterly Review of Economics and Finance 67: 36–44. [Google Scholar] [CrossRef]
- Bonga-Bonga, Lumengo, and Mthokozisi M. Manguzvane. 2020. Assessing the Extent of Contagion of Sovereign Credit Risk among BRICS Countries. Economics Bulletin 40: 1017–32. [Google Scholar]
- Cappiello, Lorenzo, Robert F. Engle, and Kevin Sheppard. 2006. Asymmetric Dynamics in the Correlations of Global Equity and Bond Returns. Journal of Financial Econometrics 4: 537–72. [Google Scholar] [CrossRef]
- Chittedi, Krishna Reddy. 2015. Financial Crisis and Contagion Effects to Indian Stock Market: DCC–GARCH Analysis. Global Business Review 16: 50–60. [Google Scholar] [CrossRef]
- Cho, Jin Hyuk, and Ali M. Parhizgari. 2009. East Asian Financial Contagion under DCC-GARCH. International Journal of Banking and Finance 6: 17–30. [Google Scholar] [CrossRef]
- Corbet, Shaen, Yifan Hu, Yifan Hou, and Les Oxley. 2022. Financial Contagion among COVID-19 Concept-Related Stocks in China. Applied Economics 54: 2439–52. [Google Scholar] [CrossRef]
- Cuadro-Sáez, Luis, Marcel Fratzscher, and Christian Thimann. 2009. The Transmission of Emerging Market Shocks to Global Equity Markets. Journal of Empirical Finance 16: 2–17. [Google Scholar] [CrossRef]
- Çelik, Sıtkı. 2012. The More Contagion Effect on Emerging Markets: The Evidence of DCC-GARCH Model. Economic Modelling 29: 1946–59. [Google Scholar] [CrossRef]
- Dimitriou, Dimitrios, Dimitrios Kenourgios, and Theodore Simos. 2013. Global Financial Crisis and Emerging Stock Market Contagion: A Multivariate FIAPARCH–DCC Approach. International Review of Financial Analysis 30: 46–56. [Google Scholar] [CrossRef]
- Dungey, Mardi, and Dharma Gajurel. 2014. Equity Market Contagion during the Global Financial Crisis: Evidence from the World’s Eight Largest Economies. Economic Systems 38: 161–77. [Google Scholar] [CrossRef]
- Eichengreen, Barry, Andrew K. Rose, and Charles Wyplosz. 1996. Contagious Currency Crises. NBER Working Paper 5681. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Federal Reserve Bank of St. Louis. 2009. The Financial Crisis: A Timeline of Events and Policy Actions. St. Louis: Federal Reserve Bank of St. Louis. [Google Scholar]
- Fernández, Andrés, Stephanie Schmitt-Grohé, and Martín Uribe. 2017. World Shocks, World Prices, and Business Cycles: An Empirical Investigation. Journal of International Economics 108, (Suppl. 1): S2–S14. [Google Scholar]
- Forbes, Kristin J., and Roberto Rigobon. 2002. No Contagion, Only Interdependence: Measuring Stock Market Comovements. The Journal of Finance 57: 2223–61. [Google Scholar] [CrossRef]
- Gaddy, Clifford G., and Barry W. Ickes. 2010. Russia after the Global Financial Crisis. Eurasian Geography and Economics 51: 281–311. [Google Scholar] [CrossRef]
- Hamao, Yasushi, Ronald W. Masulis, and Victor Ng. 1990. Correlations in Price Changes and Volatility across International Stock Markets. Review of Financial Studies 3: 281–307. [Google Scholar] [CrossRef]
- Hemche, Omar, Sofiane B. Maliki, Frédéric Jawadi, and Abderrazak I. Cheffou. 2016. On the Study of Contagion in the Context of the Subprime Crisis: A Dynamic Conditional Correlation–Multivariate GARCH Approach. Economic Modelling 52: 292–99. [Google Scholar] [CrossRef]
- Hwang, Eui Jung, Byung Hee Kim, Hyung-Geun Min, and Hail Kim. 2013. Determinants of Stock Market Comovements among US and Emerging Economies during the US Financial Crisis. Economic Modelling 35: 338–48. [Google Scholar] [CrossRef]
- Joseph, Mathew. 2009. Global Financial Crisis: How Was India Impacted. Paper presented at InWEnt-DIE Conference on Global Financial Governance—Challenges and Regional Responses, Vienna, Austria, September 3–4. [Google Scholar]
- Kenourgios, Dimitrios. 2014. On Financial Contagion and Implied Market Volatility. International Review of Financial Analysis 34: 21–30. [Google Scholar] [CrossRef]
- Kenourgios, Dimitrios, and Dimitrios Dimitriou. 2015. Contagion of the Global Financial Crisis and the Real Economy: A Regional Analysis. Economic Modelling 44: 283–93. [Google Scholar] [CrossRef]
- Kenourgios, Dimitrios, Nidhaleddine Naifar, and Dimitrios Dimitriou. 2016. Islamic Financial Markets and Global Crises: Contagion or Decoupling? Economic Modelling 57: 36–46. [Google Scholar] [CrossRef]
- Khrushcheva, Olga, and Tomas Maltby. 2016. The Future of EU-Russia Energy Relations in the Context of Decarbonisation. Geopolitics 21: 799–830. [Google Scholar] [CrossRef]
- Lawlor, Philip. 2020. Not All Emerging Markets Are Equal: Tread Carefully When Chasing Returns. Investec. Available online: https://www.investec.com/en_za/focus/global-investment-strategy-group/not-all-emerging-markets-are-equal-tread-carefully-when-chasing-returns.html (accessed on 26 April 2025).
- Li, Qi, Esfandiar Maasoumi, and Jeffrey S. Racine. 2009. A Nonparametric Test for Equality of Distributions with Mixed Categorical and Continuous Data. Journal of Econometrics 148: 186–200. [Google Scholar] [CrossRef]
- Mensi, Walid, Duc Khuong Nguyen, Shawkat Hammoudeh, and Seungho H. Kang. 2016. Global Financial Crisis and Spillover Effects among the US and BRICS Stock Markets. International Review of Economics & Finance 42: 257–76. [Google Scholar] [CrossRef]
- Mensi, Walid, Syed Jawad Hussain Shahzad, Shawkat Hammoudeh, Rami Zeitun, and Muhammad Umer Rehman. 2017. Diversification potential of Asian frontier, BRIC emerging and major developed stock markets: A wavelet-based value at risk approach. Emerging Markets Review 32: 130–47. [Google Scholar] [CrossRef]
- Naoui, Khaled, Sami Khemiri, and Nabil Liouane. 2010. Crises and financial contagion: The subprime crisis. Journal of Business Studies Quarterly 2: 15. [Google Scholar]
- Narayan, Paresh Kumar, and Susan Sunila Sharma. 2015. Does data frequency matter for the impact of forward premium on spot exchange rate? International Review of Financial Analysis 39: 45–53. [Google Scholar] [CrossRef]
- Naresh, Gokul, Ganesh Vasudevan, Subramaniam Mahalakshmi, and S. Thiyagarajan. 2018. Spillover effect of US dollar on the stock indices of BRICS. Research in International Business and Finance 44: 359–68. [Google Scholar] [CrossRef]
- Pretorius, Elna. 2002. Economic determinants of emerging stock market interdependence. Emerging Markets Review 3: 84–105. [Google Scholar] [CrossRef]
- Reuters. 2020. Pandemic Won’t Cause Euro Debt Crisis, but a North-South Divide. Available online: https://www.reuters.com/article/us-health-coronavirus-eu-debt-analysis-idUSKCN2240N6 (accessed on 24 April 2025).
- Rigobon, Roberto. 2002. International Financial Contagion: Theory and Evidence in Evolution. Charlottesville: Research Foundation of AIMR. [Google Scholar]
- Soylu, Pelin Kizilkaya, and Bülent Güloğlu. 2019. Financial contagion and flight to quality between emerging markets and US bond market. The North American Journal of Economics and Finance 50: 100992. [Google Scholar] [CrossRef]
- Sutela, Pekka. 2010. Russia’s Response to the Global Financial Crisis. Available online: http://carnegieendowment.org (accessed on 24 April 2025).
- Tajoli, Lucia. 2022. Too much of a good thing? Russia-EU international trade relations at times of war. Journal of Industrial and Business Economics 49: 807–34. [Google Scholar] [CrossRef]
- Wälti, Sébastien. 2012. The myth of decoupling. Applied Economics 44: 3407–19. [Google Scholar] [CrossRef]
- Willett, Thomas D., Ping Liang, and Nan Zhang. 2011. Global contagion and the decoupling debate. In The Evolving Role of Asia in Global Finance. Edited by Yin-Wong Cheung, Vikas Kakkar and Guonan Ma. Bingley: Emerald Group Publishing Limited, pp. 215–34. [Google Scholar] [CrossRef]
- Zhang, Yan. 2016. Emerging markets and international asset allocation. Journal of International Financial Markets, Institutions and Money 44: 56–80. [Google Scholar]
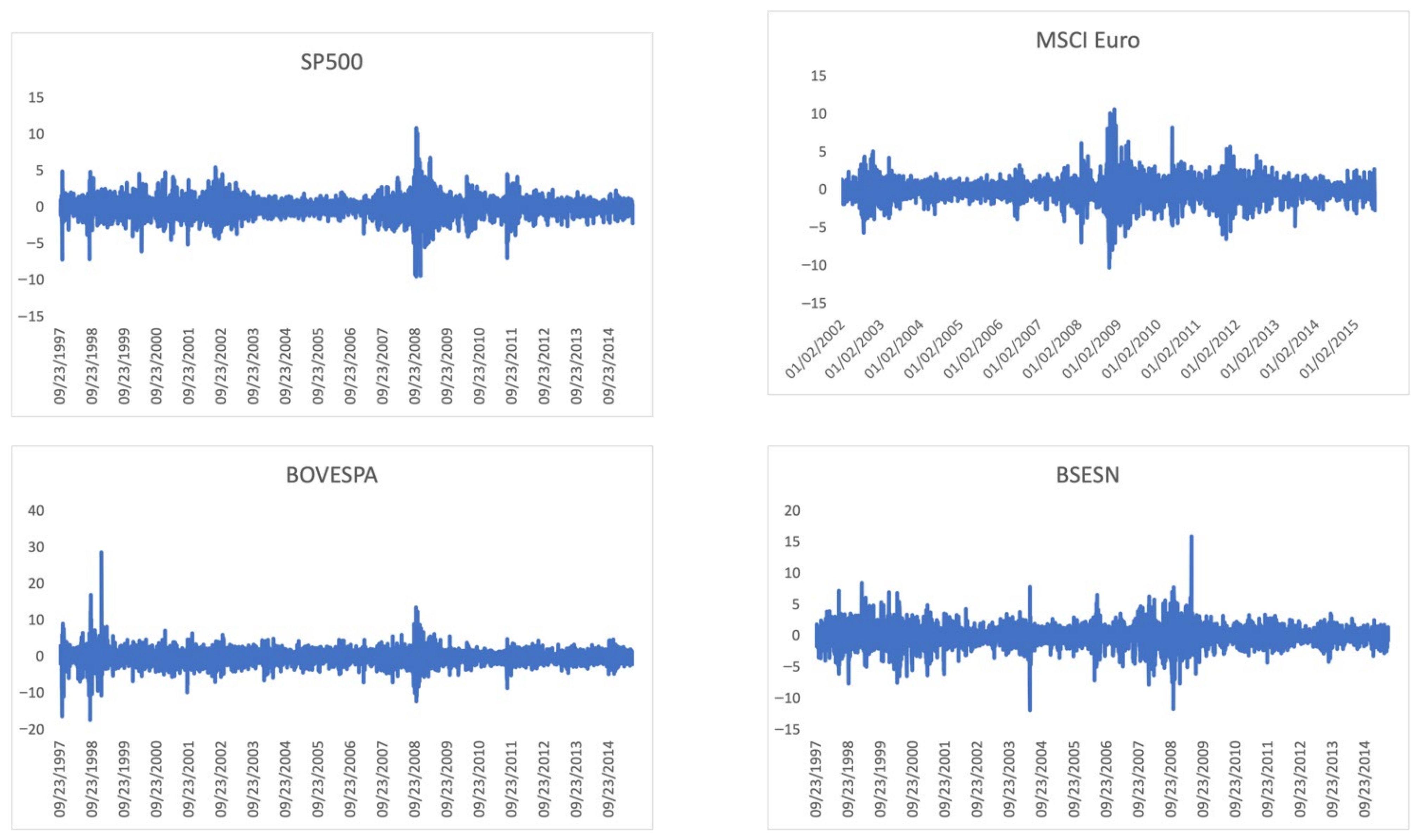
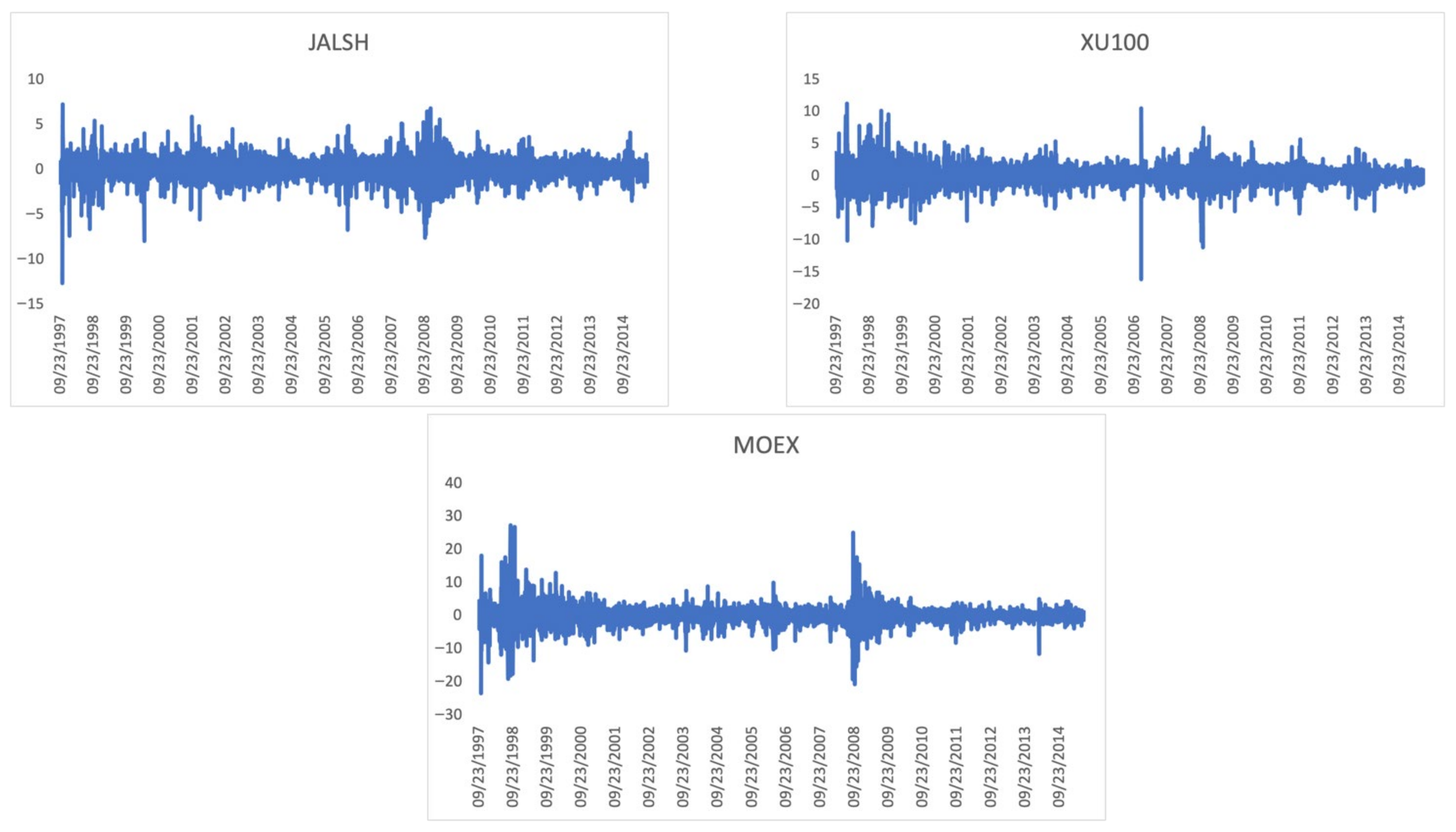
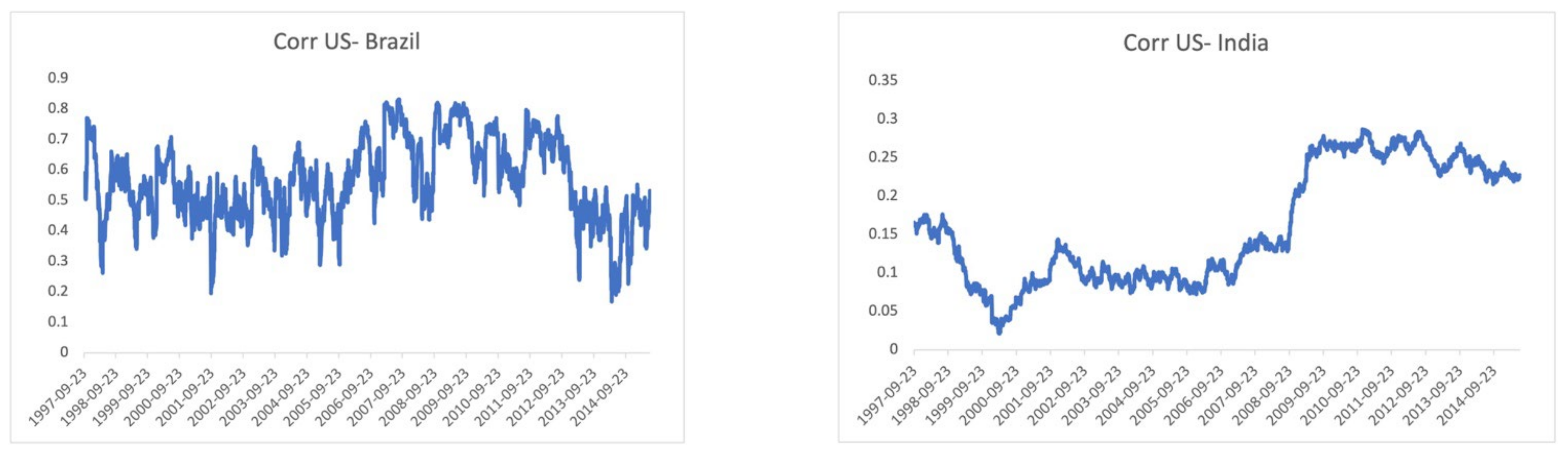
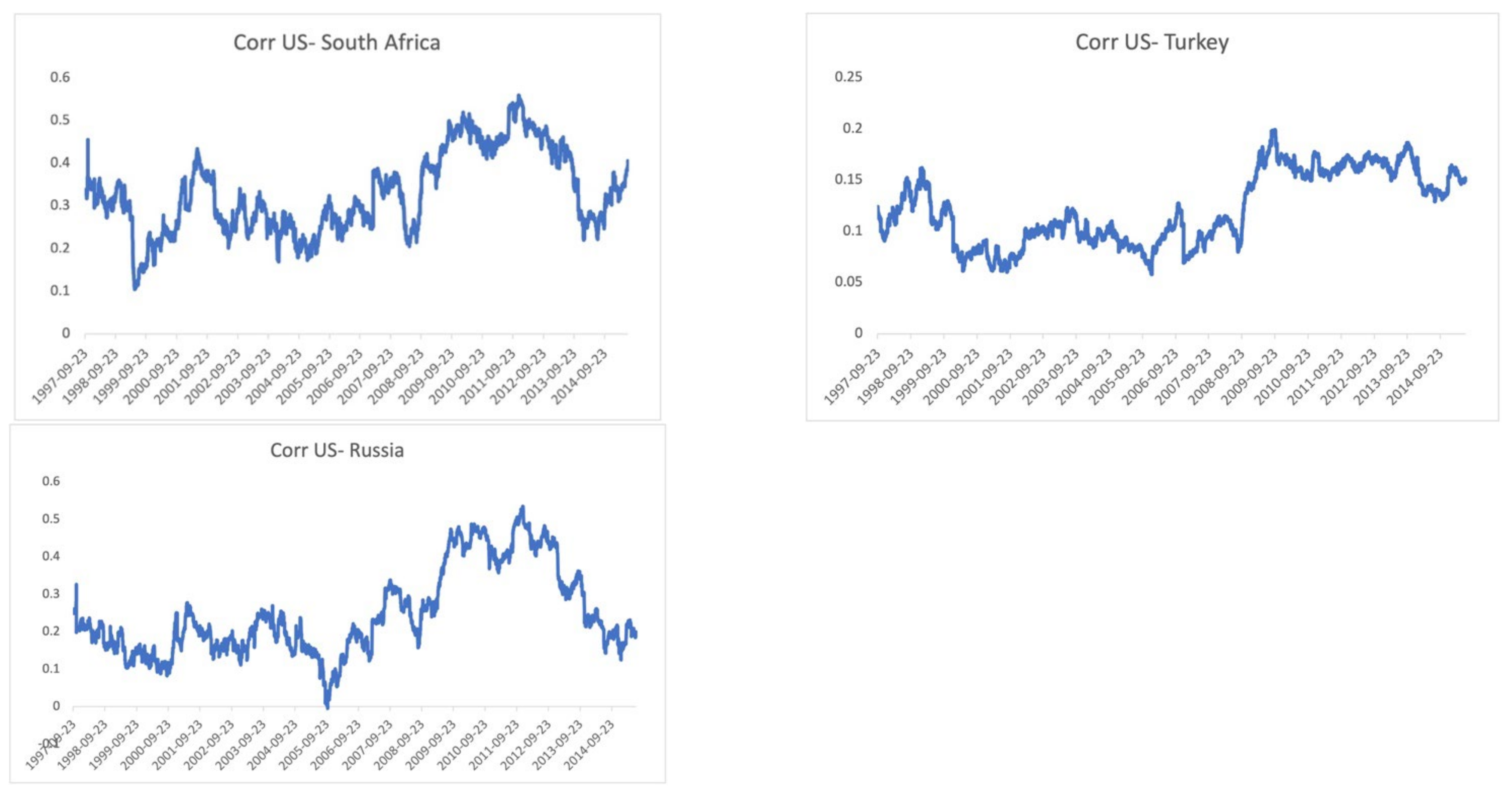
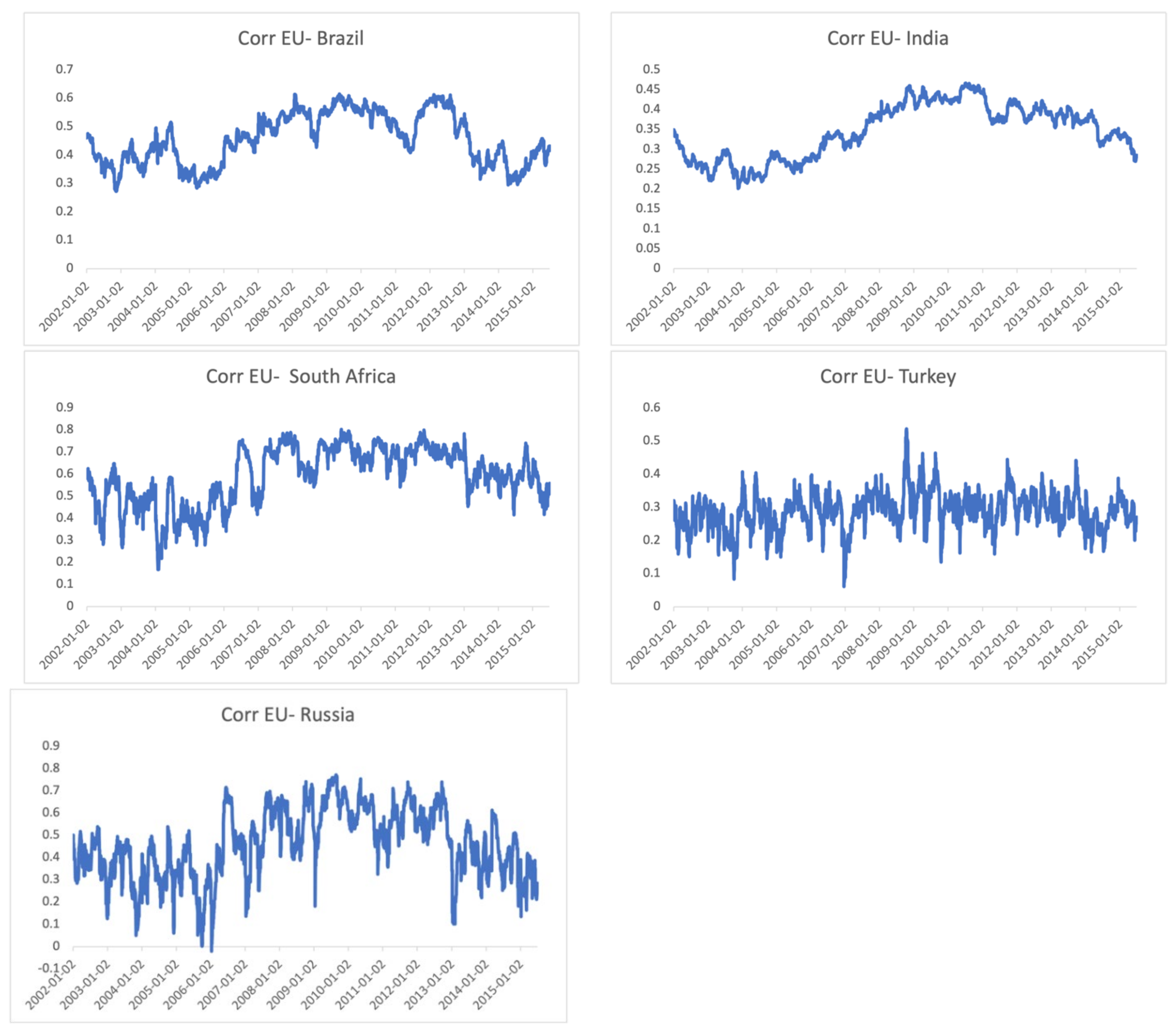
| Variable | Classification |
|---|---|
| S&P 500 (US) MSCI Europe Index (EU) | Source market (developed) Source market (developed) |
| BOVESPA (Brazil) | Recipient market (Latin American emerging market) |
| BSESN (India) | Recipient market (Asian emerging market) |
| JALSH (South Africa) | Recipient market (African emerging market) |
| XU100 (Turkey) | Recipient market (Middle East emerging market) |
| MOEX (Russia) | Recipient market (European emerging market) |
| GFC | ESDC | |
|---|---|---|
| Entire crisis period | August 2007–March 2009 | November 2009–July 2012 |
| Phases (economic approach) | ||
| Phase 1 | 1 Aug 2007–15 Sept 2008 (dubbed “initial financial turmoil”) | 5 November 2009–22 April 2010 (announcement of Greek budget deficit) |
| Phase 2 | 16 Sept 2008–31 Dec 2008 (defined as “sharp financial market deterioration”) | 23 April 2010–14 July 2011 (announcement that the austerity packages were not enough and request for bailout from IMF or EU) |
| Phase 3 | 1 Jan 2009–31 Mar 2009 (dubbed “macroeconomic deterioration”) | 15 July 2011–onwards (begins when banking stress tests were published by the European authorities and the first austerity package was announced by Italy) |
| Phase 4 | 1 Apr 2009–30 Nov 2009 (described as a phase of “stabilization and tentative signs of recovery”) | |
| Phases (statistical approach) | ||
| Phase 1 | 24 Jul 2007–29 Aug 2007 | 19 Jan 2010–8 Feb 2010 |
| Phase 2 | 31 Oct 2007–11 Nov 2007 | 16 Apr 2010–2 Sept 2010 |
| Phase 3 | 2 Jan 2008–6 Feb 2008 | 2 Nov 2010–3 Dec 2010 |
| Phase 4 | 28 Feb 2008–1 Apr 2008 | 31 May 2011–1 Feb 2012 |
| Phase 5 | 5 Jun 2008–16 Jul 2009 | 26 Mar 2012–6 Aug 2012 |
| Test Statistic Sp | p-Value | Outcome | |
|---|---|---|---|
| US–Brazil | 0.1992422 | 2.22 × 10−16 *** | rejected |
| US–India | 0.1988645 | 2.22 × 10−16 *** | rejected |
| US–South Africa | 0.1992422 | 0.000000 *** | rejected |
| US–Turkey | 0.1989548 | 2.22 × 10−16 *** | rejected |
| US–Russia | 0.196512 | 0.000000 *** | rejected |
| EU–Brazil | 0.2213491 | 0.000000 *** | rejected |
| EU–India | 0.1924623 | 2.22 × 10−16 *** | rejected |
| EU–South Africa | 0.1759779 | 2.22 × 10−16 *** | rejected |
| EU–Turkey | 0.2112558 | 0.000000 *** | rejected |
| EU–Russia | 0.206611 | 2.22 × 10−16 *** | rejected |
| US–Brazil | US–India | US–South Africa | US–Turkey | US–Russia | |
|---|---|---|---|---|---|
| 0.75749053 (0.000000) *** | −0.1710778 (8.591 × 10−34) *** | 0.2054267 (6.547 × 10−260) *** | 0.09508578 (1.385 × 10−297) *** | 0.30636772 (1.1311 × 10−16) *** | |
| DMGFC | 0.05059396 (2.7437 × 10−19) *** | 0.02990513 (2.101 × 10−19) *** | 0.03847949 (7.09 × 10−32) *** | 0.00841855 (5.1556 × 10−05) *** | −0.0498957 (5.159 × 10−10) *** |
| Exchange rate | −0.0394569 (5.2727 × 10−36) *** | 0.00644579 (3.4417 × 10−88) *** | 0.00729892 (3.4535 × 10−23) *** | 0.02187474 (5.3031 × 10−44) *** | −0.0020963 (0.09748546) * |
| Interest rate differential | 0.00622531 (1.117 × 10−104) *** | −0.0058543 (3.5853 × 10−62) *** | −0.0017017 (8.6098 × 10−08) *** | 0.00015832 (5.1981 × 10−15) *** | −0.018169 (8 × 10−147) *** |
| SE | 0.107698 | 0.06288446 | 0.09871251 | 0.04046941 | 0.11757167 |
| p-value | 6.99 × 10−206 | 5.103 × 10−232 | 1.0375 × 10−77 | 1.17 × 10−105 | 0.000000 |
| EU–Brazil | EU–India | EU–South Africa | EU–Turkey | EU–Russia | |
|---|---|---|---|---|---|
| 0.6492135 (0.000000) *** | 0.10892246 (5.3771 × 10−69) *** | 0.29577398 (5.951 × 10−138) *** | 0.32615524 (0.000000) *** | 0.6015557 (3.024 × 10−202) *** | |
| DMESDC | 0.05934492 (1.9945 × 10−67) *** | 0.08429326 (6.412 × 10−276) *** | 0.14149668 (5.226 × 10−189) *** | 0.00446084 (0.06973659) * | 0.1567137 (4.708 × 10−143) *** |
| Exchange rate | −0.0325584 (3.0311 × 10−21) *** | 0.00377976 (1.043 × 10−211) *** | 0.02633883 (2.519 × 10−176) *** | −0.0088868 (0.00108001) *** | −0.005272 (9.4971 × 10−24) *** |
| Interest rate differential | 0.00948557 (1.466 × 10−156) *** | 0.00335053 (4.0995 × 10−16) *** | 0.00127841 (0.19180879) | 0.00139337 (2.2256 × 10−36) *** | −0.0105106 (3.1155 × 10−33) *** |
| SE | 0.06644035 | 0.0495412 | 0.10533372 | 0.05474849 | 0.13964641 |
| p-value | 0.000000 | 0.000000 | 0.000000 | 5.2451 × 10−51 | 4.003 × 10−167 |
| Test Statistic Sp | p-Value | Outcome | ||
|---|---|---|---|---|
| US–Brazil | Phase 1 Phase 2 Phase 3 | 0.2034821 0.1954202 0.2101099 | 2.22 × 10−16 *** 2.22 × 10−16 *** 0.000000 *** | rejected rejected rejected |
| US–India | Phase 1 Phase 2 Phase 3 | 0.1925159 0.2054686 0.1801679 | 2.22 × 10−16 *** 0.000000 *** 2.22 × 10−16 *** | rejected rejected rejected |
| US–South Africa | Phase 1 Phase 2 Phase 3 | 0.2178756 0.178754 0.2200741 | 0.000000 *** 2.22 × 10−16 *** 2.22 × 10−16 *** | rejected rejected rejected |
| US–Turkey | Phase 1 Phase 2 Phase 3 | 0.2052791 0.2162047 0.2041979 | 2.22 × 10−16 *** 0.000000 *** 2.22 × 10−16 *** | rejected rejected rejected |
| US–Russia | Phase 1 Phase 2 Phase 3 | 0.2103451 0.20185 0.1870066 | 0.000000 *** 2.22 × 10−16 *** 0.000000 *** | rejected rejected rejected |
| EU–Brazil | Phase 1 Phase 2 Phase 3 | 0.2013982 0.2024698 0.1925159 | 0.000000 *** 2.22 × 10−16 *** 2.22 × 10−16 *** | rejected rejected rejected |
| EU–India | Phase 1 Phase 2 Phase 3 | 0.201031 0.1881834 0.1989455 | 2.22 × 10−16 *** 2.22 × 10−16 *** 0.000000 *** | rejected rejected rejected |
| EU–South Africa | Phase 1 Phase 2 Phase 3 | 0.1951405 0.2062592 0.1872081 | 2.22 × 10−16 *** 0.000000 *** 2.22 × 10−16 *** | rejected rejected rejected |
| EU–Turkey | Phase 1 Phase 2 Phase 3 | 0.1802886 0.2036417 0.1926393 | 0.000000 *** 2.22 × 10−16 *** 2.22 × 10−16 *** | rejected rejected rejected |
| EU–Russia | Phase 1 Phase 2 Phase 3 | 0.1905485 0.1894249 0.2029673 | 2.22 × 10−16 *** 0.000000 *** 0.000000 *** | rejected rejected rejected |
| US–Brazil | US–India | US–South Africa | US–Turkey | US–Russia | |
|---|---|---|---|---|---|
| 0.77367792 (0.000000) *** | −0.1667311 (2.0446 × 10−28) *** | 0.22612807 (4.554 × 10−123) *** | 0.09851885 (0.000000) *** | 0.02319544 (0.57691663) | |
| DMGFC0.1 | −0.0036838 (0.57673909) | 0.02968052 (9.484 × 10−13) *** | −0.0285798 (2.067 × 10−06) *** | −0.0065242 (0.00755262) *** | 0.04914055 (8.8913 × 10−07) *** |
| DMGFC0.2 | 0.17308156 (2.2055 × 10−45) *** | 0.00995136 (0.17590405) | 0.03417071 (0.00422677) *** | 0.03109311 (1.619 × 10−11) *** | −0.1204906 (8.3394 × 10−16) *** |
| DMGFC0.3 | 0.13492855 (4.662 × 10−24) *** | 0.05237262 (7.5512 × 10−11) *** | 0.02704641 (0.03711181) ** | 0.0497887 (1.2658 × 10−22) *** | −0.2210546 (3.3205 × 10−44) *** |
| Exchange rate | −0.044899 (1.7507 × 10−47) *** | 0.00633479 (1.4974 × 10−75) *** | 0.0182704 (1.8802 × 10−50) *** | 0.01946067 (8.217 × 10−36) *** | 0.00743625 (1.942 × 10−07) *** |
| Interest rate differential | 0.0065552 (3.676 × 10−120) *** | −0.0060499 (5.3527 × 10−65) *** | 0.00505418 (1.0829 × 10−23) *** | 0.00017391 (3.211 × 10−18) *** | −0.0191256 (2.263 × 10−165) *** |
| SE | 0.10487855 | 0.06277711 | 0.09872266 | 0.03981979 | 0.11290405 |
| p-value | 1.73 × 10−249 | 8.764 × 10−233 | 9.8839 × 10−77 | 1.133 × 10−131 | 6.605 × 10−251 |
| EU–Brazil | EU–India | EU–South Africa | EU–Turkey | EU–Russia | |
|---|---|---|---|---|---|
| 0.65945353 (0.000000) *** | 0.10601597 (6.6203 × 10−66) *** | 0.29015018 (4.848 × 10−132) *** | 0.33942379 (0.000000) *** | 0.59968117 (2.228 × 10−199) *** | |
| DMESDC,1 | 0.06880884 (4.4314 × 10−28) *** | 0.0834809 (6.0216 × 10−71) *** | 0.10257756 (1.78 × 10−25) *** | −0.0025006 (0.6256701) | 0.17991653 (1.5339 × 10−42) *** |
| DMESDC,2 | 0.02293735 (1.7818 × 10−07) *** | 0.10406578 (1.315 × 10−234) *** | 0.14945174 (3.616 × 10−114) *** | −0.013092 (0.00010564) *** | 0.14377266 (6.3541 × 10−65) *** |
| DMESDC,3 | 0.09223161 (5.1094 × 10−90) *** | 0.05864846 (1.5977 × 10−66) *** | 0.15111135 (1.703 × 10−102) *** | 0.02667543 (6.8028 × 10−14) *** | 0.16171822 (2.3468 × 10−70) *** |
| Exchange rate | −0.0375013 (4.2474 × 10−28) *** | 0.00378595 (2.018 × 10−209) *** | 0.02652683 (9.418 × 10−178) *** | −0.0142266 (2.5792 × 10−07) *** | −0.0052097 (5.6117 × 10−23) *** |
| Interest rate differential | 0.00912175 (6.617 × 10−158) *** | 0.0027629 (1.1407 × 10−10) *** | 0.00069465 (0.48106004) | 0.00154696 (5.0357 × 10−44) *** | −0.0103228 (1.7161 × 10−31) *** |
| SE | 0.06490592 | 0.04870241 | 0.10506061 | 0.05417054 | 0.13955925 |
| p-value | 0.000000 | 0.000000 | 0.000000 | 1.526 × 10−65 | 4.794 × 10−166 |
| Test Statistics Sp | p-Value | Outcome | ||
|---|---|---|---|---|
| US–Brazil | Phase 1 Phase 2 Phase 3 Phase 4 Phase 5 | 0.2223439 0.6681207 0.9765144 0.2120574 0.4687102 | 2.22 × 10−16 *** 2.22 × 10−16 *** 0.000000 *** 2.22 × 10−16 *** 0.000000 *** | rejected rejected rejected rejected rejected |
| US–India | Phase 1 Phase 2 Phase 3 Phase 4 Phase 5 | 0.2091447 0.2062592 0.2120574 0.2036417 0.1870535 | 2.22 × 10−16 *** 2.22 × 10−16 *** 0.000000 *** 0.000000 *** 2.22 × 10−16 *** | rejected rejected rejected rejected rejected |
| US–South Africa | Phase 1 Phase 2 Phase 3 Phase 4 Phase 5 | 0.2032956 0.1894249 0.2101099 0.2200741 0.2104964 | 0.000000 *** 0.000000 *** 0.000000 *** 0.000000 *** 0.000000 *** | rejected rejected rejected rejected rejected |
| US–Turkey | Phase 1 Phase 2 Phase 3 Phase 4 Phase 5 | 0.2223439 0.2120574 0.2103451 0.1801679 0.2024698 | 2.22 × 10−16 *** 2.22 × 10−16 *** 0.000000 *** 2.22 × 10−16 *** 0.000000 *** | rejected rejected rejected rejected rejected |
| US–Russia | Phase 1 Phase 2 Phase 3 Phase 4 Phase 5 | 0.2060604 0.2223439 0.2178756 0.1644527 0.1881834 | 0.000000 *** 2.22 × 10−16 *** 2.22 × 10−16 *** 0.000000 *** 0.000000 *** | rejected rejected rejected rejected rejected |
| EU–Brazil | Phase 1 Phase 2 Phase 3 Phase 4 Phase 5 | 0.2032956 0.1907429 0.2129627 0.2007392 0.18313 | 0.000000 *** 0.000000 *** 2.22 × 10−16 *** 2.22 × 10−16 *** 0.000000 *** | rejected rejected rejected rejected rejected |
| EU–India | Phase 1 Phase 2 Phase 3 Phase 4 Phase 5 | 0.1917481 0.1911886 0.1940323 0.2019162 0.1901609 | 2.22 × 10−16 *** 0.000000 *** 0.000000 *** 2.22 × 10−16 *** 2.22 × 10−16 *** | rejected rejected rejected rejected rejected |
| EU–South Africa | Phase 1 Phase 2 Phase 3 Phase 4 Phase 5 | 0.2018207 0.1835359 0.2108033 0.175078 0.2000702 | 2.22 × 10−16 *** 0.000000 *** 0.000000 *** 0.000000 *** 2.22 × 10−16 *** | rejected rejected rejected rejected rejected |
| EU–Turkey | Phase 1 Phase 2 Phase 3 Phase 4 Phase 5 | 0.1989548 0.2079274 0.1930285 0.1940544 0.2153276 | 0.000000 *** 2.22 × 10−16 *** 0.000000 *** 0.000000 *** 0.000000 *** | rejected rejected rejected rejected rejected |
| EU–Russia | Phase 1 Phase 2 Phase 3 Phase 4 Phase 5 | 0.196512 0.2003858 0.1870974 0.2185429 0.1819469 | 2.22 × 10−16 *** 2.22 × 10−16 *** 2.22 × 10−16 *** 0.000000 *** 2.22 × 10−16 *** | rejected rejected rejected rejected rejected |
| US–Brazil | US–India | US–South Africa | US–Turkey | US–Russia | |
|---|---|---|---|---|---|
| Intercept | 0.75377281 (0.000000) *** | −0.1503148 (6.9524 × 10−27) *** | 0.21990285 (2.012 × 10−118) *** | 0.0959276 (0.000000) *** | 0.20344365 (1.6179 × 10−11) *** |
| DMGFC0.1 | 0.18465667 (1.1212 × 10−19) *** | 0.05567735 (4.5118 × 10−06) *** | 0.00757591 (0.69181076) | −0.0230984 (0.00250967) *** | 0.08359866 (0.00016313) *** |
| DMGF0.2 | 0.07916516 (3.8691 × 10−05) *** | 0.05586833 (1.318 × 10−06) *** | 0.04928584 (0.00658841) *** | −0.0008955 (0.90174537) | 0.06249287 (0.00339338) *** |
| DMGFC0.3 | −0.0176848 (0.39068741) | 0.04738597 (0.0001286) *** | 0.00980031 (0.61441901) | 0.00861945 (0.26836151) | 0.09558955 (2.6757 × 10−05) *** |
| DMGFC0.4 | 0.00701396 (0.74331571) | 0.02808854 (0.02865917) ** | −0.0768375 (0.00015227) *** | 0.00751072 (0.35373342) | 0.01905637 (0.42499997) |
| DMGFC0.5 | 0.1050502 (7.0154 × 10−59) *** | 0.04346329 (3.1292 × 10−29) *** | 0.01866183 (0.00426834) *** | 0.03484958 (2.8814 × 10−45) *** | −0.1212583 (4.1288 × 10−49) *** |
| Exchange rate | −0.0409276 (4.745 × 10−41) *** | 0.00594891 (1.1416 × 10−76) *** | 0.01883108 (5.32 × 10−54) *** | 0.01981426 (7.8659 × 10−38) *** | 0.00133614 (0.19985118) |
| Interest rate differential | 0.00601103 (2.165 × 10−104) *** | −0.0060228 (1.6049 × 10−67) *** | 0.00509948 (7.3635 × 10−24) *** | 0.00015302 (8.4315 × 10−15) *** | −0.0208021 (3.516 × 10−196) *** |
| EU–Brazil | EU–India | EU–South Africa | EU–Turkey | EU–Russia | |
|---|---|---|---|---|---|
| 0.69321599 (0.000000) *** | 0.11558727 (1.2774 × 10−66) *** | 0.33443991 (8.192 × 10−165) *** | 0.32977139 (0.000000) *** | 0.58642092 (2.662 × 10−180) *** | |
| DMESDC,1 | 0.07525547 (1.4173 × 10−5) *** | 0.07401748 (1.01 × 10−7) *** | 0.07422926 (0.00897249) *** | 0.03277883 (0.02009827) ** | 0.11260497 (0.00254565) *** |
| DMESDC,2 | 0.05841933 (1.2254 × 10−16) *** | 0.1276584 (8.157 × 10−113) *** | 0.1772119 (9.3013 × 10−55) *** | 9.6443E−05 (0.98634625) | 0.2095044 (3.1317 × 10−45) *** |
| DMESDC,3 | 0.01321868 (0.33735716) | 0.12251791 (2.3531 × 10−28) *** | 0.12434667 (3.594 × 10−08) *** | 0.02112169 (0.05916379) * | 0.03021221 (0.30695081) |
| DMESDC,4 | 0.0478586 (1.5968 × 10−18) *** | 0.04995985 (5.9198 × 10−31) *** | 0.14848582 (3.3324 × 10−64) *** | 0.02850333 (3.8343 × 10−11) *** | 0.16396512 (1.455 × 10−47) *** |
| DMESDC,5 | 0.09025856 (6.5096 × 10−37) *** | 0.03223726 (1.6528 × 10−8) *** | 0.11604533 (7.5363 × 10−24) *** | 0.01856492 (0.00106904) *** | 0.12355319 (3.6133 × 10−16) *** |
| Exchange rate | −0.0477714 (4.0575 × 10−49) *** | 0.00365727 (2.199 × 10−173) *** | 0.0251471 (3.026 × 10−151) *** | −0.0114085 (3.5223 × 10−05) *** | −0.0044778 (1.8785 × 10−16) *** |
| Interest rate differential | 0.00909995 (4.503 × 10−150) *** | 0.0012286 (0.00632257) *** | 0.00365464 (0.00033674) *** | 0.00137611 (7.8676 × 10−38) *** | −0.0096825 (2.3784 × 10−26) *** |
| SE | 0.06673247 | 0.05348605 | 0.10968062 | 0.05434496 | 0.14401552 |
| p-value | 0.000000 | 0.000000 | 3.864 × 10−246 | 2.5095 × 10−59 | 1.235 × 10−116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonga-Bonga, L.; Ndiweni, Z.L. Contagion or Decoupling? Evidence from Emerging Stock Markets. Risks 2025, 13, 165. https://doi.org/10.3390/risks13090165
Bonga-Bonga L, Ndiweni ZL. Contagion or Decoupling? Evidence from Emerging Stock Markets. Risks. 2025; 13(9):165. https://doi.org/10.3390/risks13090165
Chicago/Turabian StyleBonga-Bonga, Lumengo, and Zinzile Lorna Ndiweni. 2025. "Contagion or Decoupling? Evidence from Emerging Stock Markets" Risks 13, no. 9: 165. https://doi.org/10.3390/risks13090165
APA StyleBonga-Bonga, L., & Ndiweni, Z. L. (2025). Contagion or Decoupling? Evidence from Emerging Stock Markets. Risks, 13(9), 165. https://doi.org/10.3390/risks13090165




