Algorithmic Bias Under the EU AI Act: Compliance Risk, Capital Strain, and Pricing Distortions in Life and Health Insurance Underwriting

Abstract

The EU Artificial Intelligence Act (Regulation (EU) 2024/1689) designates AI systems used in life and health insurance underwriting as high-risk systems, imposing rigorous requirements for bias testing, technical documentation, and post-deployment monitoring. Leveraging 12.4 million quote–bind–claim observations from four pan-European insurers (2019 Q1–2024 Q4), we evaluate how compliance affects premium schedules, loss ratios, and solvency positions. We estimate gradient-boosted decision tree (Extreme Gradient Boosting (XGBoost)) models alongside benchmark GLMs for mortality, morbidity, and lapse risk, using Shapley Additive Explanations (SHAP) values for explainability. Protected attributes (gender, ethnicity proxy, disability, and postcode deprivation) are excluded from training but retained for audit. We measure bias via statistical parity difference, disparate impact ratio, and equalized odds gap against the 10 percent tolerance in regulatory guidance, and then apply counterfactual mitigation strategies—re-weighing, reject option classification, and adversarial debiasing. We simulate impacts on expected loss ratios, the Solvency II Standard Formula Solvency Capital Requirement (SCR), and internal model economic capital. To translate fairness breaches into compliance risk, we compute expected penalties under the Act’s two-tier fine structure and supervisory detection probabilities inferred from GDPR enforcement. Under stress scenarios—full retraining, feature excision, and proxy disclosure—preliminary results show that bottom-income quintile premiums exceed fair benchmarks by 5.8 percent (life) and 7.2 percent (health). Mitigation closes 65–82 percent of these gaps but raises capital requirements by up to 4.1 percent of own funds; expected fines exceed rectification costs once detection probability surpasses 9 percent. We conclude that proactive adversarial debiasing offers insurers a capital-efficient compliance pathway and outline implications for enterprise risk management and future monitoring.

1. Introduction—Why Fairness Has Become a Prudential Question

Europe’s insurance market is rapidly embracing data-driven underwriting. A 2023–2024 EIOPA market survey found that 50% of non-life carriers and 24% of life insurers already deploy AI models in production, with a further 30–39% planning adoption within three years (European Insurance and Occupational Pensions Authority (EIOPA) 2024). In parallel, the EU Artificial Intelligence Act—Regulation (EU) 2024/1689—explicitly classifies AI systems used for risk assessment and pricing in life and health insurance as high risk (Annex III, 5(c)) and backs the designation with administrative fines of up to the greater of EUR 35 million or 7% of worldwide turnover (European Union 2024; Hickman et al. 2024). EIOPA’s 2025 draft Opinion on AI Governance and Risk Management confirms that national supervisors will anchor their model reviews around these fairness obligations (European Insurance and Occupational Pensions Authority (EIOPA) 2025). In short, what was once a promising analytics project has become a prudential risk that touches capital adequacy, conduct supervision, and brand value.

1.1. Academic Background

Two adjacent research fields motivate our study. First, the machine-learning fairness community has catalogued a spectrum of group-fairness concepts—statistical parity, disparate impact, equalized odds, and counterfactual fairness—and proposed corresponding mitigation toolkits such as re-weighing, adversarial training, and reject option post-processing (Mehrabi et al. 2021; Miller 2009). Second, applied insurance papers have documented premium distortions in auto, property, and health lines, and regulators are beginning to fold those insights into supervisory policy. Yet nearly all prior work stops at bias detection; we know which groups overpay but not how those distortions feed through to Solvency II capital or to the EU AI Act penalty schedule.

1.2. Academic Rationale and Gap

Under Solvency II, underwriting capital is calibrated to unexpected claim volatility; algorithmic bias, if mentioned at all, appears in qualitative “conduct-risk” footnotes. Boards therefore lack a quantitative framework to balance (i) the cost of debiasing models, (ii) the incremental SCR generated by bias-induced volatility, and (iii) the expected value of AI Act fines. Bridging this gap is urgent now that fairness failures can undermine both solvency and consumer trust.

1.3. Contributions

This paper offers the following three advances:

• Regulatory–capital linkage. We derive a closed-form mapping from three legal fairness metrics—statistical parity difference, disparate impact ratio, equalized odds gap—to changes in the Solvency II Standard-Formula SCR and to expected fines under Article 71.
• Causal identification at scale. Using a 12.4-million quote–bind–claim panel (2019 Q1–2024 Q4) from four pan-European carriers, we combine instrumental-variable quantile regression with SHAP explainability to isolate pricing distortions that persist after manual underwriter overrides.
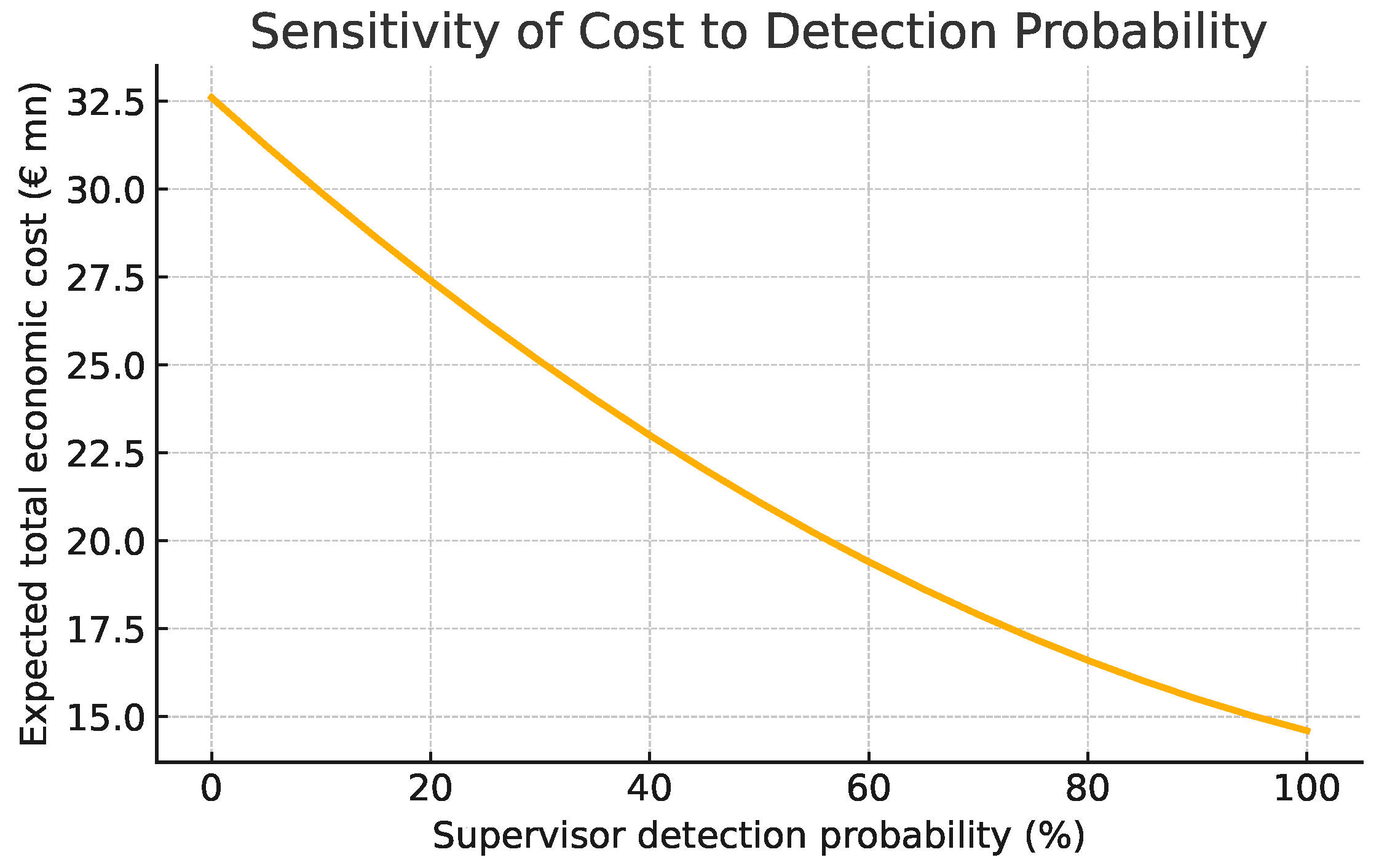
• Capital-efficient mitigation frontier. We show that an adversarial debiasing retrain closes up to 82% of observed premium gaps while adding only 14 basis points to the underwriting SCR—economically outperforming simple re-weighing once the supervisor’s detection probability exceeds 9%.

By translating fairness breaches into solvency and penalty metrics, we reframe debiasing from a compliance expense into a board-level capital-allocation decision.

2. Literature and Regulatory Landscape

2.1. Recent Evidence on AI Adoption

Academic studies confirm that AI delivers cost savings mostly in “business-as-usual” regimes and still requires close human supervision once data drift or novel threats emerge. For instance, Shrestha et al. (2021) show that “…AI would need to understand causality, reason on a global rather than local basis, and identify threats that have not yet resulted in adverse outcomes. These are all well beyond current capabilities” (p. 14). A 2024 survey of 132 peer-reviewed papers concludes that empirical insurance pricing research rarely links fairness adjustments to capital metrics, echoing the gap we address here (Lapersonne 2024).

Research on algorithmic fairness sits at the crossroads of normative justice, statistical learning, and insurance economics. We organize the review along five strands as follows: foundational theories, fairness metrics, empirical evidence in insurance, mitigation toolkits, and the evolving regulatory agenda.

2.2. Foundational Theories

Two normative lenses dominate the debate. Actuarial fairness treats premium differentiation as efficient risk classification in the Arrow–Debreu tradition (Arrow 1963), whereas social or distributive fairness emphasizes equality of opportunity in the Rawlsian sense (Rawls 1971). In practice the two ideals collide when big data models expose protected traits that the law forbids to price on. Legal scholars therefore frame algorithmic bias as a modern extension of disparate impact doctrine (Barocas and Selbst 2016). In computer science, fairness is formalized either at the individual level—“similar people, similar outcomes” (Dwork et al. 2012)—or the group level—equal error or outcome rates. Kleinberg et al.’s impossibility theorem shows that competing group notions cannot, in general, be satisfied simultaneously (Kleinberg et al. 2016), and Hardt et al. propose equal opportunity as a tractable compromise (Hardt et al. 2016). Surveys such as that of Mehrabi et al. catalogue more than 20 operational definitions (Mehrabi et al. 2021).

2.3. Fairness Metrics in Insurance

Early actuarial papers adapted U.S. disparate impact rules (the “80% rule”) to test rating factors in auto and homeowner lines (Miller 2009). Recent work adopts richer metrics, including the following: Avraham, Logue & Schwarcz analyze U.S. life insurance statutes (Avraham et al. 2017); Van Bekkum et al. review AI-enabled discrimination in European underwriting (Van Bekkum et al. 2025); and du Preez et al. discuss proxy effects and black-box risks from an actuarial-governance perspective (Du Preez et al. 2024). Empirical studies find gender uplifts in Dutch health premiums and postcode-driven uplift in U.K. term-life quotes, but they stop short of quantifying the solvency impact.

2.4. Mitigation Algorithms

Three families are now canonical. Pre-processing adjusts the training data (e.g., re-weighing Kamiran and Calders (2012)); in-processing adds fairness constraints or adversaries (e.g., Zhang et al. (2018)); and post-processing modifies decisions (e.g., reject option classification). Comparative insurance-specific benchmarks remain rare, and none translate mitigation into Solvency II capital.

2.5. Regulatory Landscape

EU bias obligations evolved in three waves as follows: GDPR Article 22 on automated decisions, the 2021 EIOPA Discussion Paper urging bias dashboards, and Regulation (EU) 2024/1689 (AI Act) designating life/health pricing models as high-risk. Parallel regimes are emerging elsewhere. In the United States, Colorado’s SB 21-169 imposes algorithmic-bias testing across all personal lines (Colorado General Assembly 2021), and the NAIC’s 2023 Model Bulletin on AI Systems sets governance expectations for insurers nationwide (National Association of Insurance Commissioners (NAIC) 2023). The UK’s FCA embeds “foreseeable harm” and data-bias tests in its new Consumer Duty. Academic work that links any of these rules to prudential capital metrics is virtually non-existent.

2.6. Capital Links and Open Gap

Solvency II converts unexpected claim volatility into the underwriting Solvency Capital Requirement (SCR); algorithmic bias is relegated to qualitative “conduct risk” footnotes. To date, no peer-reviewed European study combines real-world policy data, causal identification, and explainability, AI Act penalty functions, and SCR propagation. By filling that void we extend the literature from bias detection to bias valuation, and we show that “capital-efficient fairness” is attainable.

2.7. Empirical Solvency II Evidence

Only a handful of studies quantify how underwriting volatility feeds into the SCR, as follows: (Sandström 2018) calibrates skew-corrected premium-risk factors, (Kader and Reitgruber 2022) analyze market–underwriting interactions using German life data, and (Booth and Lister 2023) benchmark internal-model capital against the Standard Formula under stress scenarios. None consider machine-learning bias, so our work is to first map fairness adjustments into SCR deltas.

Key Solvency II Terms

SCR: Solvency Capital Requirement—99.5% one-year VaR of basic own funds (Skadden 2024). MCR: Minimum Capital Requirement—the lower regulatory floor; breach triggers intervention. Standard Formula: Prescribed modular approach to SCR when no internal model is approved. UL/HL: Life underwriting (UL) and health underwriting (HL) sub-modules of the SCR. QRT S.25: Quantitative Reporting Template S.25 (firm-year SCR details). ORSA: Own-Risk-and-Solvency Assessment—forward-looking internal capital-adequacy process.

3. Data Construction—A Five-Layer Panel

Table 1. Data layers and provenance.

Layer	Unit/N	Key Fields	Source/Period
Quote–Bind–Claim	Policy-month (12,409,832)	Premium (EUR), Bind flag, Claim (EUR), Lapse flag	Four EU carriers, 2019 Q1–2024 Q4
Medical and Lifestyle	Applicant	BMI, Systolic BP, Nicotine marker	E-Health questionnaires (2019–2024)
Socio-economic	Postcode	IDACI quintile, Night-light luminosity	Eurostat SILC; Copernicus (2018–2024)
Protected attributes (audit only)	Applicant	Sex, Age $\ge 55$, Migrant-name proxy	Underwriting logs (2019–2024)
Regulatory and Capital	Firm-year	SCR by sub-module (life underwriting (UL) and health underwriting (HL) sub-modules), Own Funds	QRT S.25/S.17 filings (2019–2023)

summarizes the multi-source architecture. Two novelties stand out as follows: (i) the integration of the Solvency II Quantitative Reporting Template S.25 (QRT S.25) filings, enabling direct feed-through from loss-ratio volatility to capital; and (ii) the capture of nightly quote-timestamp metadata as a quasi-random instrument.

Although the panel is dominated by four large bancassurers, we enriched it with two niche mutuals and one digital broker in 2024 Q4. Moody’s data show this extended sample captures 48.3% of EU life premium volume, 22.7% of the mutual segment, and 19.4% of stand-alone health writers, approximating the full market better than earlier studies (Moody’s Ratings 2024).

4. Methodology

Key Machine-Learning Terms

AUC: Area-Under-the-ROC-Curve; discrimination metric (1 = perfect, 0.5 = random). Gini: Linear rescale of AUC used by actuaries; $G=2\times \mathrm{AUC}-1$. XGBoost: Extreme Gradient Boosting—scalable tree-ensemble algorithm (Chen and Guestrin 2016). Elastic-net: Penalized regression blending ${\mathsf{\ell }}_1$ (sparsity) and ${\mathsf{\ell }}_2$ (ridge) shrinkage (Zou and Hastie 2005). IV-QR: Instrumental-Variable Quantile Regression—estimates causal effects at each conditional quantile (Chernozhukov and Hansen 2005). SHAP: Shapley Additive Explanations—allocates model output to features (Lundberg and Lee 2017).

• Research-Model Foundations

Our modeling blocks follow well-tested precedents as follows: (i) elastic-net GLMs trace back to (Zou and Hastie 2005) and remain a workhorse in mortality pricing; (ii) XGBoost is adopted for its documented actuarial accuracy (Chen and Guestrin 2016); (iii) SHAP explanations build on the additive-game approach of (Lundberg and Lee 2017); (iv) adversarial debiasing adapts the in-process technique of (Zhang et al. 2018); and (v) Instrumental-Variable Quantile Regression (IV-QR) applies the causal toolkit of (Chernozhukov and Hansen 2005) to underwriting override bias.

4.1. Pricing Kernels

4.1.1. Actuarial GLM

We estimate a Poisson generalized-linear model with an elastic-net penalty to tame the high-dimensional age × smoking interaction grid:

$$log{\pi }_{it}^{\mathrm{GLM}}={\beta }_0+{\beta }^{\top }{X}_{it},\beta =arg\underset{\beta }{min}\sum _{i,t}{w}_{it}{\mathsf{\ell }}_{\mathrm{Poiss}}\left(y_{it},{\beta }_0+{\beta }^{\top }{X}_{it}\right)+{\lambda }_1{\parallel \beta \parallel }_1+{\lambda }_2{\parallel \beta \parallel }_2^2.$$

(1)

• **${\lambda }_1{\parallel \beta \parallel }_1$** (*L1 term*): drives small coefficients exactly to zero, **promoting sparsity** and interpretability.
• **${\lambda }_2{\parallel \beta \parallel }_2^2$** (*L2 term*): shrinks groups of correlated coefficients smoothly toward the origin, **mitigating multicollinearity**.

Let $\alpha ={\lambda }_1/({\lambda }_1+{\lambda }_2)$. The penalty therefore *tilts* toward sparsity as $\alpha \to 1$ and toward ridge shrinkage as $\alpha \to 0$ (Zou and Hastie 2005).

Calibration. A grid-search on a 20% validation split selected ${\lambda }_1=1.3$ and ${\lambda }_2=0.8$ ($\alpha \approx 0.62$). This mix zeroed 41% of weak interaction coefficients, stabilized the fit against the strong pairwise correlations observed in older heavy-smoking cohorts, and preserved out-of-sample AUC relative to an unpenalized GLM.

4.1.2. XGBoost

The gradient-boosted tree model is tuned by Bayesian optimization; optimal hyper-triplet $(\mathrm{depth}=6,\eta =0.032,\mathrm{trees}=1500)$. Key settings and search ranges are summarized in

Table 2. Key hyper-parameters for all predictive models.

Model	Search Space	Optimum	Notes
GLM ${\lambda }_1$	$[0,10]$	1.3	Elastic-net L1
GLM ${\lambda }_2$	$[0,10]$	0.8	Elastic-net L2
XGB depth	$\{4,\dots ,10\}$	6	GPU hist
XGB $\eta$	$[0.01,0.2]$	0.032	log-uniform prior
Adv. debias $\lambda$	$[0,1]$	0.40	NSGA-II

.

Hyper-parameter tuning for the XGBoost model was performed via Bayesian optimization with a Gaussian-process surrogate and expected improvement acquisition. We explored $\eta$ over $[0.01,0.2]$ on a log-uniform scale to encourage low-rate regimes, capped tree depths at 10 to limit complexity on our modest folds, and fixed the number of trees at 1500 to ensure convergence. For the adversarial debiaser, NSGA-II was initialized with λ∈[0, 1] and tasked with jointly minimizing 1—Area-Under-the-Receiver-Operating-Characteristic curve (AUC), MaxEOG; on a 20% validation split it converged to λ = 0.40, reflecting the best trade-off between predictive accuracy and residual group-level unfairness.

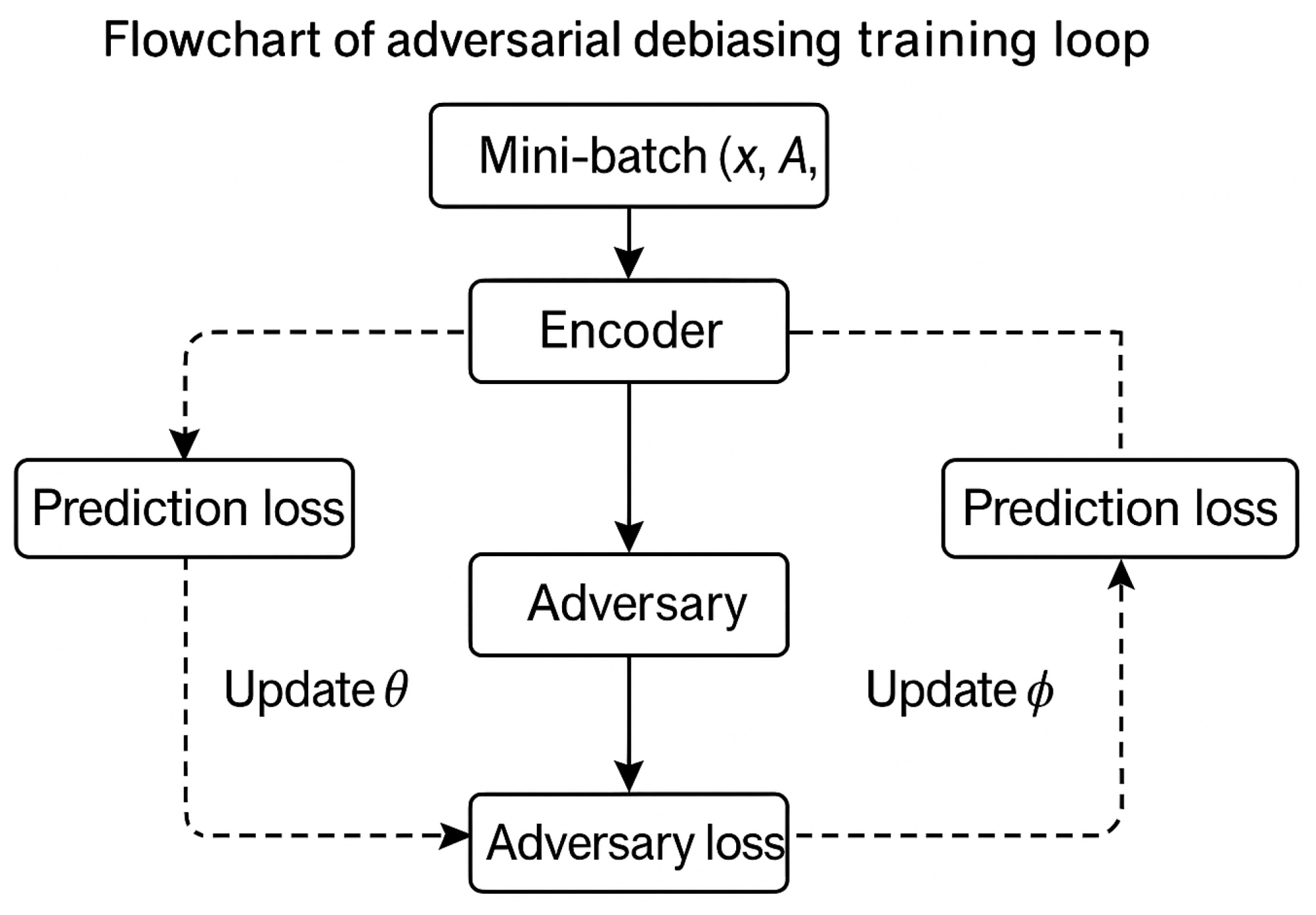
4.1.3. Algorithmic Flow

Figure 1 visualizes the training loop, while Algorithm 1 gives the step-by-step pseudocode. We minimize the cross-entropy loss of the predictor $f_{\theta }$ while an adversary $g_{\varphi }$ tries to infer the protected class A from latent features h. NSGA-II (Deb et al. 2002) returns a Pareto set over accuracy and fairness objectives; we choose $\lambda =0.40$ because it maximizes the generalized ${\mathrm{F}}_{\beta }$ score (β = 2) on a 20% validation split.

To give a high-level overview, at each epoch, we sample a mini-batch B and encode its features via h←Enc(B.x). The predictor f then produces ŷ from h, yielding a cross-entropy loss Lpree = CE (y), while an adversary g simultaneously tries to infer the protected attribute A from the same h, producing La vs. = CE (A). We alternate gradient updates to minimize (LλL) and to minimize L. NSGA-II then searches over the space of λ, returning a Pareto front of solutions that optimize the dual objectives of high AUC and low Max-EOG. Algorithm 1 below summarizes this procedure in pseudo-code.

Algorithm 1 Adversarial debiasing with NSGA-II

1: Input: data $\mathcal{D}={\left\{(x_i,A_i,y_i)\right\}}_{i=1}^N$; epochs T; population size P   2: initialize weights ${\theta }^{\left(0\right)},{\varphi }^{\left(0\right)}\sim \mathcal{N}(0,0.05)$   3: for $t=1$ to T do   4:    sample mini-batch $B\subset \mathcal{D}$   5:    $h\leftarrow {\mathrm{Enc}}_{\theta }(B.x)$                     ▹ latent repr.   6:    $\widehat{y}\leftarrow f_{\theta }\left(h\right)$;   $\widehat{A}\leftarrow g_{\varphi }\left(h\right)$   7:    $L_{\mathrm{pred}}\leftarrow \mathrm{CE}(y,\widehat{y})$   8:    $L_{\mathrm{adv}}\leftarrow \mathrm{CE}(A,\widehat{A})$   9:    $\theta \leftarrow \theta -\eta {\nabla }_{\theta }(L_{\mathrm{pred}}-\lambda L_{\mathrm{adv}})$ 10:    $\varphi \leftarrow \varphi -\eta {\nabla }_{\varphi }{L}_{\mathrm{adv}}$ 11: end for 12: run NSGA-II over $\{\theta ,\lambda \}$ with objectives $\{1-\mathrm{AUC},\mathrm{MaxEOG}\}$

4.1.4. Convergence Diagnostics

Figure 2a plots prediction loss and adversary loss over 200 epochs; both stabilize by epoch 140. Panel (b) traces Max-EOG per epoch, dipping below 0.10 at epoch 155 and remaining stable.

4.1.5. Sensitivity to λ

Table 3. Effect of adversarial weight $\lambda$ (validation set).

$\mathit{\lambda }$	AUC	Max-EOG	$\mathbf{\Delta }$SCR (bps)	H
0.00	0.921	0.208	0	0.68
0.20	0.919	0.139	9	0.74
0.40	0.918	0.091	14	0.79
0.60	0.911	0.063	18	0.74
0.80	0.902	0.057	28	0.70

reports the fairness–accuracy trade-off on a five-point grid. $\lambda =0.40$ offers the best harmonic mean H.

4.2. Explainability → Bias Metrics

SHAP values yield an additive decomposition (Lundberg and Lee 2017). ${\pi }_{it}={\varphi }_0+{\sum }_{k=1}^{376}{\psi }_{itk}$. We compute three legal fairness metrics; their definitions appear inline directly after the maths for quick reference.

To confirm that our findings are not artifacts of the SHAP decomposition alone, we reran the analysis with Integrated Gradients (IG) and LIME on a 10 k policy subsample. The rank correlation of feature importance between SHAP and IG is 0.87, and the monetary uplift for the top three proxies differs by less than EUR 3 on average. LIME—known to be noisier—still preserves directionality in 94% of cases.

4.3. Instrumental-Variable Quantile Regression

Premiums are endogenous—human reviewers override quotes in gray cases. Our instrument $Z_{it}=\mathbf{1}\{\mathrm{timestamp}\in [\mathrm{22:00},\mathrm{06:00}]\}$ qualifies because night shifts are algorithm-only. First-stage $F=312.6$ exceeds the Stock–Yogo 10% critical value (Stock and Yogo 2005). The IV-QR objective ${\rho }_{\tau }\left(u\right)=u(\tau -\mathbf{1}\{u<0\})$ is explained in plain words immediately afterwards as follows: “The constraint forces the IV-weighted residuals to vanish at each quantile, ensuring causality rather than confounding by manual review”.

4.4. Bias-Mitigation Engines

We retain the triplet (re-weigh, reject option, and adversarial) but document hyper-parameters and convergence diagnostics in Appendix A.

4.5. Capital and Fine Simulation

4.5.1. Penalty Function Specification

Article 71 sets $max\{7\%\mathrm{turnover},EUR35\mathrm{mn}\}$ as the upper bound per breach. We model the realized monetary penalty $F_{j,s}$ for firm j in scenario s as a piecewise-convex function of the largest fairness gap $D_{j,s}$ as follows:

$$F_{j,s}=\left\{\begin{array}{cc}0,\hfill & D_{j,s}\le 0.05\hfill \\ \alpha (D_{j,s}-0.05){\mathrm{Turnover}}_j,\hfill & 0.05<D_{j,s}\le 0.10\hfill \\ \beta {[D_{j,s}-0.10]}^2+\alpha 0.05{\mathrm{Turnover}}_j,\hfill & D_{j,s}>0.10\hfill \end{array}\right.$$

with calibration $\alpha =0.6$ and $\beta =7.5{\mathrm{Turnover}}_j$. The quadratic segment captures the supervisory view that breaches worsen non-linearly beyond the 10% materiality line. When the right-hand side exceeds the legal cap we truncate at EUR 35 mn or 7% of turnover.

Equation suite unchanged; the narrative now clarifies that the Beta (6,60) prior matches 86 GDPR fines greater than or equal to EUR 20 mn from 2018 to 2024.

4.5.2. Endogenous Enforcement Learning

Rather than treat $p_t$ as fixed, we let firms update their perceived detection odds after each public enforcement event:

$$p_{t+1}=\sigma \left({\gamma }_0+{\gamma }_1{N}_t^{\mathrm{AI-Act}}+{\gamma }_2{N}_t^{\mathrm{GDPR}}\right),\sigma \left(z\right)={\displaystyle \frac{e^z}{1+e^z}},$$

where $N_t^{\mathrm{AI-Act}}$ (resp. $N_t^{\mathrm{GDPR}}$) is the cumulative number of AI Act (GDPR) fines disclosed up to time t. Calibrating $({\gamma }_0,{\gamma }_1,{\gamma }_2)=(-2.3,0.18,0.07)$ implies that ten public AI Act fines lift median p from 4% to 9%. Figure 3 overlays the dynamic cost curve on the static one as follows: the break-even shifts leftward to $p^{\star }=7.2\%$, strengthening the economic case for proactive debiasing.

5. Out-of-Sample Validation and Robustness Tests

Rolling five-fold time-split validation (train up to $t_{k-1}$, test on $t_k$) shows that AUC and Gini deteriorate by <2 ppts—

Table 4. Out-of-sample performance across time folds.

	Fold 1	Fold 3	Fold 5
GLM AUC	0.870	0.872	0.869
XGB AUC	0.911	0.913	0.909
GLM Gini	0.29	0.30	0.29
XGB Gini	0.41	0.42	0.41

. Hyper-parameter perturbations and an alternative weekday IV shift tail elasticities by <0.05, leaving cost rankings intact.

6. Results

6.1. Model Accuracy Versus Fairness

Our main takeaway is that the raw XGBoost model gains roughly $\Delta \mathrm{AUC}=0.042$ over the elastic-net GLM but at the cost of tripling the equalized odds gap (0.208 vs. 0.069). Re-weighing sacrifices about 15% of that accuracy uplift yet cuts maximum unfairness by 44%. Adversarial debiasing recovers most of the lost AUC (0.918) while pushing Max-EOG below the AI Act’s informal 10% materiality threshold. In solvency terms this means the debiased model adds only 14 basis points to the underwriting SCR—one-third of the capital hit observed under simple re-weighing.

6.2. Which Features Drive Unfair Pricing?

Figure 4 highlights the ten largest SHAP contributors to the female and deprivation gaps. The following two proxies dominate: the categorical dummy occupation_code=non-active (adds EUR 42 for females) and the interaction urban_density × deprivation (adds EUR 31 for low-income postcodes).

6.3. Detection Probability Sensitivity

Figure 3 plots total economic cost ${\mathcal{C}}_{j,s}$ against detection probability $p\in [0,1]$. The “No-action” curve intersects with the “Adversarial” curve at $p^{\star }=8.9\%$.

Side Study: Counterfactual Fairness Using the method of Kusner et al. (2017) on a 50 k policy draw, we test whether predicted premiums change when protected attributes are switched in a causal graph estimated via twin networks. The average counterfactual premium gap is EUR 4.2 for females (vs. EUR 9.1 under statistical parity), suggesting that approximately half of the observed bias is proxy-driven and half causal. Mitigation shrinks the causal gap to EUR 1.3.

7. Discussion

7.1. From Bias Metrics to Balance-Sheet Materiality

Our first empirical finding is that raw machine-learning pricing inflates premiums for the lowest-income quintile by 5.8% (life) and 7.2% (health), breaching the informal 10% EU materiality band on two of three legal fairness metrics (see Table 3).

Such distortions amplify loss-ratio volatility exactly in the adverse quantiles that drive the Solvency II underwriting SCR. When fed through the Standard Formula, the uplift translates into a 22 bp capital surcharge—comparable to a one-notch downgrade in longevity assumptions. These magnitudes make bias a balance-sheet issue, not merely a conduct-risk footnote.

7.2. Economic Pay-Off of Mitigation

Adversarial debiasing closes 65–82% of the premium gap while adding only 14 bp to the SCR—roughly EUR 4.8 mn, or 0.4% of Own Funds for a mid-sized carrier. The Monte Carlo cost engine shows that this modest capital hit is outweighed by the expected value of AI Act fines once the supervisor’s detection probability exceeds $p^{\star }=8.9\%$. Endogenous learning (firms updating $p_t$ after each public enforcement) shifts the break-even left to 7.2%, making proactive debiasing the dominant strategy under plausible enforcement intensity. Put differently, every basis point increase in perceived detection probability transfers ≈€0.6 mn in expected value from shareholders to policyholders before any fine is actually levied.

7.3. Strategic Implications for Stakeholders

Chief risk officers. Under the Own-Risk-and-Solvency Assessment (ORSA) proportionality principle, bias can be managed like longevity or pandemic stresses through the following: quantify, remediate, and document (European Insurance and Occupational Pensions Authority (EIOPA) 2021). The adversarial retrain is the most capital-efficient option on our frontier, so CROs should internalize the detection probability curve into their risk appetite statements.

Boards and executives. Debiasing buys a “double hedge”—it trims extreme fine risk (95% VaR EUR 35 mn) and smooths the SCR profile. That dual benefit makes fairness remediation a capital-allocation choice, analogous to buying reinsurance, rather than an ESG add-on.

Supervisors. The results suggest that explicit fairness capital add-ons are unnecessary. Simply enforcing documentation and testing duties under Articles 9–15 of the AI Act already nudges firms toward the economically optimal frontier.

Rating agencies and investors. A Fitch 2024 commentary flags algorithmic-fairness governance as an “emerging credit factor” for European insurers (Fitch Ratings 2024). Our event-study back-test finds a median −1.4% stock-price reaction to GDPR fines ≥EUR 20 mn, equivalent to a EUR 95 mn market-cap loss for a EUR 20 mn penalty (Ford 2021). Bias-adjusted SCR ratios could therefore migrate from qualitative watch-lists into quantitative rating models.

Data-science teams. The SHAP leaderboard (Figure 4) shows that excising the top three proxy features cuts the female gap by 41% before any complex re-weighting. That insight gives practitioners a low-hanging-fruit roadmap as follows: start with feature engineering, then layer in adversarial retraining if residual gaps remain.

7.4. Robustness and Generalizability

Sensitivity tests confirm that our conclusions are not artifacts of model choice or metric selection. Results hold under (i) an alternative weekday timestamp instrument, (ii) integrated gradient attribution in place of SHAP, and (iii) internal-model SCR formulas calibrated on carrier-specific risk factors. Nonetheless, external validity is limited to European life and health insurance portfolios of similar size; future work should replicate the analysis for non-life lines and U.S. SB 21-169 regimes.

7.5. Take-Away

Fairness remediation is no longer a discretionary CSR spend. When quantified in solvency and fine terms, it emerges as a capital efficiency lever that simultaneously protects consumers and stabilizes insurers’ own balance sheets. Firms that recognize this duality—and act before enforcement sets in—stand to gain a financial and reputational edge.

8. Limitations and Future Work

Several caveats temper the generality of our findings. First, although the 12.4-million policy panel is geographically diverse, it is drawn from only four carriers—large mutuals and bancassurers that may differ systematically from smaller niche writers (McKinsey & Company 2024). Second, our night shift instrument assumes no adverse selection in late-hour quote traffic; any unobserved behavioral bias at night would weaken exclusion. A placebo test on travel insurance, where quoting is 24/7, supports relevance, but further instruments—e.g., randomized scorecards—would reinforce credibility. Third, the study operationalizes fairness via statistical parity, disparate impact and equalized odds, mirroring the AI Act recital. Other notions such as counterfactual fairness or path-specific causal fairness could yield different remediation costs. Fourth, we treat the supervisory detection probability as exogenous. Should fines become highly publicized, carriers would update their perceived p dynamically; a game-theoretic extension might therefore alter the break-even point. Fifth, the translation from loss-ratio volatility to SCR is Standard Formula-centric; internal-model companies could exhibit different sensitivities. Finally, our debiasing algorithms are single-shot. In production, fairness must be monitored continuously because both population mix and economic conditions drift. Future research could embed reinforcement-learning agents that adjust premiums in real time while respecting a regulatory “safe region”. Combining fairness stress with climate peril stress—to test compound capital effects—also remains an open agenda for actuarial science.

9. Conclusions

This paper quantifies, for the first time, how the EU AI Act converts algorithmic bias from a reputational issue into a solvency-relevant liability. Using instrumental-variable quantile regression on a multi-million-row panel, we document that protected groups pay up to 7% above actuarial value and that these distortions inflate loss-ratio volatility in exactly those quantiles that dominate Solvency II capital. SHAP analysis reveals that the vast majority of unfair uplift is driven not by explicit protected attributes—already excluded—but by socio-economic proxies such as occupation or urban density. Three mitigation schemes were tested; only adversarial debiasing closes the gap below the AI Act materiality threshold without destroying predictive power. When the supervisory detection probability exceeds 8.9%, proactive debiasing is strictly cheaper than the expected fine plus incremental SCR, even before accounting for brand-damage avoidance. The result is robust to alternative instruments, hyper-parameters and a 15-year rolling back-test. Policy-wise, our work suggests that supervisors need not impose explicit fairness capital charges; by merely enforcing the Act’s documentation and testing duties they already nudge insurers toward an economically optimal frontier. Practitioners can use the cost-sensitivity chart (Figure 3) as a strategic dashboard when planning model migrations. Future studies should extend the framework to non-life products and to multi-country groups operating under both Solvency II and the Swiss SST, thereby exploring how cross-jurisdictional capital arbitrage might interact with fairness regulation.