Copula Modeling of COVID-19 Excess Mortality

Abstract

COVID-19’s effects on mortality are hard to quantify. Issues with attribution can cause problems with resulting conclusions. Analyzing excess mortality addresses this concern and allows for the analysis of broader effects of the pandemic. We propose separate ARIMA models to analyze excess mortality for several countries. For the model of joint excess mortality, we suggest vine copulas with Bayesian pair copula selection. This is a new methodology and after its discussion we offer an illustration. The present study examines weekly mortality data from 2019 to 2022 in the USA, Canada, France, Germany, Norway, and Sweden. Previously proposed ARIMA models have low lags and no residual autocorrelation. Only Norway’s residuals exhibited normality, while the remaining residuals suggest skewed Student t-distributions as a plausible fit. A vine copula model was then developed to model the association between the ARIMA residuals for different countries, with the countries farther apart geographically exhibiting weak or no association. The validity of fitted distributions and resulting vine copula was checked using 2023 data. Goodness of fit tests suggest that the fitted distributions were suitable, except for the USA, and that the vine copula used was also valid. We conclude that the time series models of COVID-19 excess mortality are viable. Overall, the suggested methodology seems suitable for creating joint forecasts of pandemic mortality for several countries or geographical regions.

1. Introduction

The COVID-19 pandemic began in late 2019, and quickly manifested itself as a massive increase in global mortality. However, there were problems related to attribution and causation. As such, when it comes to analyzing or modeling COVID-19 mortality data, there are two approaches. The first is to specifically use COVID-19-attributed mortality. This has the benefit of a clear causal structure, where patterns in the data can be more easily connected to the spread of the pandemic (Lei and Shemyakin 2023). However, there are notable problems with respect to proper attribution. Deaths related to COVID-19 are not attributed to the disease absent a positive COVID-19 test, which is not always possible in locations unable to test (Wang et al. 2022). This is to say nothing of other infrastructure issues or potentially missing deaths not directly caused by COVID-19, but instead by complications from an existing condition or a response to the pandemic (Ahamad et al. 2020; Zińczuk et al. 2023). However, using mortality data directly attributed to COVID-19 comes with the massive benefit of no ambiguity.

The second approach is to analyze overall mortality, usually via the concept of excess mortality. This is defined as the normalized difference between an expected (historical) death count and aggregate deaths (Britt et al. 2023). Although there is some ambiguity in calculating the expected number of deaths for a particular location, this approach has the benefit of capturing systemic effects the pandemic might have had (Martinez-Folgar et al. 2021; Zińczuk et al. 2023). For example, it allows data to include the effects of increased mortality in those with existing conditions of contracting COVID-19 (Martinez-Folgar et al. 2021), or possible increases in suicides (Yan et al. 2023). However, the data will also reflect a decrease in vehicle-related deaths due to lock-downs (Wang et al. 2022). This approach captures the net effect and accurately reflects the total effect of the pandemic. However, it also carries the possible risk of masking the magnitude of the positive effect on mortality.

Regardless, multiple approaches are used to model the resulting data. The Center for Disease Control (CDC) has suggested ensemble models (Johannson et al. 2020), used also in Imperial College COVID Response Team (2022), and in Wang et al. (2022). Martinez-Folgar et al. (2021) and Basellini et al. (2021) used generalized additive models to relate different demographic or location data with mortality. These models usually address multiple covariates and require massive data collection. The approach of this paper is different. It combines ARIMA analysis of excess mortality for different geographical areas, and then applies vine copulas with Bayesian pair copula model selection to study the dependence patterns between these areas. Therefore, the model is based on open source mortality data and does not require a detailed analysis of mortality covariates.

ARIMA models have frequently been used in COVID studies. For listed examples, see Britt et al. (2023) and Wang et al. (2022). Copula models have also been used to determine the relationships between mortality and other time series data, such as the correlation of interstate trends (Kim 2022), or by combining mortality data with temperature (Alanazi 2021); however, they were rarely used in conjunction with ARIMA modeling.

Here, we follow the method laid out by Lei and Shemyakin (2023), in which ARIMA models are developed for individual locations, and the model residuals are then related to each other via copula analysis. This allows for seasonality and intra-country effects to be accounted for before addressing cross-correlation between countries. This also allows for the non-normal residuals, which while technically a violation of ARIMA assumptions, allows for the interpretation of fat-tailed residual distributions as an indication of a more complicated dependence structure.

The present paper has an objective of analyzing excess mortality time series $Y_t^{\left(i\right)}$ for different countries $i=1,\dots ,k$ during the period of T weeks $t=1,\dots ,T$ and modeling the dependence patterns in the vector $(Y_t^{\left(1\right)},\dots ,Y_t^{\left(k\right))})$ through the ARIMA residuals $({\epsilon }_t^{\left(1\right)},\dots ,{\epsilon }_t^{\left(k\right))})$.

Mortality statistics are particularly difficult to compare across countries for several reasons. First and foremost, different countries have different standards for recording deaths. For example, England records only the date a death is “registered,” while the United States records mortality statistics using the date of a death (Basellini et al. 2021; National Center for Health Statistics 2025). This means comparisons involving countries who do not record the date of a death are difficult, as actual mortality experience will not be reflected in the data. While a close reconstruction of weekly data is possible (see Martinez-Folgar et al. 2021), it still leaves open the potential problem of a death being registered several weeks after it occurs, making assigning the week it occurred impossible. Second, countries differ in how they define a “week” and how many there are in the calendar year. For example, the European countries in this study (France, Germany, Norway, Sweden) record their weekly mortality data as the sum of deaths occurring from Monday-Sunday, while the United States and Canada record theirs as the sum of deaths from Sunday to Saturday (National Center for Health Statistics 2025). This makes interpretations of resulting models somewhat weaker, but absent massive spikes for one day only, it should not affect overall trends.

2. ARIMA

Box–Jenkins models, more commonly known as ARIMA models, stand for autoregressive integrated moving average models of a time series. They have lag (order) $p=1,2,\dots$ for the single variable time series $Y_t,t=1,\dots ,T$,

$$Z_t={\beta }_0+{\beta }_1·Z_{t-1}+\dots +{\beta }_p·Z_{t-p}+{\epsilon }_t,{\epsilon }_t\sim N(0,{\sigma }^2),$$

(1)

integrated with the moving average model with lag $q=1,2,\dots$,

$$Z_t={\alpha }_0+{\alpha }_1·{\epsilon }_{t-1}+\dots +{\alpha }_q·{\epsilon }_{t-q},{ϵ}_t\sim N(0,{\sigma }^2),$$

(2)

which is applied to the differences $Z_t$ of $Y_t$ with order $d=0,1,2,\dots$,

$$Z_t=D^d{Y}_t,D{Y}_t=Y_t-Y_{t-1},D^d{Y}_t=D{D}^{d-1}{Y}_t,$$

(3)

where $d>0$ allows the specification of non-stationary models as defined as ARIMA $(p,d,q)$. Here, $d=0$ corresponds to the the stationary model ARIMA $(p,0,q)$ also known as ARMA $(p,q)$.

ARIMA model selection requires the estimation both of $p,d,q$ and the subsequent $p+q+1$ parameters in the regression models. This is usually performed via Bayesian or maximum likelihood methods. This yields fitted values of ${\widehat{Y}}_t$ for $t=1,\dots ,T$ and residuals ${\widehat{\epsilon }}_t={\widehat{Y}}_t-Y_t$.

Unit root tests or other stationarity tests can be used to determine the differencing order d, which can be further informed by the behavior of the ACF or PACF of the time series data. Afterwards, the lag order parameters can be determined via information criterion, such as the Akaike and Bayesian (Schwarz) information criteria. Note that in the case of either the AIC or BIC, there is a penalty term for the number of parameters, leading to more parsimonious models if the information criteria are used for model selection. Note also that changing the value of d does not change the number of parameters to be estimated.

Distribution Analysis of ARIMA Residuals

In general, ARIMA methods are efficient in the assumption of normality of the residuals ${\widehat{\epsilon }}_t$. However, in many applications, especially survival analysis and finance, one has to deal with asymmetric and fat-tailed residual distributions failing the normality assumption. Therefore, a skewed t-distribution model, such as the one put forward by Fernandez and Steel (1996) may be suitable to the describe the distribution of residuals. The PDF defined therein is as follows.

$$p_{{\epsilon }_t}\left(y\right)={\displaystyle \frac{2}{\xi +\frac{1}{\xi }}}{\displaystyle \frac{\Gamma \left(\frac{v+1}{2}\right)}{\Gamma \left(\frac{v}{2}\right){\left(\pi v\right)}^{1/2}}}{\left(\sigma \right)}^{-1}{[1+{\displaystyle \frac{{(y-\mu )}^2}{v\left({\sigma }^2\right)}}({\displaystyle \frac{1}{{\xi }^2}}{I}_{\left[0,\infty \right)}(y-\mu )+{\xi }^2{I}_{(-\infty ,0)}(y-\sigma ))]}^{-{\displaystyle \frac{v+1}{2}}}.$$

(4)

Regardless, fitted distributions should be compared to residual data to ensure accuracy. A common goodness-of-fit test is the Kolmogorov–Smirnov test, which compares empirical CDFs between two different samples of data and/or distributions. Once a distribution has been chosen, the residuals can be appropriately modeled as random variables.

In the case of several dependent time series $Y_t^{\left(i\right)},i=1,\dots ,k$, k separate models can be developed for the marginal distributions of ${\epsilon }_t^{\left(i\right)}$, which will help further construction of the joint distribution of $({\epsilon }_t^{\left(1\right)},\dots ,{\epsilon }_t^{\left(k\right))})$, which is the ultimate goal.

3. Copula Analysis

Copula analysis is commonly used to model non-linear statistical dependence between two or more random variables. Copulas are special functions that can describe dependence of random variables as an association between their marginal distributions. In the present paper, copula analysis is applied to model the joint distribution of ARIMA residuals $({\epsilon }^{\left(1\right)},\dots ,{\epsilon }^{\left(k\right))})$ using the marginal distributions obtained in the previous section.

Let $X,Y$ be random variables, with CDFs $u=F_X\left(x\right)$ and $v=F_Y\left(y\right)$. Then their joint distribution of $P(X\le x,Y\le y)$ can be represented using a copula function $C(u,v|r)$, where r is some set of parameters measuring the strength of dependence between the two variables.

Sklar’s theorem states that any copula function $C(u,v)$ of $u=F_X\left(x\right)$ and $v=F_Y\left(y\right)$ is a valid joint CDF, and also, any joint distribution function $F_{X,Y}(x,y)$ can be represented as a copula function of its marginals. Therein lies the advantage of copulas; the copula framework allows for modeling of the joint distribution in two steps. First, one models the marginals, and then, one uses an appropriate copula function for modeling their association.

There are many different types of copulas to be used for this purpose. For an in-depth list and definitions, see Brechmann (2010). The most popular copulas used in practice are Archimedean copulas or elliptical copulas. The former are easier to estimate parameters for, while the latter are easier to extend to higher dimensionality, e.g., more marginals.

The most popular one-parametric Archimedean pair copulas combining marginal distribution functions and their dual versions combining marginal survival functions are

• Clayton’s Copula

  $$P(X\le x,Y\le y)=C_1(u,v|\tau )=max\left[{(u^{{\displaystyle \frac{2\tau }{\tau -1}}}+v^{{\displaystyle \frac{2\tau }{\tau -1}}}-1)}^{{\displaystyle \frac{\tau -1}{2\tau }}},0\right],-1<\tau <1.$$

  (5)
• Gumbel–Hougaard’s Copula

  $$P(X\le x,Y\le y)=C_2(u,v|\tau )=exp\left[-{\left({\left[-ln\left(u\right)\right]}^{{\displaystyle \frac{1}{1-\tau }}}+{\left[-ln\left(v\right)\right]}^{{\displaystyle \frac{1}{1-\tau }}}\right)}^{1-\tau }\right],0\le \tau <1.$$

  (6)
• Dual (Survival) Clayton’s Copula

  $$P(X\ge x,Y\ge y)=C_3(1-u,1-v|\tau )=1-u-v+C_1(u,v|\tau ),0\le \tau <1.$$

  (7)
• Dual (Survival) Gumbel–Hougaard’s Copula

  $$P(X\ge x,Y\ge y)=C_4(1-u,1-v|\tau )=1-u-v+C_2(u,v|\tau ),0\le \tau <1.$$

  (8)

The first and fourth choices are especially good for addressing the lower-tail dependence, while the second and the third work well for the upper-tail dependence.

Several techniques exist for estimating copula parameters. One way of doing it is to use non-parametric measures of sample correlation, namely Kendall’s concordance $\tau$ or Spearman’s $\rho$, as many two-parameter copulas and all single-parameter copulas can have their parameters expressed as a measure of non-parametric correlation, allowing for a direct substitution (Brechmann 2010). This relationship also allows for Bayesian analysis based on sample correlation. This is discussed later. Another approach is to use maximum likelihood estimation, though this could carry computational issues relating to a lack of closed-form estimators (Brechmann 2010; Huang and Shemyakin 2020). For other parametric approaches, see Brechmann et al. (2012) and Manner (2007). For a non-parametric method, see Manner (2007).

Methods used to determine copula selection will be discussed later.

3.1. Vine Copulas

Elliptical copulas allow for a logical extension from dimension two discussed above to higher dimensions. A one-parameter Archimedean copula rarely provides an adequate model in the multivariate case due to its requirement of symmetric association between all pairs of variables. In case of different degree of association, a vine copula, also known as a pair-copula structure, may be preferable. A vine is a graphical tool for establishing the dependence structure in high-dimensional probability distributions. A regular vine is a special case for which all constraints are two-dimensional or conditional two-dimensional. Regular vines generalize trees. Vine copulas work by establishing the structure of association between the variables, where individual edges correspond to different pair copulas. Using Sklar’s theorem, the joint distribution of the data can be represented using a copula function of the marginals.

$$F(x,y,z,\dots )=C_{X,Y,Z,\dots }[F_X\left(x\right),F_Y\left(y\right),F_Z\left(z\right),\dots ].$$

(9)

From here, differentiation yields the following expression, involving a copula density $c_{X,Y,\dots Z}$ and marginal densities:

$$f(x,y,z,\dots )=c_{X,Y,Z,\dots }[F_X\left(x\right),F_Y\left(y\right),F_Z\left(z\right),\dots ]·f_X\left(x\right)f_Y\left(y\right)f_z\left(z\right)\dots .$$

(10)

For two variables, this simplifies to expression

$$f(x,y)=c_{X,Y}\left[F_X\left(x\right)F_Y\left(y\right)\right]·f_X\left(x\right)f_Y\left(y\right),$$

(11)

which using basic properties of conditional probability can be rewritten as

$$f_{X|Y}\left(x\right|y)=c_{X,Y}[F_X\left(x\right),F_Y\left(y\right)]·f_X\left(x\right).$$

(12)

Extending this to three variables yields the following result involving the conditional copula:

$$f_{X,Z|Y}(x,z|y)=c_{X,Z|Y}[F_{X|Y}\left(x\right|y),F_{Z|Y}\left(z\right|y);y]·f_{X|Y}\left(x\right|y)·f_{Z|Y}\left(z\right|y),$$

(13)

which in turn can be extended to much higher dimensions. For that and more details, see Aas et al. (2009) and Bedford and Cooke (2001). Regardless, this implies that any joint distribution can be represented as the product of marginals, pair copulas of the component vectors, and conditional pair copulas. In the case of independence between two variables,

$$c_{X,Y}[F_X\left(x\right),F_Y\left(y\right)]=1,$$

(14)

substantially simplifying the resulting structure.

Note that when working with vine copulas, the structure of the model must be specified before pair copulas can be estimated. In other words, it has to be determined first which variables are independent of each other, which variables are conditioned on the others, and in what order. For a detailed explanation why this approach is advantageous, see Aas et al. (2009) and Bedford and Cooke (2001). To estimate the vine structure, one can use the method put forth by Dissmann et al. (2013). First, the unconditional copulas are selected from the list of all possible structures, which can be exhaustive, based on which structure minimizes the reference statistic, such as AIC or BIC. Then pair copulas and their parameters are estimated for each non-independent pair. Then a variable is selected to be conditioned on, and the process repeats until all variables are exhausted.

3.2. Pair Copula Selection

Once a model structure has been specified, there are several ways to select the optimal pair copula(s). Most involve specifying a potential set of hyperparameters defined for each copula family, and then comparing them. This can be performed using the AIC (Brechmann 2010; Brechmann and Schepsmeier 2013; Manner 2007), BIC (Brechmann 2010), or other information criterion. Various goodness-of-fit tests can also be used for this purpose, allowing their statistics to be compared to select a copula (Huard et al. 2006). However, as Huard et al. (2006) point out, this approach compares single copula models with given parameter values chosen from each parametric family, instead of selecting a copula based on multiple possible parameter values.

A solution to this is to select copulas using Bayesian inference. Wifvat et al. (2020) describes the following method, which was suggested in Huard et al. (2006) and also used in Shemyakin and Kniazev (2017). First, let $H_m:m=1,2,\dots ,M$ be the hypotheses that the data come from one of M copula families, and for each pair $(i,j),i,j=1,\dots k$ test $H_k:F_{ij}({\epsilon }^{\left(i\right)},{\epsilon }^{\left(j\right)})=C_m(F_j\left({\epsilon }^{\left(i\right)}\right),F_l\left({\epsilon }^{\left(j\right)}\right))$. These hypotheses can be assumed to be mutually exclusive and exhaustive. Then, let $\tau$ be Kendall’s concordance. If all copulas considered can be written as functions of $\tau$, the posterior probabilities of the hypotheses given by the data $D=D(i,j)$ may be rewritten as

$$P\left(H_k\right|D(i,j))=\int P(H_m,\tau |D)d\tau ={\displaystyle \frac{\int P\left(D\right|H_m,\tau )P\left(H_m\right|\tau )\pi \left(\tau \right)d\tau }{P\left(D\right)}},$$

(15)

where $\pi \left(\tau \right)$ is the prior probability of $\tau$. Wifvat et al. (2020) show that this method still yields good results even for vague or non-informative priors on $\tau$. Since $\left|\tau \right|\le 1$ and in case of positive dependence $\tau \ge 0$, uniform Beta$(1,1)$ will be a suitable choice for $\pi$. Since the posterior probabilities are only to be used for selection purposes, $P\left(D\right)$ does not need to be calculated. With the discrete uniform prior on the hypothesis choice, it suffices to calculate the weights with $c_m,m=1,\dots ,M$ denoting respective copula p.d.f.:

$$W_m(i,j)={\int }_0^{1}P(D\mid H_m,\tau )\pi \left(\tau \right)d\tau ={\int }_0^1{\Pi }_{t=1}^T{c}_m(F_i\left({\epsilon }_t^{\left(i\right)}\right),F_j({\epsilon }_t^{\left(j\right)}\mid \tau ))\pi \left(\tau \right)d\tau ,m=1,\dots M,$$

(16)

or, using a Monte Carlo approach and drawing N samples from the uniform prior, evaluate

$${\widehat{W}}_m(i,j)={\displaystyle \frac{1}{N}}\sum _{r=1}^N{\Pi }_{t=1}^T{c}_m(F_j\left(e_t^{\left(i\right)}\right),F_l\left(e_t^{\left(j\right)}\right)\mid {\tau }_r).$$

(17)

and then the posteriors

$$\widehat{P}\left(H_m\right|D(i,j))={\displaystyle \frac{{\widehat{W}}_m(i,j)}{{\sum }_{m=1}^M{\widehat{W}}_m(i,j)}},$$

(18)

for each pair $(i,j),i.j=1,\dots ,k$.

4. Case Study

As an illustration of the suggested methodology, let us consider an example of COVID-19 development in several countries of Europe and North America. As stated above, data from certain countries during the pandemic may be unreliable, due to lack of infrastructure, intentional misreporting, missing data, etc. This study chose to focus on mortality data from the United States, Canada, France, Germany, Norway, and Sweden because of the easy availability of their mostly reliable data recorded in a similar time frame. For each country in this study, the following sources were used: The United States’ mortality data were obtained through the Center Disease Control’s (CDC) website. Canada’s data were obtained through Statistics Canada (2025), and they adhere to the same standards as the US (Human Mortality Database 2025). The European countries’ data were obtained entirely through EuroStat, the official statistics body for the European Union (Eurostat 2025).

To compute excess mortality, the difference between each country’s pandemic data and historical data was recorded as a percentage of the historical data for a given week in a time series. Consistently with Britt et al. (2023), the mortality rates are used rather than counts, and weekly excess mortality rate for week $t=1,\dots ,52$ of the year $s=2019,2020,\dots 2022$ is defined as the ratio

$$EMR(t,s)={\displaystyle \frac{D(t,s)-\frac{1}{5}{\sum }_{u=2014}^{2018}D(t,u)}{\frac{1}{5}{\sum }_{u=2014}^{2018}D(t,u)}}$$

(19)

where $D(t,s)$ is the weekly death count for every country in the study. The baseline death count ${\displaystyle \frac{1}{5}}{\sum }_{u=2014}^{2018}D(t,u)$ is calculated as the average for non-perturbed (pre-COVID years). Then the time series $Y_t$ for each country is obtained by concatenation $Y_t=\{EMR(t,2019),\dots EMP(t,2022)\}$. This approach to excess mortality helps to alleviate the effect of seasonality if it is generally consistent with the pre-COVID patterns.

The six countries in this study record the number of weeks in the year as the same, which is 52 (or 53) full 7-day weeks (Human Mortality Database 2025). This fixes the problem of weeks being out of alignment in which year they occur, as the data presented differ by one day only between the North American and European time series. Mortality data from 2014 to 2018 were used to make 5-year weekly averages. With 2014 being the only year with 53 weeks, this means that the week 53’s mortality average for each country is simply the last week of 2014.

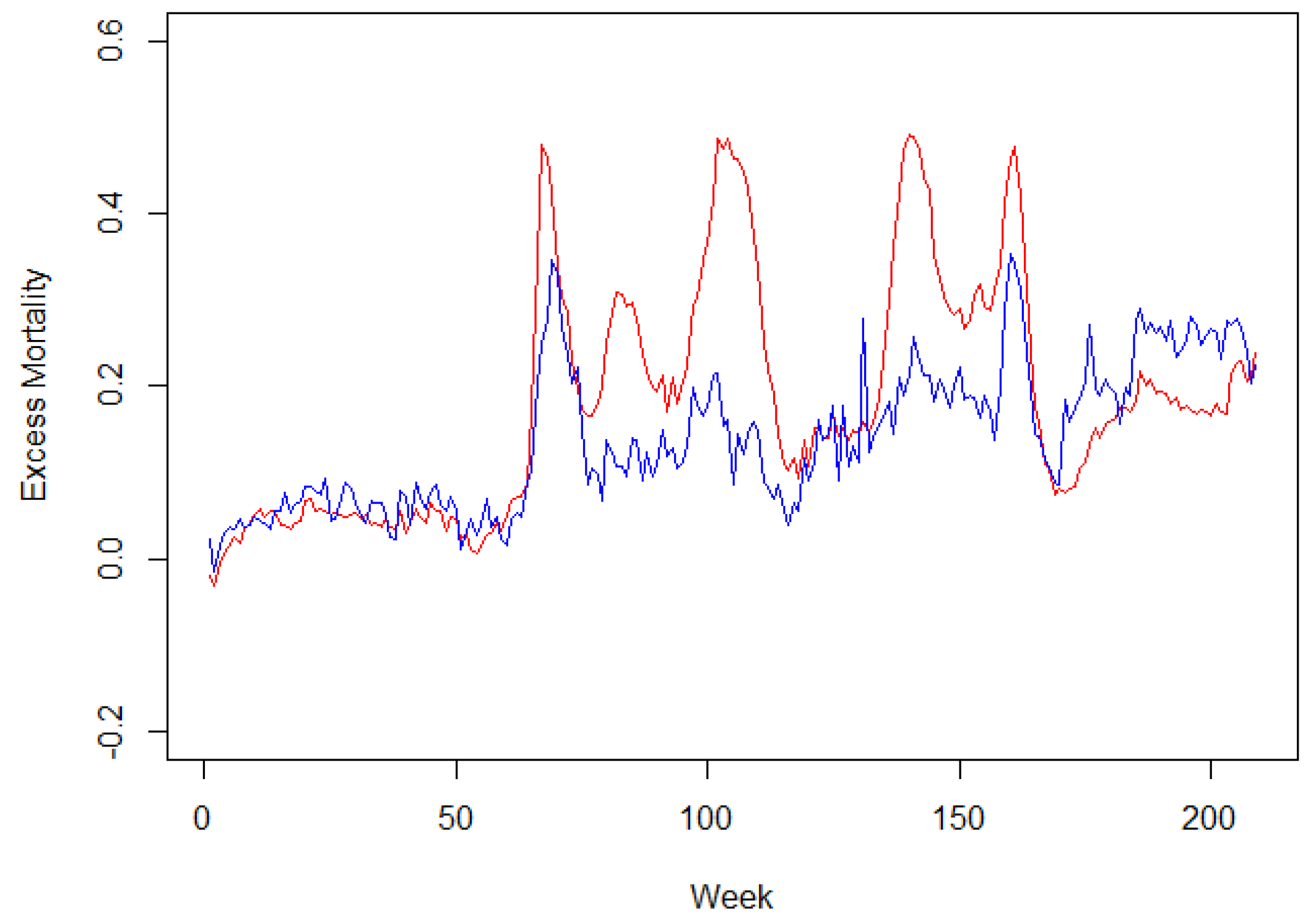
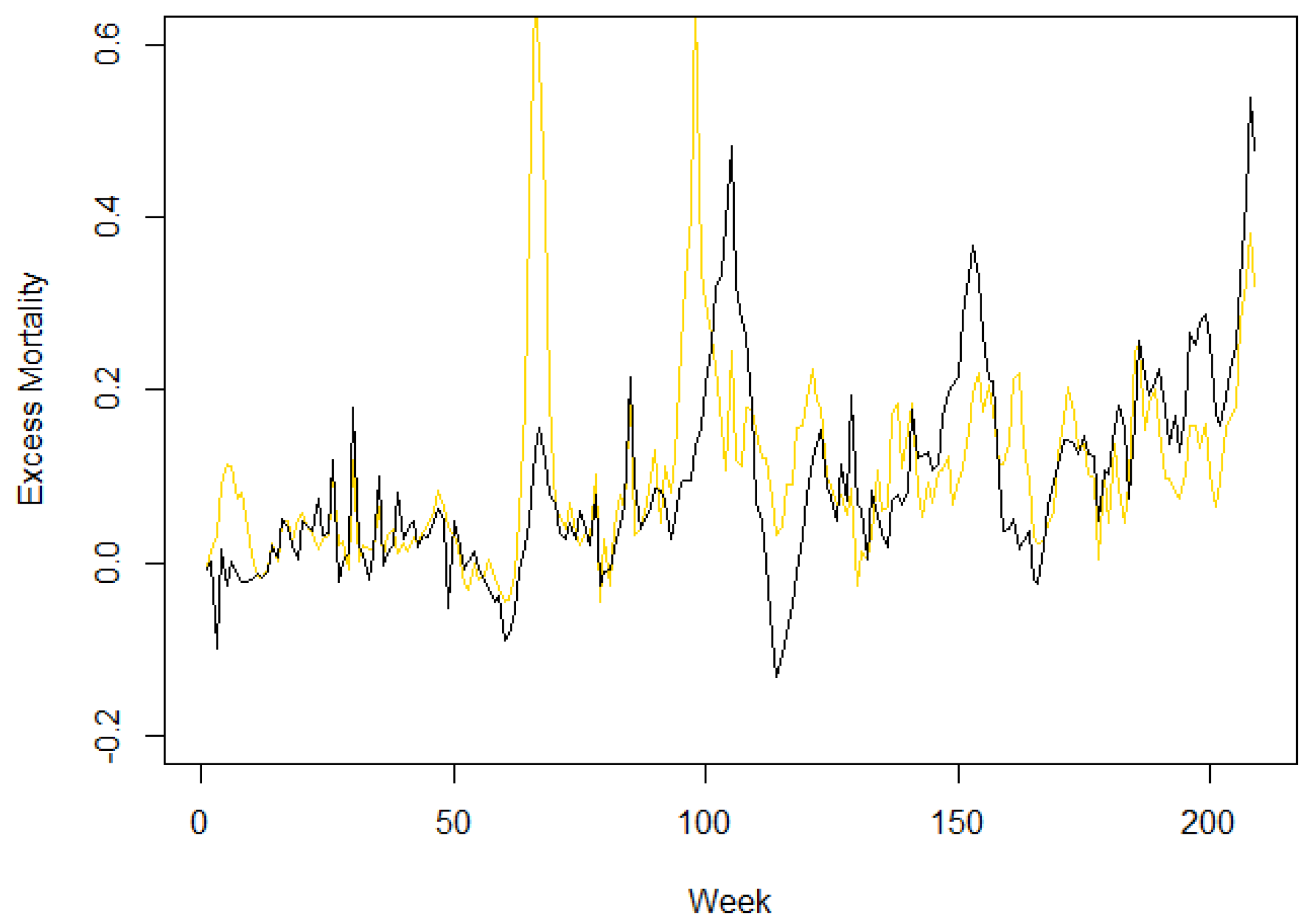
The weekly excess mortality time series from the first week of 2019 through the 52nd week of 2022 were used for all six countries. The data are summarized in

Table 1. Time series summary statistics.

Country	Min	Median	Mean	Max	$\mathit{\sigma }$
USA	$-0.032$	$0.170$	$0.183$	$0.491$	$0.134$
CAN	$-0.016$	$0.138$	$0.142$	$0.354$	$0.083$
FRA	$-0.0463$	$0.085$	$0.106$	$0.662$	$0.110$
GER	$-0.132$	$0.067$	$0.094$	$0.539$	$0.114$
NOR	$-0.195$	$0.026$	$0.040$	$0.464$	$0.090$
SWE	$-0.164$	$-0.012$	$0.013$	$0.464$	$0.101$

and three separate time series plots for three pairs of countries to avoid cluttering are presented as Figure 1, Figure 2 and Figure 3.

According to the methodology of Section 2 and Section 3, the case data are analyzed with the final goal of building a parametric joint distribution model for weekly mortality in the six countries listed, taking into account both serial and cross correlation to provide a forecasting tool. The flow chart in Figure 4 delineates the steps of model construction.

4.1. ARIMA

At the first stage, ARIMA models were constructed separately for all six countries in the study. To begin, the time series $(Y^{\left(1\right)},\dots ,Y^{\left(k\right))})$ for $k=6$ countries were tested for stationarity using the Augmented Dickey–Fuller test and KPSS tests through the tseries R 4.4 package. The p-values are summarized in

Table 2. Stationarity test p-values. $\alpha =0.05$.

Country	ADF	KPSS
USA	$0.03$	<$0.01$
CAN	<$0.01$	<$0.01$
FRA	<$0.01$	<$0.01$
GER	<$0.01$	<$0.01$
NOR	$0.25$	<$0.01$
SWE	<$0.01$	>$0.1$

. It is worth noticing that none of moving average coefficients in Equation (2) proved to be statistically significant.

The mixed results do not give a clear indication as to whether the time series are stationary or not.

From here, partial autocorrelation functions for each time series were analyzed. The United States did not show a significant correlation after a delay of 3. France, Germany, and Sweden showed no significant correlation for a lag of 2, but did have significant correlation for higher order lags. Canada and Norway showed no significant correlation after a lag of 2. After this, ARIMA analysis was performed using the ARIMA function from the R 4.4 package stats to generate potential models. Final models were selected first by those with a non-zero amount of statistically significant coefficients, and then by BIC. The models were built according to the structure of the following equation:

$$Y_t={\beta }_1·Y_{t-1}+\dots +{\beta }_p·Y_{t-p}+{\beta }_0+{\epsilon }_t,$$

(20)

where ${\epsilon }_t$ is the error terms, and ${\beta }_0$ is the intercept. The results are summarized in

Table 3. ARIMA coefficients and standard errors by country.

Coef	USA	CAN	FRA	GER	NOR	SWE
${\beta }_0$	$0.18\left(0.03\right)$	$0.14\left(0.03\right)$	$0.82\left(0.04\right)$	$0.11\left(0.04\right)$	$0.05\left(0.03\right)$	$0.02\left(0.02\right)$
${\beta }_1$	$1.41\left(0.07\right)$	$0.75\left(0.07\right)$	$0.11\left(0.02\right)$	$0.91\left(0.03\right)$	$0.56\left(0.07\right)$	$0.77\left(0.07\right)$
${\beta }_2$	$-0.29\left(0.12\right)$	$0.18\left(0.12\right)$	-	-	$0.31\left(0.07\right)$	$0.30\left(0.08\right)$
${\beta }_3$	$-0.18\left(0.03\right)$	-	-	-	-	$-0.22\left(0.07\right)$

.

After the models were selected, the residuals of each model were subjected to a Box–Ljung test using the stats R package. The results are summarized in

Table 4. Box–Ljung Tests. $\alpha =0.05$.

Country	p-Values
USA	$0.0922$
CAN	$0.4843$
FRA	$0.0553$
GER	$0.1890$
NOR	$0.4689$
SWE	$0.3456$

.

4.2. ARIMA Residual Analysis

At the second stage, the parametric models were developed for the distributions of ARIMA residuals. The Shapiro–Wilk test was performed on the residuals of each model to determine their normality. The results are summarized in

Table 5. Shapiro–Wilk tests. $\alpha =0.05$.

Country	p-Values
USA	<$0.0001$
CAN	<$0.0001$
FRA	<$0.0001$
GER	$0.0038$
NOR	$0.4416$
SWE	<$0.0001$

.

This suggests only the residuals for Norway’s model were normal. Fitting the distribution using fitdistr function from the R 4.4 package MASS yielded a normal distribution with $\mu =0$ and $\sigma =0.0036$. To fit a distribution to the others, the skewed t-distribution as defined in Fernandez and Steel (1996) was used. The results of the fitted distributions are summarized in

Table 6. Skewed t-distribution fit results.

Country	μ 1	$\mathit{\sigma }$	v	$\mathit{\xi }$
USA	0	$0.0259$	$4.6361$	$1.0340$
CAN	0	$0.0371$	$3.6201$	$1.1711$
FRA	0	$0.0720$	$2.7752$	$1.1821$
GER	0	$0.0540$	$4.0917$	$1.0257$
SWE	0	$0.0509$	$6.0996$	$1.2421$

¹ μ was found to be both $<0.005$ and have high standard error, as such as each mean was treated as zero.

.

Results were verified using the Kolmogorov–Smirnov test, which is summarized in the following

Table 7. Kolmogorov–Smirnov test statistics and p-values. $\alpha =0.05$.

Country	D	p-Value
USA	$0.0384$	$0.9177$
CAN	$0.0378$	$0.9267$
FRA	$0.0246$	$0.9996$
GER	$0.0416$	$0.8626$
SWE	$0.0377$	$0.9283$

. D is the test statistic. For the test, due to errors caused by the ks.test function used, which was not compatible with the distribution functions fitted, fitted distributions had samples randomly drawn from them to be compared, with a sample size of $N={10}^6$.

4.3. Vine Structure Selection

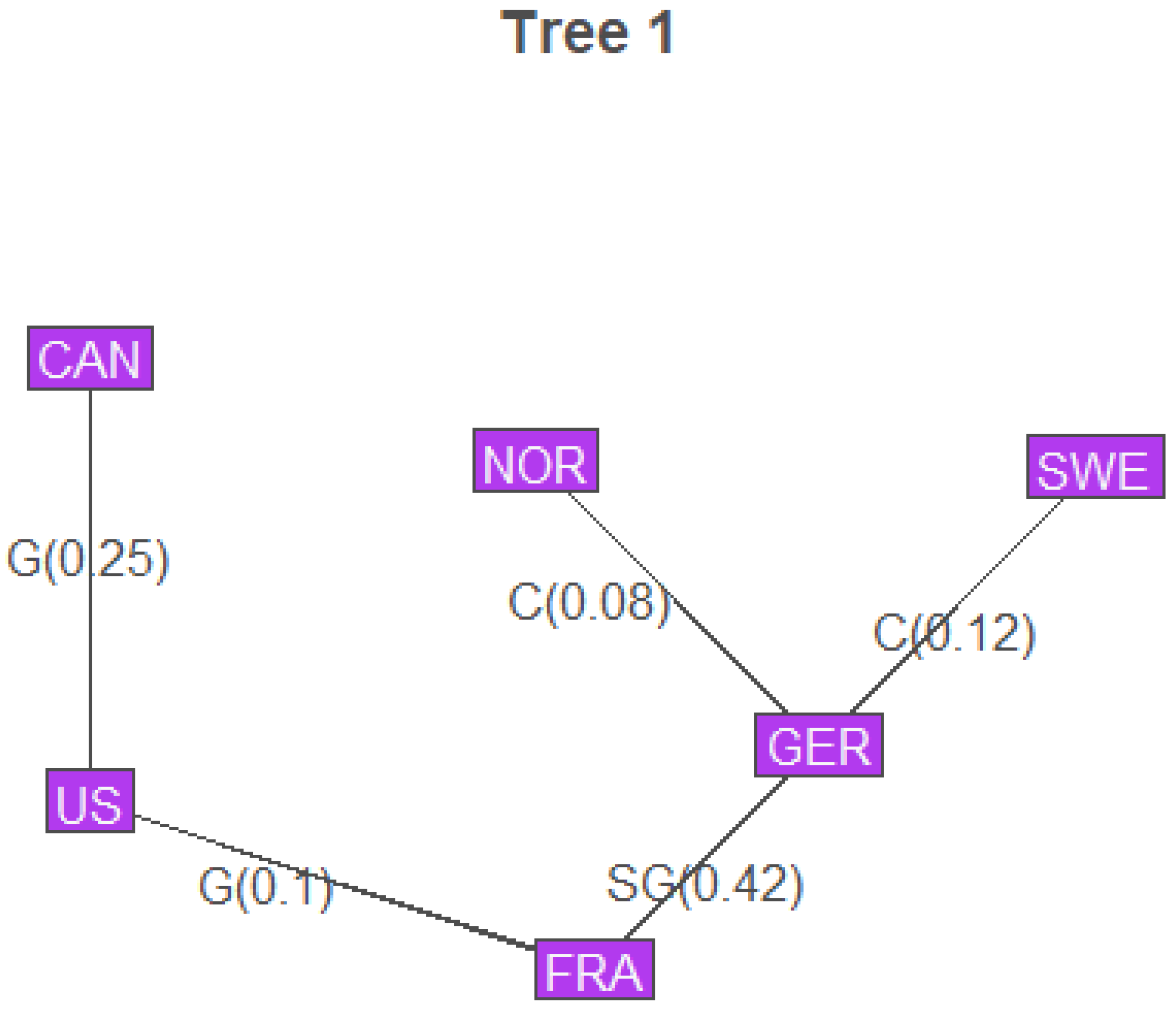
At the third stage of the analysis, the pairwise dependence patterns between the countries were determined for ARIMA residuals. Structure of the copula model for the vector of ARIMA residuals $({\epsilon }^{\left(1\right)},\dots ,{\epsilon }^{\left(6\right))})$ was determined using the RVineStructureSelect function from the VineCopula R package. Later procedures determined all copulas after the first level of conditioning to be independence copulas, so only the structure of the first level of the vine will be shown. Figure 5 illustrates the vine graph, where the edges correspond to the closest connections established between the nodes. It is reasonable to believe that these connections are mostly due to geographical reasons, but also may reflect the similarity between health policies. That is why the pair Norway/Sweden being geographically close but different at the health policy level does not share an edge at the first level of the vine.

4.4. Pair Copula Selection

Finally, the pair copula selection was performed using the Bayesian method outlined in Shemyakin and Kniazev (2017) for the choices defined in Equations (5)–(8). First, the assumption was made that each copula would fall into one of four hypothesized copula families.

Hypothesis 1 (H1).

Clayton’s Copula, C.

Hypothesis 2 (H2).

Gumbel–Hougaard’s Copula, G.

Hypothesis 3 (H3).

Dual (Survival) Clayton’s Copula, SC.

Hypothesis 4 (H4).

Dual Gumbel–Hougaard’s Copula, SG.

From here, the Monte Carlo approach described above was used, with $N=$ 10,000. The results are summarized in

Table 8. Posterior probabilities for hypothesized pair-copula families.

Countries	US/CAN	US/FRA	FRA/GER	GER/NOR	GER/SWE
H1 (C)	0	0.09	0.01	0.61	0.51
H2 (G)	0.84	0.35	0.03	0.10	0.02
H3 (SC)	0.11	0.28	0	0.04	0
H4 (SG)	0.05	0.28	0.96	0.25	0.47

, with the maximum values in each column (for each pair of countries) boldfaced.

Next, optimal $\tau$ values were selected using MLE, resulting in the following structure. In Figure 6, along with the primary connections established in Figure 5 by vine structure estimation, the selected copula and corresponding value of $\tau$ are also provided, with larger $\tau$ corresponding to a closer association between the nodes of the graph.

4.5. Validation

Validation of the model with the later (post-COVID) data was carried out on three levels: ARIMA models, distribution models for ARIMA residuals, and the vine copula structure. To validate the results, mortality data from 2023 were used. While Eurostat maintained weekly death counts throughout 2023, the CDC only maintained weekly counts for 37 weeks, and Statistics Canada only maintained weekly counts for 33 weeks. This does not impact the analysis of ARIMA models, since it is performed country-by-country, meaning that all available data can be used.

To validate the ARIMA model, the mean absolute error (MAE) of each country’s ARIMA model was calculated. This is summarized in

Table 9. MAE for ARIMA.

Country	Forecast MAE
USA	$0.103$
CAN	$0.033$
FRA	$0.064$
GER	$0.107$
NOR	$0.117$
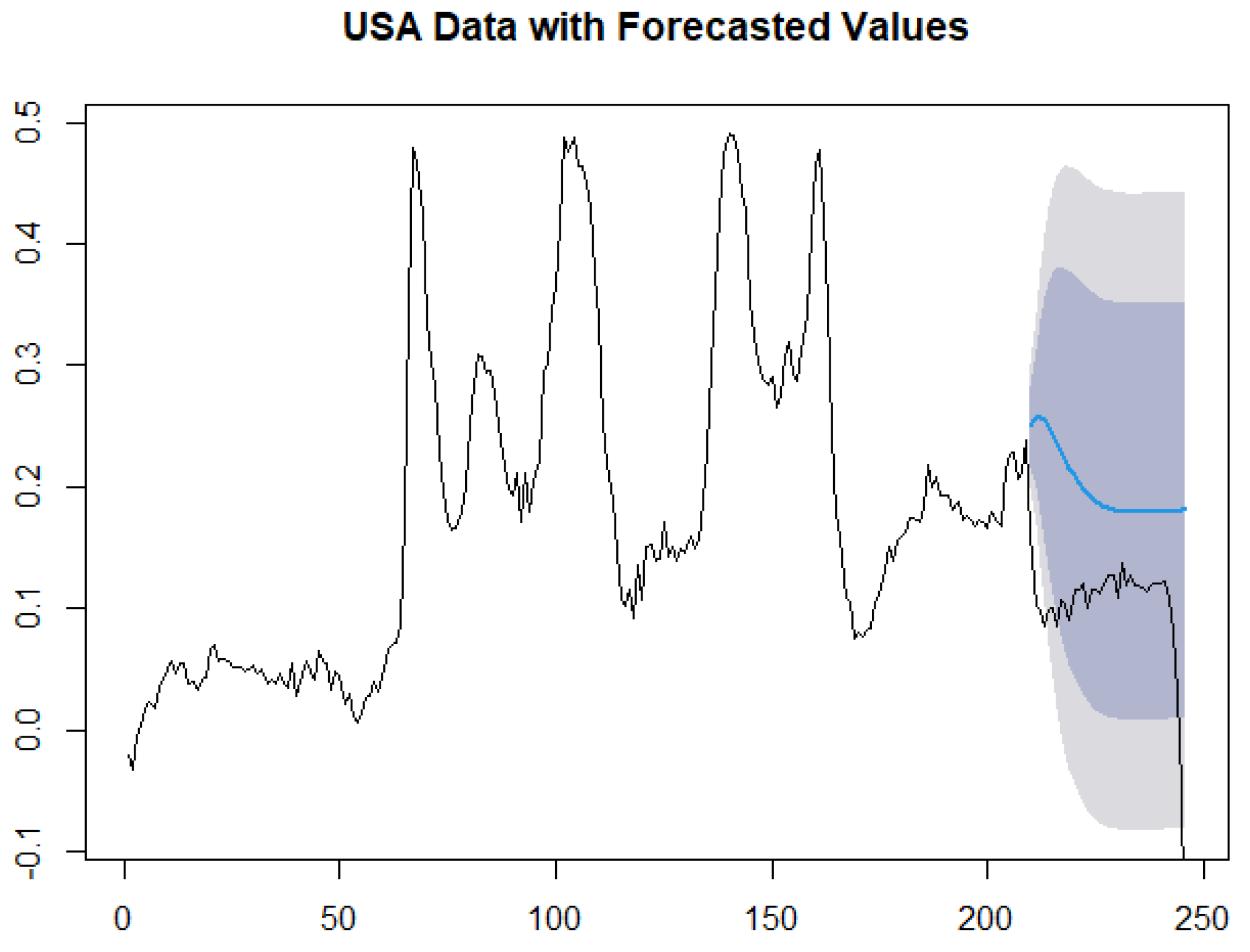
SWE	$0.077$

. The relatively low errors suggest that Canada, France, and Sweden’s ARIMA models are accurate. The larger errors of the other series makes sense, as the COVID pandemic was winding down in the USA by the time the CDC stopped updating its weekly death count in 2023. As such, models developed from the US mortality experience in 2023 would probably not be as accurate. For Germany and Norway, excess mortality temporarily plummeted in the beginning of 2023, which could explain the large average error observed. 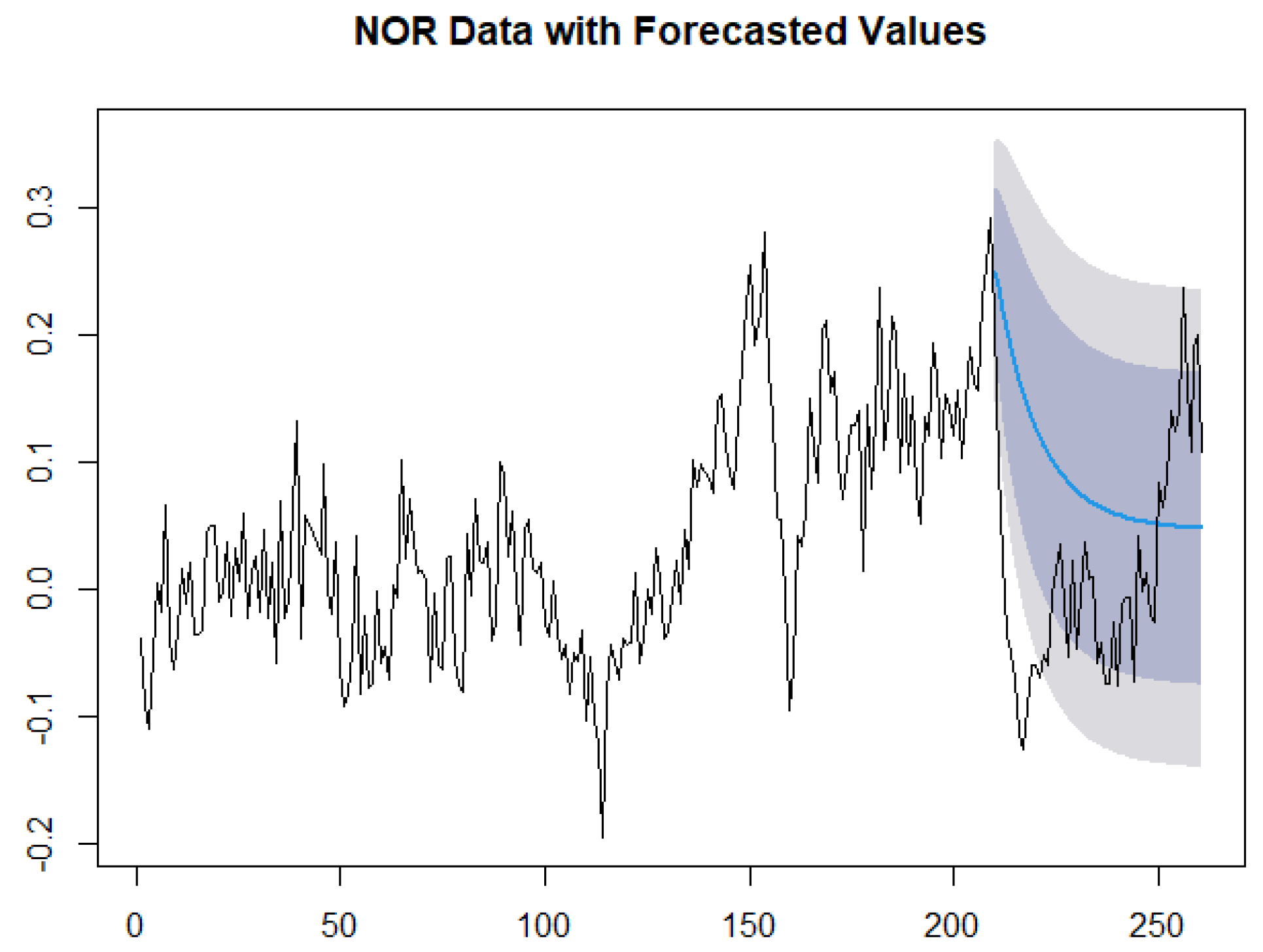Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 showing the actual out-of-sample values versus the point forecasts with 90% and 95% confidence bounds corroborate this.

To validate the marginal analysis of ARIMA residuals, the residuals generated for 2023 were compared to previously fitted marginal distributions using the Kolmogorov–Smirnov test. The results are summarized in

Table 10. Kolmogorov–Smirnov test statistics and p-values. $\alpha =0.05$.

Country	D	p-Value
USA	$0.2402$	$0.0276$
CAN	$0.1043$	$0.8652$
FRA	$0.1149$	$0.4981$
GER	$0.0646$	$0.9817$
SWE	$0.1795$	$0.0702$
NOR	$0.0822$	$0.8738$

.

This suggests that the marginal distributions of the residuals fitted in Section 4 are accurate for Canada, France, Germany, Sweden, and Norway, and less accurate for the USA where the COVID pandemic mortality abruptly dropped in 2023. This loss of predictive power is also illustrated in Figure 7. The accuracy of the other models is illustrated by the other figures, despite an initial trough in some series.

Finally, to validate the copula model proposed in Section 4, the data length had to be adjusted for each country’s residuals. To accomplish this, each dataset was limited to the first 33 weeks. Then, this sample was fitted using the VineCopula R package’s RVineGofTest function to the copula structure estimated in Section 4 using the Kolmogorov–Smirnov test (evaluated asymptotically), and the Cramer–von-Mises test (evaluated with 200 bootstrap steps). The results are summarized in

Table 11. KS and CvM test p-values for vine copula model $\alpha =0.05$.

Test	p-Value
KS	$0.7897$
CvM	$0.0650$

. For more details on how these tests are implemented in software, see Schepsmeier (2015).

This suggests that the dependence model put forth by the vine copula found in Section 4 describes the connections between the countries’ mortality experience well, even when the mortality experience differs from what is expected.

5. Discussion and Conclusions

To summarize the distinctive features of the modeling approach described in Section 2 and Section 3 and then illustrated in Section 4, we will discuss the advantages provided and the most likely applications related to these advantages. Then we will discuss the limitations of this approach. First, we suggest using separate ARIMA models for the time series of weekly excess mortality for the distinct zones (countries, geographical areas, etc). This approach is well established in mortality analysis and used in COVID-19 studies (Alabdulrazzaq et al. 2021; Ilie et al. 2020). Then, we use parametric distribution models for ARIMA residuals since they appear to be skewed and fat-tailed. This approach is quite common for financial time series but also has been applied to mortality data (Campolieti 2021). Finally, we model the joint distribution of ARIMA residuals for the zones considered above using vine copulas with the marginal distributions obtained at the previous step. This approach has been used for financial time series, see, e.g., Shemyakin and Kniazev (2017) for the general introduction and more extensive literature review, but appears to be new for mortality analysis related to epidemics (D’Urso et al. 2022).

The main advantage of using single time series ARIMA is the ease of data collection. One can use open-source data on mortality, which are often available in real time. Therefore, this approach is convenient for short-term forecast, defined by the CDC as one-week to four-weeks ahead (National Center for Health Statistics 2025). The most popular and powerful models, see Johannson et al. (2020) and Imperial College COVID Response Team (2022), use the ensemble approach and datasets including multiple predictors, which makes data collection more difficult. Using excess mortality also bypasses the necessity to properly attribute the cause of death, which can be problematic for epidemic data, especially at the epidemic’s onset, as discussed above.

Parametric distribution models for ARIMA residuals help to address extreme events of abnormally high or low weekly mortality, which can be critical in epidemic contexts. This provides more realistic tail probabilities. However, the example in Section 4 demonstrates that the multivariate effect of cross-correlation is also important. For short-term prediction of zone mortality, vine copula structure allows for an effective use of the recent history of the related zones. It also provides for a more realistic prediction of the mortality peaking simultaneously in several countries. In this regard it works like vector autoregression and network autoregression models (Britt et al. 2023; Sioofy et al. 2021). Unlike vector autoregression, however, it is not limited to linear association and is more effective in analyzing the tail behavior of joint distribution. One can also notice that the approach of the paper is not COVID-specific and can be applied to a wide range of excess mortality contexts.

The main limitation of this modeling approach is related to its strength: it does not directly allow for the use of covariates or external predictors. Therefore, there is no explanation of future mortality other than through previous experience. There is also no room for structural changes during pandemics. That makes it less suitable for longer-term forecasts or developing a realistic explanation of a pandemic’s progression versus traditional SIR and regression models (Chaurasia and Pal 2020). A possible problem is also the use of aggregated data which does not allow for the study of such factors as age, gender and socioeconomic status. The use of disaggregated data is one of the possible future directions of model development.

As we see from the illustration in Section 4, time series models of COVID-19 excess mortality built from open source countrywide mortality data are viable even without addressing mortality covariates. ARIMA models have low lags and no residual autocorrelation, but model residuals tend to be non-normal, being skewed with fat tails. In addition, there appears to exist some cross-correlation between countries not otherwise captured by ARIMA models. This cross-correlation can be modeled using vine copula structures, with pair copulas appropriately selected via Bayesian analysis of different hypothesized families. The end result also demonstrates a geographic component in determining the association between the residuals of different countries. Neighboring countries tend to have higher correlations with each other compared to countries separated by an ocean. However, this is not always the case, as Norway and Sweden’s model residuals appeared to be independent of each other and were more closely related to Germany’s residuals. It appears that copula models applied to ARIMA residuals provide an effective way to address cross-correlation between the countries and may help to predict one country’s mortality based on the others. The copula approach allows for addressing non-linear dependence patterns such as tail dependence, which cannot be captured with individual ARIMA modeling or vector autoregression. Model validation showed that real-world experience toward the end of the pandemic differed somewhat from the model predictions, possibly due to decreased mortality. However, the dependence structure held, suggesting that the conclusions derived from the vine copula model were accurate. Overall, the three-stage modeling approach (ARIMA, distribution analysis of ARIMA residuals, vine copula model for the vector of residuals) seems suitable for creating joint short-term forecasts of pandemic mortality for several countries.