Implicit Prioritization of Life Insurance Coverage: A Study of Policyholder Preferences in a Danish Pension Company

Abstract

This study evaluates the utility derived by policyholders in a Danish pension company, from their life insurance coverages. We quantify the relative importance policyholders assign to their existing coverages versus a hypothetical complete coverage scenario, thereby measuring the implicit priority of their current coverage. By analyzing these implicit priorities based on individual attributes such as age, financial situation, and company agreement limitations, we gain a comprehensive understanding of policyholders’ evaluations of their current life insurance coverage. Utilizing a continuous-time life cycle model, we optimize consumption and life insurance decisions during the accumulation phase, applying well-established theoretical findings to actual data. Our analysis identifies trends, outliers, and insights that can inform potential improvements in life insurance coverage. This tool aims to assist policyholders in prioritizing their coverage according to their life situations and provides a foundation for advisory dialogues and product development.

1. Introduction

We formalize and compare the policyholders’ preferences for life insurance coverage within the context of a Danish pension company. This is formalized by quantifying the relative importance (weights) poliyholders assign to their existing coverages and juxtaposing these with the weights they would allocate to a hypothetical scenario of complete coverage. Thus, we measure the implicit priority they place on their current coverage. A novel aspect of this study is the examination of implicit preferences derived from real-life life insurance products offered by a pension company.

Subsequently, we analyze the implicit priority for each policyholder based on their individual attributes and parameters. This analysis involves evaluating various factors such as age, financial situation, the framework and limitations of the company agreement, and personal choices by the policyholder. By aggregating and examining these priorities across the entire portfolio, we gain a comprehensive understanding of policyholders’ evaluations of their current life insurance coverage. This analysis enables us to identify trends, detect outliers, and uncover insights that can inform potential improvements or further investigations into policyholders’ current coverage. The main contributions are establishing a framework handling implicit prioritization mechanisms in a life cycle model to evaluate preferences and explore from real data the practical consequences of decisions on life insurance products on an individual personal level.

When considering optimal consumption and insurance problems, practitioners commonly ask how to incorporate these theoretical results into business. How can we gain practical tools and insights into our company through this largely investigated area?

We address this question using a continuous-time life cycle model, which is a framework to describe how policyholders make financial decisions over time, taking into account the uncertainty of the future, such as mortality and income. Our analysis is confined to the accumulation phase, as policyholders primarily acquire life insurance coverage and optimize their consumption and life insurance decisions during this period.

Policyholders’ preferences regarding risk, insurance, and consumption are fundamental to decision-making, and the measuring and quantifying of these pose significant challenges, as a standardized method is lacking. Preferences are a part of the utility functions, serving as a tool to rank different choices and clarify decisions in uncertain scenarios. Quantifying these preferences has traditionally been studied by the so-called risk aversion parameter, which is one or more parameters in the chosen utility functions. Quantification of risk aversion in decision-making was examined in some of the first studies by Pratt (1976) who, together with the work of Arrow (1973), studied the concavity of utility functions and related it to the degree of risk aversion by the agent. Our optimization uses a power utility function to model the policyholders’ preferences and risk aversion. The power utility function is also known as the constant relative risk aversion utility function and is a frequently studied choice in modeling decisions, as can be seen for instance in Wakker (2008).

The academic tradition of considering consumption–investment–insurance problems dates back to the consumption–investment framework of Merton (1969, 1971), which together with the discrete-time insurance one of Yaari (1965), was combined by Richard (1975) in his foundational work. Since then, the consumption–investment–insurance problems have been expanded in various directions, bridging the gap between financial and actuarial literature. It is worth pointing out that Pliska and Ye (2007) conducted notable work in the financial domain and Kraft and Steffensen (2008a) in the insurance domain. Further generalizations related to the market can be found in the works of Duarte et al. (2014); Shen and Wei (2016). For insights into the generalization of preferences, see Steffensen and Søe (2023); Tang et al. (2018); Zhang et al. (2021). Additionally, significant contributions regarding health risk have been made by Hambel et al. (2017); Koijen et al. (2016); Steffensen and Søe (2023). These generalizations are crucial for bridging the gap between stylized theories and the complexities and heterogeneities of the real world. We propose leveraging the extensive knowledge around choices and decision-making to analyze real-world data, focusing on policyholders’ actual preferences and implicit priorities.

The theory builds upon the Bellman principle of optimality, illustrating a relation between risk aversion and optimal investment. This concept is reversed in the work of Falden and Steffensen (2024), who calibrate risk aversion, using the investor’s real financial allocation to measure their implicit risk aversion under the assumption that the allocation is optimal. Each position of the agent leads to an equation for risk aversion, resulting in an overdetermined system and allowing them to define a mutual fund that aligns with the agent’s preferences, distinguishing it from previous solutions to estimate the risk aversion, such as Burgaard and Steffensen (2020); Conine et al. (2017); Holt and Laury (2002).

The majority of studies designed to estimate risk aversion employ revealed preference methodologies, particularly concerning decisions involving lotteries. These studies offer a framework for empirically assessing individuals’ degree of risk aversion. Noteworthy contributions to this field include the works of Azar (2006); Holt and Laury (2002); Wakker (2008). In the realm of insurance, Cohen and Einav (2007) used data on policyholders’ choices on deductible contracts to estimate risk aversion and later, Barseghyan et al. (2013) elaborated on this. Eliciting risk aversion parameters based on questionnaires has been performed by, among others, Barsky et al. (1997); Burgaard and Steffensen (2020) combined elements from the revealed preferences techniques with the propensity measure by asking agents to choose among certainty equivalents. Our approach is closer to that of Falden and Steffensen (2024) in intuition and motivation but not in methodology; the novelty of our methodology is to consider policyholders’ choices as optimal strategies and establish the concept of the implicit priority of life insurance coverage by the policyholder based on their current and possible maximum coverages, as a measure.

We obtained portfolio data from PFA Pension to analyze and compare. Due to confidentiality constraints, we do not present the raw data, but we present visual illustrations of the implicit priorities derived from the data and interpret their effects. We conducted this analysis with PFA Pension, incorporating mutual reflections on the results. Our study focuses exclusively on consumption and insurance, deliberately excluding the investment component to highlight and isolate the desired effects.

This paper is structured as follows: Section 2 presents the theoretical foundation and explains all components and variables used in the analysis. Section 3 introduces the concept of implicit priority, the conceptual idea behind the analysis and our main contribution to the evaluation of policyholders’ choices. Section 4 presents the numerical analysis, discusses the assumptions and descriptions, and presents and discusses the results. Finally, Section 5 concludes and addresses the limitations on methodology and data, and suggests further improvement and research possibilities.

2. Setup and Formulation of the Problems

In this section, we present the central optimization problem; with a corresponding solution, we compare with a special case and utilize it to define the implicit priority.

We consider a life insurance policyholder in a classical two-state life insurance model, where the policyholder can either be alive or deceased. We assume that the individual has an uncertain lifetime and denote by $\mu$ the individual’s mortality rate. The insurance company uses a deterministic interest rate r, thereby excluding the portfolio optimization, and a deterministic mortality rate ${\mu }^{*}$ for valuation purposes. The mortality rate $\mu$ is assumed to be deterministic and increases with age, thus excluding the modeling of stochastic longevity risk. However, no modeling longevity risk does not preclude us from modeling longevity itself, where mortality for a given age decreases over calendar time. If the mortality rate is deterministic, we can implement this effect by allowing the age-dependent mortality rate to vary with birth year. It is important to note that the objective mortality intensity $\mu$ may differ from the pricing mortality intensity ${\mu }^{*}$.

We specify this by the underlying stochastic processes. We let N denote the counting process, counting the number of deaths, either being 0 or 1. Thus, at time t, the process $N\left(t\right)$ equals the number of deaths, letting $I\left(t\right)$ indicate whether the policyholder is alive at time t. The expected number of deaths in the interval $[t,s]$, given the policyholder is alive at time t, is thus

$$\begin{array}{c}\hfill \mathbb{E}[N\left(s\right)-N\left(t\right)|I\left(t\right)=1]={\int }_t^s{e}^{-{\int }_t^{\tau }\mu \left(u\right)du}\mu \left(\tau \right)d\tau ,\end{array}$$

and the probability that the policyholder is alive at time s, given they are alive at time t, is

$$\begin{array}{c}\hfill \mathbb{E}\left[I\left(s\right)\right|I\left(t\right)=1]=e^{-{\int }_t^s\mu \left(u\right)du}.\end{array}$$

Using the pricing intensity, we denote with *

$$\begin{array}{cc}\hfill {\mathbb{E}}^{*}[N\left(s\right)-N\left(t\right)|I\left(t\right)=1]& ={\int }_t^s{e}^{-{\int }_t^{\tau }{\mu }^{*}\left(u\right)du}{\mu }^{*}\left(\tau \right)d\tau ,\hfill \\ \hfill {\mathbb{E}}^{*}\left[I\left(s\right)\right|I\left(t\right)=1]& =e^{-{\int }_t^s{\mu }^{*}\left(u\right)du}.\hfill \end{array}$$

In this setting, the wealth of the policyholder develops as

$$\begin{array}{cc}\hfill dX\left(t\right)& =(rX\left(t\right)+I\left(t\right)(a\left(t\right)-{\mu }^{*}\left(t\right)b\left(t\right)-c\left(t\right)))dt+b\left(t\right)dN\left(t\right),\hfill \\ \hfill X\left(0\right)& =x_0,\hfill \end{array}$$

(1)

where $x_0$ denotes the initial wealth at time 0. The policyholder earns interest at a constant rate of r. While alive, the policyholder’s financial activities include earning income a, paying life insurance premiums ${\mu }^{*}\left(t\right)b\left(t\right)$, and consuming wealth at rate c. Upon the policyholder’s death, the beneficiaries receive a lump sum payment of b and the remaining wealth x. From this point, we introduce the concept of human capital, denoted as $g\left(t\right)$. Human capital represents the financial value of expected future income. Consequently, an individual’s total wealth is given by $X\left(t\right)+g\left(t\right)$. The individual can hedge their future income by accessing the insurance market, thereby facing a complete market. Human capital is the unique value of the future income hedging portfolio. Since the future is unknown to the policyholder, a natural assumption is to let the control processes $(c,b)$ be adapted to the wealth process X; for computational ease, we go one step further and require that the controls are on a feedback form such that $\left(c\right(t),b(t\left)\right):=\left(c\right(t,X\left(t\right)),b(t,X\left(t\right)\left)\right)$ for deterministic measurable functions $c,b:[0,n]\times \mathbb{R}\to \mathbb{R}$. When used as $c\left(t\right),b\left(t\right)$, this should be understood as evaluated along the wealth process.

2.1. Central Problem

Based on the established setup, we examine the objective of maximizing the expected utility of consumption while the insured is alive and the life insurance coverage upon death until termination n, i.e.,

$$\begin{array}{c}\hfill \underset{c,b\in \mathcal{A}}{sup}\mathbb{E}\left[{\int }_0^{n}u(t,c\left(t\right))I\left(t\right)dt+v(t,b\left(t\right)+x\left(t\right))dN\left(t\right)\right].\end{array}$$

(2)

The supreme is taken over consumption and insurance processes in the set of $\mathcal{A}$ of admissible controls, and the utility functions are specified as

$$\begin{array}{cc}\hfill u(t,c)& ={\displaystyle \frac{1}{1-\gamma }}{c}^{1-\gamma }\left(t\right){\omega }^0{\left(t\right)}^{\gamma },\hfill \\ \hfill v(t,x)& ={\displaystyle \frac{1}{1-\gamma }}{x}^{1-\gamma }\left(t\right){\omega }^1{\left(t\right)}^{\gamma }.\hfill \end{array}$$

(3)

We consider the special case of power utility where both the consumption rate and the consumption upon death are measured by the same power utility function but differentiated by the coefficients ${\omega }^0$ and ${\omega }^1$ representing the different weight the policyholder places on money at time t, taken to the power $\gamma$ for mathematical convenience. As this time-weight function, some have previously chosen the exponential function $\omega \left(t\right)=e^{-\rho t}$ and let $\rho$ be the subjective discount factor since it relates to the policyholder’s utility of payments at different points in time, as was explored by Kraft and Steffensen (2008b). We do not assume a specific form of the weight function and interpret it as the weight placed upon consumption while alive or of bequest wealth. This weight, $\omega$, is particularly interesting for our analysis. The value function is correspondingly formulated as

$$\begin{array}{c}\hfill V(t,x)=\underset{c,b\in \mathcal{A}}{sup}{\mathbb{E}}_{t,x}\left[{\int }_t^{n}u(s,c\left(s\right))I\left(s\right)ds+v(s,b\left(s\right)+x\left(s\right))dN\left(s\right)\right],\end{array}$$

(4)

where ${\mathbb{E}}_{t,x}$ denotes the conditional expectation, given that $X\left(t\right)=x$ and $I\left(t\right)=1$.

We say the controls $(c,b)$ are admissible if, first, the insured does not have a negative total capital in the sense of wealth, including human capital, such that $X\left(t\right)+g\left(t\right)\ge 0$ for all $t\in [0,n]$; second, (1) needs a unique solution; third, the expectation in (4) is well defined; and finally,

$$\begin{array}{c}\hfill \mathbb{E}\left[{\int }_0^{n}b\left(t\right)(dN\left(t\right)-\mu \left(t\right)I\left(t\right)dt)\right]=0.\end{array}$$

We denote by $\mathcal{A}$ the set of admissible controls, with the value function candidate

$$\begin{array}{c}\hfill V(t,x)={\displaystyle \frac{1}{1-\gamma }}{(x+g\left(t\right))}^{1-\gamma }f{\left(t\right)}^{\gamma }.\end{array}$$

(5)

This is a specific instance of the problems addressed in, among others, Asmussen and Steffensen (2020); Kraft and Steffensen (2008b), where a verification theorem (Theorem 6.1 in Asmussen and Steffensen 2020) along with a corresponding proof for the multi-state problem with constant risk aversion is provided. The problem is addressed using dynamic programming by solving the associated Hamilton–Jacobi–Bellman equation

$$\begin{array}{cc}\hfill V_t(t,x)& =\underset{c,b}{inf}\left\{-(rx+a\left(t\right)-c-{\mu }^{*}\left(t\right)b)V_x(t,x)-u(t,c)-\mu \left(t\right)[v(t,x+b)-V(t,x)]\right\}\hfill \\ \hfill V(n,x)& =0.\hfill \end{array}$$

where the solution is presented as the solution to the differential equations for the g and f functions, which have the Feynman–Kac representation

$$\begin{array}{cc}\hfill g\left(t\right)& ={\mathbb{E}}_t^{*}\left[{\int }_t^n{e}^{-{\int }_t^{s}r\left(u\right)du}a\left(s\right)I\left(s\right)ds\right],\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill f\left(t\right)& ={\tilde{\mathbb{E}}}_t\left[{\int }_t^n{e}^{-{\int }_t^s\tilde{r}\left(u\right)du}({\omega }^0\left(s\right)I\left(s\right)ds+w^1\left(s\right)dN\left(s\right))\right].\hfill \end{array}$$

(7)

where

$$\begin{array}{cc}\hfill \tilde{r}& =-{\displaystyle \frac{\gamma }{1-\gamma }}r-{\displaystyle \frac{\gamma }{1-\gamma }}({\mu }^{*}\left(t\right)-\mu \left(t\right))+\mu \left(t\right)-\tilde{\mu }\left(t\right),\hfill \\ \hfill \tilde{\mu }\left(t\right)& ={\mu }^{*}\left(t\right){\left({\displaystyle \frac{\mu \left(t\right)}{{\mu }^{*}\left(t\right)}}\right)}^{{\displaystyle \frac{1}{\gamma }}}.\hfill \end{array}$$

Such that g is the conditional expected present financial value of future income where the expectation is taken under the ${\mathbb{P}}^{*}$, and f is the conditional expected present value of future weights where the expectation is taken under an artificial measure where N admits the intensity process $\tilde{\mu }$, or in other words, an artificial financial value of future weights applying an artificial stochastic interest rate and valuation measure. Further, the corresponding optimal controls solving the problem are

$$\begin{array}{cc}\hfill c(t,x)& ={\displaystyle \frac{{\omega }^0\left(t\right)}{f\left(t\right)}}(x+g\left(t\right)),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill b(t,x)+x& ={\displaystyle \frac{{\omega }^1\left(t\right)}{f\left(t\right)}}(x+g\left(t\right)){\left({\displaystyle \frac{\mu \left(t\right)}{{\mu }^{*}\left(t\right)}}\right)}^{{\displaystyle \frac{1}{\gamma }}}.\hfill \end{array}$$

(9)

We return to the explicit notation to emphasize the dependence of the optimal controls on both the time and the state variable. Here, the optimal consumption rate is a fraction of the total wealth, where the fraction measures the utility of present consumption against the utility of consumption in the future. Similarly, the optimal insurance and reserve payout upon death is a fraction of wealth, with an additional pricing factor. The fraction ${\omega }^1\left(t\right)/f\left(t\right)$ measures the utility of the lump sum upon dying against the utility of future consumption.

2.2. Special Case

The idea of the special case is to examine the optimal bequest formula (9), which is the wealth just before death multiplied by two factors—${\displaystyle \frac{{\omega }^1\left(t\right)}{f\left(t\right)}}$ and ${\left({\displaystyle \frac{\mu \left(t\right)}{{\mu }^{*}\left(t\right)}}\right)}^{{\displaystyle \frac{1}{\gamma }}}$—and imagine the situation where both factors are one, thus having a completely fair insurance contract with no risk/premium loading, ${\mu }^{*}=\mu$, and the weight upon bequest ${\omega }^1$ equal to the conditional expected present value of future weights, f; in other words, the significance of bequest would be the same as the significance of future consumption prior death. We speak of this as full or complete coverage inspired by Asmussen and Steffensen (2020), with $b=g$. This is a full compensation of the potential financial loss the heirs of the policyholder would experience upon the death of the policyholder.

This is a corner result and allows us, in general, to evaluate and interpret the optimal bequest (9) dependent on the preferences and price of insurance since the two factors represent deviations from the complete coverage. If the insurance is expensive ${\mu }^{*}>\mu$, the factor regarding price, ${\left({\displaystyle \frac{\mu \left(t\right)}{{\mu }^{*}\left(t\right)}}\right)}^{{\displaystyle \frac{1}{\gamma }}}$ defines depending on the preference $\gamma$ how much to under-insure compared to the complete coverage, and correspondingly, how much to over-insure if the insurance is cheap. The other factor is of great interest to this investigation since it represents the appreciation of consumption of bequest upon death through the parameter ${\omega }^1$, and the appreciation of accumulated consumption just before death is expressed by f. Thus, if the policyholder values the consumption of bequest upon death higher than consumption before death, one should over-insure compared to the complete coverage, and vice versa if consumption prior to death is valued higher than consumption upon death.

With this foundation established, we aim to isolate and emphasize the effects of interest. Therefore, instead of having two distinct weights, ${\omega }^0$ and ${\omega }^1$, in the utility functions (3), we set ${\omega }^0=1$ and redefine ${\omega }^1$ as $\omega$. This allows us to focus solely on the weight the insured places on their life insurance coverage. This weight, $\omega$, is precisely the pivotal element of our analysis, and this defined the following:

Proposition 1.

For $t\in [0,n]$, assume $X\left(t\right)=x$, ${\mu }^{*}=\mu$, and $x+g\left(t\right)\ge 0$. Let everything known from data be denoted with a bar. Assume the functions $\overline{\tilde{r}}\left(u\right)$, $\overline{\mu }\left(u\right)$, and $\overline{a}\left(s\right)$ are known and continuous over the interval $[0,n]$.

The optimal bequest strategy is defined as

$$\begin{array}{cc}\hfill \overline{b}+x& ={\displaystyle \frac{\omega \left(t\right)}{f\left(t\right)}}(\overline{x}+g\left(t\right)),\hfill \end{array}$$

(10)

with the corresponding functions

$$\begin{array}{cc}\hfill f\left(t\right)& ={\int }_t^n{e}^{-{\int }_t^s(\overline{\tilde{r}}\left(u\right)+\overline{\mu }\left(u\right))du}(1+\omega \left(s\right)\overline{\mu }\left(s\right))ds,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill g\left(t\right)& ={\int }_t^n{e}^{-{\int }_t^s(\overline{r}\left(u\right)+\overline{\mu }\left(u\right))du}\overline{a}\left(s\right)ds.\hfill \end{array}$$

(12)

Here, $g\left(t\right)$ consists of known parameters and can be calculated by numerical integration. The function $f\left(t\right)$ is dependent on ω, and thus, ω can be solved numerically.

3. Implicit Priority

This section presents the general concept and establishes the framework for constructing the implicit priority of life insurance coverage.

If we assume values for the relative risk aversion parameter based on previous studies of the Danish population by Burgaard and Steffensen (2020) and with the data we have available, the only unknowns in (10) are the weight, $\omega$, quantifying the significance the policyholder places upon the consumption of bequest upon death, compared to the consumption prior to death. In two distinct scenarios, we examine the policyholder’s choices as the optimal strategies, and with the data supplied, we can isolate the weight $\omega$ and asses the significance in the context of the insured’s overall financial strategy, and thus, their implicit priorities.

• In the first scenario, we consider the currently chosen life insurance payout to be the optimal life insurance coverage. We calculate backward to determine the following: ‘If this life insurance coverage were optimal for the insured, what weight would correspond to the insured’s valuation of it?’ In other words, we aim to understand how the insured values this life insurance payout relative to their intermediate money consumption, thereby understanding the factor ${\displaystyle \frac{\omega \left(t\right)}{f\left(t\right)}}$ and the policyholder’s appreciation for under- or over-insurance while noting that $\omega$ itself plays a role in f, as defined in (11). We denote the weight from this scenario ${\omega }^{current}$.
• The second scenario extends the special case explained in the previous Section 2.2. If, instead of the current life insurance coverage, the insured had the complete coverage equivalent to their human capital, g, we determine the weight, $\omega$, that would correspond to the insured’s valuation of this coverage. In other words, we aim to understand how the insured would value complete coverage relative to their intermediate consumption in this scenario. Serving as a reference to the examination of appreciation the policyholder has for over- or under-insurance, as this is exactly the value placed on the consumption of bequest if the policyholder had complete coverage. We denote the weight from this scenario ${\omega }^{complete}$.

From these two scenarios, we define the implicit priority of the current life insurance coverage as

$$\begin{array}{c}\hfill \mathcal{I}\left(current\right)={\displaystyle \frac{{\omega }^{current}}{{\omega }^{complete}}},\end{array}$$

(13)

where the weights in each situaiton are defined as in Proposition 1. This implicit priority, $\mathcal{I}$, can be systematically compared across policyholders to evaluate how the insured prioritizes their current coverage relative to having all future income covered. The weight assigned to the expected future income as a life insurance payout is fixed, while the individual current payout can be adjusted. A high implicit prioritization of the life insurance payout indicates that the current payout is deemed highly valuable. Conversely, a low implicit prioritization of the life insurance payout indicates that the current coverage is considered lower value. The essential aspect is that the implicit priority is based on the policyholder’s current situation, but it can be compared with the implicit priority of other policyholders.

This idea is based on several crucial assumptions. Firstly, it is assumed that the insured optimally consumes the funds until death, thereby reducing the discussion of consumption and, with the weight placed on consumption being one, still including it as a reference. Secondly, investments and an uncertain market are not considered. Lastly, the wealth used in the calculations is the accumulated value of the wealth in the pension. Our analysis focuses exclusively on policyholders who are not yet retired and are currently paying premiums.

4. Numerical Analysis

We analyze 372,667 policies with life insurance coverage from the Danish pension company PFA, with the relevant parameters chosen through mutual discussion. Our presentation focuses solely on the results derived from these data rather than the data themselves. We first outline our assumptions and describe the selected parameters, and then present and discuss the results.

4.1. Assumptions and Descriptions

We assume the mortality rates follow the Danish Financial Supervisory Authority’s (Finanstilsynet) life expectancy model1, using intensities provided by PFA Pension incorporating improvements in life expectancy. This means that the mortality intensity for women and men with age x at time t can be described as

$$\begin{array}{cc}\hfill {\mu }_{women}(x,t)& ={\mu }_{women}(x,2023){(1-R_{women}\left(x\right))}^{t-2023},\hfill \\ \hfill {\mu }_{men}(x,t)& ={\mu }_{men}(x,2023){(1-R_{men}\left(x\right))}^{t-2023}.\hfill \end{array}$$

where ${\mu }_{women}(x,2023)$ and ${\mu }_{men}(x,2023)$ for $x=0,\dots ,110$ are the current mortality for women and men, respectively, and $R_{women}\left(x\right)$ and $R_{men}\left(x\right)$ for $x=0,\dots ,110$ are the future expected life improvements for women and men, respectively. As previously explained, it is possible to have a risk loading if ${\mu }^{*}\ne \mu$, but for simplicity, we exclude this in the calculations and assume entirely fair insurance ${\mu }^{*}=\mu$, simplifying the problem significantly. Based on Burgaard and Steffensen (2020), we let the risk aversion for female be ${\gamma }_{women}:=2.25$ and for men ${\gamma }_{men}:=1.86$.

Moreover, we assume the wealth of the insured consists exclusively of the amount accumulated within the pension company. The payout upon death is equal to this accumulated wealth, the bequest wealth from the pension company, along with one other potential extra lump sum payment from outside the company made at the time of the policyholder’s death.

In our analysis, we aim to isolate the effects of various attributes on policyholder behavior by segmenting the data into distinct groups. This approach allows us to identify patterns and correlations within the portfolio. The key covariates used for this segmentation are defined as follows: First, we consider each policyholder’s coverage level. This is categorized into three distinct groups: those whose coverage is at the maximum allowable level under their agreement, those whose coverage falls between the minimum and maximum levels, and those whose coverage is at the minimum permissible level. Secondly, we classify policyholders based on their annual salary. The salary categories are defined as follows: less than 80,000 DKK, between 80,000 and 400,000 DKK, between 400,000 and 1,000,000 DKK, and greater than 1,000,000 DKK. These categories help us understand the financial background of the policyholders and its potential impact on their decisions.

Another significant covariate is the recommendation status. Policyholders who have completed an online questionnaire provided by the pension company and received some coverage recommendations are classified as having “Recommendation Viewed”. Conversely, those who have not completed the questionnaire are classified as having “Recommendation Not Viewed”. We also differentiate policyholders based on the type of life insurance benefit they have. Those who retain the default coverage provided by the agreement are classified under “Standard Life Insurance Benefit”, while those who have modified their coverage from the default are classified under “Custom Life Insurance Benefit”. Lastly, we consider whether a policy is broker-assisted. Policies managed with a broker’s assistance are classified as “Broker-Assisted”, whereas those managed without broker assistance are classified as “Non-Broker-Assisted”.

These covariates are crucial for our analysis as they allow us to group policyholders into homogeneous segments, facilitating a more granular examination of behavior and outcomes. By analyzing these segments, we can better understand the impact of different attributes on policyholder decisions and overall portfolio performance.

If a policyholder holds multiple policies, these are aggregated and evaluated cumulatively, as it is assumed that the policyholders would have rights to all policies upon death. When aggregating the policies, we have assumed some way of aggregating the variables we use to examine the results, and in turn, we have assumed the following:

• For the coverage level, it is assumed that all coverages must be at the minimum or maximum limit for the policyholder to be noted as being at the respective limit.
• The policyholder is cumulatively noted as “Recommendation Viewed” if at least one of the policies has received a recommendation.
• The policyholder is noted as “Custom Life Insurance Benefit” if this is the case for at least one of the policies.
• The policyholder is noted as “Broker-Assisted” if this is the case for at least one of the policies.

Another critical assumption is that the provided salary is constant; extending it to an adjustable wage is not tricky. The discount rate is set at 3.9%, given that the analysis’s purpose is to evaluate the value of future money placed in the PFA Pension internally, with the knowledge that it can carry risk. With the implicit priority as $\mathcal{I}\left(current\right)=w^{current}/w^{complete}$ and 110 used as the maximum possible living age, composite Simpson has been used to calculate the numerical integrals; further explanation can be found in Appendix A.

4.2. Benchmark

To assess whether the insured are generally over- or under-insured, a reference point is usually used to evaluate whether their coverage exceeds or falls short. This reference could be three times their annual income, with adjustments made in special cases where more detailed policyholder information is available. This evaluation method serves as a reference point; thus, we introduce a benchmark coverage, and thereby a simplicity priority of this benchmark $\mathcal{I}\left(Benchmark\right)$, representing the implicit prioritization a policyholder would have if their life insurance coverage were set at three times their annual income. In this calculation, we assume their life insurance coverage is precisely this benchmark and compare it in the same manner as their current coverage. Specifically, we analyze how the individual prioritizes this benchmark coverage relative to consumption, compared to having all future income covered as a life insurance sum.

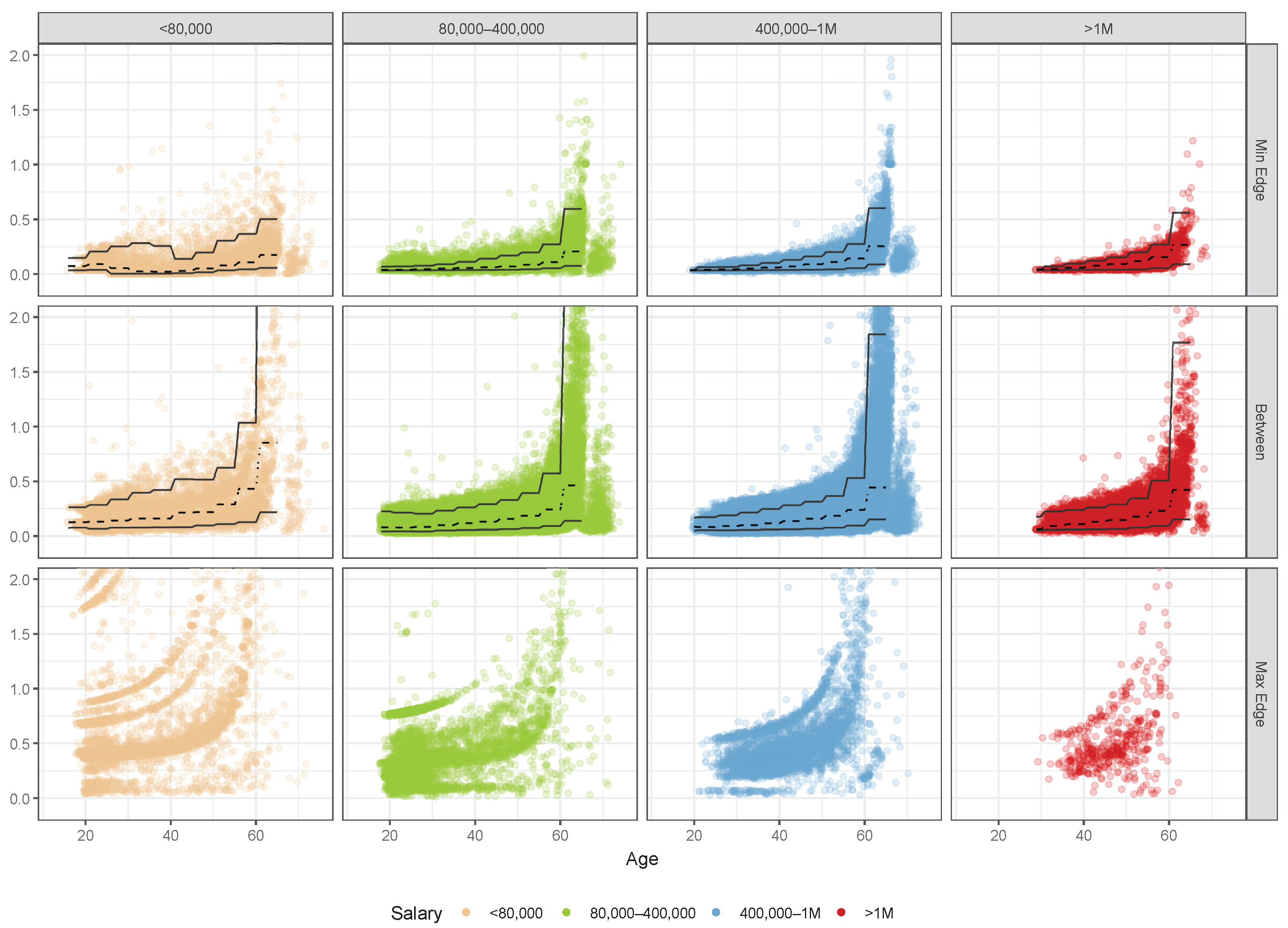
4.3. Results and Discussion

First, we examine the entire population and then break it down into individual components that we consider to be of greater significance. In all illustrations, the implicit priority $\mathcal{I}$ of the life insurance payout is depicted as a function of age. Each point represents a policyholder, illustrating how they individually prioritize their current death benefit relative to consuming funds compared to having full coverage of all future income.

When discussing implicit priority, $\mathcal{I}$, it is essential to note that we do not expect it to equal one or any other predetermined number. As previously described, having all expected future income covered is an extreme case. However, we do expect some form of consistency among groups of individuals with similar characteristics. Therefore, further investigation could be warranted if the data show tendencies towards lower or higher prioritization for several groups or subdivisions.

To illustrate the distribution of the entire population, Figure 1 displays all $\mathcal{I}\left(current\right)$ aggregated for the currently selected coverage, compared with the benchmark implicit priority $\mathcal{I}\left(Benchmark\right)$ for the entire population, marked in pink. This results in a large green cloud, where we can observe several bands that lie higher than the majority. However, due to the high number of points, it is challenging to form a clear overview.

To establish an interpretative baseline, an implicit prioritization of exactly one can be understood as the policyholder implicitly prioritizing their current coverage as highly as having all their future income covered. Those with values above one implicitly prioritize their life insurance coverage more than all the income they can expect to earn until retirement.

We aim to demonstrate how policyholders individually prioritize their life insurance coverage within the population. Assuming that somewhat similar policyholders should exhibit similar $\mathcal{I}$, we group them to highlight outliers with two main points:

• Extra information can shed light on some outliers, and their implicit prioritization might indicate a deliberate and sensible choice.
• For some, it might be essential to ensure the policyholder is aware of the prioritization of their life insurance coverage and how they compare to similar policyholders.

To identify trends, we specify the analysis and attempt to find correlations and outliers that we can discuss. This will help us identify smaller groups with more similarities, allowing us to make more specific statements about how individuals prioritize their life insurance coverage compared to similar policyholders.

Given that PFA Pension is a private pension company with a substantial portion of its population drawn from various companies, it is common for coverages to be determined by agreements specific to each company. Consequently, we aim to examine the parameters of these agreements and analyze how policyholders have made choices and prioritized within these constraints.

In Figure 2, we examine the minimum and maximum boundaries of the company agreements that policyholders are mandated to follow. For policyholders whose coverage lies on the minimum limit or between the minimum and maximum boundaries, we further illustrate where the middle $90\%$ of all data points for each age group are located, marked by black vertical lines. The prominent point here is the median for each age group. There is a wide dispersion in the cloud of points, but the band is considerably narrower when focusing on the middle $90\%$. Additionally, a relatively stable median gradually increasing until a few years before retirement age is visible. A possible interpretation could be policyholders not regularly updating their life insurance coverage, which may become less accurate over time.

It is evident that almost all notable outliers of $\mathcal{I}\left(current\right)$ in the previous plots are at the maximum boundary of their agreement, with all income levels being represented. The same division is shown in Figure 3, additionally split by income instead of overlaying the colors. Here, the middle $90\%$ of the points are between the solid lines, with the median marked by the dashed line, allowing for a clearer view of how the median and the concentration of points change across different income groups.

Assuming the boundaries are a potential limitation on the policyholder’s choices, it further depends on whether the policyholder has consciously chosen to have maximum or minimum coverage or simply stayed with a default coverage. Therefore, we examine whether the policyholder has the standard life insurance sum as coverage specified in the agreement or has chosen something different.

When a policyholder has received a recommendation, it indicates that they have completed a questionnaire regarding coverage available on PFA’s website. In Figure 4 we have included markers for the middle $90\%$ points and the median to better illustrate the development and the concentration of policyholders. In most cases, policyholders who have chosen something other than the standard coverage have opted for higher coverage. This may be due to the greater distance from the standard to the maximum compared to the standard to the minimum.

Since receiving a recommendation only indicates whether the policyholder has completed PFA’s questionnaire, we have in Figure 5 included whether the policyholder is broker-administered, as shown in the graph on the left. We assume that if they are broker-administered, the brokers have had a dialogue with the policyholder and have, therefore, gone through a form of recommendation marked in pink. The most interesting points from these graphs are possibly the policyholders who have chosen something other than the standard coverage, indicating a conscious decision, which results in a very high or very low implicit priority of life insurance coverage. Furthermore, those who are neither broker-administered nor have received a recommendation but have chosen to prioritize their coverage very highly can be seen in the lower right corner with the prominent blue high points.

Therefore, we have chosen to delve deeper and examine only those who have chosen something other than the standard coverage and how their implicit prioritization of life insurance coverage relates to the boundaries of the agreement. This is shown in Figure 6.

Here, all those who have chosen something other than the standard coverage are shown, representing a form of choice by the policyholder. Even with a conscious choice of the highest possible coverage within the agreement, many have a low implicit prioritization of their life insurance coverage compared to all their future income. This indicates that they may be under-insured in their economic situation and desire higher coverage but cannot choose it due to the agreement’s constraints; conversely, for the few who implicitly prioritize their life insurance coverage highly but have chosen the agreement’s minimum boundary.

Additionally, it remains interesting to investigate the very high implicit priorities, where policyholders prioritize their life insurance coverage much higher than all their future income.

To provide an overview and a comparison with the benchmark of three times annual income, Figure 7 shows that all the gray dots represent the policyholders’ implicit priority of the benchmark coverage, $\mathcal{I}\left(benchmark\right)$, relative to all their future income. The black vertical markers represent the middle $50\%$ of the $\mathcal{I}\left(Benchmark\right)$ values, and the purple marker illustrates where, for each group, the current middle $50\%$ of implicit prioritizations of current coverage $\mathcal{I}\left(current\right)$ are located. This clearly shows that the benchmark encapsulates policyholders who fall between the agreement’s minimum and maximum boundaries with all different income levels. However, for policyholders at the agreement’s minimum boundary, the benchmark is much too high. For the maximum boundary, the current middle $50\%$ is almost entirely outside the interval where the benchmark values lie.

This demonstrates how the benchmark can serve as a good starting point for a general guideline for most policyholders. However, to guide and examine the entire population, it may be beneficial to go down to a more individual level and find a guideline for how more policyholders can be advised based on their individual situations.

5. Conclusions and Future Work

We formalize the implicit priority based on the policyholder’s choices within a continuous-time life cycle model. Initially, we established this framework specifically for decisions related to life insurance coverage. However, extending it to include other insurance products, such as disability coverage, is of significant interest, as this would offer a more nuanced understanding of the policyholder’s actual choices. After all, the policyholder does not merely choose between life insurance coverage and immediate consumption.

Assuming the policyholder’s preferences follow a power utility function, the optimal consumption and bequest strategies are derived using the Hamilton–Jacobi–Bellman equation and used to measure the appreciation policyholders place upon their life insurance coverage compared to intermediate consumption.

We suggest a method to evaluate the implicit priority of a policyholder’s current coverage by measuring the appreciation of the life insurance coverage in two different scenarios; first, assuming the current coverage is optimal and second, concerning the complete coverage. Real data on each policyholder allow us to evaluate and compare the implicit priority across different sub-portfolios.

This study relies on the assumption of power utility functions and constant relative risk aversion. Together with the inclusion of optimal investment, it would be an intuitive step to include more refined optimal consumption and insurance solutions with more real-world aspects to reflect reality better. The exclusion of investment optimization and limiting the insurance framework to that of life insurance are deliberate choices to develop the concept of the implicit priority in the simplest possible setting, making it a starting point, and it would be a natural extension to investigate.

The data for our study are extensive but limited to one pension company. As a result, policyholders may have savings and other financial dependencies outside of this closed environment. Additionally, the specific living situations of the policyholders can significantly influence their preferences and would add depth to the analysis of implicit priorities.