Modeling Age-to-Age Development Factors in Auto Insurance Through Principal Component Analysis and Temporal Clustering
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Estimating Age-to-Age Development Factors via Principal Component Analysis
2.3. Eigenvalue Decomposition of DR
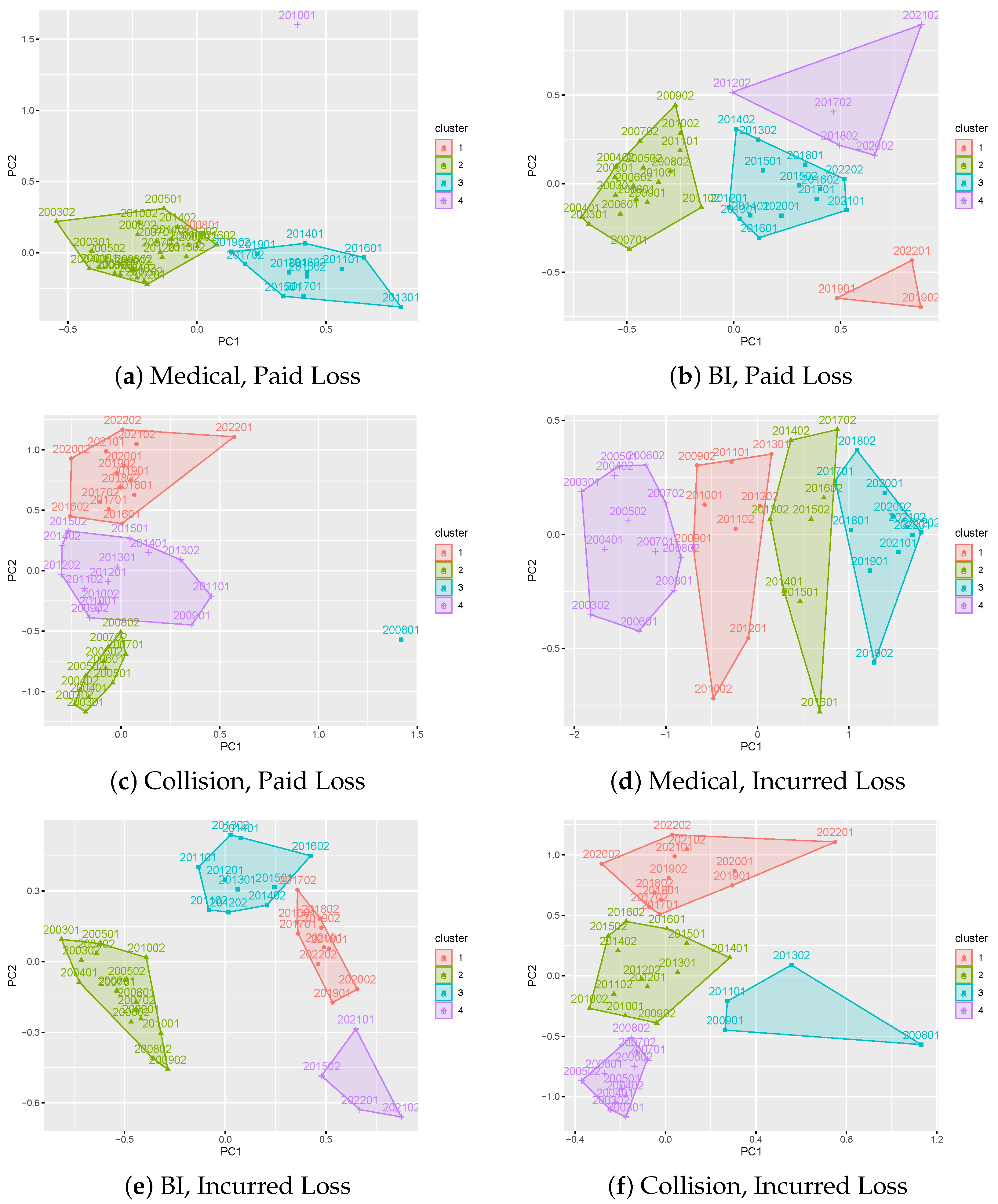
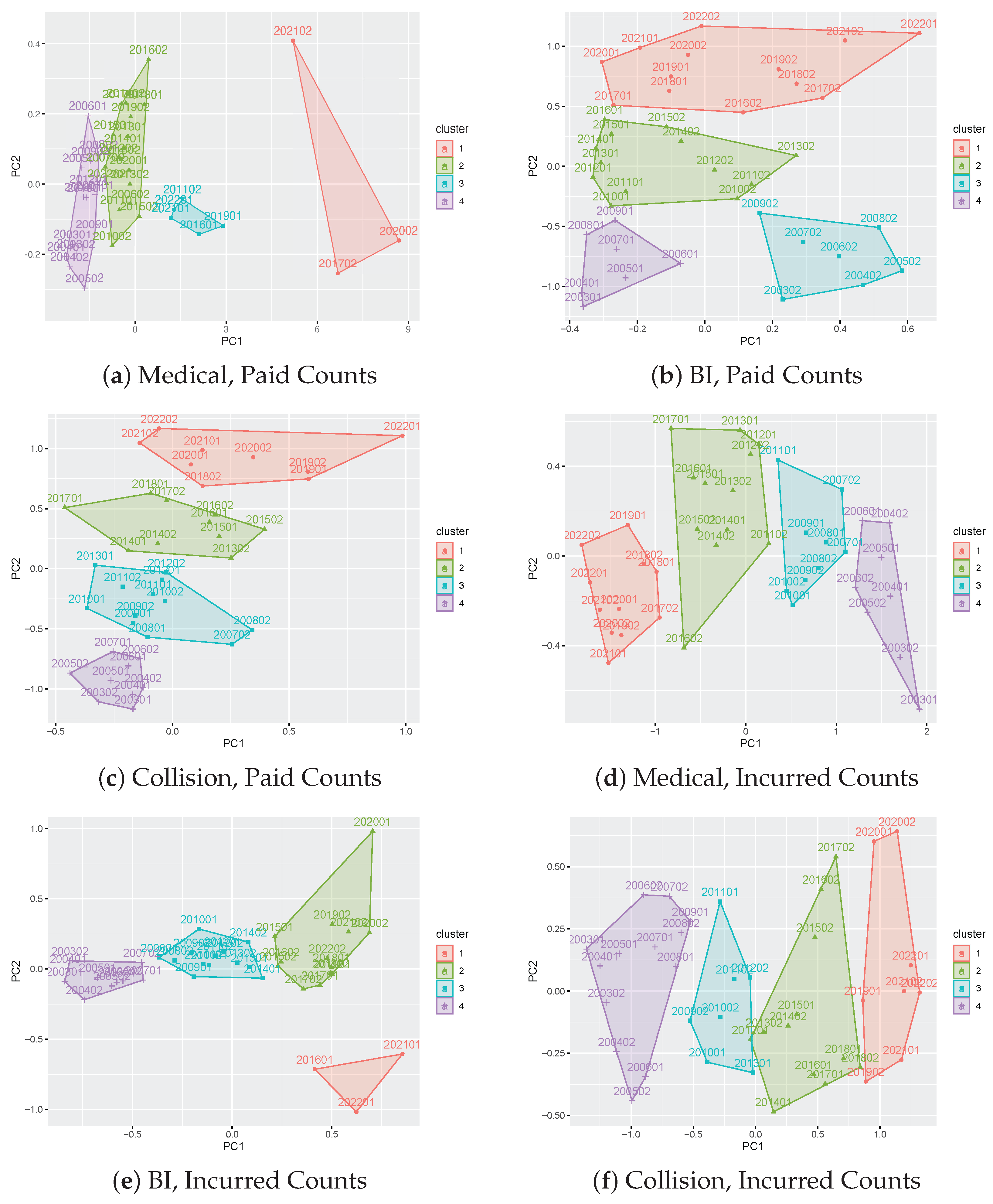
2.4. K-Means Clustering of Principal Component Scores with Contiguity Constraints in Time
| Algorithm 1 Procedure for K-Means clustering of principal component scores with contiguity constraints in time. |
|
- A weight is incorporated into the objective function to control the influence of each feature during clustering.
- Post-clustering adjustments are made to ensure that clusters maintain full temporal contiguity, and no cluster consists of a single, isolated accident half year.
2.5. Modeling Development Factors by Generalized Linear Models
2.6. Implications of Proposed Methods
3. Results
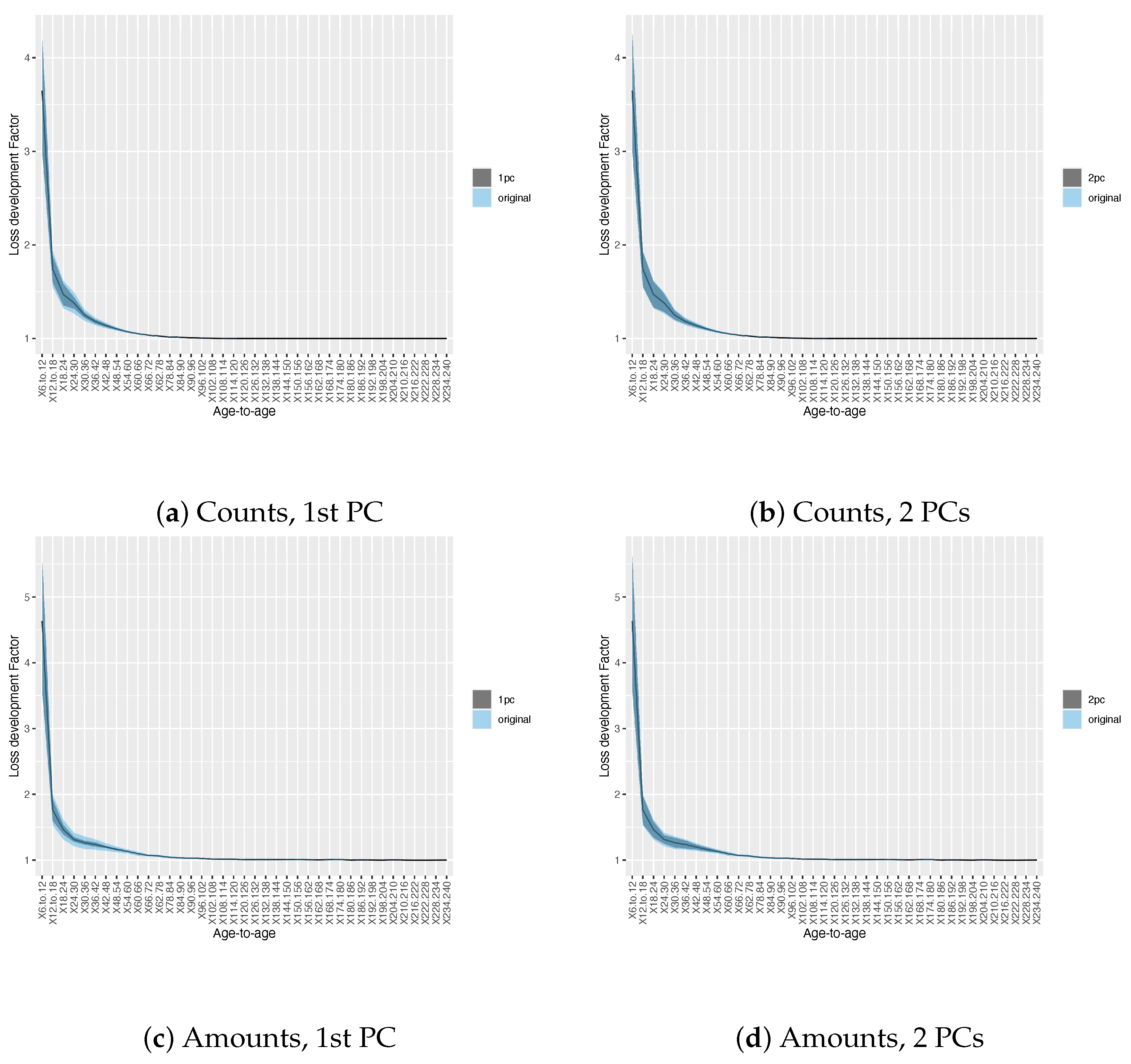
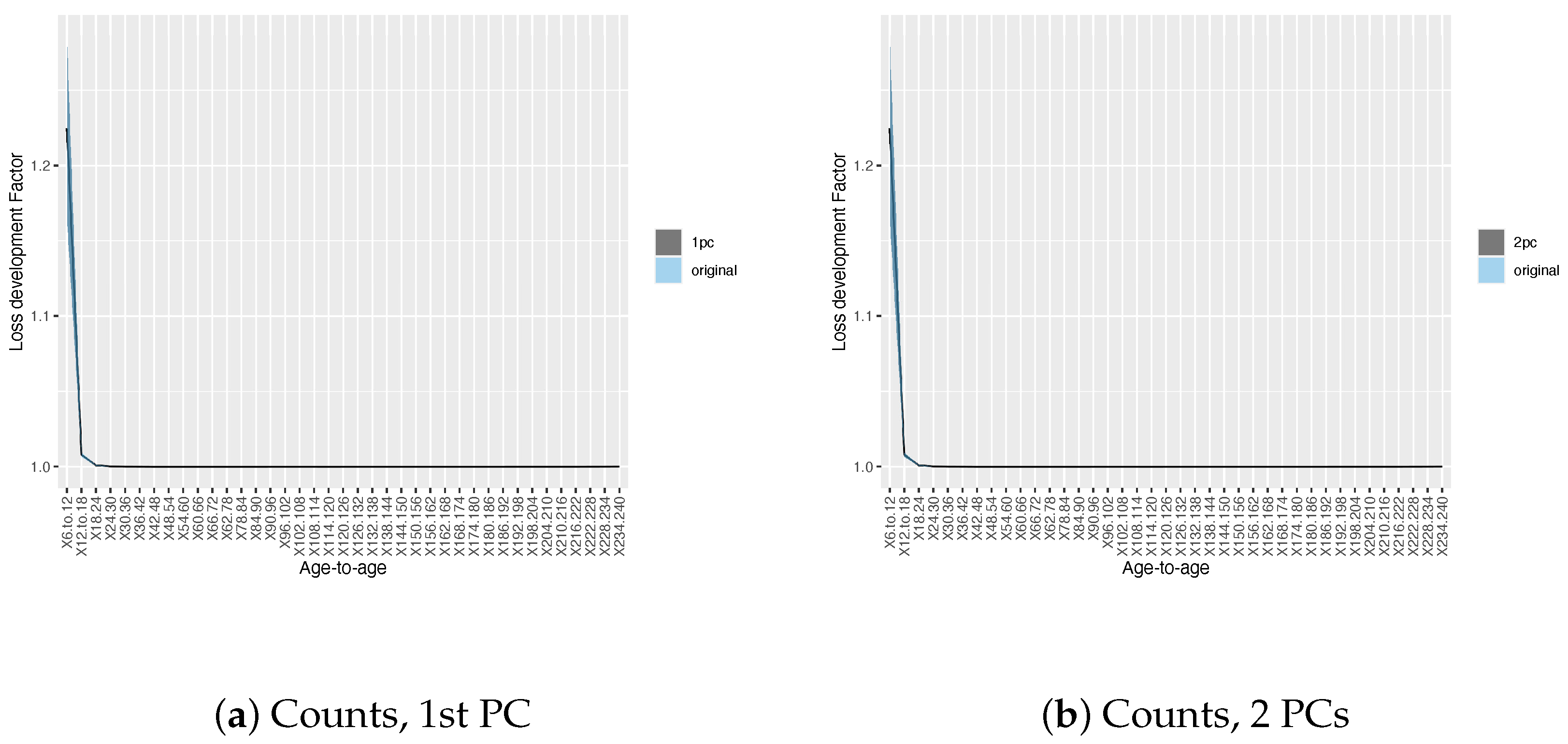
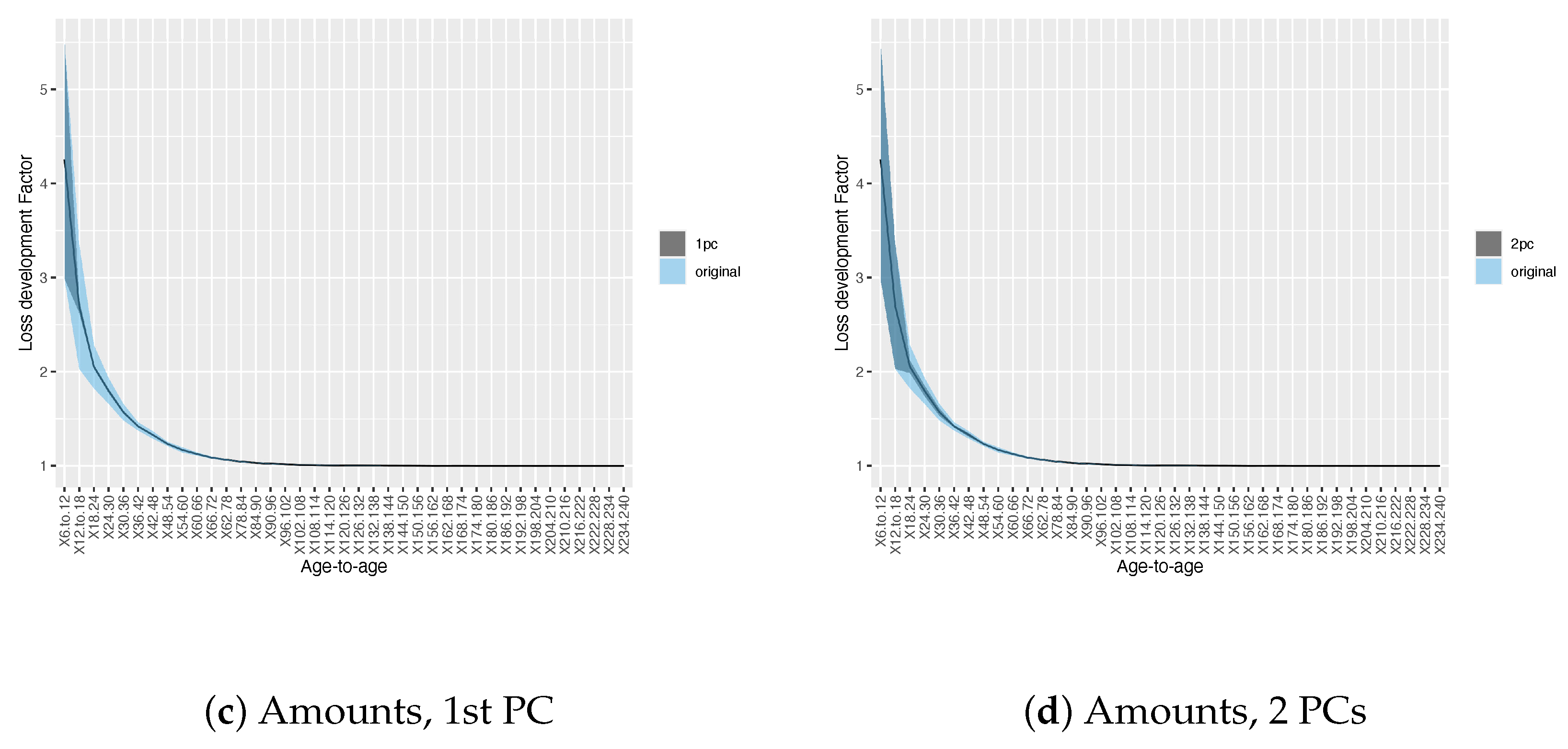
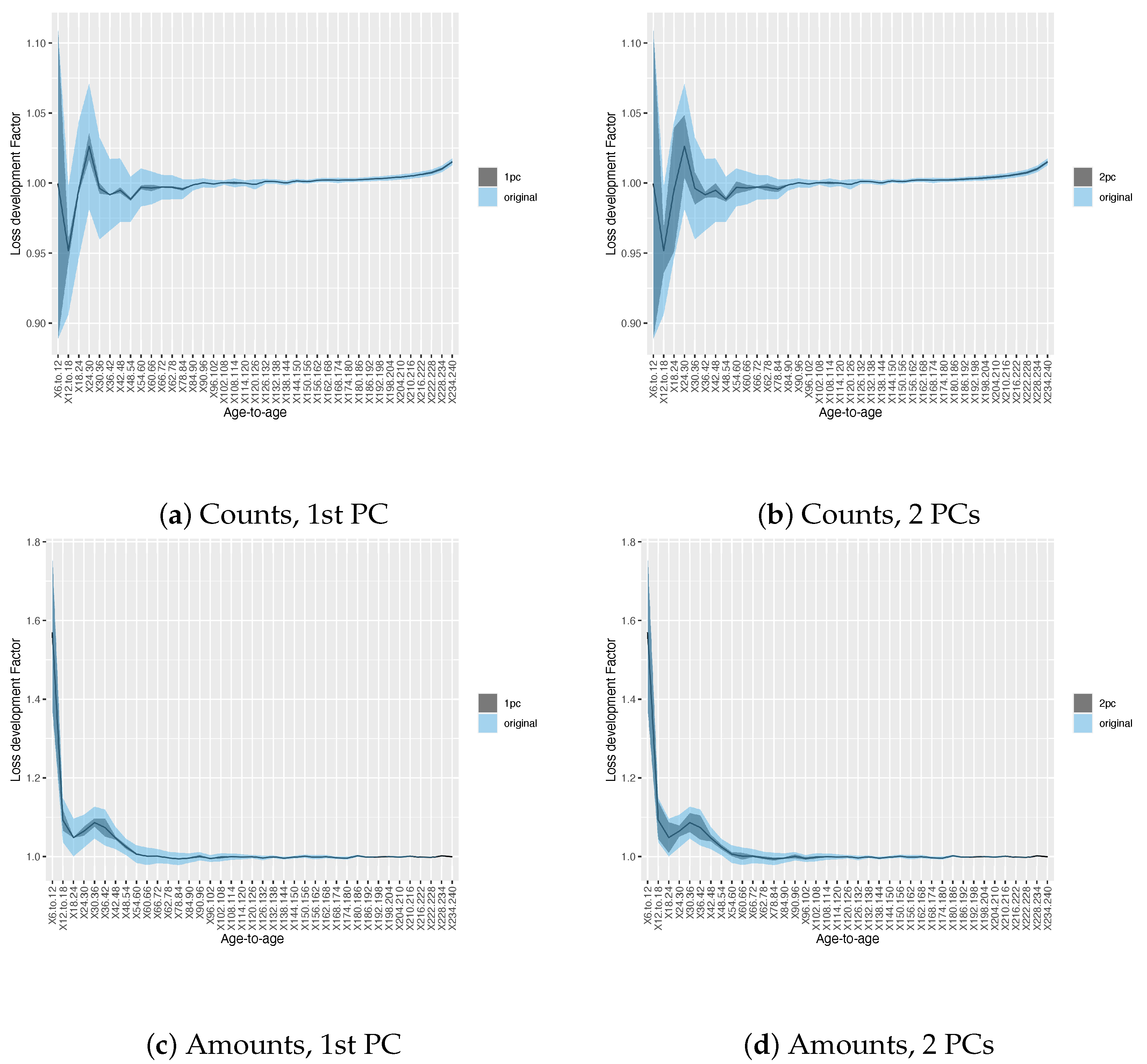
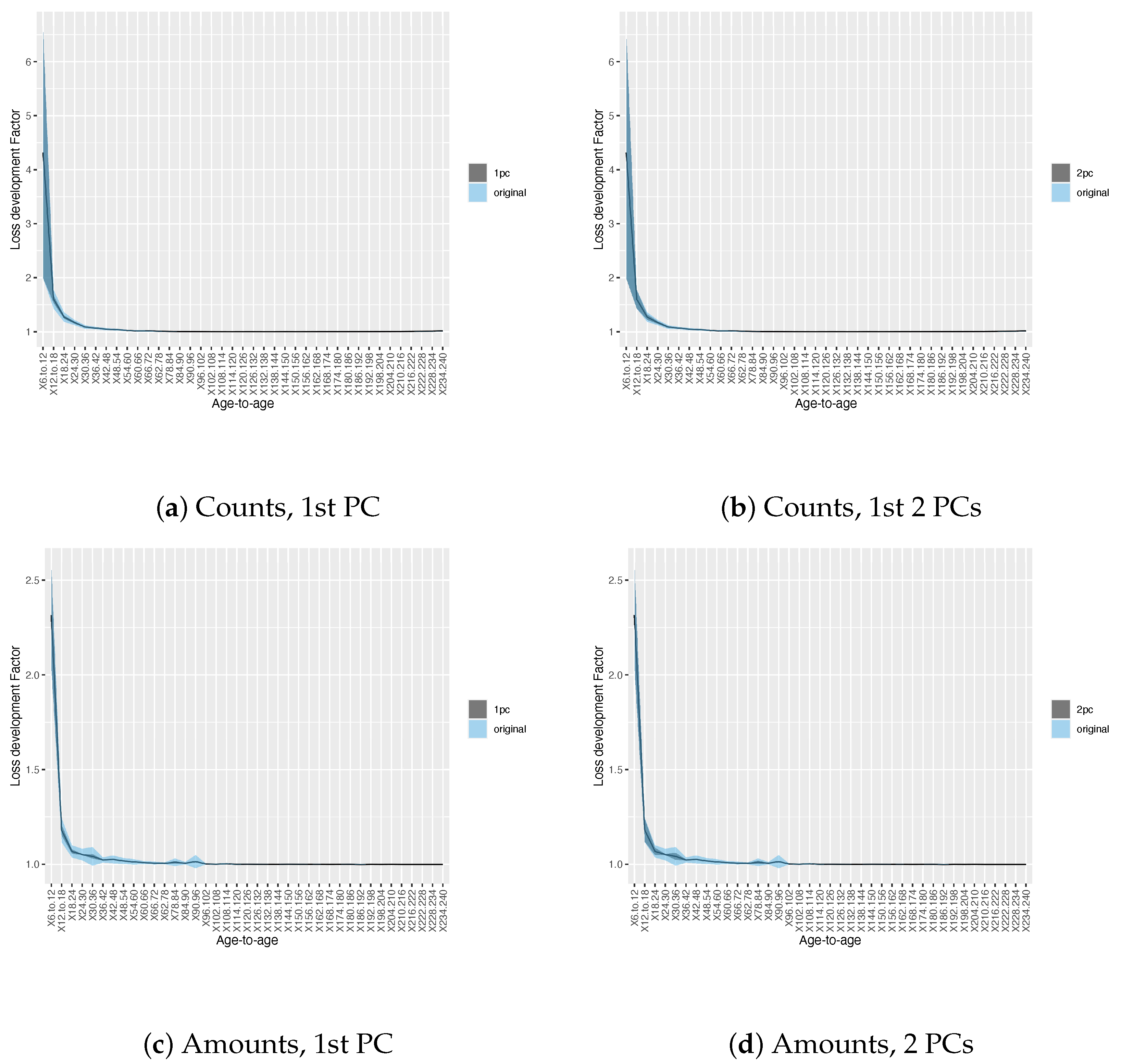
3.1. Results on Principal Component Analysis and Weighted K-Means of Development Factors
3.2. Results on Development Factor Estimates
4. Some Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Mudafer, Muhammed Taher, Benjamin Avanzi, Greg Taylor, and Bernard Wong. 2022. Stochastic loss reserving with mixture density neural networks. Insurance: Mathematics and Economics 105: 144–74. [Google Scholar] [CrossRef]
- Barlak, Jan, Matus Bakon, Martin Rovnak, and Martina Mokrisova. 2022. Heat equation as a tool for outliers mitigation in run-off triangles for valuing the technical provisions in non-life insurance business. Risks 10: 171. [Google Scholar] [CrossRef]
- Berquist, James R., and Richard E. Sherman. 1977. Loss reserve adequacy testing: A comprehensive, systematic approach. In Proceedings of the Casualty Actuarial Society. 64 vols. Arlington: Casualty Actuarial Society, pp. 123–84. [Google Scholar]
- D’Arcy, Stephen P. 1987. Revisions in loss reserving techniques necessary to discount property-liability loss reserves. In PCAS LXXIV. Arlington: Casualty Actuarial Society. [Google Scholar]
- England, Peter D., and Richard J. Verrall. 2002. Stochastic claims reserving in general insurance. British Actuarial Journal 8: 443–518. [Google Scholar] [CrossRef]
- Feng, Yu Shi, and Ira Robbin. 2022. Quantifying reserve risk based on volatility in triangles of estimated ultimate losses. CAS E-Forum. Available online: https://eforum.casact.org/article/37955-quantifying-reserve-risk-based-on-volatility-in-triangles-of-estimated-ultimate-losses (accessed on 14 May 2025).
- Frees, Edward W., Richard A. Derrig, and Glenn Meyers. 2014. Predictive Modeling Applications in Actuarial Science. Cambridge: Cambridge University Press, vol. 1. [Google Scholar]
- Han, Zhongxian, and Wu-Chyuan Gau. 2008. Estimation of loss reserves with lognormal development factors. Insurance: Mathematics and Economics 42: 389–95. [Google Scholar] [CrossRef]
- Jeong, Himchan, and Dipak Dey. 2020. Application of a vine copula for multi-line insurance reserving. Risks 8: 111. [Google Scholar] [CrossRef]
- Jeong, Himchan, Hyunwoong Chang, and Emiliano A. Valdez. 2021. A non-convex regularization approach for stable estimation of loss development factors. Scandinavian Actuarial Journal 2021: 779–803. [Google Scholar] [CrossRef]
- Kloek, Teun. 1998. Loss development forecasting models: An econometrician’s view. Insurance: Mathematics and Economics 23: 251–61. [Google Scholar] [CrossRef]
- Korn, Uri. 2015. Credibility and other modeling considerations for loss development factors. CAS E-Forum, Summer 2: 1–25. [Google Scholar]
- Mack, Thomas. 1995. Distribution-free calculation of the standard error of chain ladder reserve estimates. Insurance Mathematics and Economics 3: 277–78. [Google Scholar] [CrossRef]
- Mack, Thomas. 1999. The standard error of chain ladder reserve estimates: Recursive calculation and inclusion of a tail factor. ASTIN Bulletin: The Journal of the IAA 29: 361–66. [Google Scholar] [CrossRef]
- Neuhaus, Walther. 2023. Consistent development patterns. Scandinavian Actuarial Journal 2023: 933–45. [Google Scholar] [CrossRef]
- Nugraha, Ruth Cornelia, and Danang Teguh Qoyyimi. 2022. Predicting claim reserves when the loss development factors are unstable: A case study from indonesia’s general insurance company. In International Conference on Educational Technology and Administration. Berlin/Heidelberg: Springer, pp. 109–30. [Google Scholar]
- Okyere Dwebeng, Daniel. 2016. Projecting Loss Reserves Using Tail Factor Development Method a Case Study of State Insurance Company (Motor Insurance). Ph.D. thesis, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana. [Google Scholar]
- Pittarello, Gabriele, Gian Paolo Clemente, and Diego Zappa. 2022. An Individual Model for Claims Reserving Based on Bayesian Neural Networks. Technical Report. Rome: Sapienza Università di Roma. [Google Scholar]
- Raço, Endri, Kleida Haxhi, Etleva Llagami, and Oriana Zaçaj. 2022. Comparison of statistical methods for claims reserve estimation using r language. WSEAS Transactions on Mathematics 21: 547–52. [Google Scholar] [CrossRef]
- Radtke, Michael. 2016. Cape cod method. In Handbook on Loss Reserving. Berlin/Heidelberg: Springer, pp. 43–52. [Google Scholar]
- Sakthivel, K. M. 2016. A nonparametric approach for validation of chain ladder methods in claims reserving. International Research Journal of Engineering and Technology 3: 1616–19. [Google Scholar]
- Schmidt, Klaus D., and Mathias Zocher. 2007. The Bornhuetter-Ferguson Principle. Göttingen: Institut für Mathematische Stochastik. [Google Scholar]
- Shi, Peng, and Brian M. Hartman. 2016. Credibility in loss reserving. North American Actuarial Journal 20: 114–32. [Google Scholar] [CrossRef]
- Sriram, Karthik, and Peng Shi. 2021. Stochastic loss reserving: A new perspective from a dirichlet model. Journal of Risk and Insurance 88: 195–230. [Google Scholar] [CrossRef]
- Taylor, Gregory. 2012. Loss Reserving: An Actuarial Perspective. Berlin and Heidelberg: Springer Science & Business Media, vol. 21. [Google Scholar]
- Verdier, Bertrand, and Artur Klinger. 2005. Jab Chain: A Model-Based Calculation of Paid and Incurred Loss Development Factors. Zurich: ASTIN Colloquium. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=0929a8a16a2e11377c024c3c040a383156c147b9 (accessed on 1 January 2025).
- Verrall, Richard J. 2000. An investigation into stochastic claims reserving models and the chain-ladder technique. Insurance: Mathematics and Economics 26: 91–99. [Google Scholar] [CrossRef]
- Zhao, Yixing, Rogemar Mamon, and Heng Xiong. 2021. Claim reserving for insurance contracts in line with the international financial reporting standards 17: A new paid-incurred chain approach to risk adjustments. Financial Innovation 7: 71. [Google Scholar] [CrossRef]
| Accident HY | 6 to 12 | 12 to 18 | 18 to 24 | 24 to 30 | 30 to 36 | 36 to 42 | 42 to 48 | 48 to 54 | 54 to 60 | 60 to 66 | 66 to 72 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 200301 | 2.979 | 1.590 | 1.234 | 1.178 | 1.194 | 1.158 | 1.216 | 1.145 | 1.132 | 1.104 | 1.067 |
| 200302 | 3.482 | 1.504 | 1.375 | 1.318 | 1.200 | 1.181 | 1.208 | 1.169 | 1.094 | 1.101 | 1.062 |
| 200401 | 3.352 | 1.432 | 1.296 | 1.285 | 1.244 | 1.117 | 1.194 | 1.151 | 1.169 | 1.069 | 1.077 |
| 200402 | 3.557 | 1.497 | 1.489 | 1.274 | 1.219 | 1.167 | 1.153 | 1.191 | 1.148 | 1.096 | 1.102 |
| 200501 | 3.493 | 1.536 | 1.399 | 1.346 | 1.323 | 1.148 | 1.124 | 1.131 | 1.119 | 1.038 | 1.052 |
| 200502 | 4.219 | 1.649 | 1.462 | 1.244 | 1.146 | 1.191 | 1.210 | 1.149 | 1.113 | 1.095 | 1.075 |
| 200601 | 3.814 | 1.543 | 1.338 | 1.228 | 1.191 | 1.165 | 1.207 | 1.168 | 1.145 | 1.086 | 1.074 |
| 200602 | 4.204 | 1.513 | 1.317 | 1.286 | 1.212 | 1.239 | 1.145 | 1.114 | 1.168 | 1.059 | 1.057 |
| 200701 | 3.506 | 1.464 | 1.326 | 1.255 | 1.188 | 1.168 | 1.157 | 1.095 | 1.080 | 1.145 | 1.076 |
| 200702 | 3.977 | 1.540 | 1.286 | 1.231 | 1.212 | 1.202 | 1.207 | 1.093 | 1.101 | 1.066 | 1.075 |
| 200801 | 3.779 | 1.493 | 1.330 | 1.299 | 1.188 | 1.180 | 1.129 | 1.079 | 1.102 | 1.088 | 1.063 |
| 200802 | 4.331 | 1.540 | 1.248 | 1.205 | 1.148 | 1.146 | 1.121 | 1.134 | 1.096 | 1.070 | 1.062 |
| 200901 | 3.653 | 1.490 | 1.313 | 1.179 | 1.119 | 1.108 | 1.104 | 1.119 | 1.128 | 1.090 | 1.066 |
| 200902 | 4.478 | 1.560 | 1.277 | 1.151 | 1.124 | 1.137 | 1.106 | 1.127 | 1.080 | 1.101 | 1.040 |
| 201001 | 3.964 | 1.580 | 1.253 | 1.163 | 1.120 | 1.118 | 1.125 | 1.084 | 1.062 | 1.046 | 1.062 |
| 201002 | 3.069 | 1.489 | 1.296 | 1.238 | 1.160 | 1.226 | 1.138 | 1.124 | 1.118 | 1.108 | 1.095 |
| 201101 | 4.035 | 1.802 | 1.658 | 1.306 | 1.379 | 1.219 | 1.243 | 1.168 | 1.139 | 1.104 | 1.080 |
| 201102 | 4.351 | 1.787 | 1.485 | 1.404 | 1.259 | 1.364 | 1.221 | 1.239 | 1.181 | 1.117 | 1.116 |
| 201201 | 4.541 | 1.772 | 1.723 | 1.497 | 1.347 | 1.345 | 1.182 | 1.213 | 1.162 | 1.102 | 1.073 |
| 201202 | 4.607 | 1.860 | 1.380 | 1.429 | 1.389 | 1.381 | 1.213 | 1.256 | 1.135 | 1.105 | 1.052 |
| 201301 | 4.602 | 1.915 | 1.672 | 1.205 | 1.329 | 1.283 | 1.265 | 1.178 | 1.140 | 1.064 | 1.058 |
| 201302 | 4.005 | 2.045 | 1.366 | 1.465 | 1.286 | 1.370 | 1.298 | 1.217 | 1.129 | 1.082 | 1.057 |
| 201401 | 4.170 | 1.802 | 1.690 | 1.378 | 1.490 | 1.371 | 1.299 | 1.190 | 1.165 | 1.075 | 1.059 |
| 201402 | 5.042 | 1.887 | 1.575 | 1.576 | 1.300 | 1.307 | 1.360 | 1.196 | 1.150 | 1.123 | 1.090 |
| 201501 | 5.016 | 1.931 | 1.676 | 1.230 | 1.534 | 1.300 | 1.207 | 1.241 | 1.176 | 1.240 | 1.093 |
| 201502 | 7.001 | 1.868 | 1.477 | 1.516 | 1.293 | 1.361 | 1.228 | 1.226 | 1.167 | 1.115 | 1.074 |
| 201601 | 5.494 | 1.958 | 1.582 | 1.485 | 1.399 | 1.285 | 1.320 | 1.204 | 1.123 | 1.147 | 1.085 |
| 201602 | 5.419 | 2.434 | 1.459 | 1.420 | 1.250 | 1.318 | 1.216 | 1.163 | 1.130 | 1.105 | 1.083 |
| 201701 | 5.239 | 1.997 | 1.516 | 1.311 | 1.324 | 1.272 | 1.250 | 1.161 | 1.183 | 1.112 | 1.091 |
| 201702 | 4.874 | 1.977 | 1.642 | 1.391 | 1.296 | 1.261 | 1.249 | 1.167 | 1.136 | 1.128 | 1.072 |
| 201801 | 5.873 | 2.053 | 1.698 | 1.315 | 1.333 | 1.172 | 1.187 | 1.178 | 1.234 | 1.099 | 1.072 |
| 201802 | 5.325 | 2.059 | 1.576 | 1.228 | 1.405 | 1.287 | 1.139 | 1.237 | 1.130 | 1.099 | 1.072 |
| 201901 | 5.878 | 1.805 | 1.636 | 1.335 | 1.302 | 1.327 | 1.254 | 1.161 | 1.130 | 1.099 | 1.072 |
| 201902 | 5.073 | 1.957 | 1.530 | 1.404 | 1.282 | 1.295 | 1.193 | 1.161 | 1.130 | 1.099 | 1.072 |
| 202001 | 5.064 | 1.945 | 1.482 | 1.371 | 1.259 | 1.230 | 1.193 | 1.161 | 1.130 | 1.099 | 1.072 |
| 202002 | 6.043 | 1.948 | 1.717 | 1.323 | 1.241 | 1.230 | 1.193 | 1.161 | 1.130 | 1.099 | 1.072 |
| 202101 | 6.006 | 1.861 | 1.584 | 1.287 | 1.241 | 1.230 | 1.193 | 1.161 | 1.130 | 1.099 | 1.072 |
| 202102 | 7.513 | 2.086 | 1.403 | 1.287 | 1.241 | 1.230 | 1.193 | 1.161 | 1.130 | 1.099 | 1.072 |
| 202201 | 6.138 | 1.667 | 1.403 | 1.287 | 1.241 | 1.230 | 1.193 | 1.161 | 1.130 | 1.099 | 1.072 |
| 202202 | 4.160 | 1.667 | 1.403 | 1.287 | 1.241 | 1.230 | 1.193 | 1.161 | 1.130 | 1.099 | 1.072 |
| BI, Incurred Loss | Collision, Incurred Loss | Medical, Incurred Loss | ||||
|---|---|---|---|---|---|---|
| PC1 | PC2 | PC1 | PC2 | PC1 | PC2 | |
| Standard deviation | 1.066 | 0.208 | 0.030 | 0.006 | 0.202 | 0.066 |
| Proportion of Variance | 0.938 | 0.036 | 0.960 | 0.034 | 0.754 | 0.081 |
| Cumulative Proportion | 0.938 | 0.974 | 0.960 | 0.995 | 0.754 | 0.835 |
| BI, Paid Loss | Collision, Paid Loss | Medical, Paid Loss | ||||
| PC1 | PC2 | PC1 | PC2 | PC1 | PC2 | |
| Standard deviation | 1.270 | 0.670 | 0.081 | 0.005 | 0.275 | 0.060 |
| Proportion of Variance | 0.754 | 0.210 | 0.995 | 0.004 | 0.878 | 0.042 |
| Cumulative Proportion | 0.754 | 0.964 | 0.995 | 1.000 | 0.878 | 0.920 |
| BI, Incurred Counts | Collision, Incurred Counts | Medical, Incurred Counts | ||||
| PC1 | PC2 | PC1 | PC2 | PC1 | PC2 | |
| Standard deviation | 0.672 | 0.175 | 0.061 | 0.026 | 0.112 | 0.052 |
| Proportion of Variance | 0.916 | 0.062 | 0.706 | 0.125 | 0.562 | 0.123 |
| Cumulative Proportion | 0.916 | 0.977 | 0.706 | 0.831 | 0.562 | 0.685 |
| BI, Paid Counts | Collision, Paid Counts | Medical, Paid Counts | ||||
| PC1 | PC2 | PC1 | PC2 | PC1 | PC2 | |
| Standard deviation | 0.061 | 0.001 | 0.176 | 0.026 | 2.326 | 0.166 |
| Proportion of Variance | 1.000 | 0.000 | 0.964 | 0.021 | 0.993 | 0.005 |
| Cumulative Proportion | 1.000 | 1.000 | 0.964 | 0.984 | 0.993 | 0.998 |
| BI, Incurred Loss | Collision, Incurred Loss | Medical, Incurred Loss | |||||||
| Reported Year | 2020 | 2021 | 2022 | 2020 | 2021 | 2022 | 2020 | 2021 | 2022 |
| group2 | 0.021 | 0.004 | 0.018 | −0.006 *** | 0.007 *** | 0.008 *** | 0.077 | 0.024 | 0.054 *** |
| (0.110) | (0.118) | (0.139) | (0.002) | (0.002) | (0.003) | (0.078) | (0.020) | (0.018) | |
| group3 | 0.207 * | 0.195 * | 0.256 * | −0.007 *** | 0.006 ** | 0.006 ** | 0.193 ** | 0.106 *** | 0.083 *** |
| (0.116) | (0.118) | (0.131) | (0.002) | (0.002) | (0.003) | (0.076) | (0.018) | (0.018) | |
| group4 | 0.450 *** | 0.437 *** | 0.556 *** | 0.00003 | 0.006 ** | 0.007 *** | 0.132 * | 0.099 *** | 0.082 *** |
| (0.110) | (0.108) | (0.131) | (0.002) | (0.002) | (0.003) | (0.076) | (0.018) | (0.018) | |
| Mean Age-to-Age DFs | |||||||||
| Period12 | 3.917 | 3.973 | 4.008 | 1.010 | 1.069 | 1.071 | 1.688 | 1.489 | 1.518 |
| Period18 | 2.422 | 2.428 | 2.448 | 1.002 | 0.999 | 0.999 | 0.995 | 1.026 | 1.041 |
| Period24 | 1.834 | 1.832 | 1.806 | 1.003 | 0.995 | 0.995 | 0.929 | 0.984 | 0.997 |
| Period30 | 1.592 | 1.594 | 1.549 | 1.003 | 0.995 | 0.995 | 0.942 | 1.004 | 1.014 |
| Period36 | 1.381 | 1.376 | 1.324 | 1.003 | 0.995 | 0.995 | 0.923 | 1.024 | 1.035 |
| BI, Paid Loss | Collision, Paid Loss | Medical, Paid Loss | |||||||
| Reported Year | 2020 | 2021 | 2022 | 2020 | 2021 | 2022 | 2020 | 2021 | 2022 |
| group2 | 0.086 | 0.080 | 0.068 | −0.0003 | 0.022 *** | 0.019 *** | 0.073 *** | 0.073 *** | 0.073 *** |
| (0.071) | (0.077) | (0.091) | (0.006) | (0.007) | (0.007) | (0.018) | (0.018) | (0.018) | |
| group3 | 0.460 *** | 0.455 *** | 0.458 *** | −0.003 | 0.004 | 0.003 | |||
| (0.071) | (0.077) | (0.089) | (0.006) | (0.007) | (0.007) | ||||
| group4 | 0.469 *** | 0.500 *** | 0.536 *** | 0.006 | 0.007 | 0.010 | |||
| (0.071) | (0.073) | (0.085) | (0.006) | (0.007) | (0.007) | ||||
| Mean Age-to-Age DFs | |||||||||
| Period12 | 4.102 | 4.205 | 4.342 | 1.218 | 1.273 | 1.279 | 2.288 | 2.288 | 2.288 |
| Period18 | 1.485 | 1.480 | 1.472 | 1.005 | 1.004 | 1.004 | 1.153 | 1.153 | 1.153 |
| Period24 | 1.209 | 1.188 | 1.174 | 1.001 | 0.994 | 0.994 | 1.041 | 1.041 | 1.041 |
| Period30 | 1.072 | 1.049 | 1.025 | 1.000 | 0.993 | 0.993 | 1.024 | 1.024 | 1.024 |
| Period36 | 1.029 | 1.006 | 0.976 | 1.000 | 0.993 | 0.993 | 1.015 | 1.015 | 1.015 |
| BI, Incurred Counts | Collision, Incurred Counts | Medical, Incurred Counts | |||||||
| Reported Year | 2020 | 2021 | 2022 | 2020 | 2021 | 2022 | 2020 | 2021 | 2022 |
| group2 | −0.002 | −0.005 | −0.007 | 0.010 * | 0.003 | −0.003 | −0.012 | −0.010 | 0.002 |
| (0.005) | (0.004) | (0.005) | (0.005) | (0.006) | (0.006) | (0.008) | (0.009) | (0.013) | |
| group3 | −0.008 | −0.005 | −0.015 | −0.003 | −0.008 | −0.009 | 0.078 *** | 0.071 *** | −0.017 |
| (0.005) | (0.004) | (0.013) | (0.008) | (0.008) | (0.006) | (0.009) | (0.009) | (0.012) | |
| group4 | −0.003 | 0.0003 | 0.002 | −0.002 | −0.005 | 0.033 *** | 0.035 *** | 0.033 ** | |
| (0.005) | (0.005) | (0.005) | (0.005) | (0.006) | (0.006) | (0.007) | (0.013) | ||
| Mean Age-to-Age DFs | |||||||||
| Period12 | 1.225 | 1.223 | 1.227 | 1.069 | 1.076 | 1.081 | 0.754 | 0.748 | 0.995 |
| Period18 | 1.011 | 1.011 | 1.011 | 0.962 | 0.965 | 0.970 | 0.861 | 0.862 | 0.947 |
| Period24 | 1.004 | 1.004 | 1.004 | 0.981 | 0.985 | 0.987 | 0.971 | 0.972 | 0.991 |
| Period30 | 1.003 | 1.004 | 1.003 | 0.997 | 1.002 | 1.005 | 1.075 | 1.076 | 1.022 |
| Period36 | 1.003 | 1.004 | 1.003 | 0.995 | 0.999 | 1.002 | 0.965 | 0.961 | 0.992 |
| BI, Paid Counts | Collision, Paid Counts | Medical, Paid Counts | |||||||
| Reported Year | 2020 | 2021 | 2022 | 2020 | 2021 | 2022 | 2020 | 2021 | 2022 |
| group2 | 0.229 *** | 0.234 *** | 0.229 *** | 0.015 | 0.023 * | 0.014 | 0.269 *** | 0.248 *** | 0.185 |
| (0.045) | (0.050) | (0.052) | (0.013) | (0.013) | (0.015) | (0.035) | (0.039) | (0.205) | |
| group3 | 0.375 *** | 0.370 *** | 0.363 *** | 0.024 * | 0.035 *** | 0.032 ** | 0.359 *** | 0.379 *** | 0.429 ** |
| (0.044) | (0.049) | (0.053) | (0.013) | (0.013) | (0.015) | (0.036) | (0.038) | (0.205) | |
| group4 | 0.412 *** | 0.449 *** | 0.461 *** | 0.045 *** | 0.055 *** | 0.065 *** | 0.864 *** | ||
| (0.046) | (0.052) | (0.051) | (0.013) | (0.013) | (0.016) | (0.200) | |||
| Mean Age-to-Age DFs | |||||||||
| Period12 | 3.196 | 3.309 | 3.383 | 1.668 | 1.672 | 1.688 | 3.095 | 3.180 | 3.925 |
| Period18 | 1.420 | 1.449 | 1.476 | 1.061 | 1.059 | 1.061 | 1.464 | 1.507 | 1.212 |
| Period24 | 1.162 | 1.178 | 1.205 | 1.013 | 1.010 | 1.012 | 1.233 | 1.262 | 0.881 |
| Period30 | 1.085 | 1.097 | 1.115 | 1.000 | 0.996 | 0.997 | 1.154 | 1.178 | 0.778 |
| Period36 | 0.973 | 0.975 | 0.984 | 0.993 | 0.988 | 0.989 | 1.031 | 1.041 | 0.696 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, S.; Gan, C. Modeling Age-to-Age Development Factors in Auto Insurance Through Principal Component Analysis and Temporal Clustering. Risks 2025, 13, 100. https://doi.org/10.3390/risks13060100
Xie S, Gan C. Modeling Age-to-Age Development Factors in Auto Insurance Through Principal Component Analysis and Temporal Clustering. Risks. 2025; 13(6):100. https://doi.org/10.3390/risks13060100
Chicago/Turabian StyleXie, Shengkun, and Chong Gan. 2025. "Modeling Age-to-Age Development Factors in Auto Insurance Through Principal Component Analysis and Temporal Clustering" Risks 13, no. 6: 100. https://doi.org/10.3390/risks13060100
APA StyleXie, S., & Gan, C. (2025). Modeling Age-to-Age Development Factors in Auto Insurance Through Principal Component Analysis and Temporal Clustering. Risks, 13(6), 100. https://doi.org/10.3390/risks13060100







