Comparing the Effectiveness of Machine Learning and Deep Learning Models in Student Credit Scoring: A Case Study in Vietnam
Abstract
1. Introduction
2. Literature Review
2.1. Conceptual Framework of Credit Scoring and Student Loan Repayment
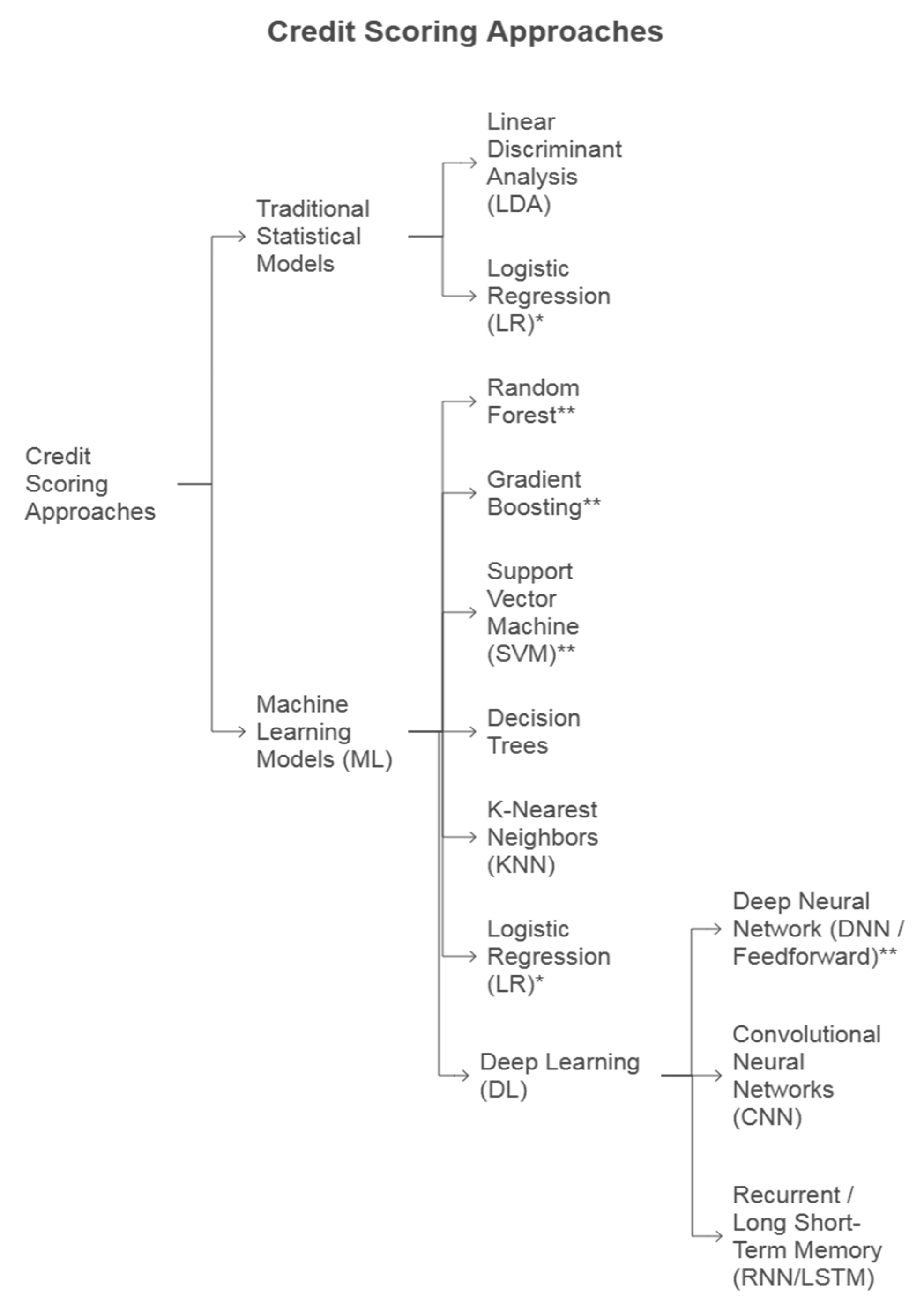
2.2. Traditional and Data-Driven Approaches in Credit Scoring
2.3. Criteria in Personal Credit Scoring
2.3.1. General Criteria in Personal Credit Scoring Models
2.3.2. Credit Scoring Criteria in the Vietnamese Context
2.3.3. Unique Considerations and Criteria for Student Credit Scoring
2.4. Machine Learning Models and Deep Learning Models in Credit Scoring
3. Model Evaluation
3.1. Evaluation Metrics
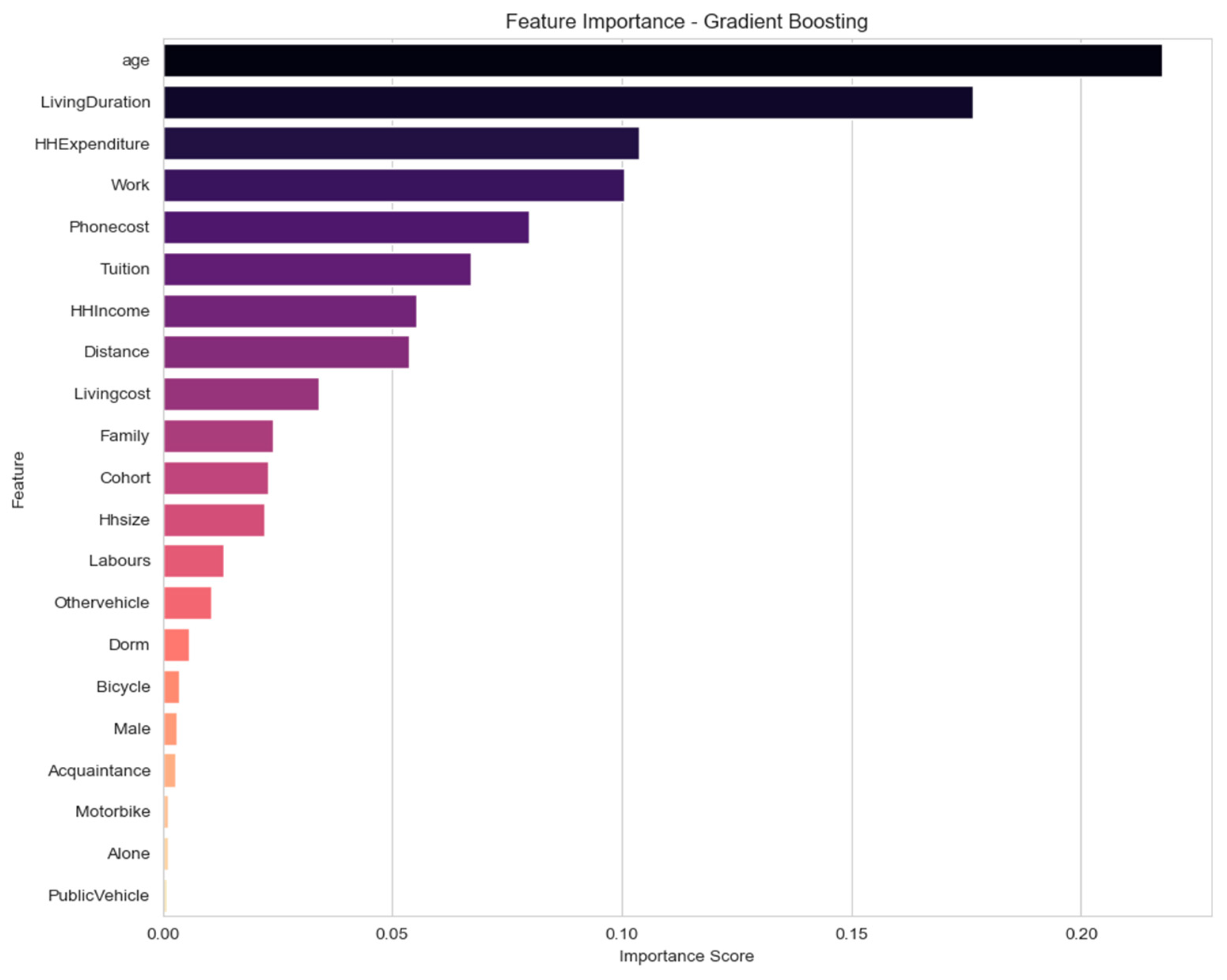
3.2. Results and Discussion
4. Methodology
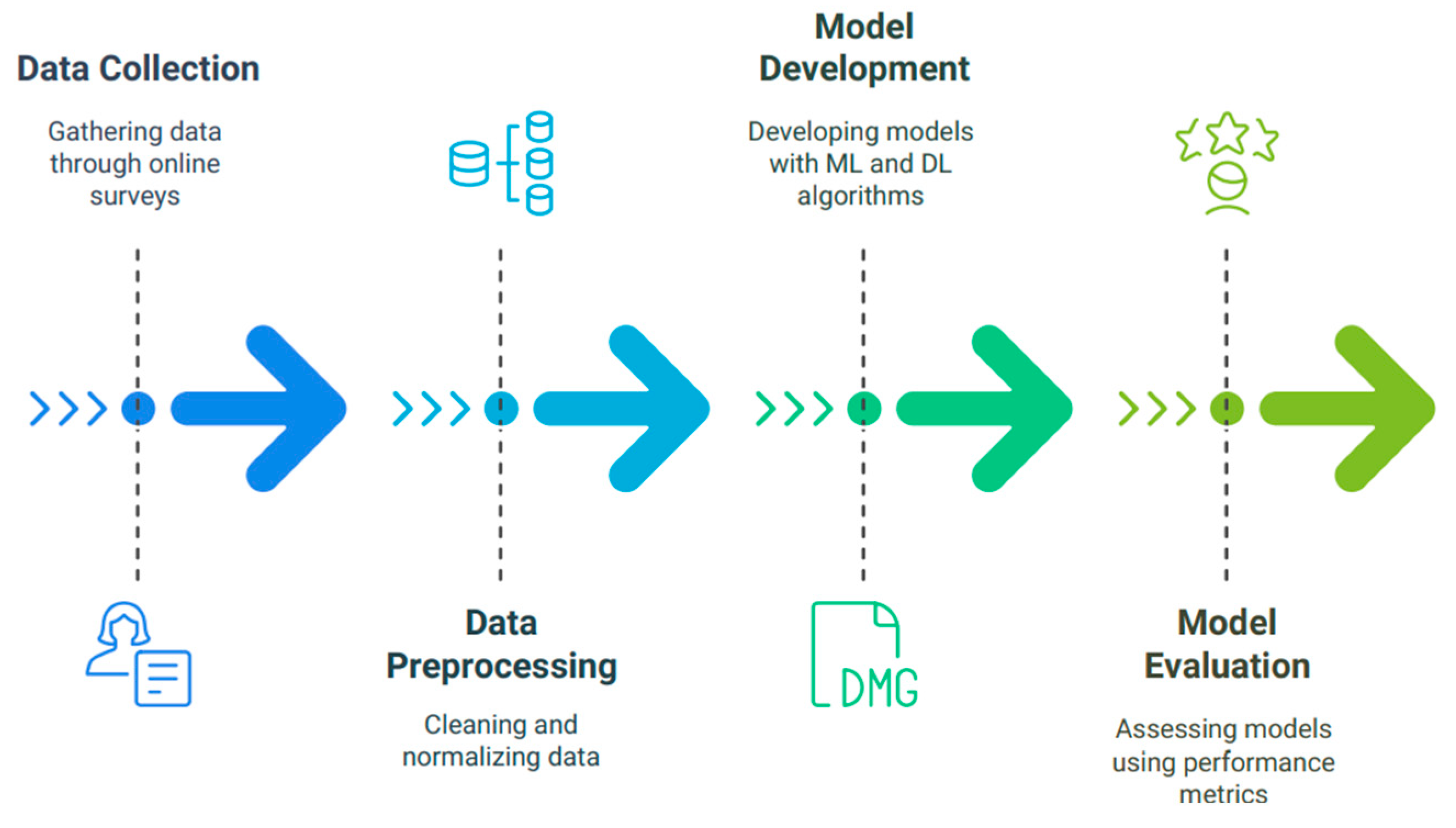
4.1. Research Design
4.2. Data Collection and Processing
4.2.1. Data Collection
4.2.2. Data Processing
4.2.3. Research Variables
4.3. Model Development and Training
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Exploratory Data Analysis (EDA)
Appendix A.1. Initial Data Overview
| # | Column | Non- | Null Count | Dtype |
|---|---|---|---|---|
| 0 | ID | 1024 | non-null | int64 |
| 1 | Loan | 1024 | non-null | int64 |
| 2 | age | 1024 | non-null | int64 |
| 3 | Male | 1024 | non-null | int64 |
| 4 | Cohort | 1024 | non-null | int64 |
| 5 | Tuition | 1024 | non-null | int64 |
| 6 | Hhsize | 1024 | non-null | int64 |
| 7 | Labours | 1024 | non-null | int64 |
| 8 | HHIncome | 1024 | non-null | int64 |
| 9 | HHExpenditure | 1024 | non-null | int64 |
| 10 | Work | 1024 | non-null | int64 |
| 11 | Dorm | 1024 | non-null | int64 |
| 12 | Family | 1024 | non-null | int64 |
| 13 | Acquaintance | 1024 | non-null | int64 |
| 14 | Alone | 1024 | non-null | int64 |
| 15 | LivingDuration | 1024 | non-null | int64 |
| 16 | Livingcost | 1024 | non-null | int64 |
| 17 | Phonecost | 1024 | non-null | int64 |
| 18 | Distance | 1024 | non-null | int64 |
| 19 | Bicycle | 1024 | non-null | int64 |
| 20 | Motorbike | 1024 | non-null | int64 |
| 21 | PublicVehicle | 1024 | non-null | int64 |
| 22 | Othervehicle | 1024 | non-null | int64 |
| Count | Mean | Std | Min | 25% | 50% | 75% | Max | |
|---|---|---|---|---|---|---|---|---|
| Age | 1024 | 19.81152 | 1.410276 | 18 | 19 | 20 | 20 | 40 |
| Hhsize | 1024 | 2.354492 | 0.63332 | 1 | 2 | 2 | 3 | 4 |
| Labours | 1024 | 1.888672 | 0.528104 | 1 | 2 | 2 | 2 | 4 |
| HHIncome | 1024 | 1.566406 | 0.850211 | 1 | 1 | 1 | 2 | 4 |
| HHExpenditure | 1024 | 2.831055 | 1.112346 | 1 | 2 | 3 | 3 | 5 |
| LivingDuration | 1024 | 2.967773 | 1.072146 | 1 | 2 | 3 | 4 | 4 |
| Livingcost | 1024 | 1.977539 | 0.816786 | 1 | 1 | 2 | 2 | 4 |
| Phonecost | 1024 | 2.147461 | 0.822897 | 1 | 2 | 2 | 3 | 4 |
| Distance | 1024 | 1.983398 | 1.03729 | 1 | 1 | 2 | 3 | 4 |
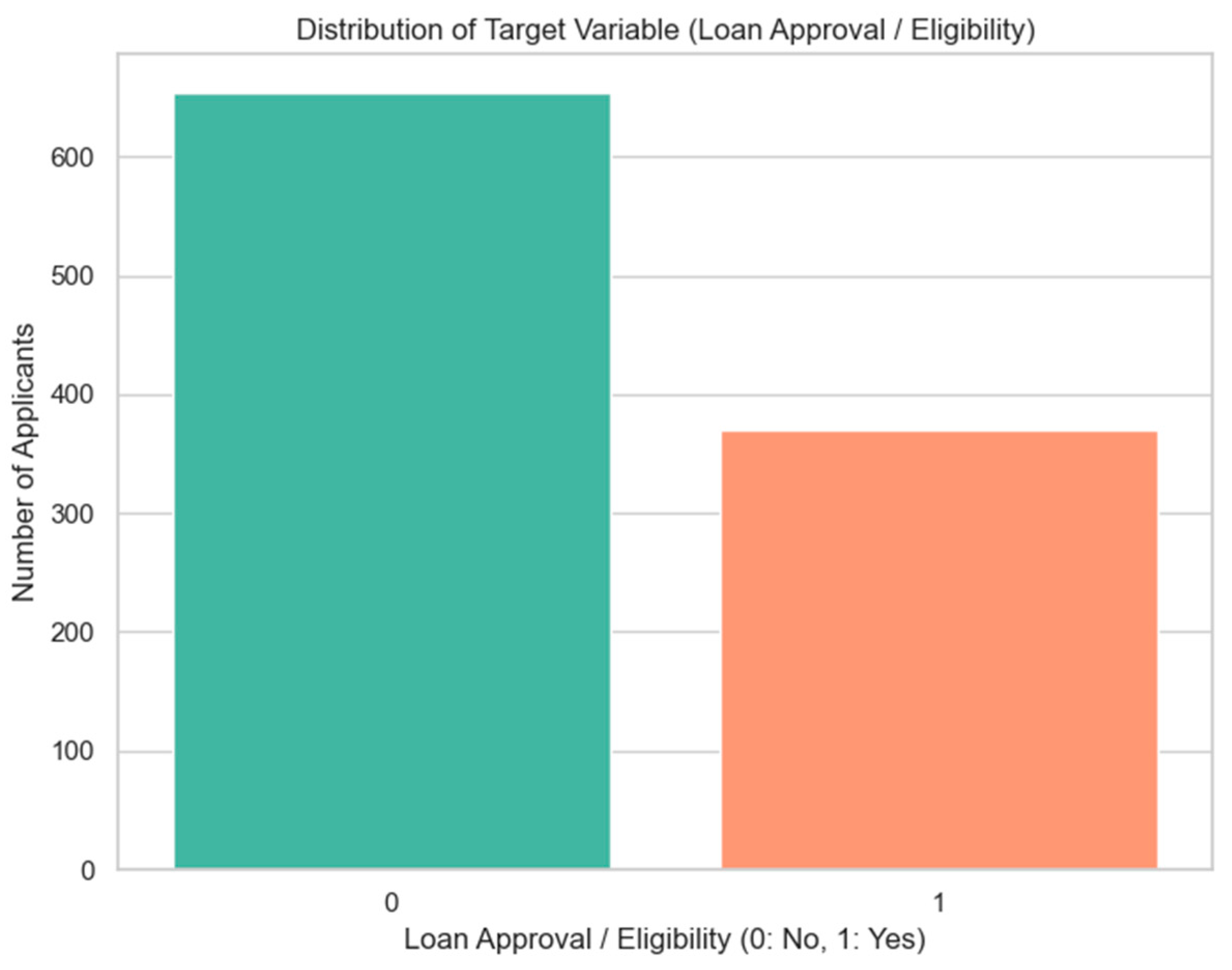
Appendix A.2. Target Variable Distribution
Appendix A.3. Univariate Analysis of Predictors
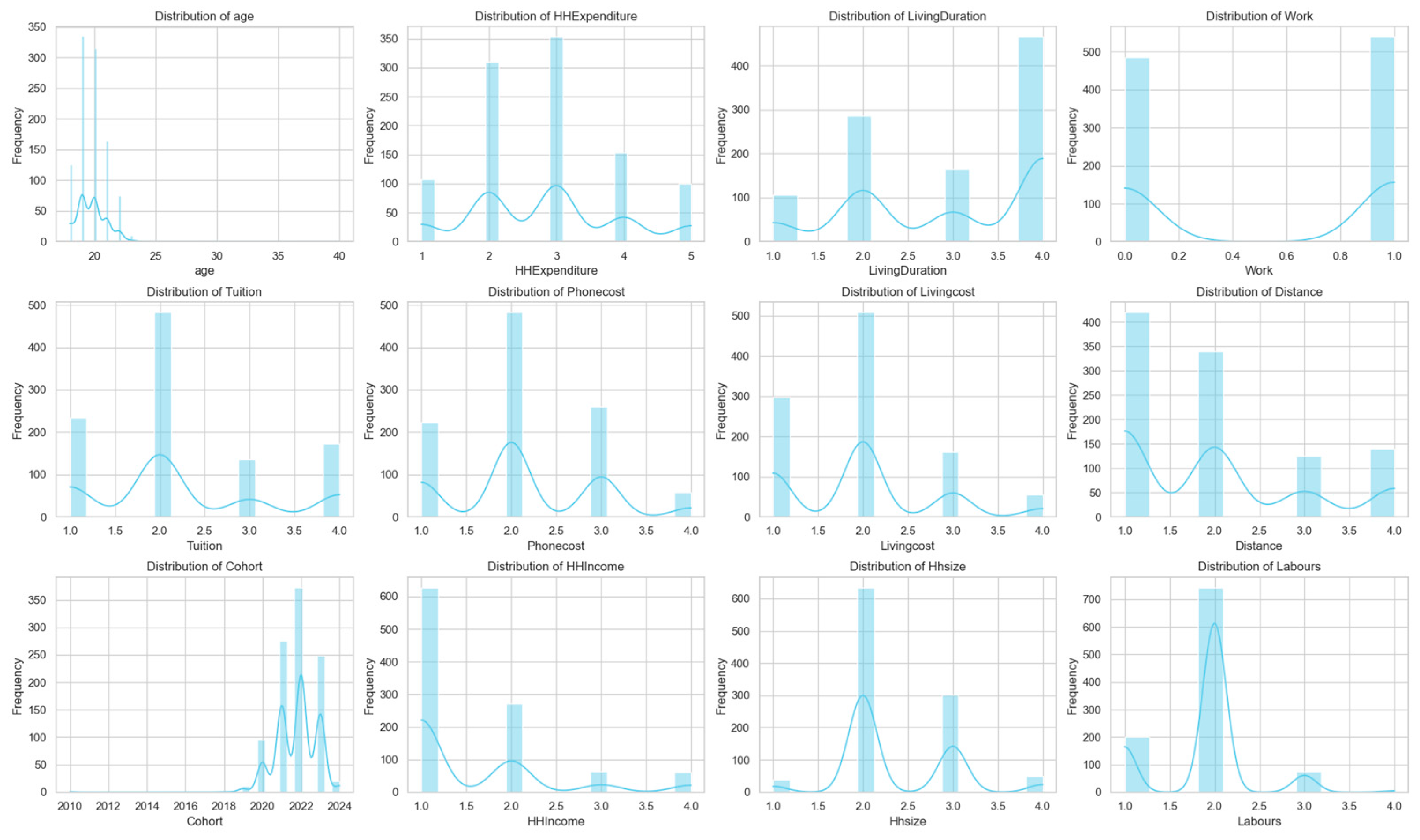
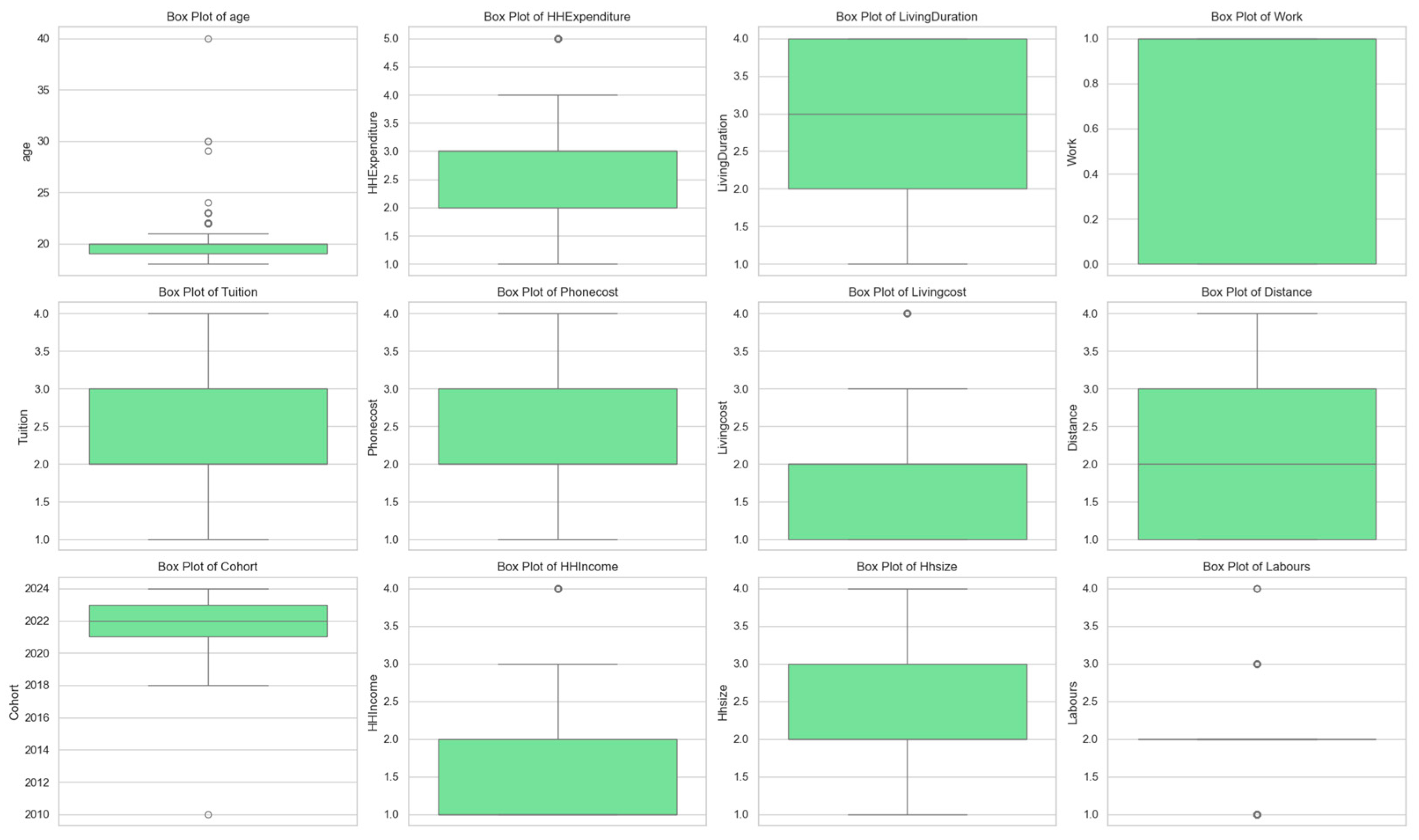
| Variable | Category (Code = 1) | Count (n = 1024) | Percentage |
|---|---|---|---|
| Male | Male | 355 | 0.347 |
| Work | Has Part-time Job | 501 | 0.489 |
| Dorm | Lives in Dorm | 64 | 0.062 |
| Family | Lives with Family | 464 | 0.453 |
| Acquaintance | Lives with Acquaintance | 346 | 0.338 |
| Alone | Lives Alone | 150 | 0.146 |
| Bicycle | Uses Bicycle | 28 | 0.027 |
| Motorbike | Uses Motorbike | 662 | 0.646 |
| PublicVehicle | Uses Public Transport | 148 | 0.145 |
| Othervehicle | Uses Other Transport | 186 | 0.182 |
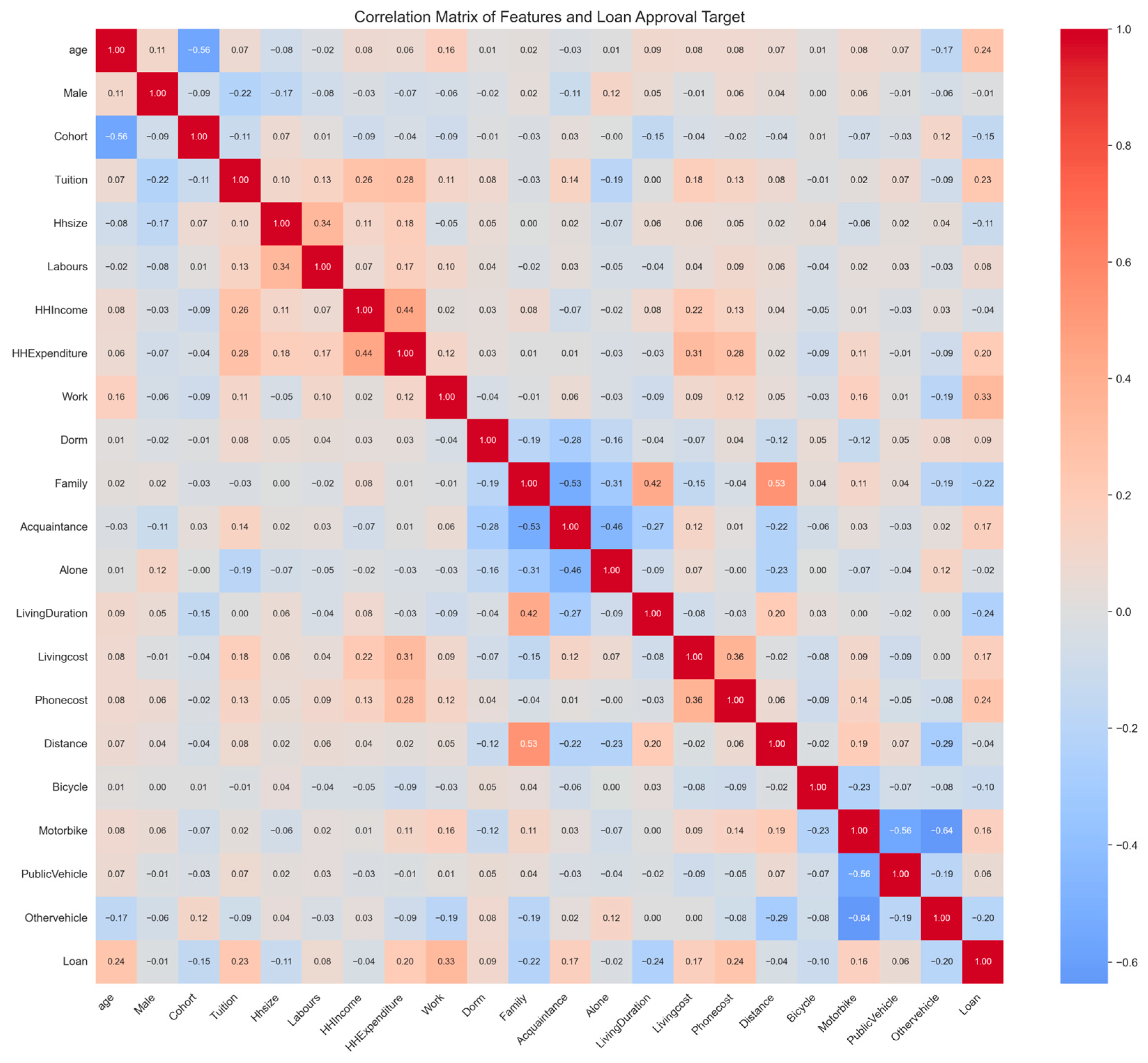
Appendix A.4. Bivariate Analysis
Appendix B. Model Specifications
| Model | Key Parameters and Settings |
|---|---|
| Random Forest (RF) | n_estimators: 100 trees Splitting Criterion: Gini Index max_depth parameter tuned via cross-validation |
| Gradient Boosting (GB) | n_estimators: 100 iterations learning_rate: 0.1 max_depth: 3 Strategy: Early stopping applied |
| Support Vector Machine (SVM) | Kernel: RBF (Radial Basis Function) Parameters C and gamma tuned via Grid Search Input Data: Scaled Probability obtained via Platt Scaling |
| Deep Neural Network (DNN) | Framework: PyTorch Architecture: Input → 2 Hidden Layers (64, 32 neurons, ReLU activation) Optimizer: Adam (Learning Rate = 0.001) Training: Max 100 Epochs with Early Stopping Input Data: Scaled |
References
- Abbas, Elaf Adel, and Nisreen Abbas Hussein. 2024. Algorithm comparison for data mining classification: Assessing bank customer credit scoring default risk. Jurnal Kejuruteraan 36: 1935–44. [Google Scholar] [CrossRef]
- Abdou, Hussein A., and John Pointon. 2011. Credit scoring, statistical techniques and evaluation criteria: A review of the literature. Intelligent Systems in Accounting, Finance and Management 18: 59–88. [Google Scholar] [CrossRef]
- Adams, Troy, and Monique Moore. 2007. High-Risk Health and Credit Behavior Among 18- to 25-Year-Old College Students. Journal of American College Health 56: 101–8. [Google Scholar] [CrossRef] [PubMed]
- Addo, Fenaba R., Jason N. Houle, and Daniel Simon. 2016. Young, black, and (still) in the red: Parental wealth, race, and student loan debt. Race and Social Problems 8: 64–76. [Google Scholar] [CrossRef]
- Adesanya, Mobolade E. 2024. Assessing credit risk through borrower analysis to minimize default risks in banking sectors effectively. International Journal of Research Publication and Reviews 5: 5479–93. [Google Scholar] [CrossRef]
- Andreeva, Ganila. 2006. European genetic scoring models using survival analysis. Journal of the Operational Research Society 57: 1180–87. [Google Scholar] [CrossRef]
- Babaei, Golnoosh, Paolo Giudici, and Emanuela Raffinetti. 2023. Explainable FinTech lending. Journal of Economics and Business 125–126: 106126. [Google Scholar] [CrossRef]
- Babaei, Golnoosh, Paolo Giudici, and Emanuela Raffinetti. 2025. A Rank Graduation Box for SAFE AI. Expert Systems With Applications 259: 125239. [Google Scholar] [CrossRef]
- Baker, Amanda R., and Catherine P. Montalto. 2019. Student loan debt and financial stress: Implications for academic performance. Journal of College Student Development 60: 115–20. [Google Scholar] [CrossRef]
- Banasik, John, and Johnathan Crook. 2007. Reject inference, augmentation, and sample selection. European Journal of Operational Research 183: 1582–94. [Google Scholar] [CrossRef]
- Banasik, John, Johnathan Crook, and L. Thomas. 2003. Sample selection bias in credit scoring models. Journal of the Operational Research Society 54: 822–32. [Google Scholar] [CrossRef]
- Bari, Hasanujamman, Shaharima Juthi, Asha Moni Mistry, and Md Kamrujjaman. 2024. A systematic literature review of predictive models and analytics in ai-driven credit scoring. Journal of Machine Learning, Data Engineering and Data Science 1: 1–18. [Google Scholar] [CrossRef]
- Baum, Sandy, and Patricia Steele. 2010. Who Borrows Most? Bachelor’s Degree Recipients with High Levels of Student Debt. The College Board Advocacy & Policy Center. Available online: https://trends.collegeboard.org/sites/default/files/trends-2010-who-borrows-most-brief.pdf (accessed on 28 March 2025).
- Bellotti, Tony, and Jonathan Crook. 2009. Support vector machines for credit scoring and discovery of significant features. Expert Systems with Applications 36: 3302–8. [Google Scholar] [CrossRef]
- Bengio, Yoshua, Aaron Courville, and Pascal Vincent. 2013. Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence 35: 1798–828. [Google Scholar] [CrossRef] [PubMed]
- Breiman, Leo. 2001. Random forests. Machine Learning 45: 5–32. [Google Scholar] [CrossRef]
- Chapman, Bruce, and Amy Y. C. Liu. 2013. Repayment Burdens of Student Loans for Vietnamese Higher Education, Crawford School Research Papers 1306, Crawford School of Public Policy, The Australian National University. Available online: https://ideas.repec.org/p/een/crwfrp/1306.html (accessed on 28 March 2025).
- Chen, Ziqeng. 2025. Machine learning in credit risk assessment: A comparative analysis of different models. Social Science Research Network. [Google Scholar] [CrossRef]
- Chen, Mu-chen, and Shih-Hsien Huang. 2003. Credit scoring and rejected instances reassigning through evolutionary computation techniques. Expert Systems with Applications 24: 433–41. [Google Scholar] [CrossRef]
- Fawcett, Tom. 2006. An introduction to ROC analysis. Pattern Recognition Letters 27: 861–74. [Google Scholar] [CrossRef]
- Fejza, Doris, Dritan Nace, and Orjada Kulla. 2022. The Credit Risk Problem—A Developing Country Case Study. Risks 10: 146. [Google Scholar] [CrossRef]
- Friedman, Jerome H. 2001. Greedy function approximation: A gradient boosting machine. The Annals of Statistics 29: 1189–232. [Google Scholar] [CrossRef]
- Géron, Aurélien. 2019. Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow: Concepts, tools, and techniques to build intelligent systems (2nd ed.). O’Reilly Media. Physical and Engineering Sciences in Medicine 43: 1135–36. [Google Scholar] [CrossRef]
- Giudici, Paolo. 2024. Safe machine learning. Statistics 58: 473–77. [Google Scholar] [CrossRef]
- Golbayani, Parisa, Ionut Florescu, and Rupak Chatterjee. 2020. A comparative study of forecasting corporate credit ratings using neural networks, support vector machines, and decision trees. The North American Journal of Economics and Finance 54: 101251. [Google Scholar] [CrossRef]
- Greene, William H. 1997. Econometric Analysis, 3rd ed. Hoboken: Prentice Hall. [Google Scholar]
- Han, Bowen. 2024. Evaluating Machine Learning Techniques for Credit Risk Management: An Algorithmic Comparison. Applied and Computational Engineering 112: 29–34. [Google Scholar] [CrossRef]
- Hand, David J., So-Young Sohn, and Yoonseong Kim. 2005. Optimal bipartite scorecards. Expert Systems with Applications 29: 684–90. [Google Scholar] [CrossRef]
- Ho, Tin Kam. 1995. Random decision forests. Paper presented at 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, August 14–16; pp. 278–82. [Google Scholar] [CrossRef]
- Houle, Jason N. 2014. Disparities in debt: Parents’ socioeconomic resources and young adult student loan debt. Sociology of Education 87: 53–69. [Google Scholar] [CrossRef]
- Hussain, Abrar, Muddasir Ahamed Khan.N, Ayub Ahamed K S, and Kousarziya. 2024. Enhancing Credit Scoring Models with Artificial Intelligence: A Comparative Study of Traditional Methods and AI-Powered Techniques. In QTanalytics Publication (Books). Delhi: QTanalytics Publication, pp. 99–107. [Google Scholar] [CrossRef]
- Huynh, Thi Tu Trinh. 2017. Improving the Business Personal Credit Scoring Model at Vietnam Bank for Agriculture and Rural Development—Hai Chau Branch, Da Nang City. Master’s thesis, Business Administration, Economics University—Da Nang University, Da Nang, Vietnam. [Google Scholar]
- Iwase, Maomi. 2011. Current Situation on Consumer Credit in Vietnam: Legal Framework for Formal Financial Sector. Japan Social Innovation 1: 40–45. [Google Scholar] [CrossRef]
- Jackson, Brandon A., and John R. Reynolds. 2013. The Price of Opportunity: Race, Student Loan Debt, and College Achievement. Sociological Inquiry 83: 335–68. [Google Scholar] [CrossRef]
- James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning. New York: Springer. [Google Scholar] [CrossRef]
- Kimani, Grace W., J.K Mwai, and E. Mwangi. 2024. A Deep Learning Based Hybrid Model Development for Enhanced Credit Score Prediction. International Journal of Research and Innovation in Applied Science IX: 250–62. [Google Scholar] [CrossRef]
- Kiviat, Barbara. 2019. The Moral Limits of Predictive Practices: The Case of Credit-Based Insurance Scores. American Sociological Review 84: 1134–58. [Google Scholar] [CrossRef]
- Knutson, Maelissa L. 2020. Credit Scoring Approaches Guidelines. World Bank Group. Available online: https://thedocs.worldbank.org/en/doc/935891585869698451-0130022020/CREDIT-SCORING-APPROACHES-GUIDELINES-FINALWEB (accessed on 28 March 2025).
- Kotb, Naira, and Chrstian R. Proaño. 2023. Capital-constrained loan creation, household stock market participation and monetary policy in a behavioural New Keynesian model. International Journal of Finance & Economics 28: 3789–807. [Google Scholar] [CrossRef]
- Kuhn, Max, and Kjell Johnson. 2018. Applied Predictive Modeling, 2nd ed. Berlin/Heidelberg: Springer. [Google Scholar]
- Lainez, Nicolas, and Jodi Gardner. 2023. Algorithmic Credit Scoring in Vietnam: A Legal Proposal for Maximizing Benefits and Minimizing Risks. Asian Journal of Law and Society 10: 401–32. [Google Scholar] [CrossRef]
- Le, Thi Thanh Tan, and Thi Viet Duc Dang. 2016. Personal customer credit rating at Vietnam National Credit Information Center. Journal of Finance 12: 42–46. [Google Scholar]
- Le, Thinh. 2017. An overview of credit report/credit score models and a proposal for vietnam. VNU Journal of Science: Policy and Management Studies 33: 36–45. [Google Scholar] [CrossRef]
- Le, Van Triet. 2010. Improving the Personal Credit Rating System of Asia Commercial Joint Stock Bank. Master’s thesis, University of Economics Ho Chi Minh City, Ho Chi Minh City, Vietnam. [Google Scholar]
- Lee, I-Fei Chen, Chih-Chou Chiu, Chi-Jie Lu, and I-Fei Chen. 2002. Credit scoring using the hybrid neural discriminant technique. Expert Systems with Applications 23: 245–54. [Google Scholar] [CrossRef]
- Lee, Tian-Shyug, and I-Fei Chen. 2005. A two-stage hybrid credit scoring model using artificial neural networks and multivariate adaptive regression splines. Expert Systems with Applications 28: 743–52. [Google Scholar] [CrossRef]
- Lessmann, Stefan, Bart Baesens, Hsin-Vonn Seow, and Lyn C. Thomas. 2015. Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. European Journal of Operational Research 247: 124–36. [Google Scholar] [CrossRef]
- Lochner, L., and A. Monge-Naranjo. 2016. Student loans and repayment. In Handbook of the Economics of Education. Edited by Eric Hanushek, Stephen Machin and Ludger Woessmann. Amsterdam: Elsevier, vol. 5, pp. 397–478. [Google Scholar] [CrossRef]
- Luo, Bin, Qi Zhang, and Somya D. Mohanty. 2018. Data-Driven Exploration of Factors Affecting Federal Student Loan Repayment. arXiv arXiv:1805.01586. [Google Scholar] [CrossRef]
- Mai, Nhat Chi. 2014. Building a Credit Rating Model for Individual Customers of DongA Commercial Joint Stock Bank. OSF Preprints, Center for Open Science. Available online: https://econpapers.repec.org/scripts/redir.pf?u=https%3A%2F%2Fosf.io%2Fdownload%2F622498921e399c02af600b78%2F;h=repec:osf:osfxxx:2z7uq (accessed on 28 March 2025).
- Malesky, Edmund J., and Markus Taussig. 2009. Where is credit due? Legal institutions, connections, and the efficiency of bank lending in Economics Vietnam. The Journal of Law, & Organization 25: 535–78. [Google Scholar] [CrossRef]
- Malik, Reza Firsandaya, and Hermawan. 2018. Credit Scoring Using CART Algorithm and Binary Particle Swarm Optimization. International Journal of Electrical and Computer Engineering (IJECE) 8: 5425. [Google Scholar] [CrossRef]
- Malohlava, Michal, and Arno Candel. 2020. Gradient Boosting Machine with H2O, 7th ed. H2O. ai. Available online: https://h2o-release.s3.amazonaws.com/h2o/rel-zahradnik/7/docs-website/h2o-docs/booklets/GBMBooklet.pdf (accessed on 28 March 2025).
- Mendes-Da-Silva, Wesley, Wilson Toshiro Nakamura, and Daniel Carrasqueira De Moraes. 2012. Credit card risk behavior on college campuses: Evidence from Brazil. BAR-Brazilian Administration Review 9: 351–73. [Google Scholar] [CrossRef]
- Meng, Xiaoqi, Lihan Jia, Shuo Chen, Yu Zhou, and Chang Liu. 2025. Comparative study of classical machine learning models in credit scoring. IET Conference Proceedings 2024: 220–26. [Google Scholar] [CrossRef]
- Mestiri, Samir. 2024. Credit scoring using machine learning and deep learning-based models. Data Science in Finance and Economics 4: 236–48. [Google Scholar] [CrossRef]
- Mienye, Ebikella, Nobert Jere, George Obaido, Ibomoiye Domor Mienye, and Kehinde Aruleba. 2024. Deep Learning in Finance: A Survey of Applications and Techniques. AI 5: 2066–91. [Google Scholar] [CrossRef]
- Mukhanova, Ayagoz, Madiyar Baitemirov, Azamat Amirov, Bolat Tassuov, Valentina Makhatova, Assemgul Kaipova, Ulzhan Makhazhanova, and Tleugaisha Ospanova. 2024. Forecasting creditworthiness in credit scoring using machine learning methods. International Journal of Power Electronics and Drive Systems 14: 5534–42. [Google Scholar] [CrossRef]
- Ong, Chorng-Shyong, Jih-Jeng Huang, and Gwo-Hshiung Tzeng. 2005. Building credit scoring models using genetic programming. Expert Systems with Applications 29: 41–47. [Google Scholar] [CrossRef]
- Organisation for Economic Co-Operation and Development. 2025. Recommendation of the Council on OECD Legal Instruments: Good Practices on Financial Education and Awareness Relating to Credit. Paris: OECD Publishing. Available online: https://legalinstruments.oecd.org/public/doc/78/78.en.pdf (accessed on 28 March 2025).
- Orgler, Yair E. 1971. Evaluation of bank consumer loans with credit scoring models. Journal of Bank Research 2: 31–37. [Google Scholar]
- Powers, David Martin Ward. 2011. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. Journal of Machine Learning Technologies 2: 37–63. [Google Scholar] [CrossRef]
- Robb, Cliff A., and Marry Beth Pinto. 2010. College students and credit card use: An analysis of financially at-risk students. College Student Journal 44: 823–35. [Google Scholar]
- Sarlija, Natasa, Mirta Benčić, and Zoran Bohacek. 2004. Multinomial model in consumer credit scoring. Paper presented at 10th International Conference on Operational Research (KOI 2004), Trogir, Croatia, September 22–24. [Google Scholar]
- Sayed, Eslam Husein, Amerah Alabrah, Kamel Hussein Rahouma, Muhammad Zohaib, and Rasha M. Badry. 2024. Machine learning and deep learning for loan prediction in banking: Exploring ensemble methods and data balancing. IEEE Access 12: 193997–4019. [Google Scholar] [CrossRef]
- Schmitt, Marc. 2022. Deep Learning vs. Gradient Boosting: Benchmarking state-of-the-art machine learning algorithms for credit scoring. arXiv arXiv:2205.10535. [Google Scholar] [CrossRef]
- Shukla, Deepak, and Sunil Gupta. 2024. A Survey of Machine Learning Algorithms in Credit Risk Assessment. Journal Electrical Systems 20: 6290–97. [Google Scholar] [CrossRef]
- Shukla, Rahul, Rupali Sawant, and Renuka Pawar. 2023. A Comparative Study of Deep Learning and Machine Learning Techniques in Credit Score Classification. International Journal of Innovative Research in Computer and Communication Engineering 11: 10004–10. [Google Scholar] [CrossRef]
- Sokolova, Marina, and Guy Lapalme. 2009. A systematic analysis of performance measures for classification tasks. Information Processing & Management 45: 427–37. [Google Scholar] [CrossRef]
- Steenackers, A., and M.J. Goovaerts. 1989. A credit scoring model for personal loans. Insurance: Mathematics and Economics 8: 31–34. [Google Scholar] [CrossRef]
- Šušteršič, Maja, Dusan Mramor, and Juze Zupan. 2009. Consumer credit scoring models with limited data. Expert Systems with Applications 36: 4736–44. [Google Scholar] [CrossRef]
- Tai, Le Quy, and Giang Thi Thu Huyen. 2019. Deep Learning Techniques for Credit Scoring. Journal of Economics, Business and Management 7: 93–96. [Google Scholar] [CrossRef]
- Teles, Germanno, Joel J. P. C. Rodrigues, Ricardo A. L. Rabêlo, and Sergei A. Kozlov. 2021. Comparative study of support vector machines and random forests machine learning algorithms on credit operation. Software: Practice and Experience 51: 2492–500. [Google Scholar] [CrossRef]
- Tran, Khanh Quoc, Binh Van Duong, Linh Quangc Tran, An Le-Hoai Tran, An Trong Nguyen, and Kiet Van Nguyen. 2021. Machine Learning-Based Empirical Investigation for Credit Scoring in Vietnam’s Banking. In Advances and Trends in Artificial Intelligence. From Theory to Practice. Cham: Springer, pp. 564–74. [Google Scholar] [CrossRef]
- Van Trung, Truong, and Ngoc Anh Nguyen Vuong. 2024. Development of a credit scoring model using machine learning for commercial banks in Vietnam. Advances and Applications in Statistics 92: 107–20. [Google Scholar] [CrossRef]
- Vapnik, Vladimir N. 1998. Statistical Learning Theory. New York: Wiley. [Google Scholar]
- Vu, Mai. 2024. Consumer credit in Vietnam from 2019 to 2023: Current situation and recommendations. Journal of Economics—Law and Banking 270. [Google Scholar] [CrossRef]
- Wang, Xiang, Min Xu, and Özgur Tolga Pusatli. 2015. A Survey of Applying Machine Learning Techniques for Credit Rating: Existing Models and Open Issues. In Neural Information Processing. ICONIP 2015. Lecture Notes in Computer Science. Edited by S. Arik, T. Huang, W. Lai and Q. Liu. Cham: Springer, vol. 9490. [Google Scholar] [CrossRef]
- Zhang, Haichao, Ruishuang Zeng, Linling Chen, and Shhangfeng Zhang. 2020. Research on personal credit scoring model based on multi-source data. Journal of Physics: Conference Series 1437: 012053. [Google Scholar] [CrossRef]

| Model | Train Accuracy | Test Accuracy | Confusion Matrix | Class 0 (Precision/Recall/F1) | Class 1 (Precision/Recall/F1) | Macro Avg F1 |
|---|---|---|---|---|---|---|
| Random Forest | 95.8% | 82% | [[121, 18], [19, 47]] | 86%/87%/0.87 | 72%/71%/0.72 | 0.79 |
| Gradient Boosting | 99.9% | 75% | [[107, 32], [20, 46]] | ~84%/~77%/0.80 | 59%/70%/0.64 | 0.72 |
| Support Vector Machine | 98.3% | 80% | [[125, 14], [25, 41]] | 83%/90%/0.87 | 75%/62%/0.68 | 0.77 |
| Pytorch DNN | 86.2% | 85.5% | [[125, 14], [20, 46]] | 86%/90%/0.88 | 77%/70%/0.73 | 0.81 |
| Model | Initial Loss | Final Loss | Number of Epochs |
|---|---|---|---|
| DL (PyTorch) | 0.5446 | 0.2256 | 20 |
| Category | Information Attributes | Relevant Literature |
|---|---|---|
| Personal Information | Age, gender, hometown, current residence, and duration of stay | Baker and Montalto (2019) |
| Academic Background | University, program, major, enrollment year (admission year), Grade Point Average, academic conduct scores, and Tuition | Jackson and Reynolds (2013); Adams and Moore (2007) |
| Family Financial Status | Household income, monthly expenses, number of dependents, and number of working-age family members | Addo et al. (2016); Houle (2014) |
| Part-time Employment | Job type, working hours, income, and job stability | Robb and Pinto (2010); Mendes-Da-Silva et al. (2012) |
| Credit and Loan History | Most recent loan, lending institution, loan amount, term, interest rate, and loan purpose | Baker and Montalto (2019); Baum and Steele (2010) |
| Living Conditions and Transportation | Housing type, living expenses, main means of transportation, and travel costs | Robb and Pinto (2010) |
| Category | Variables | Description |
|---|---|---|
| Personal Information | ID | Identifier |
| Age | Age | |
| Gender | Male, female | |
| Academic | Cohort | Cohort group (e.g., year of admission) |
| Tuition | Tuition fee | |
| Families Finance | Hhsize | Number of family members |
| Labours | Number of working members in the family | |
| HHIncome | Household income | |
| HHExpenditure | Household expenditure | |
| Employment and housing | Work | Having a part-time job or not |
| Dorm | Living in a dormitory | |
| Family | Living with family | |
| Acquaintance | Living with acquaintances | |
| Alone | Living alone | |
| LivingDuration | Duration of residence at current place | |
| Personal expenditure | Livingcost | Total living expenses |
| Phonecost | Mobile phone expenses | |
| Transportation | Distance | Distance from residence to school |
| Bicycle | Traveling by bicycle | |
| Motorbike | Traveling by motorbike | |
| PublicVehicle | Using public transportation | |
| Othervehicle | Other means of transportation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thuy, N.T.H.; Ha, N.T.V.; Trung, N.N.; Binh, V.T.T.; Hang, N.T.; Binh, V.T. Comparing the Effectiveness of Machine Learning and Deep Learning Models in Student Credit Scoring: A Case Study in Vietnam. Risks 2025, 13, 99. https://doi.org/10.3390/risks13050099
Thuy NTH, Ha NTV, Trung NN, Binh VTT, Hang NT, Binh VT. Comparing the Effectiveness of Machine Learning and Deep Learning Models in Student Credit Scoring: A Case Study in Vietnam. Risks. 2025; 13(5):99. https://doi.org/10.3390/risks13050099
Chicago/Turabian StyleThuy, Nguyen Thi Hong, Nguyen Thi Vinh Ha, Nguyen Nam Trung, Vu Thi Thanh Binh, Nguyen Thu Hang, and Vu The Binh. 2025. "Comparing the Effectiveness of Machine Learning and Deep Learning Models in Student Credit Scoring: A Case Study in Vietnam" Risks 13, no. 5: 99. https://doi.org/10.3390/risks13050099
APA StyleThuy, N. T. H., Ha, N. T. V., Trung, N. N., Binh, V. T. T., Hang, N. T., & Binh, V. T. (2025). Comparing the Effectiveness of Machine Learning and Deep Learning Models in Student Credit Scoring: A Case Study in Vietnam. Risks, 13(5), 99. https://doi.org/10.3390/risks13050099







