Abstract
The primary objective of this empirical study is to investigate the Indian equity market network by analyzing its topological properties using the disparity filtering technique, and a minimum spanning tree. It investigates the backbone structure of the reduced weighted equity network and highlights the sector-based cluster formation. This study also examines the relative importance of each sector by utilizing different key network metrics, with comparative analysis against other emerging markets. It observes a high sector-specific dominance, power imbalance, disparity, and risk concentration in the healthcare and technology sectors. It also finds that fast-moving consumer goods and the healthcare sector can play important roles in maintaining economic stability, public health, and social wellbeing. The findings of this study are highly useful in understanding the market structure, risk management, and investment decisions in the emerging market context of India.
1. Introduction
In recent years, the Indian equity market has become more volatile, which emphasizes the need for more sophisticated analytical techniques. Due to global uncertainty, a lack of liquidity, and widespread investor panic, the 2020 COVID-19 crisis caused the BSE Sensex and NSE Nifty 50 to experience historically heavy drops (Varma et al. 2021; Sreenu and Pradhan 2023). The inability of conventional risk models to adequately represent the intricate relationships between stocks during times of crisis was made evident by this era of severe volatility (Varma et al. 2021). In the aftermath, the Reserve Bank of India’s (RBI) monetary policy actions, ranging from inflation targeting and liquidity support to interest rate adjustments, have continued to shape market dynamics (Priya and Sharma 2023; Sreenu and Pradhan 2023). These events emphasize the critical need to understand systemic linkages among financial assets to allow for improved risk assessment and market stability.
The introduction of network theory to financial modelling and analysis makes it simple to understand the complex relationships that are inherent in financial markets (Bonanno et al. 2003; Jung et al. 2006; Jung et al. 2008; Mantegna 1999; Meng and Chen 2023; Onnela et al. 2003a, 2003b, 2003c; Samitas et al. 2022). However, most studies focus on western stock markets. This study extends this type of analysis to the Indian equity market, which is one of the fastest-growing economies among the BRICS nations, necessitating a more in-depth examination of its capital market (Maiti et al. 2022). The Bombay Stock Exchange is one of the oldest and is ranked among the top ten stock exchanges globally in terms of market capitalization. In terms of statistics, over five thousand four hundred companies are listed on it, with a total market capitalization of INR 42,362,278.53 crores in the beginning of June 2024 (Times Now News 2024). Plenty of regulatory measures are taken by the Security Exchange Board of India to maintain the financial stability of the Indian capital markets and retain confidence among investors. All such activities make the Indian capital market an ideal subject for a complex network study.
Given the Indian equity market’s high volatility (Kumari and Mahakud 2015), structural inefficiencies (Belhoula et al. 2024), and changeable regulatory framework, network theory is especially applicable to it. In contrast to developed markets, India’s financial ecosystem is characterized by significant cross-asset interdependencies, frequent regulatory interventions, and volatility in its liquidity (Kumari and Mahakud 2015). Investor emotions (Agarwal et al. 2025), macroeconomic developments, and regulatory changes all have an impact on the volatility of the Indian equity market (Dhingra et al. 2024), which continues to be a persistent problem. Particularly in times of financial instability, traditional risk models frequently fail to capture the complex network of stock relationships. Network-based approaches, on the other hand, provide a thorough, data-driven strategy to find hidden connections, giving greater insights into contagion routes and systemic risk (Clemente et al. 2021; 2022). Stock price dynamics are made more difficult to interpret by market inefficiencies such as inconsistent institutional participation, information asymmetry, and the dominance of major players in particular industries. By mapping these relationships, network analysis makes it possible to differentiate between equities that are essential to market stability and those that are more susceptible to speculative activity. The market’s behavior has been profoundly altered by ongoing regulatory developments, such as the Goods and Services Tax (GST) (Karmuhil and Murugesan 2024), financial market liberalization, and SEBI reforms (Kaur 2024). These changes frequently call into question the assumptions of traditional econometric models, emphasizing the necessity of adaptable, network-driven methodologies to comprehend the dynamic character of stock interrelationships. Using network analysis insights, risk managers, investors, and policymakers can better assess systemic risks, diversify their portfolios, and spot sectoral relationships that traditional models can miss (Bhattacharjee et al. 2019).
Despite the widespread use of network analysis in extant financial equity market studies in multiple geographies, most of the extant studies only employ one technique, which restricts their structural insights. Rarely used in the Indian equity market, this study employs a dual technique that combines disparity filtering (Yassin et al. 2025) and MST analysis (Barbi and Prataviera 2019), which provides a more thorough perspective by catching both important connections and subtle link heterogeneity. Prior research on the network analysis of Indian equity markets has largely focused on early-stage interconnectedness using pre-2016 data (Matia et al. 2004; Pan and Sinha 2007; Pan and Sinha 2008; Sinha and Pan 2007), limited stock samples (Kulkarni et al. 2024), or corporate interlocks (Sankar et al. 2015). In contrast, the present study offers a comprehensive examination of sectoral interconnectedness within the Indian equity market. To fill this gap in the literature and improve the comparative insights regarding other emerging economies, the current study uses an integrated technique to reveal the intricate structure of the Indian equity market. This study uses two techniques, namely, the disparity filtering technique for weighted networks (Serrano et al. 2009), and minimal spanning tree technique (Mantegna 1999). A rich dataset comprising data from over 10 years (from 1st December 2013 to 30th June 2024) is used to explore the network topology of different industrial sectors in the Indian context. This study aims to answer the following research questions:
- RQ1:
- What are the topological properties of the Indian equity market network, and how do they compare with those of other emerging markets?
- RQ2:
- How do different industrial sectors contribute to the structure and dynamics of the Indian equity market?
- RQ3:
- How does network visualization and reduction (using MST analysis and disparity filtering) improve our understanding of market dynamics?
To gain rich insights, this study estimates different sector-wise average network metrics, namely the dominance, weighted clustering coefficient, closeness centrality, influence strength, disparity, and eigenvector centrality. This study finds a strong power imbalance, disparity, and risk concentration in the Indian financial sector. Further, the fast-moving consumer goods (FMCGs) and healthcare sectors are vital in achieving financial stability and economic growth. These findings are extremely useful in understanding the overall Indian market structure. The current study offers several key contributions to the existing literature and has significant practical implications. First, it decodes the level of interconnectedness of different sectors within the Indian equity market network. Second, it provides useful insights on the topological aspects of the Indian equity market network by estimating different network metrics. Third, these estimates are then used for a comparative analysis with other emerging markets, namely, Brazil and South Africa. Lastly, this study further deploys reduced network visualization to obtain useful insights at the micro level (stock). Thus, the addition of value of the present study to the existing literature is as follows:
- Previous studies done on the network analysis of Indian equity markets are mostly focused on the study of interconnectedness at the initial level, using old study samples from before 2016 (Bhattacharjee et al. 2016), considering a smaller number of stocks for analysis (Kulkarni et al. 2024), or incorporating corporate interlock (Sankar et al. 2015). Keeping these in mind, the present study comprehensively decodes the level of interconnectedness of different sectors within the Indian equity market network;
- Thereafter, it provides useful insights into the topological aspects of the Indian equity market network by estimating six different network metrics, namely the disparity, closeness centrality, eigenvector centrality, influence strength, weighted clustering coefficient, and domination power;
- Then, this study’s estimates are used for a comparative analysis with other emerging markets, namely Brazil and South Africa;
- Lastly, this study further deploys reduced network visualization to obtain useful insights at the micro level (stock).
The remaining study is structured as follows. Section 2 reviews the literature, highlighting the need to investigate equity markets in emerging economies using network models, with a focus on emerging economies, especially the Indian equity market. Section 3 discusses the data and methodology adopted for this study. The results and discussions are presented in Section 4, followed by the managerial implications (Section 5). It concludes with a discussion of key policy implications and directives for future studies.
2. Literature Review
2.1. Network Finance Literature
In the network finance and network economics literature, scaling (Mantegna and Stanley 1995), the fractal dimension (Mandelbrot 1965), power law connection, complex network analysis (Schinckus and Jovanovic 2013), and volatility proxy identification (Ghosh and Kozarević 2019) have emerged eventually over the last century. The discipline of financial economics realizes that the traditional method of analysis has become insignificant due to the irrational and complex behavior exhibited by financial markets over time. Since Mantegna’s initial work on stock correlation networks (Mantegna 1999), numerous studies have explored the use of financial network analysis across various dimensions (Bonanno et al. 2003; Brida and Risso 2008; Gilmore et al. 2008; Jung et al. 2006; Jung et al. 2008; Meng and Chen 2023; Onnela et al. 2003a, 2003b, 2003c; Tumminello et al. 2007, 2010; Samitas et al. 2022).
According to existing studies, network models are useful for comprehending the structures of markets (Silva et al. 2016). The studies conducted by Clemente et al. (2021) and Clemente et al. (2022) highlighted the advantages of using network techniques in portfolio selection and allocation. In addition, different network centrality metrics are useful for choosing assets in times of global financial crisis (Wang et al. 2024).
2.2. Network Analysis Methods in the Extant Literature
In response to the 2008 global financial crisis, there was a growing recognition of the inadequacies of traditional approaches, prompting the adoption of advanced network analysis techniques to assess systemic risk (Zaheer et al. 2023). Extant network-based studies have highlighted significant shifts in stock market co-movements during the pandemic, revealing the profound impact of global health events on market dynamics (Zaheer et al. 2023). Table 1 provides a list of studies which introduced several network-based methods to the extant financial network analysis literature.

Table 1.
Studies introducing complex equity network filtering methodologies.
All these methods (mentioned in Table 1) have been extensively adopted over the past several years in different equity market contexts and time periods. Apart from these methods, many other nonlinear methods have been brought up in the literature on financial network analysis, such as the mutual information method (Baitinger and Papenbrock 2017), the Brownian distance method (Zhang et al. 2014), copula-based metrics (Brechmann 2013), Laplacian energy measures (Huang et al. 2023), the moving-window Bayesian network model (Chan et al. 2023), and several others. Extended methods have also been brought in for MST analysis, such as the directed bubble hierarchical tree (DBHT) (Musmeci et al. 2015; D.-M. Song et al. 2011; W.-M. Song 2011; Song et al. 2012) and triangulated maximally filtered graph (TMFG) (Barfuss et al. 2016; Massara et al. 2016; Musmeci et al. 2015) methods. Additionally, the real-time monitoring and modelling of financial market behaviours has been made possible by the integration of AI and machine learning approaches, such as dynamic correlation analysis and the use of graph neural networks (Hou and Pan 2022; Gu and Yao 2022). The significance of keeping an eye on network connectivity to evaluate systemic hazards has been shown by methods such as the use of moving-window Bayesian network models (Chan et al. 2023).
The last few years have seen a growing number of research studies that use network-based methodologies to examine the time-varying dynamics of financial markets. Chakrabarti et al. (2021) used dynamic network analysis to uncover significant shifts in global stock market co-movements during the COVID-19 pandemic, and Hatami et al. (2022) used population analysis and correlation networks to uncover underlying market structures. Nie (2020) improved our knowledge of market anomalies and their causes by creating a network-based technique to identify crucial correlation alterations.
Researchers have also ventured into distances at which it is possible to capture nonlinear relationships, entailing the use of information-theoretic measures like the mutual information (MI) method (Barbi and Prataviera 2019; Fiedor 2014; Goh et al. 2018; Guo et al. 2018), the Brownian distance (Zhang et al. 2014), Copula-based metrics (Brechmann 2013; Durante and Pappada 2015; Marti et al. 2016), and tail dependence distances (Durante et al. 2015). Nonlinear dependencies can be misleading, as evidenced by distortions in stock return series characterizations (Hartman and Hlinka 2018).
2.3. Network Based Studies on Indian Equity Market
A limited number of studies have also been performed on cross-security dependencies in the Indian capital market. The study by Matia et al. (2004) analyzed the 49 largest stocks listed on the National Stock Exchange (NSE) for the period of November 1994–June 2002. It was observed that stocks price fluctuations decay in an exponential fashion, rather than by following power law distribution. Power law distribution has normally been observable in the price fluctuations of securities in the capital markets of developed countries. A study by Pan and Sinha (2007) analyzed the high-frequency tick-by-tick data of 489 stocks belonging to the companies that constitute the S&P BSE 500 index of the Indian capital market for the period from November 1994 to May 2006. The study demonstrates that, for security price fluctuations, the inverse cubic law still holds well, even in the case of emerging markets like India. The same authors conducted another study (Pan and Sinha 2008) where they analyzed the market indices data of the BSE and NSE. They demonstrated that the price fluctuations in market indices in the Indian capital market follow inverse-cubic law distribution. Their findings point to the fact that, even though diversity exists in markets (diversity in terms of the market’s components, its interactive nature, and its predisposition to external news), there might be mechanisms of a universal nature that generate market fluctuations, as reflected by observation of the invariant properties of markets. The study by Sinha and Pan (2007) investigated the evolutionary trend of the stock price correlation structures of networks in Indian equity markets. This study presented evidence that there is a greater likelihood of cluster formation by different business sectors in cases of markets that move towards a stage of maturity; such clusters can be visualized as tightly coupled sub-graphs (Sinha and Pan 2007). Recent financial network studies on the Indian equity market have adopted various measures other than MST analysis and centrality measures, such as geometry-inspired network measures (Kulkarni et al. 2024), and random matrix theory (Pawanesh et al. 2025), to name a few.
Although network analysis has been used in many studies to investigate the dynamics of financial markets, the majority only use one methodological technique, which may restrict the breadth and depth of their structural findings. A dual strategy that combines minimum spanning tree (MST) analysis and disparity filtering—two complementary techniques that capture both the backbone structure and finer network nuances of the market—has rarely been used to analyze the Indian equity market. While disparity filtering preserves statistically significant edges and the heterogeneity of link strengths (Yassin et al. 2025), MST analysis efficiently draws attention to the most important connections in a condensed tree structure (Barbi and Prataviera 2019). A more thorough and accurate depiction of the market’s underlying structure can be obtained by combining these techniques. Furthermore, there are not many comparative studies that compare the network centrality of the Indian equity market to that of other emerging markets, which limits our comprehension of how the systemic importance and market interconnection differ depending on the setting. Our study fills these gaps by using a dual-method network approach and performing cross-market centrality comparisons. This helps to improve the existing methodological toolset for financial network analysis and provides a more comprehensive understanding of emerging market dynamics. Thus, given the importance of financial networks in understanding the complexities inherent in financial markets, this study characterizes the topology of the Indian equity market networks using the disparity filtering technique and minimal spanning tree (MST) analysis.
3. Data and Methodology
3.1. Data
This study chose the S&P BSE 500 Index to represent the Indian stock market, as it represents all major twenty industrial segments. The dataset spans from 1st December 2013 to 30th June 2024. The study period (2013–2024) was chosen to reflect significant SEBI regulatory reforms, advancements in trading infrastructure post-2013, and enhanced market stability. SEBI’s corporate governance initiatives that were instituted from 2003 to 2013, such as mandatory quarterly disclosures and the inclusion of independent directors, strengthened transparency and investor protection. The selected period also captures a notable rise in IPO activity, with 298 companies raising $16.6 billion in 2024 alone (ANI 2024). Aligning with similar research in emerging markets, this timeframe ensures methodological consistency and relevance. The period between 2013 and 2024 is very important with respect to the Indian stock market due to several reasons. Before 2013, the economic growth was slower, marked by high inflation, policy paralysis, corruption, and scandals. However, thereafter, several reforms were seen in the form of political and economic reforms (GST implementation (2017) (Deshmukh et al. 2022), corporate tax cuts (PTI 2019), and “Make in India” initiatives (Press Information Bureau 2017)); an increase in FPI inflows; digitalization drives (UPI, demonetization); structural shifts in the capital markets; the effects of COVID-19 (sectors like IT, pharma, and EVs booming); an increase in financial literacy programs (participation of more retail investors in stock markets).
Due to the lack of continuous historical time-series data for the entire 10-year and six-month study period, stocks with IPOs after 1 December 2013 were excluded. Consequently, the final dataset included 335 stocks. This study employs the S&P BSE 500 Index, which spans 500 companies across 20 sectors. In contrast to indices like the NIFTY 50 or Sensex that emphasize large-cap stocks, the BSE 500 encompasses large-, mid-, and small-cap firms, providing a holistic view of the systemic risk and market dynamics. To maintain data consistency, post-2013 IPOs were excluded, ensuring that all selected stocks have a continuous trading history and minimizing bias from newly listed companies. The daily closing prices were obtained from BSE historical reports, Yahoo Finance, and the CMIE Prowess Database. Adjusted closing prices are considered in this study. In cases where, for specific days, closing prices were found to be missing, the stock price values of the previous day’s closing prices were used as a substitute. This form of substitution is generally considered better than substitution with the average value of the closing price for surrounding previous days because of several reasons. First, stock prices often follow a continuous path, and the price on any given day is heavily influenced by the previous day’s price. Second, using the previous day’s closing price maintains this continuity, reflecting the typical day-to-day movements in the market. Lastly, stock markets often exhibit momentum, where the direction of price movement tends to continue for some time.
Using the previous day’s closing price preserves this momentum, which is crucial for accurately modeling and forecasting the future price behavior of a stock. Replacing a missing value with the average of surrounding days can distort the true price movement of the stock. If the stock is trending up or down, an average can misrepresent its price level, leading to inaccuracies in analysis and modeling. The volatility and daily price variations of stocks are essential characteristics of stock data. Using the previous day’s price retains the natural volatility patterns of the market, whereas averaging can smooth out these variations, leading to an underestimation of the market’s volatility. Several extant studies on financial networks have used the same methodology as an approach to handling missing closing price data (Bhattacharjee et al. 2019, 2022). Based on all of the above-mentioned data-handling procedures, a data series reflecting 10 years and six months’ worth of closing price data was obtained, which comprised the final study dataset.
3.2. Weighted Network Construction Workflow
The methodological steps for building the weighted equity network model used in this study are outlined below. The initial step entails computing the weights assigned to the edges of the equity network. Log returns are calculated for 2622 trading days, generating a dataset of 2621 log returns that represent a duration of 10 years and six months. Log returns are more commonly used than raw prices as they ensure time-additivity and stabilize variance, making log return financial time series ideal for statistical modeling
3.2.1. Rolling Window Methodology
This study examines temporal network dynamics, employing the rolling window approach to explore temporal variations in the topological metrics of the weighted equity networks. This technique was applied to a matrix comprising 2621 data points for 335 stocks. The continuous data were segmented into time-frames of 500 data points each (representing trading days), with each observation separated from the next by a 20-data-point increment. This procedure generated 106 temporally synchronized observations spanning a duration of 10 years and six months (from 1 December 2013 to 30 June 2024). Weighted networks were subsequently constructed for each time-window frame. The 500-trading-day window was chosen due to several reasons. First, it captures a long period of data that makes the analysis more reliable (Fama 1970). Second, longer periods reduce the overall market noise as compared to shorter periods, and they also account for business cycles (Shiller 2005). Lastly, longer period data may experience a minimum impact of outliers as compared to shorter periods, and are useful in capturing the long-term risk and market behavior of markets (Malkiel 2003).
3.2.2. Calculation of Edge Weights in the Network
The construction of the weighted network followed the methodology proposed by Kim et al. (2002a, 2002b). Two quantitative measures were utilized in creating the weighted network model: (i) the residual log return, denoted by Gi(t); (ii) the weighted cross-correlation coefficient, denoted by wi,j. The first measure allows capturing the inherent characteristics of stock price changes and is calculated by subtracting the mean value for a time N from each log return value Si. The computation of this measure is outlined as follows:
In the current study, the symbol Si(t) represents the log returns of stocks. The value of Si(t) is computed using Equation (1). Here, the value of N refers to 500 days. The weighted cross-correlation coefficient is computed as follows (See Equation (2)):
In this study, Pearson correlation coefficients have been used to construct the weighted network, because this metric measures the linear relationship between stock log returns and has been widely adopted in financial network analysis in the extant literature (Bhattacharjee et al. 2022; Wang et al. 2018; Marti et al. 2021). This coefficient is computationally efficient and provides an intuitive interpretation of stock dependencies, allowing for the construction of minimum spanning trees (MSTs) and other network models that identify sectoral clustering and market structures (Marti et al. 2021). Furthermore, it has been observed in several studies that financial markets often exhibit short-term linear dependencies, particularly during phases of market stability, making this coefficient a reasonable choice for detecting sectoral co-movement. Also, one can find extensive usage of this coefficient in the portfolio optimization, risk management, and systemic risk assessment literature (Laloux et al. 1999; Plerou et al. 1999; Mantegna 1999; Mantegna and Stanley 2000). Thus, its usage ensures consistency with established methodologies.
Using these weighted correlation coefficient matrices, undirected weighted stock networks were constructed, forming a graph with 335 edges representing stocks belonging to different industry sectors (Figure A1). This is a type of dense graph, and possesses 55,945 edges, wherein all vertices have N − 1 edge connections. The resultant weighted equity network can be described as follows: The vertices of the network represent the time series of the stocks’ log returns, and there is a weight wi,j associated with the edges between each pair (i,j) of nodes. Each of the 335 vertices of the weighted equity network model represents a time series of the log returns of the individual scripts of the selected 335 stocks. The weighted equity network construction is adopted from Kim (2002b). The complete weighted equity network, as shown in Figure A1, provides a holistic view of the interdependencies within the Indian market. It is very useful in understanding the overall market structure and in studying the correlations and portfolio constructions of the market. A highly connected network may represent potential channels of systemic risk flow. Identifying such potential nodes could be highly useful in dealing with the market’s stability and systemic risk. The next section covers the different network metric computations that were conducted to understand the overall market structure.
3.3. Network Metric Computation
Six network measures were calculated to characterize the topological properties of the weighted equity network. These metrics were computed for each of the 106 weighted equity networks, representing 106 temporally synchronized observations that were generated using a rolling window approach.
3.3.1. Disparity
This network metric measures the heterogeneity of the edge weights in the network (Barthélemy et al. 2005). In a vertex Vi that has a connectivity ki and possesses an influence strength si, all the weights of the edges wij will be of similar order when the value of si equals ki. Conversely, if the weight of one or a few vertices predominates over others in the network, it indicates heterogeneity. The disparity of a vertex i can be calculated using Equation (3):
where v(i) refers to the set of neighbors of i.
3.3.2. Closeness Centrality
The subsequent metric examined in the context of the weighted equity network is the “closeness centrality” (Sabidussi 1966). This metric provides an indication of how closely connected vertex i is to the other vertices within the weighted network. A higher value of closeness centrality signifies that the vertex is closer to other vertices in the network. For a vertex k within a weighted graph G, the closeness centrality can be defined as follows:
Here, the term dG(k,h) denotes the shortest distance between two vertices k and h (see Equation (4)).
3.3.3. Eigenvector Centrality
The next metric for the weighted equity network model is the eigenvector centrality, an extension of the degree of centrality. Newman (2008) introduced the equation for the eigenvector centrality of a weighted network, which forms the basis for the PageRank algorithm employed by the Google search engine (Brin and Page 1998). The basic concept behind the eigenvector centrality measure is that the significance of an edge is solely dependent on the quality of its connections. This signifies that a vertex connected to a highly central node is weightier than any other vertex connected to nodes of low centrality. The general function for an unweighted network is given in Equation (5):
where xi refers to the eigenvector centrality score for node i, and λ refers to a constant value represented by a vector–matrix system, which is represented in Equation (6):
where x refers to the eigenvector of the adjacency matrix A that has eigenvalue λ.
The theorem of Perron–Frobenius can be used to establish the fact that the largest eigenvalue is λ and that x belongs to the associated eigenvector (Friedkin 1991). Normalizing the value of x can help obtain the eigenvector centrality, which varies between the range of 0 and 1. The eigenvector centrality of the weighted network is provided by Equation (7) (Soh et al. 2010).
where refers to the average weighted centrality of node i (See Equation (7)).
3.3.4. Influence Strength
The influence strength (Barthélemy et al. 2005) of stock i in the time period k is defined as follows:
In Equation (8), wi,j represents the weighted correlation coefficient of the neighbors of vertex j.
3.3.5. Weighted Clustering Coefficient
Barrat et al. (2004) introduced the equation for the weighted clustering coefficient of a weighted network, which can be computed using Equation (9) (Sabidussi 1966):
where si is the influence strength of vertex i and ki refers to the degree of vertex i. The value of aij will be equal to 1 if there is an existence of an edge connecting i and j. The weighted clustering coefficient ranges between 0 and 1. For computing this metric, two aspects must be considered: first, how many closed triplets are adjacent to the node under consideration and, second, what the total relative weight of the node is with reference to its strength.
3.3.6. Domination Power
For computation of the domination power of a node, two things are considered. First, whether a node is accessible to the centrality in a network and, second, the direction of the edges of the node and their corresponding weights. Van Den Brink and Gilles (2000) proposed the degree-based domination measure, known as the β-measure, which is computed as shown in Equation (10):
where w (i, j) refers to the weight of the edges that link vertex i to j. The value of λ refers to the dominance weight of vertex j and is computed as shown below:
This study computes the above-mentioned six network metrics for each of the 335 stocks constituting each of the 106 weighted networks (each network model represents an observation of 500 data points). The network measures are then aggregated in sector-wise dimensions, and the aggregated values are plotted graphically and investigated. The aggregated values are further plotted sector-wise for all 106 observations to examine the temporal variations in the network over the study period. The following categorical sectors are considered for analysis: financial, communication, energy, diversified, textiles, construction, metals, automobile, engineering, services, chemicals, technology, consumer durables, healthcare, and FMCGs. The industry sectors of the stocks, as listed by the BSE, are used for sector-wise aggregation, computations, and plotting.
3.4. Network Reduction Methods and Visualization
The three issues with the usage of empirical unfiltered correlation matrices for making investment models are as follows: (i) the correlation matrices are dominated by a large noise content; (ii) there is a problem of instability in the empirical correlation matrices; and, (iii) in the unfiltered empirical correlation matrix, the actual realized risk of a future investment period is magnified several-fold in comparison to the predicted risk, whereas, for filtered correlation matrices, the realized risk is only magnified by a small level (Rosenow et al. 2003). These three issues make the financial models built using such an unfiltered matrix a poor decision estimate. Deriving a filtered matrix with a high signal-to-noise ratio is, thus, necessary for building suitable decision models in the areas of finance management and investment science. Using different genres of network filtering methods, substantial noisy edge connections that are traditionally observed in the topology of equity networks can be suitably removed. Exploratory network analysis comprises visualization and insight generation. A weighted equity network for the complete dataset of 2621 data points (representing 10 years and six months’ worth of data) is constructed. In Figure A1 of Appendix A, the resulting weighted equity network for the complete dataset is also denser in the topological structure, which inhibits direct visual comprehension. We, hence, use different network filtering methods such as MST analysis and the backbone extraction method (disparity filtering) to identify the links of the reduced network.
3.4.1. Minimum Spanning Tree
The MST is the spanning tree of the shortest length and is a graph without cycles connecting all nodes with links. Mantegna (1999) introduced a methodology and distance measure to construct an MST for studying correlation-based equity networks. The MST is constructed using Prim’s algorithm (Prim 1957). The current study adopts a similar methodology and distance measure for the construction of MSTs from the study datasets
3.4.2. Disparity Filtering
The disparity filtering algorithm for weighted networks was proposed by Serrano et al. (2009). This filtering method offers a practical approach for extracting the relevant connection backbone in complex multiscale networks. It preserves the edges that represent statistically significant deviations with respect to a null model. An essential part of this technique is that it does not belittle small-scale interactions and operates at all scales, which are defined by their weight distribution. This method has been used in filtering complex networks belonging to a diverse set of fields such as food pairing networks (Ahn et al. 2011), cattle trade movement networks (Bajardi et al. 2011), human disease symptoms networks (Zhou et al. 2014), metabolic networks (Serrano et al. 2012), and other networks in the fields of social science, medicine, library science, and climate science.
The disparity filtering algorithm determines which edge should be retained for each vertex in the network by using hypothesis testing. The following is the step-wise approach for executing the disparity filtering methodology:
Step 1: Find node strength (nsi) of the ith node:
Step 2: Find the normalized weight () of each edge incident from the ith node:
Step 3: Fix the value of alpha at which statistically significant edges should be derived. Consider the value of α to be 0.1;
Step 4: State the null hypothesis (H0): the normalized weight of the edge for a certain connection of a node that has the degree k belongs to a random assignment from a uniform distribution;
Step 5: Calculate the αi,j for each of the edge connections using the following formula:
where k refers to the degree of node i
Step 5: Remove the edge connection if
Changing α, one can progressively remove the irrelevant links, thus effectively extracting the backbone structure of the weighted network. In the case of the disparity filtering, the first step consisted of obtaining an optimum alpha value for which disparity filtering could be performed. The alpha value should be such that the backbone structure that is obtained should essentially retain the multi-scale structure and the intrinsic clustering of the original network. For determining the optimum alpha value, each one of the following values was considered: 0.2, 0.15, 0.10, and 0.05. For each of these alpha values, the disparity filtering was performed on the weighted network, and backbone structures were extracted.
Next, the weighted clustering coefficients were computed for all of the backbone structures. The current study uses the weighted clustering coefficient given by Barrat et al. (2004). The equation 9 for computing the weighted clustering coefficient of a weighted network is given in Equation (9).
The Barrat weighted clustering coefficients are computed for each of the backbone structures for the range of alpha values (0.2, 0.15, 0.10, 0.05, and 0.01). The Barrat weighted clustering coefficients are also computed for the unfiltered weighted network. The weighted clustering coefficients of the backbone structures at different values of alpha are compared with that of the value of the unfiltered weighted network. The optimum alpha value is the one for which the weighted clustering coefficient of a filtered network (extracted backbone) is the closest to that of the unfiltered network. Table 1 exhibits the Barrat weighted clustering coefficient scores of the backbone structures obtained for each of the alpha values. The table also lists the value of the Barrat weighted clustering coefficient for the unfiltered network. It can be clearly seen from Table 2 that, for an alpha value of 0.1, the weighted clustering coefficient is the closest to the one obtained from the unfiltered network. Thus, the optimum alpha value determined for the disparity filtering is 0.1. The filtration of the network is next performed using the disparity filtering method, taking the α value as 0.1.

Table 2.
List of weighted clustering coefficients of backbone structures at each of the value of α.
4. Results and Discussion
4.1. Topological Properties of the Network
A topological property can be defined as a type of characteristic that is preserved under a general notion of homeomorphism, for instance, compactness and connectedness. In the context of network theory, complex networks are a type of network whose topological properties are non-trivial and non-observable in simple networks, such as random graphs or lattices. Nevertheless, the intricate topological features of these networks are indicative of networks that abstract interdependencies within real-world systems. Equity networks, classified as complex networks, possess unique topological traits that can be quantified through specific network metrics.
4.2. Aggregated Sector-Wise Average Network Measures
A plot of the sector-wise average network measures for 106 observations for the six-network metrics, i.e., dominance (Figure 1), weighted clustering coefficient (Figure 2), closeness centrality (Figure 3), influence strength (Figure 4), disparity (Figure 5), and eigenvector centrality (Figure 6), respectively, is shown below.
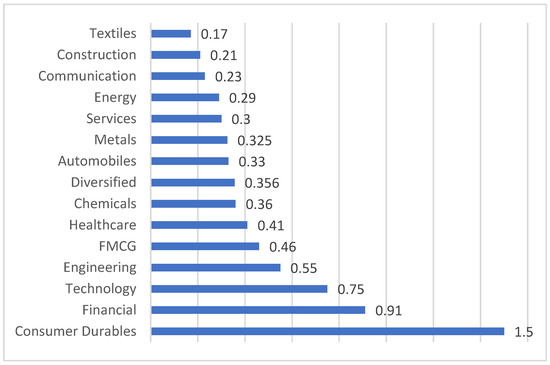
Figure 1.
Sector-wise average dominance.
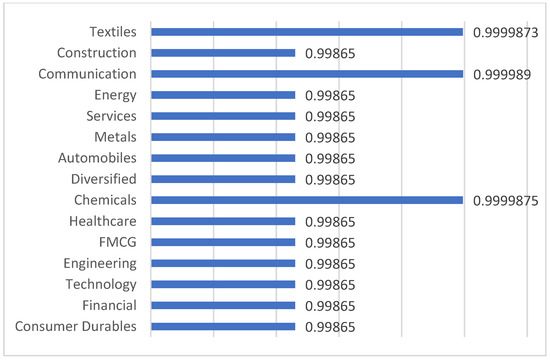
Figure 2.
Sector-wise average weighted clustering coefficients.
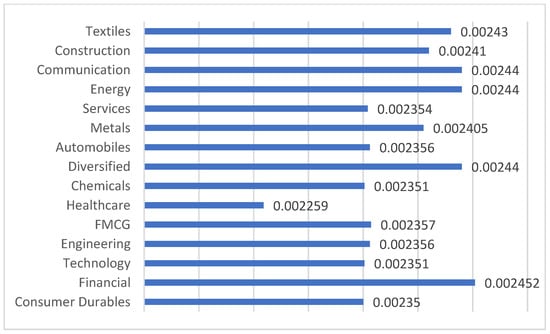
Figure 3.
Sector-wise average closeness centrality.
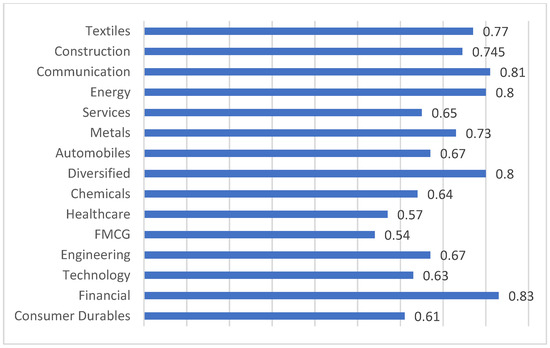
Figure 4.
Sector-wise average influence strength.
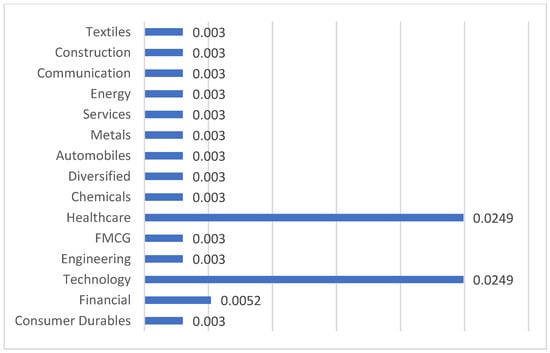
Figure 5.
Sector-wise average disparity.
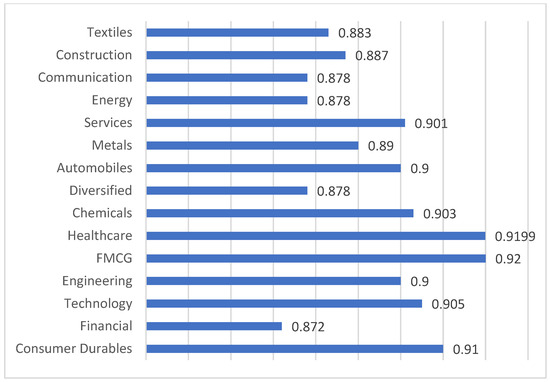
Figure 6.
Sector-wise average eigenvector centrality.
Figure 1 shows the sector-wise average dominance within the network. A high value specifies a high dominance sector that controls most connections within the network. Estimates show that, in India, the consumer durables sector has more dominance while the textiles sector has less dominance. Thus, the high value of average dominance for consumer durables indicates that major players within the sector have heavy influences. In contrast, a low value of average dominance for textiles suggests that the environment within the sector is well-balanced and competitive. Figure 2 illustrates sector-wise average weighted clustering coefficients that suggest the degree of clustering within each sector. Sectors like communications, chemicals, and textiles show a relatively high score compared to the other sectors, suggesting a strong internal connectivity and collaborative networks between them. It also implies that these sectors can benefit from innovation, knowledge-sharing, competitive advantages, and strategic planning. Figure 3 shows the sector-wise average closeness centrality, identifying which sectors are most accessible to others. Figure 4 displays the sector-wise average influence strength, with higher values indicating a stronger influence. The financial sector, with the highest score, plays a pivotal role within the network. Therefore, policy-wise, maintaining a stable financial sector is crucial for economic stability. Figure 5 shows the sector-wise average disparity of connections, with the healthcare and technology sectors having the highest scores, indicating that there are dominant players, power imbalances, and risk concentration in these sectors. Figure 6 presents the sector-wise average eigenvector centrality, identifying the most influential nodes. The estimates suggest that the FMCGs sector, followed by the healthcare sector, shows high values for its average eigenvector centrality. This metric not only measures the influence of the node but also considers the quality of its connections. The results suggest that the FMCGs and healthcare sectors can play a vital role in achieving economic stability, public health, and overall wellbeing. In summary, Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 provide diverse metrics that help to understand the different sectors within the network. This study computes six key network metrics to analyze the structural properties of the Indian stock market. Each of these metrics provides distinctive understanding regarding different aspects of risk propagation, market behavior, risk, and sectoral influence. For example, the eigenvector centrality draws attention to stocks that are substantially influential within the equity network, revealing sectors like FMCGs or healthcare that play a critical role in market stability. The closeness centrality finds stocks that are strategically positioned, implying that the price fluctuations of these stocks can promptly influence the broader market. The disparity measure shows asymmetric dependencies, assisting investors in understanding risk concentration points and diversification opportunities. These measures can be used by investors to determine sector leaders, modify portfolio allocations, and reduce systemic risks. Policymakers may use them to help them make decisions about sector-specific rules and economic actions, while market regulators might use them to keep an eye on interconnected vulnerabilities and anticipate financial contagion effects. Stakeholders can make better, data-driven financial decisions by incorporating these network insights into risk assessment, investment strategies, and systemic market analysis.
4.3. Reduced Network Visualization and Interpretation
This study visually interprets the cluster formation in networks derived from MST analysis and disparity filtering (Figure 7). It relates these clusters to common economic factors that affect industrial segments. The reduced network, representing 2621 data points from over 10 years and six months, provides a comprehensive view of all studied stocks, excluding cycles and with minimal weights being estimated, offering critical insights into stock relationships. The visualization of the MST plot (Figure 7) shows the formation of small local clusters, each possessing a mix of analogous and diverse industry group stocks in unequal proportion. However, these clusters exhibit a large degree of heterogeneity with no clearly demarcated homogenous regions emerging.
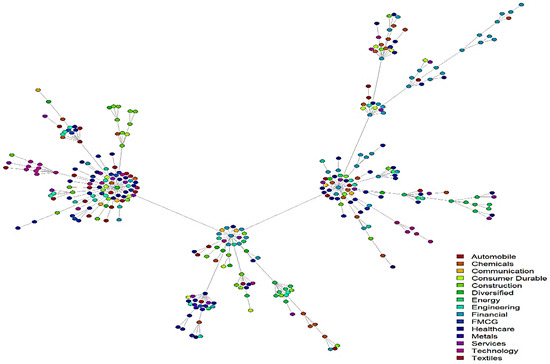
Figure 7.
Minimum spanning tree of the study dataset.
The visualization of the reduced network (Figure 8) derived using the disparity filtering method at an alpha value of 0.1 (i.e., 90 percent confidence interval) shows that stocks associated with similar industrial sectors form clearly demarcated independent clusters. The clusters derived here exhibit a high degree of variability. This study labels the clusters with serial numbers. Cluster 1 consists of government-controlled commercial banks in India, which are similarly affected by macroeconomic changes, resulting in an interconnected mesh that was observed over 10 years and six months’ worth of data. Cluster 2 shows the firms belonging to the construction and cement industries. Cluster 3 consists of minerals-sector companies, mainly steel and aluminum manufacturers. Cluster 4 includes Reliance Group’s core companies: Reliance Capital, Reliance Industries, and Reliance Infrastructure. Cluster 5 groups three government-controlled petrochemical marketing companies, Indian Oil Corporation, Bharat Petroleum Corporation, and Hindustan Petroleum Corporation, which handle downstream product distribution and retail. Cluster 6 consists of all top IT services firms. Cluster 7 consists of housing financial corporations while cluster 8 consists of three petrochemical refineries, namely Essar Oil, Chennai Petroleum, and Mangalore Refinery. Cluster 9 consists of automobile companies, namely Maruti Suzuki India Ltd. and Hero Moto Corp.
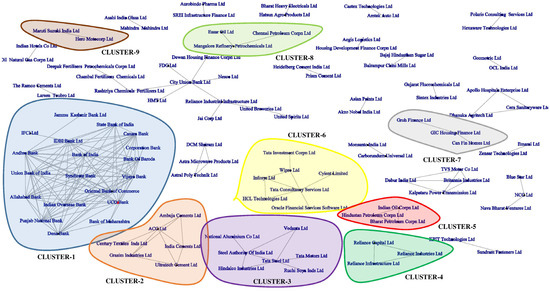
Figure 8.
Backbone structure obtained using disparity filtering algorithm with the stock names.
The use of disparity filtering and MST analysis offers two major insights into stock market relationships. The MST (Figure 7) method creates a network by retaining the most crucial connections while ensuring a cycle-free structure. This results in small, mixed-industry clusters, highlighting both inter- and intra-sector influences on market dynamics. Disparity filtering (Figure 8), on the other hand, preserves only the statistically significant links, leading to well-defined sector-based clusters. Unlike MST analysis, it does not impose a tree structure, allowing clearer industry segmentation. This method identifies dominant economic forces that influenced stock relationships, forming distinct clusters such as petrochemical companies, IT firms, and government-controlled banks which showcase similar reactions to macroeconomic factors. The comparison reveals that the MST method offers a broader view of stock interconnectivity but lacks strict industry segregation, while disparity filtering enhances the interpretability by emphasizing sectoral cohesion. The MST method captures indirect cross-industry influences, whereas disparity filtering isolates industry-specific linkages by eliminating weaker connections. The complementary nature of these methods highlights the value of multi-method network analysis in financial research. Combining both techniques provides a multi-dimensional perspective, balancing a high-level overview of market interactions with a detailed breakdown of sectoral relationships.
4.4. Comparative Analysis of Findings with Studies in Emerging Market
The findings of this study are in line with the Brazilian (Tabak et al. 2010) and South African (Majapa and Gossel 2016) contexts. Table 3 exhibits a summarized comparative analysis of the network metrics among the three markets and the associated industry rankings in each market. Similarly, Table 4 shows a comparative analysis of the findings.

Table 3.
Inference from the plots of network metrics.

Table 4.
Comparative analysis between present findings and reported findings of analogous studies in Brazilian and South African markets.
Through comparison of the MSTs of the three markets, we observed some interesting facts. First, the visual analysis of the MST shows that, in contrast to the Brazilian and South African markets where large homogeneity among clusters is formed, the MST derived from this study’s dataset does not form such clusters. Instead, there is the formation of small local clusters among analogous industry group stocks and a large degree of heterogeneity in these clusters. This study examines 335 stocks from 15 industrial sectors, compared to the 47 stocks from 8 sectors in the Brazilian market and 100 stocks from 9 sectors in the South African market. Due to the larger and more diverse sample, clear demarcated clusters are not observed, but clusters of 10–12 stocks appear in the finance, construction, and FMCGs sectors. After applying disparity filtering, distinct industry-oriented stock clusters emerge.
Our study enriches the existing literature on stock market relationships by analyzing financial network structures through disparity filtering and minimum spanning tree (MST) analysis. Specifically, our finding from the MST that economic forces cause stocks from diverse sectors to form loosely defined clusters provides evidence for sector-specific behaviors and larger market interdependencies. This suggests that, while industry-specific firms share common trends, they also do so with firms from diverse sectors. The disparity filtering, on the other hand, shed light on sectoral clustering, implying that some sectors, for example, IT firms and government-controlled banks, show highly independent and localized structures. This finding aligns with economic expectations wherein technological advancements and regulatory policies prompt distinct market behavior.
Our findings align with the existing literature (e.g., Mantegna 1999; Tumminello et al. 2005; Carvalho and Araújo 2024; Choi and Kim 2024; Rakib et al. 2024) that has demonstrated the efficacy of MST analysis in identifying financial market structures and the efficacy of disparity filtering in identifying vital interlinkages in financial networks (Serrano et al. 2009). This study is, however, unique in applying both MST analysis and disparity filtering simultaneously, which allowed us to observe heterogeneity in the MST analysis and clearer clustering in the disparity filtering, demonstrating how different methodologies can uncover complementary aspects of stock associations. For instance, stock market structures are influenced by both industry-specific dynamics and larger market inter-dependence, a fact that existing studies have failed to consider.
The novelty of this research lies in unearthing mixed-industry clusters in the MST visualization. Existing studies have identified relatively homogeneous clusters in their MST-based analyses in the context of mature markets such as Europe and the USA (Tumminello et al. 2010), whereas our study unearths greater diversity within local clusters, which can probably be attributed to the unique nature of the Indian markets, where major corporates hold business interests in diverse sectors, blurring traditional industry boundaries. For instance, India’s leading conglomerate, Reliance, operates several core companies within a single cluster despite having interests in diverse sectors, highlighting the role of group influence and corporate ownership on stock market structures.
A comparison of our findings with studies in other markets shows that developed economies show much clearer clustering, even in networks that are just based on MST analysis (Aste et al. 2010), compared to the developing economies like India, where family ownership, sectoral inter-dependencies, and government policies lead to more interconnected networks. This finding reiterates the need for tailored network analysis methods for studying diverse markets in diverse market settings.
5. Theoretical Contributions
This research enhances the existing body of work on financial network analysis by illustrating how different network-based methodologies provide complementary insights into stock market structures. Unlike previous studies (Rakib et al. 2024; Berouaga et al. 2023) that primarily employed either MST analysis or disparity filtering in a silo, this study integrates the two techniques and finds a multi-faceted perspective, with the MST analysis capturing the broader market interconnectivity while the disparity filtering highlights the most statistically significant sectoral relationships. By examining how conglomerates, government-controlled enterprises, and sector-specific factors contribute to stock clustering, this study enriches theoretical perspectives on market complexity and industry interdependencies. Contrary to conventional asset pricing models (Pástor and Stambaugh 2000) that focus primarily on returns and volatility, this study emphasizes the structural topology of financial markets, offering a novel understanding of stock relationships beyond price dynamics.
Our findings also contribute to ongoing discussions on network resilience and systemic risk (Peron et al. 2012; Cerqueti et al. 2024; Glasserman and Young 2016) by demonstrating variations in internal cohesion across industries. This has important implications for financial stability theories, illustrating that, while highly clustered industries may be more resilient to localized disruptions, loosely connected sectors could facilitate the spread of systemic risk. The network analysis throws light on market stability, systemic risk, and investment strategies. FMCG and healthcare stocks with high eigenvector centrality are key nodes, amplifying shocks during crises and stabilizing the market. Their significant interconnectivity and influence within the obtained network indicate that they serve as critical nodes, amplifying market shocks when under financial distress. This underscores the importance of continuous monitoring of these highly central stocks to enhance portfolio risk management and mitigate contagion effects.
The MST analysis reveals clear sectoral clustering, especially among government-owned banks, IT companies, and petrochemical firms, which is indicative of strong inter- and intra-sector connections within the Indian stock market. These clusters correspond with economic cycles, such that IT firms react to global demand, financial institutions to macroeconomic shifts, and commodity sectors to price changes in raw material. Insights into these patterns can help investors create sector-focused diversification strategies in order to minimize correlated risks and improve their returns. Sectoral disparities in the network analysis provide key insights when viewed through the lens of modern portfolio theory (MPT) (Lukomnik and Hawley 2021; Akkaya 2021) and factor models (Ng et al. 1992; L’Her et al. 2004). Increased disparity levels in certain sectors signal structural imbalances and differing degrees of systemic relevance. These findings will enable investors to optimize their portfolio allocation by reducing their exposure to highly volatile or tightly interconnected sectors. For example, strong connections among petrochemical companies indicate that shocks like crude oil price changes could affect the entire sector. Understanding such interdependencies enables the development of resilient, risk-adjusted investment strategies that protect against downturns while supporting long-term growth. Based on the investment and systemic risk frameworks, this study offers actionable guidance for investors, analysts, and policymakers in navigating the complexities of the Indian stock market.
6. Managerial Implication of the Study
Empirical evidence from the existing literature demonstrates that the filtered networks used herein, derived from various network pruning techniques, are statistically robust and capable of handling both non-stationarity and fat-tailed distributions in equity market time-series data. Additionally, applying network filtering methods in equity networks can be utilized for portfolio selection tasks by investment and portfolio managers. The data-driven insights generated from this cross-security interdependency study provide key information for the systemic risk monitoring of Indian equity markets by financial policymakers, mutual fund managers, and the fund managers of foreign Portfolio investors, pension funds, and hedge funds. Currently, as foreign portfolio investors increasingly invest in Indian markets for stable and high returns, this information is crucial. Unlike past decades, today’s Indian equity market is highly integrated with major global markets, making country-level diversification insufficient for hedging systemic shocks. In such scenarios, inside a country-specific equity market, increasing understanding of the collective dynamics of the price fluctuations of companies belonging to different sectors or industries and their susceptibilities to systemic shocks through the use of network metrics as decision support tools will be helpful in furthering risk management functionality.
7. Conclusions
This study examines the abstraction and capturing of interdependencies of equity returns in a complex system framework using network models. The initial inquiry was focused on determining the most suitable method for capturing the inter-stock dependencies among asset returns. The analysis showed that weighted network models form the best approximation strategy to capture such interdependencies. The second set of questions addressed the topological measures of equity network models, concluding that six network metrics capture intrinsic information and can differentiate and diagnose industry-specific asset return interdependencies. Sector-wise analysis suggests that stocks in the financial, FMCGs, healthcare, technology, and diversified sectors are more significant and influential. Therefore, continuous monitoring of equity patterns using network metrics could be a valuable strategy for portfolio managers. The third series of inquiries compared equity network models from Indian markets with those of other emerging markets. The analysis concludes that each market has unique financial traits, such as taxation regimes, circuit filters, and volume allowances, leading to distinct asset interdependency patterns with few similarities. Therefore, an investment strategy that performs well in one emerging market may encounter failure in the other. The fourth set of questions addresses reduced network visualization. Our analysis shows that more efficient disparity filtering produces an information-rich, noise-poor network compared to MST analysis. Disparity filtering effectively visualizes ‘local interdependency patterns’ in asset returns, unlike MST analysis.
Visualizing network clusters provides a multidimensional view of stock interconnections, revealing cross-sector and inter-industry linkages that are not immediately apparent through traditional analysis. In diverse markets, such as India, the role of these linkages in minimizing investment risk requires further analysis. Unlike traditional strategies, network-based clustering can identify hidden correlations among stocks, which in turn, enables greater portfolio diversification and the dynamic mapping of real-time interactions, thereby reducing exposure to highly interconnected stocks that are vulnerable to sector-wide disruptions. However, not all stocks within a group behave uniformly, given the heterogeneous nature of the observed clusters. Some clusters include a mix of industries in varying proportions, which can result in risk spillovers. Conglomerates and cross-sector linkages within clusters may also introduce more uncertainties, necessitating complementary financial indicators for accurate risk assessment. To enhance risk mitigation, cluster-based approaches should be integrated with other financial analysis techniques, including stress testing, macroeconomic factor evaluation, and volatility modeling under various market conditions. Identifying clusters that remain stable over time may also provide insights into long-term sectoral resilience, whereas highly volatile clusters may indicate increased risk exposure.
Future research could refine this approach by examining temporal shifts in network structures to understand how they evolve during financial crises or economic booms. Sensitivity analyses with varying time windows (beyond the standard 500 trading days) would also help to determine whether patterns remain consistent across periods, reinforcing the robustness of the methodology. While Pearson correlation captures linear dependencies, it may not fully reflect extreme market conditions or nonlinear relationships. Alternative dependency measures, such as Kendall’s tau or Spearman’s rank correlation, offer a more detailed analysis of stock relationships, particularly during periods of increased volatility. Exploring these methods would enhance the understanding of market dynamics and improve risk management strategies in the Indian stock market.
The findings and the methodological approach of the current study have significant implications for qualified institutional buyers, foreign institutional investors, domestic institutional investors, and foreign direct investments, as the traits of all of them emerge distinctively. The findings of this study highlight the possibilities for investigating the dynamics of stock price movements in equity markets and could also be suitably employed for systemic risk monitoring of the Indian equity market. The issues of cross-country and intra-country systemic spread have become even more relevant in today’s highly inter-connected world, where large data-streams pass through most of the emerging economy at a brisk pace. Rather unwillingly, a tiny turbulence in one corner of the globe generates a ‘butterfly effect’ in another remote corner, making these complex constructs brittle. To minimize the sudden shocks which may impact the system in a destructive fashion, fund managers could well be using these complex network constructs as supporting instruments to avoid humiliation. Further research could examine samples from the Chinese and Greek market crashes to observe how network metrics and industry sector significance evolved during these periods.
Author Contributions
Conceptualization, B.B. and M.M.; Methodology, B.B.; Software, B.B.; Validation, B.B.; Formal analysis, B.B. and M.M.; Investigation, M.M.; Resources, M.M.; Data curation, B.B.; Writing—original draft, B.B. and M.M.; Writing—review & editing, B.B. and M.M.; Visualization, B.B. All authors have read and agreed to the published version of the manuscript.
Funding
Moinak Maiti is funded by the National Research Foundation (NRF), South Africa by Knowledge Interchange & Collaboration (KIC) Grants for International Conference 2025.
Data Availability Statement
Publicly available datasets are analyzed in this study. This data can be found here: https://www.bseindia.com/markets/equity/EQReports/StockPrcHistori.html?flag=0 (accessed on 20 December 2024).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Figure A1.
Complete weighted equity network of 335 stocks. This graph represents one of the 100 temporally synchronized observations, each of which captures 500 data points.
References
- Agarwal, Vineet, Richard J. Taffler, and Chenyang Wang. 2025. Investor emotions and market bubbles. Review of Quantitative Finance and Accounting 4: 339–69. [Google Scholar] [CrossRef]
- Ahn, Yong-Yeol, Sebastian E. Ahnert, James P. Bagrow, and Albert-László Barabási. 2011. Flavor network and the principles of food pairing. Scientific Reports 1: 196. [Google Scholar] [CrossRef] [PubMed]
- Akkaya, Murat. 2021. Behavioral Portfolio Theory. In Applying Particle Swarm Optimization. Edited by Burcu Adıgüze Mercangöz. International Series in Operations Research & Management Science. Cham: Springer, vol. 306. [Google Scholar] [CrossRef]
- ANI. 2024. India’s IPO Fundraising Set for Landmark Year 2024. LiveMint. Available online: https://www.livemint.com/market/ipo/indias-ipo-fundraising-set-for-landmark-year-2024-s-p-global-market-intelligence-11733635115553.html (accessed on 3 April 2025).
- Aste, Tomaso, William Shaw, and Tiziana Di Matteo. 2010. Correlation Structure and Dynamics in Volatile Markets. New Journal of Physics 12: 085009. [Google Scholar] [CrossRef]
- Baitinger, Eduard, and Jochen Papenbrock. 2017. Interconnectedness Risk and Active Portfolio Management: The Information Theoretic Perspective. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2909839 (accessed on 20 January 2025).
- Bajardi, Paolo, Alain Barrat, Fabrizio Natale, Lara Savini, and Vittoria Colizza. 2011. Dynamical Patterns of Cattle Trade Movements. PLoS ONE 6: e19869. [Google Scholar] [CrossRef]
- Barbi, Alex Quintino, and Gilberto Aparecido Prataviera. 2019. Nonlinear dependencies on Brazilian equity network from mutual information minimum spanning trees. Physica A: Statistical Mechanics and Its Applications 523: 876–85. [Google Scholar] [CrossRef]
- Barfuss, Wolfram, Guido Previde Massara, Tiziana Di Matteo, and Tomaso Aste. 2016. Parsimonious modeling with information filtering networks. Physical Review E 94: 062306. [Google Scholar] [CrossRef]
- Barrat, Alain, Marc Barthelemy, Romualdo Pastor-Satorras, and Alessandro Vespignani. 2004. The architecture of complex weighted networks. Proceedings of the National Academy of Sciences USA 101: 3747–52. [Google Scholar] [CrossRef]
- Barthélemy, Marc, Alain Barrat, Romualdo Pastor-Satorras, and Alessandro Vespignani. 2005. Characterization and modeling of weighted networks. Physica A 346: 34–43. [Google Scholar] [CrossRef]
- Belhoula, Mohamed Malek, Walid Mensi, and Kamel Naoui. 2024. Impacts of investor’s sentiment, uncertainty indexes, and macroeconomic factors on the dynamic efficiency of G7 stock markets. Quality & Quantity 58: 2855–86. [Google Scholar] [CrossRef]
- Berouaga, Younes, Cherif El Msiyah, and Jaouad Madkour. 2023. Portfolio optimization using minimum spanning tree model in the Moroccan Stock exchange market. International Journal of Financial Studies 11: 53. [Google Scholar] [CrossRef]
- Bhattacharjee, Biplab, Muhammad Shafi, and Animesh Acharjee. 2016. Investigating the influence relationship models for stocks in Indian equity market: A weighted network modelling study. PLoS ONE 11: e0166087. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, Biplab, Muhammad Shafi, and Animesh Acharjee. 2019. Network mining based elucidation of the dynamics of cross-market clustering and connectedness in Asian region: An MST and hierarchical clustering approach. Journal of King Saud University-Computer and Information Sciences 31: 218–28. [Google Scholar] [CrossRef]
- Bhattacharjee, Biplab, Rajiv Kumar, and Arunachalam Senthilkumar. 2022. Unidirectional and bidirectional LSTM models for edge weight predictions in dynamic cross-market equity networks. International Review of Financial Analysis 84: 102384. [Google Scholar] [CrossRef]
- Boginski, Vladimir, Sergiy Butenko, and Panos M. Pardalos. 2005. Statistical analysis of financial networks. Computational Statistics & Data Analysis 48: 431–43. [Google Scholar]
- Bonanno, Giovanni, Guido Caldarelli, Fabrizio Lillo, and Rosario N. Mantegna. 2003. Topology of correlation-based minimal spanning trees in real and model markets. Physical Review E 68: 046130. [Google Scholar] [CrossRef]
- Brechmann, Eike Christian. 2013. Hierarchical Kendall Copulas and the Modeling of Systemic and Operational Risk. Ph.D. thesis, Technical University of Munich, Munich, Germany. [Google Scholar]
- Brida, Juan Gabriel, and Wiston Adrián Risso. 2008. Multidimensional minimal spanning tree: The Dow Jones case. Physica A 387: 5205–10. [Google Scholar] [CrossRef]
- Brin, Sergey, and Lawrence Page. 1998. The anatomy of a large-scale hypertextual web search engine. Computer Networks and ISDN Systems 30: 107–17. [Google Scholar] [CrossRef]
- Carvalho, Lucas, and Tanya Araújo. 2024. The dynamics of exchange traded funds: A geometrical and topological approach. Applied Network Science 9: 73. [Google Scholar] [CrossRef]
- Cerqueti, Roy, Hayette Gatfaoui, and Giulia Rotundo. 2024. Resilience for financial networks under a multivariate GARCH model of stock index returns with multiple regimes. Annals of Operations Research, 1–27. [Google Scholar] [CrossRef]
- Chakrabarti, Prasenjit, Mohammad Shameem Jawed, and Manish Sarkhel. 2021. COVID-19 pandemic and global financial market interlinkages: A dynamic temporal network analysis. Applied Economics 53: 2930–45. [Google Scholar] [CrossRef]
- Chan, Lupe S. H., Amanda M. Y. Chu, and Mike K. P. So. 2023. A moving-window bayesian network model for assessing systemic risk in financial markets. PLoS ONE 18: e0279888. [Google Scholar] [CrossRef]
- Choi, Insu, and Woo Chang Kim. 2024. A multifaceted graph-wise network analysis of sector-based financial instruments’ price-based discrepancies with diverse statistical interdependencies. The North American Journal of Economics and Finance 75: 102316. [Google Scholar] [CrossRef]
- Clemente, Gian Paolo, Rosanna Grassi, and Asmerilda Hitaj. 2021. Asset allocation: New evidence through network approaches. Annals of Operations Research 299: 61–80. [Google Scholar] [CrossRef]
- Clemente, Gian Paolo, Rosanna Grassi, and Asmerilda Hitaj. 2022. Smart network based portfolios. Annals of Operations Research 316: 1519–41. [Google Scholar] [CrossRef]
- Deshmukh, Arun Kumar, Ashutosh Mohan, and Ishi Mohan. 2022. Goods and Services Tax (GST) Implementation in India: A SAP–LAP–Twitter Analytic Perspective. Global Journal of Flexible Systems Management 23: 165–83. [Google Scholar] [CrossRef] [PubMed]
- Dhingra, Barkha, Shallu Batra, Vaibhav Aggarwal, Mahender Yadav, and Pankaj Kumar. 2024. Stock market volatility: A systematic review. Journal of Modelling in Management 19: 925–52. [Google Scholar] [CrossRef]
- Durante, Fabrizio, and Roberta Pappada. 2015. Cluster analysis of time series via Kendall distribution. In Strengthening Links Between Data Analysis and Soft Computing. Cham: Springer, pp. 209–16. [Google Scholar]
- Durante, Fabrizio, Enrico Foscolo, Roberta Pappada, and Hao Wang. 2015. A Portfolio Diversification Strategy via Tail Dependence. DEAMS Research Paper Series 3/2015, University of Trieste. Available online: https://www.openstarts.units.it/server/api/core/bitstreams/7db38d5e-d1fe-49c4-9722-3c6f71c471c8/content (accessed on 20 January 2025).
- Fama, Eugene F. 1970. Efficient capital markets. Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Fiedor, Paweł. 2014. Networks in financial markets based on the mutual information rate. Physical Review E 89: 052801. [Google Scholar] [CrossRef]
- Friedkin, Noah E. 1991. Theoretical Foundations for Centrality Measures. American Journal of Sociology 96: 1478–504. [Google Scholar] [CrossRef]
- Ghosh, Bikramaditya, and E. Kozarevic. 2019. Multifractal analysis of volatility for detection of herding and bubble: Evidence from CNX Nifty HFT. Investment Management and Financial Innovations 16: 182. [Google Scholar] [CrossRef]
- Gilmore, Claire G., Brian M. Lucey, and Marian Boscia. 2008. An ever-closer union? Examining the evolution of linkages of European equity markets via minimum spanning trees. Physica A 387: 6319–29. [Google Scholar] [CrossRef]
- Glasserman, Paul, and H. Peyton Young. 2016. Contagion in financial networks. Journal of Economic Literature 54: 779–831. [Google Scholar] [CrossRef]
- Goh, Yong Kheng, Haslifah M. Hasim, and Chris G. Antonopoulos. 2018. Inference of financial networks using the normalised mutual information rate. PLoS ONE 13: e0192160. [Google Scholar] [CrossRef]
- Gu, Yuxin, and Yinhong Yao. 2022. Dynamic correlation analysis on the financial institutions in Shanghai, Shenzhen, and Hong Kong stock markets based on complex network. Procedia Computer Science 214: 737–46. [Google Scholar] [CrossRef]
- Guo, Xue, Hu Zhang, and Tianhai Tian. 2018. Development of stock correlation networks using mutual information and financial big data. PLoS ONE 13: e0195941. [Google Scholar] [CrossRef] [PubMed]
- Hartman, David, and Jaroslav Hlinka. 2018. Nonlinearity in stock networks. Chaos: An Interdisciplinary Journal of Nonlinear Science 28: 083127. [Google Scholar] [CrossRef]
- Hatami, Zahra, H. Ali, D. Volkman, and P. Chetti. 2022. A new approach for analyzing financial markets using correlation Hong Kong stock markets based on complex network. Procedia Computer Science 214: 737–46. [Google Scholar]
- Hou, Lei, and Yueling Pan. 2022. Evaluating the connectedness of commodity future markets via the cross-correlation network. Frontiers in Physics 10: 1017009. [Google Scholar] [CrossRef]
- Huang, Chuangxia, Yunke Deng, Xin Yang, Xiaoguang Yang, and Jinde Cao. 2023. Can financial crisis be detected? Laplacian energy measure. The European Journal of Finance 29: 949–76. [Google Scholar] [CrossRef]
- Huang, Wei-Qiang, Xin-Tian Zhuang, and Shuang Yao. 2009. A network analysis of the Chinese stock market. Physica A: Statistical Mechanics and Its Applications 388: 2956–64. [Google Scholar] [CrossRef]
- Jung, Woo-Sung, Okyu Kwon, Fengzhong Wang, Taisei Kaizoji, Hie-Tae Moon, and H. Eugene Stanley. 2008. Group dynamics of the Japanese market. Physica A 387: 537–42. [Google Scholar] [CrossRef]
- Jung, Woo-Sung, Seungbyung Chae, Jae-Suk Yang, and Hie-Tae Moon. 2006. Characteristics of the Korean stock market correlations. Physica A 361: 263–71. [Google Scholar] [CrossRef]
- Karmuhil, Annadurai, and Ramasamy Murugesan. 2024. Examining the nexus of GST and selected stock indices: A multivariate time series and vector auto-regressive machine learning model. International Journal of Enterprise Network Management 15: 133–58. [Google Scholar] [CrossRef]
- Kaur, Jaspreet. 2024. Investors’ perception towards investor protection measures taken by the government of India and SEBI: An ordinal approach. International Journal of Law and Management 66: 720–51. [Google Scholar] [CrossRef]
- Kim, Hyun-Joo, In-mook Kim, Youngki Lee, and Byungnam Kahng. 2002a. Scale-free network in stock markets. Journal of the Korean Physical Society 40: 1105–8. [Google Scholar]
- Kim, Hyun-Joo, Youngki Lee, Byungnam Kahng, and In-mook Kim. 2002b. Weighted scale-free network in financial correlations. Journal of the Physical Society of Japan 71: 2133–36. [Google Scholar] [CrossRef]
- Kulkarni, Saumitra, Hirdesh K. Pharasi, Sudharsan Vijayaraghavan, Sunil Kumar, Anirban Chakraborti, and Areejit Samal. 2024. Investigation of Indian stock markets using topological data analysis and geometry-inspired network measures. Physica a Statistical Mechanics and Its Applications 643: 129785. [Google Scholar] [CrossRef]
- Kumari, Jyoti, and Jitendra Mahakud. 2015. Does investor sentiment predict the asset volatility? Evidence from emerging stock market India. Journal of Behavioral and Experimental Finance 8: 25–39. [Google Scholar] [CrossRef]
- Laloux, Laurent, Pierre Cizeau, Jean-Philippe Bouchaud, and Marc Potters. 1999. Noise Dressing of Financial Correlation Matrices. Physical Review Letters 83: 1467–70. [Google Scholar] [CrossRef]
- L’Her, Jean-François, Tarek Masmoudi, and Jean-Marc Suret. 2004. Evidence to support the four-factor pricing model from the Canadian stock market. Journal of International Financial Markets, Institutions and Money 14: 313–28. [Google Scholar] [CrossRef]
- Lukomnik, J., and J. P. Hawley. 2021. Moving Beyond Modern Portfolio Theory. Oxon: Routledge eBooks. [Google Scholar] [CrossRef]
- Maiti, Moinak, Darko Vukovic, Yaroslav Vyklyuk, and Zoran Grubisic. 2022. BRICS capital markets co-movement analysis and forecasting. Risks 10: 88. [Google Scholar] [CrossRef]
- Majapa, Mohamed, and Sean Joss Gossel. 2016. Topology of the South African stock market network across the 2008 financial crisis. Physica A 445: 35–47. [Google Scholar] [CrossRef]
- Malkiel, Burton G. 2003. The efficient market hypothesis and its critics. Journal of Economic Perspectives 17: 59–82. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit. 1965. Self-similar error clusters in communications systems and the concept of conditional stationarity. IEEE Transactions on Communication Technology 13: 71–90. [Google Scholar] [CrossRef]
- Mantegna, Rosario N. 1999. Hierarchical structure in financial markets. The European Physical Journal B-Condensed Matter and Complex Systems 11: 193–97. [Google Scholar] [CrossRef]
- Mantegna, Rosario N., and H. Eugene Stanley. 1995. Scaling behaviour in the dynamics of an economic index. Nature 376: 46–49. [Google Scholar] [CrossRef]
- Mantegna, Rosario N., and H. Eugene Stanley. 2000. An Introduction to Econophysics: Correlation and Complexity in Finance. Cambridge: Cambridge University Press. [Google Scholar]
- Marti, Gautier, Frank Nielsen, and Philippe Donnat. 2016. Optimal copula transport for clustering multivariate time series. Paper presented at the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March; pp. 2379–83. [Google Scholar]
- Marti, Gautier, Frank Nielsen, Mikołaj Bińkowski, and Philippe Donnat. 2021. A Review of Two Decades of Correlations, Hierarchies, Networks and Clustering in Financial Markets. In Progress in Information Geometry. Signals and Communication Technology. Edited by Frank Nielsen. Cham: Springer. [Google Scholar] [CrossRef]
- Massara, Guido Previde, Tiziana Di Matteo, and Tomaso Aste. 2016. Network filtering for big data: Triangulated maximally filtered graph. Journal of Complex Networks 5: 161–78. [Google Scholar] [CrossRef]
- Matia, Kaushik, Mukul Pal, H. Salunkay, and H. Eugene Stanley. 2004. Scale-dependent price fluctuations for the Indian stock market. Europhysics Letters 66: 909–14. [Google Scholar] [CrossRef]
- Meng, Sun, and Yan Chen. 2023. Market Volatility Spillover, Network Diffusion, and Financial Systemic Risk Management: Financial Modeling and Empirical Study. Mathematics 11: 1396. [Google Scholar] [CrossRef]
- Musmeci, Nicolò, T. Aste, and T. Di Matteo. 2015. Bootstrapping topological properties and systemic risk of complex networks using the fitness model. Journal of Network Theory in Finance 1: 1–20. [Google Scholar] [CrossRef]
- Namaki, Ali, Amir H. Shirazi, R. Raei, and G. R. Jafari. 2011. Network analysis of a financial market based on genuine correlation and threshold method. Physica A: Statistical Mechanics and Its Applications 390: 3835–41. [Google Scholar] [CrossRef]
- Newman, Mark E. J. 2008. The mathematics of networks. The New Palgrave Encyclopedia of Economics 2: 1–12. [Google Scholar]
- Ng, Victor, Robert F. Engle, and Michael Rothschild. 1992. A multi-dynamic-factor model for stock returns. Journal of Econometrics 52: 245–66. [Google Scholar] [CrossRef]
- Nie, Chun-Xiao. 2020. A network-based method for detecting critical events of correlation dynamics in financial markets. Europhysics Letters 131: 50001. [Google Scholar] [CrossRef]
- Onnela, Jukka-Pekka, Anirban Chakraborti, Kimmo Kaski, and Janos Kertesz. 2003a. Dynamic asset trees and Black Monday. Physica A 324: 247–52. [Google Scholar] [CrossRef]
- Onnela, Jukka-Pekka, Anirban Chakraborti, Kimmo Kaski, Janos Kertesz, and Antti Kanto. 2003b. Asset trees and asset graphs in financial markets. Physica Scripta 2003: 48. [Google Scholar] [CrossRef]
- Onnela, Jukka-Pekka, Anirban Chakraborti, Kimmo Kaski, Janos Kertesz, and Antti Kanto. 2003c. Dynamics of market correlations: Taxonomy and portfolio analysis. Physical Review E 68: 056110. [Google Scholar] [CrossRef]
- Pan, Raj Kumar, and Sitabhra Sinha. 2007. Self-organization of price fluctuation distribution in evolving markets. European Physics Letters 77: 1–5. [Google Scholar] [CrossRef]
- Pan, Raj Kumar, and Sitabhra Sinha. 2008. Inverse-cubic law of index fluctuation distribution in Indian markets. Physica A: Statistical Mechanics and Its Applications 387: 2055–65. [Google Scholar] [CrossRef]
- Pawanesh, Pawanesh, Imran Ansari, and Niteesh Sahni. 2025. Exploring the core–periphery and community structure in the financial networks through random matrix theory. Physica A Statistical Mechanics and Its Applications 661: 130403. [Google Scholar] [CrossRef]
- Pástor, Ľuboš, and Robert F. Stambaugh. 2000. Comparing asset pricing models: An investment perspective. Journal of Financial Economics 56: 335–81. [Google Scholar] [CrossRef]
- Peron, Kauê Dal’Maso Thomas, Luciano da Fontoura Costa, and Francisco A. Rodrigues. 2012. The structure and resilience of financial market networks. Chaos an Interdisciplinary Journal of Nonlinear Science 22: 013117. [Google Scholar] [CrossRef]
- Plerou, Vasiliki, Parameswaran Gopikrishnan, Bernd Rosenow, Luis A. Nunes Amaral, Thomas Guhr, and H. Eugene Stanley. 2002. Random matrix approach to cross correlations in financial data. Physical Review E 65: 1–18. [Google Scholar] [CrossRef] [PubMed]
- Plerou, Vasiliki, Parameswaran Gopikrishnan, Bernd Rosenow, Luís A. Nunes Amaral, and H. Eugene Stanley. 1999. Universal and Nonuniversal Properties of Cross Correlations in Financial Time Series. Physical Review Letters 83: 1471–74. [Google Scholar] [CrossRef]
- Press Information Bureau. 2017. 10 Years of Make in India Transforming India into a Global Manufacturing Powerhouse. Available online: https://pib.gov.in/PressNoteDetails.aspx?NoteId=153203&ModuleId=3®=3&lang=1 (accessed on 3 April 2025).
- Prim, Robert Clay. 1957. Shortest Connection Networks and Some Generalizations. The Bell System Technical Journal 36: 1389–401. [Google Scholar] [CrossRef]
- Priya, Pragati, and Chandan Sharma. 2023. COVID-19 related stringencies and financial market volatility: Sectoral evidence from India. Journal of Financial Economic Policy 15: 16–34. [Google Scholar] [CrossRef]
- PTI. 2019. Big Bang Mini-Budget: Government Slashes Corporate Tax Rate to 25.17%. Available online: https://timesofindia.indiatimes.com/business/india-business/big-bang-mini-budget-government-slashes-corporate-tax-rate-to-25-17/articleshow/71221589.cms (accessed on 3 April 2025).
- Rakib, Mahmudul Islam, Md Jahidul Alam, Nahid Akter, Kamrul Hasan Tuhin, and Ashadun Nobi. 2024. Change in hierarchy of the financial networks: A study on firms of an emerging market in Bangladesh. PLoS ONE 19: e0301725. [Google Scholar] [CrossRef]
- Rosenow, Bernd, Parameswaran Gopikrishnan, Vasiliki Plerou, and H. Eugene Stanley. 2003. Dynamics of cross-correlations in the stock market. Physica A 324: 241–46. [Google Scholar] [CrossRef]
- Sabidussi, Gert. 1966. The centrality index of a graph. Psychometrika 31: 581–603. [Google Scholar] [CrossRef]
- Samitas, Aristeidis, Elias Kampouris, and Stathis Polyzos. 2022. COVID-19 pandemic and spillover effects in stock markets: A financial network approach. International Review of Financial Analysis 80: 102005. [Google Scholar] [CrossRef]
- Sankar, C. Prem, K. Asokan, and K. Satheesh Kumar. 2015. Exploratory social network analysis of affiliation networks of Indian listed companies. Social Networks 43: 113–20. [Google Scholar] [CrossRef]
- Schinckus, Christophe, and Franck Jovanovic. 2013. Towards a transdisciplinary econophysics. Journal of Economic Methodology 20: 164–83. [Google Scholar] [CrossRef]
- Serrano, M. Ángeles, Marián Boguná, and Alessandro Vespignani. 2009. Extracting the multiscale backbone of complex weighted networks. Proceedings of the National Academy of Sciences USA 106: 6483–88. [Google Scholar] [CrossRef]
- Serrano, M. Ángeles, Marián Boguná, and Francesc Sagués. 2012. Uncovering the hidden geometry behind metabolic networks. Molecular Biosystems 8: 843–50. [Google Scholar] [CrossRef]
- Shiller, Robert J. 2005. Irrational Exuberance, 2nd ed. Princeton: Princeton University Press. ISBN 978-0691123356. [Google Scholar]
- Silva, Thiago Christiano, Solange Maria Guerra, Benjamin Miranda Tabak, and Rodrigo Cesar de Castro Miranda. 2016. Financial networks, bank efficiency and risk-taking. Journal of Financial Stability 25: 247–57. [Google Scholar] [CrossRef]
- Sinha, Sitabhra, and Raj Kumar Pan. 2007. Uncovering the Internal Structure of the Indian Financial Market: Large Cross-correlation Behavior in the NSE. In Econophysics of Markets and Business Networks: Proceedings of the Econophys-Kolkata III. Edited by Bikas K. Chakrabarti. Milan: Springer, pp. 3–19. [Google Scholar]
- Soh, Harold, Sonja Lim, Tianyou Zhang, Xiuju Fu, Gary Kee Khoon Lee, Terence Gih Guang Hung, Pan Di, Silvester Prakasam, and Limsoon Wong. 2010. Weighted complex network analysis of travel routes on the Singapore public transportation system. Physica A 389: 5852–63. [Google Scholar] [CrossRef]
- Song, Dong-Ming, Michele Tumminello, Wei-Xing Zhou, and Rosario N. Mantegna. 2011. Evolution of worldwide stock markets, correlation structure, and correlation-based graphs. Physical Review E 84: 026108. [Google Scholar] [CrossRef]
- Song, Won-Min, Tiziana Di Matteo, and Tomaso Aste. 2011. Nested hierarchies in planar graphs. Discrete Applied Mathematics 159: 2135–46. [Google Scholar] [CrossRef]
- Song, Won-Min, Tiziana Di Matteo, and Tomaso Aste. 2012. Hierarchical information clustering by means of topologically embedded graphs. PLoS ONE 7: e31929. [Google Scholar] [CrossRef]
- Sreenu, Nenavath, and Ashis Kumar Pradhan. 2023. The effect of COVID-19 on Indian stock market volatility: Can economic package control the uncertainty? Journal of Facilities Management 21: 798–815. [Google Scholar] [CrossRef]
- Tabak, Benjamin M., Thiago R. Serra, and Daniel O. Cajueiro. 2010. Topological properties of stock market networks: The case of Brazil. Physica A 389: 3240–49. [Google Scholar] [CrossRef]
- Times Now News. 2024. Stock Market Investors Richer by ₹3.6 Lakh Crore as Bulls Celebrate Modi’s Return; RBI’s Revised GDP Projection Among Others. Times Now. Available online: https://www.timesnownews.com/business-economy/markets/stock-market-investors-richer-by-3-6-lakh-crore-as-bulls-celebrate-modis-return-rbis-revised-gdp-projection-among-others-article-110861670 (accessed on 20 January 2025).
- Tumminello, Michele, Fabrizio Lillo, and Rosario N. Mantegna. 2010. Correlation, hierarchies, and networks in financial markets. Journal of Economic Behavior & Organization 75: 40–58. [Google Scholar]
- Tumminello, Michele, Tiziana Di Matteo, Tomaso Aste, and Rosario N. Mantegna. 2007. Correlation based networks of equity returns sampled at different time horizons. The European Physical Journal B 55: 209–17. [Google Scholar] [CrossRef]
- Tumminello, Michele, Tomaso Aste, Tiziana Di Matteo, and Rosario N. Mantegna. 2005. A tool for filtering information in complex systems. Proceedings of the National Academy of Sciences USA 102: 10421–26. [Google Scholar] [CrossRef]
- Van Den Brink, René, and Robert P. Gilles. 2000. Measuring domination in directed networks. Social Networks 22: 141–57. [Google Scholar] [CrossRef]
- Varma, Yashraj, Renuka Venkataramani, Parthajit Kayal, and Moinak Maiti. 2021. Short-Term Impact of COVID-19 on Indian Stock Market. Journal of Risk and Financial Management 14: 558. [Google Scholar] [CrossRef]
- Wang, Gang-Jin, Chi Xie, and H. Eugene Stanley. 2018. Correlation Structure and Evolution of World Stock Markets: Evidence from Pearson and Partial Correlation-Based Networks. Computational Economics 1: 607–35. [Google Scholar] [CrossRef]
- Wang, Gang-Jin, Huahui Huai, You Zhu, Chi Xie, and Gazi Salah Uddin. 2024. Portfolio optimization based on network centralities: Which centrality is better for asset selection during global crises? Journal of Management Science and Engineering 9: 348–75. [Google Scholar] [CrossRef]
- Yassin, Ali, Hocine Cherifi, Hamida Seba, and Olivier Togni. 2025. Backbone extraction through statistical edge filtering: A comparative study. PLoS ONE 20: e0316141. [Google Scholar] [CrossRef]
- Zaheer, Kashif, Faheem Aslam, Yasir Tariq Mohmand, and Paulo Ferreira. 2023. Temporal changes in global stock markets during COVID-19: An analysis of dynamic networks. China Finance Review International 13: 23–45. [Google Scholar] [CrossRef]
- Zhang, Xin, Boris Podobnik, Dror Y. Kenett, and H. Eugene Stanley. 2014. Systemic risk and causality dynamics of the world international shipping market. Physica A: Statistical Mechanics and Its Applications 415: 43–53. [Google Scholar] [CrossRef]
- Zhou, XueZhong, Jörg Menche, Albert-László Barabási, and Amitabh Sharma. 2014. Human symptoms disease network. Nature Communications 5: 4212. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).