The Business Cycle’s Impact on Volatility Forecasting: Recapturing Intrinsic Jump Components

Abstract

This study investigates the leverage effect and realized volatility (RV) of stocks in the presence of asymmetric jumps across economic expansions and contractions. We extend the heterogeneous autoregressive-realized volatility (HAR-RV) model by incorporating a two-period Markov regime-switching model to capture Taiwan’s economic expansion and contraction. Using Taiwan’s COVID-19 insurance-oversold events as a case–control setting, we compare the asymmetric jump risk effects on RV and realized semivariance (RSV). The results reveal that business cycle (BC) effects offset jump risk impacts, rendering intrinsic jump components statistically insignificant when BC information is omitted. During contraction periods, asymmetric jumps generate stronger negative RSV shocks, amplifying the leverage effect. Moreover, the predictive accuracy of RV critically depends on the prevailing business cycle state. By incorporating BC effects into the model, we recapture significant jump components and enhance volatility forecasting performance.

1. Introduction

Stock volatility plays a critical role in derivative pricing, hedging, portfolio selection, and risk management. As such, modeling and forecasting stock market volatility has become essential for academia, financial market participants, and policymakers. Tong et al. (2023) demonstrated that economic uncertainty amplifies market volatility and that the effects of such volatility depend on economic conditions and the degree of investor risk aversion. Yu et al. (2021) reported that global economic policy uncertainty considerably affects stock market volatility in emerging economies, and Boubaker et al. (2023) revealed that energy shocks, inflation, and other global uncertainties contribute to episodes of extreme volatility, with asymmetric effects that heighten systemic risk and cross-market contagion. Furthermore, Tran and Vo (2023) indicated that economic, policy, and financial uncertainty influence Asia-Pacific markets’ volatility, and the levels of such influence differ by market maturity and integration levels. In addition, Giudici and Pagnottini (2019) showed that high-frequency return and volatility spillovers evolve over time, highlighting the importance of capturing dynamic transmission effects when modeling market volatility and systemic risk. Economically, when financial markets encounter volatile shocks, the underlying assets’ prices typically exhibit jumps, thereby leading to an increase in asset volatility (Bollerslev et al. 2015). Buncic and Gisler (2017) investigated international equity indices and found that the jump risk effect had no relevant impact on market volatility. Dew-Becker and Giglio (2016) also showed a similar result under certain conditions. In contrast to Buncic and Gisler (2017), Zeng et al. (2022) found that the jump components of international equity indices were useful for predicting market volatility in international stock markets during the COVID-19 pandemic. Intuitive economic trends can explain the discrepancy between the results of Zeng et al. (2022) and those of Buncic and Gisler (2017). Stock prices react significantly and positively to bad news in economic contraction. However, negative stock news may have little influence on stock prices during economic expansion. Therefore, the state effect of the business cycle should be considered in the response behavior of stock prices. Hamilton and Lin (1996) proposed the regime-switching (RS) model and also confirmed this view. They concluded that economic recessions are the primary factor that drives fluctuations in stock returns and causes high volatility. Thus, the omission of the business cycle (BC) effect on volatility processes can lead to a significant bias in volatility forecasting.

This paper proposes an extended heterogeneous autoregressive (HAR) model that includes the BC effect. The HAR-type model not only can identify the RV as the short-, medium-, and long-term volatility components but also can decompose the RV into the continuous sample path and the discontinuous jump components. The former is called the HAR-RV-J model and the latter the HAR-RV-CJ model (Andersen et al. 2007b). The HAR-RV model has performed well empirically. Çelik and Ergin (2014) concluded that the HAR-RV model outperforms the GARCH process when predicting the volatility of the Turkish equity market. Though the HAR model is widely used by academic scholars, it still fails to show the significance of intrinsic significant jump parameters. Souček and Todorova (2014) found this problem of mis-identifying the intrinsic significant jump parameters as the insignificant ones and used a multivariate HAR model to solve this problem. In contrast, we solve this problem more effectively in our model by incorporating the BC effect into the HAR model.

Numerous studies use the HAR model to explore the relationship between the jump risk and leverage effects on RV (Xu and Wang 2017; Qu et al. 2018; Clements and Preve 2021; Bu et al. 2023). By including the leverage effect, Liu and Pan (2020) showed that negative returns are always more related to higher future volatility than are positive returns. The leverage effect is affected not only by good and bad news but also by the state of economic expansion and contraction (Halling et al. 2016; Nuno and Thomas 2017). The impact of negative returns on RV in economic contraction is significantly greater than that in economic expansion, implying that the BC effect has a strong correlation with the leverage effect. As a result, the leverage effect should be incorporated into the HAR model.

Because good and bad surprises cause different jump risk effects, RV is further defined as realized semivariance (RSV). We can use the extended HAR model to examine RSV, asymmetric jumps and the leverage effect. Audrino and Hu (2016) proposed a method of estimating quadratic changes and jump sizes in past volatility, classifying jumps into good and bad jump uncertainties. They find that bad jump risk is more informative than is good jump risk in predicting future volatility (Liang et al. 2021; Li et al. 2022). When volatility information is differentiated into good and bad news, the impact on the volatility of the state of the business cycle becomes more critical to identify that the impact of bad news on RV is greatly amplified in economic contraction. In addition, a downward jump also leads to a leverage effect (Souček and Todorova 2014; Liang et al. 2022). Specifically, when a shock causes a downward jump, it easily leads to negative returns and an increase in volatility, which causes a rise in feedback effects and leverage effects. In addition, the impact on financial markets of good and bad news was empirically found to be asymmetric. Patton and Sheppard (2015) decomposed RV into positive and negative intraday return volatility and found evidence of RSV. They also found that negative RSV has a more significant and lasting impact on future RV than does positive RSV. However, no other relevant literature examines the relationship between the BC effect and the asymmetric jump risk. To capture time-varying volatility, our model includes the two-period Markov regime-switching (MRS) effect.

To consider a different way of treating shocks, many researchers incorporate RS models into the time series framework, particularly within GARCH-type volatility models (Marcucci 2005). With parameters switching between low and high volatility regimes, the MRS-GARCH model demonstrates superior fitting performance relative to its single-regime counterparts (Zhang and Zhang 2023). Liang et al. (2022) also employed a Markov regime-switching (MRS) process in their model, incorporating a larger set of significant parameters to enhance volatility forecasting. It is recognized that the MRS framework captures more relevant and nuanced information, particularly in distinguishing the effects of good versus bad news. However, although this approach improves volatility forecast accuracy, it lacks macroeconomic interpretation and thus fails to reflect systemic responses to macroeconomic shocks. Our study addresses this important gap.

The challenge of verifying the impact of the BC effect on RV is that it is difficult to find a real scenario in which good news always occurs in expansion, while bad news always arises in contraction. We use the data from the Taiwan COVID-19 insurance-oversold event to construct a real scenario and utilize the data to construct a case–control study that includes a case group and a control group to create a scenario in which the BC effect is presented.

Data Description and Case–Control Study

The impact of surprises brought by the systemic risk of stock prices exhibits different responses to the state of the economy in expansion and in contraction. Boyd et al. (2005) found that an announcement of rising unemployment is good news to stock prices in economic expansion, and bad news in economic contractions. Their research showed that the stock market’s response to a macroeconomic surprise depends on the BC effect. In addition, Heinlein and Lepori (2022) documented that the effects of macroeconomic surprises are contingent not only upon the state of the economy but also on the state of the stock market. However, the financial econometric literature on realized volatility dynamics mostly ignores the important macroeconomic factors that affect the volatility pattern in the high-frequency domain due to the frequency mismatch. Karanasos and Yfanti (2020) used the high-frequency variables to replace the economic variables in the HEAVY model and showed that higher UK policy uncertainty increases the leverage effect and the macro effect on credit and commodity across European markets. Thus, frequency mismatch has been a problem in time series econometrics. Many monthly economic and financial indicators are often aggregated to align with quarterly macroeconomic series, such as Gross Domestic Product (Franco and Mapa 2014). Hence, when we construct a case–control study to examine how the BC effect can be integrated into the HAR model, we face three key challenges: Challenge 1, the same event must have occurred twice in the financial market; Challenge 2, the two event occurrences must take place in the distinct phases of the business cycle, that is, one in an expansion period and the other in a contraction period; Challenge 3, the scale of the event should be sufficiently significant to be representative, implicitly implying that it is an important significant event.

Taiwan’s COVID-19 insurance-oversold event is adopted in our empirical study because the event satisfies the three abovementioned conditions (or challenges). To verify the impact on the fall of Taiwan’s Financial Insurance Index (TFII) caused by Taiwan’s COVID-19 insurance-oversold events. The stratified analysis is used to ensure the accuracy of the empirical result, and the different states of Taiwan’s economy are regarded as the extraneous variables. The behavior of the TFII’s responses to each state is analyzed separately in the following sections.

During the COVID-19 period from year 2019 to 2021, Taiwan experienced a business cycle (discussed in subsequent sections), and the two COVID-19 insurance-oversold events also occurred in this period, in which the TFII was greatly influenced. To verify the BC effect using the HAR model, we construct a framework similar to a case–control study in which the TFII is regarded as a control group in Taiwan’s economic contraction, while the TFII in Taiwan’s economic expansion is a case group.

As noted above, Condition 1 is necessary to satisfy Condition 2. However, major events rarely repeat within a short time period in the financial market. Additionally, to examine the magnitude and direction of jumps, it is essential to have a control case for the stock market’s response to the identical events. Condition 2 is even more challenging to fulfill due to the relatively low frequency of the business cycle. To address this issue, we use the Taiwan Monitoring Indicator to represent Taiwan’s monthly business cycle, which has a high frequency relative to Taiwan’s GDP data. The COVID-19 insurance-oversold event in Taiwan from year 2019 to 2021 is a unique event and a special example that meets the abovementioned criteria.

Our study contributes to the literature from three significant perspectives. Firstly, we show how the BC effect can cause the intrinsic significant coefficients of the HAR model to become insignificant. This fact is usually ignored by former researchers. Secondly, using the case–control study of Taiwan’s COVID-19 insurance-oversold event, we find that a close relationship exists between the BC effect and asymmetric jumps. Thirdly, the existence of the BC effect strengthens the leverage effect, and then, through the feedback effect, the leverage effect increases the accuracy in forecasting the positive and negative RSV.

The rest of the paper is organized as follows. Section 2 provides the methodology and shows how to estimate jumps and asymmetric jumps based on the distinct stages of the business cycle. The data and Taiwan’s business cycle are described in Section 3, which also provides the case–control study and the shock scenario during Taiwan’s COVID-19 insurance-oversold event. Section 4 provides empirical results. The conclusion is given in Section 5.

2. Methodology and Model Setting

2.1. Realized Volatility, Bi-Power Variation, Jumps, and Stages of the Business Cycle

Consider a two-period MRS model (MRS-2) in which the variable $X_t$ is the unobservable state of a business cycle. In addition, the state of the business cycle follows a two-state Markov chain. The notations $X_t$ = 1 and $X_t$ = 2 represent, respectively, economic contraction and expansion. A two-state MRS process with a fixed transition probability matrix is presented as follows

$$p(X_t=j\left|X_{t-1}=j\right.)=p_{jj},p(X_t=i\left|X_{t-1}=j\right.)=p_{ji},\forall i,j=1,2,$$

where $p_{11}+p_{12}=p_{21}+p_{22}$ = 1. The stochastic process $X_t$ is a stationary process with $0<p_{ii}<1$, $\forall i=1,2$. Following Hamilton’s (1989) approach, Taiwan’s business cycle from 2018 to 2022 can be divided into two phases: expansion and contraction. For a detailed discussion, refer to Section 3.

Let $S_t{|}_{X_t}$ denote the stock price at time $t$ conditioned on the regime $X_t$, and assume that the stock price process evolves in continuous time as a jump-diffusion under the MRS-2 model

$$d\log S_t{|}_{X_t}=\mu {|}_{X_t}dt+\sigma {|}_{X_t}d{W}_t+J{|}_{X_t}d{q}_t,$$

(1)

where $\mu {|}_{X_t}$ and $\sigma {|}_{X_t}$ are the drift and diffusion terms conditioned on the regime $X_t$, $W_t$ is a standard Brownian motion, $q_t$ is a Poisson jump process with intensity $\lambda {|}_{X_t}$, and $J{|}_{X_t}$ refers to the corresponding log jump size distributed as normal $(\alpha {|}_{X_t},{\delta }^2{|}_{X_t})$. The continuous and jump components of all parameters, including the jump intensity, depend on Taiwan’s economic regime.

The intraday returns conditioned on the regime $X_t$ are defined as $r_i{|}_{X_t}=S_{\Delta }{|}_{X_t}-S_{(i-1)\Delta }{|}_{X_t}$, where $r_i{|}_{X_t}$ represents the i-th intra-day return on day t and $\Delta$ denotes the sampling frequency within each day. By following Andersen and Bollerslev (1998), realized variance (RV) conditioned on the regime $X_t$ is defined as follows:

$${\mathrm{RV}}_t{|}_{X_t}={\displaystyle \sum _{i=1}^N{r}_{t,i}^2}{|}_{X_t}.$$

(2)

We apply the same approach as proposed by Barndorff-Nielsen and Shephard (2004) to realize bi-power variance (BV). They prove that RV can be calculated using BV as $\Delta \to 0$, and realized bi-power variance conditioned on the regime $X_t$ is given as follows:

$${\mathrm{BV}}_t{|}_{X_t}={\displaystyle \frac{\pi }{2}}\left[{\displaystyle \frac{N}{N-2}}\right]{\displaystyle \sum _{i=2}^N\left|r_{t,i}{|}_{X_t}\right|}\left|r_{t,i-1{|}_{X_t}}\right|\mathrm{as}\Delta \to 0.$$

(3)

Additionally, they measure the contribution of jumps to the variation of asset prices using the following concepts: $\underset{\Delta \to 0}{\lim }{\mathrm{BV}}_t={\displaystyle {\int }_{t-1}^t{\sigma }_s^2}ds+{\displaystyle \sum _{t-1<s\le t}{J}_s^2}={\mathrm{CV}}_t+{\mathrm{JV}}_t$, where $J_s$ is the jump size; and ${\mathrm{CV}}_t$ and ${\mathrm{JV}}_t$ represent, respectively, the continuous and jump parts of realized variance. In other words, ${\mathrm{BV}}_t$ distinguishes jumps from continuous sample-path price movements. By incorporating the MRS-2 model into the jump part in realized variance and referring to Barndorff-Nielsen (2006) and Yi (2019), the jump statistics conditioned on the regime $X_t$ are expressed by

$$Z_t{|}_{X_t}={\Delta }^{-{\displaystyle \frac{1}{2}}}{\displaystyle \frac{({\mathrm{RV}}_t{|}_{X_t}-{\mathrm{BV}}_t{|}_{X_t}){\mathrm{RV}}_t{{|}_{X_t}}^{-1}}{\sqrt{(\frac{{\pi }^2}{4}+\pi -5)\max (1,\frac{{\mathrm{TQ}}_t{|}_{X_t}}{{({\mathrm{BV}}_t{|}_{X_t})}^2})}}},$$

(4)

where realized tri-power quarticity ${\mathrm{TQ}}_t{|}_{X_t}$ conditioned on the regime $X_t$ is equal to

$$\begin{gathered} {\mathrm{TQ}}_{t+1}{|}_{X_t}={\Delta }^{-1}{\mu }_{4/3}^{-3}{\displaystyle \sum _{i=3}^N{\left|r_{t+i\cdot \Delta ,\Delta }{|}_{X_t}\right|}^{4/3}{\left|r_{t+(i-1)\cdot \Delta ,\Delta }{|}_{X_t}\right|}^{4/3}{\left|r_{t+(i-2)\cdot \Delta ,\Delta }{|}_{X_t}\right|}^{4/3}}\mathrm{and} \\ {\mu }_p=2^{p/2}\cdot {\displaystyle \frac{\mathsf{\Gamma }(\raisebox{1ex}{$(p+1)$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}{\mathsf{\Gamma }(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.)}}. \end{gathered}$$

(5)

Please refer to Andersen et al. (2007b).

Let $1_{\left\{\cdot \right\}}$ be an indicator function. To make the jumps be non-negative, we follow Barndorff-Nielsen and Shephard (2004) and Andersen et al. (2007a) to provide the jump component (RJ) under the MRS-2 model as follows

$${\mathrm{RJ}}_t{|}_{X_t}=\max \left[{\mathrm{RV}}_t{|}_{X_t}-{\mathrm{BV}}_t{|}_{X_t},0\right]1_{\left\{Z_t{|}_{X_t}>{\varphi }_{\alpha }\right\}},$$

(6)

where ${\varphi }_{\alpha }$ is the distribution function of the normal distribution with the confidence level $\alpha$. After the Z-test of Equation (4), the estimated parameters of the jump components under the MRS-2 model which includes the jump frequency and the jump size mean. Jump size volatility is estimated as follows:

$$\stackrel{⌢}{\lambda }={\displaystyle \frac{\mathrm{Number}\mathrm{of}\mathrm{realized}\mathrm{jump}\mathrm{days}}{\mathrm{Number}\mathrm{of}\mathrm{total}\mathrm{trading}\mathrm{days}}};$$

(7)

$$\stackrel{⌢}{\alpha }=\mathrm{mean} \mathrm{of} \mathrm{realized} \mathrm{jumps};$$

(8)

$$\stackrel{⌢}{\delta }=\mathrm{standard} \mathrm{deviation} \mathrm{of} \mathrm{realized} \mathrm{jumps}.$$

(9)

2.2. Upside and Downside Realized Semivariance and State of the Business Cycle

By considering the asymmetric jump case with a regime shift, we extend the upside and downside realized semivariance (${\mathrm{RSV}}^{+}$ and ${\mathrm{RSV}}^{-}$), which are proposed by Barndorff-Nielsen et al. (2010). The ${\mathrm{RSV}}_t^{+}$ and ${\mathrm{RSV}}_t^{-}$ under the MRS-2 model are given by

$${\mathrm{RSV}}_t^{+}{|}_{X_t}={\displaystyle \sum _{i=1}^N{r}_{t,i}^2{|}_{X_t}}{1}_{\left\{r_{t,i}{|}_{X_t}>0\right\}}\mathrm{and}{\mathrm{RSV}}_t^{-}{|}_{X_t}={\displaystyle \sum _{i=1}^N{r}_{t,i}^2}{|}_{X_t}{1}_{\left\{r_{t,i}{|}_{X_t}<0\right\}}.$$

(10)

To capture the signed asymmetry of the volatility process, the continuous and jump variation are decomposed using intraday returns. Both the continuous variation ${\mathrm{CSV}}_t^{sign}{|}_{X_t}$ and the jump variation ${\mathrm{JSV}}_t^{sign}{|}_{X_t}$ can be decomposed into signed semivariation. Define the upside continuous variance conditioned on the regime $X_t$ as ${\mathrm{CSV}}_t^{+}{|}_{X_t}$ and the jump variance conditioned on the regime $X_t$ as ${\mathrm{JSV}}_t^{+}{|}_{X_t}$. Downside realized variance is defined in a similar way. Then ${\mathrm{RSV}}_t^{+}{|}_{X_t}={\mathrm{JSV}}_t^{+}{|}_{X_t}+{\mathrm{CSV}}_t^{+}{|}_{X_t}$ and ${\mathrm{RSV}}_t^{-}{|}_{X_t}={\mathrm{JSV}}_t^{-}{|}_{X_t}+{\mathrm{CSV}}_t^{-}{|}_{X_t}$.

To measure ${\mathrm{JSV}}_t^{+}{|}_{X_t}$ and ${\mathrm{JSV}}_t^{-}{|}_{X_t}$, we use the method provided by Audrino and Hu (2016). The proposed test statistic for jump existence is defined as

$$\begin{gathered} {\mathcal{L}}_{t,i}{|}_{X_t}={\displaystyle \frac{r_{t,i}{|}_{X_t}}{\sqrt{\frac{1}{K-1}{\displaystyle \sum _{u=1}^{K-1}\left|r_{t,i-u}{|}_{X_t}\right|\left|r_{t,i-u-1}{|}_{X_t}\right|}}}};W_N={\displaystyle \frac{1}{{\mu }_1{(2\log N)}^{\frac{1}{2}}}}; \\ {\beta }^{*}=-\log (-\log (1-\alpha )); \end{gathered}$$

$C_N={\displaystyle \frac{{(2\log N)}^{\frac{1}{2}}}{{\mu }_1}}-{\displaystyle \frac{\log \pi +\log (\log N)}{2{\mu }_1{(2\log N)}^{\frac{1}{2}}}}$; $K=\sqrt{270}$ and ${\mu }_1$ follows Equation (5).

The rejection region $\mathsf{\Theta }$ set is given by

$$\mathsf{\Theta }=\left\{\mathrm{the}\mathrm{arrival}\mathrm{time},i_u:1_{\left\{{\displaystyle \frac{\left|{\mathcal{L}}_{t,i}{|}_{X_t}\right|-C_N}{W_N}}>{\beta }^{*}\right\}}=1\right\}.$$

(11)

Assumption 1.

The rejection region is where the null of no jumps between time $(t,i-1)$ and $(t,i)$ is rejected, and suppose that $r_{t,i}$ is fully caused by a jump.

According to Assumption 1, if time t is in the rejection region, then Equation (11) can be rewritten under the MRS-2 model as follows:

$${\mathrm{JSV}}_t^{+}{|}_{X_t}={\displaystyle \sum _{s\in \mathsf{\Theta }}{r}_{t,s}^2{|}_{X_t}\cdot }{1}_{\left\{r_{t,s}{|}_{X_t}>0\right\}}\mathrm{and}{\mathrm{JSV}}_t^{-}{|}_{X_t}={\displaystyle \sum _{s\in \mathsf{\Theta }}{r}_{t,s}^2{|}_{X_t}\cdot }{1}_{\left\{r_{t,s}{|}_{X_t}<0\right\}}$$

(12)

Consequently, the continuous semivariance is estimated by

$$\left\{\begin{array}{c}{\mathrm{RSV}}_t^{sign}{|}_{X_t}={\mathrm{JSV}}_t^{sign}{|}_{X_t},{\mathrm{CSV}}_t^{sign}{|}_{X_t}=0,\mathrm{if}s\in \mathsf{\Theta },\forall sign=+,-\\ {\mathrm{RSV}}_t^{sign}{|}_{X_t}={\mathrm{CSV}}_t^{sign}{|}_{X_t},{\mathrm{JSV}}_t^{sign}{|}_{X_t}=0,\mathrm{if}s\notin \mathsf{\Theta },\forall sign=+,-\end{array}\right..$$

(13)

According to Equations (12) and (13), we calculate, respectively, ${\mathrm{RSV}}_t^{sign}{|}_{X_t}$, ${\mathrm{JSV}}_t^{sign}{|}_{X_t}$, and ${\mathrm{CSV}}_t^{sign}{|}_{X_t}$ in the economic contraction and expansion periods. And we extend the HAR-RV model to find whether RV prediction ability and asymmetric jumps show different behavior in the economic contraction and expansion periods.

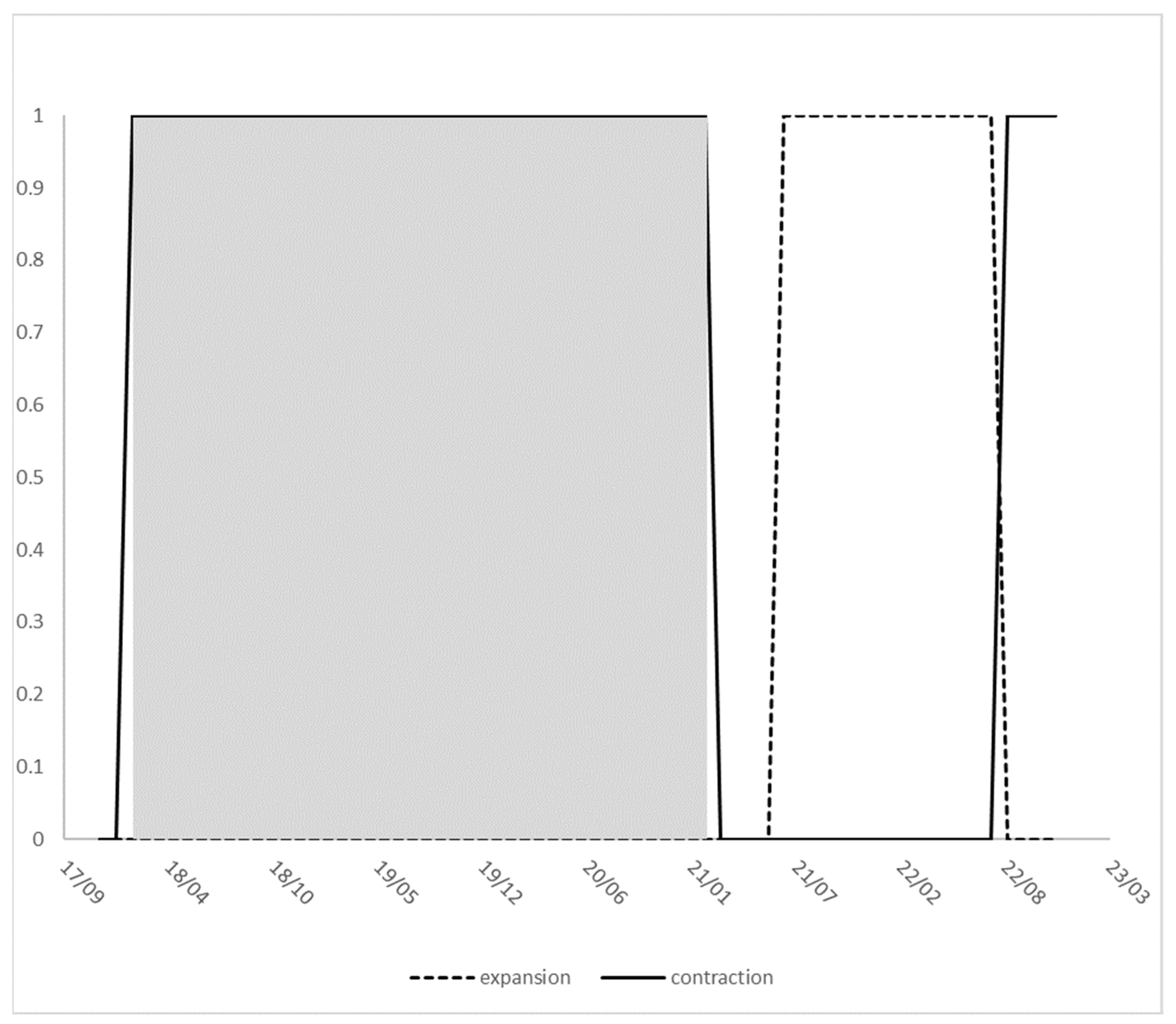
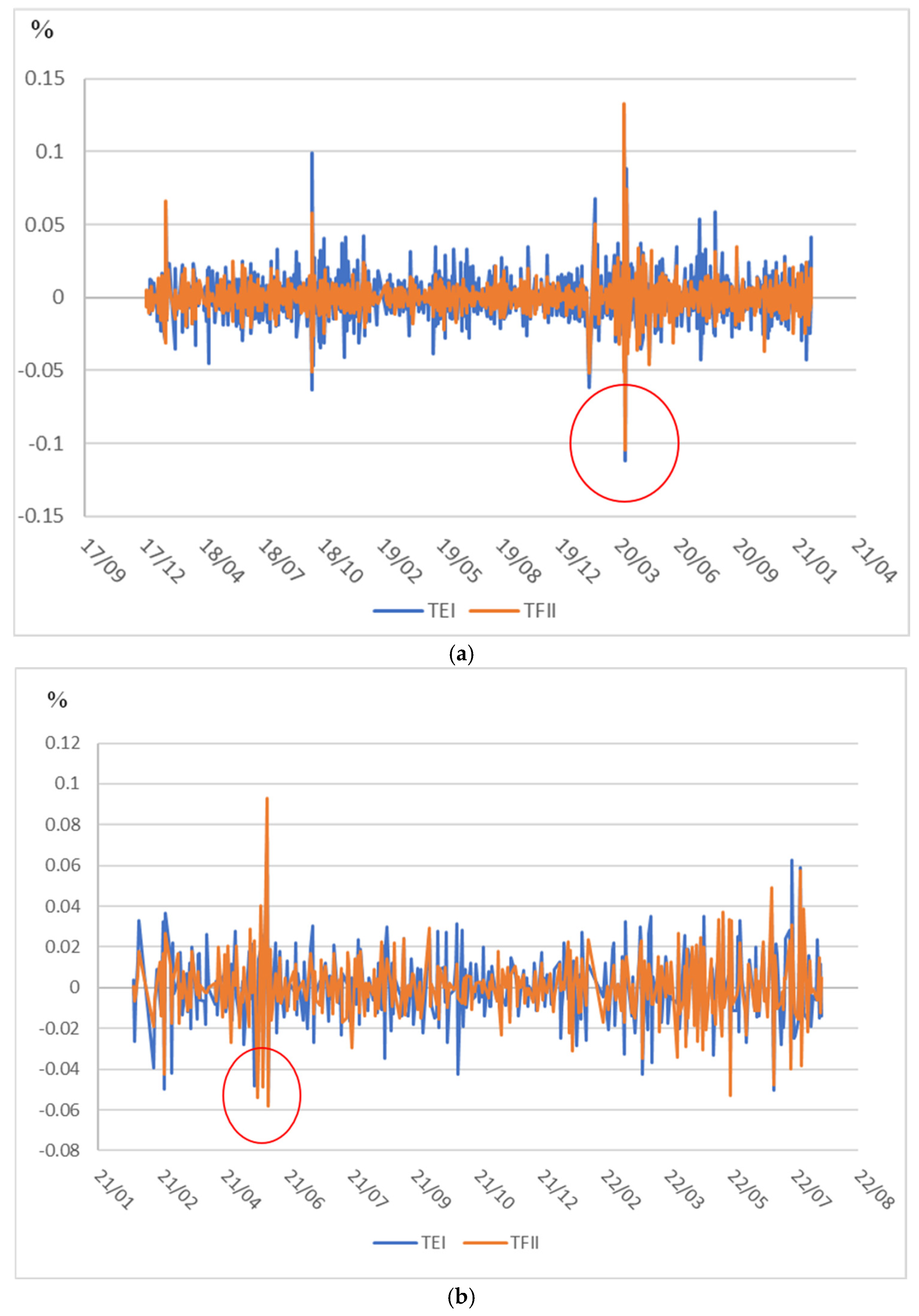
3. Data Description and Business Cycle Detection

The Taiwan Monitoring Indicator (TMI) is used to represent Taiwan’s business cycle. The TMI is issued by the National Development Council, and the frequency is monthly information. The TFII is drawn from the Taiwan Stock Exchange with a five-minute time frequency, which is high-frequency data. All data is drawn from 1 January 2018 to 31 December 2022.

We use the TMI to identify periods of economic expansion and contraction in Taiwan from 2018 to 2022, following the methodology of Hamilton (1989).1 The shaded area in Figure 1 indicates that the economic contraction ($X_t$ = 1) started from 1 January 2018 and continued to 31 January 2021, while the economic expansion ($X_t$ = 2) went from 1 February 2021 to 31 July 2022. To enhance transparency and data reproducibility, we provide summary descriptive statistics for key variables such as realized volatility (RV), bi-power variance (BV), realized jumps (RJs), and realized semivariances (CSV⁺, CSV⁻, JSV⁺, JSV⁻). These statistics correspond to periods of contraction and expansion and are reported in

Table A1. Descriptive statistics of volatility and jump measures during contraction period.

Variable	Mean	Std Dev	Min	Max
RJ	7.54 × 10−7	4.39 × 10−6	0	8.33 × 10−5
RV	1.39 × 10−5	3.03 × 10−5	9.74 × 10−7	0.000386
BV	1.45 × 10−5	3.25 × 10−5	1.16 × 10−6	0.000446
CSV+	3.68 × 10−6	9.48 × 10−6	1.16 × 10−7	0.00025
CSV−	5.08 × 10−6	1.70 × 10−5	2.81 × 10−7	0.00025
JSV+	2.91 × 10−6	3.57 × 10−7	0	0.000169
JSV−	4.29 × 10−6	6.39 × 10−7	0	0.00025

RJ, realized jumps; RV, realized volatility; BV, bi-power variance. ${\mathrm{CSV}}_{\mathrm{t}}^{+}$/${\mathrm{CSV}}_{\mathrm{t}}^{-}$ and ${\mathrm{JSV}}_{\mathrm{t}}^{+}$/${\mathrm{JSV}}_{\mathrm{t}}^{-}$ refer to positive and negative conditional and jump semivariances, respectively. All variables are reported as daily frequencies. In total, 697 observations are recorded during the contraction period.

and

Table A2. Descriptive statistics of volatility and jump measures during expansion period.

Variable	Mean	Std Dev	Min	Max
RJ	1.55 × 10−6	4.82 × 10−6	0	6.01 × 10−5
RV	3.24 × 10−5	6.26 × 10−5	2.09 × 10−6	0.001048
BV	3.41 × 10−5	6.74 × 10−5	1.63 × 10−6	0.001109
CSV+	0.000646	0.008806	−0.04904	0.031407
CSV−	8.20 × 10−6	1.76 × 10−5	5.83 × 10−7	0.000176
JSV+	9.90 × 10−6	3.00 × 10−5	7.20 × 10−7	0.000433
JSV−	7.40 × 10−6	1.74 × 10−5	0	0.000174

RJ, realized jumps; RV, realized volatility; BV, bi-power variance. ${\mathrm{CSV}}_{\mathrm{t}}^{+}$/${\mathrm{CSV}}_{\mathrm{t}}^{-}$ and ${\mathrm{JSV}}_{\mathrm{t}}^{+}$/${\mathrm{JSV}}_{\mathrm{t}}^{-}$ refer to positive and negative conditional and jump semivariances, respectively. All variables are reported as daily frequencies. In total, 367 observations are recorded during the expansion period.

. The statistics confirm that volatility and jump measures exhibit higher dispersion and intensity during contraction periods, a result that is consistent with the stronger downside risks present under adverse market conditions.

Shock Scenario Design During the COVID-19 Insurance Event

To identify the effects of asymmetric jumps during periods of economic expansion and contraction, the TFII is employed as the base index for the following reasons. One is that Taiwan’s COVID-19 insurance-oversold event (2018–2022) caused a substantial big fall in the stock market prices, thereby dragging down the insurance stock prices and causing a big drop in the value of insurance financial holdings. The other reason is that during the contraction period and the COVID-19 event, only one insurance company was affected, resulting in a loss of TWD 1.96 billion, which is considered a small shock. In contrast, Taiwan’s four large-scale insurance companies were affected during the expansion period, resulting in losses totaling TWD 169.3 billion, which is considered a large shock.2 The contraction period should exhibit a slight negative impact, while the expansion period should show a significant negative impact. In addition, Figure 2 shows the first-order differenced returns of the TSEC Electronics Index (TEI) and the TFII during periods of economic contraction and expansion, under the influence of other external factors (including pandemic severity and global market conditions).3

The red circle highlights the COVID-19 insurance-oversold event. During the economic contraction period, the blue line shows a larger negative value than the orange line, indicating that the TEI was more severely affected than the TFII in Figure 2a. In contrast, during the economic expansion period, the orange line exhibits a much larger negative value than the blue line, suggesting that only the TFII was affected in Figure 2b. In summary, the adverse changes in the TFII associated with the COVID-19 insurance-oversold event appear in both the economic contraction and expansion periods, though with varying degrees of impact between the two.

The following scenarios are used to illustrate the positive and negative jump terms of the jump semivariance.

Table 1. The explanation of the business cycle effect for the index on jumps.

	BC Effect	Large Shock	Net Effect	Case		BC Effect	Small Shock	Net Effect	Case
Contraction					Contraction
up-jump	0	--	--		up-jump	0	-	-	(c)
down-jump	--	--	----		down-jump	--	-	---	(d)
Expansion					Expansion
up-jump	++	--	0	(a)	up-jump	++	-	+
down-jump	-	--	---	(b)	down-jump	-	-	--

BC effect, business cycle effect; +, positive effect; -, small negative effect; --, large negative effect; ---, relatively large negative effect; ----, extremely large negative effect. ++, large positive effect; 0, no effect. Additional explanations of these notations are provided in the main text.

shows that good and bad surprises have a different effect on the stock prices in economic expansion and contraction. For example, a good surprise may have no effect (or little effect) on the stock prices in the contraction period. The notations in Table 1 also show that in the contraction period, the BC effect combined with the up-jump may have no effect on the stock prices, indicated by “0”, and the BC effect combined the down-jump strengthens the down-jump effect, denoted by “--”. On the other hand, an up-jump may exhibit no effect or even show the opposite effect when a negative impact appears in the expansion period, which is denoted by “--” in both expansion and contraction. The combination of a shock and BC effects determines the net effect, and so on. In addition, the notation “-” represents a negative effect, “+” denotes a positive effect, “-” represents a relatively small effect, “--” shows a relatively significant effect, and so on. If the “net effect” is denoted by zero, the index’s BC effect may offset the jump effect. Thus, Table 1 shows the eight possible cases under mutual interference between the shock and BC effect.

Additionally, recalling the outcome from the COVID-19 insurance event in real time, we have four cases (a)–(d). Noticeably, the regression coefficients show insignificant because the BC effect offsets the jump effect, which is the consequence of ignoring the BC effect in Cases (a) or (c). To avoid the two-effect mutual offset that results in insignificant jump coefficients, we identify the existence of the BC effect and compare our empirical results with other related studies in the literature.

4. Empirical Results

4.1. Examining Jumps in Economic Contraction/Expansion

Based on Equations (7)–(9), the descriptive statistics can be obtained in the expansion and contraction periods. The jump parameter set is represented as (${\stackrel{⌢}{\lambda }}_{con}$, ${\stackrel{⌢}{\lambda }}_{ex}$, ${\stackrel{⌢}{\alpha }}_{con}$, ${\stackrel{⌢}{\alpha }}_{ex}$, ${\stackrel{⌢}{\delta }}_{con}$, ${\stackrel{⌢}{\delta }}_{ex}$). The impact of the BC effect on realized jumps can be obtained by comparing the jump parameters.

Table 2. Descriptive statistics of variables for jump characteristics.

	$\stackrel{\mathbf{⌢}}{\mathit{\lambda }}$	$\stackrel{\mathbf{⌢}}{\mathit{\alpha }}$	$\stackrel{\mathbf{⌢}}{\mathit{\delta }}$
contraction	0.271	0.008	0.044
expansion	0.264	0.016	0.048

$\stackrel{⌢}{\lambda }$, ratio of realized jump days to total trading days; $\stackrel{⌢}{\alpha }$, mean of realized jumps; $\stackrel{⌢}{\delta }$, standard deviation of realized jumps; Except for $\stackrel{⌢}{\lambda }$, these variables are multiplied by 10⁴ for scaling.

shows that the jump intensity (${\stackrel{⌢}{\lambda }}_{con}$) in the contraction period is higher than that (${\stackrel{⌢}{\lambda }}_{ex}$) in the expansion period. Moreover, the average jump (${\stackrel{⌢}{\alpha }}_{ex}$) in the expansion period is higher than that (${\stackrel{⌢}{\alpha }}_{con}$) in the contraction period. The jump deviation ($\stackrel{⌢}{\delta }$) is similar between the two periods. The jump narrative statistics alone cannot explain the relationship between the jumps and expansion/contraction. The following test is used to show the differential impact of the jumps in the expansion and contraction periods. Bollerslev and Zhou (2006) showed a correlation between the stock returns and stock’s RV. Define ${\mathrm{R}}_t$ as the continuously compounded return from time $t$ to $t+\Delta$. We use lag-one RV as the explanatory variable, and RV is decomposed into realized bi-power variance (BV) and the realized jump (RJ). This implies

$$\left\{\begin{array}{ll}{\mathrm{R}}_t={\upsilon }^{con}+{\theta }_1^{con}\left(\log {\mathrm{BV}}_{t-1}\right)+{\theta }_2^{con}\left(\log {\mathrm{RJ}}_{t-1}\right)+{\epsilon }_t,& \mathrm{for}{X}_t=1\\ {\mathrm{R}}_t={\upsilon }^{ex}+{\theta }_1^{ex}\left(\log {\mathrm{BV}}_{t-1}\right)+{\theta }_2^{ex}\left(\log {\mathrm{RJ}}_{t-1}\right)+{\epsilon }_t,& \mathrm{for}{X}_t=2\end{array}\right.,$$

(14)

The null hypotheses are given by

$$H_0:{\upsilon }^{con}\ne {\upsilon }^{ex}$$

(15)

$$H_0:{\theta }_i^{con}\ne {\theta }_i^{ex}\mathrm{for}\mathrm{some}i.$$

(16)

If the null hypothesis is rejected, the stages of a business cycle can further be used to describe the relationship between RV and stock returns.

We use the interaction term test to verify whether or not the null hypothesis is rejected. The t values of BV and RJ are 0.4107 and −0.8072, respectively, in

Table 3. The estimated parameters of the relationship between returns and realized jumps.

	Contraction	Expansion
$\upsilon$	0.0016	0.0024
${\theta }_1$	0.0001	0.0002
${\theta }_2$	0.0000	−0.0001

$\upsilon$, ${\theta }_1$, and ${\theta }_2$ are parameters estimated from Equation (14); they are reported separately for contraction and expansion regimes.

. By using a two-tailed test, BV fails to reject the null hypothesis, while RJ rejects the null hypothesis. Therefore, when considering the effect of jumps on stock returns, we must consider the impact of the BC effect. Furthermore, the critical issue is to know whether economic expansion or contraction can strengthen or offset the jump effect. This issue is further tested by examining the asymmetric jumps; we predict that the downside jump is weakened in the expansion period and strengthened in the contraction period.

4.2. HAR-RV Type Model with a Latent Variable

After identifying and understanding the appropriate measures of volatility and the jump size, we are curious to explore how they contribute to the accuracy of forecasting future volatility. The proposed model is built upon the heterogeneous autoregressive (HAR) framework outlined in the reference and expands it to include semivariance, returns, and volatility jumps, as well as the influence of the business cycle on continuous returns and return jumps. We highlight the impact of the business cycle on future volatility and derive the HAR model. Thus, a new HAR-RSV model is proposed. In addition, the estimated results of our model are compared with those of Maki and Ota (2021). The notable difference between our model and their study is that our model incorporates the BC effect.

4.2.1. Realized Volatility, Jumps, and BC Effects

We extend the HAR-CJ model to the HAR-CJ-BC model (Model 1) by incorporating the BC effect, while the model with considering the BC and the asymmetric jump effects is called the HAR-AsyCJ-BC model (Model 2). We further extend it to the HAR-AsyCJ-BC-R model (Model 3) by incorporating the leverage effect.

Model 1: HAR-CJ-BC model

$$\left\{\begin{array}{l}\log {\mathrm{RV}}_{t+1}={\kappa }_0^{con}+{\gamma }_d^{con}\log {\mathrm{BV}}_t+{\gamma }_w^{con}\log {\mathrm{BV}}_{t-5}+{\gamma }_m^{con}\log {\mathrm{BV}}_{t-22}+{\rho }_d^{con}\log {\mathrm{RJ}}_t+{\epsilon }_{t+1},\mathrm{for}{X}_t=1\\ \log {\mathrm{RV}}_{t+1}={\kappa }_0^{ex}+{\gamma }_d^{ex}\log {\mathrm{BV}}_t+{\gamma }_w^{ex}\log {\mathrm{BV}}_{t-5}+{\gamma }_m^{ex}\log {\mathrm{BV}}_{t-22,}+{\rho }_d^{ex}\log {\mathrm{RJ}}_t+{\epsilon }_{t+1},\mathrm{for}{X}_t=2\end{array}\right.$$

(17)

where ${\gamma }_d$, ${\gamma }_w$, and ${\gamma }_m$ represent, respectively, the daily, weekly and monthly parameters of BV in the contraction and expansion periods; ${\rho }_d$ denotes the daily parameter of RJ which depends on economic contraction and expansion; ${\mathrm{BV}}_{t-5}={\displaystyle \frac{1}{5}}{\displaystyle {\sum }_{k=t-4}^t{\mathrm{BV}}_k}$; ${\mathrm{BV}}_{t-22}={\displaystyle \frac{1}{22}}{\displaystyle {\sum }_{k=t-21}^t{\mathrm{BV}}_k}$; and ${\epsilon }_{t+1}$ is the error term.

Table 4. The HAR-CJ model with BC effects.

Regression Coefficients	Contraction	Expansion
${\kappa }_0$	−1.588 ***	−2.727 ***
${\gamma }_d$	0.246 ***	0.319 ***
${\gamma }_w$	0.507 ***	0.466 **
${\gamma }_m$	0.116	−0.037
${\rho }_d$	−0.010 *	0.003

Parameters are estimated from Equation (17). ***, **, and * denote rejection of the null hypothesis at the 1%, 5%, and 10% significance levels, respectively. The subscript “d” stands for day, “w” for week, and “m” for month.

shows that the first three coefficients of Equation (17) are significant, and the sign direction in the contraction/expansion period is the same as the estimated results of Maki and Ota’s (2021) symmetric HAR model. In addition, the coefficient ${\rho }_d$ in the contraction period is significant at the 1% level. In contrast, the estimated coefficient of the jump is not significant in Maki and Ota’s (2021) symmetric HAR model. In fact, the positive coefficient is more reasonable for realized volatility, when the stock’s index encounters a shock, which indicates a need for further distinguishing up-jumps from down-jumps. The parameters of the five-day moving average, ${\gamma }_m$, are not significant in neither the contraction period nor the expansion period. The results indicate that the model poorly predicts monthly information. Because the monthly RV estimate is not significant, we drop the monthly parameter in the model that is presented in the next section.

4.2.2. Realized Volatility, Asymmetric Jumps, and Stages of the Business Cycle

Next, we consider the BC and asymmetric jump effects in the HAR model, and we differentiate the HAR-AsyCJ-BC model from Model 2-1 and Model 2-2. Equations (11)–(13) are used, respectively, to compute jump semivariance (JSV) and continuous semivariance (CSV). The estimated coefficients associated with g, b, d, and w are defined, respectively, as a good surprise, a bad surprise, and daily and weekly data.

Model 2-1

$$\left\{\begin{array}{ll}\log {\mathrm{RV}}_{t+1}={\kappa }_0^{con}+{\varphi }_{g,d}^{con}\log {\mathrm{CSV}}_t^{+}+{\varphi }_{b,d}^{con}\log {\mathrm{CSV}}_t^{-}+{\rho }_{g,d}^{con}\log {\mathrm{JSV}}_t^{+}+{\rho }_{b,d}^{con}\log {\mathrm{JSV}}_t^{-}+{\epsilon }_{t+1},& \mathrm{for}{X}_t=1\\ \log {\mathrm{RV}}_{t+1}={\kappa }_0^{ex}+{\varphi }_{g,d}^{ex}\log {\mathrm{CSV}}_t^{+}+{\varphi }_{b,d}^{ex}\log {\mathrm{CSV}}_t^{-}+{\rho }_{g,d}^{ex}\log {\mathrm{JSV}}_t^{+}+{\rho }_{b,d}^{ex}\log {\mathrm{JSV}}_t^{-}+{\epsilon }_{t+1},& \mathrm{for}{X}_t=2\end{array}\right.,$$

(18)

where ${\kappa }_0$ represents the intercept term; ${\varphi }_{g,d}$ and ${\varphi }_{b,d}$ represent, respectively, the daily good and bad surprise parameters of CSV; and ${\rho }_{g,d}$ and ${\rho }_{b,d}$ represent, respectively, the daily good and bad surprise parameters of JSV.

Model 2-2

$$\left\{\begin{array}{ll}\log {\mathrm{RV}}_{t+1}& ={\kappa }_0^{con}+{\varphi }_{g,d}^{con}\log {\mathrm{CSV}}_t^{+}+{\varphi }_{b,d}^{con}\log {\mathrm{CSV}}_t^{-}+{\varphi }_{g,w}^{con}\log {\mathrm{CSV}}_{t-5}^{+}+{\varphi }_{b,w}^{con}\log {\mathrm{CSV}}_{t-5}^{-}\\ & +{\rho }_{g,d}^{con}\log {\mathrm{JSV}}_t^{+}+{\rho }_{b,d}^{con}\log {\mathrm{JSV}}_t^{-}+{\epsilon }_{t+1},for{X}_t=1\\ \log {\mathrm{RV}}_{t+1}& ={\kappa }_0^{ex}+{\varphi }_{g,d}^{ex}\log {\mathrm{CSV}}_t^{+}+{\varphi }_{b,d}^{ex}\log {\mathrm{CSV}}_t^{-}+{\varphi }_{g,w}^{ex}\log {\mathrm{CSV}}_{t-5}^{+}+{\varphi }_{b,w}^{ex}\log {\mathrm{CSV}}_{t-5}^{-}\\ & +{\rho }_{g,d}^{ex}\log {\mathrm{JSV}}_t^{+}+{\rho }_{b,d}^{ex}\log {\mathrm{JSV}}_t^{-}+{\epsilon }_{t+1},for{X}_t=2\end{array}\right.,$$

(19)

where ${\mathrm{CSV}}_{t-5}^{sign}={\displaystyle \frac{1}{5}}{\displaystyle {\sum }_{k=t-4}^t{\mathrm{CSV}}_k^{sign}}$; ${\varphi }_{g,w}$ and ${\varphi }_{b,w}$ represent, respectively, the weekly good and bad surprise parameters of JSV.

Regardless of an expansion period or a contraction period, we expect that the RV under a bad surprise will be greater than that under a good surprise because shocks increase RV.

Table 5. The HAR-AsyCJ model with BC effects.

	Model 2-1		Model 2-2	Case		Case
	Contraction	Expansion	Contraction		Expansion
${\kappa }_0$	−4.1512 ***	−3.8979 ***	1.8710 **		1.5864
${\varphi }_{g,d}$	0.2819 ***	0.1909 ***	0.0227	(c)	−0.0004	(a)
${\varphi }_{b,d}$	0.2884 ***	0.3186 ***	0.0494	(d)	0.1626 **	(b)
${\varphi }_{g,w}$			0.3600 ***	(c)	0.4248 ***	(a)
${\varphi }_{b,w}$			0.5972 ***	(d)	0.3431 ***	(b)
${\rho }_{g,d}$	0.0038	0.0423	0.0045	(c)	0.0542	(a)
${\rho }_{b,d}$	0.0089	0.0049	0.0100	(d)	0.0132	(b)
R2	0.2043	0.1851	0.3450		0.2687
Adjusted R2	0.1997	0.1761	0.3393		0.2565

Parameters are estimated using Models 2-1 and 2-2. *** and ** denote rejection of the null hypothesis at the 1% and 5% significance levels, respectively. The subscripts g, b, d, and w represent good surprise, bad surprise, day, and week, respectively.

shows that ${\varphi }_{b,d}$ > ${\varphi }_{g,d}$ in the Model 2-1 no matter what the economic stage is, which is consistent with our expectation, and the results are significant at the 1% level. These test results are similar to those of the asymmetric model given in Maki and Ota (2021). In contrast, the jump components ${\rho }_{g,d}$ and ${\rho }_{b,d}$ are not significant in Model 2-1. Because the BC effect tends to be a long-term effect, asymmetric volatility persistence is considered in Model 2-2. The test result shows that the negative jump component increases RV, which also applies to ${\varphi }_{g,w}$ and ${\varphi }_{b,w}$ in the contraction period. However, several parameters in Model 2-2 are not significant. The opposite result occurs in the expansion period for Model 2-2, which indicates that the BC effect is greater than the jump risk effect in Case (a). Therefore, we have verified the fact that the BC effect can cause the intrinsic significant coefficient to become insignificant.

A large shock occurs in Cases (a) and (b) for the TFII in the expansion period, while a small shock appears in Cases (c) and (d) for the TFII in the contraction period. The test result of ${\varphi }_{b,w}^{ex}$ < ${\varphi }_{g,w}^{ex}$ in the expansion period indicates that the BC effect not only exists but is also even greater than the jump risk effect. The weekly good surprise parameter ${\varphi }_{b,w}^{con}$ in the contraction period is as high as 0.5972 despite a small shock, while the corresponding parameter ${\varphi }_{b,w}^{ex}$ in the expansion period is equal to 0.3431 for a large shock. The above evidence shows that the BC effect strengthens RV. In addition, the daily good surprise parameter ${\varphi }_{b,d}^{con}$ is equal to 0.1626 in the contraction period, which is lower in value compared with Maki and Ota (2021). The daily bad surprise parameter ${\varphi }_{b,d}^{ex}$ in the expansion period is clearly influenced by the BC effect. On the basis of the above empirical results, we conclude that when the BC effect is incorporated in our model, the coefficients in Cases (a) and (c) will be insignificant, including ${\varphi }_{g,d}$ and ${\rho }_{g,d}$ given in Model 2-2.

To solve the problem of causing insignificant coefficients, the leverage effect is incorporated into the HAR model to differentiate an up-jump from a down-jump, which is easy to show using the relationship between returns and leverage effects.

4.2.3. RV, Asymmetric Jumps, Leverage Effects, and States of the Business Cycle

Liang et al. (2022) showed that combining the realized volatility hybrid model with the RS model to predict the United States Oil Fund results in superior forecasts of RV. Intuitively, the leverage effect is more sensitive to returns than to RV in a regime shift. In this section, we incorporate the leverage effect into the HAR model. Similar to the previous subsection, we divide the HAR-AsyCJ-BC-R model into Model 3-1 and Model 3-2.

Model 3-1

$$\left\{\begin{array}{ll}\log {\mathrm{RV}}_{t+1}& ={\zeta }_0^{con}+{\zeta }_{g,d}^{con}\log {\mathrm{CSV}}_t^{+}+{\zeta }_{b,d}^{con}\log {\mathrm{CSV}}_t^{-}+{\rho }_{g,d}^{con}\log {\mathrm{JSV}}_t^{+}+{\rho }_{b,d}^{con}\log {\mathrm{JSV}}_t^{-}\\ & +{\varsigma }_1^{con}\left|{\mathrm{R}}_t\right|+{\varsigma }_2^{con}\left(\left|{\mathrm{R}}_t\right|1_{\left\{R_t<0\right\}}\right)+{\epsilon }_{t+1},for{X}_t=1\\ \log {\mathrm{RV}}_{t+1}& ={\zeta }_0^{ex}+{\zeta }_{g,d}^{ex}\log {\mathrm{CSV}}_t^{+}+{\zeta }_{b,d}^{ex}\log {\mathrm{CSV}}_t^{-}+{\rho }_{g,d}^{ex}\log {\mathrm{JSV}}_t^{+}+{\rho }_{b,d}^{ex}\log {\mathrm{JSV}}_t^{-}\\ & +{\varsigma }_1^{ex}\left|{\mathrm{R}}_t\right|+{\varsigma }_2^{ex}\left(\left|{\mathrm{R}}_t\right|1_{\left\{R_t<0\right\}}\right)+{\epsilon }_{t+1},for{X}_t=2\end{array}\right.,$$

(20)

where ${\zeta }_0$ represents the intercept term; ${\zeta }_{g,d}$ and ${\zeta }_{b,d}$ represent, respectively, the daily good and bad surprise parameters of CSV; ${\rho }_{g,d}$ and ${\rho }_{b,d}$ represent, respectively, the daily good and bad surprise parameters of JSV; ${\varsigma }_1$ represents the daily return; and ${\varsigma }_2$ denotes the daily bad surprise return.

Model 3-2

$$\left\{\begin{array}{c}\begin{array}{ll}\log {\mathrm{RV}}_{t+1}& ={\zeta }_0^{con}+{\zeta }_{g,d}^{con}\log {\mathrm{CSV}}_t^{+}+{\zeta }_{b,d}^{con}\log {\mathrm{CSV}}_t^{-}+{\zeta }_{g,w}^{con}\log {\mathrm{CSV}}_{t-5}^{+}+{\zeta }_{b,w}^{con}\log {\mathrm{CSV}}_{t-5}^{-}\\ & +{\rho }_{g,d}^{con}\log {\mathrm{JSV}}_t^{+}+{\rho }_{b,d}^{con}\log {\mathrm{JSV}}_t^{-}+{\varsigma }_1^{con}\left|{\mathrm{R}}_t\right|+{\varsigma }_2^{con}\left(\left|{\mathrm{R}}_t\right|1_{\left\{R_t<0\right\}}\right)+{\epsilon }_{t+1},for{X}_t=1\end{array}\\ \begin{array}{ll}\log {\mathrm{RV}}_{t+1}& ={\zeta }_0^{ex}+{\zeta }_{g,d}^{ex}\log {\mathrm{CSV}}_t^{+}+{\zeta }_{b,d}^{ex}\log {\mathrm{CSV}}_t^{-}+{\zeta }_{g,w}^{ex}\log {\mathrm{CSV}}_{t-5}^{+}+{\zeta }_{b,w}^{ex}\log {\mathrm{CSV}}_{t-5}^{-}\\ & +{\rho }_{g,d}^{ex}\log {\mathrm{JSV}}_t^{+}+{\rho }_{b,d}^{ex}\log {\mathrm{JSV}}_t^{-}+{\varsigma }_1^{ex}\left|{\mathrm{R}}_t\right|+{\varsigma }_2^{ex}\left(\left|{\mathrm{R}}_t\right|1_{\left\{R_t<0\right\}}\right)+{\epsilon }_{t+1},for{X}_t=2\end{array}\end{array}\right.,$$

(21)

where ${\zeta }_{g,w}$ and ${\zeta }_{b,w}$ represent, respectively, the weekly good and bad surprise parameters of CSV.

The leverage effect shows that volatility is correlated with lagged negative returns and bad surprise has a greater impact on returns than does good surprise. So, we expect the result ${\varsigma }_1+{\varsigma }_2>{\varsigma }_2$.

Table 6. The results of the HAR-AsyCJ-BC-R model.

	Model 3-1		Model 3-2
	Contraction	Expansion	Contraction	Expansion
${\zeta }_0$	−5.9785 ***	−5.3284 ***	−0.2653	−0.6854
${\zeta }_{g,d}$	0.2583 ***	0.1412 *	0.0277	−0.0096
${\zeta }_{b,d}$	0.1942 ***	0.2856 ***	0.3451 ***	0.3361 ***
${\zeta }_{g,w}$			−0.0010	0.1558 ***
${\zeta }_{b,w}$			0.5123 ***	0.2979 ***
${\rho }_{g,d}$	0.0081	0.0470	0.0078	0.0559 *
${\rho }_{b,d}$	0.0028	−0.0057	0.0051	0.0025
${\varsigma }_1$	56.0609 ***	48.8531 ***	43.9546 ***	44.1281 ***
${\varsigma }_2$	28.2129 **	19.8264 **	29.0156 ***	17.3063 **
R2	0.3098	0.3139	0.4186	0.3697
Adujst R2	0.3038	0.3024	0.4118	0.3556

Parameters are estimated from Equations (19) and (20). ***, **, and * denote rejection of the null hypothesis at the 1%, 5%, and 10% significance levels, respectively. The subscripts g, b, d, and w represent good surprise, bad surprise, day, and week, respectively.

shows that Model 3-1 and Model 3-2 in both the contraction and expansion periods satisfy the abovementioned characteristics of the leverage effect. In addition, the daily return parameter ${\varsigma }_1$ and the daily bad surprise parameter ${\varsigma }_2$ are statistically significant. Because a massive shock to the TFII occurs when $X_t=2$, the daily bad surprise parameter ${\varsigma }_2$ in the expansion period (${\varsigma }_2^{ex}$) should be greater than that in the contraction period (${\varsigma }_2^{con}$). However, the daily bad surprise parameter (${\varsigma }_2^{ex}$) in the expansion period is smaller than the corresponding parameter (${\varsigma }_2^{con}$) in magnitude in the contraction period, implying that the BC effect offsets the impact on negative returns of the down-jump. This result is consistent with our previous educated guess where Case (a) or Case (c) occurs, and the parameters ${\zeta }_{g,d}^{con}$, ${\zeta }_{g,w}^{ex}$, and ${\rho }_{g,d}^{con}$ are statistically insignificant, while the parameter ${\rho }_{g,d}^{ex}$ is significantly positive, indicating that the BC effect is more significant than is the jump effect. This result leads to the insignificant correlation between the daily bad surprise jump parameter ${\rho }_{b,d}^{ex}$ and the good surprise jump parameter ${\rho }_{b,d}^{con}$. As a result, if the BC effect is excluded in the model, a bias arises in examining the relationship between volatility and jump risk, thereby causing a failure to capture the intrinsic significant jump components.

In summary, our study has shown that the incorporation of the BC effect in the HAR-AsyCJ-BC-R model can explain the reason behind the cause of the insignificant coefficients and recapture the intrinsic significant jump risk component.

5. Conclusions

Studying the effects of jump risk and asymmetric jump risk across business cycle phases has long been constrained by the frequency mismatch between macroeconomic indicators and high-frequency financial data. We address this challenge by leveraging a rare natural experiment: Taiwan’s COVID-19 insurance-oversold event, which occurred during both economic expansion and contraction. This setting enables the construction of a case–control framework to examine the differential effects of systemic jump shocks under distinct business cycle states.

To empirically validate this framework, we employ three variations of the HAR model that incorporate latent variables. Using interaction term tests, we confirm the presence of asymmetric jumps that depend on the state of the economy. Comparing Model 1 with Model 2 highlights the critical role of the business cycle effect in recovering statistically significant jump components. Moreover, comparing Model 2 with Model 3 reveals that the business cycle effect significantly amplifies the leverage effect, particularly during economic contractions. In addition to its econometric contributions, this study holds several crucial implications for financial practitioners and regulators. Specifically, the amplified downside jumps observed in our results during economic contractions suggest that insurers, portfolio managers, and risk officers should employ state-dependent volatility models—such as the proposed HAR-AsyCJ-BC-R framework—to effectively capture asymmetric jump risks. Incorporating macroeconomic indicators such as the TMI or policy uncertainty indices can increase the accuracy of real-time volatility forecasts and stress-testing outcomes. Our findings also indicate that ignoring cyclical asymmetries may lead to systematic underestimation of the downside risk in expansionary phases. Therefore, regulators and supervisors should integrate regime-switching dynamics into macroprudential policy and capital buffers to strengthen financial systems’ resilience. These insights underscore the value of using econometric modeling to enhance policy-oriented applications in dynamic financial environments.

In summary, our findings demonstrate that ignoring the business cycle effect can lead to a misestimation of both jump components and leverage effects. Future studies on volatility and jump risk should explicitly incorporate business cycle regimes, especially when modeling high-frequency data under macroeconomic shocks. Incorporating the business cycle effect allows for more accurate realized volatility forecasts, which, in turn, can enhance empirical research in areas such as option pricing and risk management. Additionally, our findings suggest that similar methodologies can be extended to other financial markets, including bonds and commodities such as oil, where business cycle sensitivity may also play a critical role.

This study has several limitations. First, integrating macroeconomic and high-frequency financial data results in an inherent frequency mismatch that renders the alignment of low-frequency indicators with high-frequency market variables a challenging process. Second, the identification of business cycle phases often depends on ex post statistical determinations, which may not capture dynamic shifts in real time. Third, the lack of synchronization across national or market-specific cycles complicates cross-market analysis. Finally, the model may not be robust or generalizable to other markets because of differences in the microstructure, driving forces, and responses to macroeconomic shocks. These limitations highlight the need for further refinement and indicate directions for future research to enhance real-time business cycle detection, increase robustness across heterogeneous markets, and link empirical results more directly to policy and risk management practices.