Extending Approximate Bayesian Computation to Non-Linear Regression Models: The Case of Composite Distributions

Abstract

Modeling loss data is a crucial aspect of actuarial science. In the insurance industry, small claims occur frequently, while large claims are rare. Traditional heavy-tail distributions, such as Weibull, Log-Normal, and Inverse Gaussian distributions, are not suitable for describing insurance data, which often exhibit skewness and fat tails. The literature has explored classical and Bayesian inference methods for the parameters of composite distributions, such as the Exponential–Pareto, Weibull–Pareto, and Inverse Gamma–Pareto distributions. These models effectively separate small to moderate losses from significant losses using a threshold parameter. This research aims to introduce a new composite distribution, the Gamma–Pareto distribution with two parameters, and employ a numerical computational approach to find the maximum likelihood estimates (MLEs) of its parameters. A novel computational approach for a nonlinear regression model where the loss variable is distributed as the Gamma–Pareto and depends on multiple covariates is proposed. The maximum likelihood (ML) and Approximate Bayesian Computation (ABC) methods are used to estimate the regression parameters. The Fisher information matrix, along with a multivariate normal distribution as the prior distribution, is utilized through the ABC method. Simulation studies indicate that the ABC method outperforms the ML method in terms of accuracy.

1. Introduction

Creating an accurate loss model for insurance data is a vital topic in actuarial science. Insurance industry data have distinct characteristics, including a high frequency of small losses and a scarcity of significant losses. Traditional heavy-tailed distributions often struggle to capture the skewness and fat-tailed properties inherent in insurance data. As a result, many researchers have explored alternative distributions to better fit the loss data. One promising approach is the use of composite distributions, which combine a standard distribution with positive support, such as the Exponential, Inverse Gaussian, Inverse Gamma, Weibull, and Log-Normal distributions for minor losses, with the Pareto distribution, which accounts for extreme losses that occur infrequently.

Klugman et al. (2012) provided a comprehensive discussion on modeling data sets in actuarial science. Teodorescu and Vernic (2006) examined the Exponential–Pareto composite model and derived the maximum likelihood estimator for the threshold parameter $\theta$. Preda and Ciumara (2006) utilized the composite models Weibull–Pareto and Log-Normal-Pareto to analyze insurance losses. The models described in the article have two key parameters: the support parameter, denoted as $\theta$, and the threshold parameter, represented by $\alpha$. The authors developed algorithms to find and compare the maximum likelihood estimates (MLEs) for these two unknown parameters. In their work, Cooray and Cheng (2013) estimated the parameters of the Log-Normal-Pareto composite distribution using Bayesian methods, employing both Jeffreys and conjugate priors. They opted for Markov Chain Monte Carlo (MCMC) methods instead of deriving closed mathematical formulas. Additionally, Scollnik and Sun (2012) developed several composite Weibull–Pareto models. Aminzadeh and Deng (2018) revisited the composite Exponential-Pareto distribution and provided a Bayesian estimate of the threshold parameter using an inverse-gamma prior distribution. Additionally, Bakar et al. (2015) introduced several new composite models based on the Weibull distribution, specifically designed for analyzing heavy-tailed insurance loss data. These models were applied to two real insurance loss data sets, and their goodness-of-fit was evaluated. Furthermore, Deng and Aminzadeh (2023) recently examined a mixture of prior distributions for the Exponential-Pareto and Inverse Gamma–Pareto composite models.

Teodorescu and Vernic (2013) developed the composite Gamma-Type II Pareto model and derived the composite Gamma–Pareto as its special case, which has three free parameters. However, the new composite Gamma–Pareto model proposed in this article has only two free parameters, which makes it a more desirable model to work with, particularly when used for regression modeling. This means that fewer parameters need to be estimated using a data set. Cooray and Ananda (2005) introduce a two-parameter composite Log-Normal-Pareto model and utilizes the model to analyze fire insurance data. Additionally, Scollnik (2007) discusses limitations of the composite Log-Normal-Pareto model in Cooray and Ananda (2005) and presents two different composite models based on the Log-Normal and Pareto models to address the concerns. In this article, the performance of the three composite models is discussed and compared using the fire insurance data set. More recently, Grün and Miljkovic (2019) provides a comprehensive analysis of composite loss models on the Danish fire losses data set, derived from 16 parametric distributions commonly used in actuarial science; however, the Gamma–Pareto composite model proposed in the current article is not among the best 20 fitting composite models for the fire data listed in Grün and Miljkovic (2019).

There has been limited research on regression models for composite distributions. Konşuk Ünlü (2022) considered a composite Log-Normal-Pareto Type II regression model; however, their estimation of the regression parameters relied on the Particle Swarm Optimization method to analyze household budget data. Furthermore, Bayesian inference was not addressed in that study. In contrast, the method proposed in the current article provides accurate estimates of regression parameters by directly optimizing the likelihood function using Mathematica code specifically written for this research. Additionally, the proposed method can be applied more generally to other composite distributions beyond the Gamma–Pareto composite, which serves as the example in this article.

This article presents an innovative computational tool for efficiently finding the MLEs and approximate Bayes estimates of regression parameters using the ABC algorithm, particularly when the response variable Y is linked to multiple covariates.

In Section 2, we introduce a new composite Gamma–Pareto distribution which has only two parameters. We demonstrate that the smoothness conditions of its density function allow us to simplify four parameters into a two-parameter probability density function (PDF). Additionally, we outline a numerical maximization approach for accurately computing the MLEs. Section 3 formulates the likelihood function in a regression context, establishing connections between the response variable and covariates. In Section 4, we apply a numerical optimization method and the Fisher information matrix with Mathematica to compute the MLEs of the regression parameters, ensuring reliable estimates throughout our analysis.

Section 5 discusses the ABC algorithm for estimating regression parameters. This algorithm utilizes the Fisher information matrix and assumes a multivariate normal distribution as the prior, generating a large number of samples. The samples that are “accepted” represent the posterior distribution and are used to compute the approximate Bayesian estimates. This section also outlines the steps necessary to calculate both the MLEs and ABC-based estimates for the regression parameters. A summary of the simulation results is provided in Section 6. Section 7 presents a Chi-Square test for evaluating the goodness of fit of a data set generated from the composite Pareto model. Section 8 provides a real data set labeled as “Total Auto Claims in Thousands of Swedish Kronor”. For this data, the Chi-Square test is also applied to assess how well the claims fit the Gamma–Pareto model. Mathematica codes, labeled B–D, are included in the Supplementary Materials, and Mathematica code A for the simulations involved in the regression model is available upon request.

2. Derivation of Gamma–Pareto Composite Distribution

The single-parameter exponential dispersion family (EDF) pdf for a random variable Y is given by

$$f(y|\theta )=exp\left[[{\displaystyle \frac{y\theta -b(\theta )}{\varphi }}]+c(y,\varphi )\right]$$

where $b:\mathsf{\Theta }\to \mathbb{R}$ is the cumulant functin, $\theta \in \mathsf{\Theta }$ is the canonocal parameter, $\varphi >0$ is the dispersion parameter, and $c(.;.)$ is the normalization not depending on $\theta$. Note that $\mu =E[Y]=b^{\prime }(\theta )$. Let $Y\sim \mathrm{gamma}(\alpha ,b)$ with the PDF

$$f(y|\alpha ,\gamma )={\displaystyle \frac{{\gamma }^{\alpha }}{\mathsf{\Gamma }(\alpha )}}{y}^{\alpha -1}{e}^{-\gamma y}, \alpha >0, \gamma >0,$$

and assume $\alpha$ is known. It can be shown that choosing $\varphi ={\displaystyle \frac{1}{\alpha }}, \theta =-{\displaystyle \frac{\gamma }{\alpha }}$, we get $b(\theta )=-ln(-\theta ), c(y,\varphi )=(\alpha -1)ln(y)-ln(\mathsf{\Gamma }(\alpha )+\alpha ln(\alpha )$. As a result, $b^{\prime }(\theta )=-{\displaystyle \frac{1}{\theta }}=\mu$, our canonical link is $-{\displaystyle \frac{1}{\mu }}$, and $\theta$ is the canonical parameter. Therefore, the PDF of the gamma distribution with this canonical parameterization can be written as

$$f(y|\theta ,\alpha )={\displaystyle \frac{{(-\theta \alpha )}^{\alpha }{y}^{\alpha -1}{e}^{\theta \alpha y}}{\mathsf{\Gamma }(\alpha )}}\alpha >0,\theta <0$$

which will be used in developing the Gamma–Pareto composite model proposed in the article. It is worth mentioning that with this parameterization, $\theta$ takes negative values.

In the following, we derive the PDF of the proposed Gamma–Pareto model. Let Y be a random variable with the probability density function

$$f_Y(y)=\left\{\begin{array}{cc}c{f}_1(y)\hfill & 0<y\le \rho \hfill \\ c{f}_2(y)\hfill & \rho \le y<\infty \hfill \end{array}\right.$$

where

$$f_1(y)={\displaystyle \frac{{(-\theta \alpha )}^{\alpha }{y}^{\alpha -1}{e}^{\theta \alpha y}}{\mathsf{\Gamma }(\alpha )}}0<y\le \rho ,\alpha >0,\theta <0$$

and

$$f_2(y)={\displaystyle \frac{\eta {\rho }^{\eta }}{y^{\eta +1}}}y\ge \rho .$$

The derivation of the normalizing constant c, which can be found via

$$c^{-1}={\int }_0^{\rho }{f}_1(y)dy+{\int }_{\rho }^{\infty }{f}_2(y)dy,$$

is shown below after reducing the number of parameters from four to two. $f_1(y)$ is the PDF of the Gamma distribution based on the canonical parametrization mentioned earlier with the parameters $\alpha$ and $\theta$. $f_2(y)$ is the PDF of the Pareto distribution with parameters $\eta$ and $\rho$. The advantages of the canonical parametrization for the gamma distribution are twofold: 1. It enables us to include a dispersion parameter $\varphi$ which is related to $\alpha$ through $\alpha ={\displaystyle \frac{v}{\varphi }}$, where v is the exposure or given weight. Without loss of generality, it is common to let $v=1$. Note that the smaller the $\varphi$ value, the larger the $\alpha$ value. Therefore, the selected value $\alpha$ controls the variation in the data. 2. The likelihood function becomes unimodal with a unique global maximum.

To ensure the smoothness of the composite density function, it is assumed that the two probability density functions are continuous and differentiable at $\rho$. That is,

$$f_1(\rho )=f_2(\rho ),f_1^{\prime }(\rho )=f_2^{\prime }(\rho ).$$

The equation $f_1(\rho )=f_2(\rho )$ leads to

$${\displaystyle \frac{{(-\theta \alpha )}^{\alpha }{\rho }^{\alpha -1}{e}^{\theta \alpha \rho }}{\mathsf{\Gamma }(\alpha )}}={\displaystyle \frac{\eta }{\rho }},$$

and as a result,

$$\eta ={\displaystyle \frac{{(-\theta \alpha )}^{\alpha }{\rho }^{\alpha }{e}^{\theta \alpha \rho }}{\mathsf{\Gamma }(\alpha )}}.$$

(1)

Using $f_1^{\prime }(\rho )=f_2^{\prime }(\rho )$, we have

$${\displaystyle \frac{{(-\theta \alpha )}^{\alpha }}{\mathsf{\Gamma }(\alpha )}}[(\alpha -1){\rho }^{\alpha }{e}^{\alpha \theta \rho }+\alpha \theta e^{\alpha \theta \rho }{\rho }^{\alpha +1}]=-\eta (\eta +1).$$

Using Equation (1) in the above equation, we obtain

$$\eta =-\alpha (1+\rho \theta ).$$

(2)

Equating (1) and (2) leads to

$${\displaystyle \frac{{(-\theta \alpha )}^{\alpha }{\rho }^{\alpha }{e}^{\theta \alpha \rho }}{\mathsf{\Gamma }(\alpha )}}=-\alpha -\alpha \rho \theta .$$

(3)

Letting $w=\alpha \rho \theta$, the above equation can be rewritten as

$${\displaystyle \frac{{(-w)}^{\alpha }{e}^w}{\mathsf{\Gamma }(\alpha )}}=-(\alpha +w).$$

(4)

For a selected value of $\alpha$, non-linear Equation (4), which has two solutions, can be solved for w via Mathematica. For example, if $\alpha =1.2$, the negative solution is $w=-1.5876$, and for $\alpha =1.6$, the negative solution is $w=-2.0539$. Note that the acceptable solution to (4) must be negative, as $\theta <0, \alpha >0$, and $\rho >0$. Using $w=\alpha \rho \theta$, we have $\psi =\rho \theta ={\displaystyle \frac{w}{\alpha }}$. Since for any value of $\alpha$, as mentioned, w is a function of $\alpha$ through (4), it is concluded that $\psi =\rho \theta$ is a negative number, which is only a function of $\alpha$.

It can be shown that the normalizing constant c for the Gamma–Pareto can be written as

$$c={\displaystyle \frac{\mathsf{\Gamma }(\alpha )}{2\mathsf{\Gamma }(\alpha )-\mathsf{\Gamma }(\alpha ,-w)}},$$

where $\mathsf{\Gamma }(\alpha )$ is the gamma function and $\mathsf{\Gamma }(\alpha ,-w)$ is the upper incomplete gamma function. Both functions can be computed via Mathematica. Since w is a function of $\alpha$, c is a constant that does not depend on $\theta$ or $\rho$. Therefore, the composite Gamma–Pareto density function is given by

$$f_Y(y)=\left\{\begin{array}{cc}{\displaystyle \frac{c{(-\theta \alpha )}^{\alpha }{y}^{\alpha -1}{e}^{\theta \alpha y}}{\mathsf{\Gamma }(\alpha )}}\hfill & 0<y\le \rho \hfill \\ {\displaystyle \frac{c\eta {\rho }^{\eta }}{y^{\eta +1}}}\hfill & \rho \le y<\infty \hfill \end{array}\right.$$

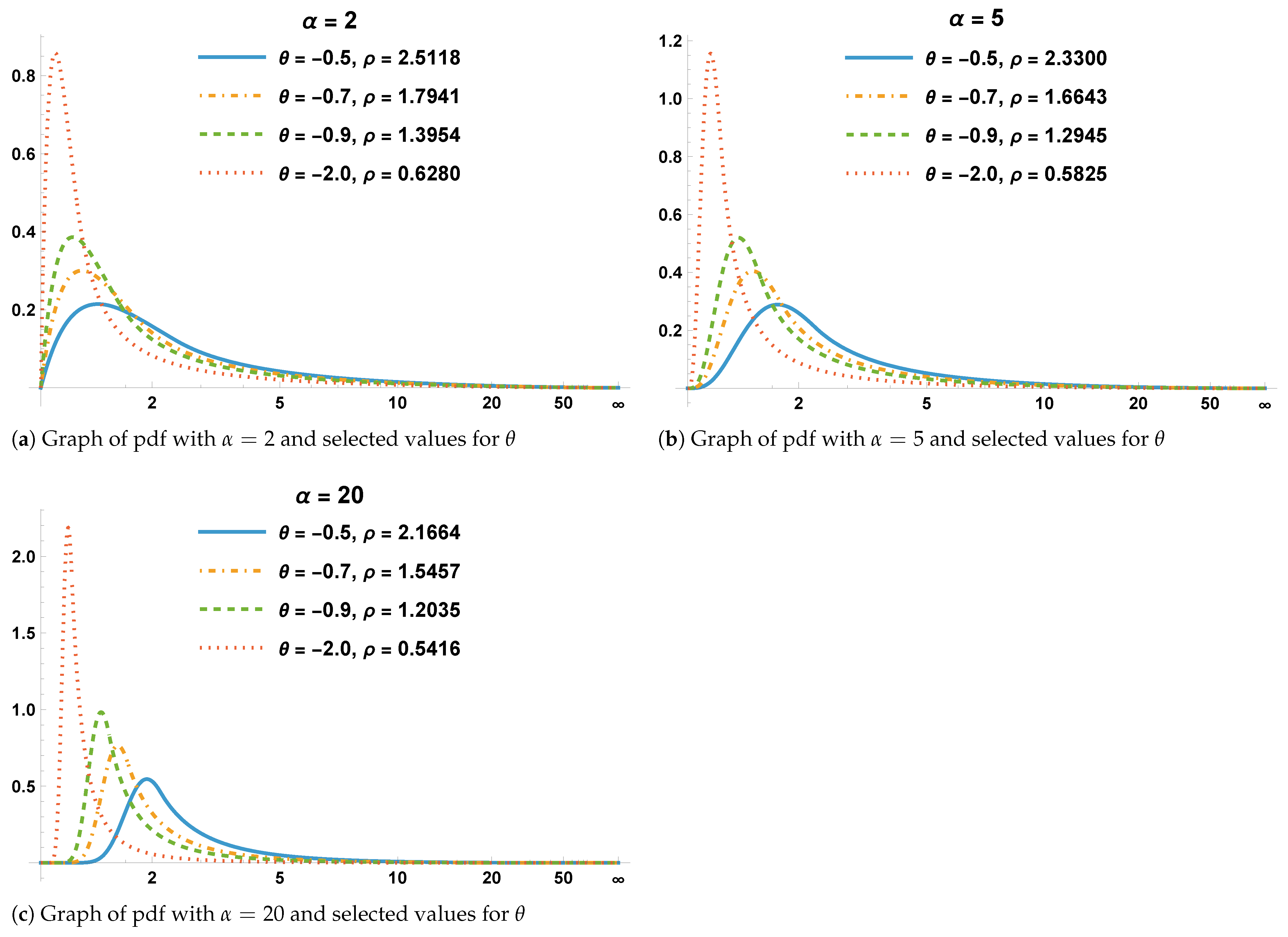
where $\eta =-\alpha (1+\psi )$ and $\rho =\psi {\theta }^{-1}$. It is worth mentioning that the above PDF has only two parameters, $\theta$ and $\alpha$. Figure 1a–c confirm that for a selected value of $\alpha$, the graph of $f_Y(y)$ is a smooth curve. Also, Figure 1a–c reveal that the dispersion decreases as $\alpha$ increases, and the PDF becomes more symmetric.

The first moment of the distribution is given in Equation (9) in the subsection titled “Maximum Likelihood Method for Regression Parameters.” The conditions for the existence of the first moment, verified by Mathematica, are $\alpha >0,\alpha +\alpha \theta \rho <0,$ which imply $\theta \rho <-1$. That is, $\psi <-1.$ It can also be shown that the conditions for the existence of the second moment are

$$\alpha >0,1+\alpha (1+\psi )<0\mathrm{or}\alpha >0,1+1+\alpha (1+\psi )>0.$$

Table 1. Values of $\psi$ and $1+\alpha (1+\psi )$ for selected values of $\alpha$.

$\mathit{\alpha }$	$\mathit{\psi }$	$\mathbf{1}\mathbf{+}\mathit{\alpha }\mathbf{(}1+\mathit{\psi }\mathbf{)}$
0.2	−1.6283	0.8744
0.5	−1.4649	0.7675
1	−1.3499	0.5501
1.5	−1.2922	0.5617
3	−1.2112	0.3664
10	−1.1173	−0.1730
20	−1.0839	−0.6780
100	−1.0372	−2.7250
350	−1.0199	−5.9650

utilizes Equation (4) and reveals that for a variety of selected values of $\alpha$, the conditions for the first and second moments are satisfied. We can see that for a positive value of $\alpha$, the condition ($\psi <0$) for the first moment is satisfied. Also, for small values of $\alpha$, Table 1 reveals that $1+\alpha (1+\psi )>0$. However, for large values of $\alpha$, we have $1+\alpha (1+\psi )<0$.

3. MLE for $\mathit{\theta }$ and the Value of $\mathit{m}$

This section proposes a numerical approach to provide the ML estimate for the parameter $\theta$ for the PDF $f_Y(y)$, derived in Section 1. For $y_1, y_2, \dots , y_n\sim \text{Gamma-Pareto}(\theta ,\alpha )$, without loss of generality, for an integer m, assume $y_1<y_2<\dots \le y_m<y_{m+1}<\dots <y_n$, where $1<m<n$. Assume that $y_1, y_2, \dots , y_m$ and $y_{m+1}, \dots , y_n$, respectively, are from the Gamma and Parerto components of the composite distribution. The log-likelihood function can be written as

$$ln(L)=m[ln(c)+\alpha ln(\alpha )-ln(\mathsf{\Gamma }(\alpha )]+\alpha \sum _{i=1}^{m}ln(-\theta ))+(\alpha -1)\sum _{i=1}^{m}ln(y_i)+\alpha \sum _{i=1}^m\theta y_i+$$

$$(n-m)ln(c)+\sum _{i=m+1}^n\left(ln(\eta )+\eta ln({\displaystyle \frac{\psi }{\theta }})-(1+\eta )ln(y_i)\right).$$

(5)

Recall from Section 2 that for a given value of $\alpha$, we can find w using Equation (4). We then define $\eta$ as $-\alpha (1+\psi )$, where $\psi ={\displaystyle \frac{w_o}{\alpha }}=\rho \theta$. Due to this reduction in the number of parameters, it is not possible to derive closed formulas for the maximum likelihood estimates (MLEs) directly through differentiation of $ln(L)$, since a specific value for $\alpha$ is required. Instead, we propose using a numerical optimization algorithm via Mathematica, specifically the NMaximize function, to search for an approximate value of $\alpha$ and the correct value of m. Code B (see the Supplementary Materials) computes the MLE of $\theta$, along with an approximate value for $\alpha$ and the correct value for m, using a sample from the Gamma–Pareto distribution.

In the simulation studies, Code C (see the Supplementary Materials) utilizes “true” values $({\alpha }_t,{\theta }_t)$ and a sample size n to generate $N=100$ samples from the composite distribution. The average maximum likelihood estimate (MLE) $\overline{\widehat{\theta }}$ and the average squared error (ASE) are calculated. For each simulated sample, the corresponding values for w and $\psi$ are determined using ${\alpha }_t$. A numerical optimization method, as outlined in Code B, is then employed to compute $\widehat{\theta }$ and the correct value of m.

Table 2. Accuracy of ML estimator for $\theta$.

${\mathit{\theta }}_{\mathit{t}}$	${\mathit{\alpha }}_{\mathit{t}}$	n	$\overline{\widehat{\mathit{\theta }}}$	$\mathit{\xi }\mathbf{(}\widehat{\mathit{\theta }}\mathbf{)}$
−1.2	2	50	−1.267	(0.087)
−1.2	2	100	−1.189	(0.034)
−1.2	2	150	−1.221	(0.018)
−1.2	5	50	−1.203	(0.018)
−1.2	5	100	−1.228	(0.007)
−1.2	5	150	−1.194	(0.006)
−0.6	2	50	−0.583	(0.012)
−0.6	2	100	−0.584	(0.007)
−0.6	2	150	−0.603	(0.003)
−0.6	5	50	−0.619	(0.004)
−0.6	5	100	−0.595	(0.002)
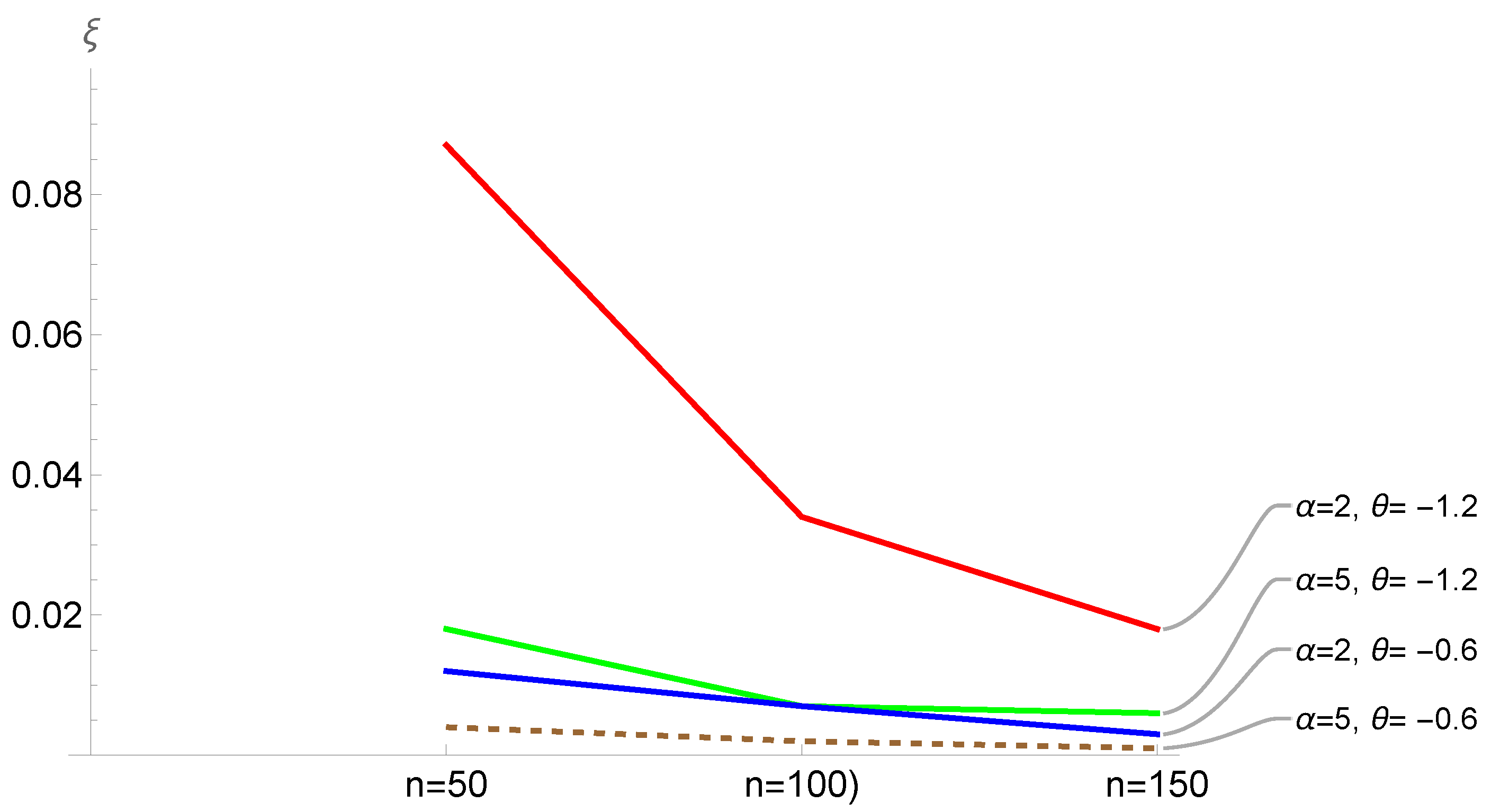
−0.6	5	150	−0.589	(0.001)

presents a summary of the simulation studies and reveals that as the sample size n increases, the Average Squared Error (ASE), given inside parentheses,

$$\xi (\widehat{\theta })={\displaystyle \frac{{\sum }_{j=1}^N{({\widehat{\theta }}_j-{\theta }_t)}^2}{N}},$$

decreases for all values of ${\alpha }_t$ and ${\theta }_t$ listed in the table. Additionally, for specific combinations of $({\theta }_t,n)$, a larger ${\alpha }_t$ results in a smaller $\xi (\widehat{\theta })$. This relation is more apparent when $\theta$ is not very small. Figure 2 provides a visual summary of the numbers in Table 2, which also supports the same conclusion. This outcome is expected, as a larger value of $\alpha$ leads to reduced variation within the sample, thereby providing a more accurate estimate for $\widehat{\theta }$.

4. Regression Model for Gamma–Pareto Composite Distribution

In this section, in the context of the regression analysis, it is assumed that $\alpha$ can be approximated through a search method (see Code B) using a random sample $y_1, \dots , y_n\sim \text{Gamma-Pareto}(\alpha ,\theta )$. Therefore, $\theta$ is the only parameter that links the response variable Y to covariates. Hence, an approximated $\alpha$ value is used in the regression analysis with the ultimate goal of estimating regression parameters through a link function for $\theta$. For each row, $x_i^{\prime }=(1, x_{i2}, \dots , x_{ip}),i=1, 2, \dots , k$, of the design matrix $X_{(k\times p)}$, let $y_i$ denote a realization of the response variable Y from the composite PDF (4), and without loss of generality, assume that $y_1<y_2<\dots \le y_m<\dots <y_k$ is an ordered random sample of size k, where $y_1, \dots , y_m$ are assumed to be from the first part (Gamma) of the composite distribution and $y_{m+1}, \dots , y_k$ are observed values from the second part (Pareto) of the composite distribution.

It is assumed that there are $p-1$ potential predictors related to the response variable Y. The first column of X contains 1’s, which accounts for the intercept parameter ${\beta }_1$. Therefore, the regression parameters are denoted by ${\beta }^{\prime }=({\beta }_1, {\beta }_2, \dots , {\beta }_p)$. As discussed in Section 2, based on the parameterization we considered, the canonical link function is $g(\mu )=\theta =-{\displaystyle \frac{1}{\mu }}$. For $Y\sim \mathrm{gamma}(\alpha ,\gamma )$, $E[Y]=\mu ={\displaystyle \frac{\alpha }{\gamma }}$. As a result, $\theta =-{\displaystyle \frac{\gamma }{\alpha }}.$ Recall that $\alpha$ is assumed to be known or can be approximated. Therefore, to define a link function in the context of regression modeling that relates $\theta$ to the covariates, we need to choose a function of covariates that is positive. There are several options:

• ${\theta }_i=-{\displaystyle \frac{1}{e^{x_i^{\prime }\beta }}}\Rightarrow {\mu }_i=e^{x_i^{\prime }\beta },i=1, 2, \dots , k.$
• ${\theta }_i=-{\displaystyle \frac{1}{x_i^{\prime }\beta }}\Rightarrow {\mu }_i=x_i^{\prime }\beta ,i=1, 2, \dots , k.$
• ${\theta }_i=-{\displaystyle \frac{1}{{(x_i\beta )}^2}}\Rightarrow {\mu }_i={(x_i^{\prime }\beta )}^2,i=1, 2, \dots , k.$

Option 3 provides a positive value for the mean, as required. However, algebraically, it may not be the best choice for optimizing the likelihood function to find MLEs of regression parameters and compute the Fisher information matrix. Option 2 is undesirable because, depending on the covariate data, it is possible that $x_i^{\prime }\beta <0$, which would make ${\theta }_i>0$; therefore, it is not acceptable. Consequently, we consider Option 1 with the exponential function that ensures ${\displaystyle \frac{1}{e^{x_i^{\prime }\beta }}}>0$, which means ${\mu }_i>0$

Note that ${\psi }_i={\theta }_i{\rho }_i$ and ${\eta }_i=-\alpha (1+{\theta }_i{\rho }_i)=-\alpha (1+{\psi }_i),i=1, 2, \dots , k$. Substituting for ${\theta }_i$ in the density function, the composite Gamma–Pareto density function is

$$f(y_i)=\left\{\begin{array}{c}{\displaystyle \frac{c{(-{\theta }_i\alpha )}^{\alpha }{y}_i^{\alpha -1}{e}^{{\theta }_i\alpha y_i}}{\mathsf{\Gamma }(\alpha )}}0<y_i\le {\rho }_i\alpha >0{\theta }_i<0\hfill \\ {\displaystyle \frac{-c\alpha (1+{\psi }_i){\rho }_i^{-\alpha (1+{\psi }_i)}}{y_i^{-\alpha (1+{\psi }_i)+1}}}{\rho }_i\le y_i<\infty .\hfill \end{array}\right.$$

(6)

It is noted that the observation $y_i$ in the second part of the PDF is related to the covariates $x_i^{\prime }=(1,x_{i2}, \dots , x_{ip})$ through

$${\rho }_i={\displaystyle \frac{{\psi }_i}{{\theta }_i}}=-{\psi }_i{e}^{x_i^{\prime }\beta }.$$

Maximum Likelihood Method for Regression Parameters

This section provides MLEs of regression parameters and utilizes the Fisher information matrix to compute the variance–covariance matrix for the estimators. Recall that ${\eta }_i=-\alpha (1+{\psi }_i), {\theta }_i=-{\displaystyle \frac{1}{e^{x_i^{\prime }\beta }}}$ and ${\rho }_i=-{\psi }_i{e}^{x_i^{\prime }\beta }i=1, 2, \dots , k$. Therefore, the global maximum for (6) with respect to the regression parameters can be found by maximizing

$$l=\alpha \sum _{i=1}^m(-x_i^{\prime }\beta -e^{-x_i^{\prime }\beta }{y}_i)-\alpha (1+{\psi }_i)\sum _{i=m+1}^k(ln(-{\psi }_i)+x_i^{\prime }\beta ).$$

NMaximize in Mathematica is used in our code to maximize l to find the MLE $\widehat{\beta }=({\widehat{\beta }}_1, {\widehat{\beta }}_2, \dots , {\widehat{\beta }}_p)$. A few predictors might not be statistically significant. We propose computing the inverse of the estimated Fisher information matrix and using Wald’s test to identify statistically significant predictors. Let

$$I_{\beta }={\displaystyle \frac{\partial l}{\partial \beta }}{I}_{\beta \beta }={\displaystyle \frac{\partial I_{\beta }}{\partial \beta }}.$$

(7)

$I_{\beta }$ is a $p\times 1$ vector. We aim to compute the $p\times p$ matrix, denoted as IFM = ${(E[I_{\beta \beta }])}^{-1}{|}_{\beta =\widehat{\beta }}$, which represents the inverse of the estimated Fisher information matrix. This matrix estimates the variance–covariance matrix for $\widehat{\beta }$. Since we are using numerical maximization with Mathematica, we will not be considering the iterative Fisher scoring algorithm. The algorithm for the parameter estimates is given by

$${\widehat{\beta }}_{v+1}={\widehat{\beta }}_v-{(E[I_{\beta \beta }])}^{-1}·I_{\beta }{|}_{\beta ={\widehat{\beta }}_v}$$

(8)

where v is the iteration index. However, calculating the Fisher information matrix is necessary for identifying statistically significant predictors in the regression model using Wald’s test statistic.

$I_{\beta \beta }$ involves Y; consequently, the computation of $IFM$ requires estimating the expected value. From the composite probability density function (PDF) discussed in Section 2, it can be shown that

$$E[Y|Y<\rho ]={\displaystyle \frac{-{(-\alpha \theta )}^{-1}[\mathsf{\Gamma }(1+\alpha ,-\alpha \psi )-\mathsf{\Gamma }(1+\alpha )]}{2\mathsf{\Gamma }(\alpha )-\mathsf{\Gamma }(\alpha ,-\alpha \psi )}}$$

(9)

$$E[Y|Y>\rho ]={\displaystyle \frac{\alpha \rho (1+c1)\mathsf{\Gamma }[\alpha ]}{(1+(\alpha (1+\psi ))\left(2\mathsf{\Gamma }(\alpha )-\mathsf{\Gamma }(\alpha ,-\alpha \psi )\right)}}.$$

In the context of regression analysis, Equation (9) can be rewritten as

$$E[Y_i|Y_i<{\rho }_i]=-{\displaystyle \frac{{\left(\frac{\alpha }{e^{x_i^{\prime }\beta }}\right)}^{-1}[\mathsf{\Gamma }(1+\alpha ,-\alpha {\psi }_i)-\mathsf{\Gamma }(1+\alpha )]}{2\mathsf{\Gamma }(\alpha )-\mathsf{\Gamma }(\alpha ,-\alpha {\psi }_i)}}$$

(10)

$$E[Y_i|Y_i>{\rho }_i]={\displaystyle \frac{\alpha (-{\psi }_i{e}^{x_i^{\prime }\beta })(1+{\psi }_i)\mathsf{\Gamma }[\alpha ]}{(1+(\alpha (1+{\psi }_i))\left(2\mathsf{\Gamma }(\alpha )-\mathsf{\Gamma }(\alpha ,-\alpha {\psi }_i)\right)}}.$$

Note that $\mathsf{\Gamma }(1+\alpha )>\mathsf{\Gamma }(1+\alpha ,-\alpha {\psi }_i)$ and ${\psi }_i<0$. Therefore, $E[Y_i]$ is a positive number, as expected, and can be estimated using $\widehat{\beta }$. The Mathematica code for this article uses (10) to compute $IFM$. Once $\widehat{\beta }$ is obtained, the Wald’s test is utilized as shown below:

$$W_g={\displaystyle \frac{{\widehat{\beta }}_g}{\sqrt{IF{M}_{(gg)}}}},g=1, 2, \dots , p$$

where ${\mathrm{IFM}}_{(gg)}$ is the gth diagonal element of IFM, and it estimates the variance of $\widehat{{\beta }_g}$. For a large sample size k, due to the asymptotic large sample property of MLE, the estimators ${\widehat{\beta }}_1, \dots , {\widehat{\beta }}_p$ are asymptotically normally distributed. Therefore, if $|W_g|<z_{q/2}$, it is concluded that at q level of significance, predictor $x_g, g=1, 2, \dots , p$ is not significant and that the matrix X should be updated accordingly. Using the updated matrix X, the new set of MLEs for the remaining regression parameters is found and tested for significance. This process continues until all remaining predictors in the model are significant.

5. Bayesian Estimation of Regression Parameters

According to the classical Bayesian approach, given a prior distribution $\rho (\xi )$ for a parameter $\xi$ (or multi-parameters $\underline{\xi }=({\xi }_1\dots {\xi }_p)$ for the distribution of a random variable Y, the corresponding posterior PDF

$$f(\underline{\xi }|y_1, \dots , y_n)=CL(\underline{y}|\underline{\xi })\rho (\xi ),$$

is formulated, where $y_1, \dots , y_n$ are observed values of Y in a sample of size n. $L(\underline{y}|\underline{\xi })$ is the likelihood function and C is a normalizing constant, defined as

$$C=\int \int \dots \int L(\underline{y}|\underline{\xi })\rho (\underline{\xi })d{\xi }_1\dots d{\xi }_p,$$

provided that $\rho (\xi )$ is a continuous prior distribution. Under the squared-error loss function, Bayes estimates of the parameters ${\xi }_1, \dots , {\xi }_p$ are analytically derived via the corresponding expected values based on the posterior distribution. This may require writing the posterior PDF as

$$f(\underline{\xi }|\underline{y})=f({\xi }_1|\underline{y})f({\xi }_2|{\xi }_1\underline{y})\dots f({\xi }_n|{\xi }_1{\xi }_2\dots {\xi }_{p-1}\underline{y}),$$

if ${\xi }_1\dots {\xi }_p$ are assumed to be dependent.

Identifying a conjugate prior for a likelihood function can often be a challenging task. This is especially true when we want the posterior distribution to belong to the same class as the prior distribution. Depending on the form of the likelihood function, it might also be impossible to express the posterior PDF in a recognizable form, which complicates deriving the Bayes estimator as the expected value of the posterior. To address these challenges, a common approach is to utilize a Markov Chain Monte Carlo (MCMC) algorithm. This method involves selecting a proposal distribution for the parameters of the posterior probability density function (PDF), which may not align with any well-known distribution class. The algorithm then performs simulations until it confirms that convergence has been achieved. For example, Aminzadeh and Deng (2022) proposes a computational method that leverages an MCMC algorithm to estimate the Bayes estimate of the renewal function when the interarrival times follow a Pareto distribution.

To develop a Bayesian algorithm using the Gamma–Pareto composite distribution and a non-linear regression model, it is essential to establish a multivariate prior distribution for the regression parameters ${\beta }_1, {\beta }_2, \dots , {\beta }_p$. Since these parameters can assume any value, the multivariate normal distribution is the most suitable choice for the prior distribution.

$$\underline{\beta }\sim N_p(\varphi ,\mathsf{\Sigma })\underline{\beta }=({\beta }_1\dots {\beta }_p),$$

(11)

where $E({\beta }_j)={\varphi }_j, j=1, 2, \dots , p$ and $\mathsf{\Sigma }$ is the corresponding $p\times p$ positive-definite variance–covariance matrix of ${\beta }_1, \dots , {\beta }_p.$

The posterior PDF via (5) and (11) is written as

$$\prod _{i=1}^m{\displaystyle \frac{c{\alpha }^{\alpha }{(-{\theta }_i)}^{\alpha }{y}_i^{\alpha -1}{e}^{\alpha {\theta }_i{y}_i}}{\mathsf{\Gamma }(\alpha )}}\times \prod _{i=m+1}^{k}c{\eta }_i{\rho }_i^{{\eta }_i}{y}_i^{-({\eta }_i+1)}$$

$$\times {(2\pi )}^{p/2}{[det(\mathsf{\Sigma })]}^{-0.5}{e}^{-0.5{(\underline{\beta }-\underline{\varphi })}^{\prime }{\mathsf{\Sigma }}^{-1}(\underline{\beta }-\underline{\varphi })}.$$

(12)

It is important to note that in total, there are $p+\left({\displaystyle \genfrac{}{}{0pt}{}{p}{2}}\right)$ hyperparameters involved in the prior distribution. Choosing appropriate values for these hyperparameters can be challenging. For the current model, we need to know values for ${\varphi }_j$ (where $j=1, 2, \dots , p$) as well as the covariances $\mathrm{Cov}({\beta }_i, {\beta }_j)$ (for $i\ne j$ and $i,j=1, 2, \dots , p$). Aminzadeh and Deng (2018, 2022) explored a data-driven approach to help select hyperparameter values when relevant information is unavailable. Their method involves using the MLEs of the parameters of interest to match the expected value of the prior distribution with the MLE while also choosing hyperparameters that minimize the prior distribution’s variance. The idea is to incorporate the information in the MLEs and assign appropriate hyperparameter values. This approach results in several equations that can be solved simultaneously to find the hyperparameters. Simulation studies in their articles suggest that this method provides accurate Bayesian estimates that outperform MLEs in terms of accuracy.

5.1. Approximate Bayesian Computation

In this article, we take a data-driven approach. However, because the posterior in Equation (12) is challenging to work with, we turn to the Approximate Bayesian Computation (ABC) method, which relies on extensive simulations. The foundational concepts of ABC date back to the 1980s when Donald Rubin introduced them. Since then, various researchers have employed this method, mainly when deriving the posterior probability density function (PDF) is intractable. Lintusaari et al. (2017) provide a comprehensive overview of recent developments in the ABC method.

5.2. Computation Steps for ML and ABC Estimates Using Simulated Data

For selected “true” values of ${\beta }_t=({\beta }_{t,1}, \dots , {\beta }_{t,p})$ and a chosen $k\times p$ design matrix X, we generate $N_s=300$ samples $y_{j1}, \dots , y_{jk}$ for $j=1, 2, \dots , N_s$ from the Gamma–Pareto composite distribution. The following steps in Mathematica Code A compute the MLEs and approximate Bayesian estimates of ${\beta }_{t1}, \dots , {\beta }_{tp}$. It is important to note that ${\beta }_{t,1}$ represents the intercept parameter, and the first column of the matrix X consists of ones.

• In the jth iteration $j=1, 2, \dots , N_S$, the numerical maximization method via NMaximize in Mathematica is applied to

  $$l=\alpha \sum _{i=1}^m(-x_i^{\prime }\beta -e^{-x_i^{\prime }\beta }{y}_i)-\alpha (1+{\psi }_i)\sum _{i=m+1}^k(ln(-{\psi }_i)+x_i^{\prime }\beta ).$$

  (see Section 4) to compute MLEs ${\widehat{\beta }}_1, \dots , {\widehat{\beta }}_p$ and Wald’s test statistic is used to identify the significant predictors that should remain in the model. Recall that we need to update the design matrix X, if necessary. This also applies to the first column of the matrix X. For ease of presentation, it is assumed that all predictors are retained in the model. The overall MLE is computed as

  $${\widehat{\beta }}_{\mathrm{ML},\mathrm{g}}={\displaystyle \frac{{\sum }_{j=1}^{N_S}{\widehat{\beta }}_{jg}}{N_S}},{\widehat{\beta }}_{ML}=({\widehat{\beta }}_{\mathrm{ML},1}, \dots , {\widehat{\beta }}_{\mathrm{ML},\mathrm{p}})$$

  and with the average squared error (ASE)

  $$\xi ({\widehat{\beta }}_{\mathrm{ML},\mathrm{g}})={\displaystyle \frac{{\sum }_{j=1}^{N_S}{({\widehat{\beta }}_{\mathrm{ML},\mathrm{g}}-{\beta }_{t,g})}^2}{N_S}}, g=1, 2, \dots , p.$$
  Note that using jth generated sample $j=1, 2, \dots , N_S$, the corresponding ${\mathrm{IFM}}_j$ matrix is computed, and then the overall variance–covariance matrix

  $$\mathrm{IFM}={\displaystyle \frac{{\sum }_{j=1}^{N_S}{\mathrm{IFM}}_j}{N_S}}$$

  is computed and is used in Wald’s test statistic.
• Using IFM, generate $Nss=3000$ random samples from a multivariate normal distribution $N_p({\widehat{\beta }}_{ML},\mathrm{IFM})$. Let ${\beta }_1^v, \dots , {\beta }_p^v$, denote the vth generated sample, $v=1, 2, \dots , Nss$.
• Based on vth simulated sample ${\beta }^v=({\beta }_1^v, \dots , {\beta }_p^v)$, generate sample of size k from the composite distribution using the ith row $x_i^{\prime }$ of the updated design matrix X and the link function ${\theta }_i=-{\displaystyle \frac{1}{e^{x_i^{\prime }{\beta }^v}}}.$ Let us denote the simulated samples by $y_1^v, y_2^v, \dots , y_k^v,$ $v=1, 2, \dots , Nss$.
• Following the ABC algorithm, simulated samples $y_1^v, y_2^v, \dots , y_k^v$ should be compared with $y_{j1}, \dots , y_{jk}j=1, 2, \dots , N_S$, using some summary statistics. If the difference in the absolute value of selected summary statistics is less than a selected tolerance error $ϵ$, then the vth simulated ${\beta }^v$ in Step 3 is accepted as a sample from the posterior distribution and is moved to the set of “accepted” samples. In this article, we use the 30th and 90th percentiles as the summary statistics. The reason for the two percentiles is that the samples from the composite distribution are expected to have small and very large values in each sample. Therefore, for a more accurate comparison, two percentiles are employed. ${ϵ}_1$ and ${ϵ}_2$, respectively, denote the tolerance errors for 30th and 90th percentiles. Note that there are $N_S$ original samples from Step 1 and $Nss$ samples in Step 3. For comparison purposes, we compare all $Nss$ samples with one of the samples from Step 1. Note that choosing only one generated sample for comparison is exactly the practical case, as we are given only one data set $y_1, \dots , y_n$ on the response variable to analyze. But in the simulation scenario, the “original sample” can be any of the $N_S$ samples from Step 1. The sample can be selected at random. In the simulation studies, two options are considered: 1. All $Nss$ samples are compared with the Average of $N_S$ samples, 2. All $Nss$ samples are compared with a Random sample selected from the $N_S$ samples. Again, it is noted that option 2 is the practical case, as only one sample in an actual application is available to analyze.
• Letting $N_a$ denote the number of acceptable simulated samples ${\beta }_1^{\nu }, \dots , {\beta }_p^{\nu }$ from the multivariate normal distribution in Step 2, we define an approximate Bayes estimate as

  $${\widehat{\beta }}_{\mathrm{Bayes},g}={\displaystyle \frac{{\sum }_{h=1}^{N_a}{\beta }_g^h}{N_a}},$$

  with the ASE,

  $$\xi ({\widehat{\beta }}_{\mathrm{Bayes},\mathrm{g})}={\displaystyle \frac{{\sum }_{h=1}^{N_a}{({\widehat{\beta }}_{\mathrm{Bayes},g}-{\beta }_{t,g})}^2}{N_a}} ,g=1, 2, \dots , p.$$

  (13)
  The values of tolerance errors ${ϵ}_1$ and ${ϵ}_2$ in the code should depend on the available $y_1, y_2, \dots , y_n$ and simulated data. Small tolerance values would lead to a small $N_a$. On the other hand, significant tolerance limits would force $N_a$ to be close to Nss. Therefore, before making all comparisons in Step 4, it is recommended to print a few values for the absolute differences between the 30th percentiles of the original and simulated samples, as well as for the 90th percentiles, to get an idea of the appropriate choices for ${ϵ}_1$ and ${ϵ}_2$. It is worth emphasizing that according to the ABC algorithm, the set of acceptable ${\beta }_1^h, \dots , {\beta }_p^h, h=1, 2, \dots N_a$ are considered random samples from the posterior distribution (14).

6. Simulation for Composite Gamma–Pareto Regression

We conduct simulation studies to compare the accuracy of ML and Bayesian methods. For selected values of k (sample size), $\beta$ (the parameter vector), $\alpha$, and p, we generate $N_S=300$ samples from the PDF (4) to obtain the MLEs. Additionally, we generate $N_{ss}=3000$ simulated samples from a multivariate normal distribution using the Approximate Bayesian Computation (ABC) algorithm to derive the Bayesian estimates of the regression parameters.

Case 1: For the sample size $k=30$ and $p=3$,

Table 3. Comparison of ML and ABC accuracies, k = 30.

	MLE						Bayes
${\beta }_1=1.5,{\beta }_2=0.5,{\beta }_3=0.5$ Average
$\alpha$	${\overline{\widehat{{\beta }_1}}}_{MLE}$	${\xi }_{{\beta }_{1MLE}}$	${\overline{\widehat{{\beta }_2}}}_{MLE}$	${\xi }_{{\beta }_{2MLE}}$	${\overline{\widehat{{\beta }_3}}}_{MLE}$	${\xi }_{{\beta }_{3MLE}}$	${\overline{\widehat{{\beta }_1}}}_{Bayes}$	${\xi }_{{\beta }_{1Bayes}}$	${\overline{\widehat{{\beta }_2}}}_{Bayes}$	${\xi }_{{\beta }_{2Bayes}}$	${\overline{\widehat{{\beta }_3}}}_{Bayes}$	${\xi }_{{\beta }_{3Bayes}}$
2	1.38317	(0.02339)	0.31571	(0.04741)	0.69946	(0.06635)	1.37884	(0.03036)	0.32004	(0.03580)	0.69851	(0.04106)
5	1.38910	(0.01788)	0.31511	(0.04286)	0.68680	(0.05153)	1.38751	(0.01772)	0.31525	(0.03567)	0.68731	(0.03570)
${\beta }_1=1.5,{\beta }_2=0.5,{\beta }_3=0.5$ Random
2	1.39066	(0.03170)	0.30534	(0.04882)	0.70131	(0.07010)	1.38496	(0.02919)	0.30951	(0.03975)	0.70154	(0.04221)
5	1.37700	(0.02349)	0.29783	(0.05531)	0.69977	(0.06285)	1.37832	(0.02217)	0.29724	(0.04256)	0.699970	(0.04051)
${\beta }_1=1.5,{\beta }_2=0.5,{\beta }_3=0.9$ Average
2	1.70788	(0.06452)	0.47799	(0.01842)	0.806311	(0.04315)	1.70809	(0.06015)	0.47973	(0.00406)	0.80209	(0.01115)
5	1.67041	(0.04057)	0.49669	(0.00919)	0.77179	(0.03343)	1.65335	(0.03230)	0.50464	(0.00188)	0.77384	(0.01655)
${\beta }_1=1.5,{\beta }_2=0.5,{\beta }_3=0.9$ Random
2	1.69979	(0.06499)	0.48245	(0.01788)	0.80149	(0.04932)	1.69068	(0.05411)	0.49788	(0.00437)	0.79125	(0.01338)
5	1.67205	(0.04008)	0.50933	(0.00848)	0.75602	(0.03138)	1.66830	(0.03442)	0.50863	(0.00130)	0.75768	(0.02084)
${\beta }_1=2.1,{\beta }_2=0.2,{\beta }_3=1.6$ Average
2	2.26742	(0.06399)	0.16432	(0.00920)	1.59097	(0.01842)	2.27079	(0.04064)	0.16356	(0.00403)	1.59021	(0.00119)
5	2.20439	(0.02051)	0.14440	(0.00898)	1.58875	(0.01309)	2.18404	(0.01156)	0.15604	(0.00284)	1.58963	(0.00050)
${\beta }_1=2.1,{\beta }_2=0.2,{\beta }_3=1.6$ Random
2	2.26540	(0.04789)	0.13791	(0.01174)	1.61942	(0.02034)	2.26681	(0.04009)	0.13997	(0.00647)	1.61678	(0.00134)
5	2.12305	(0.01890)	0.13728	(0.00938)	1.58968	(0.01050)	2.19284	(0.01236)	0.13831	(0.00470)	1.58941	(0.00059)

provides a summary of the simulation results with the “true” regression parameters $({\beta }_{t,1}=1.5, {\beta }_{t,2}=0.5, {\beta }_{t,3}=0.5)$, $({\beta }_{t,1}=1.5, {\beta }_{t,2}=0.5, {\beta }_{t,3}=0.9)$, and $({\beta }_{t,1}=2.1, {\beta }_{t,2}=0.2, {\beta }_{t,3}=1.6)$. The selected design matrix, $X^{\prime }=V_{3\times 30}^{\prime }$, is given below

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
1.3.	1.6	1.1	1.7	1.2	1.5	1.9	1.3	1.3	2.2	1.2	1.5	1.5	2.7	1.4	1.5	1.7	2.7	1.6	1.8	1.6	1.3	1.1	1.5	1.4	2.0	1.9	1.4	1.5	1.9
2.5	2.3	2.4	2.1	2.3	1.7	2.4	1.5	2.3	1.3	1.9	1.9	2.1	2.3	1.1	2.3	1.1	2.6	2.4	2.1	2.0	2.3	2.4	1.5	2.4	2.2	1.1	2.8	2.8	2.0

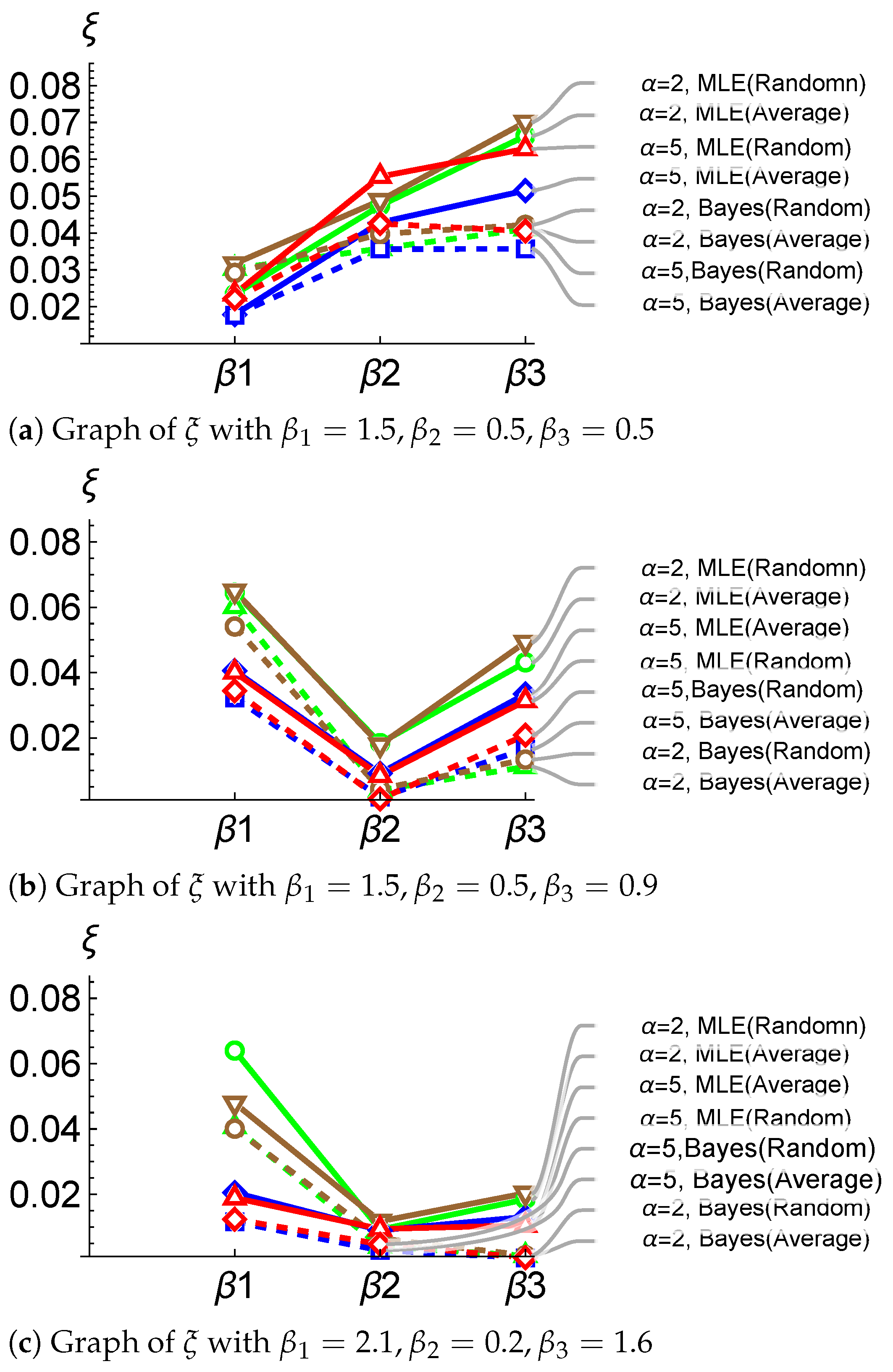
Table 3 and

Table 4. Comparison of ML and ABC accuracies, k = 50.

	MLE						Bayes
${\beta }_1=1.5,{\beta }_2=0.5,{\beta }_3=0.5$ Average
$\alpha$	${\overline{\widehat{{\beta }_1}}}_{MLE}$	${\xi }_{{\beta }_{1MLE}}$	${\overline{\widehat{{\beta }_2}}}_{MLE}$	${\xi }_{{\beta }_{2MLE}}$	${\overline{\widehat{{\beta }_3}}}_{MLE}$	${\xi }_{{\beta }_{3MLE}}$	${\overline{\widehat{{\beta }_1}}}_{Bayes}$	${\xi }_{{\beta }_{1Bayes}}$	${\overline{\widehat{{\beta }_2}}}_{Bayes}$	${\xi }_{{\beta }_{2Bayes}}$	${\overline{\widehat{{\beta }_3}}}_{Bayes}$	${\xi }_{{\beta }_{3Bayes}}$
2	1.37024	(0.02673)	0.48601	(0.00421)	0.42714	(0.01136)	1.36815	(0.02216)	0.48362	(0.00119)	0.42935	(0.00539)
5	1.35771	(0.02329)	0.46217	(0.00578)	0.43992	(0.00667)	1.35694	(0.02220)	0.46274	(0.00176)	0.44001	(0.00374)
${\beta }_1=1.5,{\beta }_2=0.5,{\beta }_3=0.5$ Random
2	1.37950	(0.02823)	0.48090	(0.00609)	0.42913	(0.00981)	1.37746	(0.01976)	0.48254	(0.00137)	0.42881	(0.00540)
5	1.36602	(0.02443)	0.47633	(0.00434)	0.42054	(0.00896)	1.36490	(0.02008)	0.47638	(0.00093)	0.42115	(0.00637)
${\beta }_1=1.5,{\beta }_2=0.5,{\beta }_3=0.9$ Average
2	1.57586	(0.01590)	0.42997	(0.01391)	0.68170	(0.05904)	1.58408	(0.01147)	0.42622	(0.00635)	0.68096	(0.04844)
5	1.56522	(0.00734)	0.44004	(0.00719)	0.65876	(0.06066)	1.55817	(0.00532)	0.44257	(0.00371)	0.66045	(0.05752)
${\beta }_1=1.5,{\beta }_2=0.5,{\beta }_3=0.9$ Random
2	1.58426	(0.01801)	0.45345	(0.01470)	0.65688	(0.06679)	1.59720	(0.01402)	0.44868	(0.00368)	0.65496	(0.06040)
5	1.57121	(0.00824)	0.43543	(0.00671)	0.66431	(0.05988)	1.57378	(0.00742)	0.43353	(0.00487)	0.66405	(0.05581)
${\beta }_1=2.1,{\beta }_2=0.2,{\beta }_3=1.6$ Average
2	2.18171	(0.02131)	0.35200	(0.03160)	1.3117	(0.08492)	2.18010	(0.00921)	0.33201	(0.02161)	1.31791	(0.05490)
5	2.11701	(0.00501)	0.35010	(0.02491)	1.29191	(0.09932)	2.11721	(0.00131)	0.32001	(0.02271)	1.28190	(0.09140)
${\beta }_1=2.1,{\beta }_2=0.2,{\beta }_3=1.6$ Random
2	2.17481	(0.00649)	0.34901	(0.03190)	1.3182	(0.0885)	2.1748	(0.00231)	0.25120	(0.02354)	1.31778	(0.05983)
5	2.10581	(0.00780)	0.33582	(0.02765)	1.30714	(0.0915)	2.10521	(0.00101)	0.33573	(0.00910)	1.30711	(0.06150)

illustrate that the ABC-based estimator generally has a lower Average Squared Error (ASE) compared to the ML estimator. Additionally, both the Random and Average options used to compare the original samples with those generated via the ABC method show nearly identical levels of accuracy. Figure 3 is derived from Table 3. Note that there are three different sets of “true” values for the regression parameters considered in Table 3 and Table 4. Solid and dashed lines represent the $\xi$ values obtained using the MLE method and the ABC method, respectively. Since the solid lines are usually higher than the corresponding dashed lines, we can conclude that the MLE method results in more variability for the estimators than the ABC method. Note that the relation between ASE values solely depends on the selected “true” values of ${\beta }_1,{\beta }_2$, and ${\beta }_3$ in simulations, as well as the covariate values in the design matrix. For example, in Figure 3b,c, $\xi \widehat{({\beta }_2)}$ is the smallest, while in Figure 3a, that is not the case. It is worth mentioning that the Random option is more realistic because it takes into account that we typically analyze only one data set in real-world scenarios. This means that the samples produced by the ABC algorithm are compared exclusively with the original data set.

Case 2: For $k=50$, $p=3$ and the same “true” regression parameters as in Case 1, a summary of simulation results is given in Table 4. The design matrix is $X^{\prime }=\left[V_{3\times 30}^{\prime },W_{3\times 20}^{\prime }\right]$, where $W_{3\times 30}^{\prime }$ is

1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
1.2	1.7	1.3	1.6	1.4	1.8	1.1	1.5	1.2	1.3	1.5	1.7	1.3	1.5	1.6	1.3	2.1	1.6	1.4	1.5
2.4	2.4	2.6	2.0	2.5	2.2	2.7	2.9	2.7	2.5	2.7	2.6	1.7	2.3	2.5	2.3	2.6	2.9	2.8	3.1

7. Goodness-of-Fit Test

This section details the goodness-of-fit of a data set to the Gamma–Pareto composite distribution. Using the composite PDF in Section 2, the CDF of the distribution can be derived as

$$F_Y(y)=\left\{\begin{array}{cc}{F}_1(y)={\displaystyle \frac{\mathsf{\Gamma }(\alpha )-\mathsf{\Gamma }(\alpha ,-y\alpha \theta )}{2\mathsf{\Gamma }(\alpha )-\mathsf{\Gamma }(\alpha ,-w)}}\hfill & 0<y\le \rho \hfill \\ \\ F_2(y)={\displaystyle \frac{1-{(\frac{y}{\rho })}^{\alpha +w}\mathsf{\Gamma }(\alpha )}{2\mathsf{\Gamma }(\alpha )-\mathsf{\Gamma }(\alpha ,-w)}})\hfill & \rho <y<\infty \hfill \end{array}\right.$$

The derivation of the CDF is based on the constraints (summarized below) on the parameters discussed in Section 2.

• For a given value for $\alpha$, w is the negative solution to ${\displaystyle \frac{{(-w)}^{\alpha }{e}^w}{\mathsf{\Gamma }(\alpha )}}=-(\alpha +w).$
• $\psi ={\displaystyle \frac{w}{\alpha }}.$
• $\rho ={\displaystyle \frac{\psi }{\theta }}$
• $\eta =-\alpha (1+\psi ).$

For a sorted data set $y_1<y_2<\dots \le y_m<y_{m+1}<\dots <y_n$ from the Gamma–Pareto distribution, the correct value of m, the MLE $\widehat{\theta }$, and an approximate value for $\alpha$ are computed via Code B and plugged into Code D (see the Supplementary Materials), which provides the Chi-Square goodness-of-fit test statistic.

The data in

Table 5. Generated sample ($n=150, {\theta }_t=-0.6, {\alpha }_t=5$).

0.173221	0.562328	0.6014	0.628722	0.684222	0.702359	0.732797	0.778164	0.8045	0.85104
0.853733	0.854449	1.01957	1.03878	1.04466	1.07031	1.0818	1.0916	1.09649	1.11931
1.12353	1.14771	1.15567	1.16688	1.17806	1.18038	1.19546	1.20516	1.2289	1.24685
1.27918	1.28665	1.34073	1.37014	1.38414	1.38951	1.41006	1.41252	1.42017	1.42077
1.45826	1.46232	1.46817	1.47453	1.51074	1.57869	1.63747	1.66341	1.71561	1.72894
1.77688	1.85376	1.85484	1.88346	1.90621	1.92309	1.93003	1.93009	1.93474	1.99243
1.99464	1.99573	2.01341	2.04042	2.24144	2.27748	2.3462	2.37468	2.38365	2.39532
2.42395	2.53448	2.54501	2.5652	2.56955	2.58355	2.59503	2.60915	2.62535	2.65666
2.68232	2.96808	2.99684	3.0168	3.02363	3.04648	3.16551	3.16612	3.16846	3.17327
3.19892	3.21764	3.22007	3.25448	3.26738	3.30428	3.354	3.35662	3.37009	3.51026
3.52236	3.5508	3.63083	3.82762	4.00392	4.11479	4.14929	4.17158	4.24731	4.42791
4.42811	4.76074	4.76354	4.91131	5.10246	5.15575	5.16438	5.42668	5.67241	6.80587
7.0751	7.18785	7.54937	7.81637	8.44419	9.05178	9.10595	9.70052	10.7409	10.7701
10.991	14.7825	15.2575	15.3069	16.9331	21.8571	22.0069	28.7049	39.6837	40.3783
56.6038	78.7244	92.4837	224.286	284.65	298.247	345.156	957.885	1120.81	1452.6

is generated from the Gamma–Pareto composite distribution. For the data set, Code B provides $\alpha \approx 4.97644, \widehat{\theta }=-0.55$, $w=-5.7142, \psi ={\displaystyle \frac{w}{\widehat{\alpha }}}=-1.16669$, and $m=59$. For this data, the Chi-Square goodness-of-fit test (see Code D) is applied using the CDF (see Section 7) and its inverse function to determine the intervals:

$$\begin{gathered} \{(0,0.962813),(0.963,1.29308),(1.2931,1.61033),(1.611,2.01341),(2.022,3.34491),(3.45,4.84397), \\ (4.844,8.07716),(8.08,47.492),(47.493,1453)\}, \end{gathered}$$

with the corresponding observed frequencies: {12, 20, 14, 17, 33, 14, 11, 16, 10}. The Chi-Square test = 7.11064. Since the critical value is ${\chi }_{(6,0.01)}^2=16.8119,$ at the 0.01 level of significance, the goodness-of-fit of the data to the Pareto-Gamma model is not rejected.

It is worth mentioning that the Gamma–Pareto model introduced in the current article does not provide an adequate fit to the Fire data that was analyzed by Grün and Miljkovic (2019). The proposed composite model, like other composite models in the literature, would be superior to common heavy-tailed distributions, such as the Gamma and Weibull distributions, provided that the data contain several extreme loss values.

8. Numerical Example

The following data represents the total payment for auto claims in thousands of Swedish Kronor.

https://www.kaggle.com/datasets/redwankarimsony/auto-insurance-in-sweden (accessed on 1 October 2025).

y = {4.4, 6.6, 11.8, 12.6, 13.2, 14.6, 14.8, 15.7, 20.9, 21.3, 23.5, 27.9, 31.9, 32.1, 38.1, 39.6, 39.9, 40.3, 46.2, 48.7, 48.8, 50.9, 52.1, 55.6, 56.9, 57.2, 58.1, 59.6, 65.3, 69.2, 73.4, 76.1, 77.5, 77.5, 87.4, 89.9, 92.6, 93., 95.5, 98.1, 103.9, 113., 119.4, 133.3, 134.9, 137.9, 142.1, 152.8, 161.5, 162.8, 170.9, 181.3, 187.5, 194.5, 202.4, 209.8, 214., 217.6, 244.6, 248.1, 392.5, 422.2}

We applied Code B and obtained the approximate values of $\alpha =0.4294$, $m=10$, and $\widehat{\theta }=-0.065559$. For this data, the Chi-Square goodness-of-fit test (see Code D) is applied using the CDF (see Section 7) and its inverse function to determine the following intervals:

$$(0,7.21433),(7.22,16.6535),(16.66,42.8439),(42.9,126.404),(126.5,423)$$

with the corresponding observed frequencies: {2, 6, 10, 25, 19}. The Chi-Square test = 7.67. Since the critical value is ${\chi }_{(2,0.01)}^2=9.21034,$ at the 0.01 level of significance, the goodness-of-fit of the data to the Pareto–Gamma model is not rejected. Given potential covariates, the proposed estimation methods in the article can be used via Code A to estimate regression parameters.

9. Summary

This article introduces a new composite distribution, the Gamma–Pareto, based on the Gamma and Pareto distributions. Several measures of this composite distribution are derived, including the CDF, which is used for the Anderson–Darling and Chi-Square goodness-of-fit tests. The article aims to provide innovative computational tools for estimating regression parameters through a link function that connects small and large response variable values to covariates. Specific Mathematica codes are provided, utilizing numerical approximations to MLEs and Bayesian estimates via the ABC algorithm. This proposed ABC method uses a multivariate normal distribution as the prior, employs a data-driven approach to select hyperparameters, and relies on the MLEs of regression parameters and the Fisher information matrix to compute approximate Bayesian estimates. The 30th and 90th percentiles serve as summary statistics to identify “acceptable samples”, which are a subset of larger samples generated from the prior. The Anderson–Darling goodness-of-fit test assesses how well the response variable aligns with the composite distribution. Simulation results indicate that the ABC method generally outperforms the ML method in terms of accuracy.