1. Introduction
The recent geopolitical tensions make it clear how important adequate risk management of electricity price risk is. Basic risk management tools are futures and options on the futures. Indeed, a large proportion of electricity is traded via future (or swap) contracts, that deliver the electricity over a specified period like a month, a quarter, or a year.
1 The delivery period has to be incorporated into the pricing model. In the geometric case, this can induce technical difficulties, and approximations have to be made. The theory of the market price of risk for delivery periods (MPDP), introduced by
Kemper et al. (
2022) and
Kemper and Schmeck (
2023), constitutes an elegant method of exact pricing. This paper provides empirical evidence for the existence of the MPDP, constituting a precise pricing framework for futures and options on electricity.
One may say that the starting point of our analysis is the existence of the delivery period in electricity markets. The futures, that are traded, e.g., at the European Electricity Exchange (EEX), typically deliver the underlying electricity over a period of time, in exchange for a fixed futures price. In this paper, we refer to these contracts with delivery periods as
swaps. In contrast, we refer to contracts with one time delivery as futures. These contracts are not traded at the exchanges, but are nevertheless useful for constructive purposes: the electricity swap price can be defined as the average with respect to the delivery time of an instantaneous stream of (artificial) futures. This approach is in the spirit of the Heath–Jarrow–Morton approach (see
Heath et al. 1990) and has been applied to energy markets by, e.g.,
Clewlow and Strickland (
1999) and
Bjerksund et al. (
2010).
The problems with the delivery period in geometric models start when averaging
arithmetically over the delivery period. The resulting swap price dynamic is neither geometric nor Markovian, due to a complex expression of the volatility term, and therefore of very limited use for further analysis. For a detailed description of the problem, we refer to
Kemper et al. (
2022) and the references therein. A solution to the problem is the approximation of the swaps volatility coefficient by the average of the futures volatility coefficient, as suggested by
Bjerksund et al. (
2010). This results in a geometric, Markovian dynamic. It is clear that any approximation always gives rise to an approximation error.
Kemper et al. (
2022) and
Kemper and Schmeck (
2023) offer a tractable framework to avoid such approximation errors and allow for precise pricing. They suggest using geometric averaging instead of arithmetic averaging. In a geometric price model as we consider it here, this corresponds to an arithmetic averaging of the drift and volatility coefficients. Indeed, the dynamics are again geometric as well as Markovian.
Kemper and Schmeck (
2023) discuss the similarities and differences between the approaches of
Bjerksund et al. (
2010) and
Kemper et al. (
2022) and introduce a numéraire caused by the different averaging techniques.
Kemper et al. (
2022) start with a stream of instantaneous futures contracts that are martingales under some pricing measure
. Incorporating the delivery period by geometric averaging does not maintain the martingale property. Therefore, they define the market price of risk for delivery periods that lead to an equivalent measure
, that is a martingale measure for the geometrically averaged swap price dynamics.
The new pricing measure
will differ from
if the volatility of the futures exhibits delivery-dependent effects as, e.g., the Samuelson effect (see
Samuelson 1965). The Samuelson effect is typically observed in energy and commodity markets (see, e.g.,
Benth and Paraschiv 2016;
Jaeck and Lautier 2016) and states that there will be an exponential increase in volatility if we come close to the maturity of the contract. In the empirical study presented herein, we focus on the MPDP that is induced by the Samuelson effect.
An additional property of the electricity swap market is the mean-reverting behavior observed under the physical measure
. As mentioned by
Latini et al. (
2019) and
Kleisinger-Yu et al. (
2020), among others, mean reversion is an important property of electricity swap prices.
Koekebakker and Ollmar (
2005) empirically validate that the short-term price varies around the long-term price, which confirms mean-reverting behavior. As
Benth et al. (
2019), we face the problem of changing from the risk-neutral measure to a mean-reverting process of the Ornstein–Uhlenbeck type. We adjust their measure change to our multi-dimensional geometric setting.
Figure 1 gives an overview over the measure changes that are involved in our analysis.
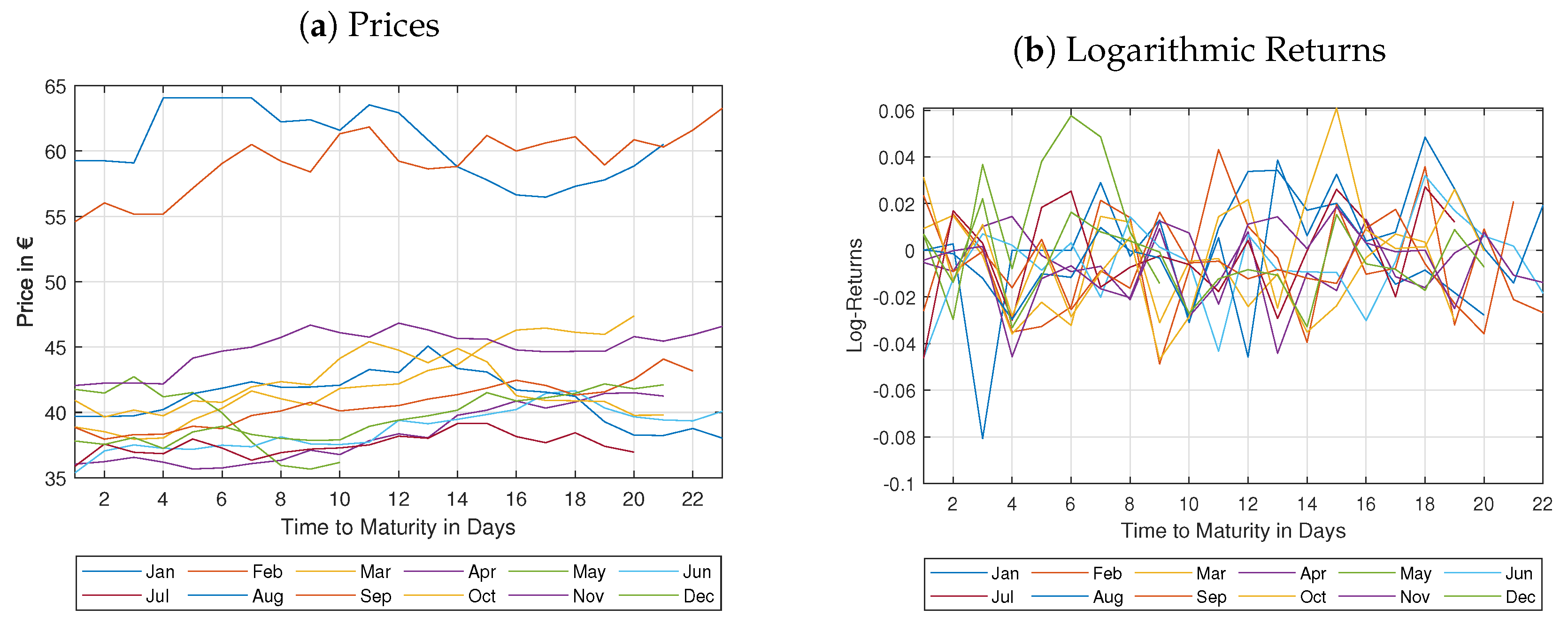
In our empirical analysis, we investigate twelve swap contracts with monthly delivery from January to December 2019 traded at the European Electricity Exchange (EEX). That is, here we concentrate on monthly delivering swap contracts exclusively and refer to
Kemper et al. (
2022) and
Piccirilli et al. (
2021) for further insights on overlapping swap contracts such as quarterly or yearly swaps.
We put our focus on the analysis of the forthcoming swap contract only, for two reasons. In electricity futures markets, the forthcoming futures is the most liquid one that is traded the most. Furthermore, we concentrate on delivery-dependent effects such as the Samuelson effect, that comes into play when approaching the beginning of the delivery period. Taking these two important aspects together, we have decided to focus on the time horizon of one month for each contract. This could be seen as a relatively short period. Nevertheless, it is only during this short period of time where it is possible to observe the effects that we are looking for. A longer time period does not necessarily improve the quality of the results that we have in mind, that is the MPDP induced by the Samuelson effect.
We fit a model indicating mean-reversion and term-structure effects in the volatility coefficient. The parameters are estimated by maximum likelihood estimation (MLE). The objective of our analysis is to provide evidence for the MPDP, but not to perform an exhaustive empirical study of swap price modeling. Note that we do not perform a term-structure fit by estimating all swap prices occurring at a fixed day since the presence of parallel contracts is limited.
In addition to mean-reversion and term-structure effects, delivery-dependent seasonal effects are observed in electricity markets.
Fanelli and Schmeck (
2019) empirically identify seasonalities in the swap’s delivery period by considering implied volatilities of electricity options. This feature has an effect on the MPDP as well, which is investigated by
Kemper et al. (
2022). To analyze the seasonality effects on the MPDP requires, however, a large set of available time series over several years. For this reason, we focus on the influence of the Samuelson term-structure effect on the MPDP exclusively.
Our main contribution to the literature is to show that our geometric averaging approach, leading to the market price of risk for delivery periods, is indeed of importance in practice. That is, we aim at showing empirically that the market price of risk for delivery periods is present in our dataset. For this, we first have to specify our model of
Kemper et al. (
2022) and
Kemper and Schmeck (
2023) in a multi-dimensional setting, as we fit several swap price dynamics simultaneously.
The paper is organized as follows:
Section 2 presents the geometric averaging approach under the artificial risk-neutral measure applied to the multi-dimensional futures curve. In addition, it presents the MPDP of diffusion risk in order to adjust to the swap’s true risk-neutral measure. Moreover, we introduce the model under the physical measure as a preparation for our empirical study. The estimation procedure and the empirical findings are presented in
Section 3. Finally,
Section 4 concludes our main findings.
2. The Model and the MPDP
In electricity markets, typically several swap contracts are tradable at the same time, endowed with different delivery periods. For example, at the EEX, the next 9 months, 11 quarters, and 6 years are available. For the scope of this paper, we concentrate on monthly delivering swap contracts.
Let us consider a market with M available swap contracts. The swap contract delivers 1 MWh of electricity during the agreed delivery month, embracing the period from until for . At a trading day before the contract expires, we denote the swap price by , settled such that the contract is entered at no cost. It can be interpreted as an average price of instantaneous delivery. Trading takes place until .
We consider
M artificial futures contracts with an
—dimensional price
. Each component
,
stands for instantaneous delivery at time
. Note that such a contract does not exist on the market but it turns out to be useful for modeling purposes when considering delivery periods (see, e.g.,
Benth et al. (
2019) and
Kemper et al. (
2022)).
Consider a filtered probability space
, where the filtration satisfies the usual conditions. At time
, let the price of the artificial futures contracts follow a geometric diffusion process evolving as
where each component of
can be characterized by the dynamics of a representative futures price
given by
with initial conditions
and where
W is an
—dimensional Brownian motion under
with independent components
. Furthermore, we assume that
is zero if
and also if
. In this way, we freeze contract
m if the time has reached the period of potential delivery and if a point of delivery is considered that is not in the delivery period of contract
m.
Remark 1. In the empirical analysis to come, we concentrate on the last trading month before maturity. Moreover, we focus on monthly contracts that do not overlap. Therefore, each contracting period is characterized by an individual Brownian motion.
We assume that the future price volatility,
, depends on both trading time
t and delivery time
. This enables us to include the Samuelson effect as follows,
such that the futures price volatility is described by a deterministic exponential function with exponential damping factor
and a final volatility value
that is reached in the end of maturity. This effect goes back to
Samuelson (
1965) and was implemented in commodity markets, for example, by
Schneider and Tavin (
2018) and
Ladokhin et al. (
2024). In addition, it is a typical feature of the electricity market, involving a more pronounced volatility closer to the end of the maturity.
Benth and Paraschiv (
2016) and
Jaeck and Lautier (
2016) provide empirical evidence for the Samuelson effect in the volatility term structure of electricity swaps. It can also be observed in the implied volatilities of electricity options, especially far out and in the money (see
Kiesel et al. 2009).
Lemma 1 (The Artificial Futures Price under
)
. The artificial futures price is a -martingale. The unique solution to Equation (2) is given by Proof. We know that the volatility
from Equation (3) is positive and deterministic as
for all
m so that suitable integrability and measurability conditions are satisfied. Hence, following
Øksendal and Sulem (
2007) (cf. Theorem 1.19) there exists a unique solution to Equation (2) given by Equation (4), which follows from the usual procedure. Moreover, from
Øksendal and Sulem (
2007) (cf. Theorem 1.17), it follows that
is a true martingale under
. □
Following
Heath et al. (
1990), we derive the electricity swap price from the artificial futures price as a next step: In order to characterize the electricity swap price appropriately, the implementation of the delivery period plays a crucial role. In particular, the swap price results from averaging an instantaneous stream of artificial futures with respect to the delivery period using a general weight function:
where
is the corresponding settlement function at
. We will follow the most popular example given by a constant settlement type
for all
such that
This corresponds to a one-time settlement that is independent of the instantaneous settlement time
. For a characterization of a continuous settlement, we refer the interested reader to
Benth et al. (
2008).
To simplify notation, we use the following representation whenever we average over the delivery period:
for some function
f and a random variable
being uniformly distributed over the delivery period. Furthermore,
denotes the variance of a random variable
X.
Traditionally,
arithmetic weighted averaging is implemented to price swaps in electricity markets (see, e.g.,
Benth et al. (
2008),
Bjerksund et al. (
2010), and
Benth et al. (
2019)). However, since the arithmetic average is tailored for arithmetic models, it requires an approximation whenever it is applied to geometric models and whenever we are seeking for explicit solutions. The approximation was first introduced by
Bjerksund et al. (
2010) in the setting of the electricity market. In order to distinguish between the averaging methods,
Kemper and Schmeck (
2023) call it the
approximated average, leading to a swap price that we denote by
. Hence, a representative swap price based on the
approximated averaging procedure is defined by
In order to avoid any kind of approximations,
Kemper et al. (
2022) suggest the use of the
geometric average customized for geometric models (see also
Kemna and Vorst 1990). The swap price based on geometric averaging will be denoted by
F. Hence, a representative swap price based on the
geometric averaging procedure is defined by
In a next step, we characterize both versions of representative electricity swaps in Equations (6) and (7), in order to investigate the consequences of the often-used approximation procedure.
Lemma 2. Under the artificial pricing measure , the dynamics of a representative swap price based on approximated averaging procedure are given by Proof. Since the volatility is deterministic, measurable, and
, we can show that
so that we can apply the stochastic Fubini Theorem (see
Protter (
2005), cf. Theorem 65, Chapter IV. 6), which gives Equation (8). □
Definition 1 (Swap Price Volatility)
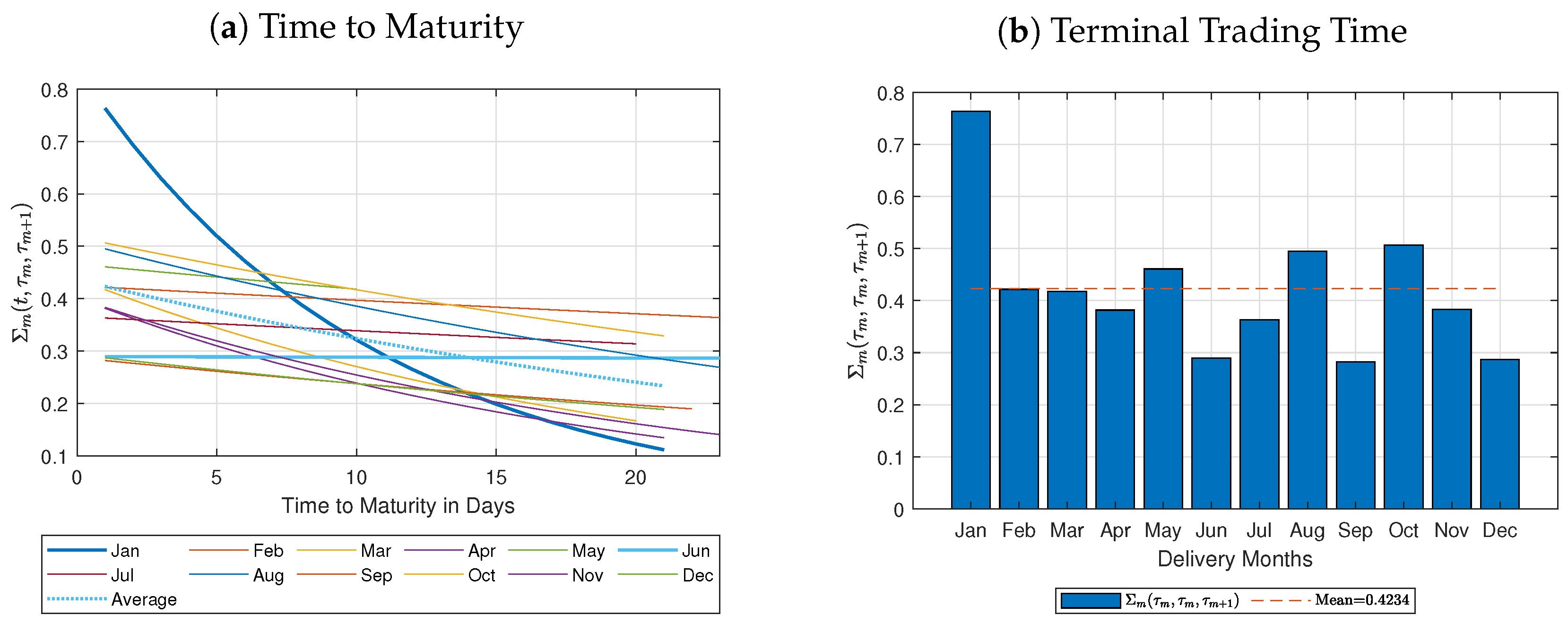
. We define the swap price volatility bywhich is the average futures price volatility over the delivery period with density . Remark 2. Note that the swap price volatility simplifies tofor a constant parameter such that the swap price volatility still preserves the Samuelson effect until maturity . Note that
actually depends on the length of the delivery period
as it is precisely denoted in
Kemper et al. (
2022) (by choosing the notation
). For simplicity we skip this dependence as we consider only monthly delivery periods in the empirical analysis to come.
In contrast,
geometric averaging originates from the arithmetic average of logarithmic returns without any need for approximations. Hence, in line with
Kemper et al. (
2022), we define the swap price originating from geometric averaging as follows.
Lemma 3 (Swap under
)
. Under the artificial pricing measure , the dynamics of a representative swap price based on the geometric averaging procedure is given bywhere U denotes the random delivery variable with density and . Proof. Consider the solution of the futures price process in (
4) and plug it into (
7). An application of the stochastic Fubini Theorem (see
Protter (
2005), cf. Theorem 65, Chapter IV.6) leads to
Then, (
12) follows using Itô’s formula (see, e.g.,
Øksendal and Sulem 2007). □
We summarize all swap prices that are available during the trading horizon
as an
—dimensional process
given by
where
is an
—dimensional Brownian motion and
is an
—dimensional deterministic drift vector.
Although the futures prices and the approximated swaps are martingales under the pricing measure , the swap price F is not a -martingale: It turns out, that the resulting swap price dynamics is a geometric process endowed with the same swap price volatility as in Lemma 2. However, note that in general the swap price dynamics in Equations (8) and (12) do not coincide, due to a non-zero drift term arising in Equation (12). More precisely, the swap price process F under has a negative drift term characterized by the swap’s variance.
Remark 3 (Swap Price Drift under
)
. We can simplify the drift term of the representative swap price tofor a constant parameter such that the swap’s drift also preserves a squared Samuelson effect until maturity . Note that again depends on the length of the delivery period, which will be skipped for notational convenience. Hence, using geometric averaging leads to a new interpretation of risk related to the delivery period going along with an adjustment of the swap’s risk-neutral measure that we denote by .
As introduced by
Kemper et al. (
2022), the gap between the classical risk-neutral measure
and the swap’s true risk-neutral measure
is characterized by the MPDP, which we define in the following:
Definition 2 (The MPDP)
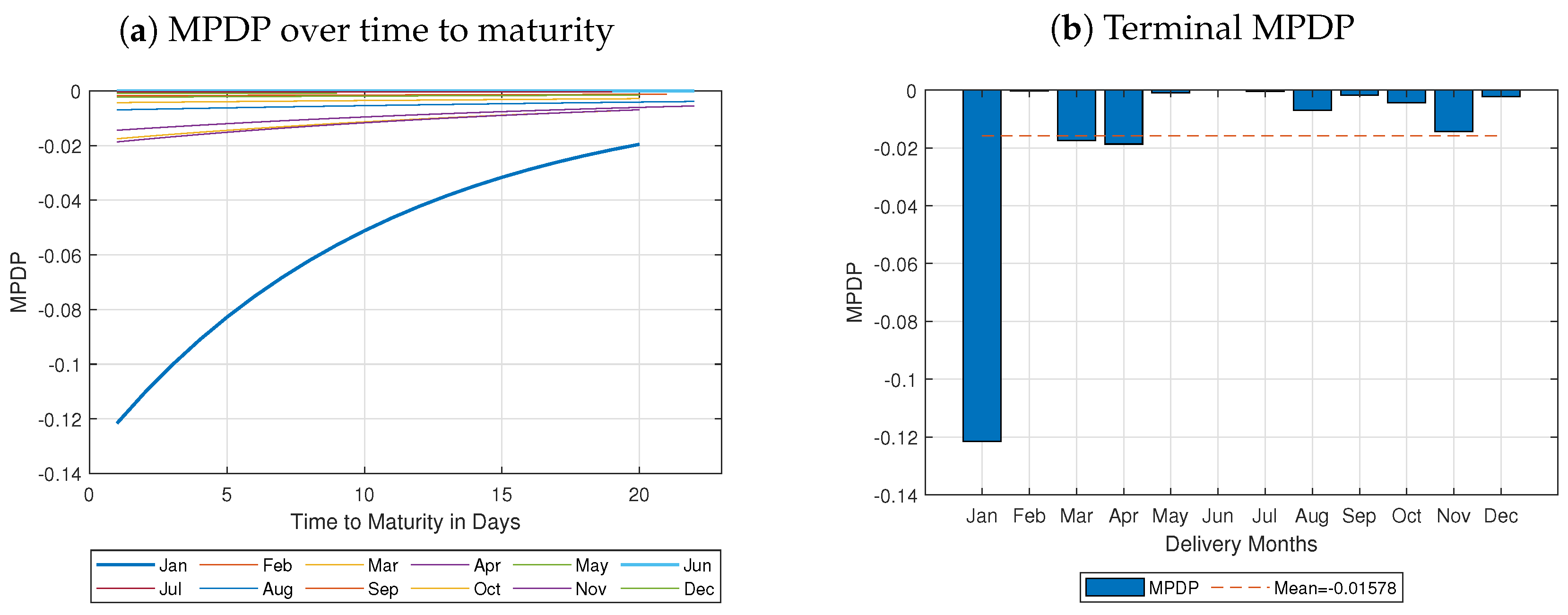
. At time , the market price of diffusion risk for delivery periods associated with all equidistant delivery periods for is defined by , where Remark 4. Using the notation above, the MPDP for a representative swap contract simplifies tosuch that the MPDP preserves the Samuelson effect until maturity . In particular,
refers to the additional diffusion risk associated with each available swap contract. Note that the MPDP of diffusion risk,
, is negative. Hence, the geometric averaging technique induces less risk than the application of the approximated arithmetic average, for which we need to pay a cost of approximation risk. Vice versa, using the geometric average induces less risk than the approximated arithmetic one such that the overall risk is lowered. Consequently, risk is reduced whenever the correct, and thus non-approximated, averaging procedure is implemented. It can be interpreted as the trade-off between the weighted average variance of a stream of futures, on the one hand, and the variance of the swap, on the other hand. Note that the MPDP of a representative swap,
, is in line with the MPDP for diffusion risk found in
Kemper et al. (
2022), where a stochastic volatility scenario is considered.
In Equation (17), we can clearly observe that the MPDP preserves the term-structure effect: The MPDP splits into a negative constant, characterized by the Samuelson parameter and the length of the delivery period , and the deterministic exponential term-structure effect. Hence, the MPDP becomes more pronounced closer to the end of maturity.
Note, if in the exceptional case that the future price volatility is independent of the delivery time, then both swap prices in Lemmas 2 and 3 directly coincide. Moreover, they are martingales under since the MPDP in Equation (16) is zero whenever delivery dependence fails to appear.
We define a new pricing measure
such that the
—dimensional swap price processes
are martingales. Following
Øksendal and Sulem (
2007), define the Radon–Nikodym density through
Assume that
is a martingale for the entire trading time. We then define the new measure
through the Radon–Nikodym density
which clearly depends on all delivery periods
.
Hence, a straightforward valuation leads to the following result.
Proposition 1 (Swap under
)
. The swap price process , defined in (14), is a martingale under . The corresponding dynamics are given bywhere is an —dimensional Brownian motion under , defined throughduring the trading horizon . Proof. We know by definition that
is a continuous deterministic process that is square-integrable since
Hence, all processes are adapted. Following
Øksendal and Sulem (
2007) (cf. Theorem 1.35), we need to show that
, defined in Equation (18), is a true martingale. Since
are independent of each other, it is enough to show, that
for
are true martingales. We can prove Novikov’s condition (see, e.g.,
Protter 2005, cf. Theorem 41, Chapter III.8) as
satisfies
Hence,
for all
m, and so
, are true martingales. Hence, we can apply Girsanov’s Theorem (see, e.g.,
Øksendal and Sulem 2007, cf. Theorem 1.35) and the assertion follows. □
In order to investigate the model empirically, we introduce the model under its physical measure
. A typical drift feature is the mean-reverting behavior (see, e.g.,
Benth et al. (
2008) and
Benth et al. (
2019)), which we implement at the swap’s
rate level following
Kemper and Schmeck (
2023).
Lemma 4 (Swap under
)
. Under the physical measure , the representative swap price process, , evolves asWe find that are independent Brownian motions under the physical measure , characterized bywhere the true market price of risk, , is defined through Proof. Analogous to
Kemper and Schmeck (
2023) (Section 2.2 and Appendix B) and to
Benth et al. (
2019) (Theorem 3.5 and Appendix B), where both references are dealing with one-dimensional swap price dynamics, either with jumps and stochastic volatility or jumps exclusively. The proof in the multi-dimensional setting can be found in
Appendix A. □
Remark 5. - (i)
The logarithmic price of a representative swap contract evolves as Hence, we observe that the mean-reverting behavior enters as a modified second term-structure effect. The Samuelson effect is exclusively present in the volatility term and strengthens the speed of mean reversion.
- (ii)
Note, that the swap’s logarithmic returns are based on logarithmic future price returns defined by
In order to discretize the model of Lemma 4 under the physical measure , we follow the Euler-type discretization procedure with step size . The discretized logarithmic price of the swap from Equation (27) is denoted by , with , and is given by the following Lemma.
Lemma 5. The discretized logarithmic price of a representative swap pricefor and is a standard normal-distributed random variable. Moreover, the coefficients to be estimated are , where , and , with and where we denote as the length of the time series with delivery during . Hence, the likelihood of our discretized model in Lemma 5 can be expressed in terms of the conditional probability density function
where
is the set of parameters, and
determines the conditional probability density function for contract
m at data point
j. In particular,
such that the conditional probability density function is given by
where the set of parameter values
is subject to
,
and
.
We recalibrate the parameters to characterize
, and
accordingly:
Remark 6. By construction, the contracts are independent of each other. We justify this assumption since we only fit the last—most liquid—trading month of the contracts and the contracts do not overlap.