A Hypothesis Test for the Long-Term Calibration in Rating Systems with Overlapping Time Windows
Abstract
1. Introduction
2. Setup and Preliminaries
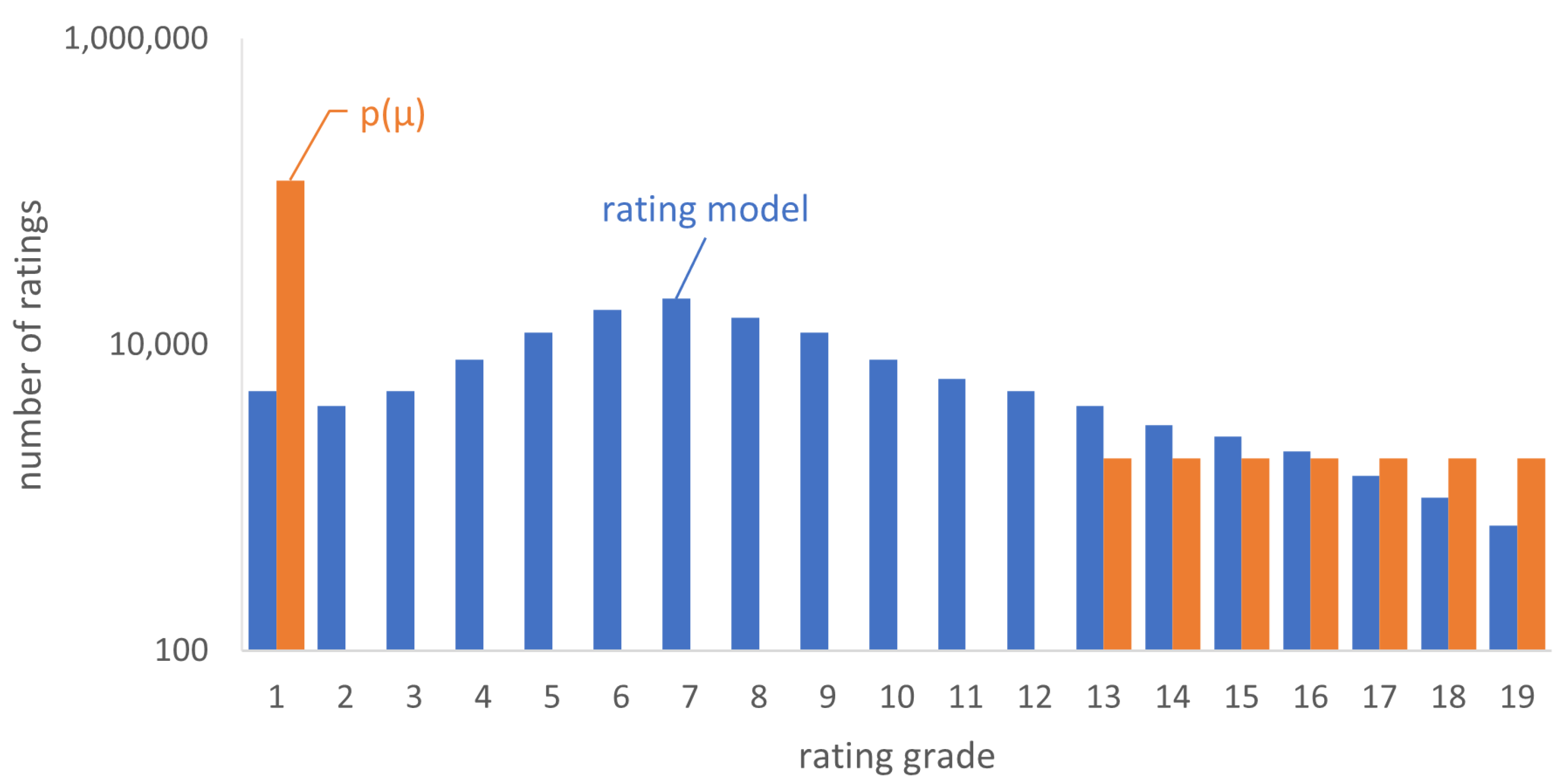
2.1. Setup and Notation
2.2. Formal Description of the Test
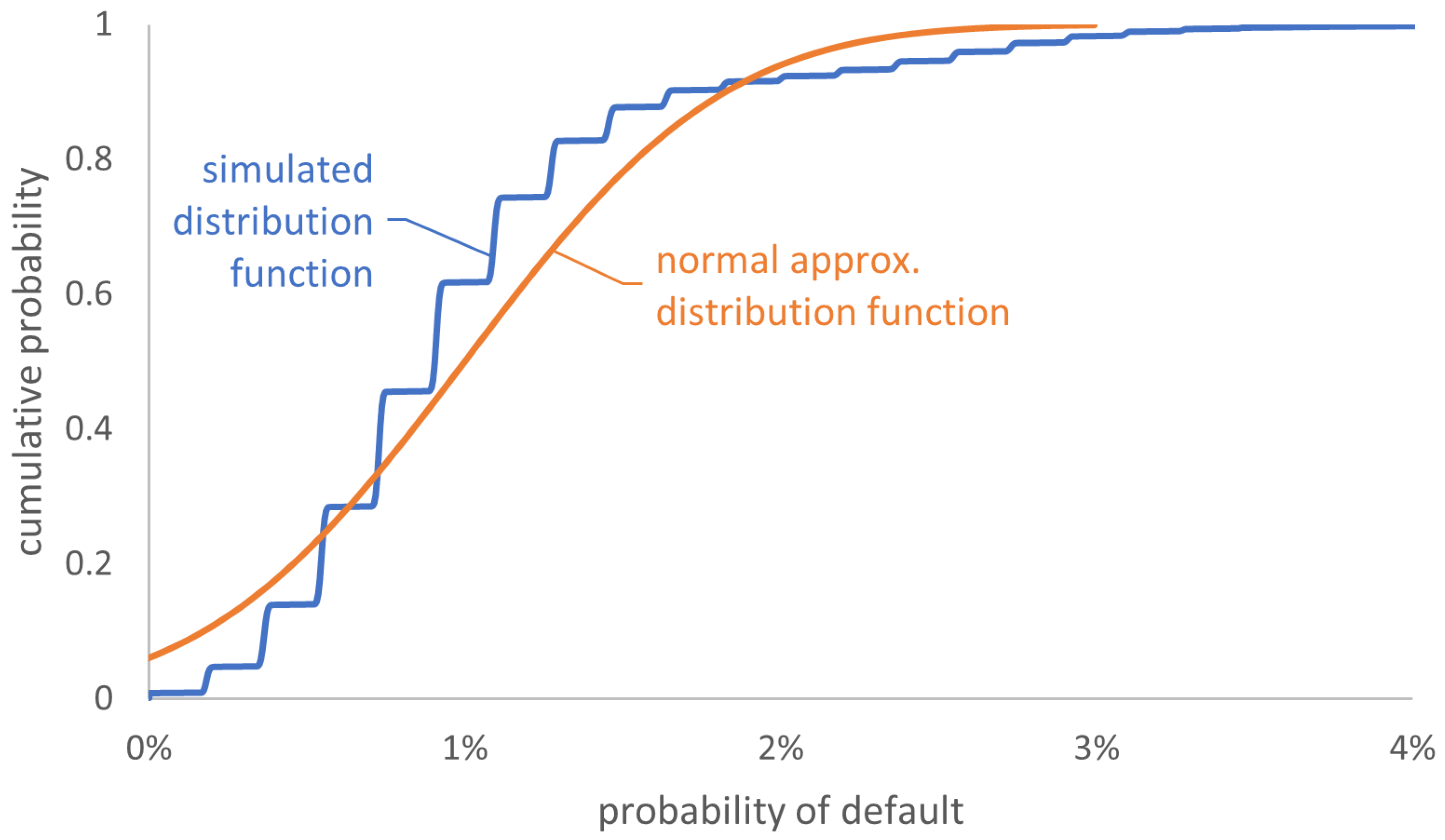
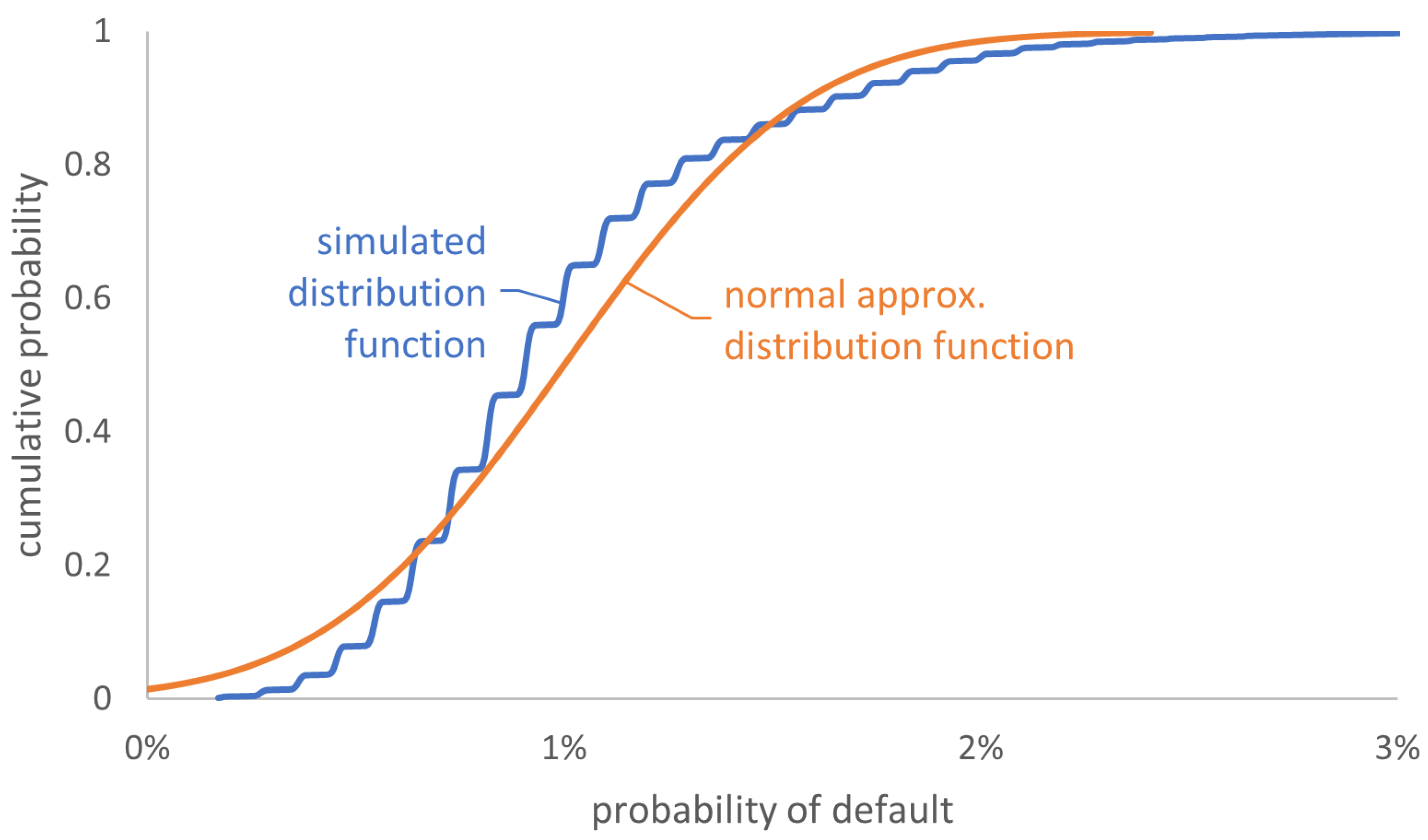
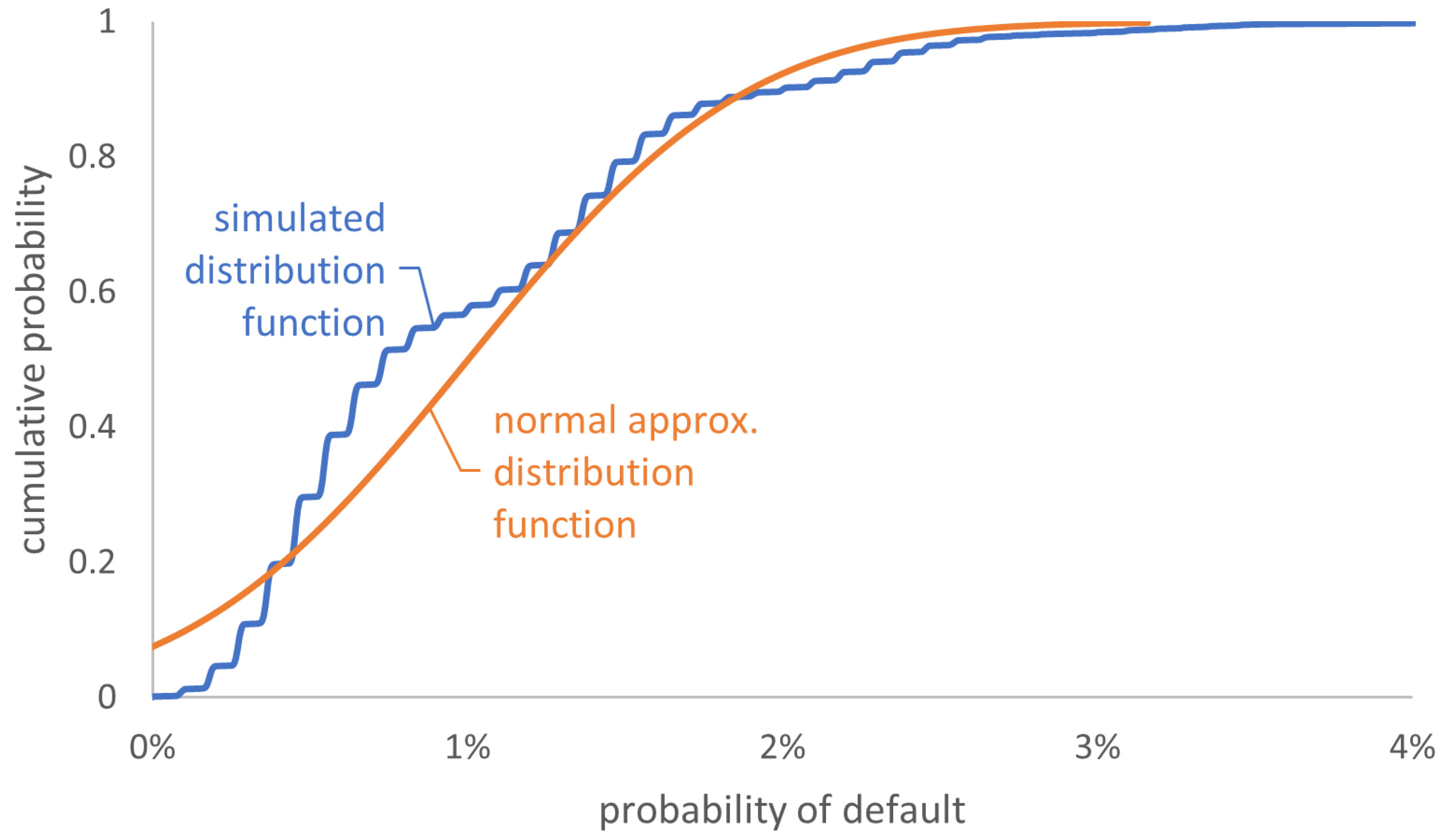
2.3. Distribution of the Long-Run Default Rate
2.4. Covariance between Default States
2.5. Covariance between Default Rates
2.6. Variance of the Long-Run Default Rate
3. Hypothesis Test for Long-Term Calibration
3.1. Statistical Test per Rating Grade
3.2. Statistical Test on Portfolio Level
4. Discussion and Further Considerations
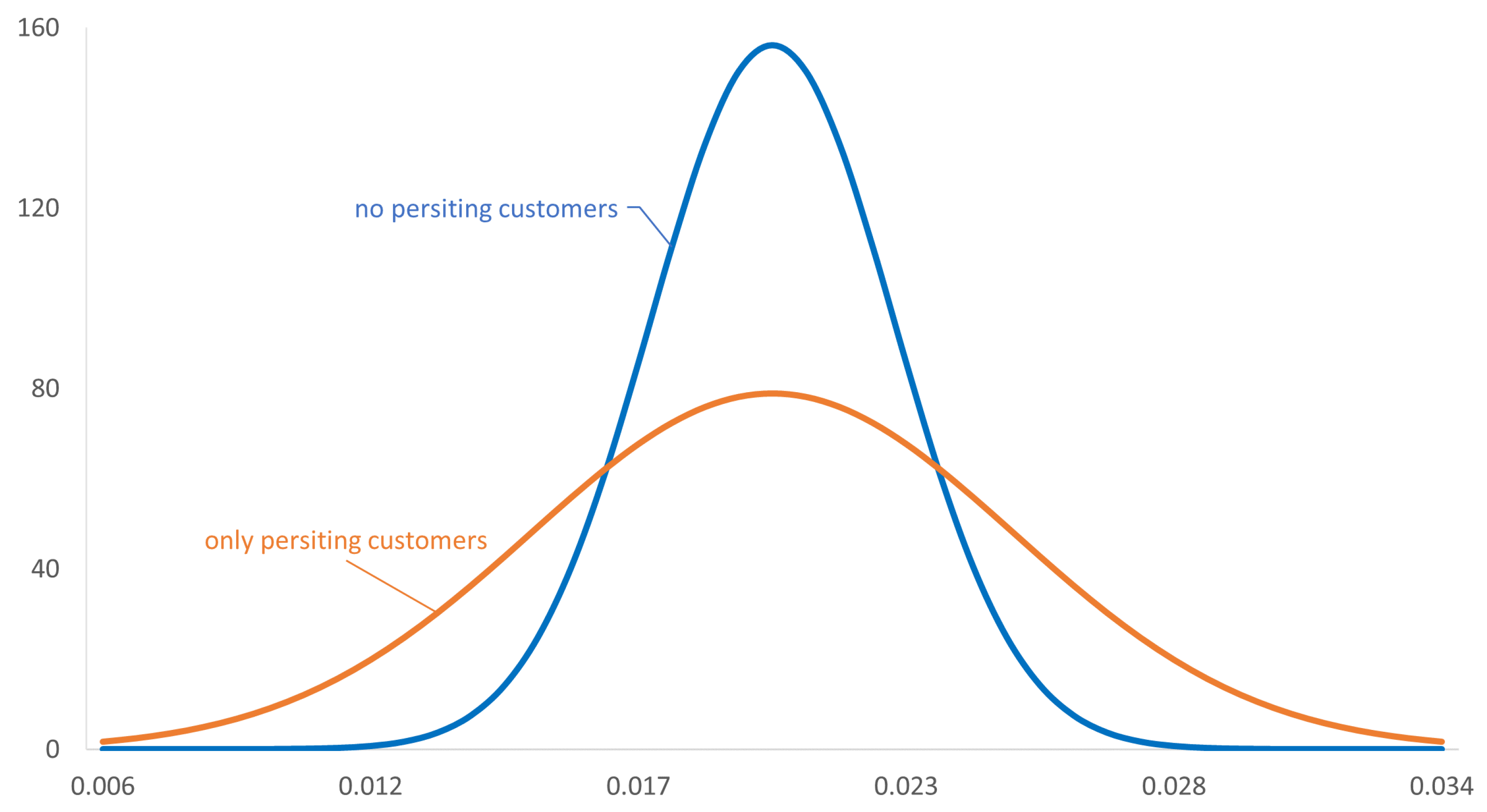
4.1. Effect of Persisting Customers on the Variance of Z
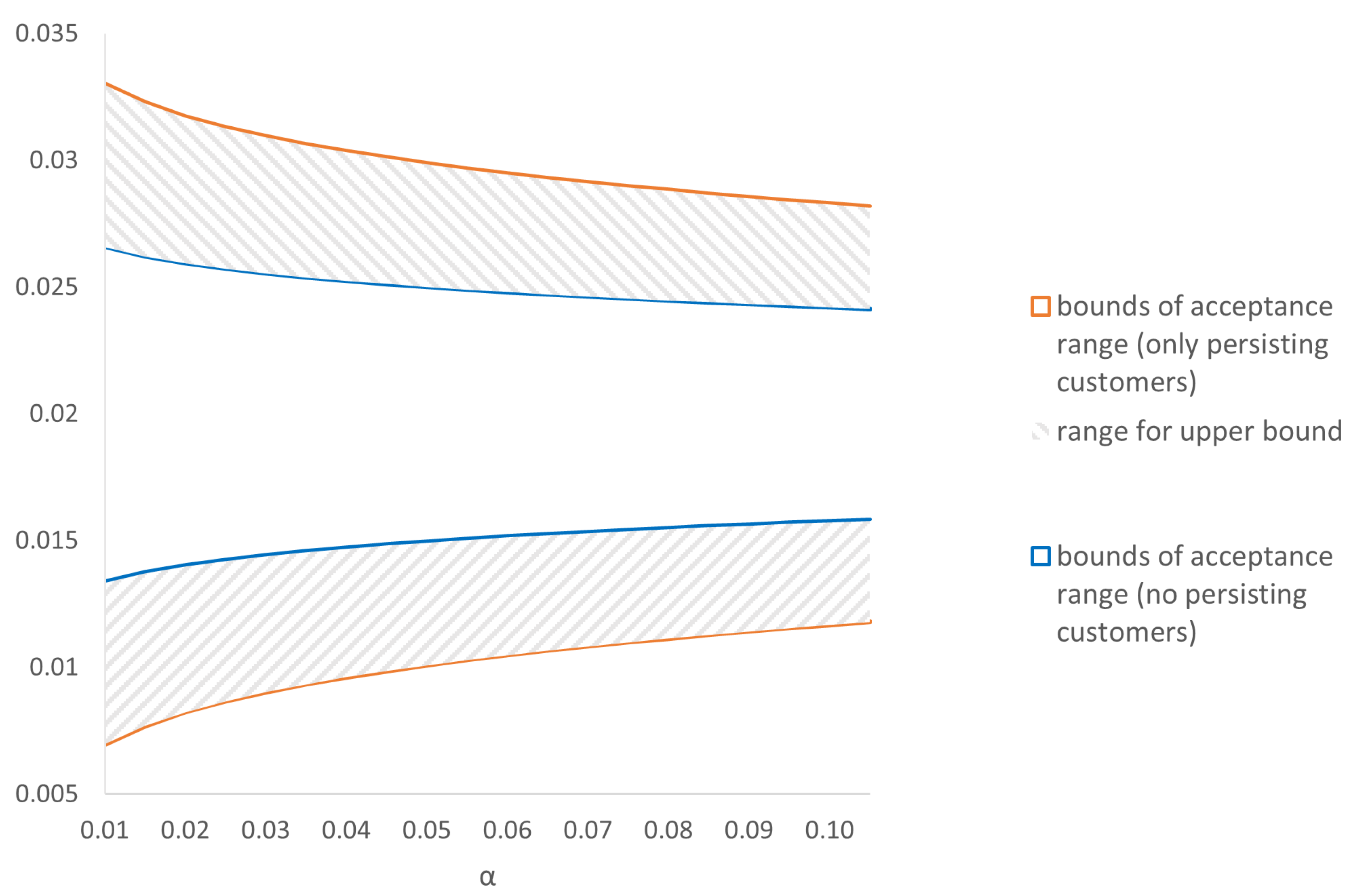
4.2. Effect of Persisting Customers on Acceptance Range
4.3. Some Thoughts on the Rate of Convergence
4.4. An Alternative Way to Bound the Variance
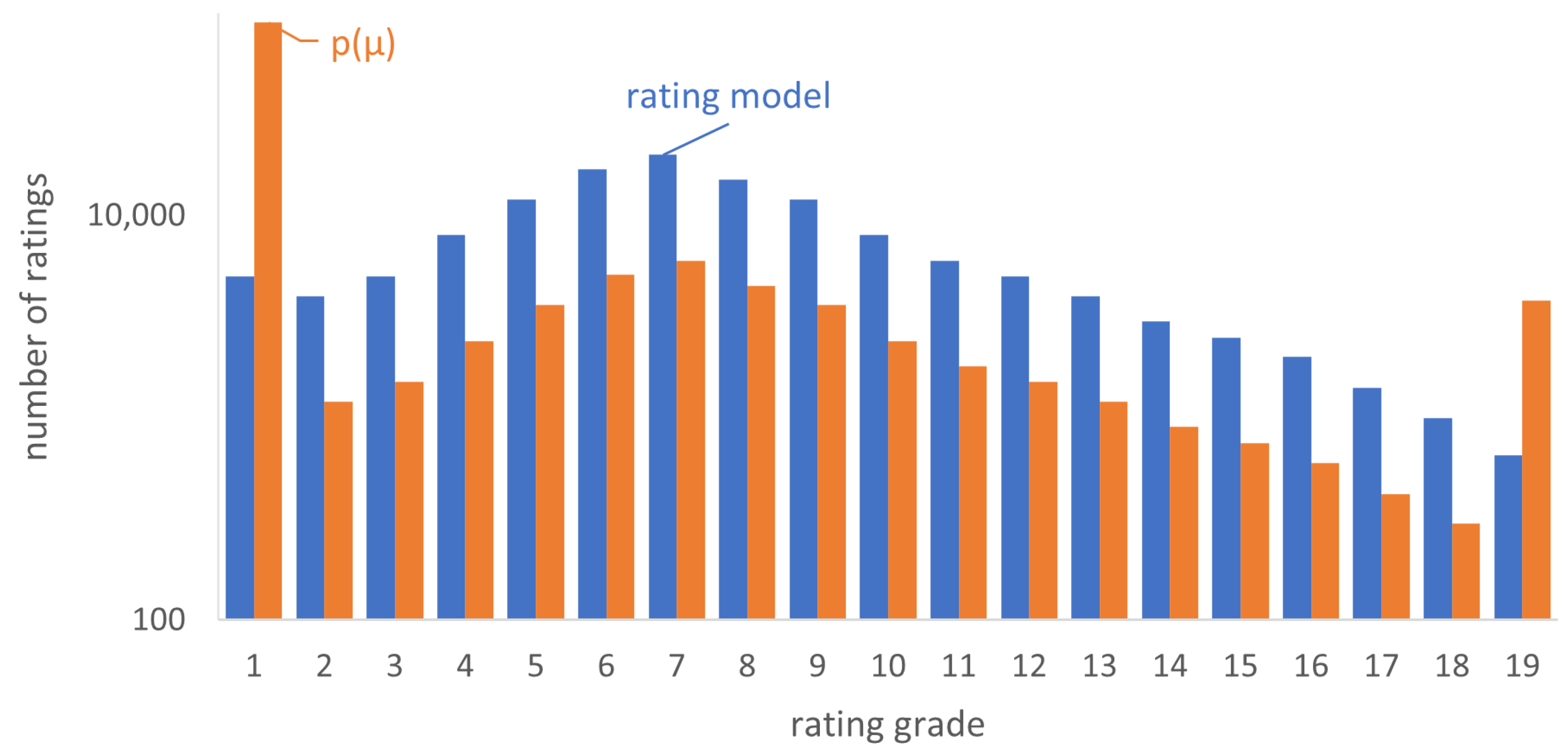
4.5. Additional Conditions on the Rating Distribution
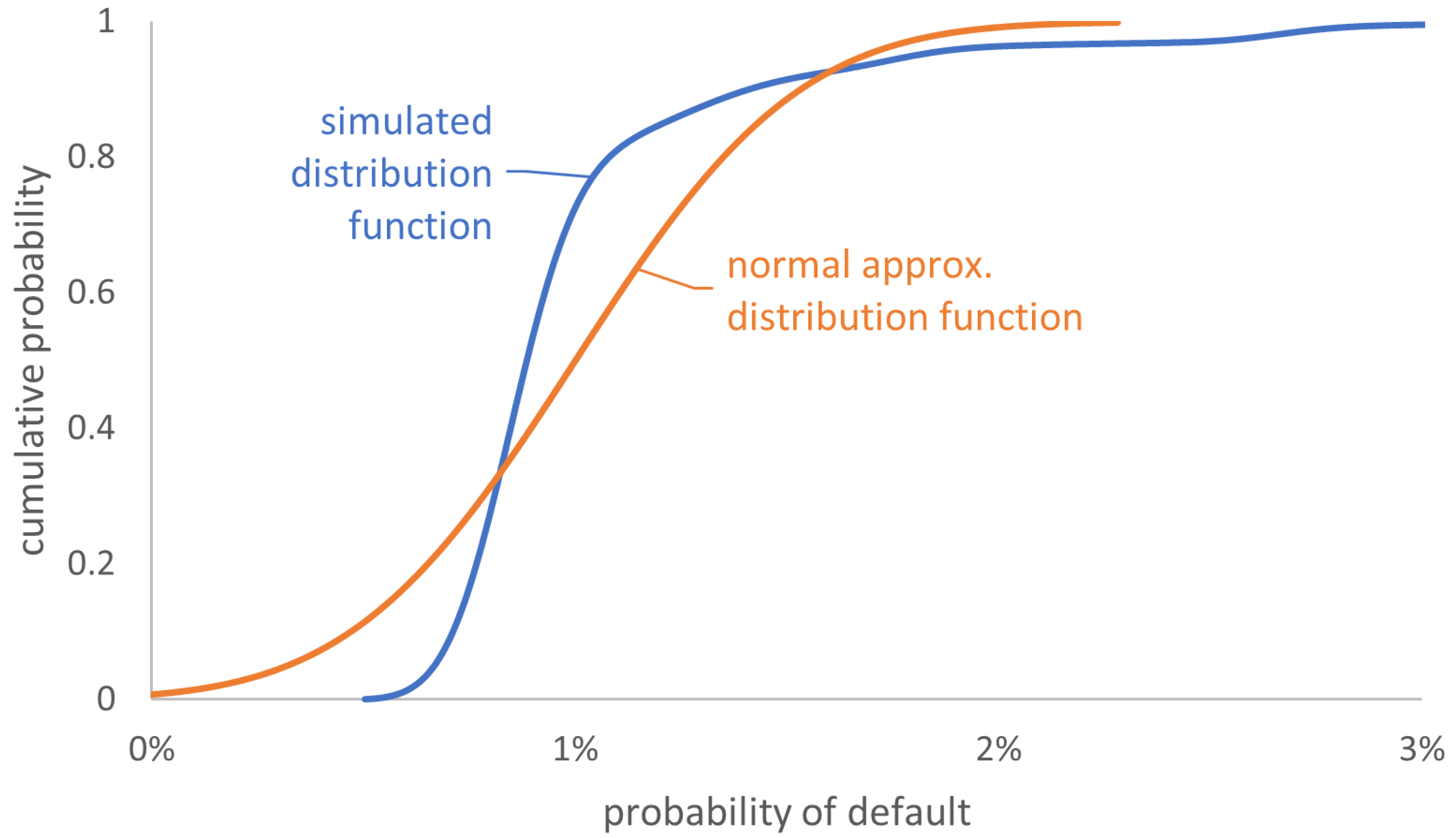
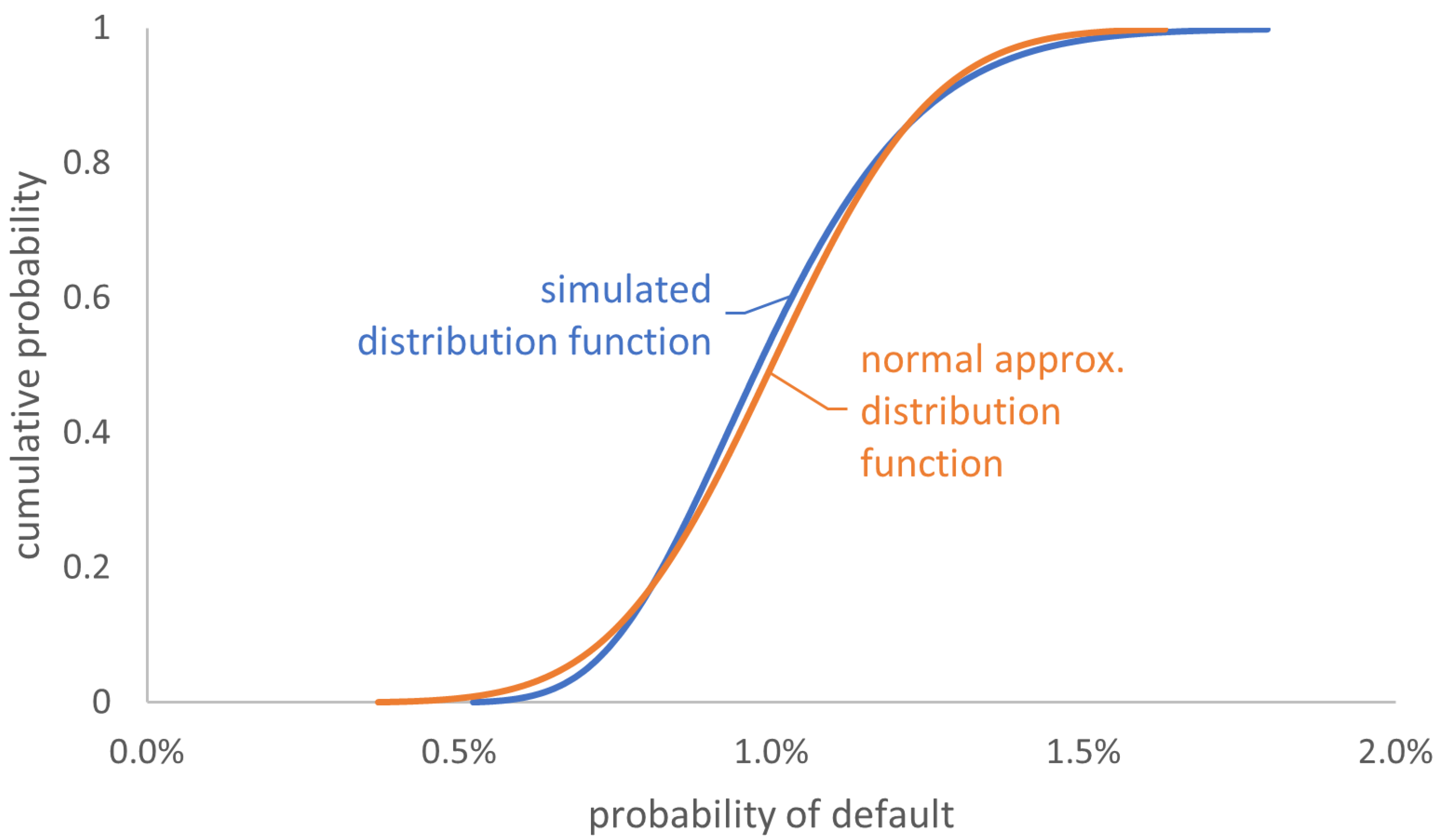
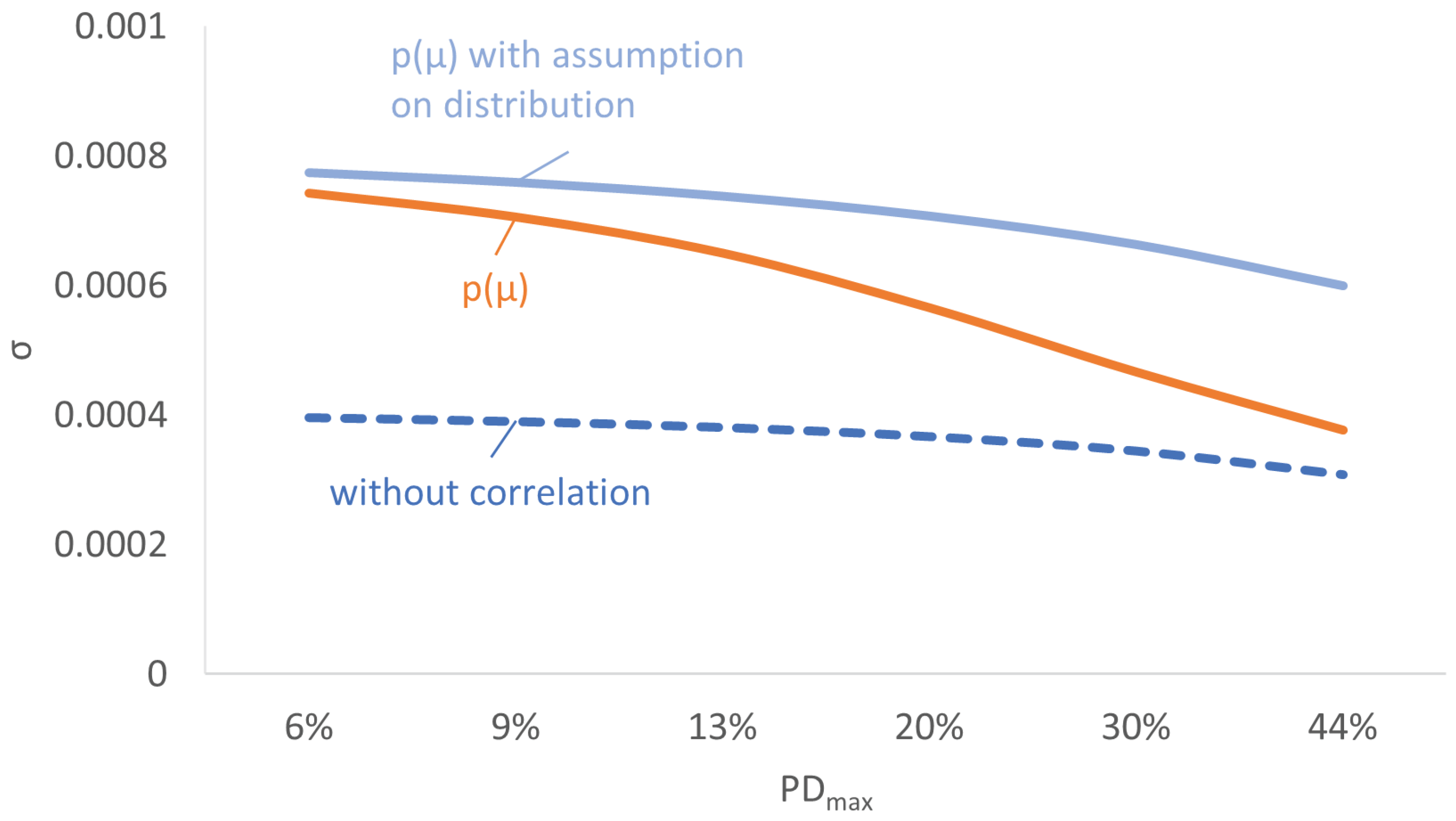
4.6. Impact of Simplification on the Acceptance Range
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols and Abbreviations
| probability of default | |
| LGD | loss given default |
| Bernoulli distribution with probability p | |
| default probability of rating grade k in the underlying master scale | |
| equal to , i.e., default probability of the best rating grade | |
| equal to , i.e., default probability of the worst rating grade | |
| reference date number t | |
| N | number of reference dates |
| set of natural numbers | |
| number of obligors on reference date | |
| set of natural numbers including zero | |
| minimal number (larger than zero) of existing obligors at any reference date | |
| maximal number of existing obligors at any reference date | |
| minimum of a set A | |
| maximum of a set A | |
| q | number of reference dates within a one-year time horizon starting from an arbitrary reference date |
| size of the overlap of observation periods with reference dates and | |
| M | total number of all customers during the history |
| set of customers at reference date | |
| one-year default rate at reference date | |
| one-year default state of an unspecified customer at reference date | |
| one-year default state of customer j at reference date | |
| probability of default over a one-year time horizon of customer j at reference date | |
| realized default rate on reference date | |
| set of indices for reference dates, where the portfolio contains at least one customer | |
| cardinality of | |
| Z | long-run default rate |
| realized long-run default rate | |
| estimated long-run default rate (long-run central tendency) | |
| expected value of the long-run default rate | |
| variance of the long-run default rate | |
| null hypothesis | |
| alternative hypothesis | |
| lower and upper bound of the acceptance range of the hypothesis test | |
| covariance of the random variables X and Y | |
| Normal distribution with expected value and variance | |
| expected value of a random variable X | |
| probability measure | |
| set of real numbers | |
| indicator function of set A | |
| cumulative distribution function for the standard normal distribution | |
| length of an interval or cardinality of a finite set I | |
| number of persisting customers with respect to reference dates and | |
| ∅ | empty set |
| solution of the minimization problem | |
| minimal value of the minimization problem | |
| absolute value of a real number x |
Appendix A. Minimization Problem
Appendix B. Test on Portfolio Level without Solving the Minimization Problem
References
- Aussenegg, Wolfgang, Florian Resch, and Gerhard Winkler. 2011. Pitfalls and remedies in testing the calibration quality of rating systems. Journal of Banking and Finance 35: 698–708. [Google Scholar] [CrossRef]
- Blochwitz, Stefan, Stefan Hohl, Dirk Tasche, and Carsten S. Wehn. 2004. Validating Default Probabilities on Short Time Series. Chicago: Capital & Market Risk Insights, Federal Reserve Bank of Chicago. [Google Scholar]
- Blochwitz, Stefan, Marcus R. W. Martin, and Carsten S. Wehn. 2006. Statistical Approaches to PD Validation. In The Basel II Risk Parameters: Estimation, Validation, and Stress Testing. Berlin and Heidelberg: Springer, pp. 289–306. [Google Scholar]
- Blöchlinger, Andreas. 2012. Validation of default probabilities. Journal of Financial and Quantitative Analysis 47: 1089–123. [Google Scholar] [CrossRef]
- Blöchlinger, Andreas. 2017. Are the Probabilities Right? New Multiperiod Calibration Tests. The Journal of Fixed Income 26: 25–32. [Google Scholar] [CrossRef]
- Caprioli, Sergio, Emanuele Cagliero, and Riccardo Crupi. 2023. Quantifying Credit Portfolio sensitivity to asset correlations with interpretable generative neural networks. arXiv arXiv:2309.08652. [Google Scholar] [CrossRef]
- Caprioli, Sergio, Riccardo Cogo, and Raphael Cavallari. 2023. Back-Testing Credit Risk Parameters on Low Default Portfolios: A Bayesian Approach with an Application to Sovereign Risk. Preprint SSRN. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4408217 (accessed on 1 February 2023).
- Council of European Union. 2013. Regulation (EU) No 575/2013 of the European Parliament and of the Council of 26 June 2013 on prudential requirements for credit institutions and investment firms and amending regulation (EU) No 648/2012. Official Journal of the European Union L 176: 1. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:32013R0575 (accessed on 1 February 2023).
- Coppens, Francois, Manuel Mayer, Laurent Millischer, Florian Resch, Stephan Sauer, and Klaas Schulze. 2016. Advances in Multivariate Back-Testing for Credit Risk Underestimation. Frankfurt am Main: European Central Bank. [Google Scholar]
- Cucinelli, Doriana, Maria Luisa Di Battista, Malvina Marchese, and Laura Nieri. 2018. Credit risk in European banks: The bright side of the internal ratings based approach underestimation. Journal of Banking and Finance 93: 213–29. [Google Scholar] [CrossRef]
- Deutsche Bundesbank. 2003. Approaches to the Validation of Internal Rating Systems. Monatsbericht September. Frankfurt am Main: Deutsche Bundesbank, pp. 59–71. [Google Scholar]
- European Banking Authority (EBA). 2016. Final Draft Regulatory Technical Standards (RTS) on the Specification of the Assessment Methodology for IRB. Available online: https://www.eba.europa.eu/activities/single-rulebook/regulatory-activities/credit-risk/regulatory-technical-standards-2 (accessed on 1 February 2023).
- European Banking Authority (EBA). 2017. Guidelines on PD Estimation, LGD Estimation and Treatment of Defaulted Assets. Available online: https://www.eba.europa.eu/regulation-and-policy/model-validation/guidelines-on-pd-lgd-estimation-and-treatment-of-defaulted-assets (accessed on 1 February 2023).
- European Central Bank (ECB). 2024. ECB Guide to Internal Models. Available online: https://www.bankingsupervision.europa.eu/ecb/pub/pdf/ssm.supervisory_guides202402_internalmodels.en.pdf (accessed on 25 June 2024).
- European Commission. 2021. Commission Delegated Regulation (EU) 2022/439. Official Journal of the European Union L 90: 1–66. [Google Scholar]
- Hogg, Robert V., and Elliot A. Tanis. 1977. Probability and Statistical Inference. New York: Macmillan Publishing Co., Inc. London: Collier Macmillan Publishers. [Google Scholar]
- Jing, Zhang, Fanlin Zhu, and Joseph Lee. 2008. Asset correlation, realized default correlation and portfolio credit risk modeling methodology. Moody’s KMV, March. [Google Scholar]
- Klenke, Achim. 2020. Probability Theory—A Comprehensive Course, 3rd ed. Universitext. Cham: Springer. [Google Scholar]
- Li, Weiping. 2016. Probability of Default and Default Correlations. Journal of Risk and Financial Management 9: 7. [Google Scholar] [CrossRef]
- Pluto, Katja, and Dirk Tasche. 2011. Estimating probabilities of default for low default portfolios. In The Basel II Risk Parameters: Estimation, Validation, Stress Testing-with Applications to Loan Risk Management. Berlin and Heidelberg: Springer, pp. 75–101. [Google Scholar]
- Tasche, Dirk. 2003. A Traffic Lights Approach to PD Validation. Preprint arXiv. Available online: https://arxiv.org/abs/cond-mat/0305038 (accessed on 1 February 2023).
- Tasche, Dirk. 2008. Validation of internal rating systems and PD estimates. In The Analytics of Risk Model Validation. Amsterdam: Elsevier, pp. 169–96. [Google Scholar]
- Tasche, Dirk. 2013. Bayesian estimation of probabilities of default for low default portfolios. Journal of Risk Management in Financial Institutions 6: 302–26. [Google Scholar] [CrossRef]
- Zhou, Chunsheng. 2001. An Analysis of Default Correlations and Multiple Defaults. The Review of Financial Studies 14: 555–76. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurth, P.; Nendel, M.; Streicher, J. A Hypothesis Test for the Long-Term Calibration in Rating Systems with Overlapping Time Windows. Risks 2024, 12, 131. https://doi.org/10.3390/risks12080131
Kurth P, Nendel M, Streicher J. A Hypothesis Test for the Long-Term Calibration in Rating Systems with Overlapping Time Windows. Risks. 2024; 12(8):131. https://doi.org/10.3390/risks12080131
Chicago/Turabian StyleKurth, Patrick, Max Nendel, and Jan Streicher. 2024. "A Hypothesis Test for the Long-Term Calibration in Rating Systems with Overlapping Time Windows" Risks 12, no. 8: 131. https://doi.org/10.3390/risks12080131
APA StyleKurth, P., Nendel, M., & Streicher, J. (2024). A Hypothesis Test for the Long-Term Calibration in Rating Systems with Overlapping Time Windows. Risks, 12(8), 131. https://doi.org/10.3390/risks12080131



